Response of laterally loaded finned piles in sand

Abstract

This paper investigates the response of finned piles in sand subjected to static lateral load through laboratory tests and full-scale field tests. Firstly, model tests were carried out on free headed single piles of different shaft diameters with and without fins in sand to explore the performance of the piles under lateral loading. The results obtained from monotonic loading tests on three series of piles of three different combination of fins and pile shaft diameters were presented. The effect of fins on improving the stiffness and ultimate lateral capacity of the piles was discussed. An equivalent diameter was proposed for a finned pile, which enabled the experimental results to be back calculated using an available elasto-plastic solution for laterally loaded piles in sand. Secondly, field tests were conducted on laterally loaded Starfin screw piles in loose to medium dense sand. The proposed approach was then used for the analysis of the measured response of Starfin screw piles and further validated against measured test results from fully instrumented finned piles in overconsolidated dense sand. The results show that the proposed equivalent diameter and approach for the analysis of finned piles provided the most satisfactory match to the measured data, ranging from the initial elastic state to the ultimate limit state.

1 Introduction

Many structures (including transmission line towers, bridges, tall buildings, and offshore structures) are founded on piles, which are designed to transmit both vertical and horizontal forces, and resulting moments to the load bearing strata. The piles supporting these structures are inevitably subjected to lateral static and cyclic load generated by waves, currents, and wind. Some methods of increasing the lateral resistance of piles have been discussed by Poulos and Davis [20]. Among them, increasing the dimension of the pile near the ground surface by attaching fins or wings to the pile shaft have been developed for both offshore monopiles [5, 7, 8] and onshore infrastructures [18]. In Australia, Star finned screw pile foundation has been developed in the late 1990s specifically for laterally loaded structures such as lighting columns, traffic lights and power transmission poles. The primary application for Starfin screw piles is to provide foundations for utility poles, particularly for lighting. As such, the foundation must resist lateral load and moment caused by wind load on the poles. The main aim of the Starfin screw pile is to transfer the loads caused by the wind load on the poles to the ground safely and within the allowable deformations. However, relatively little attention has been paid to the development of theoretical methods to predict the response of laterally loaded finned piles.

The response of laterally loaded finned piles in sand has been studied through 1 g small-scale model tests [1, 4, 7, 8, 21], centrifuge modeling [5, 27], full-scale field tests [15] and theoretical and numerical analysis [1, 3, 16, 18, 19, 31]. These studies have provided valuable insight on the effect of the length, width, position, configuration, and shape of fins as well as the effect of the relative density and stiffness of sand on the performance of finned piles under lateral loading with respect to the load transfer mechanism, load–displacement relationship and bending moment along the pile. The main findings available in the literature can be summarized as follows:

• In comparison with the unfinned piles, a greater initial stiffness and a higher lateral load capacity were generally obtained for finned piles from all the previous studies [1, 3, 4, 7, 15, 16, 18, 19, 27, 31].

• Fins placed at the top of the pile close to the ground level is more effective than fins at other locations [3, 4].

• The efficiency of the fins in enhancing the lateral load behavior generally increases with an increase in the fin length. For long flexible pile, an optimal fin length is found to be approximately 0.3 ~ 0.4 times the pile embedded length, beyond which any further increase in the fin length does not increase the lateral load capacity and reduce the pile deflection significantly [4, 16, 18]. However, no optimal fin length is observed for short rigid piles, independent of the relative density of the sand [3, 16, 18]. Increasing the fin length also reduces the maximum bending moment along the pile shaft for both short and long piles [16, 18].

• In comparison with an unfinned pile, the addition of fins reduces the maximum bending moment along the pile shaft for a given load. On the other hand, a finned pile suffers higher maximum bending moment for a given pile displacement [3, 15, 18].

• The fin efficiency increases with increasing width of the fins with the optimal width being the diameter of the pile shaft [4, 16, 18].

• Rectangular-shaped fins are more effective than triangular-shaped fins [4, 16].

• For the piles fitted with four fins (as shown in Fig. 3), the fin orientation with respect to the loading direction does not influence the lateral load–pile displacement responses up to l_fin/l = 0.25, where l_fin is the fin length and l is the embedded length of the pile, for all sand relative density. For larger ratio of l_fin/l_, the fin orientation has small influence on the lateral load capacity, but quite significantly on the maximum bending moment, for a given displacement level [3].

• The performance of the fins is highly dependent on both the sand density and stiffness. The enhancement of load capacity using fins decreases with increasing relative density of the sand. Fins are more effective in improving the lateral load-carrying capacity of piles in loose sand than in medium to dense sands [3, 16, 18].

Despite the insight, many of the previous investigations regarding the behavior of laterally loaded finned piles have predominantly focused on physical modeling using laboratory tests and numerical analysis using finite element method. There are still limited laboratory data and full-scale field tests as well as analytical solutions available for laterally loaded finned piles in sand.

This study presents experimental investigation at both small scale tests in the laboratory and full-scale field tests into the response of laterally loaded finned piles in sand. Firstly, model tests were carried out on free headed single piles of different shaft diameters with and without fins in sand to explore the performance of the piles under lateral loading in terms of the measured load–displacement and moment–rotation relationships as well the soil displacement around the piles. An equivalent diameter was proposed for a finned pile, which enabled the experimental results to be back analyzed using an existing elasto-plastic solution for laterally loaded piles in sand within the framework of p-y method. Then, field tests on laterally loaded Starfin screw piles in sand conducted in Queensland, Australia, were reported. Lastly, the measured field test results were analyzed using the proposed approach, which was further validated against measured test results from fully instrumented finned piles in overconsolidated dense sand reported in the literature.

2 Apparatus and procedures

2.1 Apparatus

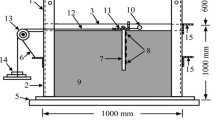
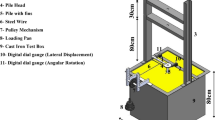
Figure 1 shows the laboratory apparatus and the experiment set up for the model pile test, which was modified from that designed by Przibilla [22] for monotonic and cyclic lateral loading of piles. Figure 2 illustrates a schematic cross section of the experimental set up. The container was made of steel and had an inner diameter of 560 mm and height of 890 mm. A steel frame with pulleys was mounted on the sides of the container. The height of the frame can be adjusted so that the load eccentricity can be varied. A model pile was installed to an embedded length, l, in the center of the container. The pile was subjected to lateral load through a flexible steel wire of 2 mm diameter attached to the pile. The wire was pulled horizontally at a height, e, above the model ground surface through the pulleys and a hanger. Dead weights were put manually on the hanger to induce lateral load on the pile. Two dial gauges with an accuracy of 0.01 mm and measurement range of 0–10 mm were attached on the frame to measure the displacements of the pile above the ground surface level.

Fig. 1

Experimental setup

Fig. 2

Schematic experimental setting up

2.2 Model pile

Tests were conducted on piles with and without fins. Circular, hollow steel pipes were used as the model piles with length of 1 m and wall thickness of 1.2 mm. The outer diameter of the pile, d_shaft was 19 mm, 25.4 mm, and 31.8 mm, with the pile embedded lengths, l = 183 mm, 245 mm, and 307 mm, respectively. The finned piles were made by welding four rectangular steel plates at 90° to the pile shaft as fins, with the fin width w_fin = 0.8d_shaft, fin length, l_fin = l/3, and fin thickness t_fin = 3 mm. Figure 3 shows the detailed configurations of the piles. The dimensions of the model finned piles were designed at approximately 1:10 scale of those of the Starfin screw piles as described in Sect. 6.1. The surface of the model pile shaft may be classified as smooth; however, the surface of the segment fitted with fins is smooth to semi-rough due to the welding. Kim et al. [12] show that the surface roughness makes appreciable difference in the lateral pile response, especially at small roughness values, but marginal change at greater roughness. The effect of the pile surface roughness was not investigated in this study, and its impact on the lateral pile response is likely to be minor [13].

Fig. 3

Detailed configuration of finned piles

2.3 Model sand ground properties

Oven dried medium coarse quartz sand was used for the tests. Figure 4 plots the particle size distribution curve of the sand with mean particle size, D₅₀ = 0.37 mm. The uniformity coefficient, C_u, and coefficient of curvature, C_c, are 3.1 and 0.74, respectively. The maximum dry unit weight and minimum dry unit weight were determined as 16.86 kN/m³ and 14.29 kN/m³, respectively, using the dry placement method according to AS 1289.5.5.1–1998 [29]. In this study, very dense samples were prepared for all the pile tests, with average unit weight of 16.79 ± 0.02 kN/m³ (average relative density D_r = 97.7% ± 0.1%). The samples were prepared by placing the desired amount of sand in the container in layers and tamped using a compaction hammer. All samples were prepared dry to simulate drained conditions. The angle of internal friction at the critical state was determined as 30° from direct shear tests at a normal stress of 100, 200 and 400 kPa.

Fig. 4

Particle size distribution of sand

2.4 Test procedures

After the sand was prepared in the container, grids of colored sand were made on the surface of the model ground, which enabled the soil displacement to be visualized and measured at the ground level. Then, the pile was driven into the model ground manually using a rubber hammer to a desired embedded length. During driving, the verticality of the piles was checked by a spirit level. Afterward, the lateral loading devices were set up and the two dial gauges were fitted to measure the pile lateral displacement. The lateral load, T_t was applied at an eccentricity, e, above the model ground surface. The resulting moment at the model ground surface was M₀ = T_t e. In addition, the pile displacement, u₀, and rotation, ω₀, at the ground surface were calculated from the dial gauge measurements.

3 Test program

Thirteen tests were conducted to investigate the effect of pile diameter, pile cross section, loading direction with respect to the fin orientation. Table 1 presents the detailed test program. Each test is denoted by a combination of letters, numbers, and symbols for easy reference.

Table 1 Details of the model and field tests

• (1) Tests C1-C4 were conducted on the circular pile with the diameter of 25.4 mm and 31.8 mm to test the apparatus as well as to investigate the repeatability and consistence between tests.

• (2) The remaining nine tests consisted of three series of tests conducted on the model piles with shaft diameter of 19 mm, 25.4 mm and 31.8 mm. Each series included a reference pile test with no fins (○), finned pile tests with crossing fins ( +) and diagonal fins ( ×), respectively. Figure 3b and d shows the loading direction and the finned pile orientations.

The boundary effect needs to be accounted for and assessed for the model tests. The pile was free-headed and subjected to lateral loading only. The pile was always installed in the center of the container. Albiker et al. [2] show that the load–displacement responses were practically not affected by the boundary provided the ratio of the diameter of the container, D_c, to the pile diameter D_c/d_shaft ≥ 10. In this study, the minimum D_c/d_shaft was about 17.6 (= 560/31.8). Numerical analyses [2, 18, 19] show that the extent of soil influence zone for a pile with fins is greater than that of an unfinned pile for a given pile head displacement, depending on the width of the fins and orientation of the fins as well as the fin length with respect to the embedded pile length. Nevertheless, with the equivalent diameter, d_eq, introduced in Sect. 5.1. The minimum D_c/d_eq was obtained as 9.6(= 560/58.4). Therefore, it was deemed that the diameter of the container is large enough for the model pile tests and the boundary effect was insignificant.

4 Test results

4.1 Load–displacement response

To ensure the reproducibility of the tests, model tests were first conducted on the unfinned piles with the diameter of 25.4 mm and 31.8 mm twice in Tests C1 to C4. The piles were loaded to a very large displacement, greater than 20% of pile diameter, so that the soil resistance against the piles can be fully mobilized. Figure 5 presents the lateral load, T_t ~ displacement measured at groundline, u₀ and the moment, M₀ ~ rotation, ω₀ response. All tests exhibited nonlinear relationships between the lateral load and displacement or moment and rotation. Under the same testing conditions, the two sets of test results are comparable. The excellent agreement suggests that the quality of the sand sample preparation was consistent, and the tests were repeatable, even though some scattering can be observed.

Fig. 5

Measured pile response of tests C1 ~ C4

Figure 6 presents the lateral load, T_t ~ displacement measured at groundline, u₀ and the moment, M₀ ~ rotation, ω₀, for the three series of laterally loaded unfinned and finned piles with the shaft diameter of 19 mm, 25.4 mm, and 31.8 mm in tests RP1-FC3. The figures demonstrate that.

• The piles with and without fins have similar pattern of T_t ~ u₀ and M₀ ~ ω₀ relationships.

• The finned piles carry higher lateral load compared to the circular piles at a given displacement level.

• The finned piles have greater initial stiffness and load capacity compared with the circular piles with the same shaft diameter.

• The addition of fins is more effective in improving the lateral load capacity and stiffness for the piles with a larger diameter.

• The variation of the test results between the piles with a crossing fin ( +) and diagonal fin ( ×) is small. Thus, the effect of the fins’ orientation to the loading direction has marginal influence on the lateral load carrying capacity. This finding is consistent with the numerical analysis results of Babu and Viswanadham [3] for piles up to l_fin/l = 0.25.

Fig. 6

Measured pile response of tests RP1 ~ FC3

4.2 Soil displacement around the pile

The effect of fins on the soil displacement around the pile can be observed at the ground surface. Sand flowing around the pile was observed during loading, along with the separation between the pile and sand, which resulted in a ‘depression’ behind the pile, and formation of a ‘mound’ from the accumulation of sand in front of the pile in the loading direction. The ‘depression’ and ‘mound’ were clearly visible and were noticed to enlarge with increasing loadings. Figures 7 and 8 show the soil displacement pattern around the circular pile of Test RP3 at the load level of 165.6 N and the pile with crossing fins ( +) in Test FC2 at 73.5 N. The ‘depression’ for the circular pile resembles a cone. However, the passive mound for the finned piles has a complex geometry associated with the dilatancy of the sand at the low stress level.

Fig. 7

Soil displacement at the ground surface around the pile in test RP3 at 165.6 N

Fig. 8

Soil displacement at the ground surface around the pile in test FC2 at 73.5 N

To quantify the soil movement pattern around the piles adjacent to the ground surface, measurements were made manually using vernier calipers. In addition, 3D models were created using Autodesk ReCap to capture and reconstruct the pile testing so that better visualization and understanding of the soil displacement field can be gained. Figure 8 shows a scheme of the 3D model developed in Autodesk ReCap. Six parameters were made to quantify the soil surface displacement around the finned pile, including the horizontal displacement of passive zone (u_p), soil vertical displacement of passive zone (v_p), width of passive zone (w_p), soil horizontal displacement of active zone (u_a), soil vertical displacement of active zone(v_a), and width of active zone (w_a). Figure 8 shows the experimental measurement for Test FC2. The values are 156.32 mm, 18.38 mm, 195.76 mm, 92.82 mm, 40.71 mm, and 118.71 mm, respectively, at the lateral load of 73.5 N.

4.3 Lateral capacity and fin efficiency

There is no clear failure point appearing on the load–displacement or moment–rotation curves in Figs. 5 and 6. As reviewed by Qin [23], several methods have been proposed for predicting the lateral capacity of rigid piles. These methods generally result in different lateral capacity predictions that can vary substantially for the same measured data. In the literature on laterally loaded finned piles, the lateral load capacity has been determined as the load at a displacement of 0.1d_shaft [3, 16, 19, 27] or 0.2d_shaft [18]. Because of the composite cross section with fins, accounting for the effect of the fins, it may be more appropriate to take the load/moment at a certain rotation angle as the lateral capacity. In this study, the lateral load capacity, T_t2°, is defined as the load at a ground level rotation of 2° as proposed by Byrne et al. [6]. Table 2 presents the lateral load capacities T_t2° of the model tests.

Table 2 Summary of calculated results

To quantify the efficiency of fins in enhancing the pile performance, the fin efficiency, η, introduced by Peng et al. [19], Babu and Viswanadham [3] was adopted in this study, which is defined as the ratio of the lateral load capacity of a finned pile to that of an unfinned pile. Note that the fin efficiency, η, is different from the load efficiency, η_H (= η-1), used by Pei and Qiu [18]. The current test results show that.

• (1) The finned piles (+ and ×) of the same diameter have similar lateral load capacities, with finned piles ( ×) having slightly smaller capacity, but the difference is generally less than 5% on average.

• (2) The magnitudes of the fin efficiency, η, are 1.36, 2.35, and 2.88 for the finned piles ( +) with a shaft diameter of 19 mm, 25.4 mm, and 38.1 mm, respectively. It seems that the addition of fins is more efficient in improving the lateral performance of piles with larger pile diameter.

5 Theoretical analysis of pile responses

5.1 Equivalent diameter for a finned pile

Numerical analysis has been carried out to investigate the behavior of laterally loaded finned piles and has brought valuable insight into the complex three-dimensional mechanism of the load transfer and pile-soil interaction [3, 18, 19]. On the other hand, Duhrkop and Grabe [8] described a modified p-y curve method for piles with fins or bulge. They showed that the effectiveness of the fin depends on its stiffness in relation to that of the soil and pile shaft. They introduced a bulge factor, κ_w, to describe the ratio of resistance provided by the finned pile section to that without fins at the same depth, which depends on the fin width, apex angle and modulus of subgrade reaction. They further suggested that in sections with fins the lateral resistance is multiplied by the bulge factor in the p-y method. In essence, the finned pile section was taken as a circular section with an equivalent diameter, d_eq = κ_wd_shaft, with κ_w = 1.2–1.5 for flat fins (i.e., apex angle of bulge δ = 0).

In this study, it is proposed that a short rigid finned pile is taken as an equivalent circular unfinned pile. The diameter of the equivalent circular pile is taken as the narrowest effective width when subjected to a load as illustrated in Fig. 3. For the finned piles with four fins,

$${\text{d}}_{{{\text{eq}}}} = 0.{7}0{7}\left( {{\text{d}}_{{{\text{shaft}}}} + {\text{2w}}_{{{\text{fin}}}} } \right)$$

(1)

For the Starfin piles with three fins as shown in Fig. 3e

$${\text{d}}_{{{\text{eq}}}} = 0.{75}\left( {{\text{d}}_{{{\text{shaft}}}} + {\text{2w}}_{{{\text{fin}}}} } \right)$$

(2)

where d_eq is the equivalent diameter, d_shaft is the diameter of the pile shaft, and w_fin is the width of the fin.

5.2 Elasto-plastic solutions

Based on the analysis of the field tests results of laterally loaded Starfin screw piles in sand, Qin [23] showed that the finned piles with the embedded pile length to equivalent diameter ratio, l/d_eq varying between 4 and 6 behave in a rigid manner. Thus, in this study, the experimental test results were back analyzed using the elasto-plastic solutions for laterally loaded rigid piles in cohesionless soil proposed by Guo [10, 11]. The solutions are briefly explained below.

A pile is defined as rigid if the pile–soil relative stiffness, E_P/G_s exceeds a critical ratio, (E_P/G_s)_c, where (E_P/G_s)_c = 0.052(l/r₀)⁴ and E_P is Young’s modulus of an equivalent solid cylindrical pile, G_s is the soil shear modulus, l is the pile embedded length, and r₀ is the outer radius of the equivalent solid pile. The elasto-plastic solutions were developed for laterally loaded rigid piles using a load transfer model. As shown in Fig. 9(a), the pile head is free with no constraints. The pile soil interaction is characterized by a series of springs distributed along the shaft. The springs have an elasto-plastic p-y (u) curve at each depth, where p is the soil lateral resistance per unit length of pile shaft and u is the pile deflection. The lateral resistance, p, is proportional to the local pile displacement, u, at that depth and the coefficient of subgrade reaction, k, i.e., p = kdu. It should be noted that d = d_eq for the finned piles and d = d_shaft for piles without fins in the theoretical analysis of the pile response. The k may be written as k₀z^m, with m = 0 and 1 being referred to as constant k and Gibson k hereafter. Where the lateral resistance reaches the limiting value p_u, relative slip takes place along the pile-soil interface and extends to a depth z₀, which is called pre-tip yield state. With increasing load, the pile-soil relative slip may also initiate from the pile tip (z = l) and expand upwards to another depth z₁ (see Fig. 9(c)). The two plastic zones tend to merge when the pile reaches the ultimate state, i.e., yield at rotation point (z₀ = z₁ = z_r). It is assumed that the p_u increases linearly with depth z and is described by p_u = A_rdz, where A_rd is the gradient of the p_u profile. The solutions allow the nonlinear responses to be readily estimated, using the two parameters k and A_r. Conversely, the two parameters can be deduced from the measured results of pile tests.

Fig. 9

Schematic analysis for a rigid pile (after Guo [10])

The solutions have been implemented into a spreadsheet program to facilitate computation. The responses of over 65 piles tested in sand have been investigated by Qin and Guo [24, 25]. It should be noted that the solutions have been recommended to calculate the lateral resistance of cantilever pole retaining walls to resist earthquake loading in the guidance Module 6 Earthquake resistant retaining wall design developed jointly by the New Zealand Geotechnical Society and the Ministry of Business, Innovation & Employment (MBIE) [17].

5.3 Analysis of test results

Back calculations were carried out by best matching between the elasto-plastic solutions and the measured responses for all tests. The measured test data and the back calculated curves with a constant k are plotted in Figs. 10 and 11, with the calculated results in lines and the measured data as scatter symbols. Excellent agreement was achieved between the calculated and measured load–displacement and moment–rotation data using the solution with a constant k. The deduced parameters A_r and k are presented in Table 2. It is calculated that the pile tip yield takes place around a rotation angle of 1.5°–2.5° for the finned piles using the solution, except tests C3 and C4. After tip yield, a minor increase in load induces large displacements and rotations of the piles. The calculated load capacity of the piles at the ultimate state, i.e., yield at rotation point, is greater than the measured load capacity at a pile rotation of 2°. The back calculated k of the finned piles is 1.875–2.57 times that of the circular piles for shaft diameter of 25.4 mm and 31.8 mm, while it has similar values for the 19 mm shaft diameter pile.

Fig. 10

Measured and back calculated responses of piles C1 ~ C4

Fig. 11

Measured and back calculated responses of piles RP1 ~ FC3

To facilitate comparison, a non-dimensional parameter N_g is defined as N_g = A_r/(γ_s′K_p²), where γ_s′ is the effective unit weight of the soil (dry unit weight above water table, and buoyant unit weight below); K_p = tan²(45° + ϕ_s′/2) is the coefficient of passive earth pressure; ϕ_s′ is the effective frictional angle, which is taken as the critical frictional angle in this study [9, 26]. The N_g was calculated for each pile test and tabulated in Table 2. The value of N_g varies from 7.0 to 10.6, which is greater than the range determined previously by Qin and Guo [24, 25] from the analysis of 65 pile test results. This may be partly due to the smaller K_p computed from the critical frictional angle. On the other hand, the relative density, the loading eccentricity, stress level, pile installation method, failure mode, etc., also had an influence on the ultimate lateral soil resistance [24, 25, 30]. This warrants further investigation with full-scale field tests in the next section.

6 Full-scale tests results

To clarify the performance of finned piles under lateral loading in sandy soil, full-scale field tests were executed on Starfin screw piles in loose to medium dense sand in this study. In addition, field experiments on instrumented winged monopiles in overconsolidated dense sand were reported by Murphy et al. [15]. These test results were analyzed and presented below.

6.1 Starfin screw pile tests

6.1.1 Site investigation

The experimental tests were carried out in July 2018 in the Boyland area, Queensland, Australia. Geotechnical investigation has shown that the test site consists of natural silty clay. A sand test bed using imported river sand and fine from a local quarry was constructed and compacted to 1.8 m deep for the purpose of creating a sand site. Prior to pile testing, a series of laboratory and field tests were conducted to determine the in situ sand properties on site. Figure 12a plots the particle size distribution curve of the sand. The coefficient of uniformity, C_u, and coefficient of curvature, C_c, were calculated as 3.1 and 1.0. The sand was classified as SP, based on the Unified Soil Classification System (USCS). The peak and critical state frictional angle were determined as 36.7° and 34.6°, respectively, from direct shear tests. Four Dynamic Cone Penetrometer (DCP) tests were conducted in accordance with AS1289.6.3.2–1997 [28] up to 1.9 m depth. Figure 12b shows the DCP results with depth. The DCP number of blows per 100 mm increment varies from 3 to 5 in the top 1.0 m. The DCP values are quite consistent with depth for the test 1 and 2, while they decrease to a lower value of 1–2 below 1.0 m in test 3 and 4, indicating that the site may have not been compacted uniformly. An average DCP value of 3–4 may be approximately obtained for the site. Using the correlation proposed by Look [14], the sand was at loose to medium dense state and the effective internal frictional angle was estimated as 35°–36°. These values are consistent with those obtained from the direct shear tests. The unit weight of the sand was determined as 17 kN/m³.

Fig. 12

Subsoil conditions at the test site for Starfin screw pile tests

6.1.2 Starfin screw piles

There is a total of six models of Starfin screw piles. Each Starfin screw pile consists of a central shaft of uniform diameter with a set of relative broad fins covering the top portion of the shaft as shown in Fig. 13a. The fins are square at the top of the shaft and the bottom portion of the fins taper from the shaft to the outside edge of the fin. An enlarged pile cross-sectional area is achieved near the pile head, improving the strength and stiffness of the pile system. The unique feature of the Starfin piles is a fin assembly at the top of the screw pile shaft designed to increase the lateral resistance of the foundation relative to a conventional screw pile. The screw pile shaft is free to rotate within the fin assembly for installation.

Fig. 13

Details of Starfin screw piles

In this study, three models, SF1, SF2 and SF3 of the Starfin screw piles were tested. Model SF1 has three fins, while model SF2 and SF3 have 4 fins as shown in Fig. 13c. The fin thickness is 6 mm for all models. The dimensions of the diameter of the shaft, d_shaft, length of the fin, l_fin, width of the fin, w_fin are presented in Table 1. In addition, a model SF2 fitted with a ‘sand kit’ (SF2SK), in which the fin length was doubled (Fig. 13b), was also tested.

6.1.3 Test setup

The installation of a Starfin screw pile consists of two stages. Firstly, the pile shaft was screwed into the ground using a hydraulic rotary until the fins touched the ground. Then, the orientation of the fins was adjusted and aligned. Afterward, the position of the fins was maintained, and the fins were dragged vertically into the ground with further screwing of the shaft until the designed length of the pile. During the second stage, the fins did not rotate with the pile shaft. The soil disturbance had some effect on the lateral responses of the piles. However, the effect was not investigated in the present study. The piles were laterally loaded using a pole mounted on top of the foundation with an excavator providing tie back force via a sling as shown in Fig. 14a. The pole was connected to the top portion of the fins by hold down bolts to ensure the force was fully transferred. The measurement equipment of the tests included a load cell with a capacity of 7500 kg and two dial gauges at two different heights set perpendicular to the pole above the ground level. The lateral load was applied in increments at an eccentric height, e, above the ground to induce a bending moment and shear force into the foundation. The deflection of the pole mounted on the Starfin pile was measured using the two dial gauges. The measurements from their readings allowed the calculation of the lateral pile displacements at the ground level and the rotation of the pole and Starfin pile foundation.

Fig. 14

Field Starfin screw pile test and measurement

Four tests were conducted. Figure 14d shows the schematic of the testing setup. The test details were summarized in Table 1. The piles were restrained by soil (free-headed) and subjected to lateral loading only. At each increment of load, the dial gauge readings were recorded. The piles were loaded in a series of stages such that a cyclic load was applied and reduced to zero for about 4 to 5 cycles. These provided a replication of the cyclic nature of the wind forces which would occur in gusting actions. In each case, the test was terminated after significant pole deflection.

6.1.4 Test results and analysis

Figure 15 shows the lateral load–displacement at ground level response and ground level moment–pile rotation curves for each tested pile. All tests exhibit nonlinear between the lateral load and displacement or moment and rotation. No clear failure point is observed on the load–displacement or moment–rotation curves.

Fig. 15

Measured and back calculated response of Starfin screw piles

During a test, the pile was gradually loaded to a certain load level, and then, the pile was unloaded to zero; afterward, the pile was reloaded to a higher load magnitude. This loading pattern was applied to simulate cyclic characteristics of wind loads. As an example, the test on SF3 includes three loading parcels with the maximum shear force of 2.4 kN, 3.6 kN, and 4.34 kN, respectively. The plotting in Fig. 15 shows: (1) a progressively accumulated lateral displacement during the cyclic loading; (2) irrecoverable pile displacement and rotation after unloading to zero; (3) a lower initial tangent stiffness; (4) a nearly elastic reaction during reloading; (5) the tangent stiffness of each reloading curve is approximately equal; (6) the reloading paths merge the load–displacement curve when the maximum past load was exceeded.

As discussed in Sect. 4.3, the lateral load capacity was determined as the lateral load/moment corresponding to 2° of rotation of the pile at the ground level. They are obtained as 3.6 kN, 3.2 kN, 3.3 kN and 1.4 kN for the pile SF3, SF2, SF2SK and SF1, respectively. Having identical embedment depth of 1.5 m, the load capacity of pile SF3 with a larger shaft diameter and longer fin length is about 12.5% higher than that of SF2. On the other hand, the load capacity of SF2 and SF2SK is similar, indicating extension of the fin length enhancing the pile load capacity slightly when the ratio l_fin/l increases from 1/3 to 2/3. The pile SF1, having 3 fins with a smaller shaft diameter and embedment depth, has a much less capacity of 1.4 kN, which is about 38% and 44% of that of the SF3 and SF2.

Back calculations were carried out by best matching between the elasto-plastic solutions and the measured load–displacement and moment–rotation responses for all tests. The deduced parameters A_r, k and k₀ are presented in Table 2. The measured test data and the back calculated curves are plotted in Fig. 15. The calculated pile responses are plotted as lines, while the measured data are plotted as scatter symbols, respectively.

To illustrate the calculation, the back analysis of test SF3 was performed and was supplemented in the Appendix. The pile had four fins and 1.5 m long 114 × 6 CHS shaft (Grade 350). The load eccentricity was 5.45 m. The fin width was 180 mm. The equivalent diameter, d_eq was calculated as 0.349 m. The pile was tested to a maximum lateral load of 5.5 kN, and the moment at ground level was 29.98 kNm with a corresponding pile head rotation angle of 5°. The back-calculated curves are plotted in Fig. 15 together with the measured results, using A_r = 345 kN/m³, k₀ = 25 MN/m⁴, and k = 25 MN/m³. The following features are observed from the comparison. (1) Taking the same value of A_r, back calculation using the solution with a constant k gives a better match with the measured T_t-u₀ relationships than using a Gibson k. (2) The ultimate load at yield at rotation point was calculated as 6.0 kN, which is independent of the k. (3) With e/l = 3.63, the z₀/l at tip yield is obtained as 0.519 (constant k) and 0.396 (Gibson k). The pile head rotation angle ω = 2.5° and ω = 1.8° is obtained at M₀ = 28.5 kNm and M₀ = 26 kNm, respectively.

Priority was given to match the measured load–displacement, yet agreement between the measured and calculated moment–rotation response was less satisfactory using the same set of input A_r, and k values. The pile tip yield took place around a rotation angle of 2°–3°. After tip yield, a minor increase in load would cause excessively large displacements and rotations of the pile. The pile should operate in the pre-tip yield state under serviceability limit state loading.

6.2 Field experiments on instrumented winged monopiles in overconsolidated dense sand

Murphy et al. [15] reported field tests on instrumented prototype scale pipe piles fitted with and without wings at Garryhesta and Blessington in Ireland. The sand deposits were relatively uniform as revealed by the CPT profiles, and the water table was below the pile tip at both sites. The test site at Garryhesta was a medium dense silty sand deposit with the relative density about 70% and the unit weight of 18.6 kN/m³. A critical state friction angle of 33° was reported, and the peak friction angle was 45° at 0.5 m and 40° at 2 m. The overconsolidation ratio was estimated as 15 at 0.5 m and 5 at 2 m below ground level. The cone tip resistance q_c distribution was relatively uniform with an average value of 6.65 MPa. The small strain shear stiffness G₀ is 200 MPa. At this site, the piles were installed by pushing/jacking. The test site at Blessington was a dense silty sand deposit with the relative density about 100% and the unit weight of 20 kN/m³. A critical state friction angle of 36.5° was reported, and the peak friction angle was 42° at 0.5 m and 44° at 2 m. The overconsolidation ratio was about 20 at 0.5 m and 10 at 2 m below ground level. At the depth of 0.3 ~ 2.0 m below the ground level, the cone tip resistance q_c increases linearly with depth. The small strain shear stiffness G₀ is 150 MPa. The piles were driven into the site.

Tests were conducted on three instrumented piles with one without fins as a reference pile (RP) and the other two fitted with fins (WP1 and WP2). The piles had an embedded length of 1.5 m, diameter of 245 mm and wall thickness of 8 mm. The width of the fins was 185 mm, and the length of the fins was 280 mm and 560 mm for WP1 and WP2, respectively. Only a pair of fins were fixed to the pile shaft, perpendicular to the loading direction. The load eccentricity was 0.4 m. At both sites, the piles were loaded statically until the pile head displacement continued without addition of a further load increment.

The measured lateral load T_t ~ pile displacement at the ground level u₀ of the reference piles RP is plotted in Fig. 16a and 16b for the piles at Blessington and Garryhesta sites, respectively. The calculated T_t ~ u₀ curves by best matching the measured curves are also plotted for comparison. The deduced parameters A_r, k and k₀ are presented in Table 2. The solution with a Gibson k provides an excellent match of the initial elastic response up to a pile displacement, u₀ of 6.4 mm and 6.8 mm for the RP tests at Blessington and Garryhesta, respectively, which is about 3% (u₀/d_shaft = (6.4 ~ 6.8)/245 ≈ 3%) of the pile diameter, and the ultimate load at excessively large pile displacement against the measured T_t ~ u₀ curves for the two piles tested in the overconsolidated sand, although the middle transition parts were slightly overestimated. The pile tips yielded at a ground level rotation angle about ω₀ ≈ 1° and displacement u₀ ≈ 20 mm (u₀/d_shaft ≈ 8%) using Gibson k for both sites at 41 kN and 31.4 kN. The ultimate loading capacities at the state of yielding at rotation point T_u are calculated as 48 kN and 37 kN for the tests at Blessington and Garryhesta sites, respectively. They are approximately 6% higher than the ultimate capacities of 45 kN and 35 kN at a pile displacement of 30 mm (u₀/d_shaft = 12%) determined from the measured load ~ displacement curve, beyond which the pile displacement increases substantially with no further load increment. The bending moment profiles along the pile obtained using the strain measurements at three load levels are plotted in Fig. 16c and d. The back calculated bending moment profiles were also included for comparison. Generally, the bending moment distributions with depth were accurately captured, except the maximum bending moment was overestimated by about (5 ~ 15)%, particularly at a large load level.

Fig. 16

Measured and back calculated response of RP at Blessington and Garryhesta

The measured lateral load T_t ~ pile displacement at the ground level u₀, bending moment profiles of the two finned piles WP1 and WP2 are presented in Figs. 17 and 18 for the two sites. Two approaches were used to calculate the measured pile responses, accounting for the composite pile diameter along the length of the pile: (a) an equivalent diameter of 0.435 m computed using d_shaft = 0.245 m and w_fin = 0.185 m from Eq. (1), and (b) the diameter of the pile shaft of 0.245 m. The deduced parameters A_r, k and k₀ are presented in Table 2. The studies show.

• (1) Using either approach the measured pile response can be well estimated and matched but resulting in different values for the deduced parameters A_r, k and k₀. Only the calculated pile responses using the equivalent diameter are plotted in Figs. 17 and 18 for comparison.

• (2) For the constant fin width and shaft diameter, i.e., w_fin/d_shaft = 0.185/0.245 = 0.755, the values of the A_r, k and k₀ increase approximately linearly with the increasing length of the fins from l_fin/l = 0 to 0.373, implying enhanced lateral capacity and stiffness of the piles with increasing fin length.

• (3) The ratio of the values of A_r and k₀ deduced using the equivalent diameter to those obtained using the pile shaft diameter is about 0.56, which is inverse to the ratio of d_eq/d_shaft = 1.775. This is expected because the predicted initial elastic response and ultimate pile load capacity are proportional to the pile diameter for the same measured load–displacement responses.

• (4) The maximum bending moment was over estimated, and its depth moves down the pile, especially at a larger load level, at both sites.

• (5) The fin efficiency, η, calculated from T_u, increases with the length of the fins. They can be estimated as η = 1 + 0.85l_fin/l.

• (6) The average modulus of subgrade reaction along the pile embedded depth, k₀d1/2, is 26–66 MPa and 18–51 MPa for the Blessington and Garryhesta test site, respectively, which are only (17–44)% and (9 ~ 25)% of the small strain shear modulus, G₀.

• (7) The dimensionless factor N_g deduced using the actual pile shaft diameter increases approximately linearly with l_fin/l, giving N_g = 2.86 + 2.12l_fin/l and N_g = 3.27 + 2.14l_fin/l for the piles at Blessington and Garryhesta test site, respectively.

Fig. 17

Measured and back calculated response of WP1 and WP2 at Blessington

Fig. 18

Measured and back calculated response of WP1 and WP2 at Garryhesta

7 Concluding remarks

This paper presents experimental investigation of the effect of fins on the response of piles under static lateral loading in sand. Model tests were conducted on piles of different shaft diameters without and with the addition of four fins to enable the performance of finned piles to be evaluated and compared with that of a regular circular pile. The measured lateral load–displacement and moment–rotation responses of the piles were back-calculated using the elasto-plastic solutions with the equivalent pile diameter proposed for finned piles. The following conclusions are drawn:

• 1. Piles with fins allow significant enhancement of the lateral stiffness and ultimate lateral load capacity compared with a regular circular pile. The test results in this study show that the load capacity was increased by 207%, 146% and 32% for the finned piles with diameters of 38.1 mm, 25.4 mm and 19 mm, respectively, compared to non-finned piles of the same shaft diameter.

• 2. The orientation of the fins with respect to the lateral loading direction has only a minor effect on the performance of the finned piles. The ultimate load capacity of finned piles with the same shaft diameter is within a range of approximately 5% for the two fin orientations investigated in the experimental study.

• 3. The addition of fins is more efficient in improving the lateral performance of piles with larger pile diameter.

• 4. The soil movement field around a finned pile has a complex pattern near the ground surface, rather than a simple conic depression that occurs for a circular pile.

• 5. In general, the elasto-plastic solution with a constant k and a linear increasing ultimate soil resistance can accurately reproduce the responses of the laterally loaded finned piles with the equivalent diameter. However, the assumption of a Gibson k is required to capture the initial linear elastic response of the piles in overconsolidated dense sand.

• 6. The back calculated ultimate load capacity of the piles is greater than the measured load capacity defined as the load that causes a pile rotation of 2°.

• 7. The measured pile response can be well back calculated and matched using either the equivalent diameter or the diameter of the pile shaft but resulting in different values for the deduced parameters A_r, k and k₀. For the constant fin width and shaft diameter, the values of the Ar, k and k₀ increase approximately linearly with the increasing length of the fins, implying enhanced lateral capacity and stiffness of the piles with increasing fin length.

• 8. The fin efficiency η and the dimensionless factor N_g increase approximately linearly with fin length.