A mechanistic model for porosity and permeability in deformable hydrate-bearing sediments with various hydrate growth patterns

Abstract

A stress-dependent porosity and permeability model is proposed to predict the microstructure evolution and the physical properties and mechanical behavior of deformable hydrate-bearing sediments (HBS) with various hydrate growth patterns under engineering disturbance. First, according to Hertzian contact theory and the proposed mesoelastic–plastic damage model (Gurson-DP model), the correction formula of the pore size under the influence of the effective confining pressure and the overburden pressure is given, and the stress-dependent porosity model is derived. Second, the fractal capillary bundle model is used to describe the stress-dependent permeability of HBS with different hydrate saturations considering the grain-cementing hydrate and the universal-growth hydrate. Finally, the proportions of hydrates with various growth patterns, such as pore filling (PF), wall coating (WC), and grain cementing (GC), are determined based on the equivalent flow assumption to reasonably evaluate the hydrate growth habit in HBS. This paper comprehensively studies the stress-dependent porosity and permeability models of deformable HBS and thus, provides a theoretical basis for quantitative evaluation and prediction of the physical properties (such as porosity and permeability) and mechanical behavior of HBS.

Appendices

Appendix 1: Derivation of stress-dependent permeability for HBS

1.1 Fractal capillary bundle permeability model of sediments in the absence of hydrates

Experimental results show that pores in the sediments have similar fractal scaling laws, so that fractal theory can be used to describe the complex and random geometric microstructure of the pores. According to fractal geometry theory, regardless of the influence of hydrates, the cumulative size distribution of the pores in the sediments obeys the fractal scale law and satisfies the scale law [34, 35]:

$$N(\varepsilon \ge r) = (r_{\max 0} /r)^{{D_{f} }}$$

(40)

where N is the number of pores or capillary bundles, ε is the length scale, r is the pore size, the minimum and maximum pore radii are defined as r_min and r_max, respectively, and the pore fractal dimensions D_f in two and three dimensions are taken as 0 < D_f < 2 and 0 < D_f < 3, respectively.

Differentiation of Eq. (40) yields the number of pores with a scale distribution between radius r and r + dr:

$$- {\text{d}}N = D_{f} r_{\max 0}^{{D_{f} }} r^{{ - (D_{f} + 1)}} {\text{d}}r$$

(41)

According to Eq. (40), the total number of pores N_t is given by:

$$N_{t} = (r_{\max 0} /r_{\min 0} )^{{D_{f} }}$$

(42)

Dividing Eq. (41) by Eq. (42), the probability density function of the pore size distribution in fractal porous media can be obtained as:

$$- {\text{d}}N/N_{t} = D_{f} r_{\min 0}^{{D_{f} }} r^{{ - (D_{f} + 1)}} {\text{d}}r = f(r){\text{d}}r$$

(43)

According to fractal theory, the Sierpinski carpet model can be used to determine the fractal dimension of the pores [35]:

$$D_{f} = d - \frac{{\ln (\phi_{0} )}}{{\ln (r_{\min 0} /r_{\max 0} )}}$$

(44)

where the parameter d is the Euclidean dimension. In the two (or three) dimensional space, the parameter should be set to 2 (or 3). In this paper, we assume that the capillary radius does not vary along the flow direction; thus, the Euclidean dimension is set to d = 2. The relationship between the porosity and fractal dimension of fractal porous media is obtained by Eq. (44):

$$\phi_{0} = (r_{\min 0} /r_{\max 0} )^{{D - D_{f} }}$$

(45)

The cross section of the pores is approximated as a circle, and its total area is determined according to the fractal scalar law of the pores [34]:

$$A_{p} = N_{t} \int_{{r_{\min 0} }}^{{r_{\max 0} }} {\pi r^{2} } f(r){\text{d}}r = \int_{{r_{\min 0} }}^{{r_{\max 0} }} {\pi r^{2} D_{f} } r_{\max 0}^{{D_{f} }} r^{{ - (D_{f} + 1)}} {\text{d}}r$$

(46)

Substituting Eq. (45) into Eq. (46) can induce the effective area of the representative element volume (REV):

$$A_{p} = \frac{{D_{f} }}{{2 - D_{f} }}\pi r_{\max 0}^{2} (1 - \phi_{0} )$$

(47)

The representative element volume (REV) area A and the representative capillary length L are as follows [32]:

$$A = \frac{{A_{p} }}{{\phi_{0} }} = \frac{{D_{f} }}{{2 - D_{f} }}\pi r_{\max 0}^{2} \frac{{1 - \phi_{0} }}{{\phi_{0} }}$$

(48)

$$L = \sqrt A$$

(49)

According to fractal theory [35], the length of the curved capillary L_τ should satisfy the following equation:

$$L_{\tau } = (2r)^{{1 - D_{T} }} L^{{D_{T} }}$$

(50)

where D_T is the tortuous fractal dimension corresponding to the two-dimensional (1≦D_T < 2) or three-dimensional (1≦D_T < 3) space. A larger value of parameter D_T indicates a more tortuous capillary. In this paper, the Euclidean dimension is set as 2, and the parameters are between 1 and 2. Yu and Cheng [34] suggested that D_T can be expressed as:

$$D_{T} = 1 + \frac{{\ln \overline{\tau }}}{{\ln [L/(2\overline{r})]}}$$

(51)

where

$$\left\{ {\begin{array}{*{20}l} {\frac{L}{{2\overline{r}}} = \frac{{D_{f} - 1}}{{\sqrt {D_{f} } }}\sqrt {\frac{1 - \phi }{{4\phi }}\frac{\pi }{{2 - D_{f} }}} \frac{{r_{\max } }}{{r_{\min } }}} \hfill \\ {\overline{\tau } = \frac{1}{2}\left[ \begin{gathered} 1 + \frac{1}{2}\sqrt {1 - (r_{\min } /r_{\max } )^{{2 - D_{f} }} } \hfill \\ + \frac{{\sqrt {[1 - \sqrt {1 - (r_{\min } /r_{\max } )^{{2 - D_{f} }} } ]^{2} + \frac{1}{4}[1 - (r_{\min } /r_{\max } )^{{2 - D_{f} }} ]} }}{{1 - \sqrt {1 - (r_{\min } /r_{\max } )^{{2 - D_{f} }} } }} \hfill \\ \end{gathered} \right]} \hfill \\ \end{array} } \right.$$

(52)

If the aperture ratio ζ = r_min/r_max is reasonably determined, the fractal dimension of pores and tortuosity can be accurately determined by using Eqs. (44) and (52), respectively. Otherwise, substituting Eq. (45) into Eq. (52), we obtain:

$$\left\{ {\begin{array}{*{20}l} {\frac{L}{{2\overline{r}}} = \frac{{D_{f} - 1}}{{\sqrt {D_{f} } }}\sqrt {\frac{1 - \phi }{{4\phi }}\frac{\pi }{{2 - D_{f} }}} \phi_{0}^{{\frac{1}{{D_{f} - 2}}}} } \hfill \\ {\overline{\tau } = \frac{1}{2}\left[ {1 + \frac{1}{2}\sqrt {1 - \phi_{0} } + \frac{{\sqrt {(1 - \sqrt {1 - \phi_{0} } )^{2} + \frac{{1 - \phi_{0} }}{4}} }}{{1 - \sqrt {1 - \phi_{0} } }}} \right]} \hfill \\ \end{array} } \right.$$

(53)

For the convenience of derivation, we define:

$$C_{f} = \frac{{3 - D_{f} + D_{T} }}{{2 - D_{f} }},\alpha_{{{\text{pf}}}} = \frac{{2 - D_{f} }}{{3 - D_{f} + D_{T} }},\beta_{{{\text{pf}}}} = 2 - \left( {1 - \frac{2}{{\ln S_{h} }}} \right)(1 - S_{h} ),C_{{{\text{pf}}}} = \frac{{1 - D_{f} + D_{T} }}{{2 - D_{f} }}.$$

When the pressure drop is ∆p, the flow rate q(r) of the fluid through the capillary with radius r and length L_τ in the porous medium satisfies the modified Hagen–Poiseuille equation [34]:

$$q(r) = \frac{\pi }{8}\frac{{r^{4} }}{{\mu_{m} }}\frac{\Delta p}{{L_{\tau } }}$$

(54)

where μ_m is the fluid viscosity and the subscript m is the movable fluid (m = g for the gas phase and m = mw for the movable water phase). The total flow rate in the pore medium is given by:

$$\begin{gathered} Q = N_{t} \int_{{r_{\min 0} }}^{{r_{\max 0} }} {q(r)f(r){\text{d}}r} = \int_{{r_{\min 0} }}^{{r_{\max 0} }} {\frac{{\pi r^{4} }}{{8\mu_{m} }}\frac{\Delta p}{{(2r)^{{1 - D_{T} }} L^{{D_{T} }} }}D_{f} r_{\max 0}^{{D_{f} }} r^{{ - (D_{f} + 1)}} {\text{d}}r} \hfill \\ { = }\frac{1}{{2^{{4 - D_{T} }} }}\frac{\Delta p}{{\mu_{m} L^{{D_{T} }} }}\frac{{D_{f} }}{{3 - D_{f} + D_{T} }}(1 - \phi_{0}^{{C_{f} }} )\pi r_{\max 0}^{{3 + D_{T} }} \hfill \\ \end{gathered}$$

(55)

According to Eq. (55) and Darcy's law, in the absence of hydrate, the permeability K₀ of the sediments is given by:

$$K_{0} = \frac{{\alpha_{{{\text{pf}}}} }}{{2^{{4 - D_{T} }} L^{{D_{T} - 1}} }}\frac{{\phi_{0} }}{{1 - \phi_{0} }}(1 - \phi_{0}^{{C_{f} }} )r_{\max 0}^{{1 + D_{T} }}$$

(56)

According to Eqs. (48)–(49), Eq. (56) can be simplified as:

$$K_{0} = \frac{{\alpha_{{{\text{pf}}}} }}{{2^{{4 - D_{T} }} }}\left( {\frac{{\pi D_{f} }}{{2 - D_{f} }}} \right)^{{\frac{{1 - D_{T} }}{2}}} (1 - \phi_{0}^{{C_{f} }} )\left( {\frac{{\phi_{0} }}{{1 - \phi_{0} }}} \right)^{{\frac{{1 + D_{T} }}{2}}} r_{\max 0}^{2}$$

(57)

1.2 Permeability model of wetting and non-wetting phases for sediments in the absence of hydrates

All capillaries of radius r ≦ r_c are assumed to be completely saturated with the wetting fluid (such as water), while capillaries of size r ≥ r_c are occupied only by the non-wetting fluid (such as gas) at a given capillary pressure value. The saturation of wetting fluid is given by [32]:

$$S_{w} = \frac{{\int_{{r_{\min 0} }}^{{r_{c} }} {\pi r^{2} ( - dN)} }}{{\int_{{r_{\min 0} }}^{{r_{\max 0} }} {\pi r^{2} ( - dN)} }} = \frac{{(r_{c}^{{2 - D_{f} }} - r_{\min 0}^{{2 - D_{f} }} )}}{{(r_{\max 0}^{{2 - D_{f} }} - r_{\min 0}^{{2 - D_{f} }} )}}$$

(58)

The effective pressure at the critical capillary radius r_c can be expressed as $p = 2\sigma \cos \theta /r_{c}$, where σ is the surface tension of the wetting phase and θ is the liquid–solid contact angle. Then, Eq. (58) can be rewritten as:

$$S_{w} = \left[ {\left( {\frac{2\sigma \cos \theta }{{pr_{\max 0} }}} \right)^{{2 - D_{f} }} - \phi_{0} } \right]/(1 - \phi_{0} )$$

(59)

Assuming that the incompressible fluid is in steady and laminar flow in the capillary, according to the Hagen–Poiseuille equation, the wetting and non-wetting phase volume flow rates Q_w and Q_nw, respectively, are given by:

$$\begin{gathered} Q_{w} = N_{t} \int_{{r_{\min 0} }}^{{r_{c} }} {q(r)f(r){\text{d}}r} = \int_{{r_{\min 0} }}^{{r_{c} }} {\frac{{\pi r^{4} }}{{8\mu_{w} }}\frac{{\Delta p_{w} }}{{(2r)^{{1 - D_{T} }} L^{{D_{T} }} }}D_{f} r_{\max 0}^{{D_{f} }} r^{{ - (D_{f} + 1)}} {\text{d}}r} \hfill \\ { = }\frac{\pi }{{2^{{4 - D_{T} }} }}\frac{{\Delta p_{w} }}{{\mu_{w} L^{{D_{T} }} }}\frac{{D_{f} r_{\max 0}^{{D_{f} }} }}{{3 - D_{f} + D_{T} }}(r_{c}^{{3 - D_{f} + D_{T} }} - r_{\min 0}^{{3 - D_{f} + D_{T} }} ) \hfill \\ \end{gathered}$$

(60)

$$\begin{gathered} Q_{nw} = N_{t} \int_{{r_{c} }}^{{r_{\max 0} }} {q(r)f(r){\text{d}}r} = \int_{{r_{c} }}^{{r_{\max 0} }} {\frac{{\pi r^{4} }}{{8\mu_{nw} }}\frac{{\Delta p_{nw} }}{{(2r)^{{1 - D_{T} }} L^{{D_{T} }} }}D_{f} r_{\max 0}^{{D_{f} }} r^{{ - (D_{f} + 1)}} {\text{d}}r} \hfill \\ { = }\frac{\pi }{{2^{{4 - D_{T} }} }}\frac{{\Delta p_{nw} }}{{\mu_{nw} L^{{D_{T} }} }}\frac{{D_{f} r_{\max 0}^{{D_{f} }} }}{{3 - D_{f} + D_{T} }}(r_{\max 0}^{{3 - D_{f} + D_{T} }} - r_{c}^{{3 - D_{f} + D_{T} }} ) \hfill \\ \end{gathered}$$

(61)

According to Eqs. (60), (61) and Darcy's law, the effective permeability of the wetting phase K_w and non-wetting K_nw is written as:

$$K_{w} = \frac{\pi }{{2^{{4 - D_{T} }} }}\frac{{\phi S_{w} }}{{A_{p} L^{{D_{T} - 1}} }}\frac{{D_{f} r_{\max 0}^{{D_{f} }} }}{{3 - D_{f} + D_{T} }}(r_{c}^{{3 - D_{f} + D_{T} }} - r_{\min 0}^{{3 - D_{f} + D_{T} }} )$$

(62)

$$K_{nw} = \frac{\pi }{{2^{{4 - D_{T} }} }}\frac{{\phi S_{nw} }}{{A_{p} L^{{D_{T} - 1}} }}\frac{{D_{f} r_{\max 0}^{{D_{f} }} }}{{3 - D_{f} + D_{T} }}(r_{\max 0}^{{3 - D_{f} + D_{T} }} - r_{c}^{{3 - D_{f} + D_{T} }} )$$

(63)

According to Eqs. (43)–(57), Eqs. (62), (63) are, respectively, rewritten as follows:

$$K_{w} = \frac{{\alpha_{{{\text{pf}}}} S_{w} }}{{2^{{4 - D_{T} }} }}\left( {\frac{{\pi D_{f} }}{{2 - D_{f} }}} \right)^{{\frac{{1 - D_{T} }}{2}}} \left( {\frac{{\phi_{0} }}{{1 - \phi_{0} }}} \right)^{{\frac{{1 + D_{T} }}{2}}} \left\{ {[(1 - \phi_{0} )S_{w} + \phi_{0} ]^{{C_{f} }} - \phi_{0}^{{C_{f} }} } \right\}r_{\max 0}^{2}$$

(64)

$$K_{nw} = \frac{{\alpha_{{{\text{pf}}}} S_{nw} }}{{2^{{4 - D_{T} }} }}\left( {\frac{{\pi D_{f} }}{{2 - D_{f} }}} \right)^{{\frac{{1 - D_{T} }}{2}}} \left( {\frac{{\phi_{0} }}{{1 - \phi_{0} }}} \right)^{{\frac{{1 + D_{T} }}{2}}} \left\{ {1 - [(1 - \phi_{0} )S_{w} + \phi_{0} ]^{{C_{f} }} } \right\}r_{\max 0}^{2}$$

(65)

1.3 Stress-dependent permeability of HBS with a universal growth pattern

In the presence of hydrates, considering the particle arrangement of the maximum effective porosity, the effective porosity is substituted into Eqs. (57) and (64), (65), and the relative permeability of HBS ($k_{h}$), the wetting phase ($k_{h}^{w}$) and the non-wetting phase ($k_{h}^{nw}$) are written as:

$$k_{h} = \frac{{K_{h} }}{{K_{0} }}{ = }\frac{{[1 - (1 - S_{h} )^{{C_{f} }} \phi_{0}^{{C_{f} }} ]}}{{1 - \phi_{0}^{{C_{f} }} }}\left[ {\frac{{(1 - S_{h} )(1 - \phi_{0} )}}{{1 - (1 - S_{h} )\phi_{0} }}} \right]^{{\frac{{3 + D_{T} }}{2}}}$$

(66)

$$k_{h}^{w} = \frac{{K_{w} }}{{K_{h} }} = S_{w} \frac{{[(1 - \phi )S_{w} + \phi ]^{{C_{f} }} - \phi^{{C_{f} }} }}{{1 - (1 - S_{h} )^{{C_{f} }} \phi^{{C_{f} }} }}\frac{{1 - (1 - S_{h} )\phi }}{{(1 - S_{h} )(1 - \phi )}}$$

(67)

$$k_{h}^{nw} = \frac{{K_{nw} }}{{K_{h} }} = S_{nw} \frac{{1 - [(1 - \phi_{0} )S_{w} + \phi_{0} ]^{{C_{f} }} }}{{1 - (1 - S_{h} )^{{C_{f} }} \phi_{0}^{{C_{f} }} }}\frac{{1 - (1 - S_{h} )\phi_{0} }}{{(1 - S_{h} )(1 - \phi_{0} )}}$$

(68)

Ignoring the influence of saturation S_h on r_c and considering the attenuation effect of the sediment on the permeability and the correction of the effective pressure on the pore size, Eq. (14) is substituted into Eqs. (57) and (64), (65) to obtain the stress-dependent absolute permeability for HBS ($K_{h}$), the wetting phase ($K_{h}^{w}$) and the non-wetting phase ($K_{h}^{nw}$), respectively:

$$\begin{aligned} K_{h} & = \frac{{\alpha_{{{\text{pf}}}} }}{{2^{{4 - D_{T} }} }}\left( {\frac{{\pi D_{f} }}{{2 - D_{f} }}} \right)^{{\frac{{1 - D_{T} }}{2}}} \left[ {1 - \left( {\frac{{\phi_{0} + \varepsilon_{v} }}{{1 + \varepsilon_{v} }}} \right)^{{C_{f} }} (1 - S_{h} )^{{C_{f} }} } \right] \\ & \quad \cdot \left[ {\frac{{(\phi_{0} + \varepsilon_{v} )(1 - S_{h} )}}{{1 + \varepsilon_{v} - (\phi_{0} + \varepsilon_{v} )(1 - S_{h} )}}} \right]^{{\frac{{1 + D_{T} }}{2}}} r_{\max 0}^{2} \eta^{4} (1 - S_{h} )^{N} \\ \end{aligned}$$

(69)

$$\begin{aligned} K_{h}^{w} & = \frac{{\alpha_{{{\text{pf}}}} S_{w} }}{{2^{{4 - D_{T} }} }}\left( {\frac{{\pi D_{f} }}{{2 - D_{f} }}} \right)^{{\frac{{1 - D_{T} }}{2}}} \left[ {\frac{{(\phi_{0} + \varepsilon_{v} )(1 - S_{h} )}}{{1 + \varepsilon_{v} - (\phi_{0} + \varepsilon_{v} )(1 - S_{h} )}}} \right]^{{\frac{{1 + D_{T} }}{2}}} \\ & \quad \cdot \left\{ {\left[ {\frac{{(1 - \phi_{0} )S_{w} + (\phi_{0} + \varepsilon_{v} )}}{{1 + \varepsilon_{v} }}} \right]^{{C_{f} }} - \left( {\frac{{\phi_{0} + \varepsilon_{v} }}{{1 + \varepsilon_{v} }}} \right)^{{C_{f} }} } \right\}r_{\max 0}^{2} \eta^{4} (1 - S_{h} )^{N} \\ \end{aligned}$$

(70)

$$\begin{aligned} K_{h}^{nw} & = \frac{{\alpha_{{{\text{pf}}}} S_{nw} }}{{2^{{4 - D_{T} }} }}\left( {\frac{{\pi D_{f} }}{{2 - D_{f} }}} \right)^{{\frac{{1 - D_{T} }}{2}}} \left[ {\frac{{(\phi_{0} + \varepsilon_{v} )(1 - S_{h} )}}{{1 + \varepsilon_{v} - (\phi_{0} + \varepsilon_{v} )(1 - S_{h} )}}} \right]^{{\frac{{1 + D_{T} }}{2}}} \\ & \quad \cdot \left\{ {1 - \left[ {\frac{{(1 - \phi_{0} )S_{w} + (\phi_{0} + \varepsilon_{v} )}}{{1 + \varepsilon_{v} }}} \right]^{{C_{f} }} } \right\}r_{\max 0}^{2} \eta^{4} (1 - S_{h} )^{N} \\ \end{aligned}$$

(71)

where N is the permeability attenuation index.

1.4 Stress-dependent permeability model of HBS with various hydrate growth patterns

With a pressure drop ∆p, the flow rate equations of PF-hydrate and WC-hydrate are as follows [16]:

$$v_{{{\text{pf}}}} = \frac{\Delta p}{{4\mu_{m} L_{\tau } }}\left[ {(r_{h}^{2} - r^{2} ) + (r_{m}^{2} - r_{h}^{2} )\frac{{\ln (r/r_{h} )}}{{\ln (r_{m} /r_{h} )}}} \right]$$

(72)

$$\begin{array}{*{20}c} {v_{{{\text{wc}}}} = \frac{ - \Delta p}{{\mu_{m} L_{\tau } }}\frac{{r^{2} - r_{m}^{2} }}{4},} & {0 < r \le r_{m} } \\ \end{array}$$

(73)

Integrating Eqs. (72) and (73), the volume flow rates of PF-hydrate and WC-hydrate in a single capillary, respectively, are:

$$q_{{{\text{pf}}}} = \int_{{r_{h} }}^{{r_{w} }} {2\pi rv_{\text{pf}} {\text{d}}r} = \frac{{\pi \Delta p(r_{m}^{4} - r_{m}^{2} r_{h}^{2} )}}{{4\mu_{m} L_{\tau } }} - \frac{{\pi \Delta p(r_{m}^{2} - r_{h}^{2} )}}{{8\mu_{m} L_{\tau } }}\left[ {1 + \frac{1}{{\ln (r_{m} /r_{h} )}}} \right]$$

(74)

$$q_{{{\text{wc}}}} = \int_{0}^{{r_{m} }} {2\pi rv_{{{\text{wc}}}} {\text{d}}r} = \frac{{\pi \Delta pr_{m}^{4} }}{{8\mu_{m} L_{\tau } }}$$

(75)

According to Eqs. (74) and (75), the total volume flow rates of PF-hydrate and WC-hydrate are, respectively, given by:

$$\begin{gathered} Q_{{{\text{pf}}}} = N_{t} \int_{{r_{\min 0} }}^{{r_{\max 0} }} {q_{\text{pf}} f(r)} {\text{d}}r = r_{\max 0}^{{D_{f} }} \int_{{r_{\min 0} }}^{{r_{\max 0} }} {q_{\text{pf}} D_{f} } r^{{ - (D_{f} + 1)}} {\text{d}}r \hfill \\ { = }\frac{{\pi \Delta pD_{f} r_{\max 0}^{{D_{f} }} }}{{2^{{4 - D_{T} }} \mu_{m} L^{{D_{T} }} }}\int_{{r_{\min 0} }}^{{r_{\max 0} }} {r^{{D_{T} - D_{f} - 2}} \left\{ \begin{gathered} 2(r - \delta )^{4} - 2S_{h} (r - \delta )^{2} r^{2} - \hfill \\ [(r - \delta )^{2} - S_{h} r^{2} ]^{2} [1 + \frac{1}{{\ln [(r - \delta )/(\sqrt {S_{h} } r)]}}] \hfill \\ \end{gathered} \right\}{\text{d}}r} \hfill \\ \end{gathered}$$

(76)

$$Q_{{{\text{wc}}}} = N_{t} \int_{{r_{\min 0} }}^{{r_{\max 0} }} {q_{{{\text{wc}}}} f(r)} {\text{d}}r = r_{\max 0}^{{D_{f} }} \int_{{r_{\min 0} }}^{{r_{\max 0} }} {\frac{{\pi \Delta p(r - \delta_{{{\text{wc}}}} - \delta_{w} )^{4} }}{{8\mu_{m} L_{\tau } }}D_{f} } r^{{ - (D_{f} + 1)}} {\text{d}}r$$

(77)

$$\delta_{w} = a_{1} re^{{ - a_{2} r}} (\Delta p)^{{ - a_{3} }} \mu_{rw}$$

(78)

where $\delta_{{{\text{wc}}}} = (1 - \sqrt {1 - S_{h} } )r$, δ_w is the water film thickness, the parameters a₁, a₂, and a₃ are constants, and μ_rw is the viscosity of the residual water. When the water film thickness δ_w is ignored, according to Eqs. (14), (76)–(77) and Darcy's law, the stress-dependent permeability of HBS with pore-filling and wall-coating patterns can be written as:

$$K_{{{\text{pf}}}} = \frac{{\alpha_{{{\text{pf}}}} \beta_{{{\text{pf}}}} }}{{2^{{4 - D_{T} }} }}\left( {\frac{{\pi D_{f} }}{{2 - D_{f} }}} \right)^{{\frac{{1 - D_{T} }}{2}}} \left[ {1 - \left( {\frac{{\phi_{0} + \varepsilon_{v} }}{{1 + \varepsilon_{v} }}} \right)^{{C_{f} }} } \right]\left( {\frac{{\phi_{0} + \varepsilon_{v} }}{{1 - \phi_{0} }}} \right)^{{\frac{{1 + D_{T} }}{2}}} r_{\max 0}^{2} \eta^{4} (1 - S_{h} )^{1 + N}$$

(79)

$$K_{{{\text{wc}}}} = \frac{{\alpha_{{{\text{pf}}}} }}{{2^{{4 - D_{T} }} }}\left( {\frac{{\pi D_{f} }}{{2 - D_{f} }}} \right)^{{\frac{{1 - D_{T} }}{2}}} \left[ {1 - \left( {\frac{{\phi_{0} + \varepsilon_{v} }}{{1 + \varepsilon_{v} }}} \right)^{{C_{f} }} } \right]\left( {\frac{{\phi_{0} + \varepsilon_{v} }}{{1 - \phi_{0} }}} \right)^{{\frac{{1 + D_{T} }}{2}}} r_{\max 0}^{2} \eta^{4} (1 - S_{h} )^{2 + N}$$

(80)

The stress-dependent permeability of HBS with grain-cementing pattern is given by:

$$K_{{{\text{gc}}}} = \frac{{\pi \alpha_{\text{pf}} }}{{2^{{4 - D_{T} }} }}\left( {\frac{{D_{f} }}{{2 - D_{f} }}} \right)^{{\frac{{1 - D_{T} }}{2}}} \left[ {\frac{1}{{\alpha (H_{2} )^{2} }}\frac{{\phi_{0} + \varepsilon_{v} }}{{(1 - \phi_{0} )}}} \right]^{{\frac{{1 + D_{T} }}{2}}} \left[ {1 - \left( {\frac{{\phi_{0} + \varepsilon_{v} }}{{1 + \varepsilon_{v} }}} \right)^{{C_{f} }} } \right]r_{\max 0}^{{3 + D_{T} }} \eta^{4} (1 - S_{h} )^{2 + N}$$

(81)

and its derivation is shown in Appendix 2.

Appendix 2: Derivation of stress-dependent permeability for HBS with grain-cementing hydrates

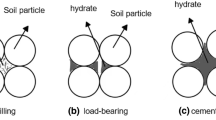
Figure 

Fig. 13

Schematic diagram of particle arrangement for maximum effective porosity

13 shows a representative element volume (REV) of the particle arrangement for maximum effective porosity, and the area of particles is πd²/4; thus, the area A_REV can be expressed as:

$$A_{REV} = \frac{{\pi \overline{d}^{2} }}{{4(1 - \phi_{0} )}}$$

(82)

where the average diameter of particles is defined as $\overline{d}$. If the pore is equivalent to a circle, the maximum pore area can be written as:

$$A_{p}^{\max } = \pi r_{\max 0}^{2} = A_{REV} - \frac{{\pi \overline{d}^{2} }}{4} = \frac{{\pi \overline{d}^{2} \phi_{0} }}{{4(1 - \phi_{0} )}}$$

(83)

According to the geometric relationship, the maximum pore radius and the average particle diameter are related by:

$$r_{\max 0} = \frac{{\overline{d}}}{2}\sqrt {\frac{{\phi_{0} }}{{1 - \phi_{0} }}}$$

(84)

In the following derivation, the diameter d is the particle diameter corresponding to the distribution of pore radius r. According to the geometric relationships, the area of REV (A_REV), the area of pore space (A_p) and the area of hydrate (A_h) are, respectively:

$$A_{REV} = (d + h_{cr} )^{2}$$

(85)

$$A_{p} = (d + h_{cr} )^{2} - \frac{\pi }{4}d^{2}$$

(86)

$$A_{h} = S_{h} A_{p} = S_{h}\left[(d + h_{cr} )^{2} - \frac{\pi }{4}d^{2}\right]$$

(87)

Figure 

Fig. 14

Simplified diagram of intergranular cementation of hydrates in sediments

14 shows the simplified diagram of intergranular cementation of hydrates in sediments. According to the geometric relationship of GC hydrates:

$$B = \sqrt {d^{2} - (d - h_{cr}^{max} + h_{cr} )^{2} }$$

(88)

$$A_{h} = B(h_{cr}^{{{\text{max}}}} + h_{cr} + d) - 2arcsin\left( \frac{B}{d} \right)d^{2}$$

(89)

Assuming that the cementation thickness h_cr is proportional to the pore size, such as the radius r, i.e., $h_{cr} \user2{(}r\user2{)} \propto r$ and $h_{cr}^{max} \user2{(}r\user2{)} \propto r$, we obtain:

$$\begin{array}{*{20}c} {h_{cr} (r) = \frac{r}{{r_{\max 0} }}H_{{1}} ;} & {h_{cr}^{{{\text{max}}}} (r) = \frac{r}{{r_{\max 0} }}H_{{2}} } \\ \end{array}$$

(90)

Meanwhile, the cementation thickness is assumed to be related to the growth law $f_{{{\text{grow}}}}^{h} (S_{h} )$:

$$\begin{array}{*{20}c} {\gamma = \gamma_{0} f_{{{\text{grow}}}}^{h} (S_{h} ),} & {\beta = \beta_{0} f_{{{\text{grow}}}}^{h} (S_{h} )} \\ \end{array}$$

(91)

$$h_{cr}^{{{\text{max}}}} (r) = h_{cr} (r) + \beta d = (\gamma + \beta )d$$

(92)

where β₀ and γ₀ are the ratios of pore spacings H₁ and H₂ to the particle size at the maximum hydrate saturation, respectively. Arranging Eqs. (88), (90)–(92), we can deduce that:

$$B = \sqrt {1 - \left[ {1 - \left( {\frac{r}{{r_{\max 0} }}} \right)\beta } \right]^{2} } d = kd$$

(93)

$$d = \frac{r}{{r_{\max } }}\frac{{H_{{2}} }}{\beta + \gamma }$$

(94)

$$H_{1} = \frac{\gamma }{\beta + \gamma }H_{{2}}$$

(95)

When B/d is small, the second-order Taylor expansion form is:

$$\arcsin \left( \frac{B}{d} \right) = \arcsin \left( {\sqrt {1 - \left[ {1 - \left( {\frac{r}{{r_{\max } }}} \right)\beta } \right]^{2} } } \right) \approx k + \frac{{k^{3} }}{6}$$

(96)

Combining Eqs. (87)–(92), we obtain:

$$S_{h} \left[ {(1 + \gamma )^{2} - \frac{\pi }{4}} \right] = k(2\gamma + \beta + 1) - 2\left( {k + \frac{{k^{3} }}{6}} \right)$$

(97)

We note that the area equality of Eqs. (87) and (89) cannot be strictly guaranteed, and we therefore ignore the geometry of GC hydrates here. The effective pore area $A_{p}^{e}$ of a single capillary bundle and the total pore area $A_{p}^{t}$ of the REV are given by:

$$A_{p}^{e} = (1 - S_{h} )\left[ {(1 + \gamma )^{2} - \frac{\pi }{4}} \right]\left( {\frac{1}{\beta + \gamma }} \right)^{2} \left( {\frac{r}{{r_{\max 0} }}} \right)^{2} (H_{{2}} )^{2} = \alpha (1 - S_{h} )\left( {\frac{r}{{r_{\max 0} }}} \right)^{2} (H_{{2}} )^{2}$$

(98)

$$\alpha = \left[ {(1 + \gamma )^{2} - \frac{\pi }{4}} \right]\left( {\frac{1}{\beta + \gamma }} \right)^{2}$$

(99)

$$\begin{aligned} A_{p}^{t} & = (1 - S_{h} )\alpha (H_{{2}} )^{2} \int_{{r_{\min 0} }}^{{r_{\max 0} }} {D_{f} r_{\max 0}^{{D_{f} }} \left( {\frac{r}{{r_{\max 0} }}} \right)^{2} r^{{ - (D_{f} + 1)}} {\text{d}}r} \\ & = (1 - S_{h} )\alpha (H_{{2}} )^{2} \frac{{D_{f} }}{{2 - D_{f} }}\left[ {1 - \left( {\frac{{r_{\min 0} }}{{r_{\max 0} }}} \right)^{{2 - D_{f} }} } \right] \\ \end{aligned}$$

(100)

According to the definition of Eq. (100) and porosity, the total cross-sectional area A of REV is given by:

$$A = \frac{{A_{p}^{t} }}{{\phi_{0} (1 - S_{h} )}} = \alpha (H_{{2}} )^{2} \frac{{D_{f} }}{{2 - D_{f} }}\frac{{1 - \phi_{0} }}{{\phi_{0} }}$$

(101)

According to the effective pore radius ($r = \sqrt {1 - S_{h} } r_{0}$), combining Eqs. (49), (55), (101) and Darcy's law, the fractal capillary bundle permeability of hydrate-bearing sediments (HBS) with a grain-cementing pattern is given by:

$$K_{{{\text{gc}}}} = (1 - S_{h} )^{2} \frac{{\pi \alpha_{\text{pf}} }}{{2^{{4 - D_{T} }} }}\left( {\frac{{D_{f} }}{{2 - D_{f} }}} \right)^{{\frac{{1 - D_{T} }}{2}}} \left[ {\frac{1}{{\alpha (H_{{2}} )^{2} }}\frac{{\phi_{0} }}{{1 - \phi_{0} }}} \right]^{{\frac{{1 + D_{T} }}{2}}} (1 - \phi_{0}^{{C_{f} }} )r_{\max 0}^{{3 + D_{T} }}$$

(102)

Considering the effect of the permeability attenuation index and effective pressure on sediments, Eq. (14) is substituted into Eq. (102) to obtain the stress-dependent permeability expression of HBS with a grain-cementing pattern:

$$K_{{{\text{gc}}}} = \frac{{\pi \alpha_{\text{pf}} }}{{2^{{4 - D_{T} }} }}\left( {\frac{{D_{f} }}{{2 - D_{f} }}} \right)^{{\frac{{1 - D_{T} }}{2}}} \left[ {\frac{1}{{\alpha (H_{2} )^{2} }}\frac{{\phi_{0} + \varepsilon_{v} }}{{(1 - \phi_{0} )}}} \right]^{{\frac{{1 + D_{T} }}{2}}} \left[ {1 - \left( {\frac{{\phi_{0} + \varepsilon_{v} }}{{1 + \varepsilon_{v} }}} \right)^{{C_{f} }} } \right]r_{\max 0}^{{3 + D_{T} }} \eta^{4} (1 - S_{h} )^{2 + N}$$

(103)

Appendix 3: Derivation of cementation thickness

In Fig. 14, according to the area relationship:

$$\left[ {(\overline{d} + h_{cr} )^{2} - \frac{\pi }{4}\overline{d}^{2} } \right] - 8\left[ {\frac{{\frac{{h_{cr} }}{2} + \frac{{h_{cr}^{\max } }}{2} + \frac{{\overline{d}}}{2}}}{2}\frac{B}{2} - \frac{{\arcsin \left( {\frac{B}{{\overline{d}}}} \right)}}{4}\overline{d}^{2} } \right] = (1 - S_{h} )\pi r_{\max 0}^{2}$$

(104)

Rearranging Eq. (104), the maximum pore diameter is related to the average particle diameter as follows:

$$r_{\max 0} = \sqrt {\frac{1}{{\pi (1 - S_{h} )}}\left[ {(1 + \gamma )^{2} - \frac{\pi }{4} - k(2\gamma + \beta - 1) + \frac{{k^{2} }}{3}} \right]} \overline{d} = \omega \overline{d}$$

(105)

$$k = \sqrt {1 - \left( {1 - \frac{{3 - D_{p} }}{{4 - D_{p} }}\beta } \right)^{2} }$$

(106)

Substituting Eqs. (48), (49) and (105) into (102), the following can be obtained:

$$K_{{{\text{gc}}}} = \frac{{\alpha_{{{\text{pf}}}} \pi }}{{2^{{4 - D_{T} }} L^{{D_{T} - 1}} }}\frac{{1 - \phi^{{C_{f} }} }}{{\alpha (H_{2} )^{2} }}\frac{\phi }{1 - \phi }(\omega \overline{d})^{{3 + D_{T} }}$$

(107)

Substituting Eqs. (49) and (84) into (107) yields the permeability expression of HBS with a grain-cementing pattern:

$$K_{{{\text{gc}}}} = (1 - S_{h} )^{2} \frac{{\pi \alpha_{pf} }}{{2^{{4 - D_{T} }} }}\left[ {\frac{{\overline{d}^{2} }}{{\alpha (H_{2} )^{2} }}} \right]^{{\frac{{1 + D_{T} }}{2}}} \left( {\frac{{D_{f} }}{{2 - D_{f} }}} \right)^{{\frac{{1 - D_{T} }}{2}}} \left( {\frac{{\phi_{0} }}{{1 - \phi_{0} }}} \right)^{{\frac{{1 + D_{T} }}{2}}} (1 - \phi_{0}^{{C_{f} }} )\omega^{{3 + D_{T} }} \overline{d}^{2}$$

(108)

Combining Eqs. (9), (57), and (84), it is derived that:

$$K_{{{\text{gc}}}} = \frac{{\alpha_{{{\text{pf}}}} }}{{2^{{6 - D_{T} }} }}\left( {\frac{{\pi D_{f} }}{{2 - D_{f} }}} \right)^{{\frac{{1 - D_{T} }}{2}}} \left[ {1 - \phi_{0}^{{C_{f} }} (1 - S_{h} )^{{C_{f} }} } \right]\left[ {\frac{{\phi_{0} (1 - S_{h} )}}{{1 - \phi_{0} (1 - S_{h} )}}} \right]^{{\frac{{3 + D_{T} }}{2}}} \overline{d}^{2}$$

(109)

Comparing Eqs. (108) and (109), the maximum cementation thickness $H_{cr}^{\max }$ of GC hydrates is obtained as:

$$H_{cr}^{\max } = H_{2} = \sqrt {\frac{\pi }{\alpha }\frac{{\phi_{0} }}{{1 - \phi_{0} }}} \left\{ {4(1 - S_{h} )^{2} \frac{{1 - \phi_{0}^{{C_{f} }} }}{{1 - \phi_{0}^{{C_{f} }} (1 - S_{h} )^{{C_{f} }} }}\left[ {\frac{{1 - \phi_{0} (1 - S_{h} )}}{{\phi_{0} (1 - S_{h} )}}\omega^{2} } \right]^{{\frac{{3 + D_{T} }}{2}}} } \right\}^{{\frac{1}{{1 + D_{T} }}}} \overline{d}$$

(110)

Equation (110) can be abbreviated as $H_{2} = \delta \overline{d}$, where δ is defined as follows:

$$\delta = \sqrt {\frac{\pi }{\alpha }\frac{{\phi_{0} }}{{1 - \phi_{0} }}} \left\{ {4(1 - S_{h} )^{2} \frac{{1 - \phi_{0}^{{C_{f} }} }}{{1 - \phi_{0}^{{C_{f} }} (1 - S_{h} )^{{C_{f} }} }}\left[ {\frac{{1 - \phi_{0} (1 - S_{h} )}}{{\phi_{0} (1 - S_{h} )}}\omega^{2} } \right]^{{\frac{{3 + D_{T} }}{2}}} } \right\}^{{\frac{1}{{1 + D_{T} }}}}$$

(111)

Assuming that the particles have the same volume (area) shape factor, the fractal dimension D_p of the pore radius with the GC-growth pattern is equal to the fractal dimension D_s of the particle size:

$$D_{p} = D_{s} = 3 - \frac{{\log [1 - (1 - S_{h} )\phi_{0} ]}}{{\log (d_{\min 0} /d_{\max 0} )}}$$

(112)

The median particle size and the mean radius are considered to be approximately equal, $r_{50} = \overline{r}$ and $d_{50} = \overline{d}$. By definition:

$$r_{50} = \overline{r} = \int_{0}^{1} {r{\text{d}}s} = \frac{{3 - D_{p} }}{{4 - D_{p} }}r_{\max 0}$$

(113)

The sorting coefficient δ_p and the variation coefficient C_p are the parameters reflecting the uniformity of the pores. A smaller value of δ_p corresponds to better uniformity. Considering the continuity of the pore radius distribution:

$$\delta_{p} = r_{\max 0} \sqrt {\frac{{3 - D_{p} }}{{5 - D_{p} }} - \left( {\frac{{3 - D_{p} }}{{4 - D_{p} }}} \right)^{2} }$$

(114)

The variation coefficient C_p is the ratio of the sorting coefficient (standard deviation) to the mean radius and can be written as:

$$C_{p} = \frac{{\delta_{p} }}{{\overline{r}}} = \sqrt {\frac{{(4 - D_{p} )^{2} }}{{(3 - D_{p} )(5 - D_{p} )}} - 1}$$

(115)

The median (or average) hydrate cementation thickness can be written as:

$$H_{50} = \overline{H} = \frac{{\overline{r}}}{{r_{\max 0} }}H_{{2}} = \frac{{3 - D_{p} }}{{4 - D_{p} }}\delta \overline{d}$$

(116)

Finally, the ratio of the average cementation thickness to the median particle size can be obtained:

$$R_{cr} = \frac{{H_{cr}^{\max } }}{{d_{50} }} = \left\{ {\begin{array}{*{20}l} {0,} \hfill & {S_{h} \le S_{h}^{i0} } \hfill \\ {\frac{{3 - D_{p} }}{{4 - D_{p} }}\frac{{r_{\max 0} }}{{\overline{r}}}\delta ,} \hfill & {S_{h}^{i0} < S_{h} \le S_{h}^{f} } \hfill \\ {(R_{cr} )|_{{S_{h} = S_{h}^{f} }} ,} \hfill & {S_{h} > S_{h}^{f} } \hfill \\ \end{array} } \right.$$

(117)