1 Introduction

Shrinkage and crack formation in drying fine sediments dramatically alter the mechanical and hydraulic properties and may lead to engineering problems for many geotechnical structures, such as slopes [16, 40], embankment dams [13], and landfills [36]. Also, drying-induced polygonal cracks are commonly observed on ceramic [3], gel–sol [12] and paintings [15]. At pore-scale, desiccation cracks are driven by air invasion, thus tending to initiate at larger pores, while the non-uniform deformation resulting from subsurface constraint or surface flaws will promote local pore enlargement and the propagation of desiccation cracks [35, 41].

The formation of desiccation cracks depends on many controlling factors, e.g. soil compressibility [10], subsurface friction [18], and sample thickness [26]. Recent studies also show the impact of drying temperature [32, 38], fluid salinity [27] and wet–dry cycles [9, 37]. Researchers have tried to engineer soils with higher crack resistance by adding fibres [14], lime [33] and polymers [30]. Experimental studies on desiccation cracks typically adopt digital cameras to continuously monitor the drying surface and quantify two-dimensional (2D) displacement fields employing digital image correlation analysis [22, 35]. 2D images have been combined to measure the three-dimensional (3D) volume of drying kaolinite through photogrammetry [28]. However, digital cameras can only characterise the surface deformation, with limited information obtained about the internal deformation.

X-ray computed tomography (CT) can non-destructively characterise the 3D soil deformation by collecting multiple scans without disturbing the loading processes. Previous researchers have mainly adopted this technique in coarse-grained soils to investigate strain localisation [5, 21], particle breakage [44], internal erosion [31], etc. The high image resolution resolves the 3D morphology of individual particles and even the contact area between particles. Thus, image analysis can quantify the evolution of particle kinematics, contact fabric and particle morphology [1, 7]. However, X-ray CT resolution is typically limited to a few microns and thus can hardly resolve silt or clay particles.

Recent studies have adopted X-ray CT to monitor the drying-induced shrinkage and desiccation crack formation in fine-grained soils [14, 24, 41]. However, these studies provided limited information on the 3D soil deformation and its relationship with crack formation. Fine-grained soils could have internal textures due to the inclusions of silt or sand grains. The internal textures in X-ray images could be adopted to measure the 3D soil deformation through two primary approaches. First, digital volume correlation (DVC) considers the cross-correlation between neighbouring monitor windows to determine the 3D strain fields [34]. This method has been applied in many materials, e.g. bones [17], aluminium alloy [11], and sandstone [29]. The 3D deformation of sensitive clay during triaxial loading has been quantified with DVC [2]. However, DVC relies on sufficient image texture, typically generated by sample inhomogeneity at pixel-scale, to ensure successful tracking of searching windows. Second, the distributed markers within the samples could be tracked between sequential scans, based on their morphology and location information, and then used to measure 3D deformation [20]. For instance, mica particles embedded in a kaolinite matrix were tracked to monitor the sample deformation under 1D compression [23].

This paper adopts X-ray CT to characterise the 3D deformation of drying kaolinite samples. Entrained gas bubbles are adopted as markers to track their displacement in sequential scans. The 3D surfaces of individual bubbles are extracted to determine their location, size and shape parameters. The morphology evolution of individual bubbles during drying will be examined to understand the impact on bubble tracking. We develop an artificial neural network (ANN) algorithm to link bubbles based on their position and morphology information. Different combinations of bubble parameters are examined regarding their suitability for bubble tracking. We determine 3D displacement fields and strain fields with tracked bubbles to show internal deformation during drying and its relationship with desiccation cracks.

2 Drying tests and bubble shape analysis

2.1 Drying and scanning procedure

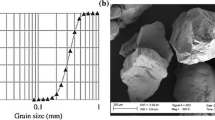
This study adopted an air-floated kaolinite with a liquid limit LL = 48% and a specific surface of 34 m2/g (Active Minerals, Georgia). The same kaolinite was used to investigate the formation of internal desiccation cracks under confinement [41]. Figure 1 shows the soil water retention curve (SWRC) measured using a dew point hygrometer WP4C [4] having a resolution of 50 kPa, resulting in large scattering for < 1 MPa. In WP4C tests, the specimens were prepared by mixing kaolinite with deionised and deaired water at a water content of 1.2 × LL. The SWRC indicates an air-entry value (AEV) of ~ 2.0 MPa, occurring at a water content of 24%, which was determined at the intersection point of two trend lines, as indicated in Fig. 1. The presence of large gas bubbles entrained by the soil matrix has limited impact on the SWRC and AEV, as they depend on the clay matrix.

Fig. 1
figure 1

Soil water retention curve of the tested kaolinite determined by WP4C dew point potentiometer (AEV, air-entry value). Using data from Zhao and Santamarina [9]

Full size image

For desiccation crack tests, kaolinite powder was mixed with deionised water to an initial water content of 151% (i.e. ~ 3 × LL). The slurry was poured into two plastic containers, giving the two test samples, each of 32.7 mm internal diameter, and allowed to dry at room temperature to achieve a water content of about 52%. The average thickness of each sample was about 4.0 mm. The gas bubbles, which are much larger than that the fine soil particles, were entrained within the saturated kaolinite matrix and may result from trapped or dissolved air during the sample preparation. These bubbles were used as the markers to monitor the deformation of each kaolinite sample during the drying process. An initial X-ray CT scan showed that most gas bubbles were spherical. We gently applied a torsional shear on the sample surface before scan 1 (i.e., S1, which was performed at a water content of 51.8%) with a flat plate to obtain irregular shaped gas bubbles (their details are revealed later in the paper). This surface torsional treatment resulted in unevenness of the soil surface. Also, some kaolinite soil adhering to the plate was taken from the sample on removing the plate.

The two samples were dried, one at room temperature and the other inside a 60 °C oven. Five high-resolution X-ray CT scans (i.e. scans S1 to S5) were collected during the drying processes of the kaolinite samples for targeted intermediary water contents that reduced from ~ 50 to 0%, as shown in Fig. 2. The water content of the sample dried at room temperature reduced by about 2.1%/h. The 60 °C sample dried much faster. Hence, after reaching the targeted water content, the container with the 60 °C sample was removed from the oven, covered with a plastic lid, and stored at room temperature to minimise further sample drying (soil deformation) occurring before performing the X-ray CT scans (S2 to S5) on both samples at approximately the same water content values. So, the drying of the 60 °C sample occurred with a stepwise water content reduction with increasing drying period as shown in Fig. 2. Note that it was not our intention to homogenise the moisture distribution for the 60 °C sample during its standing time before each scan, although when the sample container is closed, further evaporation and homogenisation are unavoidable, as shown by recent nuclear magnetic resonance measurements [42]. The two samples in the present study were scanned for each of five targeted reducing water contents using a TESCAN CoreTOM X-ray scanner at 160 keV. Both samples were scanned with the plastic lid on for maintaining their water content. Each scan took approx. 30 min to complete. The reconstructed X-ray images have a spatial resolution of 20 μm.

Fig. 2
figure 2

Water content reduction during drying of the two test samples and the X-ray scanning points

Full size image

2.2 Image processing and bubble morphology analysis

This study follows the image processing and shape analysis procedure described in Zhao and Wang [43]. Figure 3a shows a typical horizontal slice of the reconstructed X-ray images. A high grey-value contrast existed between the different materials, i.e. air, plastic (container) and kaolinite. Three primary image processing steps were conducted to extract the entrained air bubbles from the 3D greyscale images: (i) a median filter with the size of 3 × 3 × 3 voxels was used to reduce image noise (Fig. 3b); (ii) the threshold value between kaolinite and plastic was manually selected from the grey-value histogram (Fig. 4) and then applied for binarization, with kaolinite separated from both air and plastic (Fig. 3c); (iii) individual air bubbles were identified and labelled with unique IDs (Fig. 3d). The 3D view shows that gas bubbles have various size and shape, and tend to be evenly distributed in the sample. The image processing resulted in a 3D voxel matrix for each gas bubble.

Fig. 3
figure 3

Image processing for bubble-entrained kaolinite sample: (a) initial greyscale horizontal slice; (b) de-noising by 3D median filter; (c) segmented image; (d) 3D view of labelled bubbles

Full size image
Fig. 4
figure 4

Histogram of grey value for a typical horizontal slice, indicating different phases and the manually selected threshold to separate kaolinite from plastic and air

Full size image

The marching cubes algorithm was applied to each gas bubble for extracting the smooth triangular surface mesh from the 3D voxel matrix. The extracted bubble surfaces were then analysed to obtain their location and morphology information. The coordinates of the bubble centroids, determined through the average vertex weighted by face area on the surface mesh, employing the Trimesh.centroid algorithm, were used as the reference for displacement calculation. Bubble morphology was quantified with volume (V), surface area (SA), sphericity (SP) and aspect ratio (AR). The surface area of each bubble was estimated as the total area of its triangular surface mesh. To determine the volume of bubbles, we discretised them into tetrahedral elements and conducted a surface integral. This method was confirmed by counting the voxel number in each bubble. Sphericity compares the surface area of a bubble and its volume-equivalent sphere, i.e. \(SP=\sqrt[3]{36\cdot \pi {V}^{2}}/SA\). Aspect ratio compares the lengths of maximum principal dimension a, intermediate principal dimension b, and minimum principal dimension c, i.e. \(AR=(b/a+c/b)/2\). Note that bubbles smaller than 0.001 mm3 (~ 125 voxels) could result in unusual shape parameters (e.g. SP > 1). Hence, they were excluded from the morphology analysis and bubble tracking.

2.3 Bubble morphology evolution

The bubble morphology evolution during drying is briefly described here for the sample dried at room temperature. Figure 5 shows the histogram of the bubble parameters for each of the five scans (S1 to S5). A larger number of bubbles had a smaller volume (80% of them each with volume < 0.02 mm3, equivalent to 2500 voxels), which produced a fractal distribution with a fractal dimension of 0.71. Surface area shows a similar distribution. As the sample dries and shrinks, both bubble volume and surface area continuously reduce, while the cumulative distribution of bubble size remains constant. Bubbles are mostly spherical for SP > 0.8, with AR primarily ranging between 0.6 and 0.9. The change of shape parameters does not have a clear pattern between successive scans.

Fig. 5
figure 5

Cumulative probability distributions of bubble geometry parameters: (a) volume; (b) surface area; (c) sphericity; (d) aspect ratio

Full size image

We manually linked 113 bubbles between scans S1 and S2 to further investigate bubble morphology change during the drying process. Figure 6 compares the size and shape parameters of the selected bubbles whose volume ranged between 0.005 and 0.05 mm3. Bubble volume and surface area reduced slightly from S1 to S2. Although the size-reduction ratio varies, the ranking position of each bubble remained generally consistent between scans, i.e. bubbles of larger volume in S1 tend to have a larger volume in S2. This consistent size ranking indicates that volume and surface area are both suitable parameters for bubble tracking. However, SP has a small variation of between 0.8 and 0.9 in S1, and can have a relatively large reduction (of up to 0.1) in S2. Furthermore, the change of SP tends to be random, producing an inconsistent ranking sequence between S1 and S2. AR shows a similar pattern, but with a slightly larger variation. This inconsistent ranking indicates that shape parameters SP and AR are not appropriate for bubble tracking. It is anticipated that bubble shape evolution is influenced by the relationship between bubble alignment and soil shrinkage direction. Further study is required to investigate the gas bubble deformation during soil shrinkage.

Fig. 6
figure 6

Comparison of geometry parameters for manually linked bubbles between scans S1 and S2 for the sample dried at room temperature. Note: bubbles were ranked using parameters in S1

Full size image

3 ANN bubble tracking

We developed a bubble-tracking algorithm based on artificial neural networks (ANN) which can learn the correlation function from manually paired bubbles. The bubble-tracking algorithm uses the morphology and location information of individual bubbles and involves three major steps: (i) coordinate system unification between different scans; (ii) ANN model training and verification for manually linked bubbles; and (iii) implementation and optimisation of the trained ANN model. Figure 7 shows the flowchart of the ANN-enhanced bubble-tracking procedure. The algorithm is illustrated for the sample dried at room temperature.

Fig. 7
figure 7

Flowchart of ANN tracking model for data preparation, model training and implementation

Full size image

3.1 Coordination system unification

The coordination system is inconsistent between scans since the kaolinite samples were dried outside of the X-ray scanner equipment. A unique coordination system should be adopted to avoid systematic errors during the displacement calculation. We defined the coordination system considering (i) the flat contact surface between the kaolinite sample and its container  (i.e., internal base of container), and (ii) a marker on the container surface, as shown in Fig. 8a. Six randomly selected points along the circumference of the contact surface were used to define the horizontal plane (x–y) (Fig. 8b), with the origin chosen as the centre of the circle defined by the six points. The vector perpendicular to the contact surface was chosen as the z-axis. The y-axis was defined by the line connecting the origin and the centroid of the marker. All bubbles were transferred and rotated according to the unified coordination system. Figure 8c, d compares a series of manually selected bubbles in scans S1 and S2, before and after the coordination system unification. In Fig. 8d, the projections of bubbles on the x–y plane are consistent between S1 and S2, which demonstrates the effectiveness of the coordination system unification.

Fig. 8
figure 8

Coordinate system unification: (a) unique marker and six randomly selected points taken along circumference of soil–container contact surface; (b) the six selected points; (c) manually linked bubbles in S1 and S2 for initial coordination system; (d) manually linked bubbles in S1 and S2 for updated coordination system. Note: disc size in (c) and (d) are proportional to bubble volume

Full size image

3.2 ANN model training and verification

Artificial neural network (ANN) is adopted to link bubbles between successive scans, since the bubble attributes, i.e. location, size, and shape, all change during the drying process. Note that this regression analysis could also be implemented with other deep learning algorithms. Figure 9 shows the architecture of the ANN model having a three-layer structure implemented as the Sequential Model in Keras [8]. The input layer takes the parameter difference of two bubbles in various X-ray scans, ΔXi. Thus, the number of nodes in the input layer is equal to the number of parameters used for bubble tracking, i.e. \(i\in [2, 7]\). The output layer has a single node defining the correlation factor between two bubbles, Y \(\in\) [0, 1]. This study simply adopts one hidden layer with \(n=\mathrm{min}(i, 4)\) nodes since the number of input parameters is relatively small. Ideally, the numbers of hidden layers and the nodes in each one could be determined by optimisation. However, the bubble-tracking task is not a complex problem for the ANN model, and can be well solved with this simple ANN architecture, as shown later. An activation function is adopted to consider the effectiveness of each node, i.e. \(sigmod\left(x\right)=1/(1+\mathrm{exp}\left(-x\right))\).

Fig. 9
figure 9

Structure of the ANN model adopted for bubble tracking

Full size image

The number of unknown weights and bias in the ANN model equals to \((i\times n+n+n\times 1+1)\), which varies between 9 and 37. The weights and bias were determined through back analysis, considering 100 pairs of manually linked bubbles between scans S1 and S2. The trained ANN model was verified with 45 extra pairs of manually linked bubbles. The cross-validation was conducted five times by randomly dividing the 145 pairs into training and testing groups, resulting in a consistently good accuracy. Table 1 shows the performance of nine ANN models employing different groups of the bubble parameters. Group 6 adopts bubble centroid location (X, Y, and Z) and volume, and results in the best performance with the highest mean correlation factor. Another four groups (i.e. groups 1, 2, 3 and 5) show similar mean and standard deviation values of correlation factors. The root-mean-square-error (RMSE) again shows that the Group 6, with bubble location and volume, produced the best performance, with the smallest RMSE for the nine cases investigated.

Table 1 Mean, standard deviation, and root-mean-square-error (RMSE) of correlation factors obtained for nine ANN models with different combinations of bubble parameters
Full size table

3.3 ANN model implementation and optimisation

The ANN model compares randomly selected bubble pairs from different scans. The number of bubbles changes from scan to scan due to the challenge of identifying small bubbles. Thus, m × l correlation factors are estimated from all possible bubble links between two scans with m and l numbers of bubbles, respectively. We developed a ranking system that uniquely links bubbles, as follows. The two bubbles with the highest correlation factor between two scans are linked first. Then, the linked bubbles are removed from the ranking system, and another pair of bubbles with the highest correlation factor are linked from the remaining bubbles. This step is repeated until all bubbles in one scan have been linked. The extra bubbles in another scan are eliminated.

The trained ANN models were applied to link all bubbles between S1 and S2 with 2954 and 2830 bubbles, respectively. Figure 10 shows the cumulative distribution of correlation factors for 2830 linked bubbles. All ANN models with both location and volume information produced a relatively good performance, as shown in Fig. 10a. Among them, the parameter combination of X + Y + Z + V resulted in the best performance, with most correlation factors larger than 0.98. As explained earlier, shape parameters (i.e. SP and AR) are not suitable for bubble tracking, while ANN models perform well to mitigate their impact if both bubble position and size are also considered. However, it is not appropriate to track bubbles based on considering size but not location, and vice versa, as indicated by the low correlation factors in Fig. 10b.

Fig. 10
figure 10

Cumulative distributions of the correlation factors for all linked bubbles considering nine different parameter combinations: (a) combinations giving high correlation factors; (b) combinations with low correlation factors (colour figure online)

Full size image

4 Results

4.1 Suction-induced volume shrinkage and crack formation

The volume of the kaolinite matrix was calculated based on the segmented images excluding the bubbles (Fig. 3c). Note the initial volume of the two samples was different, since some soil adhered to (and was removed with) the plate used for applying torsional treatment on the surface of the deposited samples (see Sect. 2.1). Referring to Fig. 11a, the total clay matrix volume reduced linearly with reducing water content to the AEV, remaining almost constant thereafter for both samples. Assuming a kaolinite density of 2.6 g/cm3, based on soil mass and water content we estimated the kaolinite matrix volume for S1 of the room temperature dried sample as 3.50 cm3, which is comparable to the image processing result of 3.40 cm3. At each scan, we determined the suction value according to the SWRC in Fig. 1 and the void ratio of the kaolinite matrix with segmented images excluding bubbles. Figure 11b indicates the consistent volume shrinkage driven by increasing suction before the AEV, with a deduced compression index (Cc) of 0.33 for both samples. The estimated Cc refers to the clay matrix (not the bulk soil) as it was calculated based on the sample volume excluding air bubbles. Also, we assumed a full saturation before the AEV for Cc evaluation in the suction-driven shrinkage. The deduced Cc (of 0.33) is in-line with the values obtained from oedometer tests on kaolinite, varying from 0.2 to 0.4 [19, 25, 39]. For reducing water content below the AEV, void ratio remains almost constant, but suction dramatically increases as air starts invading the pores.

Fig. 11
figure 11

Evolution of (a) kaolinite matrix volume and (b) void ratio (both computed for excluding gas bubbles) responses for the two samples dried at different temperatures

Full size image

Figure 12 shows typical vertical and horizontal slices of S4 after the formation of desiccation cracks at the interface between the sample and container, and within the sample. Cracks are mostly aligned vertically and propagate horizontally along the interface between the sample bottom and container. The sample undergoes a slight curling, i.e. the soil close to the periphery moves upwards, once the horizontal cracks have detached the kaolinite from the container base. This is probably due to the non-uniform shrinkage along depth after crack formation due to variation in water content, where surface soil contracts more than the lower part [45]. Some cracks originated at the bottom interface and propagated upwards, as marked by arrows in Fig. 12a. Cracks are randomly distributed without polygonal patterns, which indicates the limited friction between the kaolinite and plastic substrate. The plastic container is hydrophobic; thus, air is easier to invade along the soil–container interface. Note that the unevenness of the sample top surface, seen in the central part in Fig. 12a, was originated from the surface torsional treatment during the sample preparation (Sect. 2.1).

Fig. 12
figure 12

Typical (a) vertical and (b) horizontal slices of scan S4 for the sample dried at room temperature. Arrows indicate the cracks originated at the bottom interface

Full size image

4.2 3D displacement field

The displacement field of internal gas bubbles was calculated by comparing the centroid location of the linked bubbles and is illustrated with the sample dried under room temperature. Figure 13 shows the projections of all displacement vectors on the vertical plane (x–z) between successive scans. The bubbles were classified into the sample upper, middle and lower layers, which are represented as green, blue and red, respectively. The bubble displacement was primarily vertical, with negligible horizontal displacement occurring before crack formation (Fig. 13a,b). Vertical displacement reduced with increasing depth (below the sample surface), resulting in the largest displacement occurring at the top central part. For example, between S1 and S2, the average vertical displacement varies from 0.77 mm close to the top surface, to about 0.02 mm close to the container base. As evident in Fig. 13c, significant horizontal displacement occurs between S3 and S4 due to the formation of vertical cracks, with the bubbles marked in the dashed circle moving upwards due to the curling (refer to Fig. 12a). The constriction of the substrate on horizontal displacement is absent, which again shows the limited impact of a hydrophobic substrate. The bubble displacement seems to be limited after the AEV (Fig. 13d).

Fig. 13
figure 13

Vertical projections of displacement field from scans (a) S1 to S2, (b) S2 to S3, (c) S3 to S4, and (d) S4 to S5. Note: colours indicate bubbles in upper (green), middle (blue) and lower (red) layers. Dashed circle in (c) shows the area of bubbles moving upwards (due to sample curling) (colour figure online)

Full size image

Based on their centroid positions, the bubbles were grouped into thin layers, each of 0.2 mm thickness, to further analyse the variation in displacement over depth. The incremental vertical displacement reduced linearly with depth for all scan intervals before the AEV, as shown in Fig. 14a. The slope of this linear relationship is inversely proportional to the vertical strain (\({\varepsilon }_{\mathrm{zz}}\)) and water content reduction occurring before the AEV. The data scattering for S3–S4 and S4–S5 may result from the uneven sample surface profile or non-uniform deformation after the AEV caused by curling and cracking. However, these aspects need to be confirmed with further tests using higher imaging resolution, as the variation is only around several voxels (i.e. < 0.1 mm). The cumulative displacement was also estimated by linking the bubbles in S1 to all following scans. As shown in Fig. 14b, the linear relationship between cumulative displacement and depth rotates around the origin.

Fig. 14
figure 14

Distributions of vertical displacement over depth: (a) incremental displacement; (b) cumulative displacement

Full size image

Figure 15a shows the projection of displacement between S3 and S4 on the horizontal plane (x–y). Major cracks formed close to the container sidewall and induce the horizontal displacement. Cracks with larger width led to higher surrounding displacement, as shown by comparing with Fig. 12b. Most bubbles move towards a shrinkage centre, marked by a grey dot in Fig. 15a. It is anticipated that soil detachment from the container at the lower part (i.e., approximately (x, y) = (−12, −12)) resulted in a larger displacement occurring in this region, such that the shrinkage centre was not in the middle. The horizontal displacement decreased as the bubbles moved closer to the shrinkage centre, indicating a limited friction constraint at the container base. There is no clear difference between the horizontal displacement patterns in the upper, middle and bottom sample layers. Figure 15b shows the average horizontal displacement of individual layers along depth. Again, the relatively uniform pattern across depth indicates a limited substrate constraint.

Fig. 15
figure 15

Horizontal displacement between S3 and S4: (a) horizontal projections; (b) distribution of mean horizontal displacement along depth. Note: colours in (a) indicate bubbles in upper, middle and lower sample layers (green, blue and red, respectively) (colour figure online)

Full size image

4.3 3D strain field

The bubble centroids are used to define tetrahedron elements for calculating the 3D strain fields based on the displacement measurements [6]. A displacement gradient tensor was calculated from the coordinates and displacements of the four vertices defining each tetrahedron element, i.e. one strain tensor was obtained for each tetrahedron element. Here, we show the cumulative strain values calculated by linking the bubbles in S1 to all later scans. Figure 16 shows the cumulative \({\varepsilon }_{zz}\) projected to the vertical and horizontal planes. \({\varepsilon }_{\mathrm{zz}}\) gradually increased to about 0.25 at S4 due to drying-induced shrinkage. The distribution is essentially uniform along the vertical and horizontal directions, although the sample’s centre region tends to have slightly smaller \({\varepsilon }_{\mathrm{zz}}\), as marked by arrows in Fig. 16b. This non-uniform \({\varepsilon }_{\mathrm{zz}}\) may be caused by the irregular top surface of the sample (Fig. 12a). It is unclear what caused the variation in strain fields between S4 and S5, since the soil deformation is limited after the AEV.

Fig. 16
figure 16

Projections of cumulative \({\varepsilon }_{\mathrm{zz}}\) from scan S1 to (a) S2, (b) S3, (c) S4 and (d) S5. Note: compressive strains are positive (colour figure online)

Full size image

The horizontal strain of the sample is quantified based on the deformation along both x- and y-axes, \({\varepsilon }_{xx}\) and \({\varepsilon }_{yy}\), respectively. Figure 17 shows the projections of cumulative \({\varepsilon }_{xx}\), which is much smaller than the cumulative \({\varepsilon }_{\mathrm{zz}}\) (see Fig. 16). Before crack formation, the horizontal strains are tiny, with a mean value of < 0.002 (Fig. 17a,b). Compared to the surrounding area, the sample’s centre region has slightly larger \({\varepsilon }_{xx}\), as marked by arrows in Fig. 17a,b. Uniform volumetric shrinkage occurred inside the sample since \({\varepsilon }_{\mathrm{zz}}\) is slightly smaller in this area. Again, this behaviour could be induced by the unevenness of the sample top surface. Before crack formation, the mean horizontal strain is close to zero, with negative horizontal strain suggesting the distance between bubbles increased slightly. However, the negative strain values reported are close to the resolution of our measurement approach, and further study is needed to confirm the inhomogeneity of horizontal strain. After crack formation, the horizontal strain significantly increases, to a mean value of 0.02 in S4 and S5, and the sample presented a horizontal strain distribution with large variance between –0.06 and 0.1. Horizontal expansions of up to –0.06 strain are typically associated with crack formation. Figure 18 presents the projections of the cumulative \({\varepsilon }_{yy}\), which are similar to the cumulative \({\varepsilon }_{xx}\) shown in Fig. 17.

Fig. 17
figure 17

Projections of cumulative \({\varepsilon }_{xx}\) from S1 to (a) S2, (b) S3, (c) S4 and (d) S5. Note: compressive strains are positive (colour figure online)

Full size image
Fig. 18
figure 18

Projections of cumulative \({\varepsilon }_{yy}\) from S1 to (a) S2, (b) S3, (c) S4 and (d) S5. Note: compressive strains are positive (colour figure online)

Full size image

All strain data points are shown with their height (using the sample container’s flat contact surface as datum) in Fig. 19a,b. The mean cumulative \({\varepsilon }_{\mathrm{zz}}\) is generally uniform with depth for all scans. At any depth, \({\varepsilon }_{\mathrm{zz}}\) has a variation within \(\pm\)0.025. This variation partially arose from the measurement precision, which mainly depends on the bubble inter-distance and the accuracy of bubble location. The mean bubble inter-distance was 45 pixels, while the smallest bubble considered in the method had a diameter of 5 pixels. Thus, a strain error of 0.022 could be generated if the estimated bubble centroid has an offset of even one pixel. Similarly, horizontal strain is uniform with height (depth) and has a variation at given depth; e.g. for S2 and S3, the horizontal strain varied from –0.04 to 0.03. Again, this variation is partially caused by the measurement precision. After crack formation, horizontal strain varied from –0.05 to 0.1, reflecting the impact of horizontal shrinkage.

Fig. 19
figure 19

Comparison of cumulative strain from S1 along sample height: (a) \({\varepsilon }_{\mathrm{zz}}\) variation; (b) \({\varepsilon }_{\mathrm{xx}}\) variation

Full size image

Figure 20 shows the cumulative distributions of \({\varepsilon }_{\mathrm{xx}}\) and \({\varepsilon }_{\mathrm{zz}}\) from S1 for the samples dried at room temperature and 60 °C. Again, \({\varepsilon }_{\mathrm{zz}}\) gradually increased before the AEV, while \({\varepsilon }_{\mathrm{xx}}\) was mainly caused by crack formation around the AEV. The distributions of strain values for the 60 °C sample are similar to those of the sample dried at room temperature. Thus, the drying temperature had insignificant impact, which is mainly due to two reasons. First, the sample thickness is relatively small, so moisture transfer can easily replenish the water evaporation occurring at the top surface for both samples. Second, before performing each scan, the sample dried at 60 °C had a significant time to homogenise (i.e. during the standing period after removal from the drying oven).

Fig. 20
figure 20

Cumulative probability distribution of (a) \({\varepsilon }_{\mathrm{zz}}\) and (b) \({\varepsilon }_{\mathrm{xx}}\) for the samples dried at room temperature (R) and 60° (H) (colour figure online)

Full size image

The precision of strain value could be increased by taking more neighbouring bubbles into the strain calculation, but at the cost of reducing the measurement spatial resolution [20]. For example, the strain error induced by one-pixel offset could be reduced to 0.01 for an increase of mean bubble inter-distance to 100 pixels. However, the effective strain measurement values will be reduced by about 90%. The trade-off between precision and resolution should be considered based on various applications.

5 Conclusion

This study investigated the 3D shrinkage and crack formation inside drying kaolinite samples using X-ray CT. A series of image processing techniques were applied to extract entrained gas bubbles and their location and morphology information. These gas bubbles were adopted as markers to monitor the sample displacements. We developed an artificial neural network (ANN) model to link corresponding bubbles in different scans based on their location and morphology information. The successful tracking of bubbles enabled the measurement of 3D displacement and strain fields.

Bubble morphology changed as the kaolinite matrix shrinks during the drying process. Bubble size has a large variation and reduced almost proportionally to the initial bubble volume during drying, which makes bubble volume and surface area good parameters for bubble tracking. However, shape parameters (e.g. AR and SP) exhibited a low variance and large random change, such that these are not suitable parameters for bubble tracking. However, further research is required to elucidate the mechanisms of changing bubble shape during shrinkage.

Nine ANN models investigated comparing bubble location, size and shape parameters, with both bubble location and size necessary for a good bubble-tracking performance, while adding further shape parameters may reduce the tracking accuracy. The coordinate system unification method developed was shown to be effective in reducing systematic errors for displacement calculation.

The drying kaolinite samples experienced uniform vertical shrinkage before the air-entry value (AEV), which leads to a vertical displacement decreasing linearly along the sample depth. Horizontal displacement was limited before the AEV, and mainly induced by large vertical cracks formed around the AEV. The sample has a uniform horizontal displacement along depth, which could be caused by the limited constraint provided by the hydrophobic (plastic) substrate.

In general, \({\varepsilon }_{\mathrm{zz}}\) was uniformly distributed with a slight variation, probably caused by irregular initial sample geometry. \({\varepsilon }_{xx}\) had a much larger variation associated with desiccation cracks. This study showed limited impact of drying temperature on the strain fields for the thin samples investigated (and long homogenisation period between scans for the 60 °C sample). Trade-off between precision and resolution should be considered for marker-based strain evaluation methods.

Air bubbles in fine-grained sediments can affect their behaviour, including the formation of desiccation cracks, such that the use of bubble tracking to evaluate internal deformation may be limited. However, it is worth noting that air bubbles occur naturally in soils, including shallow ocean sediments. Moreover, the methodology developed in this study can be applied to various embedded markers, such as addition of silt and sand particles.