1 Introduction

Unsaturated soils generally exist widespread in nature, particularly in the surface soil layers, embankment, seasonal areas, arid and semiarid areas, or locations with a deep groundwater table. Moreover, climate change in recent years has had a significant influence on the variation in water content of soils due to the evaporation and infiltration, and soils are thus subjected to a cyclic change between saturated and unsaturated states. In the interest of unsaturated soil, the soil–water characteristic curve (SWCC) plays an important role in predicting the hydraulic conductivity, shear strength, water storage function, and soil structure stability [12, 52, 53, 57, 61, 94, 95]. Because of the strong relationship between the SWCC and thermal-hydro-mechanical properties of soils, it is crucial and attractive to study the variation in SWCC and to be able to quantify the changes in thermal-hydro-mechanical behavior of unsaturated soils.

The soil–water characteristic curve naturally is representative of the potential energy variation in fluid phases and is usually described as the relationship between the soil suction and water content or saturation degree. Because the water retention test is an expensive and time-consuming procedure, several empirical models were proposed to plot the SWCC based on a limited number of test points [11, 19, 27, 82]. These models were also reviewed and discussed in detail in some other research [40, 74, 90]. In recent years, huge attention was paid to the study of SWCC variation with different factors such as density [55, 81, 92], temperature [15, 56, 73], compaction state [51], stress history [23], initial water content [8], adsorption [2], pore-size distribution [20], hydraulic hysteresis [37, 89], and soil structure [78, 93]. Among these above-mentioned factors, the initial density and temperature are of more interest to geotechnical engineers, which have a relatively significant influence on the SWCC.

The effect of soil density or porosity is one of the most important and attractive factors to be investigated when the soil density has a strong linkage with the mechanical properties of unsaturated soils [45]. It is generally known that a small change in the soil density is sufficient to lead to a significant change in the hydro-mechanical behavior of soils. Yet, the soil density is relatively sensitive to variation in the stress state of soils and environmental conditions. In this regard, the study of the density effect on the SWCC becomes a much more attractive problem and is the topic of universal interest. Several researchers thus have attempted to model the effect of soil density on the SWCCs [21, 22, 60, 67, 68, 77, 87, 96, 98]. Several of these existing models have been generated as a result of the present SWCC revision, which includes the introduction of one or more void ratio-dependent fitting parameters. Several other SWCC models were created by taking into account the variation in water content as a function of the void ratio. However, even with the same water content, it was found that variations in void ratio led to changes in SWCC [4, 41, 65, 88]. Using the soil shrinkage curve to predict SWCC with density change is another method that some researchers have used [35, 68]. However, models based on this method are typically empirical, with equations constructed based on limited data sets for a certain soil type. Moreover, these models frequently necessitate a large number of fitting parameters.

On the other hand, there are numerous geo-environmental situations where unsaturated soils relate to elevated temperature variation such as climate change [47], energy geo-structures [59, 60, 72], nuclear waste disposal [31, 97], geothermal energy storage system [85], high voltage cables buried in the ground [71]. In all such emerging problems, the effect of temperature is required to consider in thermal-hydro-mechanical behavior analysis of unsaturated soils. The need for studying the effect of temperature on the SWCC is therefore increased today. There are several efforts devoted to investigating the effect of temperature on the SWCC of unsaturated soils [15, 28, 43, 65, 66, 69]. However, several drawbacks and limitations among existing models were found and thus need to be improved. Firstly, almost all existing models considered the effect of temperature on SWCC by focusing only on the surface tension variation while other important factors (contact angle, void ratio, particle size) were neglected. This limitation might cause inaccurate results when predicting the change of SWCC with temperature. In fact, the variation in air–water surface tension with temperature was found to be small as compared to the fluctuation of air–water contact angle [5, 75]. Recently, several other authors have also dedicated efforts to investigate the effect of temperature on SWCC through considering the variation in air–water contact angle [28, 83]. Secondly, not much attention was paid to the effect of the thermal expansion of soil and water on the matric suction when the temperature is increased. However, the thermal expansion of particles and water can alter particle orientation and soil structure, potentially affecting suction dramatically. Another significant limitation is that limited consideration was given to the effect of the thermal volume change on matric suction and SWCC. This shortcoming is probably due to the fact that the relationship between temperature and the void ratio was not established well. Consequently, the temperature change continues to remain a great challenge in the field of geo-environment engineering when the effect of temperature was not addressed thoroughly.

Finally, most published research is devoted separately to the effect of density or temperature on the hydro-mechanical behavior of unsaturated soils. However, there is now broad scope where soils are exposed to both deformations and thermal conditions [24, 25, 34, 58, 65, 99]. It is therefore necessary to propose an SWCC model considering the combined effect of initial density and temperature to be able to quantify the change in the behavior of unsaturated soils under both mechanical and thermal conditions.

In that interest, this study presents an analytical model to quantify the combined effect of temperature and initial density on the SWCC. In the first step, the effect of initial density on SWCC is studied while the effect of temperature is presented in the second step. Then, two steps are combined to produce a comprehensive model for predicting the coupled effect of initial density and temperature on the SWCC. On the basis of collected twenty-two data sets of thermal volume change, this study also developed further a theoretical correlation between void ratio and temperature that is directly related to soil plasticity. The validity of the proposed model is verified by comparison with several sets of published experimental data. The proposed method is applicable to predict the single effect of temperature and initial density as well as the combined effect of both on the SWCC.

2 Modeling the effect of initial density on the SWCCs

2.1 Initial density-dependent SWCC model

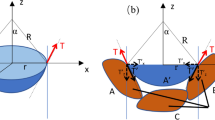
Arya and Paris [3] discovered that the soil–water characteristic curve and the particle-size distribution curve had a similar shape based on test findings on diverse materials. The particle-size distribution curve can then be converted into a soil–water characteristic curve by utilizing an equivalent pore-size distribution curve (PSDC), according to one theory. The cumulative particle-size distribution curve can theoretically be divided into multiple segments, each representing an equivalent pore volume with the same radii (Fig. 1).

Fig. 1
figure 1

Conceptual model for translation between SWCC and PSDC

Full size image

Furthermore, if the solid volume in each assemblage can be approximated by uniform-size spheres specified by the mean particle radius, then the number of spherical particles corresponding to the solid mass in the ith particle range will be ni. Meanwhile, the volume of the resulting pores can be approximated by uniform-size cylindrical capillary tubes whose radii are related to the mean particle radius. The solid volume and void volume per unit sample mass can be expressed as follows:

$$V_{s} = \frac{{m_{s} }}{{\rho_{s} }} = \frac{4}{3}\pi R_{i}^{3} \times n_{i}$$
(1a)
$$V_{v} = e \cdot \frac{{m_{s} }}{{\rho_{s} }} = \pi r_{i}^{2} l_{i}$$
(1b)
$$l_{i} = 2R_{i} \times n_{i}$$
(1c)

where Vs = solid volume per unit sample mass, Vv = void volume per unit sample mass, ms = solid mass, ρs = particle density, e = initial void ratio, li = total pore length, ri = pore radius, Ri = soil particle radius, ni = number of soil particles.

The total pore length in a natural soil material, however, is determined by the shapes and sizes of the particles. Because the actual soil particles are non-spherical, each soil particle contributes a length greater than the diameter of an equivalent sphere [60]. As a result, the number of spherical particles with radius Ri needed to trace the whole pore length in natural soil material will be greater than \(n_{i}\). The required particle number therefore will be \(n_{i}^{\delta }\), in which δ \(\ge 1\), and the total pore length must be \(l_{i} = 2R_{i} \times n_{i}^{\delta }\). Replacing \(l_{i}\) back into Eq. (1b), the void volume considering the effect of actual particle sizes, shapes, and orientations can be re-written:

$$V_{v} = e \cdot \frac{{m_{s} }}{{\rho_{s} }} = 2\pi R_{i} \times r_{i}^{2} \times n_{i}^{\delta }$$
(2)

where δ = a calibrated factor that allows minimizing the limitation of spherical particle assumption.

By dividing Eqs. (2) and (1a) side by side, the relationship between pore radius (ri) and particle radius (Ri) can be derived as follows:

$$r_{i} = R_{i} \sqrt {\frac{{2e \cdot n_{i}^{1 - \delta } }}{3}}$$
(3)

In another way, the soil suction can be estimated by the Laplace–Young equation based on the thermodynamic equilibrium theory [28, 62]:

$$\psi = u_{a} - u_{w} = \frac{{2\sigma_{s} \cdot \cos \alpha }}{{r_{i} }}$$
(4)

where \(\psi\) = matric suction, \(\sigma_{s}\) = air–water surface tension, ua = air pore pressure, uw = water pore pressure, α = air–water contact angle, cosα = wetting coefficient. It should be noted that depending on whether the soil state changes along a path of wetting or drying, the contact angle may change. The proposed model, however, uses the reference SWCC to predict how SWCC would change with temperature and density. This indicates that by using the reference SWCC, the impact of hydraulic hysteresis on the soil's retention behavior was incorporated into the proposed model.

Replacing Eqs. (3) in (4), the initial void ratio-dependent function of matric suction is given:

$$\frac{\psi }{{\rho_{w} .g}} = \frac{{2\sigma_{s} \cdot \cos \alpha }}{{R_{i} \cdot \rho_{w} \cdot g}}\sqrt {\frac{3}{{2e_{i} \cdot n_{i}^{1 - \delta } }}}$$
(5)

It is noted that the effect of pore size and sensitivity of density change on suction was considered in Eq. (5) through the parameter ni, in which soils with larger pores require a smaller number of particles and vice versus.

Considering a reference case with the initial void ratio e0, the expression for matric suction at reference state is:

$$\frac{{\psi_{{e_{0} }} }}{{\rho_{w} .g}} = \frac{{2\sigma_{s} \cdot \cos \alpha }}{{R_{i} \cdot \rho_{w} \cdot g}}\sqrt {\frac{3}{{2e_{0} \cdot [(n_{i} )_{{e_{0} }} ]^{1 - \delta } }}}$$
(6)

where \(e_{0}\) = reference initial void ratio, \((n_{i} )_{{e_{0} }}\) = number of soil particles corresponding to reference initial void ratio, \(\psi_{{e_{0} }}\) = matric suction at reference initial void ratio.

Considering an arbitrary case with the initial void ratio ei, the expression of corresponding matric suction is:

$$\frac{{\psi_{{e_{i} }} }}{{\rho_{w} .g}} = \frac{{2\sigma_{s} \cdot \cos \alpha }}{{R_{i} \cdot \rho_{w} \cdot g}}\sqrt {\frac{3}{{2e_{i} \cdot [(n_{i} )_{{e_{i} }} ]^{1 - \delta } }}}$$
(7)

where ei = arbitrary initial void ratio, \((n_{i} )_{{e_{i} }}\) = number of soil particles at an arbitrary initial void ratio, \(\psi_{{e_{i} }}\) = matric suction at arbitrary initial void ratio.

Dividing side by side of Eqs. (7) to Eq. (6) gives:

$$\frac{{\psi_{{e_{i} }} }}{{\psi_{{e_{0} }} }} = \sqrt {\frac{{e_{0} }}{{e_{i} }} \cdot \left[ {\frac{{(n_{i} )_{{e_{0} }} }}{{(n_{i} )_{{e_{i} }} }}} \right]^{1 - \delta } }$$
(8)

If the considered overall volume of a soil sample remains constant (V = Vs + Vv), the void volume component (Vv) and solid volume component (Vs) will change as the density of the soil sample changes. Variations in the number of soil particles are required because the pore volume is represented by an assemblage of particles. The physical link between void ratio and solid volume can be used to determine the number of soil particles in a soil sample as follows:

$$(n_{i} )_{{e_{0} }} = \frac{V}{{V_{{{\text{si}}}} }} \times \frac{1}{{1 + e_{0} }}$$
(9a)
$$(n_{i} )_{{e_{i} }} = \frac{V}{{V_{{{\text{si}}}} }} \times \frac{1}{{1 + e_{i} }}$$
(9b)

where V = considered total volume of a soil sample, Vsi = volume of a spherical particle.

Dividing Eqs. (9b) to (9a) gives the ratio of soil particle number corresponding to two different initial void ratios:

$$\frac{{(n_{i} )_{{e_{0} }} }}{{(n_{i} )_{{e_{i} }} }} = \frac{{1 + e_{i} }}{{1 + e_{0} }}$$
(10)

Substituting Eqs. (10) into Eq. (8) and rearranging give:

$$\psi_{{e_{i} }} = \psi_{{e_{0} }} \times \sqrt {\frac{{e_{0} }}{{e_{i} }} \cdot \left( {\frac{{1 + e_{i} }}{{1 + e_{0} }}} \right)^{1 - \delta } }$$
(11)

in which the matric suction, \(\psi_{{e_{0} }}\), can be obtained from the reference SWCC at reference initial void ratio using the equation of Fredlund and Xing [19]as follows:

$$S_{{e_{0} }} = \frac{1}{{\left\{ {\ln \left( {2.7127 + [\psi_{{e_{0} }} /a]^{n} } \right)} \right\}^{m} }}$$
(12)

where \(S_{{e_{0} }}\) = the degree of saturation for the reference SWCC; a, m, n = fitting parameters.

It should be emphasized that, depending on the defined problem and available data, the derived equation can be used to calculate with both the initial void ratio (suction is zero) and the current void ratio. This is because the current void ratio can be linked to the initial void ratio through a volume change equation that defines the relationship between void ratio and suction. As can be seen, the suggested equation provides a direct relationship between suction evolution and void ratio, and its applicability is suitable for both states of void ratio while the current void ratio is frequently used in existing models. Additionally, because the suction was connected to the change in initial void ratio, as a result, the proposed model already incorporated the effect of stress condition into account. Consolidation tests can be used to determine how the initial void ratio of soils may change under various stress states. Then, by adjusting the initial void ratio, it can use the proposed model to apply for any stress condition.

The SWCCs at an arbitrary initial void ratio can be predicted by combining Eqs. (11) and (12) as follows:

$$\left\{ {\begin{array}{*{20}c} {S_{{e_{i} }} = S_{{e_{0} }} = \frac{1}{{\ln \left( {2.7127 + [\psi_{{e_{0} }} /a]^{n} } \right)^{m} }}} \\ {\psi_{{e_{i} }} = \psi_{{e_{0} }} \times \sqrt {\frac{{e_{0} }}{{e_{i} }} \cdot \left( {\frac{{1 + e_{i} }}{{1 + e_{0} }}} \right)^{1 - \delta } } } \\ \end{array} } \right.$$
(13)

It is noted that the proposed model (Eq. 13) involves only a new calibrated parameter δ, which can be treated as a specific constant for a soil type. The parameter δ can be obtained by performing calibration from two SWCC tests or using the following equation:

$$\delta = \frac{1}{N}\mathop \sum \limits_{1}^{N} \left( {1 - {\text{log}}\,_{{\frac{{1 + e_{i} }}{{1 + e_{0} }}}}^{{\left( {\frac{{\psi_{{e_{i} }} }}{{\psi_{{e_{0} }} }}} \right)^{2} \times \frac{{e_{i} }}{{e_{0} }}}} } \right)$$
(14)

where N = number of measured data pairs for the same degree of saturation.

2.2 Performance of the proposed model

It can be observed that the proposed model has four fitting parameters, in which three fitting parameters (a, n, m) are used to control the shape of reference SWCC, and the fitting parameter δ is used to control the effect of initial density. Therefore, at least the measured data of two different SWCC tests are required to calibrate the model. One test data are used to obtain the fitting parameters (a, n, m) for a reference SWCC, and the second test data for a different initial void ratio are used to get the calibrated fitting δ. When all four fitting parameters are obtained, the calibrated model can then be used to predict the SWCC at an arbitrary initial void ratio. The procedure of the proposed model application in predicting the SWCC variation with soil density is presented by a flow chart in Fig. 2.

Fig. 2
figure 2

Flow chart for the procedure of proposed model application

Full size image

In order to check the validity of the analytical model, selected test data sets must include the measured data of at least three SWCCs for three different initial void ratios. To illustrate the calibration procedure as well as to verify the performance of the proposed model, two independent sets of laboratory test data are presented in this section. It should be noted that the success of the calibration procedure, as well as prediction performance of the proposed model, is assessed by using the average relative error (ARE), which is expressed as follows:

$${\text{ARE}} = \frac{{\left| {S_{{{\text{predicted}}}} - S_{{{\text{measured}}}} } \right|}}{{S_{{{\text{measured}}}} }}$$
(15)

where, \(S_{{{\text{predicted}}}}\) = predicted degree of saturation, \(S_{{{\text{measured}}}}\) = measured degree of saturation.

The first selected data set is from Salager et al. [68, 70], which was obtained from clayey sand samples with a broad range of initial densities ranging from 1.35 to 1.95 g/cm3. The tested soils have a plasticity index of 9.5 and specific gravity (Gs) equals 2.65. Figure 3a shows the test data of SWCCs for five different values of the initial void ratio. It should be noted that the measured data of the loosest sample corresponding to an initial void ratio of 1.01 were considered as the reference state. A reference SWCC is then plotted using Eq. (12), in which the reference fitting parameters were as follows: a = 10 kPa, m = 1.0, n = 0.7. It can be observed that the reference SWCC passes through almost all test points and the calibration is therefore reliable and successful. The calibrated parameter is then calculated using the second SWCC test data, which corresponds to an initial void ratio of 0.86. The calibrated SWCCs for five distinct values ranging from 5 to 65 are shown in Fig. 3b. The calibrated SWCC with a value of 35 generally provides the best match with the measured data, with an average relative error of only 5.2%. Following the selection of δ = 35, four fitting parameters of the proposed model are now determined, which allows using Eq. (13) to predict the SWCC at an arbitrary initial void ratio. Figure 3c shows a comparison between predicted and measured SWCCs for three different initial void ratios (ei = 0.68, 0.55, 0.44). It can be observed that all three predicted SWCCs are in good agreement with measured data. The average relative error of the proposed model among 48 test points is 2.87%. It is also interesting to note that both analytical and experimental models agree that dense soils generally produce higher SWCC than loose soil. Figure 3d demonstrates the measured against the calculated degree of saturation. The results indicate that the proposed model has an excellent performance in predicting the variation in SWCC with initial density. All three different states of SWCC including reference calibrated and predicted curves show high satisfaction with measured data.

Fig. 3
figure 3figure 3

Performance of proposed model with clayey sand (measured data source from Salager et al., [68]: a measured data and reference SWCC; b calibration curves with different values of δ; c comparison between predicted and measured SWCCs with δ = 35; d calculated against measured degree of saturation

Full size image

Another test data set from Huang et al. [33] is selected to verify further the performance of the proposed model. In this case, the silty sand was tested for six different initial void ratios ranging from 0.426 to 0.525. The fundamental properties of the tested soil are that it has a specific gravity of 2.8 and a plasticity index of 5.6. It is noted that the SWCC test data with an initial void ratio of 0.525 are used to obtain the reference SWCC. A reference SWCC was plotted using Eq. (12) as shown in Fig. 4a. To obtain the calibrated SWCC, the second test data set of the SWCC with an initial void ratio of 0.513 is used as shown in Fig. 4b. The calibrated SWCC with a value of δ = 55 is found to have an excellent match to the measured data, with an average relative error of 4.1%. It should be emphasized that the reference and calibrated curves demonstrate an excellent match with test data, and the calibration procedure, therefore, was reliable and effective. For this data set, the following four fitting parameters were found to be the best: a = 65 kPa, m = 1.2, n = 2.1, δ = 55. The proposed model after calibration can then be used to find the SWCC at an arbitrary initial void ratio. It is noted that only the reference void ratio is set because the proposed model predicts SWCC with density based on the reference SWCC. When the void ratio decreases from 0.525 to 0.426, the appropriate SWCCs are obtained in Fig. 4c. It can also be observed that the SWCC results predicted by the proposed model are in good agreement with measured data for all four different void ratios (ei = 0.49, 0.474, 0.454, and 0.426). The average relative error of the proposed model among 68 test points is 4.2%. Besides, it is also interesting to note that the effect of initial density on SWCC becomes more significant only for the suction range larger than the air entry value but smaller than 1000 kPa. Soils reaching a critical void ratio at the range of high suction can be considered as a reason behind this trend. The measured against calculated degree of saturation is shown in Fig. 4d, which indicates that the proposed model is successful in predicting the variation in SWCC with initial density.

Fig. 4
figure 4figure 4

Performance of proposed model with clayey sand (measured data source from Huang et al., 1998): a measured data and reference SWCC; b calibration curves with different values of δ; c comparison between predicted and measured SWCCs with δ = 55; d calculated against measured degree of saturation

Full size image

3 Modeling the effect of temperature on the SWCCs

3.1 General form for the temperature-dependent suction

The effect of initial density on the soil suction was presented in the previous section, which allows considering the changes in the hydro-mechanical state of unsaturated soils. In this section, the effect of temperature on soil suction will be solved so that the changes in the thermo-hydro-mechanical state of unsaturated soils can be described. According to Eq. (5), the change of soil suction depends on five different components: surface tension (σs), air–water contact angle (cos α), particle size (Ri), water density \((\rho_{w} )\), and void ratio (ei). The total differential of matric suction therefore can be expressed in involving the five independent variables as follows:

$$\frac{\partial \psi }{{\partial T}} = \frac{\psi }{{\sigma_{s} }}\frac{{\partial \sigma_{s} }}{\partial T} + \frac{\psi }{{{\text{cos}}\,\alpha }}\frac{{\partial \,{\text{cos}}\,\alpha }}{\partial T} - \frac{\psi }{{R_{i} }}\frac{{\partial R_{i} }}{\partial T} - \frac{\psi }{{e_{i} }}\frac{{\partial e_{i} }}{\partial T} - \frac{\psi }{{\rho_{w} }}\left( {\frac{{\partial \rho_{w} }}{\partial T}} \right)$$
(16)

It is noted that to study the temperature effect on matric suction, many researchers focused mainly on the first term on the right-hand side of Eq. (16) while the following four terms received less attention. In the current study, the temperature-dependent model of matric suction is investigated by incorporating simultaneously all five different terms on the right side of Eq. (16).

As a starting point, the initial temperature state of soils is defined as the reference temperature (\(T_{0}\)). An expression of matric suction at reference temperature can be written as follows:

$$\frac{{\psi_{{T_{0} }} }}{{\rho_{w} \cdot g}} = \frac{{2\sigma_{s0} \cdot \cos \alpha_{0} }}{{R_{0} \cdot \rho_{w0} \cdot g}}\sqrt {\frac{3}{{2e_{0} \cdot n_{i0}^{1 - \delta } }}}$$
(17)

where \(\psi_{{T_{0} }}\) is the matric suction at a reference temperature, \(\sigma_{s0}\) is air–water surface tension at the reference temperature, \(r_{0}\) is particle radius at the reference temperature, \(\alpha_{0}\) is air–water contact angle at the reference temperature, \(e_{0}\) is the initial void ratio of soils at the reference temperature, \(n_{i0}\) = number of soil particles at a reference temperature, \(\rho_{w0}\) = water density at the reference temperature.

And the corresponding matric suction at an arbitrary current temperature (T) can be expressed by:

$$\frac{{\psi_{T} }}{{\rho_{w} \cdot g}} = \frac{{2\sigma_{{{\text{sT}}}} \cdot \cos \alpha_{T} }}{{R_{T} \cdot \rho_{{{\text{wT}}}} \cdot g}}\sqrt {\frac{3}{{2e_{T} \cdot n_{{{\text{iT}}}}^{1 - \delta } }}}$$
(18)

where \(\psi_{T}\) is matric suction at the arbitrary current temperature, \(\sigma_{{{\text{sT}}}}\) is air–water surface tension at the current temperature, \(r_{T}\) is particle radius at the current temperature, \(\alpha_{T}\) is air–water contact angle at the current temperature, \(e_{T}\) is the initial void ratio of soils at the current temperature, \(n_{{{\text{iT}}}}\) is the number of soil particles at the current temperature, \(\rho_{{{\text{wT}}}}\) = water density at the current temperature.

Dividing Eqs. (18) to (17) side by side gives:

$$\psi_{T} = \psi_{{T_{0} }} \times \frac{{\sigma_{sT} }}{{\sigma_{s0} }} \times \frac{{\cos \alpha_{T} }}{{\cos \alpha_{0} }} \times \frac{{R_{0} }}{{R_{T} }} \times \frac{{\rho_{{{\text{wT}}}} }}{{\rho_{w0} }} \times \sqrt {\frac{{e_{0} }}{{e_{T} }} \cdot \left( {\frac{{1 + e_{T} }}{{1 + e_{0} }} \cdot \left[ {1 + \beta_{v} \cdot \Delta T} \right]} \right)^{1 - \delta } }$$
(19a)

It is mentioned that Eq. (19a) can be re-written under a simplified form as follows:

$$\psi_{T} = \psi_{{T_{0} }} \times f_{\sigma } \times f_{\alpha } \times f_{R} \times f_{e} \times f_{\rho }$$
(19b)

where

$$f_{\sigma } = \frac{{\sigma_{{{\text{sT}}}} }}{{\sigma_{s0} }}$$
(20)
$$f_{\alpha } = \frac{{\cos \alpha_{T} }}{{\cos \alpha_{0} }}$$
(21)
$$f_{R} = \frac{{R_{0} }}{{R_{T} }}$$
(22)
$$f_{e} = \sqrt {\frac{{e_{0} }}{{e_{T} }} \cdot \left( {\frac{{1 + e_{T} }}{{1 + e_{0} }} \cdot \left[ {1 + \beta_{v} \cdot \Delta T} \right]} \right)^{1 - \delta } }$$
(23)
$$f_{\rho } = \frac{{\rho_{{{\text{wT}}}} }}{{\rho_{w0} }}$$
(24)

where \(f_{\sigma }\) is the surface tension factor, \(f_{\alpha }\) is the air–water contact angle factor, \(f_{R}\) is the particle-size factor, and \(f_{e}\) is the void ratio factor, \(f_{\rho }\) is water density factor, \(\beta_{v}\) is the thermal volumetric expansion coefficient of solid particle, ΔT is the temperature increment.

3.2 Temperature-dependent function of surface tension

Surface tension is defined as the tensile force per unit length of the air–water interface. Several linearly empirical equations were established based on the low range of temperature between 0 °C and 40 °C [29]. However, Vargaftik et al. [84] presented a set of data for the surface tension up to 200 \(^\circ{\rm C}\), which presents a nonlinear form. Therefore, by using the regression analysis technique, the following equation is proposed for the temperature-dependent function of surface tension:

$$\sigma_{{{\text{sT}}}} = \left( {75.61 - 0.14245 \times T - 0.000238 \times T^{2} } \right) \times 10^{ - 3} \quad \quad \left( {{\text{N}}/{\text{m}}} \right)$$
(25)

where T is current temperature in degree Celsius (°C).

The surface tension of the air–water interface at the reference temperature is expressed as follows:

$$\sigma_{s0} = \left( {75.61 - 0.14245 \times T_{0} - 0.000238 \times T_{0}^{2} } \right) \times 10^{ - 3} \quad \quad \left( {{\text{N}}/{\text{m}}} \right)$$
(26)

where \(e_{0}\) is reference temperature in degree Celsius (°C).

For the sake of simplicity in presentation, Eq. (25) can be re-written as follows:

$$\sigma_{{{\text{sT}}}} = \lambda_{1} T^{2} + \lambda_{2} T + \lambda_{3}$$
(27)

where \(\lambda_{1}\), \(\lambda_{2}\), \(\lambda_{3}\) are constants with \(\lambda_{1} = - 0.000238 \times 10^{ - 3}\); \(\lambda_{2} = - 0.14245 \times 10^{ - 3}\); \(\lambda_{3} = 75.61 \times 10^{ - 3}\)

Replacing Eqs. (25) and (26) back into Eq. (20), the surface tension factor \(f_{\sigma }\) is derived:

$$f_{\sigma } = \frac{{\lambda_{1} T^{2} + \lambda_{2} T + \lambda_{3} }}{{\lambda_{1} T_{0}^{2} + \lambda_{2} T_{0} + \lambda_{3} }} = \,\frac{{75.61 - 0.14245 \times T - 0.000238 \times T^{2} }}{{75.61 - 0.14245 \times T_{0} - 0.000238 \times T_{0}^{2} }}$$
(28)

3.3 Temperature-dependent function of contact angle

Grant and Salehzadeh [28] assumed that a change in interfacial energy equals a change in interfacial tension. Based on the interfacial energy approach, the following expression is stated:

$$- \Delta h_{T} = \sigma_{{{\text{sT}}}} \cdot \cos \alpha_{T} - T\frac{{d\left( {\sigma_{{{\text{sT}}}} \cdot \cos \alpha_{T} } \right)}}{{{\text{d}}T}}$$
(29)

where ΔhT is immersion enthalpy per unit area at current temperature T.

Rearranging Eq. (29), the expression for the temperature dependence of contact angle can be obtained:

$$\frac{{d\cos \alpha_{T} }}{dT} = \frac{{\cos \alpha_{T} }}{T} - \frac{{\cos \alpha_{T} }}{{\sigma_{{{\text{sT}}}} }} \cdot \frac{{d\sigma_{sT} }}{dT} + \frac{1}{T} \cdot \frac{{\Delta h_{T} }}{{\sigma_{sT} }}$$
(30)

At the largest immersion enthalpy per unit area, \(\Delta h_{T} = \Delta h_{{{\text{max}}}}\), the change in wetting coefficient approaches zero:

$$\frac{{d\cos \alpha_{T} }}{dT} = 0$$
(31)

On the other hand, the derivative of surface tension with temperature is obtained as follows:

$$\frac{{d\sigma_{{{\text{sT}}}} }}{dT} = 2\lambda_{1} T + \lambda_{2}$$
(32)

Substituting Eqs. (31) and (32) back into Eq. (29) and rearranging give:

$$\Delta h_{T} = \left( {\lambda_{1} T^{2} + \lambda_{3} } \right)\cos \alpha_{T}$$
(33)

Replacing Eq. (33) into Eq. (30) and conducting an integration procedure for temperature range from T0 to T, a solution can be derived as follows:

$$\cos \alpha_{T} = \frac{{\sigma_{{{\text{sT}}}} \cdot T_{0} }}{{\sigma_{s0} \cdot T - \left( {\lambda_{1} T^{2} - \lambda_{3} } \right)\left( {T - T_{0} } \right)}}\cos \alpha_{0}$$
(34)

Replacing Eq. (34) into Eq. (21), the contact angle factor \({f}_{\alpha }\) is derived as follows:

$$f_{\alpha } = \frac{{\sigma_{{{\text{sT}}}} \cdot T_{0} }}{{\sigma_{s0} \cdot T - \left( {\lambda_{1} T^{2} - \lambda_{3} } \right)\left( {T - T_{0} } \right)}}$$
(35)

3.4 Temperature-dependent function of particle size

The volume of soil particles is supposed to expand with increasing temperature, and therefore, the particle radius is also changed [54, 58, 59]. The volumetric thermal expansion of a solid particle is considered by the equation below:

$$\frac{\Delta V}{{V_{0} }} = \beta_{v} \cdot \Delta T$$
(36)

where ΔV is volume increment of the solid particle due to temperature increase, \(V_{0}\) is the original volume of the solid particle at a reference temperature, ΔT is the temperature increment, \(\beta_{v}\) is the volumetric thermal expansion coefficient of solid particles. It is noted that the coefficient of volume expansion \(\beta_{v}\) can be predicted approximately three times the coefficient of linear expansion (\(\beta_{v}\) ≈ 3α).

Assuming the soil particles to have a spherical shape, the relation between particle radius and temperature is expressed as follows:

$$R_{T} = R_{0} \sqrt[3]{{1 + \beta_{v} \cdot \Delta T}}$$
(37)

Replacing Eq. (37) into Eq. (22), the particle-size factor is derived:

$$f_{r} = \frac{1}{{\sqrt[3]{{1 + \beta_{v} \cdot \Delta T}}}}$$
(38)

3.5 Temperature-dependent function of void ratio

It is noted that temperature increase usually induces a contraction of the soils, particularly for normally consolidated clays [32, 49, 50]. In the modeling attempts, the volumetric strain due to heating is usually determined by the following relationships:

$$\varepsilon_{v}^{T} = \frac{{\Delta e_{T} }}{{1 + e_{0} }} = \frac{{e_{0} - e_{T} }}{{1 + e_{0} }}$$
(39a)
$$\varepsilon_{v}^{T} = k.\Delta T$$
(39b)

where \(\varepsilon_{v}^{T}\) is the volumetric strain by heating, ΔeT is the void ratio change due to temperature increase, k is a material-dependent coefficient to relate the temperature change to the thermal volumetric strain.

Balancing two sides of Eqs. (39a) and (39b) gives:

$$e_{T} = e_{0} - \Delta e_{T} = e_{0} - k \cdot \Delta T \cdot \left( {1 + e_{0} } \right)$$
(40)

The void ratio factor can be obtained by replacing Eq. (40) into (23), which gives:

$$f_{e} = \sqrt {\frac{{e_{0} }}{{e_{0} - k \cdot \Delta T \cdot \left( {1 + e_{0} } \right)}} \cdot \left( {\frac{{1 + e_{0} - k \cdot \Delta T \cdot \left( {1 + e_{0} } \right)}}{{1 + e_{0} }} \cdot \left[ {1 + \beta_{v} \cdot \Delta T} \right]} \right)^{1 - \delta } }$$
(41)

According to Eq. (40), the thermal volume change depends on the accuracy of coefficient k. However, many experimental results revealed that the coefficient k depends on the property of soils including OCR, initial void ratio, plasticity index [1, 6, 7, 9, 10, 13, 14, 16, 18, 26, 30, 38, 39, 44, 46, 48, 63, 64, 76, 79, 80, 91]. Thermal volume change, on the other hand, is almost independent of suction, according to Uchaipichat and Khalili [80]. This implies that the thermal volume change function of unsaturated soil is similar to that of saturated soil. Furthermore, Demars and Charles [17] found that the volume change due to temperature is more sensitive to plasticity index (PI) than any other factor, based on laboratory test results. As a result, the plasticity index is used in this study to establish a relationship between void ratio changes and temperature.

In this study, the measured data from twenty-two laboratory test sets, which included three data sets of unsaturated soil and 19 data sets of saturated soil, are used to build an empirical relationship between thermal volume change and plasticity index. A wide range of PI between 5 and 135 were collected for different soil types. Figure 5a shows the relationship between coefficient k and the plasticity index of soils. According to the results, the value of parameter k increases significantly with increasing plasticity index. It should be noted that different test data sets tend to give a quite similar value of coefficient k if the tested soils have the same plasticity index. Furthermore, three data sets of unsaturated soils show that coefficient k is nearly independent of matric suction. As a result, the proposed equation is expected to work well for both saturated and unsaturated soils although it is well accepted that the physical mechanisms behind two kinds of soils are more complicated. Using the regression analysis technique, four different forms of the best-fit curve are plotted in Fig. 5b. It can be observed that the polynomial form of the best-fit curve produces the best agreement with measured data (coefficient of determination − R2 = 0.906). It is therefore selected to represent the relationship between coefficient k and the plasticity index in this study. The expression for the best-fit curve under the polynomial form is re-written as follows:

$$k = \frac{{\Delta e_{T} }}{{\left( {1 + e_{0} } \right) \cdot \Delta T}} = 10^{ - 8} \left( {PI} \right)^{2} + 3 \cdot 10^{ - 6} \left( {PI} \right) + 0.0002$$
(42a)

or,

$$\Delta e_{T} = [10^{ - 8} \left( {PI} \right)^{2} + 3 \cdot 10^{ - 6} \left( {PI} \right) + 0.0002]\left( {1 + e_{0} } \right) \cdot \Delta T$$
(42b)
Fig. 5
figure 5

Thermal volume change coefficient k as a function of plasticity index: a source of collected test data from literature; b different forms of best-fit curves

Full size image

Substituting Eq. (42) back into Eq. (41), the variation in void ratio factor fe with the plasticity index can be determined. Figure 6 shows the fluctuation of fe with plasticity index and temperature. It can be observed that the void ratio factor increases nonlinearly with increasing both plasticity index and temperature. It is expected that the influence of the plasticity index on the void ratio factor becomes more significant for the higher temperature ranges. It should also be noted that the void ratio factor is more influenced by temperature fluctuations for soils of high plasticity than soils of low plasticity.

Fig. 6
figure 6

Variation in void ratio factor fe with plasticity index and temperature

Full size image

3.6 Temperature-dependent function of water density

For most geotechnical engineering applications, the density of water under isothermal circumstances is commonly assumed to be 1000 kg/m3. However, the experimental data from Lide [42] and Keshky [36] showed that the water density decreases with increasing temperature. The relationship between pure water density in the liquid phase (in kg/m3) and temperature (°C) is:

$$\rho_{wT} = 999.876 -0.00588T - 0.004606T^{2}$$
(43)

The water density factor \(f_{\rho }\) can be expressed as follows:

$$f_{\rho } = \frac{{999.876 -0.00588T - 0.004606T^{2} }}{{999.876 -0.00588T_{0} - 0.004606T_{0}^{2} }}$$
(44)

3.7 Discussion of temperature-dependent suction model

To illustrate the temperature effect on surface tension, contact angle, particle size, water expansion, and void ratio, Fig. 7 depicts the relationship between matric suction and pore size with temperature fluctuation for four different cases: (1) considering temperature-dependent particle size and water density only (fσ = fα = fe = 1), (2) considering temperature-dependent particle size and surface tension only (fα = fe = 1), (3) considering temperature-dependent particle size, surface tension, and void ratio only (fα = 1), (4) considering all five temperature-dependent functions of particle size, water density, surface tension, void ratio, and contact angle. It can be observed that the change in matric suction is least significant for case 1, and most significant for case 4. The results reveal that the temperature-dependent function of contact angle has the greatest influence on matric suction as compared to other remaining functions. For example, at the pore size radius of 1 mm, the reduction in matric suction due to fluctuation in particle size, void ratio, surface tension, and contact angle is 4.1%, 8.31%, 12.9%, and 44.2%, respectively, when the temperature increases from 15 to 100 \(^\circ{\rm C}\). The results indicate that the suction change due to temperature is influenced through the following factors in descending order: air–water contact angle, surface tension, void ratio, particle-size expansion, and water density. It is therefore found that accounting only for the effects of temperature on surface tension is not sufficient to evaluate the suction change with temperature and can cause inaccurate results.

Fig. 7
figure 7

Contribution of different temperature-dependent functions to variation in matric suction

Full size image

It is obvious that the contribution of the contact angle function to the matric suction reduction due to temperature fluctuation is larger than the total contribution of the four remaining functions (surface tension, particle size, water density, and void ratio). Figure 8 demonstrates the changes in matric suction with pore size for two cases: the temperature-dependent contact angle and the temperature-independent contact angle. The comparison results between the two examined cases indicate that changes in matric suction for the temperature-independent contact angle case are relatively small as compared to the temperature-dependent contact angle case. The results, therefore, highlight the importance of considering a temperature-dependent contact angle function for multi-physics numerical simulations involving temperature effects in unsaturated soils. Unfortunately, due to the complex problem of the relationship between contact angle and temperature, not enough attention was paid to this aspect, or it was usually neglected in the existing models.

Fig. 8
figure 8

Relationship between pore size and matric suction for temperature-dependent and temperature-independent contact angles at various temperatures

Full size image

3.8 Temperature-dependent soil–water characteristic curve equation

It should be noted that the variation in soil suction with temperature can be predicted by using Eq. (19b) when all five temperature-dependent functions were addressed. The isothermal SWCC equation can then be extended to nonisothermal conditions by combining Eqs. (12) and (19b), in which Eq. (12) is used to plot the reference SWCC. Predicted SWCC at arbitrary temperature can be obtained by using Eq. (19b) to calculate matric suction change with temperature while the degree of saturation is kept constant as the one of reference SWCC. The expression for the nonisothermal SWCC equation is as follows:

$$\left\{ {\begin{array}{*{20}c} {S_{T} = S_{{T_{0} }} = \frac{1}{{\left\{ {{\text{ln}}\left( {2.7127 + [\psi_{0} /a]^{n} } \right)} \right\}^{m} }}} \\ { \psi_{T} = \psi_{{T_{0} }} \times f_{\sigma } \times f_{\alpha } \times f_{R} \times f_{e} \times f_{\rho } } \\ \end{array} } \right.$$
(45)

For sake of verification, the results obtained from the proposed model are compared with experimental data and three existing non-isothermal models [28, 66, 69]. Two sets of laboratory test data are then selected for studying the validity of the non-isothermal SWCC model in this section. The first test data set is obtained from Constantz [15], where Oakley sand was tested at 20 \(^\circ{\rm C}\) and 80 \(^\circ{\rm C}\). The sandy soil has fundamental physical properties as follows: specific gravity Gs = 2.72, dry density \({\gamma }_{d}\) = 1.77 g/cm3, initial void ratio \({e}_{0}\) = 0.52, and plasticity index PI = 1. The second data set is obtained from Wan et al. [99], which tested on the compacted bentonite at 20 \(^\circ{\rm C}\) and 80 \(^\circ{\rm C}\). The fundamental properties of the bentonite are as follows: specific gravity Gs = 2.66, dry density \({\gamma }_{d}\) = 1.70 g/cm3, saturated water content w = 10.6%, initial void ratio \({e}_{0}\) = 0.56, and plasticity index PI = 239. It is interesting to note that the case of Oakley sand has a low plasticity index while the case of compacted bentonite has a high plasticity index that may thus be sufficient to assess the performance of the proposed model at a wide range.

For the data set of Constantz [15], the SWCC test data at 20 \(^\circ{\rm C}\) are used to plot the reference SWCC, in which the fitting parameters are determined as follows: a = 7 kPa, m = 1.8, n = 1.25, δ = 10 (sand). It should be noted that the tested soil type was sand with a very low plasticity index, and the thermal volume change is therefore quite minimal. The temperature-dependent function of the void ratio is approximately close to 1, and thus has less effect on non-isothermal SWCC. Figure 9a shows the change of SWCC with temperature for four different cases. According to the results, a temperature increase generally produces lower SWCC. However, it should be emphasized that incorporating all five temperature-dependent functions of particle size, water density, surface tension, void ratio, and contact angle gives a more accurate prediction than only considering a single function. Moreover, it is also observed that the temperature-dependent function of the contact angle has a significant influence on SWCC as compared to other functions. Figure 9b demonstrates the comparison between predicted and measured SWCCs at 80 \(^\circ{\rm C}\). It is worthy to note that the predicted SWCC by the proposed model is in good agreement with measured SWCC, and generally in better accordance compared to the three existing models. The key to this difference comes from the fact that almost all existing models focused only on considering the change of surface tension with temperature while other factors were omitted. It is also found that the model of Grant and Salehzadeh [28] has a better prediction compared to the models of [69], and one of Roshani and Sedano [66]. This is because, besides surface tension function, the model of Grant and Salehzadeh (1996) considers further the effect of temperature-dependent contact angle on SWCC while the two remaining models focus only on the variation in surface tension with temperature. On the other hand, the model of Salager et al. [69] has an advance over the other models by considering the volumetric expansion of water which was ignored in the models of Grant and Salehzadeh [28], and Roshani and Sedano [66]. This explains why the model of Salager et al. [69] gives an SWCC lower than the model of Roshani and Sedano [66] for the same temperature. Figure 9c presents predicted against the measured degree of saturation. It is noted that the proposed model has a good performance in predicting the variation in SWCC with temperature. All three models underpredict the effect of temperature on the SWCC. The average relative errors of four models are 7.3%, 24.4%, 31.9%, and 43.6% for the proposed model, Grant and Salehzadeh [28], Salager et al. [69], and Roshani and Sedano [66], respectively.

Fig. 9
figure 9figure 9

Comparison outcomes for Oakley sand (measured data source from Constantz, 1991): a variation in SWCC considering various temperature-dependent functions, b comparison between predicted and measured SWCCs, c Predicted against measured degree of saturation

Full size image

The comparison results for the second data set of Wan et al. [86] are shown in Fig. 10, in which the reference SWCC is also plotted by using test data at 20 \(^\circ{\rm C}\). The fitting parameters of this reference SWCC are as follows: a = 1300 kPa, m = 1.34, n = 0.65. It should be noted that the plasticity index of the tested bentonite is very high (PI = 239), and the thermal volume change is therefore much larger than the sandy soil case of Constantz [15]. The variation in SWCC with temperature corresponding to four different cases is presented in Fig. 10a. A similar trend is also observed for bentonite when the effect of the contact angle function is more prominent than the three remaining functions. It is therefore concluded that the predictions of temperature-dependent SWCC are more effective and precise with considering the temperature-dependent function of the contact angle. Figure 10b demonstrates a comparison between the proposed model with three existing models and measured data for SWCCs at 60 \(^\circ{\rm C}\). It can be observed that the proposed model agrees well with experimental data as predicted SWCC passes through most test data points. Meanwhile, the effect of temperature on SWCC is less important according to the estimation from the three remaining models. It should be noted that test temperature in the case of Wan et al. [86] was lower than the case of Constantz [15], and the suction range of bentonite is also much higher than that of sand (about 1000 times). Finally, the limited change of surface tension with a low-temperature range is the main reason why the predicted SWCCs obtained from three existing models look very close to the reference SWCC. The results obtained from the proposed model are then extended to compare with measured data for different temperatures, as shown in Fig. 10c. A satisfactory agreement between the proposed model and test data is obtained for different temperatures ranging between 20 \(^\circ{\rm C}\) and 80 \(^\circ{\rm C}\). Figure 10d shows the predicted against the measured degree of saturation, which indicates that the proposed model is applicable to predict effectively the variation in the SWCC with temperature. The average relative error of the proposed model, Grant and Salehzadeh [28], Salager et al. [69], and Roshani and Sedano [66] is 2.2%, 15.9%, 23.7%, and 30.2%, respectively. The predictive performance of the proposed model is, therefore, higher than the other remaining models.

Fig. 10
figure 10figure 10

Comparison outcomes for bentonite (measured data source from Wan et al. 2015): a Variation in SWCC considering various temperature-dependent functions, b comparison between predicted and measured SWCCs, c proposed model against measured data for different temperatures, d predicted against measured degree of saturation

Full size image

4 Modeling the combined effect of initial density and temperature on SWCC

4.1 Coupled mechanical–thermal SWCC model

In many practical situations, unsaturated soils may experience both deformations and thermal variations. To the best knowledge of authors, unfortunately, none of the existing models are found to be able to predict the combined effect of temperature and density variations on the SWCC. With success in proposing models to predict the individual influence of initial density and temperature on the SWCCs in previous sections, this section presents a comprehensive model by combining the two models into a coupled one. By combining Eq. (13), and (45), the expression for the coupled model of SWCC can be written as follows:

$$\left\{ {\begin{array}{*{20}c} {(S_{{e_{i} }} )_{T} = (S_{{e_{0} }} )_{{T_{0} }} = \frac{1}{{\left\{ {\ln \left( {2.7127 + \left[ {\left( {\psi_{{e_{0} }} } \right)_{{T_{0} }} /a} \right]^{n} } \right)} \right\}^{m} }}} \\ {(\psi_{{e_{i} }} )_{T} = f \times (\psi_{{e_{0} }} )_{{T_{0} }} \times \sqrt {\frac{{e_{0} }}{{e_{i} }}.\left( {\frac{{1 + e_{i} }}{{1 + e_{0} }}} \right)^{1 - \delta } } } \\ \end{array} } \right.$$
(46)

where \({{(S}_{{e}_{0}})}_{{T}_{0}}\) is saturation degree corresponding to reference initial void ratio at the reference temperature, \({{(\psi }_{{e}_{0}})}_{{T}_{0}}\) is matric suction corresponding to reference initial void ratio at the reference temperature, \({{(\psi }_{{e}_{i}})}_{T}\) is matric suction corresponding to arbitrary initial void ratio at the arbitrary current temperature, f is an overall temperature-dependent function (\({f = f}_{\sigma }\times {f}_{\alpha }\times {f}_{R}\times {f}_{e}{\times f}_{\rho }\)).

It is noted that the proposed model is presented in a simplified form. By keeping the degree of saturation of the reference SWCC and replacing the reference matric suction \({{(\psi }_{{e}_{0}})}_{{T}_{0}}\) by \({{(\psi }_{{e}_{i}})}_{T}\), Eq. (46) can be used to predict the SWCC at arbitrary temperature with an arbitrary initial void ratio.

Another version of the proposed model for the SWCC using the relationship between volumetric water content and matric suction is shown as follows:

$$\left\{ {\begin{array}{*{20}c} {(\theta_{{e_{i} }} )_{T} = \frac{{\left[ {\left( {\theta_{s} } \right)_{{e_{0} }} } \right]_{{T_{0} }} \times \frac{{e_{0} }}{{e_{i} }} \cdot \left( {\frac{{1 + e_{i} }}{{1 + e_{0} }}} \right)}}{{\left\{ {\ln \left( {2.7127 + \left[ {\left( {\psi_{{e_{0} }} } \right)_{{T_{0} }} /a} \right]^{n} } \right)} \right\}^{m} }} } \\ {(\psi_{{e_{i} }} )_{T} = f \times (\psi_{{e_{0} }} )_{{T_{0} }} \times \sqrt {\frac{{e_{0} }}{{e_{i} }} \cdot \left( {\frac{{1 + e_{i} }}{{1 + e_{0} }}} \right)^{1 - \delta } } } \\ \end{array} } \right.$$
(47)

where \({{(\theta }_{{e}_{0}})}_{{T}_{0}}\) is volumetric water content corresponding to reference initial void ratio at the reference temperature, \({{(\theta }_{{e}_{i}})}_{T}\) is volumetric water content corresponding to an arbitrary initial void ratio at the current temperature.

4.2 Validity of coupled mechanical–thermal SWCC model

The validation and performance of the proposed model in modeling the combined effect of initial density and temperature on the SWCC of unsaturated soils are verified by comparison with experimental results for three test data sets. The first test data sets are obtained from Romero et al. [65], where the swelling clay (Boom clay) with a plasticity index of 27 was tested under two initial void ratios (0.97 and 0.62) at two different temperatures (22 \(^\circ{\rm C}\) and 80 \(^\circ{\rm C}\)). The second one is referenced from Imbert et al. [34], in which the Foca clay with a plasticity index of 62 was tested under four initial void ratios (0.7, 0.5, 0.47, 0.42) at three different temperatures (20 \(^\circ{\rm C}\), 50 \(^\circ{\rm C}\), and 80 \(^\circ{\rm C}\)). The last one is obtained from Gens [24], where Febex bentonite with a plasticity index of 87 was tested under three initial void ratios (0.68, 0.64, 0.59) at three different temperatures (20 \(^\circ{\rm C}\), 40 \(^\circ{\rm C}\), and 60 \(^\circ{\rm C}\)).

Figure 11a shows the comparison between predicted and measured SWCCs for the test data sets of Romero et al. [65]. It should be noted that the test data of SWCC at an initial void ratio of 0.97 and temperature of 22 \(^\circ{\rm C}\) are selected to develop the reference SWCC. The fitting parameters of the reference SWCC is as follows: a = 10 kPa, m = 0.88, n = 0.8, and δ = 45. According to the results, the predicted SWCCs are in good agreement with measured data for different cases with variations in both initial void ratio and temperature. Furthermore, it is noted that both experimental results and analytical outcomes agree that the effect of temperature on SWCC can start even from a low suction range (1 kPa in this case) while the effect of initial void ratio becomes more significant only when matric suction reaches a sufficiently large value (100 kPa in this case). Figure 11b shows the measured against calculated degree of saturation for all test points. The average relative error (ARE) for the proposed model, in this case, was only 3.40%, which indicates that the proposed model is successful in predicting the combined effect of density and temperature on the variation in SWCC.

Fig. 11
figure 11

Performance of coupled mechanical–thermal SWCC model (measured data source from Romero et al. 2001): a Comparison between predicted and measured SWCCs; b Calculated versus measured degree of saturation

Full size image

Figure 12a demonstrates the performance of the proposed model with comparison to measured data for the test data sets of Imbert et al. [34]. Concerning this case, the test data of SWCC at an initial void ratio of 0.42 and temperature of 20 \(^\circ{\rm C}\) are used to obtain the reference SWCC. The fitting parameters of the reference SWCC are as follows: a = 114 kPa, m = 1.45, n = 1.1, and δ = 25. It can be observed that the proposed model shows an excellent match to the measured data for different temperature and initial void ratios. It is found that both density and temperature have a significant influence on the variation in matric suction, and the combined effect of these two factors leads to a strong change in the SWCC. Furthermore, it is also more interesting to note that the effect of density on the SWCC is more dominant than temperature. Figure 12b shows the measured against calculated degree of saturation for 42 test points. The results indicate that the proposed model has a high performance for predicting the variation in SWCC with temperature and density. The effectiveness of the proposed model is specifically proved by the value ARE, which is about 2.95%.

Fig. 12
figure 12

Comparison between predicted and measured SWCCs (source data from Imbert et al. 2005): a comparison between predicted and measured SWCCs; b calculated versus measured degree of saturation

Full size image

Gens [24] have conducted SWCC tests for three cases, 1) different initial void ratios at the same temperature, 2) different temperatures at the same initial void ratio, and 3) different temperatures at different initial void ratios. With the variety of scenarios, the test data are more useful to evaluate the influence degree between temperature and initial density on the SWCC. The test data of SWCC at an initial void ratio of 0.68 and temperature of 20 \(^\circ{\rm C}\) are used to obtain the reference SWCC in this case study. The fitting parameters of the reference SWCC are as follows: a = 50 kPa, m = 1.1, n = 1.5, and δ = 25. The comparison between analytical and experimental models for the data sets of Gens [24] is presented in Fig. 13a. It should be noted that the proposed model shows a good match to measured data for different scenarios. It is also more interesting to note that the SWCC is influenced by the density more significantly than the temperature. Figure 13b describes the measured against calculated degree of saturation for 41 test points. The value ARE in this case was only 1.2%, which indicates that the proposed model has a good prediction performance and is proper to be used in predicting the combined effect of temperature and density on the SWCC.

Fig. 13
figure 13

Comparison between predicted and measured SWCCs (source data from Gens, 2007): a comparison between predicted and measured SWCCs; b calculated versus measured degree of saturation

Full size image

5 Conclusions

This paper presents a study for modeling the combined effect of temperature and initial density on the soil–water characteristic curve of unsaturated soils. Some key points can be summarized as follows:

A simple model was proposed to predict the effect of initial density on the soil–water characteristic curve of unsaturated soils. The initial density-dependent model of SWCC was established by translating from the particle-size distribution curve into the soil–water characteristic curve through a pore-size distribution function. The proposed model is simple and effective to be used as only one new parameter is introduced to describe the effect of initial soil density. The comparison with two test data sets showed that the analytical model has a good performance for predicting the initial density effect on the SWCC.

A non-isothermal model is also presented to estimate the effect of temperature on the soil suction as well as SWCC. The key to the proposed model is considering five different temperature-dependent functions for surface tension, contact angle, particle-size expansion, water density, and void ratio which leads to a complete method compared to existing models focusing only on surface tension. The results showed that the suction change due to temperature fluctuations is influenced through the following factors in descending order: contact angle, surface tension, void ratio, particle-size expansion, and water density. The validity of the proposed model was verified against some experimental data available in the literature. It has been shown that the non-isothermal model can capture well the temperature effect on the SWCC.

On the basis of 22 data sets of thermal volume change, this study also developed further a theoretical correlation between void ratio and temperature that is directly related to soil plasticity. It was observed that the value of the thermal void ratio increases as soil plasticity increases, and there is a nonlinear relationship between the plasticity index and the void ratio. Because of this, soils with high plasticity are more susceptible to volume changes caused by temperature fluctuations than soils with low plasticity.

A coupled mechanical–thermal SWCC model is then proposed by combining the initial density-dependent and temperature-dependent models that allow predicting the SWCC at any arbitrary initial density and temperature. The coupled mechanical–thermal SWCC model is presented in a simple form, which is more convenient to be applied in practice. The comparison results for three independent test data sets proved that the proposed model has a good performance to predict the variation in SWCC with both temperature and initial density.