Cyclic compression of sands at constant stress ratio—experimental investigations and constitutive modelling

Abstract

Several constitutive models for sands are based on an additive split of the effective stress rate into two terms. One term accounts for the deviatoric stress ratio $\varvec{r}$, the other for the mean effective stress ${p}$. While sophisticated techniques are available to account for monotonic and cyclic variations of $\varvec{r}$, the ${p}$ term is usually treated by means of rather rudimentary constitutive mechanisms. In particular, no plasticity sand model seems to exist whose functions take into account cyclic changes of ${p}$ in a realistic manner. However, cyclic changes of ${p}$ frequently occur in geotechnical boundary value problems and can cause irrecoverable deformation in non-cohesive soils. Present sand models significantly under- or overestimate these deformations. This issue is tackled in the paper. First, results from a comprehensive series of triaxial tests on Toyoura Sand are presented. The samples were loaded with cyclic changes of ${p}$ at constant stress ratio in order to study the effects of mean effective stress variations exclusively. The test results show that the samples accumulate significant irrecoverable strains throughout successive loading cycles. The results furthermore allow to investigate the effects of pressure level, pressure amplitude, stress ratio level and density on the strain evolution. Second, new constitutive functions for an existing Bounding Surface Plasticity model are proposed in the paper. They are intended to improve the simulation results obtained with the model for monotonic and cyclic changes of ${p}$ at constant stress ratio. The extended model is then carefully calibrated and validated using the experimental data from the triaxial tests. The results of the validation prove that the new constitutive functions have the desired effect.

1 Introduction

When constitutive theories for soils are formulated, it is convenient to normalise the deviatoric part of the effective stress tensor $\varvec{\sigma }_\mathrm {dev} = \varvec{\sigma } - p \varvec{I}$ with respect to the mean effective stress $p = {\text {tr}} \varvec{\sigma }/3$, yielding the stress ratio tensor $\varvec{r} = \varvec{\sigma }_\mathrm {dev} / p$. This accounts for the property of granular materials that their strength and stiffness strongly depend on the pressure level. The rate of effective stress is then decomposed by the chain rule of differentiation into

$$\begin{aligned} \dot{\varvec{\sigma }} = \dot{\varvec{r}}p + {\dot{p}}\frac{\varvec{\sigma }}{p} \,. \end{aligned}$$

(1)

The first summand of (1) describes shearing caused by changes of stress ratio $\varvec{r}$ at constant pressure ${p}$. The second summand of (1) represents what is referred to here as compression, i. e. variations of p at constant $\varvec{r}$.

Fig. 1

Stress paths for different kinds of compression loading

This work is concerned with the mechanical behaviour of sands related to the compression term of (1) only. Stress paths of pure $\dot{p}$ loading at constant stress ratio are straight lines passing through the origin in $p - q$ space (Fig. 1). Therein, $q = \sqrt{{3}/{2}}\Vert \varvec{\sigma }_\mathrm {dev}\Vert$ is the equivalent shear stress. The slopes of these lines are defined by the value of the scalar stress ratio magnitude $\eta = \sqrt{{3}/{2}} \Vert \varvec{r}\Vert = q/p$. The special case in which $\eta = \mathrm {const} = 0$ and $\dot{p} \ne 0$ is isotropic compression. A common example for loading with $\eta = \mathrm {const}$ and $\eta > 0$ is confined compression of virgin soil, for example in an oedometer device. It generates stress paths with

$$\begin{aligned} \eta = \eta _{K0} = \frac{3 ( 1 - K_0) }{1 + 2 K_0} \,, \end{aligned}$$

(2)

in which $K_0$ is the coefficient of earth pressure at rest. During laterally confined unloading and reloading, however, the coefficient of earth pressure is known to vary, resulting in ${\dot{\eta }} \ne 0$ [25, see also Fig. 1].

The soil in practical engineering problems is usually exposed to combined shearing and compression, i. e. ${\varvec{r}}$ and ${p}$ vary simultaneously. In case of cohesive soils, both terms of (1) are known to cause significant inelastic deformation. Non-cohesive soils, on the other hand, respond much stiffer to changes in ${p}$ [34]. This is the reason why several constitutive models for sand include plastic mechanisms only for the $\dot{\varvec{r}}$ term of (1) [eg. 8, 14, 17, 41, 51].

Nevertheless, there are also geotechnical initial value problems in which the soil experiences large changes in ${p}$ as well as repeated loading and unloading. This happens, for example, in the vicinity of ship lock foundations and during installation of piles by means of ramming or vibration. In these and similar situations, the $\dot{p}$ term of (1) may induce considerable amounts of irrecoverable deformation even in non-cohesive soils, especially due to strain accumulation caused by cyclic loading. This motivated to investigate the mechanical response of sands to cyclic compression by means of isotropic loading tests and oedometer tests in the works by Bauer [4], Ko and Scott [23], Mallwitz and Holzlöhner [29] Sawicki and Swidzinski [43], Wichtmann et al. [55].

A common result of the experimental investigations is that one cycle of unloading and reloading generates irrecoverable strain, even in isotropic loading of dense sand. The magnitude of irrecoverable strain depends on stress level, stress amplitude and relative density of the soil. Furthermore, previous works agree that with increasing cycle count N the amount of irrecoverable strain accumulated per cycle decreases. However, it is not clear how fast strain accumulation declines. For example, Ko and Scott [23] reported that their isotropically loaded samples reached a quasi-elastic state after only four cycles at the latest. In contrast, the results of Wichtmann et al. [55] show continued accumulation of permanent strain even after $10^{4}$ cycles of isotropic compression.

In addition, the soil response is likely affected by inherent and stress-induced anisotropy of the soil’s fabric. This has not yet been investigated with respect to cyclic compression of sands but is known from previous works on monotonic and cyclic shear loading [1, 2, 37, 47, 54, 57, 59]. For example, an effect of fabric anisotropy on the compression behaviour of sands could be that isotropic loading of a sample with isotropic initial stress not only causes volumetric strains but also deviatoric strains.

Constitutive theories that possibly could reproduce the inelastic aspects of the material behaviour described above are scarce. There are some sand models that include plastic mechanisms for the $\dot{p}$ term of (1), but these mechanisms are active only during first loading [19, 38, 48, 51, 52]. Cyclic unloading and reloading are therefore treated elastically. This is reasonable for very small stress loops because the grain skeleton of sands is indeed able to store and release elastic energy to very limited extend. For larger amplitudes of cyclic compression, however, energy dissipates and irreversible deformation is accumulated, which cannot be accounted for by treating cyclic changes of ${p}$ elastically. Only two models provide plastic $\dot{p}$ mechanisms that account for inelastic behaviour during unloading and reloading. These are MIT-S1 by Pestana and Whittle [39] and the Critical State Bounding Surface model by Li [26].

MIT-S1 was frequently used to model soil behaviour under monotonic loading, eg. by Chen et al. [11] Nikolinakou et al. [36], Pestana et al. [40]. However, no reports are available on how well effects from cyclic loading are captured. The model by Li [26], on the other hand, was successfully used for finite element simulations of model tests and benchmark problems involving cyclic loading by Carow et al. [10], Ming and Li [32], Su and Li [46]. This makes it an excellent platform for further research concerning sand behaviour under cyclic loading. Nonetheless, the model’s functions which account for changes of ${p}$ at constant stress ratio have at least one conceptual shortcoming. They were designed to simulate consolidation and one cycle of unloading and reloading only. This first cycle induces a certain amount of permanent deformation because the stress–strain loop is not closed, consistent with experimental evidence. However, each subsequent cycle with the same amplitude simply repeats the response from the first cycle. Consequently, the accumulation of strains throughout several loading cycles is greatly overestimated.

In order to resolve this issue, additional constitutive functions could be developed for the $\dot{p}$ mechanism by Li [26]. However, this requires results of element tests on the evolution of deviatoric and volumetric strains during cyclic loading with $\eta = \mathrm {const}$ and $\eta > 0$. The research works on cyclic laboratory tests referred to above do not provide this. The reason is that they cover one-dimensional problems and two distinct states of stress ratio only. These are isotropic compression ($\eta = 0$) and confined compression ($\eta \approx \eta _{K0}$). This lack of a firm experimental data basis for developing cyclic $\dot{p}$ models was also noted by Bergholz [6], Elgamal et al. [17], Taiebat and Dafalias [48].

The current state of theoretical and experimental research concerning cyclic compression of sands is summarised here as follows.

• Several plasticity models for sands rely on the stress rate decomposition (1) into a $\dot{\varvec{r}}$ term and a $\dot{p}$ term.

• Results of experiments indicate that repeated cycles of $\dot{p}$ loading induce irrecoverable strains in sands.

• Soil models which are currently available and provide plastic $\dot{p}$ mechanisms cannot capture inelastic sand behaviour during cyclic compression sufficiently realistic.

• This could be overcome by developing additional constitutive functions for the $\dot{p}$ mechanism by Li [26].

• Developing and calibrating the desired functions requires results from element tests with cyclic $\eta = \mathrm {const}$ loading on sand which currently are not available.

Two research questions may be derived from that:

• 1. How do irrecoverable strains evolve in sands during cyclic $\eta = \mathrm {const}$ loading?

• 2. How can cyclic $\eta = \mathrm {const}$ loading of sand be simulated using a constitutive model?

The present paper attempts to answer these questions. To this end, a series of triaxial tests with cyclic $\eta = \mathrm {const}$ loading of Toyoura Sand samples was conducted. The results are presented and discussed here. Then, the bounding surface framework by Li [26] is introduced as a basis for developing a model that can capture inelastic material behaviour observed in the tests. The capabilities of the model’s plastic $\dot{p}$ mechanism are analysed. Afterwards, new constitutive functions are proposed which are meant to improve simulation results for monotonic and cyclic changes of p at constant stress ratio. The extended soil model is then carefully calibrated and validated against results from the test series.

Throughout the paper, a number of assumptions and notational conventions is obeyed. Material behaviour is rate-independent. Deformations are measured by the linearised strain $\varvec{\varepsilon }$. All Stresses are effective. Stresses and strains are positive in compression. Mathematical symbols and operators are defined in Appendix A.

2 Experimental investigations

2.1 Testing programme

According to Sect. 1, experimental investigations are required to study and model the mechanical behaviour of sands with regard to cyclic changes of ${p}$ at constant stress ratio. Drained triaxial tests are chosen for that here because they allow to control and measure the volumetric as well as the deviatoric portions of stresses and deformations in soil samples. The parameters of a triaxial test with cyclic $\eta = \mathrm {const}$ loading are illustrated in Fig. 1. Hence, the stress path is characterised by the stress ratio magnitude $\eta$, the mean pressure level $p_\mathrm {av}$ and the pressure amplitude $\mathrm {\Delta }{} p$. The scalar number $\eta$ is occasionally referred to as the stress ratio if triaxial conditions are concerned. Characterising a general three-dimensional state of stress ratio, though, requires at least one more suitable stress invariant to be given, such as the Lode angle $\theta$ [26].

The aim of the test series performed for this work is to investigate how the response of sands to cyclic compression depends on the loading parameters $\eta$, $p_\mathrm {av}$ and $\mathrm {\Delta }p$ and on the relative soil density. The corresponding testing programme is summarised in Table 1.

Apart from the parameters in Table 1, the mechanical behaviour of sands is also affected by inherent and induced fabric anisotropy, as stated in Sect. 1. In order to investigate inherent anisotropy here, the method of sample preparation and the bedding plane orientation of the samples would have to be varied. Induced anisotropy can be studied by applying some kind of preloading and varying its direction. That, however, is beyond the scope of the present paper.

Table 1 Relative sample densities after consolidation $I_\mathrm {dc}$ and loading parameters for the triaxial tests with cyclic $\eta = \mathrm {const}$ loading

2.2 Material tested

Toyoura Sand was used as sample material for all triaxial tests presented in Sect. 2. It is a natural silica sand produced at Toyoura, Yamaguchi Prefecture, Japan from a deposit of weathered granite [60]. It has a 50-year history of usage for research which began with the works of Miura and Yamanouchi [33], Shibata et al. [45]. Since then, Toyoura Sand has become one of the most comprehensively described sands in soil mechanics.

The mechanical properties of Toyoura Sand are said to scatter among different batches [40, 49, 60]. Because of that, the sand’s grain-size distribution and particle shape were analysed at Technische Universität Berlin by means of Dynamic Image Analysis in a CAMSIZER^® device manufactured by Retsch Technology¹. Accordingly, the grains are flat and subangular and 99% of the grains are sized between 0,10 mm and 0,35 mm, corresponding to a poorly graded fine sand. This is consistent with the specifications given by Yasin et al. [60] and the manufacturer Toyoura Keiseki Kogyo K. K. [50]. Further parameters of the grading curve are presented and shown to agree with values from the literature in Table 2.

Table 2 Index properties of Toyoura Sand, as determined here and in previous works

The mass density of solids was determined according to German Standard DIN 18124 [15]. The result is $\rho _\mathrm {s} = {2,634}\,\mathrm{g}/\mathrm{cm}^3$. This agrees with the values reported by Toyoura Keiseki Kogyo K. K. [50] and Koseki et al. [24], for example. In other previous works, solid densities of up to 2,650 $\mathrm{g}/\mathrm{cm}^3$ were reported for Toyoura Sand [eg. 58]. This is probably attributable to inhomogeneities in the natural deposit.

The void ratios at maximum and at minimum density, respectively, were determined here as $e_\mathrm {min} = {0.569}$ and $e_\mathrm {max} = {0.910}$. As shown in Table 2, these values are below the range of values documented in the literature. This can be explained by the following argument. It is well known that $e_\mathrm {min}$ and $e_\mathrm {max}$ are no physical soil properties that can be uniquely determined. Instead, they are defined through the experimental methods by means of which their values are obtained [12]. Here, methods according to German standard DIN 18126 [16] were used. Previous works adopted Japanese, British or American standards. For that reason, it is entirely plausible that the values of $e_\mathrm {min}$ and $e_\mathrm {max}$ determined here differ from those found in the literature.

2.3 Testing equipment and procedure

Applying a cyclic loading path with $\eta = \mathrm {const}$ requires a triaxial device capable of simultaneously controlling axial and radial stresses during both loading and unloading. To this end, a so called Advanced Dynamic Triaxial Testing System device (DYNTTS) by the manufacturer GDS Instruments was employed here. A sketch of the device is shown in Fig. 2. Essentially, it follows the concept of Bishop and Wesley [7]. Thus, the sample is mounted on a ram, which can be moved in vertical direction to apply the axial load. The axial force is measured at the fixed sample head.

Fig. 2

Sketch of GDS DYNTTS triaxial cell, with LVDT added for axial strain measurement inside the cell [20]

According to the original concept by Bishop and Wesley [7], the ram would be moved hydraulically. In contrast, the DYNTTS is screw-driven by a stepper motor. That allows to measure axial deformation based on the motor steps. However, the displacements determined this way are distorted by mechanical backlash of the drive system whenever the loading direction changes. To resolve this, a linear variable displacement transducer (LVDT) was added to the GDS design. It measures the relative displacement between sample foot and sample head with a precision of $\pm {0,01}\,\mathrm{mm}$ and is not affected by backlash. See also Fig. 2.

The triaxial samples tested for this work were cylindrical and slender, with a ratio of height to diameter of two. They were prepared by dry pluviation, later flushed with CO₂ and de-aired water and then fully saturated with water by applying a back pressure of 300 kPa to the pore system. The back pressure was kept constant throughout consolidation and cyclic loading of the samples. That required water to be pumped out of the sample or into it, the amount of which was measured in order to determine the sample’s volume change. For this method to produce reliable results, loading must be applied slowly enough to allow the sample to drain completely and prevent build-up of excess pore water pressure. This is the reason why the frequency of cyclic loading was limited to 0,002 Hz here.

2.4 Results and discussion

2.4.1 Typical sample response

Figure 3 shows how strains in a medium dense sample evolved during cyclic loading with $\eta = \mathrm {const} = {0.75}$. Apparently, volumetric strains $\varepsilon _\mathrm {v}$ as well as equivalent shear strains $\varepsilon _\mathrm {q}$ were generated. The evolution of $\varepsilon _\mathrm {v}$ and $\varepsilon _\mathrm {q}$ is similar with respect to a number of aspects. During first loading, the relationships between ${p}$ and both strains are nonlinear, with the incremental stiffness becoming larger with increasing ${p}$. Furthermore, the respective values of both strains at the state of maximum stress ($p = p_\mathrm {max}$) increased after each cycle, compared to the preceding cycle. Hence, irrecoverable strains were successively accumulated. These results qualitatively agree with those reported for isotropic and confined compression by Bauer [4], Ko and Scott [23], Mallwitz and Holzlöhner [29], Sawicki and Swidzinski [43], Wichtmann et al. [55].

Figure 3 also reveals notable differences between the volumetric and the deviatoric parts of the sample response. First, $\varepsilon _\mathrm {v}$ is roughly three times larger than $\varepsilon _\mathrm {q}$ during first loading. Second, the volumetric strain curves are much steeper than the deviatoric strain curves during unloading and reloading.

Fig. 3

Typical response of Toyoura Sand to cyclic compression at $\eta = {0.75}$; 200 cycles, $I_\mathrm {Ds} = {35}\,\%$

2.4.2 Variation of stress ratio

Figure 4 depicts how strains evolve in tests with different values for $\eta$ during the consolidation stage and the first cycle with $\eta = \mathrm {const}$. In general, all results are qualitatively similar to those described in Sect. 2.4.1. The impact of $\eta$ is different for $\varepsilon _\mathrm {v}$ and $\varepsilon _\mathrm {q}$, respectively. The $\varepsilon _\mathrm {q}$ response clearly appears to become less stiff if $\eta$ is increased, i. e. $\varepsilon _\mathrm {q}$ grows faster with p. In contrast, the volumetric response does not seem to be significantly affected by different values for $\eta$.

Fig. 4

Impact of stress ratio $\eta$ on strain evolution during monotonic loading and first cycle; $I_\mathrm {Ds} \approx {35} \, \%$

Similar results were obtained in previous works. El-Sohby [18] found that during monotonic $\eta = \mathrm {const}$ compression of fine sand, shear strains grew faster with ${p}$ if $\eta$ was increased. His results furthermore indicate that $\eta$ has no significant impact on the volumetric part of the response in the domain of $\eta \in [0,{1.2}]$ and $p < {1}\,\mathrm{MPa}$. The last result was also obtained by McDowell et al. [30] for $\eta \le 1$ and $p < {2}\,\mathrm{MPa}$.

The evolution of irrecoverable strains across several cycles of unloading and reloading is hard to assess using continuous stress–strain plots as in Fig. 3. Therefore, subsequent discussions focus on the relation between the cycle count ${N}$ and the accumulated irrecoverable strains. The latter are defined as follows. Let a sequence of at least two stress controlled loading cycles be given, with constant mean stress level ($p_\mathrm {av}$, $q_\mathrm {av}$) and constant amplitude ($\mathrm \Delta p$, $\mathrm \Delta q$). Furthermore, let $\varepsilon$ be some scalar strain measure. Then,

$$\begin{aligned} \mathrm \Delta \varepsilon ^\mathrm {p}(N) = \varepsilon (N) - \varepsilon (N-1) \end{aligned}$$

(3)

is the amount of irrecoverable strain induced by the ${N}$th cycle. Based on this, the accumulated irrecoverable strain after the ${N}$th cycle can be defined as

$$\begin{aligned} \varepsilon ^\mathrm {acc}(N) := \sum _{n=1}^{N} \mathrm {\Delta }\varepsilon ^\mathrm {p} (n) \,. \end{aligned}$$

(4)

Figure 5 shows accumulated strain curves for tests with different levels of stress ratio $\eta$. It is evident from the diagrams that both the volumetric component $\varepsilon \mathrm {_v^{acc}}$ and the deviatoric one $\varepsilon \mathrm {_q^{acc}}$ increase with the cycle count ${N}$. Another general result is that the slopes of all curves gradually become less steep as ${N}$ increases, implying that the rate of strain accumulation decreases. The $\varepsilon \mathrm {_v^{acc}}$ curves approach a state of more or less stagnant evolution after only 50 cycles. The accumulation of $\varepsilon \mathrm {_q^{acc}}$, on the other hand, declines less rapid. Even after 200 cycles, the deviatoric strains grow without apparently converging towards any threshold.

Fig. 5

Impact of stress ratio $\eta$ on evolution of accumulated strains; $I_\mathrm {Dc} \approx {40}\, \%$, $p_\mathrm {av} = {200} \,\mathrm{kPa}$, $\mathrm {\Delta }p = {100} \, \mathrm{kPa}$

The value of $\eta$ appears to strongly affect the deviatoric accumulated strain evolution in Fig. 5. Specifically, the larger $\eta$ is, the faster $\varepsilon \mathrm {_q^{acc}}$ increases with ${N}$. In contrast, the $\varepsilon \mathrm {_v^{acc}}$ curves for different $\eta$ scatter only slightly. The range in which all curves reside is rather narrow and no clear trend regarding the impact of $\eta$ can be identified. These properties of the sample response to repeated loading cycles are similar to those obtained from the continuous stress–strain plots in Fig. 4.

Results from previous works imply that isotropic stress changes to samples in an isotropic initial state yield volumetric strains only [55]. This does not seem to fully apply here, because according to Figs. 4 and 5 the sample with $\eta = 0$ also generated a certain amount of deviatoric strains. This is probably caused by an anisotropy of the sample’s fabric which in turn is due to the sample preparation. However, the magnitude of deviatoric strains is very small for $\eta = 0$. Thus, the overall trend with respect to the impact of $\eta$ obtained here is consistent with the ideal result that the deviatoric strains vanish for $\eta \rightarrow 0$.

The impact of $\eta$ on the test results presented in the current section is explained and interpreted as follows. Different values of $\eta$ were obtained by varying the increment $\mathrm {\Delta }q$ of the deviatoric stress. In other words, the larger $\eta$, the larger $\mathrm {\Delta }q$ compared to $\mathrm \Delta p$. Furthermore, ${q}$ is work-conjugate to ${\dot{\varepsilon }}_\mathrm {q}$ in triaxial conditions, as is ${p}$ to ${\dot{\varepsilon }}_\mathrm {v}$  [34]. Hence, it is completely plausible that the deviatoric strains are strongly affected by $\eta$, while the volumetric strains are not. With this in mind, the results allow to draw the conclusion that the volumetric response of sands to external loading with $\eta = \mathrm {const}$ is independent of the value for $\eta$ across a broad range of $\eta$. This applies to monotonic as well as to cyclic loading.

2.4.3 Variation of further test parameters

In Fig. 6, accumulated strain curves for cyclic $\eta = \mathrm {const}$ loading at different pressure levels $p_\mathrm {av}$ are presented. The results indicate that increasing $p_\mathrm {av}$ reduces the permanent deformation induced by a given pressure amplitude after any number of cycles. This interpretation can be further supported by two arguments. First, a similar effect was observed during cyclic shearing of sands at constant radial stress in drained triaxial conditions [53]. Second, sands generally become stiffer in compression with increasing p as long as no grain crushing occurs [31].

In addition to this it is apparent from Fig. 6 that $p_\mathrm {av}$ influences how fast accumulation of permanent volumetric strain declines with ${N}$. The larger $p_\mathrm {av}$ was chosen, the sooner a more or less stationary state was reached in which the soil could not be further compacted by additional loading cycles of the same amplitude. For example, compaction stopped in case of $p_\mathrm {av} = {400}\, \mathrm{kPa}$ at $N \approx 20$, whereas at $p_\mathrm {av} = {120}\,\mathrm{kPa}$ the same amplitude yielded ongoing compaction even after 200 cycles. The deviatoric strain curves in Fig. 6, on the other hand, do not converge towards an upper limit. All of them show continued strain accumulation even after 200 cycles. They differ only with respect to their slope, which gradually becomes steeper with decreasing $p_\mathrm {av}$.

Fig. 6

Impact of $p_\mathrm {av}$ on evolution of accumulated strains; $\eta = {0.6}$, $I_\mathrm {Dc} \approx {40} \,\%$, $\mathrm {\Delta }p = {100}\,\mathrm{kPa}$

Figure 7 illustrates the effect of different values for the pressure amplitude on the response of sand samples loaded cyclically at constant stress ratio. Obviously, an increase in amplitude causes the strain evolution to become steeper. A similar phenomenon was previously observed in cyclic oedometer tests [4, 29] as well as in triaxial tests with cyclic shearing at constant radial stress [53].

Regarding the accumulation rate’s gradual decline with increasing cycle count ${N}$, the results in Fig. 7 are similar to those for different $p_\mathrm {av}$ discussed above. Specifically, the smaller $\mathrm {\Delta }p$ is, the sooner volume change of the samples ceased, whereas the deviatoric response in general does not appear to have converged towards upper limits. For example, the sample loaded with a rather small amplitude of 50 kPa stopped to be significantly compacted after only 20 cycles, while permanent deviatoric strain was accumulated up to $N = 200$.

Fig. 7

Impact of $\mathrm {\Delta }{}p$ on evolution of accumulated strains; $\eta = {0.6}$, $I_\mathrm {Dc} \approx {40}\,\%$, $p_\mathrm {av} = {200}\,\mathrm{kPa}$

The impact of the relative sample density after consolidation $I_\mathrm {dc}$ on the test results can be studied by means of Fig. 8. Accordingly, the larger the density is, the less permanent strain is accumulated within a given number of cycles. This outcome was, of course, to be expected because strength and stiffness of non-cohesive soils are known to increase strongly with the soil’s density [3].

Fig. 8

Impact of relative soil density on evolution of accumulated strains; $\eta = {0.6}$, $p_\mathrm {av} = {200}\,\mathrm{kPa}$, $\mathrm {\Delta }p = {100}\,\mathrm{kPa}$

3 Bounding Surface framework

3.1 Basic concepts

The test results presented in Sect. 2 prove that cyclic compression causes significant irrecoverable deformation in sands. This emphasises the need to find a constitutive model which accounts for cyclic compression more realistically than the existing approaches discussed in Sect. 1. With regard to that, the constitutive model for sands by  Li [26] is chosen as basic framework here. Therefore, it will be introduced in detail subsequently.

The model is founded upon the Theory of Bounding Surface Plasticity [13]. Therefore, the total rate of strain is additively decomposed into an elastic and a plastic part via

$$\begin{aligned} \dot{\varvec{\varepsilon }} = \dot{\varvec{\varepsilon }}^{\mathrm {e}} + \dot{\varvec{\varepsilon }}^{\mathrm {p}}\,. \end{aligned}$$

(5)

The stress rate is calculated from an elastic rate equation of the form

$$\begin{aligned} \dot{\varvec{\sigma }} = \mathbf {c}^\mathrm {e}(e,p) : ( \dot{\varvec{\varepsilon }} - \dot{\varvec{\varepsilon }}^\mathrm {p})\,, \end{aligned}$$

(6)

in which $\mathbf {c}^\mathrm {e}$ is the fourth-order elastic stiffness tensor. The latter is a nonlinear function of void ratio ${e}$ and mean effective stress ${p}$ through the empirical equation for the shear modulus by Richart et al. [42]

$$\begin{aligned} G = G_0\frac{\left( {2.97}-e\right) ^2}{1+e}\sqrt{pp_\mathrm {a}} \,. \end{aligned}$$

(7)

Therein, $G_0$ is a dimensionless model constant and $p_\mathrm {a} = {101}\,\mathrm{kPa}$ is the atmospheric pressure, used for normalisation. The second model constant involved in forming $\mathbf {c}^\mathrm {e}$ is the Poisson’s ratio $\nu$.

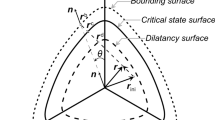
Following the approach of Wang et al. [52], the plastic strains $\dot{\varvec{\varepsilon }}^{\mathrm {p}}$ are obtained from two separate mechanisms, each of which accounts for one term of (1). The first plastic mechanism $\dot{\varvec{\varepsilon }}^\mathrm {p1}$ is driven by the stress ratio rate $\dot{\varvec{r}}$. It relies on a cone-shaped bounding surface that is shown in Fig. 9. The second plastic mechanism $\dot{\varvec{\varepsilon }}^\mathrm {p2}$ accounts for the ${\dot{p}}$ term of (1) and thus contributes irrecoverable deformations induced by changes of ${p}$ at constant $\varvec{r}$. Its bounding surface is also illustrated in Fig. 9. It is a flat cap, which closes the cone perpendicular to the hydrostatic axis. The cone and the cap mechanism are combined additively to yield

$$\begin{aligned} \dot{\varvec{\varepsilon }}^\mathrm {p} = \dot{\varvec{\varepsilon }}^\mathrm {p1} + \dot{\varvec{\varepsilon }}^\mathrm {p2} \end{aligned}$$

(8)

This work focuses on the ${\dot{p}}$ mechanism of the model, which is comprehensively described in the following section. The $\dot{\varvec{r}}$ mechanism, however, is inactive for the stress paths considered here. Because of that it will not be further addressed. Please refer to Li [26] instead.

Fig. 9

Illustration of bounding surfaces in principal stress space; adapted with permission from Carow et al. [10, p. 606], Copyright (2017) Wiley

3.2 Plastic cap mechanism

Li [26] defined the second term of (8) as

$$\begin{aligned} \dot{\varvec{\varepsilon }}^\mathrm {p2} = {\dot{\lambda }}_2 \left( \bar{\varvec{m}} + \sqrt{{2}/{27}} D_2 \varvec{I} \right) \,, \end{aligned}$$

(9)

with the deviatoric unit flow direction

$$\begin{aligned} \bar{\varvec{m}} ={\varvec{r}}/{\Vert \varvec{r}\Vert } \,. \end{aligned}$$

(10)

The magnitude of plastic flow in (9) is governed by the plastic multiplier ${\dot{\lambda }}_2$ and by the dimensionless dilatancy $D_2$. The discussion of the formula for $D_2$ is postponed to the subsequent section. First, more constitutive ingredients proposed by Li [26] are recalled in order to derive an expression for the plastic multiplier ${\dot{\lambda }}_2$.

The equation of the cap is

$$\begin{aligned} F_2 = {\bar{p}} - H_2 = 0 \,, \end{aligned}$$

(11)

in which the hardening parameter $H_2$ defines the position of the cap on the hydrostatic axis and ${{\bar{p}}}$ is the bounding surface image of ${p}$. This image is obtained by means of the mapping rule

$$\begin{aligned} {\bar{p}} = {\left\{ \begin{array}{ll} H_2 &{} \text {if } {\dot{p}} > 0 \,, \\ 0 &{} \text {if } {\dot{p}} < 0 \,. \end{array}\right. } \end{aligned}$$

(12)

The hardening rule that formally controls the evolution of $H_2$ is

$$\begin{aligned} {\dot{H}}_2 = {\bar{K}}_{\mathrm {p}2}{\dot{\lambda }}_2\,, \end{aligned}$$

(13)

with ${\bar{K}}_\mathrm {p2}$ being the plastic modulus. Combining the differential form of (11) with (13) results in the condition of consistency

$$\begin{aligned} \dot{{\bar{p}}} - {\bar{K}}_{\mathrm {p}2}{\dot{\lambda }}_2 = 0 \,. \end{aligned}$$

(14)

The Theory of Bounding Surface Plasticity then allows to map (14) from ${{\bar{p}}}$ onto ${p}$, yielding

$$\begin{aligned} {\dot{p}} - K_{\mathrm {p}2}{\dot{\lambda }}_2 = 0 \,. \end{aligned}$$

(15)

By substituting (15) and (10) into (9), the strain rate of the plastic cap mechanism can finally be expressed as

$$\begin{aligned} \dot{\varvec{\varepsilon }}^{\mathrm {p}2} = \left( \frac{1}{K_{\mathrm {p}2}}\frac{\varvec{r}}{\Vert \varvec{r}\Vert } + \sqrt{\frac{2}{27}}\frac{D_2}{K_{\mathrm {p}2}}\varvec{I}\right) {\dot{p}}\,. \end{aligned}$$

(16)

Its scalar invariants, as defined in Appendix A, are

$$\begin{aligned} {\dot{\varepsilon }}^\mathrm {p2}_\mathrm {q} = \sqrt{\frac{2}{3}}\frac{1}{K_{\mathrm {p}2}}{\dot{p}}\,,\quad {\dot{\varepsilon }}^\mathrm {p2}_\mathrm {v} = \sqrt{\frac{2}{3}}\frac{D_2}{K_{\mathrm {p}2}}{\dot{p}} \,. \end{aligned}$$

(17)

3.3 Plastic modulus and dilatancy

The plastic modulus introduced with (15) is defined as

$$\begin{aligned} K_{\mathrm {p}2} = G(e,p) h_4 \left( \frac{M_\mathrm {c}g(c, \theta )}{\eta }\right) h_\beta \ {\operatorname {sgn}} \, {\dot{p}} \end{aligned}$$

(18)

In this equation, $h_4$ is a constitutive parameter that directly controls the magnitude of $\dot{\varvec{\varepsilon }}^\mathrm {p2}$. The quantity $M_\mathrm {c}$ in (18) is the critical state stress ratio encountered when a triaxial sample is sheared to large strains by increasing the axial load while keeping the lateral stress constant. It is considered a unique soil property, consistent with the classical Critical State Soil Mechanics [44].

The function $g(c, \theta )$ in (18) prescribes the cone’s shape in the deviatoric plane. It depends on the Lode angle $\theta$ and the model constant $c = M_\mathrm {e} / M_\mathrm {c}$, in which $M_\mathrm {e}$ is the critical state stress ratio measured in triaxial extension. The product $M_\mathrm {c}g(c, \theta )$ is the generalised critical state stress ratio for the current shear mode. The argument ${c}$ of ${g}$ is suppressed subsequently for the sake of a clear presentation.

Furthermore, (18) includes the term

$$\begin{aligned} h_\beta = \left( {{\bar{\rho }}_2}/{\rho _2}\right) ^a \,, \end{aligned}$$

(19)

which is referred to here as cyclic loading factor. It accounts for the soil’s stress history in terms of the bounding surface distances

$$\begin{aligned} {\bar{\rho }}_2 = |{\bar{p}} - \beta |\quad \text {and} \quad \rho _2 = |p - \beta |\,, \end{aligned}$$

(20)

with the so-called projection centre $\beta$ being defined as the value of ${p}$ at the most recent reversal of ${\operatorname {sgn}} \, \dot{p}$. The model parameter ${a}$ in (19) controls to what extend the plastic strain rate is modified by $h_\beta$.

The dilatancy function by Li [26] reads

$$\begin{aligned} D_2 = d_2 \left\langle \frac{ M_\mathrm {c} g(\theta ) }{ \eta } - 1 \right\rangle {\operatorname {sgn}} \, {\dot{p}} \,. \end{aligned}$$

(21)

The only additional symbol introduced there is the model constant $d_2$. It allows to adjust the magnitude of the plastic volumetric strain rate.

According to (17), (18) and (21), the value of $\eta$ influences the plastic strain rate of the $\dot{p}$ mechanism by Li [26] as follows.

• ${{\dot{\varepsilon }}}\mathrm {_q^{p2}}$ vanishes for isotropic states ($\eta = 0$) and grows with increasing $\eta$. This is consistent with results of triaxial tests on sand samples by El-Sohby [18].

• ${{\dot{\varepsilon }}}\mathrm {_v^{p2}} = 0$ for $\eta \ge M_\mathrm {c}g(\theta )$. This was implemented in order to comply with the hypothesis of Critical State Soil Mechanics that the void ratio is constant at the critical state.

• ${{\dot{\varepsilon }}}\mathrm {_v^{p2}}$ increases with decreasing $\eta$ and has its maximum at $\eta = 0$. This point is further addressed in Sect. 4.2.

3.4 Description of model operation

Consider a soil element in an anisotropic stress state that is loaded along a path with constant stress ratio. Furthermore, let $\eta = {0.6}$ and the initial condition $\beta = 0$ be given. Then, as long as $\dot{p} > 0$,

• the cap hardens isotropically ($\dot{{\bar{p}}} > 0$).

• the stress point remains on the cap ($p = {{\bar{p}}}$).

• the cyclic loading factor is inactive (${{\bar{\rho }}}_2 / \rho _2 = 1$).

Please note that the model response is elastic-plastic from the very beginning. No yield criterion or range of purely elastic response is involved. This fact is illustrated by Fig. 10. It shows how the model response to the loading example described above is composed from the contributions of the elastic and the plastic model components.

Fig. 10

Role of elastic and plastic model components during simulation of triaxial compression with $\eta = \mathrm {const} = {0.6}$; $d_2 = 3.0$

As soon as the loading direction reverses at $p = p_\mathrm {max}$, indicated by a change in ${\operatorname {sgn}} \, \dot{p}$, the stress history is updated:

• The image point ${{\bar{p}}}$ is relocated to the origin (${{\bar{p}}} \rightarrow 0$).

• The projection centre is relocated to the point of maximum pre-stress ($\beta \rightarrow p_\mathrm {max}$).

In the course of an unloading phase with $\dot{p} < 0$, the factor $h_\beta$ evolves from infinity at $p = p_\mathrm {max}$ to one at $p = 0$. Therefore, the plastic strain rate is zero initially and increases continuously afterwards. The effect of that becomes apparent from Fig. 10 by comparing the full model’s output to the response obtained with $h_\beta = {1.0}$, i. e. without the cyclic loading factor.

If the direction of $\dot{p}$ changes from unloading to loading at some lower bound $p = p_\mathrm {min}$, the process described above is repeated, but this time with $\beta = p_\mathrm {min}$ and ${{\bar{p}}} = p_\mathrm {max}$. As soon as reloading exceeds the level of maximum pre-stress, the cyclic loading factor automatically becomes inactive due to $p = {{\bar{p}}}$. Hence, the elastic-plastic stiffness is then obtained in the same way as during first loading.

4 Modifications to the model

4.1 Aims and methods

In order to realistically capture the behaviour of sands due to cyclic compression at constant stress ratio, the theoretical formulation of the $\dot{p}$ mechanism by Li [26] requires some refinements. The current section aims to carefully analyse which model components need to be enhanced and how that can be achieved.

The remainder of the paper relies on graphical representations of computation results which were obtained by means of two tools. First, the numerical implementation of the model with explicit time integration and adaptive error control described by Carow and Rackwitz [9] was employed. Second, the software IncrementalDriver by Niemunis [35] was used to apply loading paths of idealised element tests at stress point level and for post-processing.

Unless stated otherwise, constitutive parameters for Toyoura Sand according to Table 3 were used. For most results presented in Sect. 4, though, the dilatancy parameter $d_2$ was enlarged in order to illustrate the role of the model’s dilatancy function more clearly.

Please note that in Sect. 4 the constitutive model’s properties are discussed referring to hypothetical loading situations and experimental investigations from previous works only. This way, the results of the test series described in Section 2 are preserved exclusively for calibrating and validating the extended model in Sect. 5.

Table 3 Constitutive parameters for Toyoura Sand [26]

4.2 Volumetric strain rate at different stress ratios

The volumetric strain rate of the plastic $\dot{p}$ mechanism proposed by Li [26] varies with the stress ratio magnitude $\eta$, as described in Sect. 3.3. In contrast, no major impact of $\eta$ on the volume change of sand samples was observed in the experimental data presented in Sect. 2. In order to further investigate this discrepancy, the model was employed to reproduce constant stress ratio compression tests by El-Sohby [18]. The constitutive parameters listed in Table 3 were adopted for that, with the values of $h_4$ and $d_2$ optimised to achieve the best-possible fit of the computation results to the experimental data.

The outcome is presented in Fig. 11. It confirms what has already been suspected. The volumetric strains are largely insensitive to different values of $\eta$ in the tests, but vary significantly with $\eta$ in the model output.

Fig. 11

Simulation vs. experiment for triaxial loading with $\eta = \mathrm {const}$ for loose initial state; model formulation by Li [26]; $h_4 = {1.7}$, $d_2 = {2.6}$; experimental data by El-Sohby [18]

To overcome this issue, the dilatancy function $D_2$ introduced with (21) has to be modified. The simplest solution would be to remove the term $-1$, rendering the volumetric plastic strain rate (17) completely stress ratio independent. In fact, this suffices to reproduce the test results for compression with different $\eta$ reported here and by El-Sohby [18]. However, it leads to a non-zero plastic volumetric strain rate at the critical state, for which $\eta = M_\mathrm {c} g(\theta )$. That negatively affects simulation results obtained by the model for undrained shearing.

A more convenient remedy emanates from the work by Gao and Zhao [19]. Accordingly, the dilatancy function is reformulated as

$$\begin{aligned} D_2 = d_2 \frac{M_\mathrm {c}g(\theta )}{ \eta } \left\langle 1- \left( \frac{ \eta }{M_\mathrm {c}g(\theta )}\right) ^X \right\rangle {\operatorname {sgn}}\,{\dot{p}} \,. \end{aligned}$$

(22)

In this equation, the exponent X is a constant. If it is assigned a sufficiently large value, say $X = 10$, the terms in (22) related to $\eta$ act in the manner of switches rather than inducing a continuous variation of ${\dot{\varepsilon }}_\mathrm {v}^\mathrm {p2}$ with $\eta$. Thus, the volumetric plastic strain rate becomes largely independent of $\eta$ for stress ratios below the critical state, but still vanishes for $\eta \ge M_\mathrm {c}g(\theta )$.

Simulation results with the modified dilatancy (22) are presented in Fig. 12. They clearly prove that due to the modification the experimental data is much better reproduced than in Fig. 11.

Fig. 12

Simulation vs. experiment for triaxial loading with $\eta = \mathrm {const}$ for loose initial state; model formulation by Li [26] with modified dilatancy (22); $h_4 = {1.6}$, $d_2 = {2.6}$; experimental data by El-Sohby [18]

4.3 Impact of void ratio

The strength and stiffness properties of non-cohesive soils vary considerably with void ratio ${e}$, or equivalently, soil density. This is clear from standard text books [eg. 3] as well as from the constant stress ratio compression tests described in Sect. 2. A comprehensive soil model would naturally be expected to account for the influence of ${e}$. This is the reason why the plastic modulus and the dilatancy of the $\dot{\varvec{r}}$ mechanism by Li [26] were formulated in terms of ${e}$ and the state parameter $\psi$. The latter is a combined measure for density and pressure level, first proposed by Been and Jefferies [5].

The plastic strain rate of the $\dot{p}$ mechanism, on the other hand, depends on ${e}$ only through the empirical formula (7) for the elastic shear modulus ${G}$, see (17) and (18). In order to explore whether this approach yields realistic results, constant stress ratio compression tests with different initial void ratios reported by El-Sohby [18] were simulated. Figure 13 shows the results. Apparently, the model can reproduce the behaviour of the “loose” sample quite well. This is because the parameters $h_4$ and $d_2$ were calibrated to the “loose” response. In case of the ”dense” sample, however, the computed strain curves evolve much faster with ${p}$ than the experimental data. This implies that the stiffness obtained from the constitutive functions varies too little with ${e}$.

Fig. 13

Simulation vs. experiment for triaxial loading with $\eta = \mathrm {const} = {0.75}$ and different initial densities; model by Li [26]; $h_4 = {1.7}$, $d_2 = {2.6}$; experimental data by El-Sohby [18]

In order to improve the model, an extension for the plastic modulus is proposed. More specifically, the parameter $h_4$ in the original formula (18) is replaced by a new function $\omega (h_4,e)$. The extended plastic modulus then becomes

$$\begin{aligned} K_{\mathrm {p}2} = G (p,e) \omega (h_4,e) \left( \frac{M_\mathrm {c}g(\theta ) }{\eta }\right) h_\beta \ {\operatorname {sgn}} \, {\dot{p}} \,. \end{aligned}$$

(23)

Parametric studies were conducted to find a specific expression for $\omega$. This revealed that $\omega$ should evolve nonlinearly and rather steep with ${e}$. The best compromise with respect to realistic simulation results as well as mathematical simplicity was achieved with

$$\begin{aligned} \omega = \frac{ h_4 e }{ e-e_\mathrm {min} } \,. \end{aligned}$$

(24)

Therein, $e_\mathrm {min}$ is the void ratio at densest packing of the soil. This is not considered a new constitutive parameter, since it is usually determined in the course of any geotechnical investigation by standard compaction tests.

The extension proposed above was applied to the same test case that had been considered before to assess the model’s abilities regarding different initial void ratios. The simulation results, shown in Fig. 14, fit the experimental data considerably better than was possible with the original constitutive equations, compare Fig. 13. The modifications (23) and (24) therefore are proven to work as intended.

Fig. 14

Simulation vs. experiment for triaxial loading with $\eta = \mathrm {const} = {0.75}$ and different initial densities; model by Li [26] with modifications (22) and (23); $h_4 = {0.4}$, $d_2 = {1.0}$; experimental data by El-Sohby [18]

4.4 Impact of pressure level

Next, a rather subtle issue of the $\dot{p}$ mechanism by Li [26] is discussed, which is not readily apparent from the theoretical formulation. It was identified while attempting to reproduce experimental data for cyclic compression at different pressure levels $p_\mathrm {av}$. Please see Fig. 15 for an illustration. Therein, the model response to isotropic loading cycles with two different $p_\mathrm {av}$ is compared.

Figure 15 (a) shows how $\varepsilon _\mathrm {v}$ evolves with ${p}$ in a computation with $p_\mathrm {av} = {200}\,\mathrm{kPa}$. Accordingly, the value of $\varepsilon _\mathrm {v}$ after each complete cycle is larger than at the beginning of that cycle. Thus, the simulated soil element is gradually compacted, which is consistent with basic findings of all experiments referred to in Sect. 1 and 2. For $p_\mathrm {av} = {120}\,\mathrm{kPa}$, on the other hand, the computed $\varepsilon _\mathrm {v}$ at the end of each cycle is smaller than at its beginning, as shown in Fig. 15 (b). Hence, the model predicts that the soil becomes looser during cyclic isotropic loading. That obviously contradicts real sand behaviour. Compare for example the results of triaxial tests presented in Fig. 6.

Further investigations revealed that the problem is due to the model responding too stiff during reloading if the preceding unloading phase ended at a pressure level with $p \ll {100}\mathrm{kPa}$. One possible remedy would be to use different elastic stiffness parameters for unloading and reloading, respectively, as suggested by Pestana and Whittle [39]. Incorporating this approach into the model by Li [26], however, would also change the response to shearing. Therefore, modifications to the plastic $\dot{\varvec{r}}$ mechanism would be required, which should be avoided here.

Instead, the present work proposes to increase the amount of plastic volumetric strains generated by the $\dot{p}$ mechanism during reloading. This is accomplished by equipping the dilatancy function (22) with a cyclic loading factor $h_{\gamma }$ via

$$\begin{aligned} D_2 = d_2 \frac{M_\mathrm {c}g(\theta )}{\eta } \left\langle 1- \left( \frac{\eta }{M_\mathrm {c}g(\theta )}\right) ^X \right\rangle h_\beta h_\gamma \ {\operatorname {sgn}}\,{\dot{p}} \,, \end{aligned}$$

(25)

in which

$$\begin{aligned} h_\gamma = \left( \frac{\rho _2}{{\bar{\rho }}_2} \right) ^a + \gamma _0 \left( 1 - \left( \frac{\rho _2}{{\bar{\rho }}_2} \right) ^a \right) \frac{1+{\operatorname {sgn}} \, \dot{p}}{2} \,. \end{aligned}$$

(26)

The main implications of (25) and (26) are:

• ${\dot{\varepsilon }}\mathrm {_v^{p2}}$ according to (17) becomes independent of $h_\beta$.

• During first loading ($\rho _2 = {{\bar{\rho }}}_2$) as well as during unloading (${\operatorname {sgn}} \, \dot{p} = -1$), $D_2$ according to (22) is retained.

• $\gamma _{0}$ is the initial value of $h_\gamma$ immediately after ${\operatorname {sgn}} \, \dot{p}$ switched from ${-1}$ to 1.

• During reloading (${\operatorname {sgn}} \, \dot{p} = 1$), $\rho _2$ evolves from 0 to ${{\bar{\rho }}}_2$. Hence, $h_\gamma$ varies between $\gamma _0$ and 1.

• Setting $\gamma _0 = 0$ yields the same plastic strain rate as the model by Li [26]

In order to illustrate the effect of the extension, different values for $\gamma _0$ were adopted for the simulation of isotropic loading, unloading and reloading. The results are shown in Fig. 16. They demonstrate that $\gamma _0$ affects only the reloading branch and that the larger $\gamma _0$ is, the more strain is produced. Consequently, the total strain difference $\mathrm {\Delta }\varepsilon _\mathrm {v}$ between the end points of first loading and reloading increases with $\gamma _0$. The cyclic loading factor for $D_2$ thus works as intended.

Assuming $\gamma _0$ to be constant would of course be inconvenient for a comprehensive soil model. Instead, Fig. 15 suggests that the smaller ${p}$ is at the onset of reloading, the larger $\gamma _0$ should be. This dependency can be expressed through a suitable function of the dimensionless quantity

$$\begin{aligned} \gamma _\mathrm {rev} = \left( \frac{ p_\mathrm {max} - p_\mathrm {min} }{ p_\mathrm {max} } \right) ^a \,, \end{aligned}$$

(27)

which is the value of $h_\beta$ at the end of the unloading phase. The stress reversal points where termed $p_\mathrm {min}$ and $p_\mathrm {max}$ for clarity here, consistent with Fig. 1. Nevertheless, their values are not stored at stress point level, but are obtained from the internal state variables $\beta$ and ${{\bar{p}}}$.

As a first approximation, $\gamma _0$ is assumed to depend linearly on $\gamma _\mathrm {rev}$. Thus,

$$\begin{aligned} \gamma _0 = m_d \gamma _\mathrm {rev} + n_d \,. \end{aligned}$$

(28)

Validating this approach and determining the constants $m_d$ and $n_d$ is postponed to Sect. 5.4 because these tasks require experimental data.

Fig. 15

Simulation of cyclic isotropic compression; model formulation by Li [26]; $e_0 = {0.778}$, $d_2 = {3.0}$

Fig. 16

Simulation of cyclic isotropic compression; model formulation by Li [26] with extended dilatancy (25); $e_0 = {0.778}$, $d_2 = {3.0}$

4.5 Excessive plastic strain accumulation

4.5.1 Problem statement

Sect. 3.3 and 3.4 explained how the $\dot{p}$ mechanism by Li [26] handles unloading and reloading. Accordingly, the stress history is accounted for in terms of the two internal state variables $\beta$ and ${{\bar{p}}}$, the values of which vary within each loading cycle between $p_\mathrm {max}$, $p_\mathrm {min}$ and zero. See Fig. 1 for a definition of the stress parameters. The sequence of that variation does not change across cycles. Therefore, the response to the first cycle is repeated for every following cycle.

The effect of this has already been briefly mentioned in Sect. 1. Nevertheless, it should be demonstrated here. To this end, cyclic isotropic compression was simulated using the model. Figure 17 (a) depicts the computed evolution of the void ratio with ${p}$. It is evident that each cycle reduces ${e}$ by the same amount as the previous cycle. That means, irrecoverable deformation is accumulated, with the increment per cycle being constant. Consequently, the soil is continuously compacted, without a lower limit being recognisable in the course of 20 cycles. This complies with the foregoing notes on the model formulation. However, it contradicts basic findings from the experiments described in Sect. 1 and 2, according to which the rate of strain accumulation strongly declines with increasing ${N}$.

4.5.2 Solution approach

The excessive accumulation of irrecoverable deformation in the computation is obviously caused by the plastic functions of the constitutive model. So one way to obtain a more realistic response is to successively deactivate these functions. To this end, a new factor $H_\mathrm {c}$ is proposed to be incorporated into (23), by virtue of which

$$\begin{aligned} K_{\mathrm {p}2} = G(p,e) \omega (h_4,e) \left( \frac{M_\mathrm {c}g(\theta ) }{\eta }\right) h_\beta H_\mathrm {c} \ {\operatorname {sgn}} \, {\dot{p}} \,. \end{aligned}$$

(29)

The term $H_\mathrm {c}$ should be unity during monotonic loading and gradually increase during repeated unloading and reloading. This way, $K_\mathrm {p2}$ would also grow, reducing the magnitudes of both ${\dot{\varepsilon }}\mathrm {_v^{p2}}$ and ${\dot{\varepsilon }}\mathrm {_q^{p2}}$ according to (17). So in essence, the extension causes the plastic strain rate to successively decline. Therefore, $H_\mathrm {c}$ will be referred to as degradation factor subsequently.

4.5.3 Shape of the degradation factor

The model extension (29) relies on the assumption that the constitutive functions yield reasonable results for monotonic loading. Thus, the degradation factor should only be in effect during unloading and reloading. This is achieved by shaping $H_\mathrm {c}$ as

$$\begin{aligned} H_\mathrm {c} =\left( \frac{\rho _2}{{\overline{\rho }}_2}\right) ^X +h_\kappa \left( 1-\left( \frac{\rho _2}{{\overline{\rho }}_2}\right) ^X\right) \,. \end{aligned}$$

(30)

The actual constitutive response induced by (30) comes from the term $h_\kappa$, to be defined later. The exponent X is a constant, default to $X = 10$, as has already been discussed with respect to (22). Consequently, those terms in (30) which are raised to the power of X act as switches. They are unity as long as $\rho _2 = {{\bar{\rho }}}_2$ (monotonic loading) and near to zero when $\rho _2 < {{\bar{\rho }}}_2$ (unloading and reloading). This leads to the desired result

$$\begin{aligned} H_\mathrm {c} \approx {\left\{ \begin{array}{ll} 1, &{}\text {if }\rho _2 = {{\bar{\rho }}}_2 \,,\\ h_\kappa , &{}\text {if }\rho _2 < {{\bar{\rho }}}_2\,. \end{array}\right. } \end{aligned}$$

4.5.4 Choosing a state variable

The main input of the function $h_\kappa$ introduced with (30) should be an internal state variable which tracks the soil’s deformation history through multiple loading cycles. In plasticity theories, such variables are most naturally derived from some measure of accumulated plastic strain. One of the earliest works proposing that was the one by Ghaboussi and Momen [21]. Li [26] also adopted this approach for the $\dot{\varvec{r}}$ mechanism by rendering the plastic modulus of the cone bounding surface a function of the cone’s accumulated plastic shear strain $\lambda _1$.

The extension (29) of the $\dot{p}$ mechanism is supposed to work for anisotropic as well as for isotropic loading paths. The latter only induce volumetric strains, as noted in Sect. 3.3. Therefore, the degradation factor cannot be formulated in terms of plastic shear strains. Rather than that, the accumulated value $\kappa _2$ of the plastic volumetric strain ${\dot{\varepsilon }}\mathrm {_v^{p2}}$ is used. It can be formally defined through

$$\begin{aligned} \kappa _2(t) = \kappa _2(t_0) + \int _{t_0}^{t}{\dot{\varepsilon }}_\mathrm {vol}^{\mathrm {p}2}(\tau )\mathrm {d}\tau \,. \end{aligned}$$

(31)

The actual value of $\kappa _2$ depends on the reference point for the plastic strains $\varvec{\varepsilon }^\mathrm {p2}$, which in general may be chosen arbitrarily. If $h_\kappa$ were formulated in terms of $\kappa _2$ alone, the model response would depend on the choice for that reference point. This unnecessarily restricts the generality of the model. Therefore, the relative accumulated strain $\kappa _2 - \kappa _\mathrm {ref}$ is used as argument for $h_\kappa$ here, with $\kappa _\mathrm {ref}$ being the value of $\kappa _2$ at the first reversal of the loading direction.

4.5.5 Expression for $h_\kappa$

Once activated by the switch terms in (30), the function $h_\kappa$ should steadily increase with $(\kappa _2 - \kappa _\mathrm {ref})$. Various kinds of mathematical expressions could be used for $h_\kappa$ to obtain that kind of behaviour. For the sake of simplicity and numerical robustness, a linear formula is proposed here as follows:

$$\begin{aligned} h_\kappa = h_5\left( \frac{\kappa _2-\kappa _\mathrm {ref}}{{0.001}}\right) + 1 \end{aligned}$$

(32)

The constitutive parameter $h_5$ controls how quickly $h_\kappa$ grows. The relative plastic strain is divided by 0.001 because its value is expected to be rather small in engineering problems and thus needs to be amplified. Without this amplification, the degradation factor would not have a pronounced effect on the evolution of $K_\mathrm {p2}$, or the parameter $h_5$ would have be to be assigned a very large value.

4.5.6 Degradation of volumetric plastic strain rate

The experimental results presented in Section 2 indicate that the volumetric component of the accumulated strains declines faster with the cycle count ${N}$ than the deviatoric one. To account for this, the degradation factor is also incorporated into the dilatancy (25), yielding

$$\begin{aligned} D_2 = d_2 \frac{M_\mathrm {c}g(\theta )}{\eta } \left\langle 1- \left( \frac{\eta }{M_\mathrm {c}g(\theta )}\right) ^X \right\rangle h_\beta h_\gamma H_\mathrm {c}^{-h_6} \ {\operatorname {sgn}} \, {\dot{p}} \,. \end{aligned}$$

(33)

The implications of this are twofold. First, the degradation factor $H_\mathrm {c}$ enters ${\dot{\varepsilon }}\mathrm {_v^{p2}}$ through $K_\mathrm {p2}$ as well as through $D_2$, see (17). Thus, the volumetric plastic strain rate should degenerate faster than the deviatoric one, consistent with the experimental data. Second, the additional constitutive parameter $h_6$ allows to specifically adjust the degradation of ${\dot{\varepsilon }}\mathrm {_v^{p2}}$. In contrast, the parameter $h_5$ introduced with (32) enters both ${\dot{\varepsilon }}\mathrm {_q^{p2}}$ and ${\dot{\varepsilon }}\mathrm {_v^{p2}}$ directly.

4.5.7 Effect of the modifications

In order to demonstrate that the modifications proposed in Sect. 4.5 yield the desired effect, the simulation of cyclic isotropic compression discussed initially was repeated with the extended model. For the parameters $h_5$ and $h_6$ fictitious values of 3 and 1 were assumed.

Figure 17 (b) shows the outcome. Apparently, each of the first three cycles reduces ${e}$ permanently by a noticeable amount. Afterwards, the gaps between the ${e}$-${p}$ loops become smaller, which means that the increment of permanent deformation per cycle declines. This implies that the degradation factor successively reduced the accumulation of plastic strains, as intended.

The calibration and validation of the degradation factor with respect to experimental data is detailed in Sect. 5.

Fig. 17

Simulation of 20 isotropic loading cycles; $d_2 = {3.0}$; sub-figure (b): model formulation by Li [26] with modifications (29) and (33) but extensions for void ratio and pressure level deactivated by $\omega (h_4, e ) = \gamma _0 = 0$ 

5 Calibration and validation of the extended model

5.1 Preliminaries

In order to validate the modified constitutive functions, they should be used to simulate the cyclic triaxial tests on Toyoura Sand described in Sect. 2. For that purpose, the model parameters of the $\dot{p}$ mechanism for Toyoura Sand reported by Li [26] and listed here in Table 3 could not be used. First, because they have never been validated against actual test results, or at least there are no reports on that. Second, because the modifications proposed in Sect. 4 shifted the parameter’s meaning slightly. Hence, it became necessary to carefully calibrate all parameters which are exclusively related to the extended $\dot{p}$ mechanism. This is described comprehensively in Sect. 5.2 to 5.5. Nevertheless, the parameter set from Table 3 served as basis for the calibration procedure and was thus used for all computations unless noted otherwise.

Apart from the plastic parameters, the model response to $\eta = \mathrm {const}$ compression is also affected by the elastic constants ($G_0$, $\nu$) and the critical state parameters $M_\mathrm {c}$ and ${c}$. The relevant values can be adopted from Table 3 because they were proven to fit experimental data for Toyoura Sand by Li and Dafalias [27, 28].

The computations presented in the subsequent sections cover only the first 50 cycles of the test results from Sect. 2. This is the usual range of applicability for constitutive models which link rates of stresses and strains, such as the one considered here [53]. If more cycles are simulated, numerical errors distort the results and the computational costs become too high.

5.2 Calibration of parameters related to monotonic loading

The model parameters $h_4$ and $d_2$ have already been present in the original $\dot{p}$ mechanism by Li [26]. They control the magnitude of the plastic strain rate during monotonic as well as during cyclic loading. This has been discussed in detail in Sect. 3.3.

Li [26] proposed to calculate $d_2$ from $K_0$ and then calibrate $h_4$ to ${e}$-${p}$ lines obtained from isotropic compression. This was found here to yield unsatisfactory results for anisotropic $\eta = \mathrm {const}$ compression. The method was probably motivated by the fact that no tests results with respect to $\eta = \mathrm {const}$ compression were available for Toyoura Sand. This is now resolved by the data for anisotropic consolidation presented in Sect. 2.4.2, which allows to calibrate both $h_4$ as well as $d_2$ directly.

The constant for $h_4$ can be found by calibrating the model output to fit the $\varepsilon _\mathrm {q}$ curve of a triaxial test with monotonic $\eta = \mathrm {const}$ loading and $\eta \gg 0$. This is demonstrated in Fig. 18 based on the anisotropic consolidation phase of test No. TCR04. The best fit was achieved here with $h_4 = {1.0}$. Please note that $h_4$ also affects the $\varepsilon _\mathrm {v}$ evolution because $K_\mathrm {p2}$ enters both components of the plastic strain rate in (17). However, this is of no relevance here and therefore the impact of $h_4$ on $\varepsilon _\mathrm {v}$ is not shown in Fig. 18.

Fig. 18

Calibration of model parameter $h_4$ to the shear strain evolution during triaxial loading at constant $\eta$ with $\eta = {0.75}$; $I_\mathrm {Dc} = {39} \, \%$

An appropriate value for the dilatancy parameter $d_2$ is found by fitting computation results to the volumetric component of the experimental data that has already been used to calibrate $h_4$. As shown in Fig. 19, the optimal value turned out to be $d_2 = {3.2}$ here. Since $d_2$ has no effect on the deviatoric strain curves, these are not included in Fig. 19. Instead, see the graph for $h_4 = {1.0}$ in Fig. 18, which was obtained in all computations performed to calibrate $d_2$.

Fig. 19

Calibration of model parameter $d_2$ to the volumetric strain curve of the same triaxial test already referred to in Fig. 18; $h_4 = {1.0}$

5.3 Calibration of cyclic loading factor exponent

The third and last constitutive parameter that has already been included in the original model formulation is the exponent ${a}$ of the cyclic loading factor (19). According to Li [26, p. 180], it “provides a means to adjust the opening of the ${e}$-${p}$ hysteretic loop under the swelling-recompression cycles”. Besides, the exponent ${a}$ turned out to strongly affect the amount of irrecoverable strain induced by unloading and reloading. This results from the fact that the ${e}$-${p}$ loops produced by the model are not closed, but leave some irrecoverable deformation.

No method for determining a suitable value for ${a}$ was described in previous works. Therefore, a custom approach had to be found here. Since ${a}$ is included in $K_\mathrm {p2}$, it affects both ${\dot{\varepsilon }}_\mathrm {v}$ and ${\dot{\varepsilon }}_\mathrm {q}$ during unloading and reloading. In addition to that, the extended model according to Sect. 4 contains a second cyclic loading factor $h_\gamma$, which has been incorporated into the dilatancy function with (25). It allows to control ${\dot{\varepsilon }}_\mathrm {v}$ independent from ${\dot{\varepsilon }}_\mathrm {q}$. Therefore, it is convenient to first calibrate ${a}$ with respect to the deviatoric strains and then adjust the volumetric component by means of $h_\gamma$.

The deviatoric response of both sand model and sand samples to unloading and reloading is shaped like a “<” sign in $\varepsilon _\mathrm {q}$-p space, as is apparent from Fig. 10 and 4. The value of ${a}$ controls the width of the gap between the two branches as well as their slope. The width is chosen as the key parameter that should be optimised by calibrating ${a}$. To this end, it is quantified by the strain difference $\mathrm {\Delta }{}\varepsilon _\mathrm {q}$. See Fig. 20 for an illustration with respect to triaxial test No. TCR04.

So the goal of the calibration procedure is to find a value for ${a}$ that yields an optimal match between $\mathrm {\Delta }{} \varepsilon _\mathrm {q,sim}$ (computation) and $\mathrm {\Delta }{}\varepsilon _\mathrm {q,exp}$ (experiment). This is accomplished here by choosing $a = {1.4}$, as can be seen in Fig. 20.

The results presented in Fig. 20 furthermore reveal that the computed strain evolution during unloading and reloading is much steeper than the experimental strain path. This is the case even though the values of $\mathrm {\Delta }{}\varepsilon _\mathrm {q,sim}$ and $\mathrm {\Delta }{}\varepsilon _\mathrm {q,exp}$ match perfectly. Different methods could possibly resolve this, at least partially:

• Increase the elastic constant $G_0$ and decrease $h_4$ while keeping the first loading curve constant; this yields more plastic strains and less elastic ones

• Use different elastic stiffness functions during unloading and reloading, as proposed by Pestana and Whittle [39]

• Modify $h_\beta$ to give more plastic strains during unloading

All three solutions would complicate the model formulation and the calibration procedure. However, they cannot improve the computation results with regard to irrecoverable strains caused by cyclic loading. Thus, no benefit with respect to the aim of the present work would be gained. The issue is therefore not further investigated here.

Fig. 20

Calibration of constitutive parameter ${a}$ for triaxial loading at constant $\eta$ with $\eta = {0.75}$; $h_4 = {1.0}$, $d_2 = {3.2}$, $I_\mathrm {Dc} = {39}\,\%$

5.4 Calibration of cyclic dilatancy

Section 4.4 investigated how to improve the volumetric response of the constitutive model during reloading by incorporating a cyclic loading factor $h_\gamma$ into the dilatancy $D_2$. According to (26), the key parameter of $h_\gamma$ is its initial value $\gamma _ 0$. The latter was postulated to depend on the normalised pressure variable $\gamma _\mathrm {rev}$, defined in (27). The current section should explore how to determine suitable values for the parameters $m_d$ and $n_d$ of the function (28) that relates $\gamma _0$ to $\gamma _\mathrm {rev}$.

The approach chosen here is somewhat similar to the calibration of ${a}$. Specifically, the value of $\gamma _0$ was optimised to achieve an optimal match of numerical and experimental results in terms of the volumetric strain difference $\mathrm {\Delta }{} \varepsilon _\mathrm {v}$ between first loading and reloading. Please refer back to Fig. 16 for a graphical definition of $\mathrm {\Delta }{} \varepsilon _\mathrm {v}$. This was done for multiple configurations of loading parameters that differ with respect to their $\gamma _\mathrm {rev}$. The results are summarised in Table 4.

Table 4 Calibrated values of $\gamma _0$; test numbers are defined in Table 1

The calibrated $\gamma _0$ were then plotted against $\gamma _\mathrm {rev}$. Furthermore, (28) was curve-fitted to the data points. The fit function of gnuplot² was used for that, which according to Williams and Kelley [56, p. 74] is based on “the nonlinear least-squares Marquardt–Levenberg algorithm”. The results are presented in Fig. 21. Accordingly, the optimised parameters are $m_d = {0.94}$ and $n_d = {-0.36}$. Moreover, it turns out that the linear function matches the empirical data surprisingly well. This implies that $m_d$ and $n_d$ can be obtained from only two triaxial tests.

Fig. 21

Relation between $\gamma _0$ and $\gamma _\mathrm {rev}$; data from Table 4

In order to illustrate that the cyclic dilatancy extension improves the model, the original formulation and the extended one were used to simulate the consolidation and the first cycle of triaxial test No. TCR05. All constitutive parameters determined so far were used for that. Figure 22 shows the results. Clearly, the cyclic dilatancy factor $h_\gamma$ has no effect during the first loading and the unloading phase, as was intended by the theoretical formulation (26). This is proven to be convenient here because up to the second reversal point at $p_\mathrm {min} = {20} \, \mathrm{kPa}$, the strain evolution computed by both model versions fits the test results very well. This changes in the course of the reloading stage. There, the model response without $h_\gamma$ is far too stiff and therefore ends below the first loading curve, implying that the soil loosened during the first cycle. This non-sense outcome is consistent with the theoretical investigations presented in Sect. 4.4. In contrast, the extended model yields a reloading stiffness which is similar to the one encountered in the experiment and correctly predicts that the unloading and reloading sequence compacts the soil.

The bottom line is that the cyclic dilatancy can be easily and accurately calibrated and that the extension significantly improves the model. This comes at the cost of two additional constitutive parameters, the determination of which requires results from at least two unloading and reloading tests with different $p_\mathrm {min}$. The experience gained from the present work suggests that $m_d$ and $n_d$ are somehow related to ${a}$. Perhaps future investigations can explore this further and thereby reduce the number of independent parameters.

Fig. 22

Impact of cyclic dilatancy on simulation results for triaxial loading with $\eta = {0.6}$ and $p_\mathrm {av} = {120}\,\mathrm{kPa}$; $I_\mathrm {Dc} = {37}\,\%$, $h_4 = {1.0}$, $d_2 = {3.2}$, $a = {1.4}$; sub-figure (b): $m_d = {0.94}$, $n_d = {-0.36}$

5.5 Calibration of degradation function

The last task to be solved before validating the model was to determine appropriate values for the parameters $h_5$ and $h_6$ of the plastic strain degradation function $H_\mathrm {c}$. As shown in Sect. 4.5, $h_5$ enters both $K_\mathrm {p2}$ and $D_2$, while $h_6$ is only present in $D_2$. Based on that, one might suspect that $h_5$ could be calibrated first, affecting ${\dot{\varepsilon }}_\mathrm {q}$ as well as ${\dot{\varepsilon }}_\mathrm {v}$ and that afterwards $h_6$ could be adjusted to optimise only the volumetric response. In fact, that was one motivation for equipping both $K_\mathrm {p2}$ and $D_2$ with $H_\mathrm {c}$. In practice, however, the situation is slightly more complicated.

Both components of the plastic strain rate are linked by the plastic modulus $K_\mathrm {p2}$, as seen in (17). In the original model, this dependency existed only in one direction, i. e. ${\dot{\varepsilon }}_\mathrm {q}$ was independent from ${\dot{\varepsilon }}_\mathrm {v}$. This is no longer true with $H_\mathrm {c}$ having been incorporated into $K_\mathrm {p2}$. Now, the deviatoric strain rate is a function of the accumulated volumetric strain $\kappa _2$ defined in (31). Any changes to the volumetric plastic strain rate therefore also affect the deviatoric component. Because of that, a calibration process is proposed in the course of which it becomes necessary to simultaneously vary $h_5$ and $h_6$.

A first estimate for $h_5$ can be found by setting $h_6 = {1.0}$ and then fitting the accumulated deviatoric strains obtained from the model to the experimental data. This lead to $h_5 = {2.6}$ here. See Fig. 23 for the final result.

Based on $h_6 = {1.0}$, the volumetric accumulated strains usually turn out too large. This is tackled in a second calibration step in which both $h_6$ and $h_5$ are gradually increased. Meanwhile, the shape of the $\varepsilon \mathrm {_q^{acc}}$ curve is to be kept constant. The process is illustrated in Fig. 23. It finally resulted in $h_5 = {4.3}$ and $h_6 = {1.8}$ for the case considered here.

Fig. 23

Calibration of constitutive parameters $h_5$ and $h_6$ for cyclic triaxial loading at $\eta = {0.75} = \mathrm {const}$; $I_\mathrm {Dc} = {39} \, \%$, $p_\mathrm {av} = {200}\,\mathrm{kPa}$, $\mathrm {\Delta }p = {100}\,\mathrm{kPa}$, $h_4 = {1.0}$, $d_2 = {3.2}$, $a = {1.4}$, $m_d = {0.94}$, $n_d = {-0.36}$

Table 5 Constitutive parameters of the extended $\dot{p}$-mechanism for Toyoura Sand; model parameters not listed here are adopted from Table 3

5.6 Simulation of cyclic triaxial tests

The previous sections detailed how the parameters of the extended constitutive model were calibrated. The resulting parameters are summarised in Table 5. With this accomplished, the model proposed by Li [26] and extended in Sect. 4 could be used to simulate the cyclic triaxial tests on Toyoura Sand described in Sect. 2. The outcome will be presented and discussed subsequently with respect to the irrecoverable strain evolution.

In Fig. 24, results from tests and computations are compared in which the soil was cyclically compressed at different stress ratio levels $\eta$. Apparently, the deviatoric strains evolved very similarly in laboratory tests and numerical computations. Minor differences are encountered regarding the impact of different $\eta$ on the volumetric response. In the simulations, $\varepsilon \mathrm {_v^{acc}}$ was nearly unaffected by $\eta$. This obviously is the effect which the modification (22) was intended to achieve. In contrast, the experimental $\varepsilon \mathrm {_v^{acc}}$ curves scatter slightly and unsystematically with $\eta$. However, the scatter of the experimental data in terms of $\varepsilon \mathrm {_v^{acc}}$ is small and can be explained by imperfections of the soil fabric which are induced by the sample preparation. Naturally, this cannot be taken into account by the constitutive model because the initial states for all simulations with different $\eta$ are identical expect for the level of stress ratio. With this in mind, the simulation results presented in Fig. 5 can be considered to match the experimental data very well.

Fig. 24

Simulation vs. experiment for cyclic compression at different stress ratio levels; $I_\mathrm {Dc} \approx {40} \, \%$, $p_\mathrm {av} = {200}\,\mathrm{kPa}$, $\mathrm {\Delta }p = {100} \, \mathrm{kPa}$, model parameters according to Table 5

According to Fig. 25, different $p_\mathrm {av}$ have the same effect in the numerical simulations as in the experiments, i. e. the smaller $p_\mathrm {av}$, the faster grow $\varepsilon \mathrm {_v^{acc}}$ and $\varepsilon \mathrm {_q^{acc}}$ with ${N}$. Even in detail, the computations appear to match the test results reasonably well for $p_\mathrm {av} = 200\,/\,300\,/\,{400} \, \mathrm{kPa}$. This also applies to the deviatoric response obtained with $p_\mathrm {av} = {120} \, \mathrm{kPa}$. However, the volumetric strain curve predicted by the model for $p_\mathrm {av} = {120}\, \mathrm{kPa}$ turned out considerably less steep than the curve from the corresponding triaxial test. Therefore, the model underestimates how much the soil is compacted by the cyclic load. To address this discrepancy, the degradation factors incorporated into $K_\mathrm {p2}$ and $D_2$ by virtue of (29) and (33) would probably need to be extended by additional terms that depend on p.

Fig. 25

Simulation vs. experiment for cyclic compression at different pressure levels; $\eta = {0.6}$, $I_\mathrm {Dc} \approx {40} \, \%$, $\mathrm {\Delta }p = {100} \, \mathrm{kPa}$  model parameters according to Table 5

The model performance regarding cyclic compression with different pressure amplitudes $\mathrm {\Delta }{}p$ can be assessed by means of Fig. 26. It turns out that nearly all simulation results match their experimental counterparts very well. The influence of $\mathrm {\Delta }{}p$ therefore is realistically captured by the extended constitutive model. Only the $\varepsilon \mathrm {_v^{acc}}$ curves obtained from computations and laboratory tests for $\mathrm {\Delta }p = {150} \, \mathrm{kPa}$ differ considerably. That is, the test sample was compacted faster than the simulated soil element. A similar phenomenon has already been described for the influence of $p_\mathrm {av}$ (Figure 25). Most likely, both issues can be resolved by the same approach, i. e. an extension of the degradation functions by a term related to ${p}$.

Fig. 26

Simulation vs. experiment for cyclic compression with different amplitudes; $\eta = {0.6}$, $I_\mathrm {Dc} \approx {40} \, \%$, $p_\mathrm {av} = {200} \, \mathrm{kPa}$, model parameters according to Table 5

Finally, the calculation results for different relative soil densities are discussed, which are shown in Fig. 27. Judging from the diagrams, the constitutive model responds to changes in density in the same way as was observed in the triaxial tests. More precisely, the smaller $I_\mathrm {D}$, the greater the accumulated irreversible strains in both simulation and experiment. In detail, the computed strain evolution differs slightly from the test results. More accurate results could probably be obtained by adding a term to the plastic strain degradation function that depends on the void ratio ${e}$. However, this effort is considered unnecessary here because the discrepancies are relatively small.

Fig. 27

Simulation vs. experiment for cyclic compression with different initial densities; $\eta = {0.6}$, $p_\mathrm {av} = {200} \, \mathrm{kPa}$, $\mathrm {\Delta }p = {100} \, \mathrm{kPa}$, model parameters according to Table 5

6 Conclusions

Within this paper, the constitutive behaviour of sands with respect to cyclic compression at constant stress ratio has been studied. As stated in Sect. 1, two research questions were to be answered.

The first question is: How do irrecoverable strains evolve in sands during cyclic $\eta = \mathrm {const}$ loading? This has been explored by means of cyclic triaxial tests on Toyoura Sand. The key findings from that are:

• Cyclic $\eta = \mathrm {const}$ loading causes accumulation of irrecoverable volumetric and deviatoric strains.

• The amount of irrecoverable strain induced per cycle decreases with the cycle count ${N}$.

• Volumetric strain accumulation declines faster with ${N}$ than deviatoric strain accumulation.

• The amount of volumetric and deviatoric irrecoverable strain induced per cycle increases with

  • increasing amplitude $\mathrm {\Delta }{}p$.

  • decreasing pressure level $p_\mathrm {av}$.

  • decreasing relative density $I_\mathrm {D}$.

• Increasing the stress ratio magnitude $\eta$ leads to more deviatoric strain but does not significantly affect the volumetric response.

The second research question to be addressed is: How can cyclic $\eta = \mathrm {const}$ loading of sands be simulated using a constitutive model? In order to investigate this, the bounding surface framework by Li [26] has been chosen as a basis. The shortcomings of the theoretical formulation have been analysed. To overcome them, new functions have been proposed to be incorporated into the model. Then, the model parameters have been determined for Toyoura Sand. Most of the parameters can be calibrated with respect to a single triaxial test. Only for the cyclic dilatancy factor, four other tests have been considered. However, it turned out that this was actually unnecessary, because a total of two tests would have sufficed.

Finally, the extended model has been validated by simulating the triaxial tests with cyclic $\eta = \mathrm {const}$ loading conducted for this work. The main conclusions from this are as follows.

• The degradation factors incorporated into $K_\mathrm {p2}$ and $D_2$ by virtue of (29) and (33) enable the model to reproduce the gradual decline of irrecoverable strain accumulation seen in the laboratory tests.

• Thanks to the modified dilatancy (22), the concept of which is due to Gao and Zhao [19], the model can realistically capture the impact of $\eta$ on the evolution of irrecoverable volumetric strains.

• The extended model can reproduce the effects of different pressure levels and different pressure amplitudes encountered in the experiments. A crucial prerequisite for this is the cyclic dilatancy extension (25).

• Extending $K_\mathrm {p2}$ by a void ratio dependent factor via (23) allows the effects of different initial densities on the soil’s behaviour to be accounted for in a way that is consistent with the test results.

Overall, the validation has shown that the extended model is able to capture salient aspects of constitutive behaviour that have been observed in the experiments. Both the original model and the extensions proposed here contribute to that result.

A couple of points should be further explored in future works. For one thing, it is not entirely clear for which configurations of soil densities and loading parameters the assumption applies that the volumetric sample response is unaffected by $\eta$. In order to clarify this, further tests need to be conducted, which cover a broader range of values for $\eta$ and different combinations of stress ratios and soil densities.

In addition, the extended sand model should be validated for sands other than Toyoura as well as for combined cyclic loading situations in which stress ratio and pressure vary simultaneously. The model could also be further refined. First, the number of independent parameters of the cyclic dilatancy can probably be reduced by finding a relationship between $m_d$, $n_d$ and ${a}$. Second, the degradation function (30) could be extended in order to better account for the effect of small $p_\mathrm {av}$ and large $\mathrm {\Delta }{}p$ on the evolution of accumulated volumetric strains.

Last but not least, the experimental results presented here could be further used. They were obtained from triaxial tests on Toyoura Sand. This is a standard sand in soil mechanical research, so its constitutive parameters are known for a large variety of soil models. Therefore, the test results can easily be employed to calibrate and enhance constitutive theories other than the one used in this work. Among the models with plastic $\dot{p}$ mechanisms mentioned in Sect. 1, the one by Gao and Zhao [19] is particularly interesting because it can describe the evolution of the fabric anisotropy of sands in shear as well as in compression. If its $\dot{p}$ mechanism were extended to cover inelastic behaviour during unloading and reloading, the evolution of irrecoverable strains in cyclic compression of sands could possibly be linked to the soil fabric. The resulting sand model would be closer related to actual microstructural processes between individual grains than the phenomenological approach adopted in Sect. 4.

A. Notation

$\varvec{A} : \varvec{B} = A_{ij} B_{ij}$ – Double contraction

$\varvec{I}$ – Second-order unit tensor

${\text {tr}}(\varvec{A}) = A_{kk}$ – Trace operator

$\varvec{A}_\mathrm {dev} = \varvec{A} - (1/3){\text {tr}}(\varvec{A}) \varvec{I}$ – Deviatoric tensor

$\Vert \varvec{A}\Vert = \sqrt{ \varvec{A} : \varvec{A} }$ – Euclidean norm

$\dot{\varvec{A}}$ – Material time derivative

${\operatorname {sgn}} \, x = x / |x|$ – Sign function

$\langle x \rangle = (x+|x|)/2$ – Macaulay brackets

e – Void ratio

$\varvec{\varepsilon }$ – Linearised strain tensor

$\varepsilon _\mathrm {v} = {\text {tr}} \varvec{\varepsilon }$ – Volumetric strain

$\varepsilon _\mathrm {q} = \sqrt{2/3} \Vert \varvec{\varepsilon }_\mathrm {dev}\Vert$ – Equivalent shear strain

$I_\mathrm {ds}$ – Relative density before consolidation

$I_\mathrm {dc}$ – Relative soil density after consolidation

$\varvec{\sigma }$ – Effective stress tensor

$p = (1/3){\text {tr}}(\varvec{\sigma })$ – Mean effective stress

$q = \sqrt{3/2}\Vert \varvec{\sigma }_\mathrm {dev}\Vert$ – Equivalent shear stress

$\varvec{r} = ( \varvec{\sigma } - p \varvec{I} )/ p$ – Stress ratio tensor

$\eta = \sqrt{3/2} \Vert \varvec{r} \Vert$ – Stress ratio magnitude