Use of interaction domains for a displacement-based design of caisson foundations

Abstract

Caisson foundations, typically adopted for both onshore and offshore structures, are usually subject to combined loading acting during working conditions and exceptional events such as earthquakes. Assessment of their performance under general loadings is therefore fundamental, for both serviceability and ultimate limit states. In this study, a simplified displacement-based approach, aimed at preliminary designing caisson foundations subjected to combined loading, is presented. Such an approach requires the definition of both interaction domains (IDs) and generalised pushover curves, together with the assumption of an associative flow rule. The IDs and pushover curves are obtained by interpreting the results of a set of 3D finite element nonlinear static analyses, where the response of massive cylindrical onshore caisson foundations, embedded in a layered soil profile and subjected to both centred vertical (N) and combined loads (N–Q–M), is investigated. Following previous works, the influence of initial loading factor and caisson embedment ratio on both IDs shape and size is investigated. Additionally, the effect of soil drainage conditions on the IDs is discussed. Role of load reference point (LRP) is also assessed, since a suitable choice of LRP may strongly simplify the geometrical representation of the ID. Analytical expressions for dimensionless IDs and pushover curves are presented and used at a preliminary design stage to evaluate the maximum generalised load acting on the caisson for a given threshold generalised displacement, so as not to exceed either serviceability or ultimate limit states.

1 Introduction

Caissons are embedded foundations characterised by large mass and stiffness, typically employed for both offshore and onshore structures, and usually subject to combined loading acting during working conditions (weights of superstructure and traffic, wind, etc.) as well as exceptional events (strong earthquakes, storms, etc.).

According to an ultimate limit state approach, a foundation must be designed so that the load combinations expected during its service life are lower than the collapse loads, thus guaranteeing an adequate factor of safety. However, if the collapse load is attained for displacements incompatible with serviceability of the superstructure, a displacement-based approach is recommended when evaluating the soil-foundation system capacity, as in the case of large-diameter piles. Such an approach may be particularly useful for caisson foundations, as failure mechanisms involve large soil volumes due to their noticeable dimensions, leading to high axial and lateral loading capacity. This need is supported by these foundations being typically used for critical facilities characterised by tall superstructures, such as long-span bridges and wind turbines, whose limit conditions are typically defined in terms of generalised displacements and permanent rotations rather than generalised forces.

In view of the above, developing a simplified procedure aimed at computing the limit load acting on caissons for a given threshold displacement may prove useful, as an expeditious tool to be used at a preliminary design stage. Such a procedure would require the definition of: (1) the combined N–Q–M failure domain of the soil-foundation system, where N and Q are the vertical and horizontal forces and M is overturning moment; (2) the generalised load–displacement curve describing the response of the system from the onset of loading until its failure condition. For foundations subject to combined loads, interaction diagrams (IDs, i.e. three-dimensional failure envelopes in the N–Q–M space) are a useful tool to relate the different loading components at failure. The use of IDs would allow to define the factor of safety either as the minimum distance of the current N–Q–M combination from the envelope or the distance evaluated along the load path [16, 27].

Interaction diagrams have been investigated for a variety of foundations by employing different approaches (i.e. experimental, analytical and numerical): shallow footings [7, 9, 18, 30, 33], solid and skirted shallow foundations for offshore structures typically characterised by an embedment ratio H/D < 1 (H being the embedment depth and D the in-plane dimension) [5, 37] and spudcan footings employed for jack-up units [23]. Less studies have been devoted to failure conditions of massive caisson foundations for onshore structures subjected to combined loads, concerning either cuboid-shaped [2, 17, 38] or cylindrical caissons [3, 8], both with values of H/D ≥ 1. Furthermore, most of the numerical studies [4, 5, 18, 19, 37] are based on 2D plane-strain numerical analyses, while just a few account for the three-dimensional stress/strain state properly [3, 8, 17, 38]. Under undrained conditions, the analyses are always carried out in terms of total stresses [3, 5, 17, 18, 37], where the soil is described as an equivalent single-phase medium, therefore ignoring its two-phase nature.

In this study, the IDs of massive cylindrical caisson foundations are obtained for different embedment ratios H/D = 0.5, 1, 2, installed in a layered alluvial deposit under both centred vertical and combined N–Q–M loads. The IDs are computed through a series of 3D finite element (FE) nonlinear static analyses carried out assuming both fully undrained and drained conditions. To account for the two-phase nature of the saturated soil, the undrained analyses have been performed in terms of effective stresses, rather than the typically adopted total stress approach. For the sake of simplicity, a linear elastic-perfectly plastic behaviour is assumed for the foundation soils. This choice, in agreement with what already done by many other authors also in the recent past [3,4,5, 19], is justified by the theoretical objectives of the paper, aimed at defining the mechanical response of the system, irrespective of the specific datum. In fact, when monotonic loads are applied and hydro-mechanical coupling is disregarded, the use of more sophisticated constitutive relationships could modify the values but not the nature of the system mechanical response.

In the first part of the paper, after giving insights on the problem layout (Sect. 2) and the numerical model (Sect. 3), the results of the numerical analyses are presented and discussed (Sect. 4). The FE results are validated against those coming from the application of limit analysis (LA) and those discussed by [5, 17, 38] for a homogeneous soil. Additionally, the choice of considering a two-layer foundation soil showed that, for a given profile of shear strength (either constant or linearly increasing with depth), the size of IDs is governed by the stratigraphic profile but not its shape: this allowed to generalise the obtained results to a large number of practical applications in which a colluvial stratum is positioned on a cohesive one. Following previous works by [17, 38], influence of foundation geometry (H/D) and initial loading factor (χ) on the IDs have been first investigated, showing a good agreement with their results. Furthermore, the comparison of the IDs obtained in the two limit drainage conditions is provided for a given geometry and initial loading factor, showing that drainage scales the ID size rather than influencing its shape. A short discussion on how the choice of the load reference point (LRP) affects the shape of the IDs is also given, with the caisson centroid being the most suitable choice as it strongly simplifies the geometrical representation of the ID.

In the second part of the paper, based on the results of the nonlinear static analyses, the authors propose an approach for the assessment of the performance of caisson foundations: (1) an analytical expression for ID in the non-dimensional N–Q–M space for both drainage conditions (Sect. 5) and (2) the equation of dimensionless generalised pushover curves (Sect. 6). The expressions (1) and (2) are integrated in a displacement-based simplified approach; moreover, the hypothesis of an associative flow rule, confirmed by previous experimental and numerical works [35, 38], allows to compute the displacement components, for an assigned load path and a given threshold for generalised displacements.

2 Problem layout

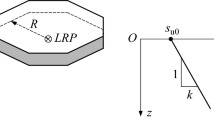
IDs have been obtained by performing nonlinear static (i.e. pushover) analyses on different cylindrical caisson foundations subject to combined N–Q–M loading until the collapse is attained. In Fig. 1a, a sketch of the adopted geometrical scheme is illustrated. A rigid cylindrical caisson of diameter D = 12 m and height H is embedded in an alluvial deposit consisting of a 5-m-thick layer of gravelly sand and a layer of silty clay. Water table is located at the bottom of the gravelly sand layer: an initial hydrostatic pore water pressure regime is imposed. While the diameter of the caisson is kept constant over the parametric study, three embedment ratios H/D = 0.5, 1, 2 are considered. In this study, the load reference point (LRP), defined as the point where loads and displacements are referred to, is chosen to be coincident with the caisson centroid unless specified differently; the sign convention adopted in the analyses is also illustrated in Fig. 1a.

Fig. 1

Problem definition: a schematic layout; b OCR and G₀ profiles assumed in the analyses; plan (c) and section (d) view of the FE model

The profiles of both overconsolidation ratio OCR and small-strain shear modulus G₀ are plotted in Fig. 1b. The silty clay is assumed to be slightly overconsolidated with an OCR profile consistent with a uniform erosion process (unloading vertical stress Δσ_v = − 340 kPa), reproduced in the analyses by means of the stepwise profile of Fig. 1b. G₀ is assumed to increase with depth according to the empirical relationship proposed by [20] for gravelly sands (assuming a maximum void ratio e_max = 0.8, a minimum e_min = 0.4 and a relative density D_r = 60%) and by [29] for the silty clay (assuming a plasticity index I_P = 25%). The earth pressure coefficient at rest is evaluated by using the relationship proposed by [24]. A linear elastic-perfectly plastic behaviour is assumed for the foundation soils with a Mohr–Coulomb failure criterion. The influence of the choice of such a constitutive law on the numerical results is discussed in “Appendix 1”. The physical and mechanical properties adopted in the analyses are listed in Table 1, where γ is the unit weight, ν the Poisson’s ratio, G/G₀ the ratio between the current and the small-strain shear modulus, c' the cohesion, φ' the internal friction and ψ the dilatancy angles.

Table 1 Properties of the foundation soils and parameters adopted in the soil constitutive model

3 Numerical modelling

The numerical analyses have been carried out by using the FE code Plaxis 3D AE [6]. In case of H/D = 0.5 and 1, the numerical model shown in Fig. 1c, d has been used: the 3D mesh consists of 95,500 10-node tetrahedral elements with 4 Gaussian points [12]. In case of H/D = 2, the depth z of the model has been doubled using a mesh of approximately 188,000 elements. Thanks to the problem symmetry with respect to the x-axis, only half domain has been modelled. Lateral boundaries are located at a distance x = y = 6.25 D from caisson axis, where the contours of both soil displacements and stresses have been checked not to be affected by the mesh boundaries (e.g.: [13, 14]). Horizontal displacements on vertical boundaries, as well as horizontal and vertical displacements at the base, are not allowed.

In the analyses, the caisson is always “wished in place”, neglecting the simulation of the construction process. A linear-elastic behaviour is assumed for the caisson with a Young’s modulus E_c = 30 GPa and a Poisson’s ratio ν = 0.15; the unit weight of reinforced concrete is assumed equal to γ_c = 25 kN/m³. At the soil–caisson interface, purely attritive interface elements with Mohr–Coulomb failure criterion are inserted to simulate relative sliding, with a friction angle δ = tan⁻¹ [2/3 tanφ']. The choice of such a value of δ, although consistent with common practice, does not affect the generality of the numerical results since, as shown by [17, 38], the friction angle at the foundation-soil interface seems to have a slight influence on the IDs especially for high values of H/D.

4 Analyses and results

Two series of 3D FE analyses have been performed to investigate the bearing capacity of the caissons (1) under centred vertical loading and assuming drained conditions, (2) under a general combination of N, Q and M, assuming both drained and undrained conditions for the foundation soils. Specifically, in (2) drainage conditions have been varied only in the calculation phases during which horizontal forces and overturning moments are applied, bearing in mind that such components can be representative of seismic-induced inertial forces acting under undrained conditions. Conversely, drained conditions are always considered for the vertical load, assuming that the excess pore water pressures in the foundation soil, due to the construction of the superstructure, are fully dissipated at the end of the construction phase.

4.1 Centred vertical loading

To investigate the bearing capacity under a centred vertical load, three displacement-controlled analyses have been performed. They consist of the following calculation phases: (1) initialisation of the effective stress state; (2) wished-in-place caisson activation; (3) progressive application of a vertical displacement w. For each embedment ratio H/D, the resulting N–w curves are plotted in Fig. 2a. As was expected, the limit load increases with H/D and is attained for very large values of w. Ultimate loads are compared with the values of N_lim provided by the code OPTUM G3 [26], where LA calculations are combined with the FE method [32]. The numerical model, characterised by the same dimensions and boundary conditions as the ones described in Sect. 3, comprises the soil and the caisson, the latter modelled as a rigid body. The soil domain is discretised by means of solid elements characterised by a rigid-perfectly plastic behaviour assuming a Mohr–Coulomb failure criterion and an associative flow rule. In each analysis, an adaptive mesh with automatic refinement in proximity of plastic strain localisations has been used. After a few iterations, the analysis stops when the range of the upper and lower bounds to the bearing capacity is small enough to give an accurate estimation of the exact solution.

Fig. 2

Pushover curves under centred vertical loading: a dimensional; b dimensionless plane

The drained FE analyses, carried out by assuming a non-associative flow rule (dilatancy is nil), cannot provide bearing capacities coincident with those obtained from LA calculations, where associativeness is imposed. For this reason, FE results have been compared with LA results computed using both the original strength parameters, c′ and φ′, and the reduced values, c′_red and φ′_red, evaluated as proposed by [10]. Since the role of dilation is more crucial for deeper failure mechanisms, as it was expected, the agreement between FE and LA results, the latter obtained with the original strength parameters, is better for H/D = 0.5, whereas the opposite is true for H/D = 2 (Fig. 2a). H/D = 1 may be considered as an intermediate case.

In Fig. 2b, the N–w curves are plotted in the non-dimensional plane N/N_lim–w/w_el, where w_el corresponds to the elastic vertical displacement calculated for N = N_lim: therefore, w_el = N_lim/K₀, where K₀ is the initial tangent stiffness of the N–w curves. By definition, all normalised curves exhibit an initial linear-elastic response with tangent stiffness equal to 1, followed by a nonlinear load–displacement curve until the ultimate condition (N/N_lim = 1) is attained. The nonlinear and irreversible response of caisson foundations to vertical load is strongly influenced by the embedment ratio: as H/D increases, the “structural hardening” related to the progressive increase in the plastic zone developing in the soil surrounding the caisson’s base and shaft becomes more and more evident. Similarly to what observed in [11] for the unloading occurring at the face of a deep tunnel, the progressive loading of the foundation causes an expansion of the plastic domain: yielding starts from the edges of the foundation’s base to deepen and widen as loading increases, with plastic strains spreading over the soil surrounding the caisson. As soon as the mechanism reaches the upper boundary, the horizontal asymptote of the load–displacement curve is attained and failure occurs. In Fig. 3, the progressive evolution of the yielded volume during the unloading at the face of a deep tunnel (Fig. 3a) and that computed for a caisson with H/D = 2 (Fig. 3b) is shown. Under the assumption of a sufficiently large ratio of the cover to tunnel diameter, the mechanism (Fig. 3a) involves the soil surrounding the tunnel face and lining without reaching the ground surface, this resulting in the absence of a plateau in the load–displacements curve [11].

Fig. 3

Evolution of the plastic volume: a during the unloading of the tunnel front (modified after [11]); b during the loading of the H/D = 2 caisson (this study). LSR indicates the load sharing ratio as defined by [36]

The following analytical expression of the non-dimensional N–w curves is proposed to simulate the numerical results:

$$\left\{ {\begin{array}{*{20}l} {\frac{N}{{N_{{{\text{lim}}}} }}\left[ {1 + \left( {k - 1} \right)\left( {\frac{N}{{N_{{{\text{lim}}}} }}} \right)^{\text{r}} } \right] = \frac{w}{{w_{{{\text{el}}}} }}} \hfill & {\frac{w}{{w_{{{\text{el}}}} }} \le k} \hfill \\ {\frac{N}{{N_{{{\text{lim}}}} }} = 1} \hfill & {\frac{w}{{w_{{{\text{el}}}} }} \ge k} \hfill \\ \end{array} } \right.$$

(1)

This represents a modified hyperbole with the following properties: (1) the initial tangent stiffness is equal to 1; (2) the ultimate condition (N/N_lim = 1) is reached for a finite value of w/w_el = k, where k describes the “structural hardening” not governed by the upper boundary and uniquely determined once the constitutive relationship and the constitutive parameters are assigned; (3) the curve is discontinuous in the first derivative for w/w_el = k; (4) parameter r = 1.9 is chosen to best-fit the curves obtained from the numerical analyses. The discontinuity of the curve for w/w_el = k emphasises the sudden change in stiffness observed when the plastic zone reaches the upper boundary. In Table 2, the values of k evaluated for each embedment ratio are listed. The non-dimensional N–w curves computed using Eq. (1) are compared in Fig. 2b with those obtained numerically. The agreement is more than satisfactory. Bearing in mind that the limit vertical load is attained for high values of the vertical displacement, definitely incompatible with the superstructure operating conditions, Eq. (1) can be employed to introduce an alternative criterion to define the attainment of an ultimate limit state, based on limit values of settlement, as in case of large-diameter piles.

Table 2 Values of parameter k obtained from the numerical results

4.2 Combined N–Q–M loading

To investigate the bearing capacity under a general load combination, about 370 load-controlled pushover numerical analyses have been performed. After the initialisation of effective stresses and the caisson activation, the following calculation phases are completed: (1) drained application of a vertical load atop the caisson; (2) either drained or undrained progressive application at constant ratio α = M_T/Q_T up to failure of both horizontal force Q_T and overturning moment M_T atop the caisson (“T” standing for “top”). Values of Q_T and M_T are then transposed into equivalent forces and moments referred to the foundation centroid, chosen as load reference point: Q_G = Q_T and M_G = M_T + Q_T·H/2 = (α + H/2)·Q_T = α_G·Q_G, where subscripts G and T stand for load components referred to foundation centroid and top, respectively. Ratio α_G represents the lever arm of the load component Q_G measured from the centroid: when α_G is nil the resultant horizontal force is applied at the caisson LRP, when α_G >  < 0 above it or below it, respectively. For α_G =  ± ∞, an overturning moment is only applied clockwise or anticlockwise, respectively. In the following, unless specified otherwise, omitted subscripts refer to load components calculated for LRP.

The interaction domain obtained under drained conditions for a caisson with H/D = 1 is plotted in Fig. 4a in the N_net–Q–M/D load space. Net vertical load, N_net, denotes the net disturbance N_net = N + W_c– σ_v(z = H)·A_c, where N is referred to the top of the caisson, W_c and A_c are the caisson weight and cross-section area, respectively, whereas σ_v is the total vertical stress acting at the embedment depth z = H. Three cross sections of the failure envelope are also reported in the planes of equation N_net = 117 MN (Fig. 4b), corresponding to a safety factor under centred vertical loading F_Sv = N_lim,net/N_net = 5, or equivalently to an initial loading factor χ = 1/F_Sv = 0.2, Q = 0 (Fig. 4c) and M/D = 0 (Fig. 4d). Arrows are introduced in the figures to indicate some of the loading paths imposed in the numerical analyses: during phase (1), the vertical load is increased until a value of N_net = 117 MN (horizontal arrow in Fig. 4c, d); during phase (2), several radial numerical tests in the Q–M/D plane, at imposed α_G (constant vertical load), are performed (Fig. 4b) until the ultimate condition is reached. The cross sections in Fig. 4c, d are characterised by an envelope which is convex with a maximum/minimum in terms of M/D and/or Q corresponding to an intermediate value of N_net, similarly to what observed for IDs of (1) reinforced concrete sections subject to combined compression and bending actions and (2) shallow foundations. In contrast to what observed for shallow footings [7, 25], in case of caisson foundations: (1) when N_net = 0 bearing capacity is different from zero; (2) owing to the shaft resistance ID extends also for N_net < 0 (traction); and (3) similarly to what observed also by [17, 38], the ID section in the Q–M/D plane shows a nonzero strength even for N_net very close to N_lim,net; in any case, this portion of the load space has not been investigated further in this paper.

Fig. 4

ID for the H/D = 1 caisson under drained conditions: a N_net–Q–M/D space; b N_net = 117 MN plane; c Q = 0 plane; d M/D = 0 plane

From the results of the numerical analyses, the collapse of the soil-foundation system under a general N–Q–M load combination (plateau of the pushover curves) may be inferred to be attained for values of displacements varying in a wide range: from centimetres to metres, depending on (1) the loading path (α_G), (2) the embedment ratio (H/D), (3) the vertical load (N_net) and (4) the drainage conditions. The highest values of displacements are attained for the deepest caissons (H/D = 1, 2) subject to high vertical loads and under drained conditions. Therefore, as was suggested by [17, 38], a different criterion to define the ultimate condition is adopted here in the following: the attainment by the tangent stiffness of the pushover curve of the 1% of the initial stiffness (K_tan/K₀ = 1%) (Fig. 5a). Such a condition leads to the evaluation of limit loads corresponding to computed displacements much smaller than those referred to the plateau of the pushover curves. For H/D = 1, N_net = 7 MN and drained conditions in Fig. 5b, IDs obtained by employing the two different criteria, plateau (solid line) and K_tan/K₀ = 1% (solid line with crosses), respectively, are compared. The pushover curve for α_G = 0 in Fig. 5a is represented in the non-dimensional generalised force–displacement plane |$\overline{F}$|–|$\overline{u}$|, defined as:

$$\begin{aligned} & |\overline{F}| = \sqrt {\left( {\frac{Q}{{N_{{\text{lim,net}}} }}} \right)^{2} + \left( {\frac{M}{{D \cdot N_{{\text{lim,net}}} }}} \right)^{2} } = Q\sqrt {\left( {\frac{1}{{N_{{\text{lim,net}}} }}} \right)^{2} + \left( {\frac{{\alpha_{{\text{G}}} }}{{D \cdot N_{{\text{lim,net}}} }}} \right)^{2} } \\ & |\overline{u}| = \sqrt {\left( \frac{u}{D} \right)^{2} + \left( \theta \right)^{2} } \\ \end{aligned}$$

(2)

Fig. 5

Different criteria for defining the ultimate loads: a pushover curve for the load path α_G = 0; b ID for the H/D = 1 caisson subject to N_net = 7 MN under drained conditions

In case the tangent stiffness criterion is adopted, a value |$\overline{u}$|= 0.015 is obtained for the case under consideration, whereas |$\overline{u}$|= 0.089 is computed at last step of convergence.

Owing to its symmetry with respect to the origin of the M/D–Q plane, half of the envelope is represented in Fig. 5b. IDs obtained by using the different criteria are characterised by the same shape and this is true for Fig. 4b–d as well, where the other sections are plotted. The same may be inferred in case of loci corresponding to assigned values of $|\overline{u}|$ ($|\overline{u}|$= 0.005, 0.015, 0.025, 0.035, 0.045): an almost homothetic expansion of the envelopes correspond to an increase in $|\overline{u}|$, progressively less spaced as ultimate condition is approached. This observation, in view of modelling the soil-foundation response to general load combinations by means of a macro-element approach [22, 25, 28, 31, 35] based on the theory of elasto-plasticity, seems to suggest the adoption of an isotropic hardening rule in the Q–M plane. Finally, in Fig. 5b the results of FE pushover analyses are compared with those obtained by employing limit analysis and in particular code OPTUM G3, in which strength parameters are reduced as proposed by [10]: again, the agreement is generally good for all loading paths (for any values of α_G) although less satisfactory for high vertical loads. As was previously discussed (Sect. 4.1), the reduction to be applied to strength parameters is however problem dependent.

The model capability to predict the bearing capacity under a general loading combination has also been checked by comparing the IDs obtained for the H/D = 1 caisson subject to N = 0 assuming in turn (1) undrained and (2) drained conditions with published data (Fig. 6). The results are represented in the non-dimensional plane Q/Q_u–M/M_u, where Q_u and M_u denote the values of Q and M bringing the soil–caisson systems to collapse when the other load component is zero: Q_u = Q_(M=0) and M_u = M_(Q=0). For case (1), the solutions obtained by [5, 17] by means of 2D and 3D total stress analyses are shown, the former assuming a shear strength constant (S_u = const.) or linearly increasing with depth (S_u = k z), the latter assuming S_u = const. only. For case (2), instead, the comparison is made with the ID obtained in [38] by means of 3D numerical analyses where the foundation soil consists of a layer of sand.

Fig. 6

IDs for the H/D = 1 caisson subject to N = 0: comparison to results reported a by [5, 17] for undrained conditions and b by [38] for drained conditions

In case (1), the IDs are referred to the base of the caisson, chosen by [5] as LRP. The best agreement is obtained with the ID computed in [5] under the assumption of S_u = k⋅ z, as the same assumption of a soil shear strength increasing with depth is made. For both drainage conditions, the comparison is satisfactory showing that, for the case of a two-layer soil deposit hereby considered, the ID shape is very slightly affected by the assumed soil profile (i.e. dimensionless ID is almost the same), while IDs are influenced by the soil shear strength profile (e.g. constant or linearly increasing).

4.3 Parametric study

In this section, the role in affecting the shape and size of IDs of (1) the initial loading factor χ = 1/F_Sv, where F_Sv denotes the safety factor in case of centred vertical loads under drained conditions, (2) the caisson embedment ratio (H/D) and (3) drainage conditions is discussed. The values of the centred vertical load applied under drained conditions prior to applying Q and M have been selected to impose the desired value of χ, so as to attain equal initial mobilisation of the soil shear strength for all the caissons. Five values of χ have been chosen (χ = 0, 0.09, 0.21, 0.42, 0.63) these resulting in values of F_Sv = ∞, 11, 4.7, 2.4, 1.6.

Prior to showing the results of the parametric study, a discussion on how the LRP location affects the shape of failure envelopes is presented. Given that LRP can be chosen arbitrarily, the most frequently adopted location is the top [17, 38], the centroid [23] and the base of the foundation [5]. The effect of LRP location is presented in Fig. 7a, b for the envelopes relative to H/D = 0.5 and 2, respectively, subject to undrained Q–M loading (χ = 0). Two different LRPs are considered in the figure: the centroid (G) and the top of the caissons (T). As was expected, the largest ID corresponds to the deepest caisson, since in this case the soil volume involved in the failure mechanism is larger: two different scales are then adopted to plot the results. The diagrams referred to the top of the caisson (T) are characterised by a “stretched” shape in the IV quadrant (Q > 0, M/D < 0), where Q and M act in opposite directions: indeed, the overturning moment counterbalances the moment produced by the horizontal force applied atop the caisson. The domains referred to caisson centroid (G) tend instead to become symmetric with respect to the axes. For the shallowest caisson (H/D = 0.5, Fig. 7a), the envelope is almost perfectly symmetric and crosses the x and y-axes perpendicularly: this is due to the decoupling between the rotational and horizontal degrees of freedom. In view of developing a macro-element model for caisson foundations, it is evident that both symmetry and decoupling are desirable for an easy analytical representation of ID. Decoupling is however lost for higher values of embedment (Fig. 7b). To highlight this item, vector plots of some failure mechanisms computed for the two caissons are shown in Figs. 8 and 9 together with the relevant contours of the deviatoric strain. IDs, relative to the caissons centroid, are represented in the non-dimensional plane Q/Q_u–M/M_u to focus on their shape. In Fig. 8, the caisson with H/D = 0.5, subject to M only (α_G = ∞, point A), undergoes an almost pure clockwise rotational mechanism around a point close to the centroid (“scoop” mechanism, according to [38]). Similarly, when subject to Q only (α_G = 0, point C), the caisson undergoes a pure translational mechanism with deviatoric strains developing in front and at the back of the caisson, where pseudo-active and pseudo-passive wedges are detected. Between points A and B, a coupled (“scoop-slide”) mechanism is attained with the caisson rotation pole moving downwards from the centroid to infinite (in point C). Between points B and D, a translational mechanism is observed, while after point D the mechanism is coupled again, with an anticlockwise rotation of the caisson (“reverse-scoop”) and the rotation pole progressively approaching the caisson centroid again, moving from above as Q decreases (points E and F). Similar failure mechanisms are observed for the deeper caisson (H/D = 2, Fig. 9). However, a rotation about a point deeper than the centroid is observed in A and a coupled mechanism in C: both symmetry and orthogonality of the failure envelope with respect to both x and y-axes are lost. The way the coupling effect of sliding and rotation affects the depth of the rotation point has also been observed in [3, 38]. This condition becomes more and more evident as H/D increases, as the lever arm of the resultant force transferred to the caisson centroid increases with H. Indeed, for the caisson with H/D = 2, the pure translational mechanism is attained when the horizontal force is applied to a point deeper than the centroid, at a depth z = H/2-$\alpha_G$ = 16 m = 2/3·H (point D in Fig. 9).

Fig. 7

Influence of the LRP location: IDs obtained for caissons subject to χ = 0 under undrained conditions, characterised by a H/D = 0.5 and b H/D = 2

Fig. 8

Failure mechanisms for the H/D = 0.5 caisson subject to χ = 0 and undrained conditions: vector plots and deviatoric strain contours

Fig. 9

Failure mechanisms for the H/D = 2 caisson subject to χ = 0 and undrained conditions: vector plots and deviatoric strain contours

4.3.1 Influence of the initial loading factor

For increasing vertical loads (χ = 0.63, F_sv = 1.6), symmetry and orthogonality of ID are lost even for H/D = 0.5 (Fig. 10). Higher values of vertical load induce a deepening of failure mechanisms, as shown by the comparison between the contour plots plotted in Figs. 8 and 10, with a more pronounced asymmetry in the Q–M plane, this resulting in a different shape of the envelope, especially between points B and D, where decoupling between rotational and horizontal degrees of freedom is lost.

Fig. 10

Failure mechanisms for the H/D = 0.5 caisson subject to χ = 0.63 and undrained conditions: vector plots and deviatoric strain contours

To better appreciate the influence of the vertical load on both ID size and shape, in Fig. 11 these are plotted for caissons with H/D = 0.5 and 1, for undrained applications of Q and M, both in the dimensional Q–M/D and non-dimensional Q/Q_u–M/M_u planes. Owing to the progressive change in the failure mechanisms geometry, which become deeper and more asymmetric (Figs. 8, 10), at increasing values of χ failure envelopes in Fig. 11a, c, first harden and subsequently shrink, in accordance with [38]. Specifically, at increasing χ values up to a certain threshold, the bearing capacity increases since larger volumes of soil are involved as mechanisms deepen. However, above a threshold value of χ, bearing capacity reduces since the asymmetry of the mechanisms seems to prevail, with a contraction of the failure envelopes.

Fig. 11

Influence of the vertical load (χ): IDs obtained for a, b H/D = 0.5 and c, d H/D = 1 caissons under undrained conditions

Comparison of Fig. 11b, d allows us to appreciate the influence of χ on the shape of IDs: this is more pronounced for the shallower caisson (H/D = 0.5). A significant change in the shape is evident by comparing envelopes obtained by assuming χ < 0.1 and χ > 0.1. Conversely, for embedment ratios H/D = 1 (Fig. 11d) and H/D = 2 (here omitted for the sake of brevity), non-dimensional IDs almost superimpose.

4.3.2 Influence of caisson embedment ratio

While the influence of embedment ratio H/D on IDs size has been already discussed (Sect. 4.3), here the focus is on the role of H/D in affecting the shape of IDs (Fig. 12) in case undrained conditions are accounted for. Consistently with the results shown by [17], a significant change in the shape of IDs is observed for small vertical loads, χ ≤ 0.21, as H/D increases (Fig. 12a, b): the envelope eccentricity progressively increases in the IV quadrant of the non-dimensional plane. By contrast, the influence of H/D vanishes for higher vertical loads (Fig. 12c, d).

Fig. 12

Influence of the embedment ratio (H/D): IDs obtained under undrained conditions for a χ = 0, b χ = 0.21, c χ = 0.42, d χ = 0.63

4.3.3 Influence of drainage conditions

The influence of drainage conditions, on both size and shape of IDs, is illustrated in Fig. 13, where IDs obtained imposing both undrained and drained conditions are compared for χ = 0.09 and different embedment ratios. As was expected for compression loading paths, undrained soil behaviour always results into smaller envelopes with respect to those computed under drained conditions (Fig. 13a, c, e). Indeed, due to the excess pore water pressure, foundation soils undergo an effective stress and in turn a shear strength reduction. Conversely, drainage conditions do not affect the shape of the failure envelopes (Fig. 13b, d, f). This observation may lead to assuming a failure envelope hardening homothetically as drainage occurs with time, until reaching the drained envelope.

Fig. 13

Influence of drainage conditions: IDs obtained for χ = 0.09 and caissons with a, b H/D = 0.5, c, d H/D = 1, e, f H/D = 2

5 Proposed relationships for interaction diagrams

An analytical expression for IDs is proposed to fit all the conditions investigated in this study. The general equation, valid for every initial loading factor χ, embedment ratio H/D and for both undrained and drained conditions, is that of a unit circle in the ξ′–μ′ plane:

$$\left( {\xi ^{\prime}} \right)^{2} + \left( {\mu ^{\prime}} \right)^{2} = 1$$

(3)

By scaling Eq. (3), the equation of an ellipse is obtained in the form

$$\left( {\frac{\xi ^{\prime}}{{a_{\xi } }}} \right)^{2} + \left( {\frac{\mu ^{\prime}}{{a_{\mu } }}} \right)^{2} = 1,$$

(4)

where a_ξ and a_μ, defined in the following, are a function of χ, H/D and drainage conditions. Equation (4) is then mapped into the ξ–μ plane by applying a rotation of an angle ω (positive if counterclockwise)

$$\left( {\begin{array}{*{20}c} {\xi ^{\prime}} \\ {\mu ^{\prime}} \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\cos \omega } & {\sin \omega } \\ { - \sin \omega } & {\cos \omega } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} \xi \\ \mu \\ \end{array} } \right)$$

(5)

where ξ and μ, following [7], are defined as

$$\begin{aligned} & \xi = \frac{Q}{{N_{{\text{lim,net}}} }} \\ & \mu = \frac{M}{{DN_{{\text{lim,net}}} }} \\ \end{aligned}$$

(6)

Hence, the proposed equation in the ξ–μ plane (Eq. 7) is that of a rotated ellipse having semi-axes, a_ξ and a_μ, and rotation angle, ω, depending on χ, H/D and drainage conditions:

$$\left( {\frac{{\cos^{2} \omega }}{{a^{2}_{\xi } }} + \frac{{\sin^{2} \omega }}{{a^{2}_{\mu } }}} \right)\xi^{2} + \left( {\frac{{\sin^{2} \omega }}{{a^{2}_{\xi } }} + \frac{{\cos^{2} \omega }}{{a^{2}_{\mu } }}} \right)\mu^{2} + \sin 2\omega \left( {\frac{1}{{a^{2}_{\xi } }} - \frac{1}{{a^{2}_{\mu } }}} \right)\xi \mu = 1$$

(7)

The numerical IDs corresponding to the five values of χ under consideration have been first interpolated by ellipses to obtain the values of $\omega$, $a_{\xi }$ and $a_{\mu }$ plotted by symbols in Fig. 14, for each H/D ratio and for both drainage conditions. In turn, these values have been best-fitted to define the following functions of χ:

$$\omega \left( \chi \right) = c_{11} {\kern 1pt} \chi^{2} + c_{12} {\kern 1pt} \chi + c_{13}$$

(8)

Fig. 14

Dependency of ω, a_ξ and a_μ on χ: values obtained for the best-fitting ellipses against Eqs. (8–9) for undrained (a–c) and drained (d–f) conditions

and

$$\begin{aligned} & a_{\xi } \left( \chi \right) = c_{21} (\chi - c_{\min } )^{{c_{22} }} (c_{\max } - \chi ) \\ & a_{\mu } \left( \chi \right) = c_{23} (\chi - c_{\min } )^{{c_{24} }} (c_{\max } - \chi ) \\ \end{aligned}$$

(9)

where the non-dimensional parameters c_i are listed in Table 3 as a function of H/D and the drainage conditions. Figure 14 shows a satisfactory agreement between the proposed Eqs.  (8–9) and the values of $\omega$, $a_{\xi }$ and $a_{\mu }$ represented by symbols.

Table 3 Values of the parameters in Eqs. (8–9) for each H/D ratio and both drainage conditions

The ξ–μ plane locus is obtained from the analytical expression above according to the method illustrated in Fig. 15. Specifically, with reference to undrained conditions and H/D = 0.5, the unit circle (Fig. 15a) is first distorted to the ellipse (Fig. 15b), by applying Eq. (4), and then rotated by the values of ω provided by Eq. (8) (Fig. 15c).

Fig. 15

Analytical IDs for H/D = 0.5 and undrained conditions: unit circle [Eq. (3)] (a); introduction of the distortion given by a_ξ and a_μ [Eq. (9)] (b) and the rotation ω [Eq. (8)] (c)

In Fig. 16a, the three-dimensional ID under drained conditions provided by Eq. (7) is plotted for H/D = 0.5: black lines are added to put in evidence the rotation with χ of the elliptical cross sections. In addition, cross sections for χ = 0.21 (b), ξ = 0 (c) and μ = 0 (d) for each value of embedment are also plotted. A comparison with the analytical solution proposed by [7] for shallow footings resting on sand is also presented (dotted line). It is evident that: (1) IDs increase in size with H/D, and (2) in contrast to the case H/D = 0, the cross sections of the caissons IDs in planes ξ = 0 and μ = 0 (Fig. 16c, d) do not close neither for χ = 0 nor for χ = 1 (Sect. 4.2). Conversely, in the solution proposed by [7], an almost perfectly symmetric to χ = 0.5 parabola is suggested. Finally, in planes χ = const., the solution proposed for shallow footings is an ellipse rotated by a constant angle ω = − 14°, while for embedded caisson foundations the rotation angle ω is found to vary with χ, especially for low values of H/D. The IDs provided by Eq. (7) for undrained conditions and each embedment ratio are plotted in Fig. 17. Similarly to what observed for drained conditions, the tendency of failure domains not to close for χ = 1 becomes more evident as H/D increases: however, such an opening is less pronounced due to the stiffer response of foundation soils under undrained loading.

Fig. 16

Analytical solutions of the 3D IDs under drained conditions for shallow footings (H/D = 0, [7]) and caissons (H/D = 0.5, 1, 2, this study)

Fig. 17

Analytical solutions of the 3D IDs under undrained conditions for each embedment ratio (H/D = 0.5, 1, 2)

6 Simplified displacement-based approach

Since the ultimate Q–M values are attained for high values of both caisson horizontal displacement and rotation, a displacement-based criterion can be proposed not to exceed either serviceability or ultimate limit states for the superstructure (e.g. a bridge pier). The numerical generalised load–displacement curves (LDCs), obtained for different load paths (i.e. values of α_G), under undrained conditions are represented in Fig. 18 (grey line) for each H/D and for χ = 0.09 and 0.21 in the ${{\left| {\overline{F}} \right|} \mathord{\left/ {\vphantom {{\left| {\overline{F}} \right|} {\left| {\overline{F}} \right|_{{{\text{lim}}}} }}} \right. \kern-\nulldelimiterspace} {\left| {\overline{F}} \right|_{{{\text{lim}}}} }} - {{\left| {\overline{u}} \right|} \mathord{\left/ {\vphantom {{\left| {\overline{u}} \right|} {\left| {\overline{u}} \right|_{{{\text{el}}}} }}} \right. \kern-\nulldelimiterspace} {\left| {\overline{u}} \right|_{{{\text{el}}}} }}$ plane, where $\left| {\overline{u}} \right|_{{{\text{el}}}} = {{\left| {\overline{F}} \right|_{{{\text{lim}}}} } \mathord{\left/ {\vphantom {{\left| {\overline{F}} \right|_{{{\text{lim}}}} } {K_{0} }}} \right. \kern-\nulldelimiterspace} {K_{0} }}$ denotes the elastic generalised displacement corresponding to $\left| {\overline{F}} \right|_{{{\text{lim}}}}$ and K₀ is the initial tangent stiffness of the $\left| {\overline{F}} \right| - \left| {\overline{u}} \right|$ curves. As it is evident in Fig. 18, for deep caissons, in contrast to what is observed in case of low values of H/D (≤ 1), the dependency of LDCs on α_G is less significant, being the scatter not marked. The same observation does apply for drained conditions, although the representation is here omitted for the sake of brevity. In view of defining a pre-design simplified approach, the following equations of LDCs are proposed for both drainage conditions:

$$\begin{array}{*{20}l} {\frac{{|\overline{F}|}}{{|\overline{F}|_{{{\kern 1pt} {\text{lim}}}} }} = 1 - \exp \left( { - \frac{{|\overline{u}|}}{{|\overline{u}|_{{{\kern 1pt} {\text{el}}}} }}} \right)} \hfill & {{\text{undrained}}\;{\text{conditions}}} \hfill \\ {\frac{{|\overline{F}|}}{{|\overline{F}|{\kern 1pt}_{{{\text{lim}}}} }} = \frac{{\frac{{|\overline{u}|}}{{|\overline{u}|{\kern 1pt}_{{{\text{el}}}} }}}}{{1 + \frac{{|\overline{u}|}}{{|\overline{u}|_{{{\kern 1pt} {\text{el}}}} }}}}} \hfill & {{\text{drained}}\;{\text{conditions}}} \hfill \\ \end{array}$$

(10)

Fig. 18

Dimensionless generalised LDCs: comparison between Eq. (10)₁ and numerical curves obtained under undrained conditions for χ = 0.09 (a, c, e) and χ = 0.21 (b, d, f)

These simple expressions, neglecting the dependency of LDCs on parameters χ, H/D, α_G, are justified by the range of values of ${{\left| {\overline{u}} \right|} \mathord{\left/ {\vphantom {{\left| {\overline{u}} \right|} {\left| {\overline{u}} \right|_{{{\text{el}}}} }}} \right. \kern-\nulldelimiterspace} {\left| {\overline{u}} \right|_{{{\text{el}}}} }}$ considered for design purposes, far from ${{\left| {\overline{F}} \right|} \mathord{\left/ {\vphantom {{\left| {\overline{F}} \right|} {\left| {\overline{F}} \right|_{{{\text{lim}}}} }}} \right. \kern-\nulldelimiterspace} {\left| {\overline{F}} \right|_{{{\text{lim}}}} }} = 1$. In preliminary design computations, the user can evaluate $\left| {\overline{F}} \right|_{{{\text{lim}}}}$ from the rotated ellipse discussed in Sect. 5 (Eq. 7) and K₀ from the elastic solutions proposed by [15, 21, 34] (see “Appendix 2”), as a function of input parameters such as χ, H/D, α_G and drainage conditions. Then, the threshold displacement ratio ${{\left| {\overline{u}} \right|} \mathord{\left/ {\vphantom {{\left| {\overline{u}} \right|} {\left| {\overline{u}} \right|_{{{\text{el}}}} }}} \right. \kern-\nulldelimiterspace} {\left| {\overline{u}} \right|_{{{\text{el}}}} }}$ needs to be selected only in Eqs. (10).

As an example, here $\left| {\overline{u}} \right| = \theta$ [i.e. u/D = 0, see Eqs. (2)] is assumed, and an ultimate state threshold value of 1 ‰, typically adopted for bridge piers of critical facilities, is considered. The elastic generalised displacement $\left| {\overline{u}} \right|_{{{\text{el}}}}$ does not change significantly with α_G and H/D, mainly depending on χ instead, due to (1) the increase in $\left| {\overline{F}} \right|_{{{\text{lim}}}}$ and (2) the decrease in K₀ related to the development of plastic strains in the soil. Numerical results show that item (2) is particularly evident for low values of H/D: as χ increases from 0 to 0.21, the mean reduction of K₀ is of 40%, 25%, 10% for H/D = 0.5, 1 and 2, respectively. The computed values of ${{\left| {\overline{F}} \right|} \mathord{\left/ {\vphantom {{\left| {\overline{F}} \right|} {\left| {\overline{F}} \right|_{{{\text{lim}}}} }}} \right. \kern-\nulldelimiterspace} {\left| {\overline{F}} \right|_{{{\text{lim}}}} }}$, evaluated through Eqs. (10), are listed in Table 4, for three values of χ and both drainage conditions, correspondingly to $\left| {\overline{u}} \right|_{{{\text{lim}}}} = 1\permille$. As it is shown in Fig. 18, for undrained conditions, in the range of values of ${{\left| {\overline{u}} \right|} \mathord{\left/ {\vphantom {{\left| {\overline{u}} \right|} {\left| {\overline{u}} \right|_{{{\text{el}}}} }}} \right. \kern-\nulldelimiterspace} {\left| {\overline{u}} \right|_{{{\text{el}}}} }}$ here considered for design purposes, ${{\left| {\overline{u}} \right|} \mathord{\left/ {\vphantom {{\left| {\overline{u}} \right|} {\left| {\overline{u}} \right|_{{{\text{el}}}} }}} \right. \kern-\nulldelimiterspace} {\left| {\overline{u}} \right|_{{{\text{el}}}} }} \le 1$, the analytical expressions [Eqs. (10)] fairly match the curves obtained from the numerical analyses. It is worth mentioning that one can also compute the displacement components, u and θ, starting from the definition of $\left| {\overline{u}} \right|$ [Eqs. (2)], under the hypothesis of associative flow rule, once the same shape is assumed for both the yielding and the failure envelope, as discussed in Sect. 4.2.

Table 4 Admissible values of |$\overline{F}$|/|$\overline{F}$|_lim corresponding to the limit value of |$\overline{u}$|= 1 ‰ suggested in design under undrained and drained conditions

7 Conclusions

Rigid and massive caisson foundations are typically subject to combined loading conditions, thus withstanding vertical and horizontal forces at the same time, as well as moment. For this reason, interaction domains may be a useful tool to assess their safety against limit states when designing these foundations, as the distance of the image generalised stress point from the boundary of the interaction domain may be interpreted as a sort of safety factor. However, as full mobilisation of the caissons capacity under general loading conditions tends to be achieved for large displacements not compatible with working conditions, a displacement-based approach for assessing the safety factor at a preliminary design stage may be preferred. This approach has been followed in this paper, based on the non-dimensional expressions provided for both the IDs and generalised load–displacement curves obtained by performing FE analyses. Indeed, the response of massive cylindrical onshore caisson foundations in a two-layer soil, subject to general loading conditions, has been investigated by means of a series of 3D elastic–plastic FE numerical analyses.

Bearing capacity under a centred vertical load is first investigated by assuming a drained response for the foundation soil and three different values for the embedment ratio. Numerical results testify that load–displacement relationships are severely affected by the caisson embedment ratio: indeed, structural hardening related to spatial propagation of the plastic zone, from the caisson base to the upper horizontal boundary of the FE mesh, becomes more and more pronounced as H/D increases.

Ultimate response of the caissons under a general combination of vertical and horizontal loads (N, Q), as well as overturning moment (M), is also investigated. The 3D envelopes in the N–Q–M/D space present a rugby-ball shape, similar to that obtained for shallow footings in previous works. However, soil–caisson strength under Q–M combinations is different from zero when the vertical load is equal to zero and close to its limit value (N_lim,net), differently from shallow foundations.

From the comparison of the results obtained in this study (two-layer soil) with those from previous ones (homogeneous soil), it follows that IDs shape is very slightly affected by the assumed soil layering, whereas it is influenced by the profile of shear strength (constant or linearly increasing with depth).

A parametric study has been carried out to understand the factors mainly affecting both size and shape of failure envelopes in the N–Q–M space. The influence of initial loading factor (χ) and caisson embedment ratio (H/D) has been evaluated for both fully undrained and drained conditions, showing that the assumed drainage condition scales up the ID size rather than modifying its shape. The influence of the load reference point location is also discussed, with the centroid of the caisson being usually the most suitable choice, as this strongly simplifies the shape of ID, leading to decoupling of rotational and horizontal degrees of freedom for low embedment ratios (H/D = 0.5).

Analytical expressions best-fitting the three-dimensional interaction diagrams computed in the non-dimensional N–Q–M/D load space, together with the generalised load–displacement curves are also proposed, for both undrained and drained conditions: these are integrated according to a simplified approach proposed as a useful tool at a preliminary design stage to ensure the foundation displacements to be compatible with the desired structural performance, for both serviceability and ultimate limit states. Future work will be oriented towards integrating the obtained results in an elastic–plastic isotropic hardening macro-element model, where the ID equation can be used to define the yield function.

Appendices

Appendix 1

The influence of the soil constitutive law on the IDs is shown in Fig. 

Fig. 19

Influence of the constitutive law under undrained conditions: ID for the H/D = 1 caisson subject to χ = 0.21 obtained assuming the elastic-perfectly plastic (black) and the HS Small (grey) model for the soil (a); pushover curve for the load path α_G = 0 (b)

19. For the H/D = 1 caisson subject to χ = 0.21, the IDs have been obtained from two sets of purely undrained numerical analyses where the following models have been used to describe the soil behaviour: (1) linear elastic-perfectly plastic and (2) nonlinear elastic–plastic model with isotropic hardening (Hardening Soil with small-strain stiffness, [1]), both assuming a Mohr–Coulomb failure criterion. Table 

Table 5 Properties of the foundation soils and parameters of the HS Small model

5 summarises the parameters assumed for HS Small: details about the meaning and choice of such parameters can be found in [13]. The choice of different constitutive laws affects the evolution of the soil stiffness and, consequently, the excess pore pressure arising under undrained conditions. This affects the evolution of the generalised force–displacement curves attaining a different plateau, as shown in Fig. 19b for α_G = 0. However, Fig. 19a shows that the choice of the constitutive law does not affect the shape of the IDs and that the overestimation of the Q–M strength does not exceed the 10%. Under drained conditions, instead, nor the shape neither the dimensions of the IDs are affected since the plateau attained by the curves is the same as a consequence of the same failure criterion assumed by the two models (Fig. 

Fig. 20

Influence of the constitutive law under drained conditions: pushover curve for the load path α_G = 0 and the H/D = 1 caisson subject to χ = 0.0 assuming the elastic-perfectly plastic (black) and the HS Small (grey) model for the soil

20).

If a criterion different from the plateau is used to obtain the IDs, as those based on the K_tan/K₀ ratio or on the generalised displacement |$\overline{u}$| described in Sect. 4.2, its influence on the IDs shape and dimensions is negligible though the constitutive law affects the evolution of the generalised force–displacement curves. In view of the above and of the purpose of the paper, a less complex constitutive law has been adopted in the parametric numerical study, thus taking advantage of a lower computational effort.

Appendix 2

To calculate $\left| {\overline{u}} \right|_{{{\text{el}}}} = {{\left| {\overline{F}} \right|_{{{\text{lim}}}} } \mathord{\left/ {\vphantom {{\left| {\overline{F}} \right|_{{{\text{lim}}}} } {K_{0} }}} \right. \kern-\nulldelimiterspace} {K_{0} }}$, stiffness K₀ is to be evaluated as follows

$$K_{0} = \frac{{\left\| {\begin{array}{*{20}c} {\frac{1}{{N_{{\text{lim,net}}} }}} \\ {\frac{{\alpha_{G} }}{{DN_{{\text{lim,net}}} }}} \\ \end{array} } \right\|}}{{\left\| {{\kern 1pt} {\kern 1pt} \left[ {\begin{array}{*{20}c} \frac{1}{D} & { \pm \frac{H}{2D}} \\ 0 & 1 \\ \end{array} } \right]{\varvec{C}}\left[ {\begin{array}{*{20}c} 1 \\ {\alpha_{{\text{G}}} \pm \frac{H}{2}} \\ \end{array} } \right]{\kern 1pt} {\kern 1pt} } \right\|}}$$

(11)

where ||⋅|| stands for the matrix norm. In Eq. (11) C represents the elastic compliance matrix of the soil–caisson system calculated as the inverse of the stiffness matrix

$${\varvec{C}} = \left[ {\begin{array}{*{20}c} {{\text{K}}_{x}^{emb} } & {{\text{K}}_{x - ry}^{emb} } \\ {{\text{K}}_{x - ry}^{emb} } & {{\text{K}}_{ry}^{emb} } \\ \end{array} } \right]^{ - 1}$$

(12)

The translational, rotational and coupled stiffness terms in Eq. (12) can be evaluated according to [15, 21] for H/D ≤ 1 and to [34] for H/D = 2. The ± sign in Eq. (11) is introduced to properly exploit the previously cited elastic solutions since they assume the caisson base (+) as LRP for H/D ≤ 1 and the caisson top (−) for H/D = 2, respectively.