1 Introduction and motivation

Design and assessment procedures of geotechnical infrastructure increasingly rely on constitutive models capable of describing the crucial aspects of soil behaviour. However, when soft organic soils as peats are encountered, many difficulties arise. Lack of sound geotechnical description of the behaviour of peats represents one of the greatest concerns currently faced by geotechnical engineers. The deviatoric behaviour of peats is particularly challenging, due to contradictory results and knowledge gaps remaining in the interpretation and the modelling of field and laboratory tests.

Attempts to model the deviatoric behaviour of peats are scarce. Most of the contributions in the literature tackle the simulation of experimental data from laboratory tests or field tests by introducing minor changes in well-known constitutive models originally developed for other soils. It is worth mentioning the first contribution due to Yamaguchi et al. [48], who coupled a Modified Cam clay model [42] with an experimentally based stress–dilatancy relationship. Good agreement with the experimental results at the ultimate state was found despite significant overestimation of both the shear stiffness and the excess pore pressure over the pre-failure response. Yang et al. [49] adopted the elastic–plastic model developed by Li and Dafalias [29] with a modified stress–dilatancy function and plastic hardening modulus. The comparison with laboratory data was satisfactory though limited to a series of standard undrained triaxial tests. More recently, Muraro et al. [36] proposed an attempt to model drained and undrained triaxial compression tests on peats in the framework of hypo-plasticity. Starting from the model by Mašín [31], the authors introduced an experimentally based boundary surface and the corresponding asymptotic strain rate directions.

An application of the well-established Soft Soil Creep model for clays is reported by den Haan and Feddema [15]. The model capabilities were tested against data from the IJkdijk macro-stability experiment at Booneschans, with the results showing reasonable agreement with the measured field displacements [51]. Applicability of the anisotropic version of the Soft Soil Creep model to peats was discussed by den Haan [12]. However, comparison with experimental data was not reported, leaving the validation of the formulation and the determination of the model parameters open to further study. To this end, information from probe tests can provide experimental evidence to support some of the model ingredients, such as the rotational hardening rule, and to identify a convenient range for the model parameters. Recent modelling attempts also include a kinematic bubble model though at a very early stage [5].

Regardless of the different modelling approaches, the development of constitutive models for soils is typically supported and validated on data from laboratory tests interpreted as soil element tests. Muraro and Jommi [35] found significant differences between the material behaviour and the sample behaviour of peats caused by the adoption of conventional rough end platens in the triaxial apparatus. Shear stresses at the interface between the sample and the porous stone restrain the radial displacement of the sample to a large extent, in turn introducing an apparent contribution to anisotropy along compression paths and altering the computed dilatancy. End restraint also contributes to largely overestimating the shear strength of peats. Overestimation of the deviatoric stress and the excess pore pressure measured at the bottom of the sample was found by Muraro and Jommi [37] on a series of undrained triaxial tests. These results have a twofold implication. On the one hand, constitutive models for peats should be developed based on experimental data from laboratory tests as triaxial tests where smooth end platens are adopted. On the other hand, when this is unfeasible, end restraint must be accounted for when elaborating the experimental data.

The recent work by Muraro and Jommi [37] on the interpretation of triaxial tests underpins the analysis of the pre-failure behaviour of peats presented here. A series of drained triaxial compression tests on reconstituted peat performed in triaxial apparatus are presented to substantiate the derivation of the ingredients that an elastic–plastic model for peats should contain. The yield locus, the hardening mechanism and the flow rule are analysed, in an attempt to improve the current elastic–plastic models capabilities though keeping the description of the soil as simple as possible. The capabilities and the limitations of the adopted elastic–plastic constitutive law are eventually discussed against laboratory data.

2 Experimental programme

2.1 Tested material

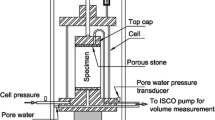
The material used in the experimental investigation was collected from the Leendert de Boerspolder in the Netherlands, between 1 and 1.5 m below the ground surface. Reconstituted samples were prepared by mixing the natural material with demineralised water to a slurry with a water content of 855%, corresponding to 1.4 times the liquid limit. The material was consolidated in \( K_{0} \) conditions under a vertical stress of 10 kPa and eventually mounted in the triaxial apparatus. The triaxial system includes a submersible 1 kN load cell, a back pressure and cell pressure volume controllers with an accuracy of ± 1 kPa on pressure and ± 300 mm3 on volume (0.15% full scale range). Relevant index properties of the samples are reported in Table 1, together with the pre-consolidation mean effective stress, \( p '_{\text{c}} \), the mean effective stress, \( p '_{0} \) and the void ratio, \( e_{0} \), at the start of the shear, and a description of the stress path followed during each test. The specific gravity, Gs, and the organic content, OC, were determined in accordance with the D5550-14 [11] and the D2974-14 [10]. Fibre content determination gave an average value of 0.14 [9]. Figure 1 displays a picture obtained from X-ray micro-CT on the tested peat, after 2 days of drying at a temperature of 14 °C and relative humidity of 80%. The fibrous structure is characterised by diffused small fibres having a maximum length of about 3 mm.

Table 1 Index properties, initial state and stress path of the tested specimens
Full size table
Fig. 1
figure 1

Micro-CT scan of the reconstituted peat used in the experimental investigation

Full size image

The nominal size of the tested specimens was 38 mm in diameter and 76 mm in height. Preliminary comparison of TxCU results on 38-mm-diameter and 50-mm-diameter samples confirmed the absence of any significant effect of the sample diameter on the stress–strain response of the tested peat. To reduce the shear stresses at the sample extremities, modified end platens were used [37]. A suction cap was used to assure perfect contact between the load cell and the top cap given the low effective confining stresses adopted in the experimental investigation, representative of the field stress of surficial peat layers in the Netherlands (\( \sigma '_{\text{v}} \) ≅ 10–40 kPa). All the drained tests were performed under stress control assuring limited excess pore pressure generation. The maximum excess pore pressure remained below 4% of the mean effective stress of the samples. The resulting average axial displacement rate, \( \dot{u}_{\text{a}} \), reported in Table 1, is approximately ten times lower than that theoretically required to guarantee a pore pressure dissipation degree of 95% [3].

2.2 Stress and strain variables

The experimental data are elaborated by assuming axisymmetric test conditions and adopting the common triaxial stress–strain variables: mean effective stress p′, deviatoric stress q, volumetric strain, \( \varepsilon_{\text{p}} \), and deviatoric strain, \( \varepsilon_{\text{q}} \). Natural strains are adopted to account for the large displacements undergone by peat samples [30, 19]:

$$ \varepsilon_{\text{p}} = \varepsilon_{\text{a}} + 2\varepsilon_{\text{r}} = \ln \left( {\frac{{V_{0} }}{V}} \right) $$
(1)
$$ \varepsilon_{\text{q}} = \varepsilon_{\text{a}} - \frac{{\varepsilon_{\text{p}} }}{3} = \ln \left( {\frac{{H_{0} }}{H}} \right) - \frac{1}{3}\ln \left( {\frac{{V_{0} }}{V}} \right) $$
(2)

where \( V_{0} \) and \( H_{0} \) are the initial volume and height of the sample, while V and H are the current values during the test. Compressive stresses and strains are assumed positive.

2.3 Stress paths

To investigate the volumetric behaviour, sample S-I was isotropically compressed to \( p' \) = 100 kPa and isotropically unloaded to \( p' \) = 7 kPa. A \( K_{0} \) consolidation test was performed on sample S-\( K_{0} \) to \( p' \) = 70 kPa to determine the coefficient of earth pressure at rest. The test was performed with a radial stress ramp with volume change and axial displacement back measurement allowing for automatic adjustment to guarantee negligible radial strains. Sample S-M1 and sample S-M2 were firstly isotropically consolidated to a mean effective stress \( p '_{\text{c}} \) = 34 kPa and \( p '_{\text{c}} \) = 37 kPa, respectively, and subsequently isotropically unloaded to \( p '_{0} \) to give an initial overconsolidation ratio \( {\text{OCR}} = p '_{\text{c}} / p '_{0} \) of about 2 and 2.6, respectively. The final shearing stage consisted in a series of mixed isotropic and deviatoric loading, unloading and reloading paths, as summarised in Fig. 2a, b.

Fig. 2
figure 2

Experimental stress paths followed for a isotropic volumetric behaviour and \( K_{0} \) consolidation and for b deviatoric behaviour

Full size image

3 Experimental results

3.1 Compression behaviour

The isotropic compression path performed on sample S-I allows determining the slope of the ISO-NCL and ISO-URL lines on the \( v - \ln p' \) space, resulting in \( \lambda \) = 2.0 and \( \kappa \) = 0.3 as reported in Fig. 3a. The compression indexes agree with previous research on fibrous peat where a ratio \( \kappa / \lambda \) = 0.1–0.3 is often reported [48, 33]. To better evaluate the response of the sample upon isotropic compression, the test was performed by controlling separately the axial and the radial stresses and measuring the axial displacement and the volume change separately. The inclination of the plastic strain increment vectors, \( \beta \), defined in Eq. (3) is plotted as a function of the mean effective stress in Fig. 3b.

Fig. 3
figure 3

Specific volume a and b inclination of the plastic strain increment vectors during isotropic compression of reconstituted peat sample S-I

Full size image
$$ \tan \beta = \frac{{\delta \varepsilon_{\text{q}}^{\text{p}} }}{{\delta \varepsilon_{\text{p}}^{\text{p}} }}. $$
(3)

The volumetric and the deviatoric plastic strain increments, \( \delta \varepsilon_{\text{p}}^{\text{p}} \) and \( \delta \varepsilon_{\text{q}}^{\text{p}} \), have been derived from the total ones by computing the elastic strains with a hypo-elastic law with constant Poisson’s ratio, \( \nu \) = 0.3 and \( \kappa \) = 0.3 [35].

The previous stress history experienced by the sample in the 1D consolidometer justifies the initial anisotropic response observed at the beginning of the isotropic compression. However, the initial anisotropy is progressively erased over the isotropic loading path. At mean effective stress of about 30 kPa (Fig. 3a, b), roughly corresponding to four times the one experienced in the consolidometer, the response already turns to be isotropic with horizontally aligned plastic strain increment vectors (\( \beta \) → 0). The exceptional compressibility of peats allows accumulating high irrecoverable strains [24], which contribute to erasing the initial anisotropy faster than for other soils [20, 28, 34, 41, among others].

The 1D compression behaviour was investigated by a \( K_{0} \) consolidation path on sample S-\( K_{0} \) (Fig. 4) which gave \( K_{0} \) = 0.33 in the range indicated by previous findings [13, 16, 18]. The \( K_{0} \) value is consistent with the simplified Jaky’s formula [21], \( K_{0} \cong 1 - \sin \varphi ' \), assuming a friction angle \( \varphi ' \) ≅ 43° obtained from undrained triaxial compression tests with smooth end platens on the same reconstituted peat [37].

Fig. 4
figure 4

Lateral stress ratio for the tested peat from \( K_{0} \) consolidation path (data from [37])

Full size image

3.2 Yield locus

Yielding of soils is associated with a transition in stiffness of the response. In general, this transition is gradual and a degree of judgement must be exercised in estimating the yield stress [45, 46]. To infer the position of the yield locus for the tested peat, the multiple stress paths applied on samples S-M1 and S-M2 in Fig. 2b have been elaborated following various criteria. Estimates of the yield points, Y, have been obtained on each stress–strain plane shown in Figs. 5 and 6. The cumulative work input per unit of volume, W, versus the length of the stress path, S, is also considered to assist in the estimate of the yield points [2, 46], with

Fig. 5
figure 5

Estimates of the yield points for sample S-M1 along the radial path AC (a, b), the isotropic loading DE (c), and the deviatoric path FG (d)

Full size image
Fig. 6
figure 6

Estimates of the yield points for sample S-M2 along the radial path AC (a, b) and the isotropic loading DE (c, d)

Full size image
$$ W = \int p^{\prime}\delta \varepsilon_{\text{p}} + q \delta \varepsilon_{\text{q}} $$
(4)
$$ S = \int \delta s = \int \sqrt {\delta{{{\text{p}}'}}^{2} + \delta{\text{q}}^{2} } $$
(5)

where \( \delta \varepsilon_{\text{p}} \) and \( \delta \varepsilon_{\text{q}} \) are the total volumetric and deviatoric strain increments. Eventually, the chosen yield points for each test were the ones best matching all the criteria.

The yield points in Figs. 5 and 6 allow drawing a tentative yield locus for the tested peat. To fit the experimental points, the generalised expression proposed by McDowell and Hau [32] is used, which allows enough flexibility in the shape of the yield locus through the coefficient \( \chi_{\text{f}} \), though keeping the formulation extremely simple:

$$ f = 0 = q^{2} + \frac{{M_{\text{f}}^{2} }}{{1 - \chi_{\text{f}} }}\left( {\frac{p'}{{p_{\text{c}}^{\prime } }}} \right)^{{\frac{2}{{\chi_{\text{f}} }}}} p_{\text{c}}^{\prime 2} - \frac{{M_{\text{f}}^{2} p^{\prime 2} }}{{1 - \chi_{\text{f}} }}. $$
(6)

In Eq. (6), \( p '_{\text{c}} \) is the pre-consolidation mean effective stress and \( M_{\text{f}} \) is the stress ratio corresponding to a horizontal tangent to the yield locus in the \( p ' \) − q plane. The latter is different from the critical stress ratio, which is ruled by the non-associated plastic potential. Figure 7 displays the trace of the yield locus compared to the Modified Cam clay, which corresponds to \( \chi_{\text{f}} \) = 2 [42]. As displayed in Fig. 7, the experimental yield locus (full symbols) fitted by Eq. (6) with \( M_{\text{f}} \) = 1.5 and \( \chi_{\text{f}} \) = 3 lays slightly below the traditional Modified Cam clay. The open symbol was plotted after fixing \( p '_{\text{c}} \) with the previous yield shape.

Fig. 7
figure 7

Trace of the yield locus on the \( p' \) − \( q \) space from the estimated yield points

Full size image

3.3 Hardening mechanism

Critical state models assume that the hardening of the soil is controlled merely by plastic volumetric strains. This assumption can be considered acceptable for fine-grained materials as clays but not for granular materials as sands and intermediate soils as silts. Information on the hardening of peat is very scarce. Experimental evidence about the hardening mechanism of peat is presented here, based on the results of both drained and undrained triaxial tests.

3.3.1 Drained triaxial tests

Figure 8a reports the evolution of the pre-consolidation mean effective stress, \( p '_{\text{c}} \), with the volumetric plastic strains, \( \varepsilon_{\text{p}}^{\text{p}} \), computed for each radial path. The current value of \( p '_{\text{c}} \) is normalised with the value at the onset of plastic strains.

Fig. 8
figure 8

Evolution of the pre-consolidation mean effective stress with a volumetric plastic strain and b the combination of volumetric and deviatoric plastic strains for different radial paths

Full size image

As displayed in Fig. 8a, the evolution of the hardening variable is not ruled by the plastic volumetric strain solely over different stress paths. If \( p '_{\text{c}} \) is assumed to depend on a simple linear combination of volumetric and deviatoric plastic, \( \varepsilon_{\text{p}}^{\text{p}} + D\varepsilon_{\text{q}}^{\text{p}} \), the experimental data well fit a unique line with D an empirical coefficient equal to 0.95 (Fig. 8b). The result suggests that both volumetric and deviatoric strains rule the hardening mechanism of the tested peat and that the relevance of the deviatoric component increases with the stress ratio.

3.3.2 Undrained triaxial tests

Indirect information on the hardening mechanism also come from undrained compression triaxial tests by means of the pore pressure parameter, a, defined as [46]

$$ a = - \frac{{\Delta p^{\prime}}}{{\Delta q}} $$
(7)

Figure 9 reports the stress path and the evolution of the parameter a with the stress ratio, \( \eta \), computed from the sample S-U sheared in undrained conditions. The pore pressure parameter firstly increases until a stress ratio of about 1 and then decreases approaching zero in correspondence of the critical stress ratio \( M_{\text{g}} \) = 1.75 (Fig. 9b).

Fig. 9
figure 9

Stress path a and b pore pressure parameter from undrained triaxial compression test on sample S-U

Full size image

The two data sets suggest that a generalised mixed hardening rule proposed for granular soils [38, 39] can be adopted for the tested peat:

$$ \frac{{\delta p'_{\text{c}} }}{{p'_{\text{c}} }} = \frac{v}{\lambda - \kappa }\left( {\delta \varepsilon_{\text{p}}^{\text{p}} + D \delta \varepsilon_{\text{q}}^{\text{p}} } \right). $$
(8)

In Eq. (8), \( v \) is the specific volume of the soil, \( \lambda \) and \( \kappa \) are the slope of the normal compression and unloading–reloading lines, respectively, and \( \delta \varepsilon_{\text{p}}^{\text{p}} \) and \( \delta \varepsilon_{\text{q}}^{\text{p}} \) are the volumetric and deviatoric plastic strain increments. The coefficient D accounts for the deviatoric strain-dependent hardening. When D is set equal to zero, the usual volumetric hardening law is recovered. If not, D can be assumed either constant [17, 23, 38, 50], or better a function of the deviatoric plastic strain to reduce the dilatancy at failure. A possible expression is [44]

$$ D = D_{0} { \exp }\left( { - D_{1} \varepsilon_{\text{q}}^{\text{p}} } \right). $$
(9)

The implications of the adopted hardening rule are shown with reference to the case of an undrained compression test as the one in Fig. 9. From Eq. (8), the constraint of constant global volume, \( \delta \varepsilon_{\text{p}}^{\text{p}} = - \delta \varepsilon_{\text{p}}^{\text{e}} \), gives

$$ \kappa \frac{\delta p'}{p '} = - \left( {\lambda - \kappa } \right)\frac{{\delta {p^{\prime}} _{\text{c}} }}{{p^{\prime}_{\text{c}} }} + vD\delta \varepsilon_{\text{q}}^{\text{p}}. $$
(10)

By introducing the definition of the pore pressure parameter, a, in infinitesimal form in Eq. (10), it follows

$$ a\frac{\delta q}{p '} = \frac{\lambda - \kappa }{\kappa }\frac{{\delta p^{\prime}_{\text{c}} }}{{p^{\prime}_{\text{c}} }} - \frac{vD}{\kappa } \delta \varepsilon_{\text{q}}^{\text{p}}. $$
(11)

For a contractive soil response, the first term on the right-hand side of Eq. (11) is always positive. The same holds for the second term considering that D ≥ 0. Equation (11) shows that for a stable deviatoric response (i.e. \( \delta q \)  ≥ 0), even in the contractive range the pore pressure parameter firstly increases and then decreases depending on the magnitude of the distortional term \( D\delta \varepsilon_{\text{q}}^{\text{p}} \), as the experimental results in Fig. 9b show. As an instructive case, Fig. 10 reports the comparison between the deviatoric response predicted by the Modified Cam clay with standard volumetric hardening (D = 0) and with the mixed hardening law in Eq. (9) for \( D_{0} \) = 0.95 and \( D_{1} \) = 7.

Fig. 10
figure 10

Implication of mixed volumetric and distortional hardening rule on a the stress path and on b the pore pressure parameter

Full size image

The results in Fig. 10 compared with Fig. 9 confirm that a purely volumetric hardening is not adequate to describe the deviatoric response of peats, as the evolution of the pore pressure parameter in Fig. 9 cannot be replicated assuming D = 0. Depending on the magnitude of the distortional hardening coefficient D, Eq. (8) introduces the occurrence of dilation in the hardening regime with the possibility of reaching failure for a stress ratio higher than the critical stress ratio, \( M_{\text{g}} \), with non-null dilatancy. It is worth noticing that evidence of dilation in the hardening regime for natural fibrous peats was firstly reported by Oikawa and Miyakawa [40] in undrained compression tests and confirmed later on by Kanmuri et al. [22], Boulanger et al. [4], Mesri and Ajlouni [33] and De Guzman and Alfaro [14]. The geometrical rearrangement/realignment of the small fibrous network present in the fabric of the tested peat may provide the physical ground of Eq. (8) as the geometrical rearrangement of particles does for granular soils [46].

3.4 Stress–dilatancy relationship

A dedicated experimental and numerical investigation to derive the stress–dilatancy relationship for the tested peat was presented by Muraro and Jommi [35]. For the sake of clarity, only the main conclusions are briefly recalled. The expression by McDowell and Hau [32] introduced for the shape of yield locus is also adopted for the plastic potential:

$$ g = q^{2} + \frac{{M_{\text{g}}^{2} }}{{1 - \chi_{\text{g}} }}\left( {\frac{p '}{{p '_{\text{g}} }}} \right)^{{\frac{2}{{\chi_{\text{g}} }}}} p_{\text{g}}^{\prime 2} - \frac{{M_{\text{g}}^{2} p^{\prime 2} }}{{1 - \chi_{\text{g}} }} $$
(12)

with \( p '_{\text{g}} \) being a dummy variable.

Equation (12) gives the following expression for dilatancy:

$$ d = \frac{{\delta \varepsilon_{\text{p}}^{\text{p}} }}{{\delta \varepsilon_{\text{q}}^{\text{p}} }} = \frac{{M_{\text{g}}^{2} - \eta^{2} }}{{\chi_{\text{g}} \eta }}. $$
(13)

The value of the shape parameter \( \chi_{\text{g}} \) was determined requiring zero lateral strain along the \( K_{0} \) path on sample S-\( K_{0} \) (Fig. 2a), and neglecting the elastic component of the deviatoric strain for the sake of simplicity [1] resulting in

$$ \chi_{\text{g}} = \frac{2}{9}\frac{\lambda }{\lambda - \kappa }\frac{{M_{\text{g}} \left[ {\left( {6 - M_{\text{g}} } \right)^{2} - 9} \right]}}{{6 - M_{\text{g}} }}. $$
(14)

For compression indexes \( \lambda \) = 2.0 and \( \kappa \) = 0.3 and a critical stress ratio \( M_{\text{g}} \) = 1.75, a value of \( \chi_{\text{g}} \) = 0.98 is obtained. Figure 11 displays the resulting stress–dilatancy rule.

Fig. 11
figure 11

Stress–dilatancy rule derived from the \( K_{0} \) consolidation path on sample S-\( K_{0} \) (redrawn from [35])

Full size image

4 Constitutive modelling

The capabilities and the limitations of an elastic–plastic model built on the previous experimental findings are discussed by simulating the drained triaxial compression tests displayed in Fig. 12 with a focus on the pre-failure behaviour. Table 2 reports the characteristics of each sample.

Fig. 12
figure 12

Drained triaxial tests with multiple loading paths used to evaluate the model capabilities

Full size image
Table 2 Index properties and relevant stress levels of the specimens used for the model simulations
Full size table

The model parameters used in the numerical simulations are summarised in Table 3. All of them are based on the direct experimental evidence previously discussed, except the distortional hardening coefficient \( D_{1} \), which was chosen after a sensitivity analysis.

Table 3 Parameters adopted in the model simulations
Full size table

The comparison between the model simulations and the experimental results is reported in Figs. 13, 14 and 15 on different stress–strain spaces.

Fig. 13
figure 13

Experimental results and model simulations of the volumetric response of sample a S-M3 and b S-M4

Full size image
Fig. 14
figure 14

Experimental results and model simulations of the deviatoric response of sample a S-M3 and b S-M4

Full size image
Fig. 15
figure 15

Experimental results and model simulations of the strain paths of sample a S-M3 and b S-M4

Full size image

The model simulations show good qualitative and quantitative agreement with the experimental results both in the volumetric and in the deviatoric response, for a wide range of strains up to 20%, encompassing representative strain levels for field applications. For higher strains, the agreement is less satisfactory as shown in Fig. 14a. However, it is worth mentioning that at high strain levels membrane effects and the restraint offered by the O-rings may have affected the homogeneity of the response, which can hardly be interpreted as a pure material response [43].

The model capabilities are also tested for the undrained compression triaxial test on sample S-U with the same parameters reported in Table 3.

The model simulation in Fig. 16a shows a good agreement in the deviatoric stress–strain response compared to the experimental results despite slightly overestimating the initial stiffness for deviatoric strains up to 2%. On the contrary, the model prediction in terms of excess pore pressure development disagrees with the experimental data for the entire pre-failure domain (Fig. 16b) which seems to suggest differences in the plastic deformation response of sample S-U compared to the previous tests.

Fig. 16
figure 16

Experimental results and model simulations of the undrained compression test on sample S-U in terms of a deviatoric response and b excess pore pressure

Full size image

5 Discussion

A critical discussion of the model capabilities is presented stemming from the previous comparison between the model simulation and the experimental results. The stress–dilatancy data obtained from sample S-U is investigated in Fig. 17 in an attempt to provide a plausible explanation for the discrepancy reported in Fig. 16.

Fig. 17
figure 17

Stress–dilatancy data a from sample S-U sheared in undrained conditions compared to the one discussed in Fig. 11 and b corresponding plastic strain increment vectors along three radial paths

Full size image

As displayed in Fig. 17a, the experimental data from the undrained compression test align on a stress–dilatancy rule very different from the one presented in Fig. 11 and adopted in the numerical simulations in Fig. 16. To interpolate the experimental data in Fig. 17a, the shape parameter of the plastic potential in Eq. (12) should be increased dramatically to \( \chi_{\text{g}} \) = 5 compared to \( \chi_{\text{g}} \) = 0.98 which was derived from the \( K_{0} \) consolidation test (Eq. 14). The theoretical consequences of this apparent inconsistency are displayed in Fig. 17b, where the plastic strain increment vectors predicted using the two different values of \( \chi_{\text{g}} \) are compared to each other at the same stress state. The comparison suggests that undrained compression magnifies the role of distortional strains on the plastic deformation mechanism and marks the limitations of the previous modelling approach.

5.1 Stress–strain path dependence of the plastic deformation mechanism

Similar experimental evidence was presented by Cotecchia and Chandler [7, 8], who found very different stress–dilatancy relationships from drained and undrained triaxial tests on Pappadai clay. To explain the stress path dependency of the experimental results, the authors indicated that different structural degradation is likely to occur over different stress paths. This explanation suggests that the inconsistency on the \( \chi_{\text{g}} \) values may be justified by directional fabric changes.

Natural fibrous peats are claimed to exhibit inherent anisotropy related to the initial fibres orientation [25, 47]. The tested peat contains small fibres but without clear initial preferential orientation (Fig. 1). However, the results in Fig. 17 suggest the development of a directional response over progressive strains. Evidence of plastic strain increment vectors following the rotation of the stress increment vectors was firstly reported by Le Lievre and Poorooshasb [26] testing kaolin, Calabresi [6] testing a silty clay, and Lewin and Burland [27] testing a powdered slate dust. In an attempt to facilitate the interpretation of the experimental results, Fig. 18 shows an insight into the plastic strain increment vectors for three samples which were first isotropically consolidated up to \( p '_{\text{c}} \) = 34 kPa and then sheared along different loading directions. The sample S-D was sheared under drained conditions along a controlled stress path reproducing the one followed by the sample S-U. The incremental plastic deformation response of the three samples is compared in Fig. 18a at the same stress ratio \( \eta \cong 0.75 \), which was reached with similar deviatoric strains (\( \varepsilon_{\text{q}} \cong 2{-}3\% \)) and at similar void ratio, namely 7.08 for sample S-M1, 6.87 for sample S-U and 7.55 for sample S-D.

Fig. 18
figure 18

Stress paths a and b corresponding stress–dilatancy relationship for samples with two different loading directions

Full size image

The data show that the samples S-D and S-U, which had experienced the same stress path, show similar response, irrespective of the drainage conditions. On the contrary, the sample S-M1 shows a different incremental response after having followed a different stress path. The dependence of the stress–dilatancy rule on the stress path is confirmed by the data in Fig. 18b showing similar behaviour of the two samples S-D and S-U over the entire deviatoric stage, which differs from the one in Fig. 11. The experimental results confirm a dependence of the incremental response on the previous stress history, which can justify the difference between data and simulations in Fig. 16. On a physical ground, this dependence is likely to come from the interaction between the fibrous network and the peat matrix, with reorientation of the fibres depending on the strain path.

In Fig. 19a, the experimental axial–radial strain paths experienced by the different samples are plotted together with the reference theoretical response expected over the different stress paths. In Fig. 19b, the corresponding expected deformation of the fibrous network is sketched.

Fig. 19
figure 19

Experimental radial–axial strain paths a and b simplified scheme of the evolution of the fibrous network along different strain directions

Full size image

When the stress path triggers compressive radial strains, fibres–matrix interaction is limited. Over isotropic compression (\( \varepsilon_{\text{a}} \) = \( \varepsilon_{\text{r}} \)), fibres entanglement is expected to dominate. On the other extreme, over a \( K_{0} \) path (\( \varepsilon_{\text{r}} \) = 0) both fibres flattening and distortion may occur, still without any substantial stretching.

On the contrary, stress paths allowing fibres stretching promote kinematic interaction between the matrix and the fibres with local stress redistribution. It is expected that with radial expansion of the sample, the interaction between the soil matrix and the fibrous network alters the plastic deformation response, with isochoric tests (S-U and S-D) magnifying the tendency.

6 Conclusions

Reliable modelling of the behaviour of peats is of primary importance for many transport and flood defence infrastructure where peats serve as foundation layers. Contrarily to the volumetric behaviour, the deviatoric response of peats is not fully understood, and available models are scarce and not yet satisfactory. The vast majority of experimental studies on the stress–strain response of peats upon deviatoric loading were limited to undrained triaxial compression tests, which limit the experimental evidence supporting a rational development of constitutive models for the deviatoric behaviour of peats.

A dedicated experimental investigation was presented to partially fill this gap, in an attempt to derive minimum requirements for a simple elastic–plastic model for peats, including the yield locus, the stress–dilatancy relationship and the hardening rule. The experimental results suggest that the yield locus can be better described by reshaping a Modified Cam clay and that purely volumetric hardening is not adequate for fibrous peats, especially at high stress ratios. A mixed volumetric and distortional hardening rule better normalises the evolution of the hardening variable along radial paths with different loading directions, as a function of both volumetric and deviatoric strains.

A tentative simple stress–dilatancy relationship can be calibrated on the results of few relevant stress paths, including isotropic and \( K_{0} \) compression, and accounting for the mobilised friction angle at null volumetric plastic strain increments. However, the comparison between drained compression tests with different loading directions provided experimental evidence of the influence of the previous stress history on the plastic deformation response.

If the latter evidence is disregarded, simple simulations show reasonable qualitative and quantitative agreement with the experimental results on various compression tests. Both the volumetric and the deviatoric responses were reasonably reproduced for a large interval of axial strains, up to 20%, well above the shear strains attained by peat layers in field applications. However, excluding the previous strain path dependency of the deformation response limits the predictive capabilities of the simple model, whenever the non-holonomic fibres–matrix interaction is expected to play a significant role on the pre-failure response. Stress paths accompanied by directional contraction of the soil seem not to cause relevant changes on the plastic deformation response compared to the classical response of fine-grained materials. On the contrary, stress paths with significant directional expansion, such as isochoric compression, magnify the relevance of the deviatoric strain component in the plastic deformation response.