Constitutive modelling of granular materials using a contact normal-based fabric tensor

Abstract

This paper presents a fabric tensor-based bounding surface model accounting for anisotropic behaviour (e.g. the dependency of peak strength on loading direction and non-coaxial deformation) of granular materials. This model is developed based on a well-calibrated isotropic bounding surface model. The yield surface is modified by incorporating the back stress which is proportional to a contact normal-based fabric tensor for characterising fabric anisotropy. The evolution law of the fabric tensor, which is dependent on both rates of the stress ratio and the plastic strain, rules that the material fabric tends to align with the loading direction and evolves towards a unique critical state fabric tensor under monotonic shearing. The incorporation of the evolution law leads to a rotational hardening of the yield surface. The anisotropic critical state is assumed to be independent of the initial values of void ratio and fabric tensor. The critical state fabric tensor has the same intermediate stress ratio (i.e. b value) and principal directions as the critical state stress tensor. A non-associated flow rule in the deviatoric plane is adopted, which is able to predict the non-coaxial flow naturally. The stress–strain relation and fabric evolution of model predictions show a satisfactory agreement with DEM simulation results under monotonic shearing with different loading directions. The model is also validated by comparing with laboratory test results of Leighton Buzzard sand and Toyoura sand under various loading paths. The comparison results demonstrate encouraging applicability of the model for predicting the anisotropic behaviour of granular materials.

1 Introduction

Fabric anisotropy has a significant influence on the strength and deformation characteristics of granular materials as reported in both experimental [3, 41, 46,47,48, 50, 77, 84, 88] and numerical observations [34, 69, 81, 86]. In the past years, various effects caused by fabric anisotropy have been taken into account in constitutive models using different concepts.

The concept of rotational hardening, first proposed by Sekiguchi [64], has been widely used in constitutive modelling of geomaterials for describing initial anisotropy as well as induced anisotropy (e.g. [2, 10, 20, 27, 54, 67, 76]). Hashiguchi [19] discussed similarities and differences between the rotational hardening and the kinematic hardening [98] for metals. There are several general features of the rotational hardening rule in general stress spaces:

• A second-order traceless anisotropy tensor is used to reflect the material anisotropy, and it is introduced into the yield function through the back stress concept;

• The evolution of the anisotropy tensor is linked to the plastic strain rate. The tensor can reach a ‘saturated’ value [2] under monotonic shearing. In other words, the anisotropy tensor stops changing at large strains, for example, by introducing a rotational limit surface [20].

In the concept of rotational hardening, the anisotropy tensor, in general, is indirectly linked to the material fabric based on some microscopic evidence, but usually lacks clear physical meaning at a microscopic level. Hence the evolution of the tensor is hard to be calibrated directly even while microstructural information is available.

Recently, several constitutive models have been proposed using different fabric tensors associated with various microstructural quantities (see the references of [33, 73]) such as the orientation of the long axis of particles [30, 31], void vector [14, 32] and contact normal [1, 96, 97]. As contacts may represent the most fundamental fabric of granular materials, contact normal-based fabric tensors receive increasing attention, and potential effects of the fabric anisotropy show a strong link to this fabric tensor. Micromechanical analyses of the stress–force–fabric relationship showed that anisotropy of the orientation distribution of contact normals (or anisotropy of the contact normal-based fabric tensor) may play an important role in contributing to the shear strength of granular materials [35, 52, 60]. Meanwhile, the non-coincidence between the fabric tensor and the stress tensor is a key source of non-coaxial deformation [36].

In evolution laws of contact normal-based fabric tensors, the rate of the fabric tensor has often been related to stress rate [75], elastic strain rate [96, 97], or plastic strain rate [42, 43]. As the elastic strain rate and stress rate can be easily linked by an elastic model, the responses of evolution laws in terms of them are essentially similar. Evolution laws associated with the stress (or elastic strain) rate alone (the first type) can capture the characteristics of peak strength under monotonic shearing with various loading directions. However, they rarely show a unique critical state fabric tensor. On the contrary, fabric evolution laws associated with the plastic strain rate alone (the second type) tend to give a unique critical value of the fabric tensor, but they cannot capture the characteristics of peak strength upon monotonic shearing easily. Although these types of evolution laws may be able to qualitatively account for some experimental and numerical observations, quantitative calibrations with microscale fabric evolution data have rarely been achieved.

Most of the above-mentioned constitutive models, incorporating either a rotational hardening or a fabric tensor, are based on the critical state concept which has been widely recognised as the cornerstone of modern constitutive modelling of soils [63, 78]. Conventionally, the critical state is defined as a state at which the soil behaves like a frictional fluid with a constant void ratio and stress ratio, regardless of the initial state of the soil. It is clear that this definition makes no reference to other fabric-related entities than the scalar-valued void ratio. Consequently, it cannot provide necessary constraints on the evolution of the anisotropic fabric towards the critical state. However, microstructural investigations reveal that material fabric at the critical state is anisotropic [61] and contact normal-based fabric tensors at the critical state seem to be independent of the initial fabric [22, 81, 82, 95]. For more realistically modelling the anisotropic behaviour within the framework of the critical state concept, it is necessary to revisit the conventional critical state theory [9, 32].

The main aim of this paper is to present a critical state constitutive model for granular materials taking the fabric anisotropy into account. The model is developed on the basis of the isotropic bounding surface model named CASM_b [89, 90]. A contact normal-based fabric tensor is additionally incorporated, and its evolution is formulated by using the hybrid evolution law proposed by the first author [21]. In the new hybrid evolution law, the rate of the fabric tensor is related to both the stress ratio rate and the deviatoric plastic strain rate.

In short, the model can capture the following common effects of fabric anisotropy on the strength and deformation behaviour of granular materials:

• the dependency of the peak strength on loading directions;

• the uniqueness of the anisotropic critical state under different loading directions with a constant b value and mean effective stress;

• the non-coaxial plastic flow.

Effects of the intermediate stress ratio on the soil strength and deformation are also hierarchically considered in this model. Predictions by the new model are compared with results from DEM simulations and laboratory tests. It is demonstrated that the new constitutive model can capture both the stress–strain relation and the evolution of the fabric tensor with a high degree of satisfaction.

2 Anisotropic critical state

2.1 Definition of fabric tensor

In most cases of three-dimensional materials, the frequency distribution of contact normals in a granular assembly can be expressed by a spherical harmonic series with the second-order approximation [21, 93] as

$$E\left( \varvec{n} \right) = \frac{1}{4\pi }\left( {1 + \varvec{F}:\varvec{n} \otimes \varvec{n}} \right)$$

(1)

where $\varvec{n}$ denotes the unit contact normal at a contact. According to Kanatani [23], the tensor F in Eq. (1) is known as the second-order fabric tensor of the third kind in terms of unit contact normals. The fabric tensor F is traceless, and it can be used to describe fabric anisotropy in the assembly. Practically, the fabric tensor F can be estimated as follows:

$$\varvec{F} = \frac{15}{2}\left( {\frac{1}{{N_{c} }}\mathop \sum \limits_{{c \in N_{c} }} \varvec{n}^{c} \otimes \varvec{n}^{c} - \frac{1}{3}\varvec{I}} \right)$$

(2)

where $\varvec{I}$ denotes unit second-order tensor and $N_{\text{c}}$ is the total number of discrete directional contact normal $\varvec{n}^{\text{c}}$ of a granular assembly.

2.2 Description of the anisotropic critical state

Since granular materials like sands usually lack a unique, natural stress-free state, the critical state is important for constitutive modelling as it provides a useful reference state to characterise the granular materials under shearing. Based on the critical state concept, many constitutive models have been proposed, including a series of CASMs by Yu [90]. However, the fabric anisotropy at the critical state is often overlooked. Benefiting from the development of advanced laboratory test [12, 83] and numerical simulation technologies [13, 26, 44, 79, 81, 82, 95], the fabric effect on the critical state is further studied in recent years (e.g. [30, 32, 85], in particular, from a microscopic perspective. Increasing evidence shows that a unique critical state exists, which is independent of the initial sand density and the initial fabric anisotropy. In the light of the above discussion, the conventional definition of the critical state is revisited and modified considering the role of anisotropic fabric as follows.

The mean effective stress, p, and deviatoric stress tensor, S, can be expressed as:

$$p = 1/3tr\left(\varvec{\sigma}\right)$$

(3)

$$\varvec{S} =\varvec{\sigma}- p\varvec{I}$$

(4)

where $\varvec{\sigma}$ is the effective stress tensor. The intermediate stress ratio (i.e. b value) is given as:

$$b = \frac{{\sigma_{2} - \sigma_{3} }}{{\sigma_{1} - \sigma_{3} }} = \frac{1}{2}\left[ {\sqrt 3 { \tan }\left( {\theta_{l} } \right) + 1} \right]$$

(5)

where $\sigma_{1} , \sigma_{2} , \sigma_{3}$ are the principal values of $\varvec{\sigma}$ in descending order (i.e.$\sigma_{1} > \sigma_{2} > \sigma_{3}$), and $\theta_{l}$ is the Lode’s angle, which equals:

$${ \sin }\left( {3\theta_{l} } \right) = - 3\sqrt 6 \frac{{{ \det }\left( \varvec{S} \right)}} {\left\| {{\varvec{S} }} \right\|^{3}}$$

(6)

where ${\left\| \varvec{*} \right\|} = \sqrt {*:\varvec{*}}$ denotes the norm of any symmetrical second-order tensor *. A stress ratio tensor can be defined as:

$$\varvec{\eta}= \varvec{S}/p$$

(7)

The deviators of tensors $\varvec{S}, \varvec{\eta},\varvec{ F}$ are rewritten as $q, \eta , F$, respectively.

$$q = \left\|3/2\varvec{S}\right\|$$

(8)

$$\eta = \left\|3/2\varvec{\eta}\right\|$$

(9)

$$F = \left\|3/2\varvec{F}\right\|$$

(10)

The conventional definition of the critical state can be expressed in Eqs. (11) and (12), which describes that plastic shearing could continue indefinitely without changes in volume or stress ratios while the critical state is ultimately reached. For characterising the anisotropic critical state, an extra constraint on the fabric tensor at the critical state is defined in Eq. (13) [21].

$$e_{\text{c}} = - \lambda { \ln }\left( {p_{\text{c}} } \right) + \varGamma - 1;$$

(11)

$$\eta_{\text{c}} = M;$$

(12)

$$\varvec{F}_{c} = (M_{F} /M)\varvec{\eta}_{c}$$

(13)

where $\lambda$ and $\varGamma$ are the slope and intercept of the critical state line in the $v - { \ln }p$ space, respectively; M, so-called critical state stress ratio, is the slope of the critical state line in the p–q space; $\eta_{c} ,\varvec{\eta}_{c}$ and $\varvec{F}_{\text{c}}$ are the values of $\eta$, $\varvec{\eta}$ and $\varvec{F}$ at the critical state, receptively; $M_{F}$ is the critical state fabric ratio. Obviously, there is $M_{\text{F}} = F_{\text{c}}$ where $F_{\text{c}}$ is the value of F at the critical state.

Equation (13) defines that the critical state fabric tensor is only dependent on the stress state at the critical state. It imposes a constraint on the evolution of the fabric tensor towards the critical state. At the critical state, the fabric tensor $\varvec{F}_{\text{c}}$ is proportional to the corresponding stress ratio tensor $\varvec{\eta}_{\text{c}}$. In other words, $\varvec{F}_{\text{c}}$ has the same principal directions and b value as $\varvec{\eta}_{\text{c}}$. However, the deviators of $\varvec{F}_{\text{c}}$ and $\varvec{\eta}_{\text{c}}$ are allowed to be different, as $F_{\text{c}} = M_{\text{F}}$ while $\eta_{\text{c}} = M$. The above description of the critical state is a development of, but actually does not contradict to, the conventional thinking of the critical state [32]. The assumption of Eq. (13) is consistent with numerical observations [44, 81, 82, 95].

It should be noted that the critical state line in the $e - { \ln }p$ plane might be nonlinear due to the breakage of particles under relatively high pressure (normally greater than 1 MPa for silica sands) [5]. In this situation, the relationship between e_c and ${ \ln }p_{\text{c}}$ is better to be replaced by a bilinear relationship [5] or a nonlinear relationship [28]. As the effect of particle breakage is ignored in this work, we adopt the same linear relationship between e_c and ${ \ln }p_{\text{c}}$ as that employed in the original CASM [89]. This relationship is valid until particle breakage occurs according to the results of laboratory tests [74, 91], as shown in Fig. 1. In a general stress space, it is found that both M and M_F are dependent on the b value [93]. For simplicity, we first take M and M_F as constants here, and their dependency on the b value will be discussed in Sect. 3.6.

Fig. 1

Critical state lines in the $v - { \ln }p$ plane for Toyoura sand and Portaway sand

It should be noted that Li and Dafalias [32] proposed an alternative description of fabric anisotropy at the critical state by using a void-vector fabric tensor. They also argued that the critical state fabric tensor has the same principal directions and b value as those of the deviatoric stress tensor. A joint invariant consisting of the critical state fabric tensor normalised by $\left\| \varvec{F}_{c} \right\|$ was adopted, and, as a consequence, M_F always equals $\sqrt {3/2}$ therein. As the back stress is more closely dependent on the fabric deviator F_c rather than the normalised value, the more direct analytical description of the critical state fabric tensor with respect to F_c defined in Eq. (13) is used here while incorporating the fabric tensor into the yield function using the back stress concept as shown later.

2.3 Fabric evolution law

The rate of fabric tensor $\dot{\varvec{F}}$ is related to both the stress ratio rate $\dot{\varvec{\eta }}$ and the plastic strain rate in terms of $\dot{\varLambda } = \dot{\varvec{e}}^{\text{p}}$ where $\dot{\varvec{e}}^{\text{p}}$ is the deviatoric plastic strain rate. The hybrid fabric evolution law proposed by the first author [21] [i.e. Eq. (14)] is used. The derivation and validation of the fabric evolution law refer to the reference of [21], and an extension for incorporating the intermediate stress ratio effect is presented in the Ref. [93].

$$\dot{\varvec{F}} = C_{1} \left( {1 + C_{2}} {\left\| {\varvec{\eta}} \right\|} \right)\dot{\varvec{\eta }} + C_{3} \left( {\frac{{M_{\text{F}} }}{M}\varvec{\eta}- \varvec{F}} \right)\dot{\varLambda }$$

(14)

where C₁, C₂ and C₃ are material constants controlling the rate of the fabric evolution. At the critical state $\dot{\varvec{F}} = 0$ and $\dot{\varvec{\eta }} = 0$, there should be $\varvec{F}_{\text{c}} = M_{\text{F}}\varvec{\eta}_{\text{c}} /M$. The evolution law satisfies the requirement of the principle of material frame indifference together with the assumptions of rate independence and uniqueness of the critical state fabric tensor [i.e. Eq. (13)] [21].

Initially, the plastic strain rate is small whereas the stress ratio increases rapidly under monotonic shearing. In this case, the fabric evaluation is dominated by variations of the stress ratio. The fabric evolution law (14), therefore, can be simplified as:

$$\dot{\varvec{F}} = C_{1} \left( {1 + C_{2}} {\left\| \varvec{\eta} \right\|} \right)\dot{\varvec{\eta }}$$

(15)

From Eq. (15), it can be deduced that the deviator $F_{q}$ of the fabric tensor is formulated as a parabolic function of the stress ratio $\eta$ under monotonic shearing. This is supported by experimental [49, 75] and numerical results [25].

As shearing continues, the plastic strain rate increases considerably while the rate of the stress ratio drops, especially, near the critical state. In this stage, the contribution of the second term of the right side of Eq. (14) prevails, and the fabric tensor evolves towards the critical state value of Eq. (13). In this case, the fabric evolution can be approximated by:

$$\dot{\varvec{F}} = C_{3} \left( {\frac{{M_{F} }}{M}\varvec{\eta}- \varvec{F}} \right)\dot{\varLambda }$$

(16)

Equations (15) and (16) are special cases of the hybrid evolution law of Eq. (14) while taking C₃ = 0 and C₁ = 0, respectively. It is clear that the parameters C₁ and C₂ control the rate of fabric evolution at the initial stage of a monotonic shearing, while C₃ controls the rate of fabric evolution towards the critical state at relatively large strains. Upon continuous shearing, the evolution law transitions from the first type to the second type gradually, and hence, the aforementioned disadvantages that exist in evolution laws taking the form of only one of them may be overcome.

From a microstructural perspective, the evolution laws (15) and (16) may roughly represent two typical mechanisms of fabric evolution, respectively [21, 93]. At the initial stage of shearing, contacts are forced to reorganise to stabilise the potential buckling of force chain responding to the applied shear stress [71]. At this stage, the stress ratio increases rapidly whereas plastic strains develop relatively slowly. Therefore, changes in the spatial distribution of contact normals, i.e. evolution of the fabric tensor (e.g. a considerable amount of contact disruptions in the minor principal fabric direction and contact creations along the major principal fabric direction [25, 69]), are more efficiently expressed in terms of the rate of the stress ratio. At relatively large shear strains, the net rate of contact creation/disruption decreases considerably. Instead, the fabric evolution is primarily controlled by the reorientation and migration of the contacts through sliding and rolling of particles across each other which is usually accompanied by more plastic deformation [25, 26]. Therefore, the fabric evolution is more reasonably related to the plastic strain rate at this stage.

3 Constitutive model

This constitutive model is developed based on CASM_b [90] which is known as an isotropic critical state model using the bounding surface framework. A contact normal-based fabric tensor is incorporated into the yield surface and the flow rule in the $\pi$ plane to account for fabric anisotropy, and the anisotropic critical state defined in Eq. (13) is adopted. However, it should be noted that no attempt is made to account for the potential effects of fabric anisotropy in the dilatancy function and the elastic model in this paper.

The constitutive model is presented in the general stress space. The model described here is applicable to both fully saturated and dry soils. All stress quantities are to be understood as effective stress quantities in this paper. Our attention is restricted to the small deformation regime, isothermal conditions and rate-independent behaviour. Thus, the strain rates are split as follows:

$$\dot{\varvec{e}} = \dot{\varvec{e}}^{e} + \dot{\varvec{e}}^{p} ; \dot{\varepsilon }_{v} = \dot{\varepsilon }_{v}^{e} + \dot{\varepsilon }_{v}^{p}$$

(17)

where $\dot{\varvec{e}},\dot{\varvec{e}}^{e} ,\dot{\varvec{e}}^{p}$ are the rates of total, elastic and plastic deviatoric strains, respectively; $\dot{\varepsilon }_{v} ,\dot{\varepsilon }_{v}^{e} ,\dot{\varepsilon }_{v}^{p}$ are the rates of total, elastic and plastic volumetric strains, respectively.

3.1 Elastic model

The hypoelastic model used in CASM is followed here. Potential effects of the fabric anisotropy on the elastic behaviour are ignored as purely elastic strains are relatively small compared with plastic strains. The response associated with the elastic volumetric part is expressed in terms of the bulk modulus K which is assumed to be a linear function of the mean effective stress p:

$$\dot{\varepsilon }_{v}^{e} = \frac{{\dot{p}}}{K}; \;K = \left( {1 + e} \right)p/\kappa$$

(18)

where $\kappa$ is the slope of the swelling line in the $v - {\text{ln }}p$ plane.

The deviatoric elastic strain is calculated by using the shear modulus as:

$$\dot{\varvec{e}}^{e} = \frac{{\dot{\varvec{S}}}}{2G};\varvec{ }\;G = \frac{{3\left( {1 - 2\upsilon } \right)}}{{2\left( {1 + \upsilon } \right)}}K$$

(19)

where $\upsilon$ is Poisson’s ratio. A constant value of Poisson’s ratio is assumed, which implies that the shear modulus is dependent on the mean effective stress in the same way as the bulk modulus. The advantages and disadvantages of a constant Poisson’s ratio compared with a constant shear modulus were discussed by Yu [89]. Note that various other relationships of the shear modulus for uncemented sands at small strains have also been proposed in the literature (e.g. [17]).

From Eqs. (18) and (19), the rate of the stress tensor can be expressed in terms of the strain rates as:

$$\dot{\varvec{\sigma }} = 2G\left( {\dot{\varvec{e}} - \dot{\varvec{e}}^{P} } \right) + K\left( {\dot{\varepsilon }_{v} - \dot{\varepsilon }_{v}^{P} } \right)\varvec{I}$$

(20)

3.2 Yield surface

Plastic deformation of granular materials with hard grains is induced in the process of sliding and rolling of individual grains across each other at contact points. As frictional resistance increases, rolling becomes more dominant. At a mesoscale, it may be assumed that dilatant simple shearing over several interacting sliding planes produces the resultant macroscopic deformation, which is often accompanied by induced fabric anisotropy. By applying the Mohr–Coulomb yield condition at sliding planes, Nemat-Nasser [42] proposed a yield surface considering the fabric effect. The kernel idea is that the shear resistance at the sliding plane can be divided into two parts: an isotropic part due to a Coulomb-type isotropic resistance and an anisotropic part due to fabric anisotropy. The resistance due to fabric anisotropy is estimated by the micromechanically based stress–force–fabric relationship. From this approach, it was found that the back stress is proportional to the contact normal-based fabric tensor in a two-dimensional (2D) analysis. Actually, in this estimation it was assumed that the total back stress stems from an anisotropic stress tensor $\varvec{\sigma}^{\text{r}}$ which is resulted from the fabric tensor $\varvec{F}$. Similarly, one can obtain the back stress $\varvec{S}_{\text{b}}$ in the three-dimensional (3D) domain from the stress–force–fabric relationship obtained by Ouadfel and Rothenburg [52] as follows:

$$\varvec{S}_{\text{b}} =\varvec{\sigma}^{r} = \zeta p\varvec{F};\;\zeta = 2/5$$

(21)

Detailed derivation process of the back stress refers to the reference of [21]. In Eq. (21), $\zeta = 2/5$ is a constant coefficient obtained by spatial integration of the stress–force–fabric relation. In a 2D case, the coefficient ζ equals 1/2 [60] as the same as that obtained by Nemat-Nasser [42].

The yield surface can be expressed in terms of stress tensor and fabric tensor F as:

$$f =\left\|\varvec{S} - \zeta p\varvec{F}\right\| - M_{\text{f}} p = 0$$

(22)

where M_f is the frictional coefficient, which is generally dependent on the void ratio and fabric tensor. M_f gives the elastic range of the yield surface. Back stress $\zeta p\varvec{F}$ determines the location and orientation of the yield surface. If we regard that the isotropic yield surface used in CASM is a special case of Eq. (22), a suitable form of M_f in Eq. (22) can be chosen. The yield surface with the inclusion of the back stress can now be expressed as follows:

$$f = \left( {\frac{{\tilde{q}}}{mp}} \right)^{n} + \frac{1}{{{ \ln }\left( {r^{{\prime }} } \right)}}\ln \left( {\frac{p}{{p_{0} }}} \right) = 0$$

(23)

$$\tilde{q} = \left\|3/2\left( {\varvec{S} - \varvec{S}_{b} } \right)\right\|$$

(24)

where n and $r^{{\prime }}$ are material constants; $m = M; p_{0}$ is the reference consolidation pressure. The conventional stress deviator $q = \left\| 3/2\varvec{S} \right\|$ is replaced by $\tilde{q}$. It is clear that when the material fabric is isotropic, namely $\varvec{S}_{\text{b}} = 0$ in Eq. (24), Eq. (23) recovers the original yield function of CASM.

In the original CASM [89], the spacing ratio r was introduced to represent the distance between the reference consolidation line and the critical state line in the $v - { \ln }p$ space. The spacing ratio can be calculated as $r = p_{0} /p_{\text{c}}$ where $p_{\text{c}}$ is the mean effective stress at the critical state on a given yield surface. It is noted that this distance should remain unaltered for the anisotropic critical state model. With this assumption, the spacing ratio r is replaced by a new material constant $r^{\prime}$ using the following equation:

$${ \ln }r^{{\prime }} = { \ln }r\left( {1 - \zeta M_{F} /M} \right)^{ - n}$$

(25)

This equation is obtained by applying the critical state stress condition and fabric tensor [i.e. Eqs. (12) and (13)] to the yield function with the condition that $p_{0} /p_{c} = r$. Through Eqs. (23) (24) and (25), the fabric tensor is introduced into the isotropic yield surface with clear physical meaning.

3.3 Hardening law

It is noted that the yield surface in Eq. (23), in fact, involves both isotropic and rotational hardening. At first, the isotropic hardening rule adopted in the original CASM [89] is followed. The size of the yield surface is controlled by the reference consolidation pressure $p_{0}$ which varies with the plastic volumetric strain as defined in Eq. (26).

$$\dot{p}_{0} = \frac{{\left( {1 + e} \right)p_{0}}}{\lambda - \kappa }\dot{\varepsilon }_{v}^{p}$$

(26)

If elastic strains are ignored, we can integrate Eq. (26) and then find that $p_{0}$ can be expressed in terms of the void ratio. It indicates that the yield surface is dependent on the void ratio if $p_{0}$ is replaced, which is consistent with the suggestion on M_f by Nemat-Nasser and Zhang [43].

The rotational hardening is introduced due to the evolution law of the fabric tensor [i.e. Eq. (14)] as illustrated in Fig. 2 in the triaxial stress space with a cross-anisotropy. The slope of the axis of the yield surface (i.e. green line) represents the degree of fabric anisotropy. Specifically, the slope is equal to 2/5(F₁ − F₂) in the axial-symmetrical case. Upon shearing, the degree of fabric anisotropy varies as defined by the fabric evolution law (14). Therefore, the slope of the green line changes, which results in rotations of the yield surface in the $p_{0}$-normalised p–q space. When the critical state is reached, the slope of the axis of the yield surface will rest on a value corresponding to the critical state value of the fabric anisotropy. Mathematically, Eq. (13) acts as a rotational limit surface of the anisotropy tensor [20]. It defines that rotational hardening of the yield surface will cease once the critical state is reached. One important feature of this law is that the fabric deviator F can both harden and soften as the stress ratio $\eta$ might harden and soften during a monotonic shearing. The slope of the axis can be even larger than the critical state value as demonstrated by Hu [21].

Fig. 2

Illustration of rotational hardening in the triaxial stress space with cross-anisotropy. Note F₁, F₂ and F₃ are the principal values of the fabric tensor F (F₂ = F₃ for cross-anisotropy)

3.4 Flow rule

From the viewpoint of thermodynamics [6, 7] and micromechanics [11], the flow rule is non-associated in nature for frictional geomaterials like sands. To model this behaviour, the volumetric plastic strain rate $\dot{\varepsilon }_{v}^{p}$ and the deviatoric plastic strain rate $\dot{\varvec{e}}^{p}$ are determined separately as follows.

3.4.1 Flow rule in the deviatoric space

The deviatoric plastic strain rate can be generally expressed as:

$$\dot{\varvec{e}}^{p} = \dot{\varLambda }\varvec{l}^{{\prime }} ;\; \dot{\varLambda } = \left\|\dot{\varvec{e}}^{p}\right\| ;\varvec{ }\;\varvec{l}^{{\prime }} :\varvec{l}^{{\prime }} = 1$$

(27)

where $\dot{\varLambda }$ is the plastic multiplier index; $\varvec{l}^{{\prime }}$ is a unit normal deviatoric tensor representing the flow direction in the deviatoric space.

In conventional plasticity theory, the flow direction $\varvec{l}^{{\prime }}$ is determined by the normal of the potential surface. Although the flow rule for granular materials is widely recognised to be non-associated, it is generally assumed that the non-associativity of the plastic flow is restricted to its volumetric components. Under this assumption, the deviatoric flow direction $\varvec{l}^{{\prime }}$ should be the same as the loading direction of the yield surface in the deviatoric space as:

$$\varvec{l}^{{\prime }} = \varvec{l}_{1} = \frac{{\varvec{\eta}- \zeta \varvec{F}}} {\left\|{\varvec{\eta}- \zeta \varvec{F}}\right\|}$$

(28)

For sands with initial fabric anisotropy, the fabric tensor is not necessarily coaxial with the stress tensor. Upon proportional loading with different loading directions, this flow rule can predict non-coaxial flow as the fabric tensor is generally non-coaxial with the stress tensor. As the critical fabric tensor is coaxial with the stress tensor [see Eq. (13)], the flow direction $\varvec{l}_{1}$ at the critical state will be coaxial with the stress tensor [81]. However, it is found that the associated flow rule may overestimate the non-coaxial angle of plastic flow. For example, for pre-sheared sands with considerable initial cross-anisotropic fabric, as the magnitude of the stress ratio is smaller than $\zeta \varvec{F}$ under initial shearing, the flow direction is opposite to that of the stress tensor. To overcome this limitation, a new flow direction $\varvec{l}^{{\prime }}$ is assumed as:

$$\varvec{l}^{{\prime }} = \varvec{l}_{2} = \frac{{\varvec{L} - 3/2\zeta \varvec{F}}}{\left\| {\varvec{L} - 3/2\zeta \varvec{F} }\right\|};\quad \varvec{L} = \frac{\varvec{S}}{\left\|{\varvec{S}}\right\|}$$

(29)

In Eq. (29), it is found that the magnitudes of the components of L are always larger than $3/2\zeta \varvec{F}$ even with strong initial fabric anisotropy. This feature can restrict the non-coaxial angle in a reasonable range. The flow direction defined by Eq. (29) also implies that the flow rule in the deviatoric space becomes non-associated. According to Eq. (13), $\varvec{F}_{\text{c}}$ will be coaxial with both S and L. As a result, the plastic flow will be coaxial at the critical state.

3.4.2 Dilatancy

The volumetric plastic strain rate is determined in terms of dilatancy function D as:

$$\dot{\varepsilon }_{v}^{p} = \sqrt {2/3} \dot{\varLambda }D$$

(30)

The phenomenon of dilatancy was first reported by Reynolds [58]. Since then, numerous models for predicting dilatancy behaviour were proposed. Among them, Rowe [62] established a famous stress-dilatancy model for plane strain or triaxial stress conditions, by considering the discrete feature and the microscopic deformation mechanism of simple granular assembly as well as assuming the hypothesis of minimum energy ratio. This flow rule was adopted in the original CASM [89]. However, it has been pointed out that this stress-dilatancy relation is not very suitable for soils at low stress ratio conditions [90]. In fact, apart from the stress ratio, dilatancy is affected by many other factors, including fabric anisotropy [75], void ratio [29], non-coaxiality of the plastic flow [15], and the number of shearing cycles [57]. For simplicity, a Cambridge-type stress–dilatancy relation proposed by Nova and Wood [45] [i.e. Eq. (31)] is used in this model, which has been shown as a rather good stress–dilatancy relation for modelling sand behaviour in comparison with several commonly used flow rules [4].

$$D = C_{\text{d}} \left( {M - \eta } \right)$$

(31)

where C_d is a material constant. Miura and Toki [41] validated this equation for Toyoura sand and generalised it by considering the b value effect. The essential constraint underlying the stress–dilatancy relation in Eq. (31) is that at the critical state where $\eta_{\text{c}} = M$, there is D = 0. This means that the volumetric strain does not change further with unlimited shear strains. Note that another feature of this relation is that the stress ratio at the critical state equals that at the phase transformation state.

3.5 Bounding surface and mapping law

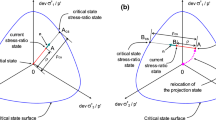
For sands, it is normally difficult to detect a clear transition from elastic to plastic behaviour. Some researchers argued that the fabric keeps unaltered only when the strain is applied up to the level of 10⁻⁵ [68]. Beyond this level, sliding and rolling will occur at contacts among particles, resulting in energy dissipation and plastic deformation. Strictly speaking, the purely elastic deformation for granular materials may tend to be vanishingly small [24]. In order to allow plastic strain to occur before the stress state reaches the yield surface [e.g. Eq. (23)], the concept of bounding surface is introduced. It is assumed that the loading [i.e. Eq. (32)] and bounding [i.e. Eq. (33)] surfaces [8, 90] take the same shape as the yield surface but are different in size:

$$f = \left( {\frac{{\tilde{q}}}{mp}} \right)^{n} + \frac{1}{{{ \ln }\left( {r^{{\prime }} } \right)}}\ln \left( {\frac{p}{{\beta p_{0} }}} \right) = 0$$

(32)

$$\bar{f} = \left( {\frac{{\bar{\tilde{q}}}}{{m\bar{p}}}} \right)^{n} + \frac{1}{{{ \ln }\left( {r^{{\prime }} } \right)}}\ln \left( {\frac{{\bar{p}}}{{p_{0} }}} \right) = 0$$

(33)

where $\beta = p/\bar{p} = \tilde{q}/\bar{\tilde{q}} \in \left( {0,1} \right]$ is the mapping ratio between current state stress $\left( {p,\bar{p}} \right)$ on the loading surface and a mapping point $\left( {\bar{p},\bar{\tilde{q}}} \right)$ on the bounding surface, as shown in Fig. 3a. When $\beta = 1$, the loading surface coincides with the bounding surface (i.e. full mobilisation of the shear resistance).

Fig. 3

Bounding and loading surfaces in the $p_{0}$-normalised p–q plane and the π plane with cross-anisotropy: $M_{cc} = 1, l_{1} = 3/4, n = 2, r^{\prime} = 40, F_{1} = 0.5, F_{2} = F_{3} = - 0.25$

In this model, a radial mapping law [18] is used. The evolution of the parameter $\beta$ is defined as:

$$\dot{\beta } = - C_{\text{b}} \dot{\varLambda }{ \ln }\beta$$

(34)

where $C_{\text{b}}$ is a constant controlling the evolution rate of $\beta$. Initially, the soil deforms in a stress state far from the fully yielding stage. As the hardening modulus is very large (i.e. $\beta$ is small), the material behaves more elastically. Upon further shearing, $\beta$ increases quickly, and the rate of $\beta$ reduces rapidly. While $\beta = 1,$ the bounding surface coincides with the yield surface. Taking material constants for Toyoura sand listed in Table 3, Fig. 4 presents example results showing the effect of $C_{\text{b}}$ on the evolution of $\beta$ in an initially anisotropic sand sample under undrained shearing. It is evident that a larger value of $C_{\text{b}}$ leads to a higher speed approaching the final state of $\beta = 1$. Although this radial mapping law is different from the common method based on interpolations of the hardening modulus (e.g. [8]), it was shown that these two methods can be equivalently transformed into each other [38].

Fig. 4

Effects of $C_{b}$ on the evolution of mapping ratio $\beta$

3.6 Effects of shear mode

Results of laboratory tests (e.g. [72, 88] and numerical simulations (e.g. [70, 87, 93]) demonstrated that the shear mode has a significant influence on the strength and deformation behaviour of granular materials. The shear mode is normally measured by the intermediate stress ratio (b value) or Lode’s angle $\theta_{l}$. The relationship between b value and $\theta_{l}$ is given in Eq. (5). It should be noted that the incorporation of the shear mode effects will remarkably increase the complexity degree of the formulation and numerical implementation.

3.6.1 Effect of shear mode on the critical state

Here the function proposed by Sheng et al. [65] is employed to characterise the relationship between M and Lode’s angle $\theta_{l}$:

$$M\left( {\theta_{l} } \right) = M_{\text{cc}} h_{1} \left( {\theta_{l} } \right); \quad h_{1} \left( {\theta_{l} } \right) = \left( {\frac{{2l_{1}^{4} }}{{1 + l_{1}^{4} + \left( {1 - l_{1}^{4} } \right){ \sin }\left( {3\theta_{l} } \right)}}} \right)^{1/4}$$

(35)

where $l_{1} = M_{\text{ct}} /M_{\text{cc}}$ is a shape parameter; $M_{\text{cc}}$ and $M_{\text{ct}}$ are the critical state stress ratios for triaxial compression and extension, respectively. In Eq. (35), $h_{1} \left( {\theta_{l} } \right)$ determines the shape of $M\left( {\theta_{l} } \right)$ in the $\pi$ plane. For triaxial compression, $\theta_{l} = - \pi /6, \;h_{1} \left( {\theta_{l} } \right) = 1, \;M = M_{\text{cc}} ;$ for triaxial extension, $\theta_{l} = \pi /6, \;h_{1} \left( \theta \right) = l_{1} ,\; M = M_{\text{ct}}$. According to Loukidis and Salgado [37], the value of $l_{1}$ is generally in the range of 0.67–0.75 for silica sands. This shape function is convex for a larger range of $l_{1}$ as compared with other kinds of shape function. In particular, the shape function is still convex when $l_{1}$ is as low as 0.6. If we assume that the critical state friction angles for triaxial extension and compression are equal, $M_{\text{cc}}$ and $M_{\text{ct}}$ can be estimated as follows:

$$M_{\text{cc}} = \frac{{6{ \sin }\left( {\phi_{\text{cv}} } \right)}}{{3 - { \sin }\left( {\phi_{\text{cv}} } \right)}}; M_{ct} = \frac{{6{ \sin }\left( {\phi_{\text{cv}} } \right)}}{{3 + { \sin }\left( {\phi_{\text{cv}} } \right)}}$$

(36)

where $\phi_{\text{cv}} = { \sin }^{ - 1} \left( {\frac{{\sigma_{1} - \sigma_{3} }}{{\sigma_{1} + \sigma_{3} }}} \right)_{\text{c}}$ is the critical state frictional angle. Hence, $l_{1}$ can be expressed in terms of $M_{\text{cc}}$ as:

$$l_{1} = \frac{3}{{3 + M_{\text{cc}} }}$$

(37)

This relationship was proven to be realistic when compared with results of laboratory tests and DEM simulations [95] (e.g. Fig. 5). The shape function becomes very similar to that proposed by Matsuoaka and Nakai [39].

Fig. 5

Theoretical prediction and DEM results [95] of critical state stress ratio in the $\pi$ plane

A similar shape function is observed for the critical state fabric ratio M_F from DEM simulations [81]. The critical state fabric ratio M_F is assumed to be a function of Lode’s angle as:

$$M_{\text{F}} \left( {\theta_{l} } \right) = M_{\text{Fc}} h_{2} \left( {\theta_{l} } \right); \quad h_{2} \left( {\theta_{l} } \right) = \left( {\frac{{2l_{2}^{4} }}{{1 + l_{2}^{4} + \left( {1 - l_{2}^{4} } \right){ \sin }\left( {3\theta_{l} } \right)}}} \right)^{1/4}$$

(38)

where $l_{2} = M_{\text{Ft}} /M_{\text{Fc}}$, and $M_{\text{Fc}}$ and $M_{\text{Ft}}$ are the critical fabric ratios for triaxial compression and extension, respectively. In Eq. (38), $h_{2} \left( { - \pi /6} \right) = 1, M_{\text{F}} = M_{\text{Fc}} ;$$h_{2} \left( {\pi /6} \right) = l_{2} , M_{\text{F}} = M_{\text{Ft}}$. It is noted that in some DEM simulations under high pressures [44, 61, 66], the value of M_F for triaxial extension may be even greater than that for triaxial compression. These observations suggest that the shape parameter for M_F might be different from that for the critical state stress ratio M [93]. l₁ and l₂ in Eq. (38) could be different, and they can be chosen dependently (e.g. a reciprocal relationship $l_{1}$ = $1/l_{2}$ [93]) or independently for more general cases. Detailed discussions about the relation between l₁ and l₂ are out of the scope of this paper.

It is indicated by Eq. (25) that different values of l₁ and l₂ will lead to a dependency of $r^{\prime}$ on the b value as we assumed that the spacing ratio r is a constant. Vice versa, a constant $r^{\prime}$ means that r is dependent on b value, which further implies that the reference consolidation line and critical state line cannot be independent of the shear mode simultaneously. For simplicity, they are assumed as identical [i.e. Eq. (39)] in the following analysis and model predictions.

$$l_{2} = l_{1}$$

(39)

This assumption implies that the proportional coefficient between the critical state stress and fabric ratios, i.e. $M_{\text{F}} /M = M_{\text{Fc}} /M_{\text{cc}}$, is a constant.

3.6.2 Effect of shear mode on the yield function

The dependency of M on Lode’s angle makes the yield (loading) function in the $\pi$ plane not circular. If we generalise the yield surface by using $m = M\left( {\theta_{l} } \right)$, the yield surface would be singular at $q = 0$ (see Fig. 3a). To avoid this problem, we replace Lode’s angle $\theta_{l}$ [i.e. Eq. (6)] in $M\left( {\theta_{l} } \right)$ by another local Lode’s angle $\theta$ measured from a deviatoric stress tensor $\varvec{t} = \varvec{S} - \varvec{S}_{b}$:

$$m\left( \theta \right) = M_{\text{cc}} h_{1} \left( \theta \right); { \sin }\left( {3\theta } \right) = - 3\sqrt 6 { \det }\left( \varvec{t} \right)/\left\|\varvec{t}\right\|^{3}$$

(40)

After this replacement, we can see that the loading and bounding surfaces are continuous at $q = 0$ in the $p_{0}$-normalised $p - q$ plane, and they have the same shape as the critical state surface in the $\pi$ plane (see Fig. 3b). Changes in the fabric anisotropy enable that the yield surface rotates in the $p - q$ plane and translates in the $\pi$ plane. However, the critical state surface is centred at the origin of the $\pi$ plane, even though an anisotropic critical stress ratio is assumed.

3.6.3 Effect of shear mode on the flow rule

As M is expressed in terms of Lode’s angle $\theta_{l}$ in Eq. (35), the stress-dilatancy function defined in Eq. (25) is also dependent on the b value.

Considering that the volumetric strain rate is zero at the critical state, the plane strain condition requires that the b value of the plastic strain rate at the critical state should be near 0.5. At the critical state, the fabric tensor has the same b value as the stress tensor. If the flow direction in Eqs. (28) or (29) is applied, the b value of the critical state stress tensor under plane strain conditions, denoted as $b_{\text{c}}^{\text{PS}}$, should equal 0.5 as well. However, it has been reported (e.g. [88]) that the b value at large strains is between 0.2 and 0.4. Most sands exhibit that the values of $b_{c}^{PS}$ are very close to 0.25. This discrepancy suggests that the flow direction may also be dependent on the b value. Therefore, the flow direction $\varvec{l^{\prime}}$ is expressed by:

$$\varvec{l}^{{\prime }} = \varvec{l}_{4} = \frac{\varvec{r}}{ \left\|\varvec{r}\right\|}; \;\varvec{r} = \left( {1 + A} \right)\varvec{l}_{2} - B\left( {\varvec{l}_{2}^{2} - \frac{1}{3}\varvec{I}} \right)$$

(41)

in which

$$A = \frac{{3\left( {1 - l_{3} } \right)g\left( {\theta^{{\prime }} } \right)\chi }}{{2l_{3} }}$$

(42)

$$B = \frac{{3\sqrt 6 \left( {1 - l_{3} } \right)g\left( {\theta^{\prime}} \right)}}{{2l_{3} }}$$

(43)

$$\chi = - \sin \left( {3\theta^{{\prime }} } \right) = 3\sqrt 6 { \det }\left( {\varvec{l}_{2} } \right)$$

(44)

$$g\left( {\theta^{{\prime }} } \right) = \frac{{2l_{3} }}{{1 + l_{3} + \left( {1 - l_{3} } \right){ \sin }\left( {3\theta^{{\prime }} } \right)}}$$

(45)

where $g\left( {\theta^{{\prime }} } \right)$ is a shape function of the potential function in the deviatoric space. The flow direction $\varvec{l}_{4}$ is the unit-norm normal of the potential function. When $l_{3} = 1$, there is $g\left( {\theta^{\prime}} \right) = 1$; hence, $\varvec{l}_{4} = \varvec{l}_{2}$ and the potential function becomes circular in the deviatoric plane [21].

The shape parameter $l_{3}$ determines the value of $b_{\text{c}}^{\text{PS}}$. According to Potts and Gens [55], $l_{3}$ can be linked to the critical state Lode’s angle for plane strain problems (i.e.$\theta_{c}^{ps}$) as follows:

$$l_{3} = \frac{{\left( {{ \sin }\left( {3\theta_{\text{c}}^{\text{ps}} } \right) + 1} \right){ \tan }\left( {\theta_{\text{c}}^{\text{ps}} } \right) + 3{ \cos }\left( {3\theta_{\text{c}}^{\text{ps}} } \right)}}{{\left( {{ \sin }\left( {3\theta_{\text{c}}^{\text{ps}} } \right) - 1} \right){ \tan }\left( {\theta_{\text{c}}^{\text{ps}} } \right) + 3{ \cos }\left( {3\theta_{\text{c}}^{\text{ps}} } \right)}}$$

(46)

Combing with the relationship between $b_{\text{c}}^{\text{ps}}$ and $\theta_{\text{c}}^{\text{ps}}$ in Eq. (5), the relationship between $l_{3}$ and $b_{\text{c}}^{\text{ps}}$ can readily be established, as depicted in Fig. 6. When $b_{\text{c}}^{\text{ps}}$ is set between 0.2 and 0.4, the value of $l_{3}$ ranges roughly from 0.7 to 0.9. If such data are not available, $b_{\text{c}}^{\text{ps}}$ can be taken around 0.25, which corresponds to $l_{3} = 0.75$. Alternatively, it can be chosen based on available data for sands with similar index properties [37].

Fig. 6

Relationship between shape parameter $l_{3}$ and $b_{c}^{ps}$

3.7 Stress–strain relationship in the rate form

The consistency condition of the loading surface [i.e. Eq. (32)] gives:

$$\dot{f} = f_{\varvec{S}} :\dot{\varvec{S}} + f_{p} \dot{p} + f_{\beta } \dot{\beta } + f_{{p_{0} }} \dot{p}_{0} + f_{\varvec{F}} :\dot{\varvec{F}} = 0$$

(47)

where $f_{\varvec{S}} , f_{p} ,f_{\beta } ,f_{{p_{0} }}$ and f_F are partial derivatives of the loading surface f with respect to $\varvec{S},p,\beta ,p_{0}$ and $\varvec{F}$ respectively. The derivatives are detailed in Appendix 1. By inserting the evolution equations with regard to $\dot{\beta }, \dot{p}_{0}$ and $\dot{\varvec{F}}$ into Eq. (47), we can obtain the plastic multiplier as:

$$\dot{\varLambda } = \left( {f_{\varvec{S}} :\dot{\varvec{S}} + f_{p} \dot{p} + C_{F1} f_{\varvec{F}} :\dot{\varvec{\eta }}} \right)/H$$

(48)

where $C_{F1} = C_{1} \left( {1 + C_{2} {\left\| \varvec{\eta}| \right|}} \right)$ and H is the hardening modulus:

$$H = - \left( {C_{3} f_{\varvec{F}} :\left( {\frac{{M_{F} }}{M}\varvec{\eta}- \varvec{F}} \right) + f_{{p_{0} }} \frac{{\left( {1 + e} \right)p_{0}}}{\lambda - \kappa }\sqrt {2/3} D - f_{\beta } C_{b} { \ln }\beta } \right)$$

(49)

By substituting the elastic model and flow rule into Eq. (48), the plastic multiplier can be rewritten in terms of total strain rates as:

$$\dot{\varLambda } = \frac{{2G\left( {f_{\varvec{S}} + C_{F1} /pf_{\varvec{F}} } \right):\dot{\varvec{e}} + K\left( {f_{p} - C_{F1} f_{\varvec{F}} :\varvec{\eta}/p} \right)\dot{\varepsilon }_{v} }}{{H + 2G\left( {f_{\varvec{S}} + C_{F1} /pf_{\varvec{F}} } \right):\varvec{l^{\prime}} + \sqrt {2/3} KD\left( {f_{p} - C_{F1} /pf_{\varvec{F}} :\varvec{\eta}} \right)}}$$

(50)

With the used of Eq. (20), the elastoplastic stress–strain relationship can be written in the rate form as:

$$\dot{\varvec{\sigma }} = 2G\left( {\dot{\varvec{e}} - \dot{\varLambda }\varvec{l}^{{\prime }} } \right) + K\left( {\dot{\varepsilon }_{v} - \dot{\varLambda }\sqrt {2/3} D} \right)\varvec{I}$$

(51)

4 Prediction and comparison

Ignoring the potential effects of shearing mode, in total 13 parameters are involved in the new model. $M_{\text{F}} ,C_{1 } , C_{2} ,C_{3}$ represent four newly introduced parameters describing the evolution of the fabric tensor. These four parameters and the initial fabric tensor can be readily determined via regression analysis of relevant microscopic information (e.g. from DEM simulations). However, these parameters are hard to be obtained directly from laboratory tests due to the difficulties in measuring the microscopic structures and their evolution within a soil sample. Alternatively, a trial-and-error method can be used as demonstrated later. Other parameters inherited from CASM_b can be calibrated by the method reported by Yu et al. [91, 92]. If the above effects of the shear mode are considered, two additional shape parameters l₁ and l₃ need to be determined. M_F and M should be interpreted as the corresponding critical fabric values for triaxial compression, i.e. M_FC, M_CC. In general, l₁ can be determined by performing conventional triaxial extension tests when M_CC is known, and l₃ can be determined from plane strain type tests (for example, simple shear test). Alternatively, l₁ can be estimated by using Eq. (37), and l₃ can be approximately set as 0.75. With given initial values of the stress state, void ratio, and fabric tensor, the initial reference consolidation pressure p_0i and the mapping ratio β_i can be determined, as shown in Appendix 2.

As aforementioned, the initial fabric tensor and the parameters related to the fabric tensor evolution can be determined directly based on DEM simulation results. Therefore, we first validate the model using the results of DEM simulations in Sect. 4.1. Afterwards, comparisons between the model predictions and laboratory test results are presented in Sect. 4.2. It needs to point out that the focus will be placed on the performance of the new model in capturing influences of the fabric anisotropy on the shear strength and non-coaxial flow of granular materials in the following analyses.

4.1 Comparison with DEM simulations

The model is compared with DEM simulations under monotonic shearing with constant mean effective stress p and b value. The DEM tests were carried out by Yang [81] using PFC3D. In the simulations, the samples consist of two-sphere clusters and have highly anisotropic fabric at the initial state due to pre-shearing. The samples were prepared by the deposition method. After isotropic consolidation to 500 kPa, the samples were pre-sheared triaxially (i.e. b = 0) up to 10% of shear strain, followed by unloading to an isotropic stress state (see Fig. 7c for the pre-loading history). During further monotonic shearing, the mean effective stress p remains constant with b = 0.4, and the direction of the major principal stress is fixed at 0°, 15°, 30°, 45°, 60°, 75°, 90° respectively, with respect to the deposition direction (see Fig. 7a). Results of the fabric evolution are presented in terms of the fabric deviator F_q = √3/2║F║, the intermediate fabric ratio F_b = (F₂ − F₃)/(F₁ − F₃), and the principal direction of the fabric tensor γ_F (see Fig. 7b). F_q, F_b and γ_F give a complete description of the fabric tensor in a triaxial loading path.

Fig. 7: a

Definition of loading direction; b definition of principal fabric direction; c loading history of the pre-shearing of DEM samples

The model parameters for the complete theoretical scheme (SC1) are listed in Table 1. It should be noted that in this section possible effects of the shear mode are ignored. Hence $M_{\text{Fc}}$ and $M_{\text{cc}}$ are taken as constants and are evaluated at b = 0.4. The fabric tensor after pre-loading is characterised as $F_{qi} = 0.7, \;F_{bi} = 0, \;\gamma_{Fi} = 0$. The same initial values of the model parameters for all the simulations are taken as follows:

Table 1 Material constants of the DEM samples

• Initial void ratio $e_{i} = 0.65$;

• Initial fabric tensor $F_{xxi} = F_{yyi} = - \frac{1}{3}F_{qi} ,F_{zzi} = \frac{2}{3}F_{qi} ,F_{xyi} = F_{yzi} = F_{xzi} = 0$;

• Initial reference consolidation pressure $p_{0i} = 26049{\text{kPa}}$;

• Initial value of mapping ratio $\beta_{i} = 0.0269$.

In addition, three additional theoretical schemes as summarised in Table 2 are also applied for the comparison analysis. The theoretical scheme 2 (SC2) using the flow direction of Eq. (28) is to more clearly reveal the effects of associativity of flow rule in the deviatoric space. All the material constants used in SC2 are the same as those in SC1. In order to examine the influence of the fabric evolution law on the predicted stress–strain relations, model predictions with the evolution laws in Eqs. (15) and (16), respectively, are also performed. Material constants used in SC3 and SC4 are the same as those used in SC1. The initial values are identical in all theoretical schemes.

Table 2 Summary of theoretical schemes

4.1.1 Fabric evolution

Figures 8, 9 and 10 show results of the fabric evolution obtained from both DEM simulations and model predictions in terms of the fabric deviator $F_{q}$, intermediate fabric ratio $F_{b}$, and principal fabric direction $\gamma_{F}$, respectively. At large strains, DEM results under various loading directions show that:

Fig. 8

Stress ratio vs fabric deviator: a DEM; b SC1; c SC3; d SC4

Fig. 9

Stress ratio vs intermediate fabric ratio: a DEM; b SC1; c SC3; d SC4

Fig. 10

Stress ratio vs principal fabric direction: a DEM; b SC1; c SC3; d SC4

• the intermediate fabric ratio $F_{b}$ evolves towards the intermediate stress ratio, i.e. $F_{b} = b = 0.4$;

• the principal fabric direction $\gamma_{\text{F}}$ evolves towards the principal direction of stress tensor; hence, the fabric tensor becomes coaxial with the stress tensor;

• the fabric deviator $F_{\text{q}}$ evolves towards a unique value of $F_{\text{q}} = M_{\text{F}} = 1$.

Therefore, the fabric tensor tends to evolve towards a unique critical fabric tensor $\varvec{F}_{\text{c}}$, which is independent of the loading direction. This behaviour was also observed in other DEM simulations with different initial fabric tensors (e.g. [82, 95]). If we set the coordinate system coincident with the loading directions, initial components of the fabric tensors in the new coordinate system may vary with the loading direction. In other words, the unique critical fabric tensor is essentially independent of the initial fabric tensors. The critical state fabric tensor is proportional to the critical state stress tensor as postulated in Eq. (13). When $\alpha \le 45^{ \circ }$, $F_{\text{q}}$ will increase to a peak value and then decreases gradually to the critical state value $M_{\text{F}} = 1$; when $\alpha > 45^{^\circ }$, $F_{\text{q}}$ will decrease initially to a minimum value, increase gradually afterwards to a peak value and then decrease again to the critical state value.

All these features of the fabric evolution are well captured by SC1 [namely, while using the fabric evolution law of Eq. (14)]. The only imperfection in the predictions of Eq. (14) is that $F_{\text{q}}$ converges to $M_{\text{F}} = 1$ more quickly than the DEM simulation results while $\alpha \le 45^{^\circ }$. This may be due to that the chosen value of parameter $C_{3}$ is slightly large. A smaller value of $C_{3}$ will ensure that the fabric evolution approaches the critical state slower. The fabric evolution predicted by SC2 (not presented here for brevity) is almost the same as those by SC1. It implies that the flow direction does not exert a significant effect on fabric evolution. This is consistent with the fact that the fabric evolution law (14) is dependent only on the norm, rather than the direction, of the deviatoric plastic strain rate. SC3 can capture the fabric evolution at a low stress level, but it has poor performance at large strains as the predicted fabric tensors do not generally evolve towards the critical state fabric tensor. SC3 performs relatively better when the angle of the loading direction is small. SC4 can capture the critical state characteristics of the fabric tensor but does not perform well at the pre-softening stage. This is due to that the plastic strain rate is very small before the peak stress ratio, and the fabric hardly evolves according to the fabric evolution law (16) at this stage.

4.1.2 Strength and volumetric response

Figures 11 and 12 present DEM simulation results and model predictions of the stress ratio and the volumetric strain under different loading directions. Not surprisingly that SC1 gives best predictions of the stress–strain behaviour over the entire loading paths. With increases of the loading direction angle, the peak strength decreases and the shear strain required to mobilise the peak strength increases. The response of the sample is softer and more contractive in tests with a larger loading direction angle. At large shear strains, both the stress ratio and void ratio evolve towards a unique value. SC3 captures the trend of the effects of loading direction on the peak strength, but it fails to predict a unique void ratio for tests with different loading directions. This can be explained by the fact that SC3 cannot predict a unique fabric tensor at large strains. After the peak stress ratio, the fabric tensor predicted by SC3 obviously deviates from DEM results. The performance of SC3 is better for a small loading direction angle. SC4 captures the volumetric deformation behaviour satisfactorily, but it fails to predict the effects of loading direction on the peak strength. The comparison of results predicted using different flow rules in the deviatoric space (i.e. SC1 and SC2) shows that the flow direction has an insignificant effect on the stress ratio and the volumetric strain.

Fig. 11

Deviatoric strain vs stress ratio: a DEM; b SC1; c SC3; d SC4

Fig. 12

Deviatoric strain vs volumetric strain: a DEM; b SC1; c SC3; d SC4

4.1.3 Fabric anisotropy and non-coaxiality

Figure 13 presents DEM simulation results and theoretical predictions of principal directions of the total strain increment (diamond) and the plastic strain increment (circle), in reference to the principal direction of the stresses. As it is not easy to distinguish the elastic strain increment from the total strain increment in DEM results, only results of the total strain increment are presented. Generally, the value of the non-coaxial angle increases with an increase in the loading direction angle for α ranging from 0° to 45°, and decreases are shown with further increases of the loading direction while α is larger than 45°. At 0° and 90° directions, the total strain increment is coaxial with the stress tensor, which is due to that the fabric tensor is coaxial with the stress tensor, as shown in Fig. 10. While the loading direction varying between 0° and 90°, the non-coaxial angle will reduce to zero gradually after the peak stress ratio as the fabric tensor evolves towards the critical state at which the fabric tensor is coaxial with the stress tensor. All these features are captured by SC1 and SC2 in terms of the total strain increments. However, the predictions of SC1 and SC2 are different in terms of the plastic strain increments. When the stress ratio is low, the predicted principal directions of the plastic strain increments by SC2 are unrealistically large in comparison with those by SC1. In theoretical predictions, at a low stress ratio the total strain increment is nearly coaxial with the stress even though the principal direction of the plastic strain obviously deviates from that of the stress tensor. Considering that the elastic strain increment is always coaxial with the stress tensor as an isotropic elastic model is assumed, it can be inferred that the plastic strain develops gradually and is smaller than the elastic strain at a low stress ratio. However, the DEM simulation results show that even at a very low stress ratio, the strain increment is non-coaxial with the stress tensor. This may imply that the elastic behaviour is also anisotropic or the plastic strain increment should be larger than the predicted values by SC1 and SC2. As the stress ratio increases, predicted principal directions of the total strain increment and plastic strain increment become coincident, which implies that the elastic strain increment becomes ignorable when compared with the plastic strain increment. SC3 and SC4 adopt the same flow rule as SC1, but SC3 is not able to predict coaxial deformation at large strains as the fabric tensor cannot evolve to be coaxial with the stress tensor. Overall, from the comparison, it can be concluded that deformation non-coaxiality is highly related to fabric evolution and is significantly influenced by the flow rule in the deviatoric space.

Fig. 13

Principal directions vs stress ratio: a DEM; b SC1; c SC2; d SC3; e SC4

4.2 Comparison with laboratory tests

The applicability of the model is further assessed by comparing with experimental results in the literature. Model predictions for tests on different sands with various loading paths under both drained and undrained conditions are performed.

A series of tests investigating the drained behaviour of air-pluviated Leighton Buzzard sand (Faction B) have been performed by Yang [80]. The maximum and minimum void ratios of the sand are 0.79 and 0.52, respectively. The specific gravity G_s is 2.65. Only limited test results were reported for the Faction B Leighton Buzzard sand. As Portaway sand has index properties very similar to this sand, the elastic and critical state parameters are taken as suggested by Yu et al. [91] for Portaway sand ($G_{\text{s}} = 2.65, e_{ \hbox{min} } = 0.46, e_{ \hbox{max} } = 0.79$). The dilatancy parameter C_d is calibrated using the response between the volumetric strain and the shear strain in triaxial compression tests. The spacing ratio $r$ is estimated by assuming the maximum state parameter equals 0.07, which is also close to the value calibrated for Portaway sand (i.e. 0.06).

Model predictions are also compared experimental results from drained true triaxial tests [40] and simple shear tests [56] and undrained true triaxial and simple shear tests [88] with Toyoura standard sand. For Toyoura sand, the elastic parameters follow those suggested by Gutierrez and Ishihara [16], and the critical state parameters are determined from the data reported by Verdugo and Ishihara [74], as shown in Fig. 1. Parameters $M_{\text{cc}}$ and $l_{1}$ are obtained from the test results and $l_{3}$ is determined as $b_{\text{c}}^{\text{ps}} = 0.25$ from simple shear tests at large strains as reported by Yoshimine et al. [88]. The spacing ratio $r$ is determined by assuming that the maximum state parameter equals 0.1. The dilatancy coefficient $C_{\text{d}}$ is taken from Miura and Toki [40].

The initial fabric tensor and the model parameters related to the fabric evolution are optimised through trial-and-error with reference to the values calibrated from the previous DEM simulations. The material parameters for both sands are summarised in Table 3. It is reasonable to assume that the initial fabric tensor is cross-anisotropic, namely $F_{\text{b}} = 0$. Initial values of the fabric deviator for Leighton Buzzard sand and Toyoura sand are set as 0.375 and 0.488, respectively. In all of the following predictions, the influence of b value is considered.

Table 3 Summary of material parameters

4.2.1 Drained behaviour of Leighton Buzzard sand

Figures 14, 15, 16 and 17 compare test data and model predictions for air-pluviated Leighton Buzzard sand under monotonic shearing with constant values of b and α. In all these tests, the mean stress was kept constant at 200 kPa. The loading condition and test setups were elaborated by Yang [80]. Overall, the constitutive model generally captures the influences of the loading direction and the b value on the drained behaviour of Leighton Buzzard sand. In general, an increase of either the angle α or the b value may lead to lower shear strength and more contractive behaviour.

Fig. 14

Comparison between model predictions and measured data for drained shear tests of air-pluviated Leighton Buzzard sand (Faction B) with different loading directions at b = 0.5. a Deviatoric strain vs. stress ratio; b deviatoric strain vs. volumetric strain

Fig. 15

Comparison between model predictions and measured data for drained shear tests of air-pluviated Leighton Buzzard sand (Faction B) with different b values at $\alpha = 0^{^\circ }$. a Deviatoric strain vs. stress ratio; b deviatoric strain vs. volumetric strain

Fig. 16

Comparison between model predictions and measured data for drained shear tests of air-pluviated Leighton Buzzard sand (Faction B) with different b values at $\alpha = 30^{^\circ }$. a Deviatoric strain vs. stress ratio; b deviatoric strain vs. volumetric strain

Fig. 17

Comparison between model predictions and measured data for drained shear tests of air-pluviated Leighton Buzzard sand (Faction B) with different b values at $\alpha = 90^{^\circ }$. a Deviatoric strain vs. stress ratio; b deviatoric strain vs volumetric strain

It is shown that before the peak strength is mobilised (typically when the shear strain is lower than 10%), the predicted strength and volumetric response are in good agreement with the test results; after that, the predicted sand response is stiffer and more dilative than that measured in the tests for most cases. These differences may be attributed to the fact that after the peak stress ratio shear bands develop quickly and become obviously visible, which leads to high hetero-homogeneity of the hollow cylindrical samples in the laboratory tests (see Fig. 18a). Consequently, the hetero-homogeneity prevents the fabric evolution towards the unique critical state fabric in the tests. However, a unique critical state fabric is assumed in the constitutive model, and the model parameters related to fabric evolution were determined with reference to the DEM results. In the DEM simulations, the sample is homogenous and no shear band can be observed even at very large shear strains (see Fig. 18b). In the DEM simulations, the sample is not in a cylindrical shape but as a solid drum, and a new technique is used to control the movement of planes for generating general loading paths. The use of this technique maintains that the sample tends to be macroscopically uniform even at a large shear strain (e.g. $\varepsilon_{\text{q}} = 40\%$). Besides, the particle number used in the DEM simulations is limited when compared with that involved in laboratory tests. This may also inhibit the macroscopic development of shear bands, even though micro-shear bands of several particle diameters in width could develop. For example, in Fig. 14, the experimental results obtained from tests with different loading directions show no sign of a unique critical stress ratio or a unique void ratio to be reached at the critical state. In the model predictions, however, the volumetric strain and the stress ratio continuously evolve towards the same value as the fabric evolves towards a unique  anisotropic critical state.

Fig. 18

Typical sample shapes at a large shear strain. a laboratory tests with obvious shear bands (after [80]); b DEM tests without obvious shear bands (after [81])

In addition, the discrepancy between the predicted and measured volumetric strains (e.g. the case of $b = 1,\alpha = 0^{^\circ }$ in Fig. 15) suggests that the dilatancy function is dependent on the current fabric. Although it may increase the degree of complexity of the model, additional assumptions about the dependency of the dilatancy function on the fabric tensor need to be introduced, which can further improve the accuracy of the model prediction on the volumetric deformation response.

4.2.2 Undrained true triaxial tests of Toyoura sand

Figures 19 and 20 compare model predictions and measured results [88] for dry-deposited Toyoura sands in undrained shear tests with different loading directions and b values. It is shown that the model satisfactorily predicts the influences of the loading direction and the intermediate stress ratio as well as the relative density on the undrained behaviour of Toyoura sand. It shows that a larger value of α or b generally leads to a softer and relatively more contractive sand response, which is also often observed in tests under drained conditions. It is noted that the model captures the gradual exhibition of the existence of the ‘quasi-steady state’ with an increasing value of the loading angle. It also predicts the gradual recovery of the shear stress after the ‘quasi-steady state’. However, the model predictions show that the recovery of shear stress after the ‘quasi-steady state’ at $\alpha \ge 45^{^\circ }$ is slower than that of the measured data for samples of D_r = 39–41%, but faster than that for samples of D_r = 31–34%.

Fig. 19

Comparison between model predictions and measured data for undrained true triaxial tests of dry-deposited Toyoura sand with different loading directions at b = 0.5

Fig. 20

Comparison between model predictions and measured data for undrained true triaxial tests of dry-deposited Toyoura sand with different b values at $\alpha = 45^{^\circ }$

4.2.3 Undrained torsional simple shear test of Toyoura sand

Figure 21 shows a comparison between the model prediction and the measured data in undrained torsional simple shear tests of dry-deposited Toyoura sand [88]. The sample was torsionally sheared from an initial anisotropic consolidation state with $p = 133 {\text{kPa}}$ and $q = 100 {\text{kPa}}$. As shown in Fig. 21, the model predicts the sand response reasonably well in the case of $e_{0} = 0.835$. When shearing begins, the direction of the major principal stress rotates rapidly to the direction $\alpha = 45^{^\circ }$ and the b value increases quickly towards $b = 0.25$. Although the model predicts the measured data in trend for the case of $e_{0} = 0.858$, the shear stress recovers quicker than that measured. This may be due to that the realistic critical state line in the $v - { \ln }p$ plane is nonlinear (the slope of the critical state line decreases with an increasing void ratio). After the ‘quasi-steady state’, stresses evolve towards the critical state values, but the linear assumption for the critical state line in the $v - { \ln }p$ plane overestimates the critical state shear stress, which makes the predicted recovery of the shear stress faster than that measured in the tests with loose sand samples.

Fig. 21

Comparison between model predictions and measured data for undrained simple shear tests of dry-deposited Toyoura sand with initial anisotropic consolidation states

4.2.4 Drained triaxial test of Toyoura sand

Figure 22 presents a comparison between the model predictions and the measured data for drained shear tests on Toyoura sand samples prepared by a multiple sieving pluviation method. Although different preparation methods might induce different initial fabrics in a sample [53], the initial fabric deviator was estimated based on dry-deposited sand samples because of the insufficient relevant information in the source reference. $F_{\text{q}} = 0.485$ is used in the predictions given in Fig. 22. Despite that the stiffness and the dilation response of the sand are slightly overestimated, the influence of the loading angle on the drained behaviour of Toyoura sand is well captured by the model.

Fig. 22

Comparison between model predictions and measured data for drained triaxial shear tests of Toyoura sand prepared by a multiple sieving pluviation method

4.2.5 Drained simple shear test of Toyoura sand

Figure 23 shows predicted and measured results of drained simple shear tests that performed on air-pluviated Toyoura sand samples with different initial void ratios [56]. Prior to performing shear tests, the samples were one-dimensionally consolidated until the vertical stress $\sigma_{11} = 98 {\text{kPa}}$ was reached. During shearing, the vertical stress was kept constant. According to Okichi and Tatsuoka [51], the consolidation coefficient is calculated as $K_{0} = 0.52e_{0}$. Again, the estimated initial value of fabric deviator $F_{\text{q}} = 0.485$ is used in the model predictions. Overall, the model predictions are in agreement with the measured data.

Fig. 23

Comparison between model predictions and measured data for drained simple shear tests of air-pluviated Toyoura sand

It is shown that the prediction accuracy is relatively higher for the sample with an initial void ratio of $e_{0} = 0.798$. For the sample with a smaller initial void ratio, the predicted stress ratio is slightly larger than that measured, and the rotation of the major principal stresses are smaller than that measured. These differences may also be attributed to the fact that the realistic critical state line in the $v - { \ln }p$ plane of the Toyoura sand is nonlinear. It is shown in Fig. 23e that rotation of the principal stress axes takes place only at very early stages of shearing, which was also reported in the torsional shearing test [56]. Figure 23(e) also presents the predicted principal directions of the total strain rate, the plastic strain rate and the fabric tensor (i.e. $\alpha_{ \det } ,\alpha_{\text{dep}} ,\alpha_{F}$) and two non-coaxial angles defined as $\left( {\alpha_{ \det } - \alpha_{s} } \right)$ and $(\alpha_{\text{dep}} - \alpha_{s} )$, respectively. However, no measured data about the principal strain increments was reported. It can be seen that, as the fabric tends to align with the stress, the non-coaxial angle becomes smaller and smaller upon loading, which is generally consistent with observations from experimental tests [59] and DEM simulations [94] for granular materials.

5 Conclusions

This paper presents an anisotropic bounding surface model for granular materials with consideration of the effects of material fabric anisotropy. It is shown that this model has the following features:

• The fabric anisotropy is described by a second-order fabric tensor which characterises spatial distributions of the contact normals. The evolution of the fabric tensor is assumed to be dependent on both the stress ratio rate and the plastic strain rate, which essentially defines that the fabric evolution under a monotonic shearing is initially dominated by the stress ratio rate and eventually towards the critical state with a unique fabric tensor. It is postulated that the critical state fabric tensor is proportional to the stress tensor, which is independent of the initial void ratio and the initial fabric tensor;

• The yield surface is modified from the original yield surface of CASM by incorporating the back stress which is proportional to the fabric tensor. The proportional coefficient is obtained from the micromechanical stress-force-fabric relationship, and it is recommended to be 2/5 for 3D cases;

• A non-associated flow law in the deviatoric plane is proposed, by which the non-coaxial flow can be naturally predicted;

• The effects of the b value were incorporated into the yield function, the dilatancy function and the flow direction.

The new constitutive model was calibrated by comparing with DEM simulations under drained conditions with stress principal directions fixed in different directions. Predictions in terms of the stress-strength-deformation behaviour and the fabric evolution agree well with the DEM simulation results. In comparison with the predictions obtained using simplified evolution laws and an associated flow rule, it is concluded that:

• the fabric evolution law is crucial for modelling anisotropic behaviour of granular materials;

• the proposed evolution law which assumes that the rate of the fabric tensor is dependent on both the stress ratio rate and the plastic strain rate is reasonably valid under monotonic loading;

• an associated flow rule in the deviatoric plane may overestimate the non-coaxial angle.

Drained test results of air-pluviated Leighton Buzzard sand and undrained and drained test results of Toyoura sand prepared by different methods were used to validate the new model. Comparison results demonstrated that the model can capture the anisotropic behaviour caused by combined effects of loading directions, shear mode, and initial void ratio in granular materials.

Note that the applicability of the proposed model for tests under some complicated loading paths (e.g. those involving continuous rotations of the principal direction of the stress tensor and cyclic loading) is not validated. The effects of fabric anisotropy on the dilatancy function were ignored in this model. Further investigations on these aspects will be carried out in the future study.

Appendices

Appendix 1: Derivatives of loading surface

According to the chain rule, we can obtain the derivatives as follows:

$$f_{\varvec{S}} = f_{{\tilde{q}}} \tilde{q}_{\varvec{S}} + f_{m} m_{\varvec{S}} ;$$

(52)

$$f_{\varvec{F}} = f_{{\tilde{q}}} \tilde{q}_{\varvec{F}} + f_{m} m_{\varvec{F}}$$

(53)

$$f_{p} = f_{{\tilde{q}}} \tilde{q}_{p} + f_{m} m_{p} - \frac{n}{p}\left( {\frac{{\tilde{q}}}{mp}} \right)^{n} + \frac{1}{{{ \ln }\left( {r^{{\prime }} } \right)p}} ;$$

(54)

$$f_{\beta } = \frac{ - 1}{{\beta { \ln }\left( {r^{{\prime }} } \right)}} ;$$

(55)

$$f_{{p_{0} }} = \frac{ - 1}{{p_{0} { \ln }\left( {r^{{\prime }} } \right)}} ;$$

(56)

where

$$f_{{\tilde{q}}} = \left( {\frac{{\tilde{q}}}{mp}} \right)^{n} = \frac{n}{{\tilde{q}}}\left( {\frac{{\tilde{q}}}{mp}} \right)^{n} ; f_{m} = - \frac{n}{m}\left( {\frac{{\tilde{q}}}{mp}} \right)^{n}$$

(57)

$$\tilde{q} = \left\| 3/2\left( {\varvec{S} - \zeta p\varvec{F}} \right) \right\| = \left\|3/2\varvec{t}\right\| ;$$

(58)

$$\tilde{q}_{\varvec{S}} = \sqrt {3/2} \frac{\varvec{t}}{\left\| \varvec{t}\right\|}; \tilde{q}_{\varvec{F}} = - \sqrt {3/2} \frac{{\zeta p\varvec{t}}}{\left\| \varvec{t}\right\|}; \tilde{q}_{p} = - \sqrt {3/2} \frac{{\zeta \varvec{t}:\varvec{F}}}{\left\| \varvec{t}\right\|}$$

(59)

$$m_{\varvec{t}} = \frac{{\left( {1 - l_{1}^{4} } \right)m^{5} }}{{8\left( {l_{1} M_{cc} } \right)^{4} }}\frac{\partial \chi }{{\partial \varvec{t}}} ;$$

(60)

$$m_{\varvec{S}} = m_{\varvec{t}} ;m_{\varvec{F}} = - \zeta pm_{\varvec{t}} ; m_{p} = - \zeta m_{\varvec{t}} :\varvec{F}$$

(61)

$$\frac{\partial \chi }{{\partial \varvec{t}}} = \frac{1}{\left\| \varvec{t}\right\|}\left( {3\sqrt 6 \left( {\varvec{t}^{2} - \frac{1}{3}tr\left( {\varvec{t}^{2} } \right)\varvec{I}} \right) - \chi \frac{\varvec{t}}{\left\| \varvec{t}\right\|}} \right)$$

(62)

When the loading surface does not account for the influence of shearing mode, m is a constant and independent of t. Thus, there is $m_{\varvec{t}} = 0.$ The derivatives $f_{\varvec{S}} ,f_{\varvec{F}} ,f_{p}$ will be considerably simplified.

Appendix 2: Determination of $p_{0i}$ and $\beta_{i}$

Initial values of the reference consolidation pressure $p_{0i}$ and the mapping ratio $\beta_{i}$ can be deduced from initial values of the stress state, void ratio and fabric tensor by considering a special monotonic shearing path where p is kept constant. This special loading path will not induce elastic volumetric strain. Under monotonic shearing without elastic volumetric strain, integration of Eq. (26) leads to:

$$p_{0} = { \exp }\left( {\left( {e_{M} - e} \right)/\left( {\lambda - \kappa } \right)} \right)$$

(63)

where $e_{M}$ represents the void ratio when $p_{0} = 1$. At the initial void ratio, there is:

$$p_{0i} = { \exp }\left( {\left( {e_{\text{M}} - e_{i} } \right)/\left( {\lambda - \kappa } \right)} \right)$$

(64)

and at the critical state, there is:

$$p_{{ 0 {\text{c}}}} = { \exp }\left( {\left( {e_{\text{M}} - e_{\text{c}} \left( {p_{\text{c}} } \right)} \right)/\left( {\lambda - \kappa } \right)} \right)$$

(65)

Considering the critical state on the yield surface, it is obtained that:

$$\left( {1 - \frac{1}{\zeta }\frac{{M_{\text{F}} }}{M}} \right)^{n} + \frac{{\ln \left( {p_{\text{c}} /p_{{ 0 {\text{c}}}} } \right)}}{{{ \ln }\left( {r^{{\prime }} } \right)}} = 0$$

(66)

Combining Eq. (11) with Eqs. (65) and (66) and then eliminating $e_{M}$ from Eq. (65), we obtain:

$$p_{0i} = p_{i} { \exp }\left( {{ \ln }\left( {r^{\prime}} \right)\left( {1 - \frac{1}{\zeta }\frac{{M_{F} }}{M}} \right)^{n} + \frac{{e_{c} \left( {p_{i} } \right) - e_{i} }}{\lambda - \kappa }} \right)$$

(67)

Once $p_{0i}$ is known, $\beta_{i}$ can be easily obtained from the loading function of Eq. (32) as follows:

$$\beta_{i} = \frac{{p_{i} }}{{p_{0i} }}{ \exp }\left( {\ln \left( {r^{{\prime }} } \right)\left( {\frac{{\tilde{q}_{i} }}{{Mp_{i} }}} \right)^{n} } \right) \le 1$$

(68)