Skip to main content
SpringerLink
Log in

Nitsche-XFEM for a time fractional diffusion interface problem

  • Articles
  • Published:
Science China Mathematics Aims and scope Submit manuscript

Abstract

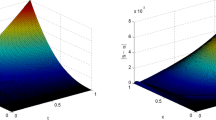
In this paper, we propose a space-time finite element method for a time fractional diffusion interface problem. This method uses the low-order discontinuous Galerkin (DG) method and the Nitsche extended finite element method (Nitsche-XFEM) for temporal and spatial discretization, respectively. Sharp pointwise-in-time error estimates in graded temporal grids are derived, without any smoothness assumptions on the solution. Finally, three numerical examples are provided to verify the theoretical results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Babuška I. The finite element method for elliptic equations with discontinuous coefficients. Computing, 1970, 5: 207–213

    Article  MathSciNet  Google Scholar 

  2. Babuška I, Banerjee U, Kergrene K. Strongly stable generalized finite element method: Application to interface problems. Comput Methods Appl Mech Engrg, 2017, 327: 58–92

    Article  MathSciNet  Google Scholar 

  3. Bramble J H, King J T. A finite element method for interface problems in domains with smooth boundaries and interfaces. Adv Comput Math, 1996, 6: 109–138

    Article  MathSciNet  Google Scholar 

  4. Burman E, Claus S, Hansbo P, et al. CutFEM: Discretizing geometry and partial differential equations. Internat J Numer Methods Engrg, 2015, 104: 472–501

    Article  MathSciNet  Google Scholar 

  5. Cai Z Q, He C Y, Zhang S. Discontinuous finite element methods for interface problems: Robust a priori and a posteriori error estimates. SIAM J Numer Anal, 2017, 55: 400–418

    Article  MathSciNet  Google Scholar 

  6. Chen S, Shen J, Wang L L. Generalized Jacobi functions and their applications to fractional differential equations. Math Comp, 2016, 85: 1603–1638

    Article  MathSciNet  Google Scholar 

  7. Chen Z M, Zou J. Finite element methods and their convergence for elliptic and parabolic interface problems. Numer Math, 1998, 79: 175–202

    Article  MathSciNet  Google Scholar 

  8. Cockburn B, Mustapha K. A hybridizable discontinuous Galerkin method for fractional diffusion problems. Numer Math, 2015, 130: 293–314

    Article  MathSciNet  Google Scholar 

  9. Cuesta E, Lubich C, Palencia C. Convolution quadrature time discretization of fractional diffusion-wave equations. Math Comp, 2006, 75: 673–696

    Article  MathSciNet  Google Scholar 

  10. Delić A, Jovanović B S. Numerical approximation of an interface problem for fractional in time diffusion equation. Appl Math Comput, 2004, 229: 467–479

    MathSciNet  Google Scholar 

  11. Ervin V J, Roop J P. Variational formulation for the stationary fractional advection dispersion equation. Numer Methods Partial Differential Equations, 2006, 22: 558–576

    Article  MathSciNet  Google Scholar 

  12. Hansbo A, Hansbo P. An unfitted finite element method, based on Nitsche’s method, for elliptic interface problems. Comput Methods Appl Mech Engrg, 2002, 191: 5537–5552

    Article  MathSciNet  Google Scholar 

  13. Huang P Q, Wu H J, Xiao Y M. An unfitted interface penalty finite element method for elliptic interface problems. Comput Methods Appl Mech Engrg, 2017, 323: 439–460

    Article  MathSciNet  Google Scholar 

  14. Jin B T, Lazarov R, Pasciak J, et al. Error analysis of semidiscrete finite element methods for inhomogeneous time-fractional diffusion. IMA J Numer Anal, 2015, 35: 561–582

    Article  MathSciNet  Google Scholar 

  15. Jin B T, Lazarov R, Zhou Z. Error estimates for a semidiscrete finite element method for fractional order parabolic equations. SIAM J Numer Anal, 2013, 51: 445–466

    Article  MathSciNet  Google Scholar 

  16. Jin B T, Lazarov R, Zhou Z. An analysis of the L1 scheme for the subdiffusion equation with nonsmooth data. IMA J Numer Anal, 2016, 36: 197–221

    MathSciNet  Google Scholar 

  17. Jin B T, Li B Y, Zhou Z. Discrete maximal regularity of time-stepping schemes for fractional evolution equations. Numer Math, 2018, 138: 101–131

    Article  MathSciNet  Google Scholar 

  18. Karaa S. Semidiscrete finite element analysis of time fractional parabolic problems: A unified approach. SIAM J Numer Anal, 2018, 56: 1673–1692

    Article  MathSciNet  Google Scholar 

  19. Le K N, McLean W, Lamichhane B. Finite element approximation of a time-fractional diffusion problem for a domain with a re-entrant corner. ANZIAM J, 2017, 59: 61–82

    MathSciNet  Google Scholar 

  20. Li B J, Luo H, Xie X P. Analysis of a time-stepping scheme for time fractional diffusion problems with nonsmooth data. SIAM J Numer Anal, 2019, 57: 779–798

    Article  MathSciNet  Google Scholar 

  21. Li B J, Wang T, Xie X P. Analysis of a temporal discretization for a semilinear fractional diffusion equation. Comput Math Appl, 2020, 80: 2115–2134

    Article  MathSciNet  Google Scholar 

  22. Li B J, Wang T, Xie X P. Numerical analysis of two Galerkin discretizations with graded temporal grids for fractional evolution equations. J Sci Comput, 2020, 85: 59

    Article  MathSciNet  Google Scholar 

  23. Li B J, Xie X P, Yan Y B. L1 scheme for solving an inverse problem subject to a fractional diffusion equation. Comput Math Appl, 2023, 134: 112–123

    Article  MathSciNet  Google Scholar 

  24. Li X J, Xu C J. A space-time spectral method for the time fractional diffusion equation. SIAM J Numer Anal, 2009, 47: 2108–2131

    Article  MathSciNet  Google Scholar 

  25. Li Z L, Lin T, Wu X H. New cartesian grid methods for interface problems using the finite element formulation. Numer Math, 2003, 96: 61–98

    Article  MathSciNet  Google Scholar 

  26. Liao H L, McLean W, Zhang J W. A discrete Grönwall inequality with applications to numerical schemes for subdiffusion problems. SIAM J Numer Anal, 2019, 57: 218–237

    Article  MathSciNet  Google Scholar 

  27. Lin Y M, Xu C J. Finite difference/spectral approximations for the time-fractional diffusion equation. J Comput Phys, 2007, 225: 1533–1552

    Article  MathSciNet  Google Scholar 

  28. Lubich C, Sloan I H, Thomée V. Nonsmooth data error estimates for approximations of an evolution equation with a positive-type memory term. Math Comp, 1996, 65: 1–17

    Article  MathSciNet  Google Scholar 

  29. Lunardi A. Analytic Semigroups and Optimal Regularity in Parabolic Problems. Basel: Birkhäuser, 1995

    Book  Google Scholar 

  30. Lunardi A. Interpolation Theory. Pisa: Edizioni della Normale, 2018

    Book  Google Scholar 

  31. Luo H, Li B J, Xie X P. Convergence analysis of a Petrov-Galerkin method for fractional wave problems with nonsmooth data. J Sci Comput, 2019, 80: 957–992

    Article  MathSciNet  Google Scholar 

  32. McLean W. Regularity of solutions to a time-fractional diffusion equation. ANZIAM J, 2010, 52: 123–138

    Article  MathSciNet  Google Scholar 

  33. Metzler R, Klafter J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys Rep, 2000, 339: 1–77

    Article  MathSciNet  Google Scholar 

  34. Mustapha K, Abdallah B, Furati K M, et al. A discontinuous Galerkin method for time fractional diffusion equations with variable coefficients. Numer Algorithms, 2016, 73: 517–534

    Article  MathSciNet  Google Scholar 

  35. Mustapha K, McLean W. Discontinuous Galerkin method for an evolution equation with a memory term of positive type. Math Comp, 2009, 78: 1975–1995

    Article  MathSciNet  Google Scholar 

  36. Persson P O, Strang G. A simple mesh generator in MATLAB. SIAM Rev, 2004, 46: 329–345

    Article  MathSciNet  Google Scholar 

  37. Ren J C, Liao H L, Zhang J W, et al. Sharp H1-norm error estimates of two time-stepping schemes for reaction-subdiffusion problems. J Comput Appl Math, 2021, 389: 113352

    Article  Google Scholar 

  38. Reusken A, Nguyen T H. Nitsche’s method for a transport problem in two-phase incompressible flows. J Fourier Anal Appl, 2009, 15: 663–683

    Article  MathSciNet  Google Scholar 

  39. Sakamoto K, Yamamoto M. Initial value/boundary value problems for fractional diffusion-wave equations and applications to some inverse problems. J Math Anal Appl, 2011, 382: 426–447

    Article  MathSciNet  Google Scholar 

  40. Sun Z Z, Wu X N. A fully discrete difference scheme for a diffusion-wave system. Appl Numer Math, 2006, 56: 193–209

    Article  MathSciNet  Google Scholar 

  41. Tang T, Yu H J, Zhou T. On energy dissipation theory and numerical stability for time-fractional phase-field equations. SIAM J Sci Comput, 2019, 41: A3757–A3778

    Article  MathSciNet  Google Scholar 

  42. Temam R. Infinite-Dimensional Dynamical System in Mechanics and Physics. New York: Springer, 1997

    Book  Google Scholar 

  43. Thomeé V. Galerkin Finite Element Methods for Parabolic Problems. Berlin-Heidelberg: Springer-Verlag, 2006

    Google Scholar 

  44. Xiao Y M, Xu J C, Wang F. High-order extended finite element methods for solving interface problems. Comput Methods Appl Mech Engrg, 2020, 364: 112964

    Article  MathSciNet  Google Scholar 

  45. Xu J C. Estimate of the convergence rate of finite element solutions to elliptic equations of second order with discontinuous coefficients (in Chinese). Natur Sci J Xiangtan Univ, 1982, 1: 1–5

    Google Scholar 

  46. Xu J C. Estimate of the convergence rate of finite element solutions to elliptic equations of second order with discontinuous coefficients. arXiv:1311.4178, 2013

  47. Wang F, Zhang S. Optimal quadratic Nitsche extended finite element method for solving interface problems. J Comput Math, 2018, 36: 693–717

    Article  MathSciNet  Google Scholar 

  48. Wang T, Yang C C, Xie X P. A Nitsche-eXtended finite element method for distributed optimal control problems of elliptic interface equations. Comput Methods Appl Math, 2020, 20: 379–393

    Article  MathSciNet  Google Scholar 

  49. Yang Y, Chen Y P, Huang Y Q, et al. Spectral collocation method for the time-fractional diffusion-wave equation and convergence analysis. Comput Math Appl, 2017, 73: 1218–1232

    Article  MathSciNet  Google Scholar 

  50. Zayernouri M, Karniadakis G E M. Fractional spectral collocation method. SIAM J Sci Comput, 2014, 36: A40–A62

    Article  MathSciNet  Google Scholar 

  51. Zeng F H, Li C P, Liu F W, et al. The use of finite difference/element approaches for solving the time-fractional subdiffusion equation. SIAM J Sci Comput, 2013, 35: A2976–A3000

    Article  MathSciNet  Google Scholar 

  52. Zhao Y M, Chen P, Bu W P, et al. Two mixed finite element methods for time-fractional diffusion equations. J Sci Comput, 2017, 70: 407–428

    Article  MathSciNet  Google Scholar 

  53. Zheng M L, Liu F W, Turner I, et al. A novel high order space-time spectral method for the time fractional Fokker-Planck equation. SIAM J Sci Comput, 2015, 37: A701–A724

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

Tao Wang was supported by the China Postdoctoral Science Foundation (Grant No. 2019M662947). Yanping Chen was supported by the State Key Program of National Natural Science Foundation of China (Grant No. 11931003) and National Natural Science Foundation of China (Grant Nos. 41974133 and 12126325).

Author information

Authors and Affiliations

  1. China Nuclear Power Technology Research Institute Co. Ltd., Shenzhen, 518028, China

    Tao Wang

  2. School of Mathematical Sciences, South China Normal University, Guangzhou, 510631, China

    Yanping Chen

Authors
  1. Tao Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yanping Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yanping Chen.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wang, T., Chen, Y. Nitsche-XFEM for a time fractional diffusion interface problem. Sci. China Math. 67, 665–682 (2024). https://doi.org/10.1007/s11425-021-2062-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11425-021-2062-6

Keywords

MSC(2020)

Search

Navigation