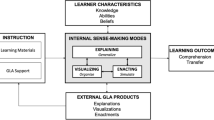
Abstract
Collaboration scripts and heuristic worked examples have been described as powerful scaffolds to support skill acquisition in CSCL. While CSCL scripts particularly facilitate argumentative discourse within groups, heuristic worked examples provide heuristics and worked out pathways to solve domain-specific tasks. Yet, both scripts and heuristic worked examples are often designed in a one-size-fits-all fashion. Granting learners the opportunity to adapt these scaffolds to their self-perceived needs might be a way to further enhance their effects. We tested this assumption in two experiments. In experiment 1, we compared the effects of learning with adaptable and non-adaptable CSCL scripts. In experiment 2, we compared the effects of learning with adaptable and non-adaptable heuristic worked examples. University students (N = 167) learned repeatedly in pairs with either adaptable or non-adaptable scaffolding in the context of mathematical conjecture problems. Results show that adaptable CSCL scripts were partly helpful for students with higher levels of self-regulation skills. Non-adaptable maximal scaffolding supported learning of distinctive skill components. Social-discursive components were best facilitated by maximal heuristic worked examples through content knowledge scaffolds. In contrast, CSCL scripts best facilitated domain-specific skill components by scaffolding learners’ engagement in social discourse about domain knowledge. The study provides recommendations for designing adaptable scaffolding by taking into account the relation between the targeted skill component and the activities scaffolded in the learning process. We suggest conducting future studies on adaptable scaffolding with a focus on supporting learning regulation and group awareness to improve learners’ success in CSCL environments.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
How to best scaffold learners in CSCL has been a major topic of CSCL research (e.g., Kollar et al., 2018). While CSCL scaffolds can be designed through various means, there is a lively debate about the amount of scaffolding that is actually needed in different phases of a learning process. On one end of the spectrum, there are arguments for highly structured scaffolds throughout the whole process of learning complex skills (Kirschner et al., 2006), while on the other, some researchers argue for as minimal structure as possible (Duffy & Jonassen, 1991). More moderate positions ask for a flexible design of scaffolds that can be adjusted to learners’ needs (Hmelo-Silver et al., 2007). To provide such a flexible design of scaffolds, we propose to give learners themselves the opportunity to adapt the scaffolds presented in a CSCL environment according to their self-perceived needs (Leutner, 2002). We argue that the mere opportunity to adapt scaffolds might trigger the reflection and planning of their learning processes (Wang et al., 2017). However, to benefit from such adaptable scaffolds, learners need to rely on their skills to regulate their own and other’s learning (Järvelä & Hadwin, 2013; Melzner et al., 2020).
This article presents two experimental studies on the effects of granting learners the opportunity to adapt the scaffolds to their self-perceived needs. More specifically, experiment 1 investigated the effects of adaptable (vs. non-adaptable) CSCL scripts, and experiment 2 looked at the effects of adaptable (vs. non-adaptable) heuristic worked examples. Our analyses focused on the socio-discursive and domain-specific learning outcomes within the context of the study (mathematical argumentation) as well as the impact of self-regulation skills and regulation activities when learning with adaptable scaffolds.
Developing argumentation skills in the context of mathematics
Successfully engaging in collaborative problem solving in various contexts is an important educational goal (OECD, 2017). Argumentation and reasoning skills play a key role, particularly when it comes to collaborative problem solving of complex tasks in STEM education (Fischer et al., 2014). Yet, students are struggling to apply the knowledge they have acquired at the transition to more constructivist learning scenarios (Nicolay et al., 2021). In particular, the transition from school mathematics to university mathematics programs has been described as challenging for students (Thomas & Klymchuk, 2012) mainly because the character of mathematics changes from a subject with a strong focus on applications to a scientific discipline that concentrates on developing axiomatic-deductive theories based on definitions and formal representations (Clark & Lovric, 2009; Kosiol et al., 2019). For this, students need skills that are crucial for a collaborative engagement in argumentative mathematical activities that are embedded in a mathematical culture oriented towards the norms of scientific mathematics. These are, for instance, developing and making use of definitions (Zandieh & Rasmussen, 2010), generating and exploring conjectures (Lin et al., 2012; Schwarz et al., 2010), selecting and organizing deductive arguments (Stylianides & Stylianides, 2008), and validating mathematical argumentation through social exchange (Alcock & Weber, 2005; Sommerhoff & Ufer, 2019). Consequently, we conceptualize mathematical argumentation skills (MAS) as the composition of a domain-specific component and a socio-discursive component. The domain-specific component accounts for the ability to explore mathematical situations in collaborative settings, formulating or evaluating a conjecture, and finally arriving at a proof or a refutation for the conjecture (Kollar et al., 2014). The socio-discursive component forms a substantial prerequisite to make effective use of domain-specific MAS components in social situations to produce new mathematical insights. It refers to the production of arguments and counter-arguments and the ability to arrive at syntheses between different arguments when solving a mathematical proof task (Kollar et al., 2014). We would like to highlight that this understanding of socio-discursive MAS is clearly catered to the context of undergraduate mathematics learning, where joint mathematical work on mathematical argumentation tasks plays a more prominent role than a joint negotiation of mathematical concepts or argumentative norms as described by socio-cultural views on mathematics school classrooms (Yackel & Cobb, 1996). To support students developing MAS, CSCL scripts guide students through sequences of necessary activities to engage socially in argumentation (Fischer et al., 2013). Heuristic worked examples offer detailed scaffolding for each step in a mathematical proof process, including activities such as exploring the problem space or identifying a plausible conjecture (Mulder et al., 2014; Reiss & Renkl, 2002).
Adaptable scaffolding in CSCL
A basic assumption of scaffolding is that scaffolds have to be adjusted to learners’ needs (Wood et al., 1976). Optimally, CSCL scripts and heuristic worked examples would continuously adjust the amount of scaffolds they provide to the learners’ current proficiency level. To realize this, a continuous assessment of the learners’ behavior, collaboration, knowledge, and skills would be necessary (Plass & Pawar, 2020). However, this may only be realized with the use of highly sophisticated intelligent tutoring technology (Diziol et al., 2010; Rummel et al., 2016). Although research showed that such automatized adaptive scaffolding can have a positive impact on learning processes, effects of learning with adaptive compared to non-adaptive CSCL scripts on learning outcomes are rare and the development of such technology may be very costly (Diziol et al., 2007; Rau et al., 2017; Walker et al., 2011).
In a less costly alternative the responsibility for adapting the scaffold is shifted to the learners themselves by making scaffolds adaptable (i.e., adjustable by the learners) rather than adaptive (i.e., adjusted by technology). For instance, a study by Wang et al. (2017) compared the effects of an adaptable CSCL script with a non-adaptable CSCL script and a non-scripted condition on the acquisition of regulation skills. The script guided groups of learners through peer-review in educational problem solving. Learners in the adaptable script condition had the opportunity to adjust the role distribution and available script prompts to their self-perceived needs and showed improved self-regulation skills as compared to non-adaptable conditions.
Adaptable scaffolding with CSCL scripts
CSCL scripts are designed to scaffold the development of cognitive schemas, so-called internal scripts, about appropriate activities within a specific social setting (e.g., an argumentative dialogue). Based on Schank (1999), Fischer et al. (2013) suggest that internal scripts are composed of a set of components on hierarchically ordered levels. The play level holds generic knowledge about the kind of situation an individual currently experiences (e.g., a group trying to explore a mathematical conjecture). At the scene level, knowledge components represent the phases that are likely to happen as the situation evolves. For example, when there is dissent about the validity of a conjecture, participants will first express their initial arguments, then their counter-arguments, and finally integrate their different arguments (Leitão, 2000). At the scriptlet level, knowledge about how to construct such arguments and counterarguments is stored. For example, a learner may hold scriptlets that guide them in bringing forward a claim, supporting the claim with concrete examples or general mathematical arguments, and integrating appropriate qualifications (Toulmin, 1958).
Externally represented CSCL scripts scaffold learners who have not yet developed functional internal scripts to engage in a situation. While CSCL scripts can be designed for various situations to facilitate different kinds of skills, one focus in CSCL research has been on scripts that are supposed to scaffold argumentation (Noroozi et al., 2013). Such CSCL scripts usually distribute roles among learners and prompt their engagement in the play, the different scenes, and scriptlets (Kobbe et al., 2007; Kollar et al., 2006). In this way, CSCL scripts may enable learners to repeatedly practice and apply argumentation skills and eventually transfer them to similar non-scaffolded tasks (van Merriënboer et al., 2003). Studies showed that CSCL scripts for argumentation in mathematics can positively affect the collaborative activities during the learning process and hereby enhance learners’ socio-discursive argumentation skills (Kollar et al., 2014; Vogel et al., 2016). By means of facilitating socio-discursive argumentation, learning with CSCL scripts may also indirectly support students’ acquisition of domain-specific knowledge: The more they are enabled to engage in socio-discursive argumentation, the more the learners may elaborate the learning material and thus acquire domain-specific knowledge about the topic of their discussion (i.e., “arguing to learn”; Andriessen et al., 2003; King, 2007). In addition, the facilitation of engaging in socio-discursive activities allows learners to decrease the distributed collaborative cognitive load. Hence, they have free capacities to explore the domain-specific content of the mathematical problem to be solved (Janssen & Kirschner, 2020).
Fischer et al. (2013) argue that a CSCL script will be most effective when it aims at the script level on which a learner’s internal script is not yet developed. A script on a too detailed level might hinder learning by “over-scripting” (Dillenbourg, 2002), which may be caused by interfering with the application of an already developed internal script and reducing motivation through the limitation of the self-determination of autonomous learners (Rienties et al., 2012). The few studies comparing the effectiveness of scripts on different levels show that scripts on the same level can sometimes be conducive, but at other times detrimental for learning outcomes (Stegmann et al., 2007; van Aalst & Chan, 2007). With an adaptable CSCL script, learners may be enabled to choose a script on the level just right for them (Tchounikine, 2016). For example, by granting learners the opportunity to receive or not receive script prompts that are designed to support their engagement in learning activities at certain script levels.
Adaptable scaffolding with heuristic worked examples
Worked examples provide learners with a full solution to a given learning task (Atkinson et al., 2000). As Schworm and Renkl (2007) have argued, worked out examples may offer information at different levels: they may provide (1) information that is related to the content knowledge necessary to solve the task (2) information about strategies to approach the respective task type, and (3) information about what is demanded during a certain task type. Traditional worked examples usually present information relating to the first and the third level. However, information about appropriate strategies and useful approaches to a problem type are deemed particularly important for complex, unstructured tasks (Hummel et al., 2006; Nadolski et al., 2005). Heuristic worked examples, in turn, offer learners a worked out heuristic solution approach that is exemplary for the task types the learners have to solve (Reiss & Renkl, 2002). This approach has been used successfully to foster scientific reasoning (Mulder et al., 2014). When applied to mathematical argumentation, they may describe an authentic problem-solving process based on an expert’s model of mathematical proof processes (e.g. Boero, 1999) and provide heuristic strategies (Hilbert et al., 2008). To scaffold domain-specific MAS, learners may then be guided through the various steps of solving mathematical proof problems, such as formulating a conjecture and exploring the problem space. Heuristic worked examples are designed to directly facilitate domain-specific MAS by showing mathematical content and heuristics. Further, heuristic worked examples offer the information needed to be able to fully engage in argumentation and hence indirectly support the development of socio-discursive MAS (Kollar et al., 2014). The facilitation for problem solving provided by heuristic worked examples may free cognitive capacities that can be utilized to practice socio-discursive argumentation more thoroughly (Renkl et al., 2009).
Similar to the research about scaffolding with CSCL scripts, worked examples have been shown to have differential effects depending on learners’ pre-requisites (Hilbert et al., 2008). Particularly due to the expertise reversal effect (Kalyuga et al., 2003), learners with higher prior knowledge may benefit less from the high structure offered by worked examples. In contrast, heuristic worked examples have the potential to privilege learners with specific characteristics regarding prior knowledge, attitudes, or self-regulation skills (Kollar et al., 2014). This may be caused by additional demands on the learners to navigate and benefit from heuristic worked examples posed by their high amount of information and structure. Designing heuristic worked examples representing the right amount of scaffolding is a delicate endeavor. When being offered adaptable heuristic worked examples, learners can be granted the opportunity to fulfill certain steps of the solution steps on their own, rather than being presented with how that step should optimally be realized.
The role of self-regulation for effective adaptation of scaffolding
The capacity to regulate one’s learning is relevant for learners who have to engage with understanding the task, planning how to achieve their goals, using strategies towards goal achievement, and adapting their strategies meta-cognitively after self-evaluation (Winne, 2011). When it comes to learning with adaptable scaffolds, learners’ self-regulation skills may play a role in different, more specific ways. Appropriate adaptation decisions demand a certain level of self-regulation skills from the learners (Gogoulou et al., 2008; Vrieling et al., 2018). More explicitly, learners need to self-assess their current learning progress correctly. Based on this assessment, they can make decisions on how to adapt the scaffold to their own needs. For this adaptation to be successful, learners need to continuously monitor, reflect on, and plan their learning (Wang et al., 2017). When this is embedded in a collaborative learning environment, the adaptation process may even turn into an act of socially shared regulation for which learners require appropriate regulation skills as well (Järvelä & Hadwin, 2013). Learners, however, often lack such skills (Miller & Hadwin, 2015). It is thus likely that some learners might be overwhelmed by the opportunity to adapt external scaffolds because they lack appropriate self-regulation strategies (Melzner et al., 2020). In addition, self-regulation may become relevant when learners do not adapt to the optimal level of scaffolding, which may demand more self-regulation skills to cope with a sub-optimal learning environment. A high amount of scaffolding may support and even take over parts of the cognitive and meta-cognitive self-regulation activities. The support with CSCL scripts is particularly focused on the regulation of social learning (Miller & Hadwin, 2015). The prompts provided by a CSCL script for argumentation serve as explicit guidance for the meta-cognitive strategies to be used to engage in socio-discursive argumentation (Noroozi et al., 2012).
Research questions
This article aims to inquire research questions in the context of two experiments: In the first experiment, we compared effects of adaptable CSCL scripts and non-adaptable CSCL scripts on learning MAS (see RQ 1). In the second experiment, we compared effects of adaptable and non-adaptable heuristic worked examples on learning MAS (see RQ 4). In the adaptable scaffolding conditions, learners were asked to adjust the learning environment to either maximum or minimum amount of scaffolding at various points throughout their learning. In each experiment, the non-adaptable scaffolding was realized by two different conditions: one with a continuously maximal amount of scaffolding and one with a continuously minimal amount of scaffolding. The study design enabled realizing the non-adaptable minimal conditions for experiments in one and the same condition. Therefore, overall only five conditions were needed with the caveat of a possible overemphasis of the minimal scaffolding condition used for both experiments. With additional research questions in each experiment (see RQs 2, 3, 5, 6), we explored the role of learning regulation in different conditions. Learning regulation is considered by means of a self-regulated learning measure and the actual regulation activities the learners show when asked to adapt the scaffolding to their needs.
Experiment 1: Adaptable CSCL scripts
-
RQ 1: What is the effect of learning with adaptable compared to non-adaptable CSCL scripts on learners’ (a) socio-discursive and (b) domain-specific MAS?
-
RQ 2: To what extent do learners’ self-regulation skills explain learning (a) socio-discursive and (b) domain-specific MAS when learning with adaptable and non-adaptable CSCL scripts?
-
RQ 3: To what extent are learners’ regulation activities related to their self-regulation skills as well as their learning of (a) socio-discursive and (b) domain-specific MAS when learning with adaptable CSCL scripts?
Experiment 2: Adaptable heuristic worked examples
-
RQ 4: What is the effect of learning with adaptable compared to non-adaptable heuristic worked examples on learners’ (a) socio-discursive and (b) domain-specific MAS?
-
RQ 5: To what extent do learners’ self-regulation skills explain learning (a) socio-discursive and (b) domain-specific MAS when learning with adaptable and non-adaptable heuristic worked examples?
-
RQ 6: To what extent are learners’ regulation activities related to their self-regulation skills as well as their learning of (a) socio-discursive and (b) domain-specific MAS when learning with adaptable heuristic worked examples?
We expected learners to gain both components of MAS with possibly differential effects in contrary directions. Learning with adaptable scaffolding may be most effective when learners succeed in adapting them to their needs, which depends on their regulation activities. Maximal scaffolding may lead to better learning outcomes due to the clearly outlined process. Yet, it may also interrupt learning by causing detrimental effects on learners’ autonomy. Minimal scaffolding, in turn, may leave opportunities for learners to practice the application of the acquired skills. Nevertheless, the lack of prompts could also overwhelm learners and lead to a decrease in their sense of being competent. Self-regulation skills may be likewise relevant in the different conditions of adaptable and non-adaptable scaffolding for regulation activities either balancing reduced scaffolding, deciding for the appropriate amount of scaffolding, or coping with competing internal scripts and external maximal scaffolding. Effects might emerge in a more differentiated way when outcomes more and less directly targeted by the scaffolds are analyzed.
Method
Both experiments were conducted in the same study context, using the same procedure, learning environment, and measures. They mainly differed in the experimental variation of the scaffolding presented in the learning environment. In the following, we first explain the context and learning environment shared by both experiments. Then, the specific experimental variation will be introduced for each experiment separately. Finally, the measures and coding procedure are presented for both experiments since instruments and coding procedure had been applied to both experiments at once.
Participants and study context
Overall, N = 167 university freshmen participated in the two experiments of the study (see Tables 1 and 2). About 59% (n = 99) of the sample were female, about 41% (n = 68) were male, and none of the participants chose other answers to indicate their gender. Their average age was Mage = 19.73 years (SDage = 2.57). The two experiments of the study were embedded in a two-week voluntary preparation course for prospective students in mathematics. The courses and the data collection took place at three different universities in Germany. At each university, participating students were randomly assigned to one of the five condition of the two experiments. Only five conditions were needed because the two minimal scaffolding conditions in both experiments shared the same instructional design. Initially, a higher number of students participated in the preparatory course and in some parts of the experiments. Yet, we only considered students who participated in all intervention sessions, had given their informed consent, and provided data for at least one component of MAS. A few missing variables (e.g., for one of the components of MAS) leads to slight differences in numbers when it comes to statistical analyses.
Procedure
Throughout the two weeks of the preparation course, we offered lectures and tutorials about the topic of elementary number theory with study-related questionnaires and pre-tests on the fourth day (see Table 3). Students were then randomly assigned to one of the experimental conditions. On the fifth, sixth, and seventh day, they participated in the three intervention sessions (45 min each). For each intervention session, students were randomly assigned to a new learning partner with comparable pre-requisites (i.e., high school grades). We decided for randomly assigning a new homogeneous learning partner in each session to reduce the effect one specific learning partner (particularly one with more diverse pre-requisites) could have on their learning. On the eighth and ninth day, students answered questionnaires and post-tests.
Learning environment
During each intervention session, students learned collaboratively in dyads on one mathematical conjecturing problem (e.g., “Choose some squared numbers. Calculate the differences of two squared numbers. Formulate a conjecture and prove it!”) that were presented in a CSCL environment. These tasks were built based on prior work related to mathematical conjecturing activities (Lin et al., 2012). The students of each dyad were seated across from one another. Each student was equipped with a laptop, a graphic tablet, and a mouse.
The CSCL environment displayed on the laptop screen was vertically divided into two parts (see Fig. 1). The left side displayed the proof problem, access to lecture notes, and a basic calculator. The right side displayed a shared graphical chat where the learning partners could type using the keyboard and draw using a graphic tablet. The same environment was used in both experiments. In general, above the shared graphical chat, students were presented with complementary script prompts. Phases of the heuristic worked examples were represented on the left side of the screen. Although the dyads were allowed to talk with each other, they were always reminded to add their most relevant contributions into the shared chat space.
Experimental variation
The learning environment varied depending on the experiment and the condition learners had been assigned to. In the following, details of the variations for each condition in Experiment 1 and Experiment 2 are described.
Experiment 1: Adaptable CSCL script
In each of the three CSCL script conditions, the learning environment offered minimal heuristic worked examples as a baseline. Beyond the proof problem itself, the minimal worked examples displayed six phases derived from Boero’s (1999) process of mathematical proof (see description of Experiment 2 below).
The minimal CSCL script guided the learners through three phases of a dialectical discussion, namely (1) argument, (2) counterargument, and (3) synthesis. For each phase, the students in a dyad received complementary prompts (“scene”; e.g.: “formulate an argument” and “listen to your partner’s argument critically”). The sequence of the three phases were shown three times per treatment session at different timepoints during mathematical problem solving represented by the baseline minimal heuristic worked example.
The maximal CSCL script included all prompts from the minimal script plus additional prompts at the scriptlet level on how to formulate sound arguments (e.g., formulate claims, data, and rebuttals) based on Toulmin’s (1958) argumentation model. These additional prompts were emphasized by the possibility of automatically inserting adequate sentence openers into the chat by pressing the respective buttons.
Students who learned with the adaptable CSCL script had the opportunity to choose between the minimal and maximal CSCL script up to six times per intervention session. At specific points within the sequence of the script (before the students were prompted to formulate an argument and before they were prompted to formulate a counterargument), a decision screen appeared that asked both learners to indicate how much support they would need during the following segment. Then, they were asked to either press a button that would lead to them learning with the minimal CSCL script or a button that would lead them to learning with the maximal CSCL script. The students were informed that if they would not come to an agreement on which script to select for the next step, they would automatically receive the maximal CSCL script.
Experiment 2: Adaptable heuristic worked examples
In the three conditions that varied the heuristic worked examples, the learning environment offered the minimal CSCL script for all students as a baseline. The minimal CSCL script repeatedly guided the learners through three phases of a dialectical discussion, namely (1) argument, (2) counterargument, and (3) synthesis. The three phases were shown three times per intervention session and were the same as the minimal CSCL script described for Experiment 1 above.
Beyond the mathematical conjecturing problem itself, the minimal heuristic worked examples displayed six central phases derived from Boero’s (1999) phases in a process model of mathematical proof:
-
1.
Exploring the problem space by calculating examples
-
2.
Formulating a reasonable conjecture
-
3.
Checking the limitations of the validity of the conjecture and collect ideas
-
4.
Formulate the conjecture more precisely using mathematical content and theorems
-
5.
Sketch a possible proof for the conjecture
-
6.
Formulate the proof in a formal way.
The maximal heuristic worked examples comprised a sequence of six detailed worked out solution steps, one for each of the phases of mathematical proof outlined above (Boero, 1999; Nadolski et al., 2005). To support the heuristic approach, the worked out examples displayed the thoughts and problem-solving steps of a fictitious learner solving the proof problem as well as reflective questions about the approach of a fictitious learner. The two students of a learning dyad were given slightly different versions of the heuristic worked example. For instance, in the phase of exploring the problem space, one worked example used sample calculations represented in tables to explore reasonable conjectures (Lockwood et al., 2016), while the other used informal diagrams to identify relevant structural features of the mathematical situations.
In the condition with the adaptable heuristic worked examples, dyads could choose between the minimal and the maximal heuristic worked examples up to six times in each treatment session. In particular, before each of the six phases of mathematical proof, students were asked how much support they would need. Then, they were asked to press a button that would either lead them to the minimal or the maximal worked examples. Again, if students would not come to an agreement, they were automatically provided with the maximal heuristic worked examples until the next phase in which they could decide again.
Measures
Socio-discursive MAS
To assess socio-discursive MAS, we conducted individual pre-tests and post-tests in which students were asked to describe typical phases and quality features of an argumentative discourse in science. Each student were given the opportunity to name and describe up to five different phases. Students’ answers were evaluated for the appearance of relevant elements in an argumentative discourse per each of the phase a student has described. The elements, derived from Leitão (2000), were (a) relating to the other’s arguments when continuing the argumentation, (b) formulating a critique of the other’s arguments, (c) balancing different arguments, (d) integrating different arguments into a synthesis. A coding schema was developed to define and describe the elements (see Table 4). Two researchers practiced the application of the coding schema in two training phases. In each phase, they coded individually the answers of 30 students who had not been included in the study at hand. Before and after each phase the raters discussed discrepancies in their coding decisions and refined the coding schema where necessary (e.g., by including more examples or specifying thresholds). After the two training phases were completed, the two raters coded a sample of 60 student answers from the actual data (30 pre-test, 30 post-test, randomized across the conditions of both experiments) and reached sufficient interrater reliability for all coded elements (Cohen’s κMean = 0.84). The remaining data was then distributed and coded by the two coders in equal parts. The final score used for the statistical analysis ranges from 0 (no element used at all) to 4 (using all relevant elements in the argumentation).
Individual-mathematical MAS
We assessed students’ domain-specific MAS by conducting parallel pre-tests and post-tests. Pre-tests were conducted one day before and post-tests one day after the treatment phase. Each of the tests comprised 17 open items (Kollar et al., 2014). Five items required schematic argumentation within elementary number theory (e.g., “Show that for all natural numbers, a and b, the following statement is true: If 7 divides a + 3b then 7 divides 2a + 13b.”). These items focused on technical skills and a basic understanding of definitions and theorems from the lectures during the first days of the two week course. We surveyed students’ proof skills in elementary number theory using six items (e.g., “Prove the following statement: The sum of five consecutive numbers is divisible by five.”). Another six items focused on open-ended argumentation problems (e.g., “Prove or refute the following statement for natural numbers a and b: If you multiply the sum of a and b with the difference of a and b, you will always obtain an even number.”) and approximated the conjecturing items used in the intervention as far as possible for a reliable test instrument. All items were coded by two trained, independent raters. Coding focused on counting the number of the main arguments that they were able to identify in the students’ solutions. Main arguments were identified based on definitions or theorems from the course that were deemed necessary for an acceptable proof. This coding widely disregarded the formal quality of the solutions (e.g., correct use of symbols), which forms a distinguishable coding dimension (Ottinger et al., 2016). Inter-rater reliability was good (Mean of ICCunjust = 0.79), but raters discussed the remaining discrepancies until they reached a consensus, nevertheless. The reliability was good for both pre-test and post-test (Cronbach’s alpha: αpre = 0.82 resp. αpost = 0.80). For the statistical analyses, a combined score was calculated and scaled to values between zero (nothing correct at all) and one (everything correct).
Self-regulation skills
To measure the participants’ self-regulation skills, we adapted an already established questionnaire (Fisher et al., 2001) in which students rated the extent to which they agreed with statements about their readiness to learn in a self-regulated way. The original instrument consists of 40 items representing three sub-scales (self-management, desire for learning, self-control) with good reliability for each scale (Cronbach’s α > 0.80). We adapted the instrument to adhere to time restrictions within the project and the native language of our participants. Thus, nine items (see Table 5) from the original scales self-management and self-control were selected and translated based on their fit to the context of the study. Participants estimated themselves as self-regulated learners by answering how much they agreed with each item on a five-point Likert scale. After excluding one item, the reliability of the resulting scale was Cronbach’s α = 0.64. Although this value does not exceed the commonly used threshold of 0.70, we decided to keep the scale as a best approximation to the participants’ self-regulation skills. Yet, the notion of it being a self-report scale with quite low internal consistency is reflected in our careful interpretation of the results.
Actual regulation activities
The adaptation choices learners made while learning with the adaptable scaffolding were logged in the CSCL environment. As a measure of their actual regulation activities, we used the frequency learners decided for adapting to the maximal scaffolding as compared to minimal scaffolding. Thus, a higher value in the actual regulation activities means that the student learned more often with the maximum scaffolding and less often with the minimum scaffolding. With a total of 18 opportunities to adapt the learning environment, the possible scores were between 0 and 18. Across both experiments, there were all types of adjustment patterns for regulating the scaffolding. These ranged the full gamut from starting with a maximum scaffold and fading to minimum scaffold to the reverse, alternating between the maximum and the minimum scaffolding, or keeping one of them across all 18 decisions. Observations of students showed that they mostly formed an agreement for a decision without extensively discussing it.
Statistical analyses
To analyze the effects of the different conditions on socio-discursive MAS, we ran repeated measures ANOVAs (as pre-test and post-test were identical). Overall, the pre-test and post-test values for socio-discursive MAS were significantly correlated (see Table 6). To analyze the effects of the different conditions on individual-mathematical MAS, we used ANCOVAs with pre-test values as the covariate (because the pre-test and post-test instruments differed from each other, even though they were significantly correlated). Small correlations between socio-discursive MAS and domain-specific MAS were not significant (see Table 6). To avoid results biased by multiple comparisons, omnibus tests were taken as an indicator of the significance of effect sizes. Significant values in post-hoc analyses were only interpreted as such when the previous omnibus test was significant.
Linear regressions were used to analyze the relevance of self-regulation skills for learning MAS. For the more exploratory analysis of the regulation data, we used correlations to explore how self-regulation skills and regulation decisions were related to learning in each condition. For all tests, the alpha level was set to 0.05. To account for not having directional hypotheses, two-tailed tests were conducted.
Results
Experiment 1: Adaptable scaffolding with CSCL scripts
RQ 1a: Effects on socio-discursive MAS
Descriptive statistics showed higher learning outcomes for learners in the adaptable script condition than in the two non-adaptable script conditions (see Fig. 2). Yet, a repeated measures ANOVA showed that these differences were not significant regarding students’ acquisition of socio-discursive MAS (F(2,94) = 0.58, p = 0.56, part. η2 = 0.01).
RQ 1b: Effects on domain-specific MAS
An ANCOVA with post-test domain-specific MAS as the dependent vairable, the type of CSCL script as the independent variable, and pre-test domain-specific MAS as the covariate revealed a significant effect of the script condition on students’ acquisition of domain-specific MAS (F(2,92) = 3.91, p = 0.02, part. η2 = 0.08). Post-hoc comparisons with Bonferroni adjustment showed that only the maximal CSCL script condition significantly outperformed the minimal CSCL script condition (MeanDiff = 0.81, SE = 0.03, p = 0.02). In contrast, learning with the adaptable CSCL script was neither significantly worse than learning with the maximal CSCL script, nor significantly better than learning with the minimal CSCL script (see Fig. 3).
RQ 2a: Relevance of learners’ self-regulation skills for learning socio-discursive MAS
To investigate the effects of learners’ subjective self-regulation skills for post-test socio-discursive MAS, we conducted exploratory regression analyses for each condition of Experiment 1 with pre-test socio-discursive MAS and self-regulation skills as predictors and post-test socio-discursive MAS as the dependent variable. Results showed that self-regulation skills significantly predicted the acquisition of socio-discursive MAS only in the adaptable script condition (see Table 7).
RQ 2b: Relevance of learners’ self-regulation skills for learning domain-specific MAS
To investigate the relevance of learners’ subjective self-regulation skills for domain-specific MAS in the post-test, we conducted exploratory regression analyses for each condition of Experiment 1 with pre-test domain-specific MAS and self-regulation skills as predictors and post-test domain-specific MAS as the dependent variable. Results showed that only in the minimal CSCL script condition, self-regulation skills were significantly positively related to post-test domain-specific MAS (see Table 8).
RQ 3: Relevance of learners’ actual regulation activities
Descriptive statistics revealed that learners from the adaptable script condition adapted the CSCL scripts to the maximal scaffolding between 0 and 15 times (M = 6.49, SD = 4.49), evenly distributed across the whole range. To find out more about the relevance of learners’ actual regulation, we conducted correlation analyses between the actual regulation of adaptable scripts (frequency of decisions for the maximum worked examples) and subjective self-regulation skills as well as pre-test and post-test measures of MAS. The correlation analyses (Pearson, 2-tailed) showed that the learners’ self-regulation skills were negatively but not significantly correlated with learners’ actual regulation on a medium level (r = -0.30; p = 0.09). The small negative correlation of actual regulation with the pre-test for socio-discursive MAS was not significant (r = -0.06; p = 0.73). Yet, there was a significant negative correlation between actual regulation and post-test socio-discursive MAS (r = -0.36, p = 0.04). This means, learners who chose more often the maximum CSCL script showed lower learning outcomes while learners who chose the minimum script more often showed better learning outcomes. Regarding domain-specific MAS, both positive correlations between actual regulation and pre-test (r = 0.15, p = 0.39) as well as post-test (r = 0.18, p = 0.31) were not significant.
Experiment 2: Adaptable scaffolding with heuristic worked examples
RQ 4a: Effects on socio-discursive MAS
A repeated-measures ANOVA with socio-discursive MAS as dependent variable and the type of heuristic worked examples as independent variable revealed a significant effect of the heuristic worked examples conditions (F(2,95) = 3.31, p = 0.04, part. η2 = 0.07). Descriptively, students in the maximal worked examples condition outperformed learners of both the minimal worked examples condition and the adaptable worked examples condition (see Fig. 4). Post-hoc comparisons did not show significant results for the specific differences between the three conditions.
RQ 4b: Effects on domain-specific MAS
An ANCOVA with post-test domain-specific MAS as the dependent variable, the type of heuristic worked examples as the independent variable, and using the pre-test domain-specific MAS as a covariate did not reveal significant differences (see Fig. 5) between the heuristic worked examples conditions (F(2,91) = 0.51, p = 0.60, part. η2 = 0.01).
RQ 5a: Relevance of learners’ self-regulation skills for learning socio-discursive MAS
To investigate the effects of learners’ self-regulation skills for post-test socio-discursive MAS, we conducted exploratory regression analyses for each condition of Experiment 2 with pre-test socio-discursive MAS and self-regulation skills as predictors and with post-test socio-discursive MAS as the dependent variable. Results showed that the measure of self-regulation skills did not serve as a significant predictor in any condition (see Table 9).
RQ 5b: Relevance of learners’ self-regulation skills for learning domain-specific MAS
To investigate the relevance of learners’ self-regulation skills for domain-specific MAS in the post-test, we conducted exploratory regression analyses for each condition of Experiment 2 with pre-test domain-specific MAS and self-regulation skills as predictors and with post-test domain-specific MAS as the dependent variable. Results showed that only in the minimal heuristic worked examples condition were self-regulation skills significantly positively related to post-test domain-specific MAS (see Table 10).
RQ 6: Relevance of learners’ actual regulation of adaptable heuristic worked examples for learning socio-discursive and domain-specific MAS
Descriptively, learners adapted their heuristic worked examples to the maximum between 1 and 17 times (M = 8.72, SD = 4.34), evenly distributed across the whole range. To find out more about the relevance of the learners’ actual regulation, we conducted correlation analyses (Pearson) between the actual regulation of adaptable heuristic worked examples (frequency of decisions for the maximum worked examples) and subjective self-regulation skills as well as pre-test and post-test measures of MAS. The correlation analyses revealed a non-significant positive correlation between self-regulation skills and learners’ actual regulation of the adaptable heuristic worked examples (r = 0.12, p = 0.51). Learners’ actual regulation of heuristic worked examples showed no significant correlation with pre-test socio-discursive MAS (r = -0.02, p = 0.89) and post-test socio-discursive MAS (r = 0.09, p = 0.63). Likewise, for the domain-specific MAS the adaptation showed no significant correlation with the pre-test (r = 0.03, p = 0.89) nor the post-test (r = -0.08, p = 0.66).
Discussion
Effects of adaptable scaffolding on MAS
Regarding the effects of adaptable scaffolding, the results show that learners in all conditions improved their MAS between pre-test and post-test, but none of the conditions turned out to be generally superior. The maximal scaffolding has been slightly more effective for learning the more indirect skills. This way, learning with the maximal CSCL script had a significant positive effect on domain-specific MAS compared to the minimal CSCL script conditions. Similarly, learning with the maximal heuristic worked examples had been related with higher scores in socio-discursive MAS, yet without being significantly better than minimal or adaptable heuristic worked examples. These effects are in line with studies in which a combination of comparable minimal CSCL scripts and heuristic worked examples had a positive effect on socio-discursive mathematical argumentation skills compared to respective control conditions (Kollar et al., 2014). They also speak for the more indirectly scaffolded skill being less prone to be disadvantaged by the lack of transfer offered when learning while being intensively scripted or with thorough worked out solutions (Noroozi et al., 2018). CSCL scripts are designed to enable learners to engage in cognitive elaboration (e.g., by discursive argumentation about the content) and that way to acquire domain-specific knowledge and skills (King, 2007; Wecker & Fischer, 2014). While the non-adaptable CSCL scripts did not yield the assumed direct effects to help learning to argue, it rather seems to have supported them in their efforts for arguing to learn (Andriessen et al., 2003) by enabling cognitive elaboration of the mathematical content through the formulation of counter-arguments and syntheses (King, 2007). The superiority of the maximal scaffolding for learning the respective less direct skills reveals that mechanisms of arguing to learn domain-specific content can work when learners are scaffolded with CSCL scripts in a mathematical context. Beyond that, being scaffolded by the aid of heuristic worked examples may have released collaborative cognitive load to be able to practice and acquire socio-discursive MAS (Janssen & Kirschner, 2020).
Regarding the effect of scaffolding the more directly supported skill, the results did not reveal significant differences. However, descriptively the results of our study showed the highest learning outcomes for adaptable CSCL scripts on the directly scaffolded socio-discursive MAS. Likewise, for adaptable heuristic worked examples, the highest outcomes were shown for directly scaffolded domain-specific MAS. The pattern shows that the adaptable scaffolds did at least not harm learning and give a hint that they may be more suitable to improve learning of more directly scaffolded learning outcomes. The maximal heuristic worked examples offered a fully worked out solution and heuristic processes for the domain-specific mathematical components of the given proof task (Reiss & Renkl, 2002). Here, learners are repeatedly engaged in scaffolded activities regarding domain-specific MAS. However, the maximum heuristic worked examples do not allow for practicing transfer of these skills to other, less scaffolded tasks (van Merriënboer et al., 2003). Similarly, the CSCL scripts engage students repeatedly in highly scaffolded socio-discursive argumentation activities (Noroozi et al., 2012; Vogel et al., 2017) but do not offer students opportunities to practice transfer of socio-discursive MAS to non-scaffolded tasks.
The role of self-regulation
When learning with the adaptable CSCL script, self-regulation skills formed a significant positive predictor for socio-discursive MAS. When learning with minimal scaffolding, self-regulation skills predicted positively the learning of domain-specific MAS. Thus, learners with higher levels of self-regulation skills tend to benefit more from learning with minimal CSCL scripts and minimal heuristic worked examples as well as adaptable CSCL scripts. The relevance of self-regulation skills for successful knowledge and skill acquisition in situations in which there is room for learners to regulate their learning (e.g., when learning with adaptable CSCL scripts) confirms research on self-, co-, and shared regulation (Järvela & Hadwin, 2013). Also, prior research points out the necessity of self-regulation skills to optimally benefit from adaptable learning environments (Gogoulou et al., 2008; Wang et al., 2017). More specific analyses about learners in the adaptable scaffolding conditions showed learners with higher scores in their self-regulation skills tended to decide more often in favor of the minimal CSCL scripts. In addition, learners who adapted their scaffolding more often to the minimal CSCL script showed higher learning outcomes regarding socio-discursive MAS. This relationship, very carefully interpreted, could give a hint how learners with better self-regulation may have benefitted from learning with the adaptable CSCL script. By deciding earlier and more often for the minimal CSCL script instead of the maximal version, they may have put themselves into more challenging learning situations, making better use of their (collaborative) cognitive load and enabling them to practice the transfer of the directly scaffolded skills (van Merriënboer et al., 2003). In contrast, learners with lower levels of self-regulation may have not been able to benefit from deciding more often to learn with the maximal CSCL script. Yet, this interpretation relies very much on exploratory analyses and would need a more detailed experiment with better power to detect the relationships between the relevant variables. In contrast, for learning domain-specific MAS, the actual adaptation was not significantly related to the outcome. Likewise, there was no significant correlation between the actual adaptation of the heuristic worked examples and either component of MAS. This may imply that uncovering effects of various approaches to adaptation would require more specific qualitative analyses of processes beyond the mere frequency of choices.
Interestingly, self-regulation skills as well as the actual regulation of the scaffold did not play a significant role when learning with adaptable heuristic worked examples. The mathematical proof task may have already posed a very high demand on learners’ self-regulation skills. Therefore, the availability of some degree of scaffolding in all heuristic worked examples conditions might have already been sufficient to reduce the relevance of self-regulation skills, even with only minimal scaffolding. It is possible that correctly self-assessing the progress in solving the mathematical proof task and deciding for the appropriate heuristic worked example may have been easier to achieve for students compared to adapting the CSCL script appropriately. The nature of heuristic worked examples that show the correct solution (Reiss & Renkl, 2002) that can be compared with individual learning progress may have facilitated the correct assessment. In contrast, a higher minimum threshold of self-regulation skills might be necessary for assessing the more complex and open-ended progress in socio-discursive argumentation given that the CSCL script does not provide a correct solution to be solved, but instead prompts induction of the relevant argumentation activities (Vogel et al., 2017). The higher self-regulation skills needed for learning domain-specific MAS when only supported with minimal scaffolding may not be connected to adaptation activities, but instead connected to other efforts (e.g., help-seeking, planning of learning, managing group work) needed to benefit in a less structured learning environment (Vrieling et al., 2018). This may also be reflected in learner’s pre-requisites being more relevant for learning domain-specific MAS when supported with CSCL scripts compared to being supported with heuristic worked examples.
Limitations and Conclusions
We carefully designed our experiments to produce insights into mechanisms that play a role when learning with adaptable scaffolding with a particular focus on self-regulation skills and regulation activities. Nevertheless, there are limitations to be discussed.
First, learners were enabled to adapt the scaffolds in a limited way by offering a decision between only two options: minimal and maximal scaffolding. Future studies may need to grant students the opportunity to choose between more fine-grained levels of scaffolding to see more differential effects of adaptation features on learning outcomes. Second, the statistical power might have been too low to detect substantial differences, given the number of different experimental conditions and learning outcomes. From this point of view, the interpretation of the results of this study may be too conservative, underestimating the true effects. Studies with higher statistical power and meta-analytical syntheses of effects from different adaptable and non-adaptable types of scaffolding would help to come to more valid conclusions. Using the studies at hand as starting point, a more substantial number of effect sizes from different studies would be needed for a useful synthesis. Third, we heavily relied on student’s self-assessment regarding the measure of self-regulation skills. The instrument showed borderline reliability and there is a risk of students overestimating or underestimating their own skills. Consequentially, interpretation of the results must be taken cautiously. Fourth, results from the minimally scaffolded condition have been used in both experiments as the same instructional design was needed and we aimed to make use of the available participants in the most efficient way. This may have led to an overrepresentation of this condition regarding RQ 1 and RQ 4. Although conditions have been randomized, a slight bias in terms of learners’ pre-requisites in the minimal scaffolding condition would lead to an unfair overestimation of the results from the minimally scaffolding condition we used in each experiment. Yet, the results in both experiments were rather related to different components of MAS and were not equally significant in both experiments. Therefore, we rather expect a marginal impact here, if any, more towards a more conservative interpretation. Nevertheless, we express interpretations of the results for these research questions carefully to balance any overestimation that could have happened and cannot be controlled for. Finally, even though we were able to randomly distribute learners across conditions, our study was embedded in a field setting. Students who participated in the experiments may differ from the average student population in important characteristics (e.g., their interest in math and conscientiousness regarding their preparation of studies). Along with this, our results were generated in the specific context of a preparatory course to undergraduate mathematics university studies. Generalization to other contexts besides undergraduate mathematics must be made very carefully and would need a greater range of studies in various contexts to be validated.
In general, our study provides evidence that adaptable scaffolding has only limited benefits when compared to non-adaptable scaffolding, particularly in the context of mathematics argumentation. It may be a too high burden on the learners to acquire self-regulation skills and apply them in such scenarios in a learning beneficial way. One approach to overcome these issues and still take advantage of adapting learning environments would be the development of CSCL technology that allows teachers to orchestrate learners and their activities (e.g., Schwarz et al., 2021). However, it should be noted that adaptable scaffolding does not seem to harm learning mathematical argumentation skills when compared to non-adaptable scaffolding. In particular, it may be worthwhile to consider adaptable scaffolding to facilitate the more direct learning outcomes, for instance scaffolding socio-discursive argumentation skills with adaptable CSCL scripts. The study shows that learners benefit most from adaptable CSCL scripts when learning socio-discursive skills under specific circumstances. First, learners may need sufficient self-regulation skills to adapt the CSCL script to their needs. Future studies should therefore explore how to support learners’ self-regulation skills to prepare them to benefit most from adaptable scaffolding. In particular, encouraging a decision for minimal scaffolding with CSCL scripts at an appropriate point in time may boost learning socio-discursive argumentation skills. Since learning regulation in collaborative contexts goes beyond individual self-regulation skills, in future studies, it would be relevant to focus on social practices when CSCL script adaptation and regulation takes place. Here, awareness of the learning group’s progress and each individual’s needs would be necessary for all learning partners to benefit most from learning with CSCL scripts. Thus, additional support for group awareness (Janssen & Bodemer, 2013) and social regulation (Miller & Hadwin, 2015) could be trialed to further improve adaptable scaffolding in CSCL learning environments.
Availability of data and material
Material that has been developed for this study will be made available upon request. Data will be made available after publication in open science repositories where applicable considering ethics and data protection policy.
Code availability
Not applicable.
References
Alcock, L., & Weber, K. (2005). Proof validation in real analysis: Inferring and checking warrants. The Journal of Mathematical Behavior, 24(2), 125–134. https://doi.org/10.1016/j.jmathb.2005.03.003
Andriessen, J., Baker, M., & Suthers, D. (2003). Argumentation, computer support, and the educational context of confronting cognitions. In J. Andriessen, M. Baker, & D. Suthers (Eds.), Arguing to learn: Confronting cognitions in Computer-Supported Collaborative Learning environments (pp. 1–25). Kluwer.
Atkinson, R. K., Derry, S. J., Renkl, A., & Wortham, D. (2000). Learning from examples: Instructional principles from the worked examples research. Review of Educational Research, 70(2), 181–214. https://doi.org/10.3102/00346543070002181
Boero, P. (1999). Argumentation and mathematical proof: A complex, productive, unavoidable relationship in mathematics and mathematics education. Preuve: International Newsletter on the Teaching and Learning of Mathematical Proof, July/August 1999. Friday, May 10. Retrieved March 1, 2022, from http://www.lettredelapreuve.org/OldPreuve/Newsletter/990708Theme/990708ThemeUK.html
Clark, M., & Lovric, M. (2009). Understanding secondary–tertiary transition in mathematics. International Journal of Mathematical Education in Science and Technology, 40(6), 755–776. https://doi.org/10.1080/00207390902912878
Dillenbourg, P. (2002). Over-scripting CSCL: The risks of blending collaborative learning with instructional design. In P. A. Kirschner (Ed.), Three worlds of CSCL. Can we support CSCL (pp. 61–91). Open University Nederland.
Diziol, D., Rummel, N., Spada, H., & McLaren, B. M. (2007). Promoting learning in mathematics: Script support for collaborative problem solving with the cognitive tutor algebra. Carnegie Mellon University. https://doi.org/10.1184/R1/6470348
Diziol, D., Walker, E., Rummel, N., & Koedinger, K. R. (2010). Using intelligent tutor technology to implement adaptive support for student collaboration. Educational Psychology Review, 22, 89–102. https://doi.org/10.1007/s10648-009-9116-9
Duffy, T. M., & Jonassen, D. H. (1991). Constructivism: New implications for instructional technology? Educational Technology, 31(5), 7–12.
Fischer, F., Kollar, I., Stegmann, K., & Wecker, C. (2013). Toward a script theory of guidance in computer-supported collaborative learning. Educational Psychologist, 48(1), 56–66. https://doi.org/10.1080/00461520.2012.748005
Fischer, F., Kollar, I., Ufer, S., Sodian, B., Hussmann, H., Pekrun, R., et al. (2014). Scientific reasoning and argumentation: advancing an interdisciplinary research agenda in education. Frontline Learn. Res., 2, 28–45. https://doi.org/10.14786/flr.v2i2.96
Fisher, M., King, J., & Tague, G. (2001). Development of a self-directed learning readiness scale for nursing education. Nurse Education Today, 21(7), 516–525. https://doi.org/10.1054/nedt.2001.0589
Gogoulou, A., Gouli, E., & Grigoriadou, M. (2008). Adapting and personalizing the communication in a synchronous communication tool. Journal of Computer Assisted Learning, 24(3), 203–216. https://doi.org/10.1111/j.1365-2729.2007.00254.x
Hilbert, T. S., Renkl, A., Kessler, S., & Reiss, K. (2008). Learning to prove in geometry: Learning from heuristic examples and how it can be supported. Learning and Instruction, 18(1), 54–65. https://doi.org/10.1016/j.learninstruc.2006.10.008
Hmelo-Silver, C. E., Duncan, R. G., & Chinn, C. A. (2007). Scaffolding and achievement in problem-based and inquiry learning: A response to Kirschner, Sweller, and Clark. Educational Psychologist, 42(2), 99–107. https://doi.org/10.1080/00461520701263368
Hummel, H. G. K., Paas, F., & Koper, R. (2006). Effects of cueing and collaboration on the acquisition of complex legal skills. British Journal of Educational Psychology, 76(3), 613–631. https://doi.org/10.1348/000709905X85629
Janssen, J., & Bodemer, D. (2013). Coordinated computer-supported collaborative learning: Awareness and awareness tools. Educational Psychologist, 48(1), 40–55. https://doi.org/10.1080/00461520.2012.749153
Janssen, J., & Kirschner, P. A. (2020). Applying collaborative cognitive load theory to computer-supported collaborative learning: Towards a research agenda. Educational Technology Research and Development, 68(2), 783–805. https://doi.org/10.1007/s11423-019-09729-5
Järvelä, S., & Hadwin, A. F. (2013). New Frontiers: Regulating learning in CSCL. Educational Psychologist, 48(1), 25–39. Scopus. https://doi.org/10.1080/00461520.2012.748006
Kalyuga, S., Ayres, P., Chandler, P., & Sweller, J. (2003). The expertise reversal effect. Educational Psychologist, 38(1), 23–31. https://doi.org/10.1207/S15326985EP3801_4
King, A. (2007). Scripting collaborative learning processes: A cognitive perspective. In F. Fischer, I. Kollar, H. Mandl, & J. M. Haake (Eds.), Scripting computer-supported collaborative learning—Cognitive, computational, and educational perspectives (pp. 13–37). Springer.
Kirschner, P. A., Sweller, J., & Clark, R. E. (2006). Why minimal guidance during instruction does not work: An analysis of the failure of constructivist, discovery, problem-based, experiential, and inquiry-based teaching. Educational Psychologist, 41(2), 75–86. https://doi.org/10.1207/s15326985ep4102_1
Kobbe, L., Weinberger, A., Dillenbourg, P., Harrer, A., Hämäläinen, R., Häkkinen, P., & Fischer, F. (2007). Specifying computer-supported collaboration scripts. International Journal of Computer-Supported Collaborative Learning, 2, 211–224. https://doi.org/10.1007/s11412-007-9014-4
Kollar, I., Fischer, F., & Hesse, F. W. (2006). Collaboration scripts—A conceptual analysis. Educational Psychology Review, 18(2), 159–185. https://doi.org/10.1007/s10648-006-9007-2
Kollar, I., Ufer, S., Reichersdorfer, E., Vogel, F., Fischer, F., & Reiss, K. (2014). Effects of collaboration scripts and heuristic worked examples on the acquisition of mathematical argumentation skills of teacher students with different levels of prior achievement. Learning and Instruction, 32, 22–36. https://doi.org/10.1016/j.learninstruc.2014.01.003
Kollar, I., Wecker, C., & Fischer, F. (2018). Scaffolding and scripting (computer-supported) collaborative learning. In F. Fischer, C. E. Hmelo-Silver, S. R. Goldman, & P. Reimann (Eds.), International handbook of the learning sciences (pp. 340–350). Routledge. https://doi.org/10.4324/9781315617572-33
Kosiol, T., Rach, S., & Ufer, S. (2019). (Which) Mathematics interest is important for a successful transition to a university study program? International Journal of Science and Mathematics Education, 17(7), 1359–1380. https://doi.org/10.1007/s10763-018-9925-8
Leitão, S. (2000). The potential of argument in knowledge building. Human Development, 43(6), 332–360. https://doi.org/10.1159/000022695
Leutner, D. (2002). Adaptivität und Adaptierbarkeit multimedialer Lehr-und Informationssysteme. In L. J. Issing & P. Klimsa (Eds.), Information und Lernen mit Multimedia und lnternet (3rd Edn, pp. 115–125). Beltz.
Lin, F. L., Yang, K. L., Lee, K. H., Tabach, M., & Stylianides G. (2012). Task designing for conjecturing and proving: Developing principles based on practical tasks. In M. de Villiers & G. Hanna (Eds.), Proof and Proving in Mathematics Education. The 19th ICMI Study (pp. 305–323). Springer.
Lockwood, E., Ellis, A. B., & Lynch, A. G. (2016). Mathematicians’ example-related activity when exploring and proving conjectures. International Journal of Research in Undergraduate Mathematics Education, 2(2), 165–196. https://doi.org/10.1007/s40753-016-0025-2
Melzner, N., Greisel, M., Dresel, M., & Kollar, I. (2020). Regulating self-organized collaborative learning: The importance of homogeneous problem perception, immediacy and intensity of strategy use. International Journal of Computer-Supported Collaborative Learning, 15(2), 149–177. https://doi.org/10.1007/s11412-020-09323-5
Miller, M., & Hadwin, A. (2015). Scripting and awareness tools for regulating collaborative learning: Changing the landscape of support in CSCL. Computers in Human Behavior, 52, 573–588. https://doi.org/10.1016/j.chb.2015.01.050
Mulder, Y. G., Lazonder, A. W., & de Jong, T. (2014). Using heuristic worked examples to promote inquiry-based learning. Learning and Instruction, 29, 56–64. https://doi.org/10.1016/j.learninstruc.2013.08.001
Nadolski, R. J., Kirschner, P. A., & Van Merriënboer, J. J. G. (2005). Optimizing the number of steps in learning tasks for complex skills. British Journal of Educational Psychology, 75(2), 223–237. https://doi.org/10.1348/000709904X22403
Nicolay, B., Krieger, F., Stadler, M., Gobert, J., & Greiff, S. (2021). Lost in transition – Learning analytics on the transfer from knowledge acquisition to knowledge application in complex problem solving. Computers in Human Behavior, 115, 106594. https://doi.org/10.1016/j.chb.2020.106594
Noroozi, O., Weinberger, A., Biemans, H. J. A., Mulder, M., & Chizari, M. (2012). Argumentation-based computer supported collaborative learning (ABCSCL). A systematic review and synthesis of fifteen years of research. Educational Research Review, 7(2), 79–106. https://doi.org/10.1016/j.edurev.2011.11.006
Noroozi, O., Weinberger, A., Biemans, H. J. A., Mulder, M., & Chizari, M. (2013). Facilitating argumentative knowledge construction through a transactive discussion script in CSCL. Computers & Education, 61, 59–76. https://doi.org/10.1016/j.compedu.2012.08.013
Noroozi, O., Kirschner, P. A., Biemans, H. J. A., & Mulder, M. (2018). Promoting argumentation competence: Extending from first- to second-order scaffolding through adaptive fading. Educational Psychology Review, 30(1), 153–176. https://doi.org/10.1007/s10648-017-9400-z
OECD. (2017). PISA 2015 assessment and analytical framework. Science, reading, mathematic, financial literacy and collaborative problem solving. Paris: OECD Publishing. https://doi.org/10.1787/9789264281820-en
Ottinger, S., Kollar, I., Ufer, S. (2016). Content and form - all the same or different qualities of mathematical arguments? In Csikos, C., Rausch, A., Szitanyi, J. (Eds.), Proceedings of the 40th Conference of the International Group for the psychology of mathematics education (vol. 4, pp. 19–26). PME.
Plass, J. L., & Pawar, S. (2020). Toward a taxonomy of adaptivity for learning. Journal of Research on Technology in Education, 52(3), 275–300. https://doi.org/10.1080/15391523.2020.1719943
Rau, M. A., Bowman, H. E., & Moore, J. W. (2017). An adaptive collaboration script for learning with multiple visual representations in chemistry. Computers and Education, 109, 38–55. Scopus. https://doi.org/10.1016/j.compedu.2017.02.006
Reiss, K., & Renkl, A. (2002). Learning to prove: The idea of heuristic examples. ZDM the International Journal on Mathematics Education, 34(1), 29–35. https://doi.org/10.1007/BF02655690
Renkl, A., Hilbert, T., & Schworm, S. (2009). Example-based learning in heuristic domains: A cognitive load theory account. Educational Psychology Review, 21(1), 67–78. https://doi.org/10.1007/s10648-008-9093-4
Rienties, B., Giesbers, B., Tempelaar, D., Lygo-Baker, S., Segers, M., & Gijselaers, W. (2012). The role of scaffolding and motivation in CSCL. Computers & Education, 59(3), 893–906. https://doi.org/10.1016/j.compedu.2012.04.010
Rummel, N., Walker, E., & Aleven, V. (2016). Different futures of adaptive collaborative learning support. International Journal of Artificial Intelligence in Education, 26(2), 784–795. https://doi.org/10.1007/s40593-016-0102-3
Schank, R. C. (1999). Dynamic memory revisited. Cambridge University Press.
Schwarz, B. B., Hershkowitz, R., & Prusak, N. (2010). Argumentation and mathematics. In K. Littleton & C. Howe (Eds.), Educational dialogues: Understanding and promoting productive interaction (pp. 103–127). Routledge.
Schwarz, B. B., Swidan, O., Prusak, N., & Palatnik, A. (2021). Collaborative learning in mathematics classrooms: Can teachers understand progress of concurrent collaborating groups? Computers & Education, 165, 104151. https://doi.org/10.1016/j.compedu.2021.104151
Schworm, S., & Renkl, A. (2007). Learning argumentation skills through the use of prompts for self-explaining examples. Journal of Educational Psychology, 99(2), 285–296. https://doi.org/10.1037/0022-0663.99.2.285
Sommerhoff, D., & Ufer, S. (2019). Acceptance criteria for validating mathematical proofs used by school students, university students, and mathematicians in the context of teaching. ZDM Mathematics Education, 51(5), 717–730. https://doi.org/10.1007/s11858-019-01039-7
Stegmann, K., Weinberger, A., & Fischer, F. (2007). Facilitating argumentative knowledge construction with computer-supported collaboration scripts. International Journal of Computer-Supported Collaborative Learning, 2(4), 421–447. https://doi.org/10.1007/s11412-007-9028-y
Stylianides, G. J., & Stylianides, A. J. (2008). Proof in school mathematics: Insights from psychological research into students’ ability for deductive reasoning. Mathematical Thinking and Learning, 10(2), 103–133. https://doi.org/10.1080/10986060701854425
Tchounikine, P. (2016). Contribution to a theory of CSCL scripts: Taking into account the appropriation of scripts by learners. International Journal of Computer-Supported Collaborative Learning, 11(3), 349–369. https://doi.org/10.1007/s11412-016-9240-8
Thomas, M. O. J., & Klymchuk, S. (2012). The school–tertiary interface in mathematics: Teaching style and assessment practice. Mathematics Education Research Journal, 24(3), 283–300. https://doi.org/10.1007/s13394-012-0051-6
Toulmin, S. (1958). The uses of argument. Cambridge University Press.
van Aalst, J., & Chan, C. K. K. (2007). Student-directed assessment of knowledge building using electronic portfolios. Journal of the Learning Sciences, 16(2), 175–220. https://doi.org/10.1080/10508400701193697
van Merriënboer, J. J. G., Kirschner, P. A., & Kester, L. (2003). Taking the load off a learner’s mind: Instructional design for complex learning. Educational Psychologist, 38(1), 5–13. https://doi.org/10.1207/S15326985EP3801_2
Vogel, F., Kollar, I., Ufer, S., Reichersdorfer, E., Reiss, K., & Fischer, F. (2016). Developing argumentation skills in mathematics through computer-supported collaborative learning: The role of transactivity. Instructional Science, 44(5), 477–500. https://doi.org/10.1007/s11251-016-9380-2
Vogel, F., Wecker, C., Kollar, I., & Fischer, F. (2017). Socio-cognitive scaffolding with collaboration scripts: A meta-analysis. Educational Psychology Review, 29(3), 477–511. https://doi.org/10.1007/s10648-016-9361-7
Vrieling, E., Stijnen, S., & Bastiaens, T. (2018). Successful learning: Balancing self-regulation with instructional planning. Teaching in Higher Education, 23(6), 685–700. https://doi.org/10.1080/13562517.2017.1414784
Walker, E., Rummel, N., & Koedinger, K. R. (2011). Designing automated adaptive support to improve student helping behaviors in a peer tutoring activity. International Journal of Computer-Supported Collaborative Learning, 6(2), 279–306. https://doi.org/10.1007/s11412-011-9111-2
Wang, X., Kollar, I., & Stegmann, K. (2017). Adaptable scripting to foster regulation processes and skills in computer-supported collaborative learning. International Journal of Computer-Supported Collaborative Learning, 12(2), 153–172. https://doi.org/10.1007/s11412-017-9254-x
Wecker, C., & Fischer, F. (2014). Where is the evidence? A meta-analysis on the role of argumentation for the acquisition of domain-specific knowledge in computer-supported collaborative learning. Computers & Education, 75, 218–228. https://doi.org/10.1016/j.compedu.2014.02.016
Winne, P. H. (2011). A cognitive and metacognitive analysis of self-regulated learning. In D. H. Schunk & B. Zimmerman (Eds.), Handbook of self-regulation of learning and performance (pp. 15–32). Routledge. https://doi.org/10.4324/9780203839010.ch2
Wood, D. J., Bruner, J. S., & Ross, G. (1976). The role of tutoring in problem-solving. Journal of Child Psychology and Psychiatry, 17, 89–100. https://doi.org/10.1111/j.1469-7610.1976.tb00381.x
Yackel, E., & Cobb, P. (1996). Sociomathematical norms, argumentation, and autonomy in mathematics. Journal for research in mathematics education, 27(4), 458–477. https://doi.org/10.5951/jresematheduc.27.4.0458
Zandieh, M., & Rasmussen, C. (2010). Defining as a mathematical activity: A framework for characterizing progress from informal to more formal ways of reasoning. The Journal of Mathematical Behavior, 29(2), 57–75. https://doi.org/10.1016/j.jmathb.2010.01.001
Funding
Open Access funding enabled and organized by Projekt DEAL. This study has been funded by the Deutsche Forschungsgemeinschaft (DFG) under grants RE 1247/9–1 and FI 792/7–1.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflicts of Interest
The authors declare no conflict of interest in relation to this study.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Vogel, F., Kollar, I., Fischer, F. et al. Adaptable scaffolding of mathematical argumentation skills: The role of self-regulation when scaffolded with CSCL scripts and heuristic worked examples. Intern. J. Comput.-Support. Collab. Learn 17, 39–64 (2022). https://doi.org/10.1007/s11412-022-09363-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11412-022-09363-z