Introduction

In the area of judgment and decision making, researchers have long been interested in metacognitive appraisals of choices, such as the participants’ level of confidence in their decision. Subjective confidence in a decision can serve different functions, such as predicting the correctness of a decision when no external feedback is available, guiding subsequent decisions and behavior (Desender et al., 2019a, 2019b; van den Berg et al., 2016) and offering a “common currency” for integrating individual opinions when decisions are made in a group (Bang et al., 2017).

Subjective confidence has also been shown to have a serious impact in practical areas where decision-making is central, such as in judging witness testimony (Brewer & Burke, 2002) or deciding on medical diagnoses (Friedman et al., 2001; Uy et al., 2014).

Researchers have used different methods to measure confidence. Explicit reports of confidence consist simply of asking decision-makers to indicate their subjective confidence in their decisions, for example on a continuous scale (Zylberberg et al., 2012), or by a binary (Rahnev et al., 2012) or a discretized response (Spence et al., 2018). This method has been used extensively in experimental studies on human metacognition (e.g. Charles et al., 2020; Koriat et al., 2020; Li & Ma, 2020).

In post-decision wagering, deciders do not explicitly indicate their decisional confidence. Instead, after a decision has been made, they are given the opportunity to place a bet on whether their decision was correct. If the bet is high, this is taken as an indication that the decider is confident in the decision. If the bet is low, the decider is thought not to be confident. Bets can be, for example, binary (high vs. low; Moreira et al., 2018) or discretized amounts (e.g. 1 to 5; Versteeg & Steendijk, 2019). Post-decision wagering has been used as an implicit measure of confidence in humans (Carpenter et al., 2019; Moreira et al., 2018; Versteeg & Steendijk, 2019) as well as animals (Middlebrooks & Sommer, 2012; Miyamoto et al., 2017; Miyamoto et al., 2018).

Info-seeking comes in very different forms, but a common feature is that the decider has the option to either make a decision immediately, or to gather some kind of additional information before deciding, such as seeing more of the relevant stimulus (Desender et al., 2018, 2019a, 2019b), receiving a clue about the correct response (Geurten & Bastin, 2019) or asking somebody for help (Goupil et al., 2016). When the decider seeks further information, this is thought to be an indication of low confidence, while not seeking additional information is considered an indication of high confidence. Info-seeking, in the form of requesting clues, has been used successfully to measure metacognitive ability in children as young as 2.5 years (Geurten & Bastin, 2019), who were not able to report their subjective confidence explicitly.

A method often used in decision tasks to investigate which aspects of the stimulus influence choice and confidence judgments is that of reverse correlation. In a typical reverse correlation design, the participant sees some kind of perceptual stimulus, such as randomly moving dots (Okazawa et al., 2018) or two light patches with different brightness (Zylberberg et al., 2012). The participant has to make a binary choice categorizing the stimulus into one of two options (e.g. more random dots moving to the left than to the right, or the left light patch being brighter than the right). Crucially, the stimulus contains random fluctuations within a trial: the amount of left- and right moving dots is not fixed over the course of a trial, and neither is the brightness of the two light patches. Rather, the amount of stimulus information provided for the decision randomly fluctuates throughout the trial around a level necessary to achieve a pre-defined accuracy. In the random dot example, at every point throughout a trial, there is a random number of dots moving left and dots moving right, and the participant has to judge which direction is dominant.

During reverse correlation, the fluctuating stimuli preceding each response are averaged over trials, separately for each stimulus dimension (e.g. the number of dots moving left, and the number of dots moving right, are averaged over trials judged as “left dominant”; and again for trials judged as “right dominant”). This averaging yields the stimulus time course that characteristically evokes each response. The results typically show that the response-compatible stimulus dimension (e.g. left moving dots in a respond-left trial) will be increased above average before a response, while the response-incompatible dimension will be decreased (e.g. Neri & Levi, 2008). Similarly, by performing reverse correlation separately for low and high confidence trials, researchers can determine how stimulus fluctuations are related to these metacognitive judgments (Zylberberg et al., 2012). Besides humans, reverse correlation methods have also been used to analyze neural data in animals (deCharms et al., 1998).

Reverse correlation has been used to investigate how explicit reports of confidence are formed (Zylberberg et al., 2012). However, it is not currently known how the different methods used to assess confidence affect reverse correlation results. The present study aims to fill this gap, as these results are of interest to current discussions on metacognition theory. An important question is whether the different forms of metacognitive monitoring reported in the literature (judgments-of-learning, ease-of-learning, confidence judgments, etc.) reflect a singular underlying process, or whether each of these judgments is realized by specialized cognitive processes (Dunlosky & Tauber, 2014). A comparison of the different forms of confidence judgments, as discussed here, can offer further evidence to this discussion of the unity and diversity of metacognitive monitoring processes.

The aim of this study was to compare explicit reports of confidence, post-decision wagering and info-seeking with respect to their reverse correlation profiles. If all three methods assess the same underlying construct of decision confidence, they should yield similar results. In a blocked, within-participant design using the same primary numerical comparison task, the participants’ decision confidence was assessed via explicit reports, post-decision wagering and info-seeking. For each method, the stimulus fluctuations for the chosen- and not chosen stimulus dimension were averaged, separately for low- and high confidence trials. The results show that decision and confidence formation was very similar when using explicit reports and post-decision wagering, while the info-seeking method of assessing confidence yielded an inverted association of stimuli with choices for low-confidence trials. Using modelling of the behavioral data, we show how a single confidence process can explain the results of all three methods of confidence assessment if the seeking of additional stimulus information is considered to allow correction of otherwise erroneous responses to the first stimulus.

Methods

Participants

Twenty-seven participants performed the task and were included in the final analysis (mean age = 25.9 years, sd = 8.5; 2 left-handed, 15 females).Footnote 1 One additional participant was recruited but aborted the task due to feeling unwell; another participant completed the study but showed chance performance in the decision task. Participants were paid 25 € plus their accumulated winnings from the wagering condition (mean = 4.38 €, sd = 0.88 €). The local Ethics Committee of the RWTH Aachen University Hospital approved the study.

Procedure

All participants received verbal and written descriptions of the purpose and procedure of the study, and each participant’s informed consent was obtained. Participants performed the task on a laptop computer using an external mouse and keyboard. The task was divided into three conditions, which will be referred to as the explicit condition (explicitly reporting confidence), the wagering condition (measuring confidence via post-decision wagering), and the info-seeking condition (using information-seeking as a measure of confidence). The order of conditions was counterbalanced across participants. To help participants differentiate among the conditions, the colors associated with the response options were varied across conditions. The pairing of colors with conditions was counterbalanced across participants.

Participants first read a detailed explanation of all three conditions. Before each condition, they were also instructed verbally, and any remaining questions they had were answered. They could additionally consult a written explanation before each condition started.

Participants completed 505 trials per condition, which took them around 40 min. We chose a trial number that is comparable to other studies with a similar design (e.g. Okazawa et al., 2018; Zylberberg et al., 2012). Every 60 trials there was a break, which the participant could terminate by pressing the space bar. The entire experiment took an average of around 2.5 h.

Task

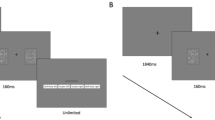
The primary decision task was a numerical comparison task (see Fig. 1). On each trial, the participant saw two groups of small squares around the screen’s center. The two groups of squares had different colors to make them distinguishable. Over the course of 1 s, the number of squares for both colors changed semi-randomly. Furthermore, to prevent simple counting of squares, their positions also changed randomly. All squares were 10 by 10 pixels in size. The squares’ positions were rasterized to a grid of 28 by 28 points around center.

Fig. 1
figure 1

Three conditions of the decision task. On each test trial, participants decided which color on average included more squares. In the explicit and wagering conditions, a response was followed by the metacognitive judgment. In the info-seeking condition, participants first decided whether they needed to see more of the stimulus, and this was followed by their response

Full size image

The participant’s task was to watch the two groups of squares and indicate by pressing the mouse which group had included more squares over the course of the entire stimulus span. Task difficulty was manipulated by changing the difference in the number of squares between the two colors. The pairing of the color with the mouse button was displayed above the stimulus. The participants had unlimited time to make their decision, but they were asked to respond quickly and accurately. On half of the trials, one color was the correct response, and on the other half, the other color was correct.

The task included two types of trials: estimation trials and test trials. Estimation trials were used to estimate the participant’s psychometric function, which was used to determine the appropriate stimulus difficulties (see the section on “stimulus generation”). Test trials measured the participants’ metacognitive judgments. The test trials differed among the three conditions. In the explicit condition, after participants had indicated their choice, a prompt appeared, asking the participants to indicate how confident they felt about their previous choice. The participant could press the keyboard’s arrow-up key to indicate high confidence, or the arrow-down key to indicate low confidence.

In the wagering condition, after the participant’s choice, a prompt appeared, asking how much the participant wanted to bet that the previous choice was correct, with the arrow-up and arrow-down keys corresponding to betting a lot or a little, respectively. If the previous choice was correct, the participant won 2.8 cents by betting high, or 1 cent by betting low. If the previous choice was incorrect, the participant lost 4 cents by betting high, or won 0.2 cent by betting low.Footnote 2 Our payoff matrix was designed to have several properties: 1) in order to assess confidence, wagering high must be advantageous when correct, while wagering low must be advantageous when incorrect; 2) even without feedback, participants can intuit their above-chance performance; therefore, wagering high when incorrect should be punished more than wagering high when correct is rewarded, otherwise participants can simply always wager high and still receive a net reward (compare Moreira et al., 2018); 3) the two degenerate strategies of always wagering high and always wagering low yield the same net reward, so neither of the two is encouraged more than the other. The participant was instructed about the potential gains beforehand, and was informed they would be paid the accumulated winnings at the end of the experiment.

In the info-seeking condition, before indicating the choice, a prompt appeared asking whether the participant needed to see more information. If the arrow-down key was pressed (“yes”), an additional 1000 ms of stimulus material was generated, in the same fashion and favoring the same response as the first stimulus, but at an easier difficulty setting. After the second stimulus, the participant indicated his/her response. Thus, this was a continuation of the previous stimulus, but easier to identify, and not a new trial. If the arrow-up key was pressed (“no”), no additional stimulus was shown, and the participant indicated their original response immediately, without seeing more of the stimulus.Footnote 3

Stimulus generation

Every condition included two types of trials: estimation and test trials. During the estimation trials, the participant’s performance was estimated using the PSI method (Kontsevich & Tyler, 1999; Prins, 2013), an adaptive stimulus placement method that efficiently estimates the psychometric function underlying a participant’s performance. The PSI method aims to estimate the different parameters of the psychometric function in as few trials as possible. We used the PSI method because it estimates the entire psychometric function, instead of just the midpoint, and this estimate was used to predict stimulus difficulty for the info-seeking condition (see below). The estimation trials never included a metacognitive judgment. Performance was estimated as the probability of giving a correct response as a function of the difference in the number of squares between the two colors, according to

$$\mathrm{p}\left(correct\right)= 0.5 +\frac{0.5 -\uplambda }{1+{e}^{-\upbeta (\mathrm{n}-\upmu )}}$$

where λ is the lapse rate, β is the slope, µ is the function’s midpoint and n is the difference in the number of squares between the two colors. A difference of n between the two colors meant that one color included \(25- \frac{n}{2}\) squares, whereas the other included \(25 + \frac{n}{2}\) squares.

Each condition started with 25 estimation trials, after which estimation and test trials were mixed in a proportion of 1 to 4, respectively, with two consecutive estimation trials at most 12 trials apart. This ensured a continuous PSI estimation throughout the task. On test trials, metacognitive judgments of confidence were measured. The current estimate of the participant’s psychometric function provided by the PSI method was used to predict the difference in number of squares for which performance was 0.7. This was the stimulus difficulty during presentation of the primary decision stimulus. Additionally, in the info-seeking condition, the square difference was determined for which performance was 0.9. This was the difficulty of the stimulus if the participant chose to see more. Thus, the additional information on info-seeking trials was more informative, but it still was not perfect.

The one-second stimulus interval consisted of 10 frames of the stimulus, each of which was presented for 100 ms. The exact position and number of the colored squares was varied semi-randomly among the frames. For the positions of the squares, two points around the center of the screen were used as the center points of two two-dimensional Gaussian distributions in screen space, one for each stimulus color. On each stimulus frame, the positions of the squares were sampled from these distributions. For each frame, the number of squares for each color was sampled from a Gaussian distribution, with the mean set by the difficulty of the current trial derived from the PSI method, as described above. The standard deviation was set to 5, i.e. 10% of the total number of squares that were visible. This procedure ensured random, time-varying variation around the stimulus value currently set by the PSI method.

Analysis and results

Task performance

Primary task performance for the three conditions was computed based on the test-trials, and compared using paired t-tests. Mean primary task performance was 0.71 (95% CI = 0.69 – 0.73) for the explicit reports condition, 0.74 (95% CI = 0.72 – 0.76) for the wagering condition, and 0.84 (95% CI = 0.8 – 0.88) for the info-seeking condition. The difference between performance in the explicit reports- and info-seeking condition was significant (t(26) = 6.89, p < 0.001), as was the comparison between the wagering- and info-seeking condition (t(26) = 4.93, p < 0.001). This was expected, because by offering an easier second stimulus in low-confidence info-seeking trials, the task effectively becomes easier. The comparison between the explicit reports- and wagering condition was marginally significant (t(26) = 2.04, p = 0.052). We think the improved performance in the wagering condition results from the participants putting in more effort to obtain a larger reward. Importantly, the performances for the explicit reports- and wagering conditions are still very similar, and thus comparable.

Reverse correlation

We further performed reverse correlation analysis for each of the three methods. First, in each of the test trials, the stimulus signal was computed as the number of squares of the color chosen by the participant, and separately of the color not chosen by the participant. The result is two time-varying signals that reflect the stimulus information presented to the participant in each trial. From each of these two stimulus signals we subtracted the expected stimulus signal for that trial, which was governed by the trial’s difficulty level. Thus, we subtracted out the expected mean stimulus signal, only leaving the random fluctuations around this pre-defined mean. These time-varying stimulus signals were averaged separately for high- and low-confidence trials for each of the three methods of confidence measurement. These averaged stimulus signals are referred to as decision weights, and are the main dependent variable in our analyses. We use these time-resolved weights for illustration, and averaged the decision weights over the ten time points for statistical analysis. Averaged weights were subjected to a 3 (condition) × 2 (selected vs non-selected) × 2 (high vs low confidence) repeated-measures ANOVA.

When time-averaged decision weights were analyzed in this way, there were significant main effects for selection (F(1, 26) = 112.88, p < 0.001, ɳG2 = 0.6) and confidence level (F(1, 26) = 9.99, p = 0.004, ɳG2 = 0.02). As can be seen in Fig. 2, the influence of stimulus information on the decision was generally positive for the stimulus dimension (dark colors) that was ultimately chosen and negative for the non-chosen dimension (light colors). Furthermore, on low-confidence trials, the influence of the stimulus on choice was weaker (broken lines) than on high-confidence trials (solid lines).

Fig. 2
figure 2

Decision weights for the three methods of confidence assessment resulting from the reverse correlation analysis. Stimulus information belonging to the option chosen by the participant is plotted in dark grey, non-chosen information in light grey. High-confidence trials are plotted as solid lines, low-confidence trials as broken lines. The x-axis represents the temporal dimension of the changing stimulus. Shaded areas indicate the SE

Full size image

In terms of interactions, the most interesting effect is the significant three way interaction between condition, selection and confidence level (F(2, 52) = 24.79, p < 0.001, ɳG2 = 0.08). This effect occurred because the decision weights were reversed for low-confidence, info-seeking trials, such that, for example, a “yellow” response on such a trial (after the additional stimulus information had been seen) was accompanied by a stronger “blue” signal during the first stimulus presentation. Post-hoc t-tests showed that for low-confidence, info-seeking trials, the non-selected stimulus option was indeed positively associated with choice (M = 0.07, t(26) = 2.89, p = 0.008, Cohen’s d = 0.56) and the selected option was negatively associated (M = -0.16, t(26) = -4.53, p < 0.001, Cohen’s d = -0.87).

It is possible that the within-participant design of our study led to the participants performing the metacognitive judgments in a more homogenous manner between the three assessment methods than would otherwise be expected. To confirm the results from our repeated-measure ANOVA, we ran another ANOVA that only included each participant’s first condition, reducing the dataset to a third of its original size. In this mixed ANOVA, condition was a between-participant factor, while selection and confidence were within-participant factors. The mixed ANOVA confirmed the pattern of results obtained in the initial analysis. The three way interaction between condition, selection and confidence was again significant (F(2, 24) = 5.28, p = 0.013, ɳG2 = 0.1). As before, the decision weights for the low-confidence trials in the info-seeking condition were reversed, with positive weights for the non-selected stimulus option (M = 0.11, t(7) = 3.03, p = 0.02, Cohen’s d = 1.07) and negative weights for the selected stimulus option (M = -0.12, t(7) = -1.85, p = 0.11, Cohen’s d = -0.65), although only the former reached statistical significance.

Model description

In the reverse correlation analysis, we found inverted decision weights for the low-confidence info-seeking trials, compared to the explicit and wagering conditions. At first glance it appears that participants responded the opposite of what the first stimulus in these trials would suggest. To determine whether a common confidence mechanism could nevertheless explain the diverging decision weights of all three methods parsimoniously, we fitted a simple decision-and-confidence model to the participants’ weights.

The primary decision is modelled after signal detection theory. Per trial:

$$\begin{array}{c}{yellow}_{external}\sim {\mathbb{N}}\left(\mu , {sd}_{external}\right)*condition\\ {blue}_{external}\sim {\mathbb{N}}\left(-\mu , {sd}_{external}\right)*condition\\ \mu =\frac{1}{2}{\Phi }^{-1}\left(0.7 | 0,\sqrt{2{{sd}_{external}}^{2}+2{{sd}_{internal}}^{2}}\right)\end{array}$$

Yellowexternal and blueexternal indicate the signal that was visually presented to the participant. It includes some random fluctuation (sdexternal) that later allows reverse correlation weights to be calculated. Condition is an indicator variable, which is coded as 1 for trials on which the yellow signal is stronger, and -1 for trials on which the blue signal is stronger. The value of µ was chosen to achieve an accuracy of 0.7 in the ultimate decision.

$$\begin{array}{c}{yellow}_{interna{l}_{1}}\sim {\mathbb{N}}\left({yellow}_{external}, {sd}_{internal}\right)\\ {blue}_{interna{l}_{1}}\sim {\mathbb{N}}\left({blue}_{external}, {sd}_{internal}\right)\\ evidenc{e}_{1}= {yellow}_{interna{l}_{1}}-{blue}_{interna{l}_{1}}\\ {r}_{first}={1} if evidenc{e}_{1}>0, \text{-1 }otherwise\\ confidence= \frac{\frac{1}{2}\varphi \left(evidenc{e}_{1} | 2\mu *{r}_{first}, \sqrt{2{{sd}_{external}}^{2}+{2{sd}_{internal}}^{2}}\right)}{\left(\begin{array}{c}\frac{1}{2}\varphi \left(evidenc{e}_{1} | 2\mu , \sqrt{2{{sd}_{external}}^{2}+{{2sd}_{internal}}^{2}}\right)+\\ \frac{1}{2}\varphi \left(evidenc{e}_{1} |-2\mu , \sqrt{2{{sd}_{external}}^{2}+{{2sd}_{internal}}^{2}}\right)\end{array}\right)}\end{array}$$

Yellowinternal1 and blueinternal1 indicate the participant’s internal estimate of the two signals. The first decision is based on the difference between these two estimates. The internal signals are subscripted as 1 because they represent the first stimulus. Confidence is low when confidence < cutoff. Cutoff is the model’s first free parameter. On low-confidence trials, a second set of internal signals is generated that is similar to the first, but with a new mean value:

$$\mu =\frac{1}{2}{\Phi }^{-1}\left(0.9 | 0,\sqrt{2{{sd}_{external}}^{2}+2{{sd}_{internal}}^{2}}\right)$$

The second response is generated as:

$${r}_{second}={1} if {yellow}_{interna{l}_{2}}>{blue}_{interna{l}_{2}}, \text{-1 }otherwise$$

For each run of the model, 100,000 trials were simulated for a specific cutoff value. The value of sdexternal was set to 1, and sdinternal to 0.3. To compute decision weights, from each trial’s external signals (yellowexternal and blueexternal) their corresponding means were subtracted, leaving only the random variation around this mean. Decision weights for the explicit- and wagering conditions were computed by averaging these signals over all trials for the selected- and non-selected color. This was based on the first response (rfirst), separately for low-confidence and high-confidence trials. For the info-seeking condition, the selected- and non-selected color was based on the second response (rsecond) for low-confidence trials, and the first response on high-confidence trials. Thus, this model assumes that the decision- and confidence mechanisms during explicit reports, wagering and info-seeking were identical. The only difference was that during low-confidence, info-seeking trials, a second stimulus with more information was offered in addition, and the ultimate response was based on this second stimulus.

Because the absolute size of the decision weights scales with sdexternal, and is therefore arbitrary, a second free parameter scale was also included. All of the output weights according to the model were first divided by this scale parameter. To quantify the difference between a simulated set of decision weights and a participant’s actual weights, the summed squared difference across all weights was used.

To fit the model to each participant, a grid search was performed in order to find a first parameter estimate for cutoff and scale. Grid values for cutoff ranged from 0.51 to 0.99 in steps of 0.04; values for scale ranged from 0.5 to 2 in steps of 0.2. From this initial estimate, the Nelder-Mead algorithm was used to find the best-fitting parameters.

To determine whether internal changes-of-mind from correct- to incorrect choices, or from incorrect- to correct choices (error-corrections) selectively contributed to the pattern of decision weights, two further models were derived from the full model above. In the “no error-corrections” model, all responses that constituted a change-of-mind from incorrect- to correct choice (i.e. the response to the first simulated stimulus was incorrect, while the response to the second stimulus was correct) were removed before computing the decision weights. In the “only error-corrections” model, all changes-of-mind from correct- to incorrect choices were removed analogously. The remainder of the two models, as well as the fitting procedure, were kept identical to the description above.

Modelling results

Figure 3 compares the time-averaged weights that were empirically observed with those derived from the fitted models. As the figure shows, the full model can accommodate the general pattern in the decision weights, without allowing any parameter to vary between the different methods of metacognitive judgment. We derived from each participant’s model fit the predicted proportion of high-confidence trials and compared it to the participant’s empirically observed proportion of high-confidence trials, averaged across the three conditions. Note that this empirical measure was not fitted by the model, which was optimized only on decision weights. The model’s prediction was correlated significantly with the empirically observed value (r(25) = 0.63, p < 0.001), further corroborating the model.

Fig. 3
figure 3

Comparison of averaged decision weights between the participants’ behavioral data (above) and model fits (below). Weights belonging to the option chosen by the decider are plotted in dark grey, non-chosen information in light grey. High-confidence trials are plotted as filled bars, low-confidence trials as shaded bars

Full size image

As can be seen in Fig. 3, when error-corrections are selectively removed from the model before computing the decision weights (“no error-corrections”) and only changes from correct- to incorrect responses are allowed, the model cannot explain the pattern of low-confidence decision weights observed. However, when only error-corrections are allowed, while changes from correct- to incorrect responses are removed (“only error-corrections”), the model is able to reproduce the pattern of results observed in the behavioral data.

Discussion

In this study, we compared and contrasted three different methods of measuring confidence – explicit reports, post-decision wagering, and info-seeking – in a within-participant design using the same basic decision task. Here we discuss the similarities and differences between the results obtained with the three methods.

A basic similarity between all three methods is the fact that response-compatible stimulus information on the whole contributed positively to choices, whereas response-incompatible information contributed negatively. This pattern has been found repeatedly in previous studies (e.g. Neri & Levi, 2008). A further commonality between all three methods is that the decision weights for low-confidence trials are overall smaller than the weights for high-confidence trials. This pattern indicates that low-confidence trials are those in which the stimulus is relatively less indicative of the chosen option than on high-confidence trials. This is to be expected if one assumes subjective confidence to scale with stimulus strength, and has been shown previously (Peirce & Jastrow, 1885).

The clearest difference in terms of the pattern of decision weights was evident between info-seeking on the one hand and explicit reports and wagering, on the other hand. On low-confidence trials – during which participants gathered more stimulus information in the info-seeking condition – decision weights were inverted compared to the explicit and wagering conditions. Thus, increased stimulus information during the first stimulus viewing was associated with the opposite, incompatible response on these low-confidence, info-seeking trials. Nevertheless, a simple model of decision and confidence, which contained only a single confidence mechanism and no parameters that distinguished the three conditions, was able to accurately fit the direction of decision weights in all three methods.

To understand how the inverted decision weights come about, the notion of a change-of-mind is important, whereby an initial binary decision is inverted. Reverse-correlation typically reveals a correlation between decision stimuli and responses, in which response-compatible stimuli are stronger and response-incompatible stimuli are reduced before a decision, as is the case in our explicit report- and wagering conditions. If in a set of trials there are a lot of changes-of-mind, meaning the decider chose to invert his/her responses after the fact, the correlation between stimuli and responses will also be inverted, because one “side” of the correlation was in effect flipped around. Now, response-compatible stimuli will be reduced and response-incompatible stimuli will be stronger before the final decision.

What happens during info-seeking is essentially an internal change-of-mind after viewing the first decision stimulus and choosing the see more before deciding. We call this change-of-mind internal because, after viewing the first stimulus and deciding to view more, there is no actual “first” response yet. Only after the second stimulus does the participant decide. However, because of the manipulated difficulty of the first stimulus, we know there would have been errors had the participant responded after viewing only the first stimulus. The second stimulus goes in the same direction as the first, but is considerably easier to judge, so by choosing to view the second stimulus, the participant can avoid many of the erroneous first responses. In effect, the participant has achieved an internal error-correction. Because of the variable nature of the stimuli, there are also instances in which the participant would have decided correctly after the first stimulus, but chooses to see more and now responds incorrectly (internal changes-of-mind from correct to incorrect). These are not as prevalent, because the second stimulus is titrated to around 0.9 accuracy.

The reason the inverted decision weights appear specifically for low confidence trials is because there is a well-known correlation between confidence and accuracy. Thus, by judging whether they are low in confidence, the participants essentially select many of the trials in which their responses would have been incorrect had they responded after the first stimulus. Many of these “internal” errors are then corrected after viewing the second stimulus, leading to the inverted decision weights. The fact that it is these internal error-corrections, and not internal changes-of-mind from correct to incorrect responses, that lead to this effect is illustrated by the fact that a model with only these latter changes-of-mind cannot fit our behavioral results (see Fig. 3). Furthermore, an interesting mechanism in this process is that a more conservative criterion in judging confidence and choosing the see the second stimulus leads to a larger proportion of internal errors among the low confidence trials, and thus more strongly inverted decision weights.Footnote 4

An open question is whether the inverted decision weights we found are strongly dependent on the second stimulus being more informative than the first. In our case, the first stimulus allowed an accuracy of 0.7, while the second stimulus was predicted to allow an accuracy of 0.9. We chose these values because they fit our intuitive idea that seeking of additional information has to be informative beyond the initial stimulus, but still require “effort” to get the response right. Generally, we would expect inverted weights as long as there is a substantial amount of “internal” error corrections. Whether this would still occur if the second stimulus was also titrated to 0.7, as was the first stimulus, depends on whether info-seeking allows what is known as “summation” of stimuli (Kingdom & Prins, 2016), i.e. integration of the decision information of the two stimuli. What is certain is that our interpretation of the inverted weights in terms of error corrections makes the prediction that the degree of inversion should scale with how much information the second stimulus adds beyond the first.

Relating our results to an influential framework of metacognition, info-seeking includes both metacognitive monitoring for the internal signal of confidence, and metacognitive control in the form of choosing to gather more information (Nelson, 1996; Nelson & Narens, 1990), whereas explicit reports and wagering only include the monitoring component. This decomposition into monitoring and control exemplifies how info-seeking lies at the conceptual intersection of metacognition- and cognitive control research. Our results illustrate that info-seeking is related to cognitive phenomena such as error detection and -correction. We think the info-seeking methodology offers an interesting experimental instrument to study the interplay of decision making, metacognition and cognitive control.

Our results are relevant to the question of whether different forms of metacognitive monitoring reflect one underlying process. According to the isomechanism view (Dunlosky & Tauber, 2014), different forms of metacognitive monitoring (e.g. judgments-of-learning, ease-of-learning; or, in our case, different ways of expressing confidence) capture the same inferential process, which uses different cues to infer the success of primary cognitive processing (see Koriat, 1997, for a description of cue-utilization models). The cues used by the inferential process can change between the different forms of metacognitive monitoring, but the process itself is essentially the same. The overlap between different forms of metacognitive monitoring is often investigated by having participants perform different kinds of judgments on the same study items, and then correlating these judgments over items. Our design does not allow for such analyses, because we tested the different forms of assessing confidence using a blocked design. However, by modelling the decision-and-confidence process, we were able to show that a unitary confidence mechanism was able to explain behavioral results in all three conditions without distinguishing between the three forms of assessing confidence. This result speaks to the isomechanism position.

One limitation to the current study is that it only demonstrates the effects of info-seeking on decision weights in a numerical comparison task, whereas reverse correlation is often used to analyze data from more perceptual decision tasks. Future work will show if similar effects are obtained in tasks involving random dot motion, luminance judgments or face discrimination (see Okazawa et al., 2018; Zylberberg et al., 2012). Based on the fact that error-detection and correction are thought to be relatively high-level processes, we would expect similar effects to appear in other primary decision tasks.

In conclusions, we showed that the methods of explicitly reporting confidence and of post-decision wagering were found to show very similar reverse correlation patterns. Low-confidence info-seeking trials, however, showed inverted decision weights compared to explicit reports and post-decision wagering. Using behavioral modelling, we showed this pattern of results to be caused by internal error-corrections.