Abstract
This article investigates the concern that assessment of metacognitive resolution (or relative accuracy—often evaluated by gamma correlations or signal detection theoretic measures such as da) is vulnerable to an artifact due to guessing that differentially impacts low as compared to high performers on tasks that involve multiple-choice testing. Metacognitive resolution refers to people’s ability to tell, via confidence judgments, their correct answers apart from incorrect answers, and is theorized to be an important factor in learning. Resolution—the trial-by-trial association between response accuracy and confidence in that response’s accuracy—is a distinct ability from knowledge, or accuracy, and instead indicates a higher-order self-evaluation. It is therefore important that measures of resolution are independent of domain-knowledge accuracy. We conducted six experiments that revealed a positive correlation between metacognitive resolution and performance in multiple-choice mathematics testing. Monte Carlo simulations indicated, however, that resolution metrics are increasingly negatively biased with decreasing performance, because multiple-choice tasks permit correct guessing. We, therefore, argue that the observed positive correlations were probably attributable to an artifact rather than a true correlation between psychological abilities. A final experiment supported the guessing-related confound hypothesis: Resolution and performance were positively correlated in multiple-choice testing, but not in free-response testing. This study brings to light a previously underappreciated limitation in assessing metacognitive resolution and its relation to task performance in criterion tasks that may involve guessing.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
To successfully improve learning, it is important that people are able to monitor what they know and what they don’t know (Bjork 1994; Flavell 1979; Metcalfe 2009; Nelson et al. 1994; Nelson and Narens 1990). This metacognitive monitoring and knowledge, when accurate, may be used to select appropriate items for further study or to seek assistance to improve comprehension. To paraphrase the oft-quoted adage: If you don’t know what you don’t know, you can’t fix it. It is therefore of paramount importance that people be metacognitively accurate in all fields of study.
The relative accuracy, or resolution, of metacognitive judgments measures the extent to which people can discriminate whether they answered (or will answer) a particular question accurately, on an item-by-item basis. A strong positive relation between a participant’s ratings about how sure they are that they are, or will be, correct on particular items and their actual correctness on those items indicates good resolution. Broadly, research has focused on two types of metacognitive ratings. Prospective ratings, such as judgments of learning (JOL), feelings of knowing (FOK) or ease of learning judgments (EOL), indicate how likely the participant thinks that a later retrieval or answer will be correct. Retrospective ratings indicate the participant’s judgment of the accuracy of a just-provided answer, typically in the form of judgments of confidence. Although these judgments are distinct, for clarity we refer to all as judgments of confidence (in the accuracy of one’s answer). Typically, the within-participant correspondence between confidence and accuracy, on an item by item basis, is referred to as metacognitive resolution, relative accuracy (Dunlosky and Metcalfe 2009), or sensitivity (Fleming and Lau 2014).
Another aspect of metacognitive accuracy, sometimes termed calibration, absolute accuracy, bias, or over/underconfidence, concerns the relationship between participants’ average level of performance and average metacognitive judgment magnitude (Dunlosky and Metcalfe 2009; Lichtenstein and Fischhoff 1977). For example, it has been found that individuals with poorer performance in a task tend to overestimate their task abilities, a phenomenon known as the Dunning-Kruger effect (Kruger and Dunning 1999). Although sometimes also called metacognitive accuracy, calibration is distinct from the topic of this manuscript, metacognitive resolution.
A long line of research indicates the general accuracy and importance of relative metacognitive judgments (Tauber and Dunlosky 2016). In the context of memory, resolution is often measured with prospective metacognitive judgments, such as JOLs, FOKs, or EOLs (Dunlosky and Metcalfe 2009; Finn and Metcalfe 2007; Hart 1965, 1967; Koriat 1997; Koriat et al. 2002; Metcalfe and Finn 2008; Metcalfe et al. 1993; Nelson and Dunlosky 1991; Nelson et al. 1994), or retrospective judgments of confidence in the correctness of a just-provided answer (Butterfield and Metcalfe 2001, 2006; Kelley and Lindsay 1993; Kelley and Sahakyan 2003; Koriat 2008, 2012). Other areas where resolution has been studied include visual perception (Desender et al. 2018; Fleming et al. 2010; Koriat 2011; Morales et al. 2018), comprehension (Glenberg and Epstein 1987; Glenberg et al. 1987; Griffin et al. 2009; Griffin et al. 2008; Maki and Berry 1984; Thiede and Anderson 2003; Wiley et al. 2016), problem solving (Baars et al. 2014a, 2014b), emotion recognition (Kelly and Metcalfe 2011), and numerosity and mathematics (O’Leary and Sloutsky 2017; Schraw 1996; Siegler and Pyke 2013; Wall et al. 2016). Across these domains of study, the overall finding has been that metacognitive judgments are positively related to the accuracy of answers on the criterion task. Although in some particular tasks the correlation between judgment and task accuracy can be small (such as with comprehension monitoring) in most tasks, people appear to know what they know and what they don’t know.
Metacognitive resolution is typically evaluated with metrics that are assumed to be independent of the participants’ performance, skill, or knowledge in the primary task. In an influential article Nelson (1984) recommended the Goodman-Kruskal gamma correlation (Goodman and Kruskal 1954) as a measure of resolution, partly because he claimed it was theoretically independent of task performance (see also Gonzalez and Nelson 1996). Other measures of resolution include Pearson’s r (Nelson and Narens 1980), the phi correlation (Kornell et al. 2007), and signal detection theoretic measures (Benjamin and Diaz 2008; Higham and Higham 2018). Although computationally different, these metrics measure the association between response accuracy and metacognitive rating and—if they are to be useful in characterizing the relation between metacognition and performance—they too need to be able to quantify the relation between metacognitive ability and task performance free of distortion. Empirically, it is possible that people who perform less well are also less able to assess accurately what they know and what they don’t know. But it is important, in evaluating the relation between resolution and skill level that the observed relation is based on metacognitive measures that are not, themselves, distorted by measurement artifact in the tasks that is used. If metacognitive resolution turns out to be empirically related to task performance, and if the relation is not due to measurement artifact, there are important implications of this purported relation for metacognitively guided study and learning, as discussed below.
Relation between metacognitive resolution and task performance
Insofar as an individual’s knowledge of what he or she knows and doesn’t know has consequences for optimal learning strategies, people with poorer knowledge of their own misconceptions may have a particularly difficult time in remedying those misunderstandings. They presumably won’t know when to seek help, or when more study is indicated, if they don’t know that they don’t know particular concepts. If metacognitions are used to guide learning, there may be a positive relation between the goodness of peoples’ metacognitive resolution and performance in the task in which their metacognitions were evaluated.
How important is metacognitive monitoring—resolution—to learning success? One review of 47 experiments found that not only do learners allocate more time to more difficult items, learners’ metacognitive judgments negatively predict the amount of time they allocate for studying that item (Son and Metcalfe 2000). These results suggest that people are aware of how well they know and use this metacognitive knowledge to guide learning. Dunlosky et al. (2020) have reviewed the conditions under which monitoring can be expected to impact learning, and have provided evidence for the relation. This relation suggests the hypothesis that students with greater metacognitive resolution may be better learners. People with good metacognition may also be people who, because they use their metacognition to learn more effectively, are good learners. If so, resolution and task performance should be positively correlated across participants. If true, this finding would further support the proposal that metacognitive monitoring is used to control learning behavior, with a positive impact on learning success (Nelson and Narens 1994).
Prior research on the resolution-performance relationship presents a mixed picture, with results varying within and between domains and methods of study. For example, the memory loss associated with amnesia is not always associated with an inability to give accurate metamemory judgments, suggesting that domain skill (i.e. memory ability) and resolution are not necessarily correlated (Janowsky et al. 1989; Shimamura and Squire 1986). Other null relations between domain skill and metacognitive monitoring have been reported in studies of children’s memory strategies (Kelly et al. 1976) emotion recognition (Kelly and Metcalfe 2011) and text comprehension (Griffin et al. 2009). However, positive relations between domain skill and resolution have also been reported, namely in memory (Thiede 1999), emotion recognition (Kelly and Metcalfe (2011); Experiment 2), and text comprehension (Griffin et al. 2008).
What could explain these mixed findings on the resolution-performance correlation? We suggest one answer: In tasks using multiple-choice responding, domain skill (task performance, or knowledge; we use these terms interchangeably) and common measures of resolution are inherently related. Although it has been repeatedly asserted that e.g. the gamma correlation does not depend on performance in the criterion test (Griffin et al. 2009; Nelson 1984; Thiede et al. 2012), we argue, here, that the truth of this assertion depends on the method of testing (multiple choice vs. free responses) (see also Galvin et al. 2003; Maniscalco and Lau 2012; Schwartz and Metcalfe 1994; Thiede and Dunlosky 1994).
For example, in one study on text comprehension, participants studied five texts and predicted their performance on upcoming short-answer tests (Griffin et al. 2009). Resolution was measured with a gamma correlation between the predicted and actual number of correct responses for each participant across the five texts. No positive correlation between metacognitive resolution and test performance was found. In this metacomprehension task with free-response tests, resolution and comprehension performance were not correlated. This interesting finding suggests that, at least in the field of text comprehension, individuals with greater domain skill/knowledge may not be better at monitoring their skill/knowledge.
However, another similar study reported that domain skill and resolution were positively related. In this two-experiment study, participants studied five texts and rated how well they understood each text (Griffin et al. 2008). After all five texts, participants were tested on their comprehension of each text with 16–20 true/false questions. Resolution was measured with a Pearson’s r correlation between comprehension ratings and proportion correct across tests for each participant. The authors reported that gamma correlations yielded similar results. In both experiments, resolution correlated positively with comprehension performance (when texts were read once, but not in a read-twice condition). These findings suggested the opposite from the Griffin et al. (2009) study, namely, that greater domain skill is associated with greater metacognitive resolution. Positive correlations in comprehension experiments have also been found by Wiley et al. (2016). Notably, this study also used multiple-choice testing. Further, manipulations that increase comprehension performance, such as re-reading texts, also increased resolution (the rereading effect; Rawson et al. 2000), suggesting that performance and resolution may be related (either as separate abilities, or due to the measurement issues discussed herein). Once again, multiple-choice testing was used.
We propose that the mixed findings regarding the resolution-performance relationship may be, at least partially, explained by features of the primary task: There was no relation between resolution and performance when performance was assessed with a free response method (Griffin et al. 2009; but see Thiede 1999). When a multiple-choice method was used, a positive correlation emerged (Griffin et al. 2008). Similarly, in an experiment investigating the relation between emotion recognition and metacognition of emotion recognition (Kelly and Metcalfe 2011, Experiment 2), a positive correlation between the overall goodness of performance and participants’ resolution was observed, leading the researchers to suggest that people’s metacognition about when they had or had not understood and correctly interpreted others’ emotions might be important in allowing them to bootstrap their emotion recognition performance. But like other experiments exhibiting a positive correlation between task performance and metacognitive resolution, across people, this study also used a multiple-choice method. The observation that two-alternative and multiple choice tasks seem to show the correlation whereas free recall may not, led us to ask if there might be a common factor that leads to associative measures of metacognitive resolution to have some inherent relation to task performance under certain testing conditions, but not others. In the present work, we focus on confidence judgments after responding on the main task, but our main argument applies equally to judgments of learning, and other metacognitive measures, before a response is provided.
Present study
Our approach to answer this question was three-fold. First, we investigated a large previously unpublished dataset from six experiments that investigated middle school and university students’ mathematics learning. These data allowed us to examine whether a performance-resolution correlation is found when multiple-choice testing is used. Based on prior literature, we hypothesized that a positive correlation would be found. Second, we developed a hypothetical model of confidence ratings, and conducted simulations to investigate potential factors contributing to the relation between metacognitive resolution and domain skill. Specifically, the simulation investigated the hypothesis that guessing may underlie the relation between domain skill and metacognitive resolution. Third, we tested the predictions of this model in an experiment that directly contrasted free-response and multiple-choice testing. In a second experiment, we hypothesized that measures of resolution in multiple-choice tasks would be i) smaller in magnitude than in free response tasks and ii) correlated to performance in the primary task more strongly than in free response tasks.
Experiment 1
In what we call Experiment 1, we collated data from six experiments investigating mathematics learning. Although these data were not collected for the purpose of this manuscript, they provided a good example case for examining the potential relationship between performance and resolution within multiple large samples. There were differences between experiments, such as testing medium (computer or paper) and age (middle school or undergraduate), but our focus here was not to investigate these factors’ impact on mathematics performance or metacognition. Rather, we used this large dataset to examine the possible relationship between metacognitive resolution and (mathematics) performance, in a multiple-choice testing context. The common procedure was that participants completed mathematics tests consisting of 4-alternative multiple-choice problems and rated their confidence in the accuracy of each of their answers. If readers are interested in the potential differences between e.g. demographics, the data is openly available for reanalyses at https://osf.io/np3cu/. Because these experiments (1A-F) were so similar, we describe all six experiments’ methods first, and then present the results together.
Experiment 1A: Method
Participants
Ninety-two 8th grade middle school students in a New York City public school participated. Parents and students provided voluntary consent. We did not query demographic information, but the school’s demographic statistics were: 12% Asian, 23% Black, 37% Hispanic, 23% White. Students with special needs: 12%. 51% were male and 49% female. 53% were below the poverty line. The experiment was approved by the Columbia University Internal Review Board and by the New York City Board of Education.
Procedure
Participants completed four tests administered on four separate days of an after-school mathematics tutorial program. There was a feedback session between each test in which a teacher provided in-class feedback on the previous test. Tests consisted of ten four-alternative multiple-choice problems, compiled from published New York State Regents Common Core tests.Footnote 1 The specific Regents problems used in Experiment 1 are listed at https://osf.io/np3cu/, and an example problem is shown in Fig. 1. The problems were classified as either ‘algebra’ or ‘functions’ in the Regents exams, and each test contained problems from only one of these classifications. Half of the students’ tests consisted of ‘algebra’ problems, and half did ‘functions’ problems. Thus, there were 80 unique problems, of which each student completed 40.
Up to 25 students at a time completed the pencil and paper tests in a single classroom under teacher supervision. Participants could use calculators and scrap paper. Each page of the test presented a single problem, and four response options printed below the problem. On the front page of the test was a grid where students entered their preferred response alternative and confidence rating for each problem. Confidence was rated with integers from 0 (“I completely guessed”) to 5 (“I am extremely confident that my answer is correct”). Students were instructed to rate their confidence immediately after completing each problem. However, although the teachers encouraged the students to enter their confidence ratings immediately following each problem, some students may have entered all their ratings in bulk after completing the whole test.
Experiment 1B: Method
Experiment 1B was a direct replication of Experiment 1A. A new sample of ninety-two 8th grade students from the same New York City public school participated. Voluntary consent was obtained from students and their parents. The experiment was approved by the Columbia University Internal Review Board and by the New York City Board of Education. The procedure was identical to Experiment 1A.
Experiment 1C: Method
Experiment 1C was a close but not exact replication of Experiments 1A and B. Ninety-one 8th grade students participated from the same New York City public school as in Experiments 1A and B. We obtained voluntary consent from the students and their parents. The experiment was approved by the Columbia University Internal Review Board and by the New York City Board of Education.
The students completed three pen-and-paper tests, separated by eight days of in-class instruction, as part of an after-school mathematics tutorial. Each test consisted of 20 four-alternative multiple-choice problems from the same pool of problems as in experiments 1A and B. Multiple problems were printed on each page of the test, but otherwise the test procedure was the same as in experiments 1A and B: Participants wrote their answers and confidence ratings—on the same scale as in the previous experiments—on a grid on the first page of the test. Participants completed the tests in groups of up to 25 students in a classroom supervised by a teacher, and had 45 min for each test.
Experiment 1D: Method
Experiment 1D was similar to previous experiments, but the tests were completed on a computer. Eighty-nine students participated. The participants were the same students as those in Experiment 1C (two students who completed Experiment 1C did not take part in Experiment 1D). In Experiment 1C, the participants had completed three pen-and-paper tests, separated by eight weeks of instruction. During those eight weeks, the participants engaged in eight computerized mathematics tutorials, once per week. Although the same students participated, the procedure was different to Experiment 1C and we therefore described it as Experiment 1D.
The participants used a website to view four-alternative multiple-choice mathematics problems. After logging on to the website, participants were presented one test problem at a time, such that the problem was shown on top of the screen, and the answer options below it. Participants clicked a small button next to their preferred response option, and then a “Submit” button to proceed to the next screen. There, they were prompted to rate their confidence in the accuracy of the preceding answer on a visual analog scale using the computer mouse. At the top of this screen the text “Sure correct or just guessing” was displayed, and a visual analog scale with endpoints labelled with “0%” on the left and “100%” was displayed below the text. In addition to the endpoints, the word “guessing” was displayed just below ¼ of the scale (without a tick mark), and “completely certain” just below the right endpoint. The word “CONFIDENCE” was printed below the scale and labels. Participants clicked on the scale to indicate their confidence, and then a “Submit” button to proceed to the next screen. After each confidence rating, participants could choose to receive feedback and/or watch instructional videos related to the problem, but those were unrelated to the current manuscript. Then, they moved on to the next problem.
In each tutorial session, the participants completed ten mathematics problems or made four errors, whichever occurred first. (They had the opportunity to redo problems which they had answered incorrectly, but those data are excluded from the current analyses.) The tests were completed on a website, and each participant completed the tests on an individual computer in a class of up to 25 students, under teacher supervision. 80 unique problems were included from the same pool as in the previous Experiments.
Experiment 1E: Method
Eighty-six Columbia University undergraduate students participated for course credit in an introductory Psychology course (36 females, 37 males, the rest did not report gender; age: 18–36 years). The experiment was approved by the Columbia University Internal Review Board.
The participants completed two tests, each consisting of 20 math problems. Each problem, and its response options, was printed on a separate page. Participants were asked to solve the problems and write their preferred response alternative and confidence rating on a separate answer sheet. Participants provided confidence ratings by writing a number from 0 (“low”) to 10 (“high”) next to their chosen response on the answer sheet. The two tests were separated by a computerized mathematics tutorial, which included videos about solving problems related to the ones on the tests, which we did not consider here. The problems were selected from the same pool of materials as in the previous experiments. Up to four individuals participated in the same room, under experimenter supervision. Participation took up to 90 min, and participants were allowed scrap paper and calculators.
Experiment 1F: Method
Experiment 1F was similar to Experiment 1E, but the mathematics tests were computerized. Ninety-nine undergraduates participated for course credit. The experiment was approved by the Columbia University Internal Review Board.
Participants completed four mathematics tests as part of an online mathematics tutorial. Each test consisted of ten problems, presented alone on the top of the screen, with the answer alternatives below. Participants chose their preferred response by clicking a box next to it. They then clicked “Submit”, and proceeded to the next screen, where they rated their confidence in the accuracy of their response by clicking on a visual analog scale. After indicating their degree of confidence, they clicked “Submit” to proceed to the next screen. The following screen allowed the participant to view different types of instructional videos related to the mathematics problems, but these are not analyzed in the current study. The tests were completed in one 90-min session, on individual computers, in groups of up to four supervised by an experimenter.
Results
Mathematics performance was quantified as proportion correct. We quantified metacognitive resolution with two common measures. First, we used the nonparametric gamma correlation (Gonzalez and Nelson 1996; Goodman and Kruskal 1954; Nelson 1984). It was recently shown that the traditional method of calculating gamma based on concordant and discordant pairs is a worse estimator of participants’ true underlying gammas than a ROC based estimator (Higham and Higham 2018). We therefore used the latter as an estimate of participants’ gamma correlations. Specifically, gamma was calculated as 2Az-1, where Az is the area under the ROC curve. However, for completeness, we also calculated gammas using the concordant-discordant pairs formula.
Second, we used the signal detection theoretic measure da (Benjamin and Diaz 2008; Masson and Rotello 2009), which measures the separation between two Gaussian latent variables weighted by the ratio of their standard deviations. We calculated da with a linear regression of the zROC, as detailed by Benjamin and Diaz (2008). However, that method ignores error on the x-axis (Higham 2007; Knoblauch and Maloney 2012), and we therefore verified these results using more robust ordinal regression methods (Bürkner and Vuorre 2019). The results were practically identical, so we focus on the former method’s results because it is more common in the existing literature. In calculating the ROC based metrics, we added 1/K (K = number of confidence categories) to all rates to account for cells with zero observations (e.g. Hautus 1995). We also did the analyses without adjusting for empty cells. That led to many participants being dropped due to indeterminate measures, but otherwise the results were practically identical. For experiments 1D and 1F, where an analogue scale was used, an ordered scale with 6 categories was created.
Most importantly, these metrics measure the within-subject, trial-by-trial association between confidence and accuracy—metacognitive resolution. Data analyses were conducted in the R statistical computing environment (R Core Team 2019), and are available at https://osf.io/np3cu/.
The mean gamma correlations and das for Experiments 1A-F are summarized in Table 1. Mathematics performance was close to 70% correct across experiments. Metacognitive resolution was good and significantly better than chance in all six experiments.
Relation between resolution and performance
We then turned to our main question, which concerned the between-subject correlation between mathematics performance and metacognitive resolution. Scatterplots of participants’ proportions correct and resolution metrics are shown in Fig. 2. Across experiments, there appeared to be a positive relation between mathematics performance and metacognitive resolution.
We then calculated Kendall’s tau correlations between proportions correct and each of the three resolution metrics, separately for each experiment. We used the nonparametric tau correlation because the resolution metrics, especially gamma, do not have the metric properties assumed by a Pearson correlation (Benjamin and Diaz 2008). The nonparametric correlation also alleviated the biasing effects of the outlying −1 concordant-discordant pairs gammas, observed in Fig. 2. Additionally, as will be shown below, the relationship between performance and resolution is unlikely to be linear, further motivating the use of a nonparametric correlation measure. As can be seen in Table 2, the correlation was positive and significant for every experiment for both ROC based metrics, and significant (or marginally so) for four out of six experiments for the concordant-discordant pairs gamma. These results strongly suggested that task performance and metacognitive resolution are positively related when multiple choice testing is used, at least in the mathematics domain.
A critical re-examination of the relation between performance and resolution
Experiment 1 found a positive correlation between mathematics performance and metacognitive resolution. This, in principle, is an important finding insofar as it suggests that students who are less accomplished at mathematics may also lack in their knowledge of what they know and do not know—a metacognitive deficit. It might even suggest that metacognitive remediation would be warranted in mathematical pedagogy. Before reaching such a bold conclusion about this result, however, we had some concerns, and suspected that there may be factors other than the students’ metacognitive abilities contributing to this relation.
In particular, it was previously noted that the number of response alternatives in multiple-choice problems positively predicts the magnitude of gamma correlations (Schwartz and Metcalfe 1994; Thiede and Dunlosky 1994). Although the number of response alternatives was constant in the present experiments, we suspected that the underlying reason for why number of alternatives positively correlates with the magnitude of observed gammas may also be an important factor in the present results.
Specifically, it was previously suggested that a smaller number of response alternatives would necessarily lead to smaller gamma correlations, because the probability of correct guesses when the participant had no actual knowledge is greater with fewer alternatives (Schwartz and Metcalfe 1994, p.95). When a participant doesn’t know the correct solution to a problem and indicates low confidence in accordance with their lack of knowledge, but nevertheless gets it right by a lucky guess, the trial will count as a “metacognitive miss”; a low confidence correct response. Such “misses” will artificially make resolution metrics appear smaller than warranted by the participant’s metacognitive accuracy.
For example, suppose there are 10 questions on the test and student A knows the answers to 2 questions, whereas student B knows the answers to 6 questions. Suppose that both students have perfect metacognition, that is, A knows that he knows the 2 questions he actually knows and knows he doesn’t know the other 8. B knows she knows the 6 she actually knows and knows she doesn’t know the other 4. When given a 4-alternative forced choice test, A gets all questions he knows he knows right and 2 questions that he doesn’t know right by guessing (for an observed score of 4/10). B gets the 6 questions she knows she knows right and only 1 question that she doesn’t know right by guessing (for an observed score of 7/10). Insofar as they both know what they know and what they don’t know, their gammas should reflect this equivalence. But if we place the correct-by-guessing items that the students didn’t really know into the metacognitive ranking of the unknown questions, A’s gamma has a mean of 0.6 (and can range from 0.0 to 1.0), while B’s gamma has a mean of 0.9 (and can range from 0.7 to 1.0): because the differential guessing results in a different proportion of metacognitive misses, it looks like B has better metacognitive resolution than does A.Footnote 2
More generally, the resolution metrics considered here attempt to measure the correspondence between domain knowledge and confidence using an imperfect indicator of knowledge (response accuracy). When guesses are present, response accuracy fails to perfectly identify knowledge, leading to biased estimates of the relationship. Therefore, we argue that Nelson’s (1984) ‘Property 3’ of gamma correlations—“feeling-of-knowing accuracy score should be independent of overall recognition performance”— is violated in multiple choice tasks (and in other tasks in which people can guess correctly without actually knowing). Participants with less knowledge, and hence poorer performance, will necessarily guess more often than participants with more knowledge: The diluting effect that guessing correctly (without real knowledge) has on resolution metrics will be greater for low than for high performers. Further, we argue that any resolution metric based on the association between response accuracy and confidence, such as the SDT measure da, has the same limitation (see also Galvin et al. 2003; Maniscalco and Lau 2012).
Subsequently, in multiple choice tasks, there will be a necessary correlation between performance, skill, or knowledge on the primary task (mathematics, recognition memory, general information testing, etc.) and metrics of metacognitive resolution: The metrics will be increasingly downward biased as performance decreases. To examine this argument in more detail, we conducted a simulation study.
Simulation study
The simulation study examined two propositions: First, gamma and da are negatively biased estimates of metacognitive resolution in tasks where correct answers may contain guesses. Second, participants’ performance on the primary task (e.g. mathematics) will impact the magnitude of bias: Lower performing participants will guess more frequently, leading to a greater bias, and a necessary relationship between performance and resolution.
Method
The simulation for one hypothetical participant was conducted as follows. First, the values of three parameters were chosen: K defined the participants knowledge as the proportion of known items. G defined the guessing probability; the probability of answering an unknown item correctly. (Generally, G = 1/M where M is the number of response alternatives in a multiple choice task.) R defined metacognitive resolution as the separation of the two latent Gaussian variables, defined in more detail below.
For each participant, 20,000 items were simulated. K defined the proportion of items that the participant knew and did not know (e.g. if K = .6, the participant knew 60% of the items, and did not know 40%). Then, correct and incorrect responses were created, such that known items were always correct, and unknown items were correct with guessing probability G (i.e. for unknown items, response accuracy was a random Bernoulli draw with probability = G). Then, a confidence rating for each item was generated: Unknown items were assigned evidence values drawn from a normal distribution with mean = 0 and standard deviation = 1. Known items were assigned evidence values from a normal distribution with standard deviationFootnote 3 = 1 and mean = R. The mean of the known items’ evidence distribution, R, defined the simulated participant’s metacognitive resolution: Higher values of R implied greater separation between unknown and known items’ evidence distributions—in standard SDT applications this parameter is called d’. Evidence values were then converted to 6-point confidence ratings via five thresholds at −1, −.5, 0, .5, and 1. Then, resolution metrics were calculated based on these simulated data.
To clarify, confidence ratings were based on knowledge, which researchers typically have no access to, rather than accuracy, which is accessible but does not perfectly identify knowledge. Therefore, the key assumption of this simulation scheme was that guessing for unknown items was random and resulted in 1/M proportion correct.
The simulations were run over a completely crossed design of K (ten levels evenly spaced between .05 and .95), G (0, 0.25, and 0.5, the latter corresponding to 4- and 2-alternative multiple-choice tasks), and R (25 levels evenly spaced between 0.1 and 2.5). The simulation was replicated 200 times at each combination of the parameters. The R code for conducting the simulation is available at https://osf.io/np3cu/.
Results and discussion
The main results of the simulation are shown in Fig. 3, which shows the relation between knowledge (K) and gamma / da. (We omitted the zROC based gamma because the result was practically identical to da). This relation is shown for different levels of actual resolution (R, colors) and guessing (G, columns). In the left column, we verified Nelson’s ‘Property 3’ of measures of resolution for both gamma and da (see Nelson 1984, Fig. 1): The mean estimates were perfectly related to the generative resolution parameter and unrelated to knowledge when there was no guessing.
However, the mean estimates of both parameters were strongly positively related to knowledge when guesses were introduced (two right columns of Fig. 3): In the presence of guessing, even when the underlying resolution parameter is constant, the estimated values change dramatically depending on the level of knowledge (and hence task performance). The consequences of this finding to analyses of resolution when guesses are possible are that metrics of resolution will be lower than the participant’s actual level of resolution, and the magnitude of this bias is related to the participant’s level of knowledge. This issue is not specific only to the measures of resolution illustrated in Fig. 3: We included in our simulations (but omit here for clarity) other measures of resolution (d’, phi, Pearson’s r, parametric and nonparametric AUCs), which were similarly impacted by knowledge when guesses were possible. (Pearson’s r and phi had an inverted-U shaped relation to knowledge even when Guessing = 0.)
Comparison of simulations to mathematics data
Next, we asked to what extent the observed performance-resolution correlation in Experiments 1A-F might be attributable to the guessing bias detailed above. To answer, we compared each experiments’ observed performance-resolution regression slope (shown in Fig. 2) against the corresponding slope obtained from the simulations, at the experiment’s mean da and guessing = 0.25. The performance-resolution slope from the data was compared to the simulation’s slope with a one-sample t-test for each experiment. One sided p-values testing whether the data slope was greater were calculated. This analysis showed that only one experiment’s da-performance correlation was marginally greater than the simulated relation, all others were not significant (Exp 1A: p = 0.218, Exp 1B: p = 0.327, Exp 1C: p = 0.224, Exp 1D: p = 0.055, Exp 1E: p = 0.473, Exp 1F: p = 0.285). The analysis was then repeated with gamma as the resolution metric; again no data slopes were significantly greater than the simulated slopes. This analysis, while far from conclusive, indicated that the data slopes—the observed performance-resolution correlations—were equal to or smaller than a relationship caused by correct guessing.
A note about calibration
Guesses may also impact measures of calibration, a different measure of metacognitive accuracy (Dunlosky and Metcalfe 2009; Lichtenstein and Fischhoff 1977). Because guesses artificially inflate measures of performance, a perfectly calibrated person’s mean judgment—which aligns with their level of knowledge, not observed performance when some answers are guesses—will be lower than their inflated performance measure: Guessing will bias measures of calibration towards underconfidence, such that the lowest-performing individuals will have the strongest guessing-induced underconfidence bias. One way to address this bias might be to estimate participants’ knowledge using e.g. Abbott’s formula (see above) instead of a simple proportion correct. As an extreme example, consider a participant in a 4AFC task who performs at chance (i.e. does not know the answer to any of the items) and accurately gives an average confidence judgment of 0%. Due to correct guessing, her observed percentage correct is 25%, leading to an observed underconfidence of 25%. However, a participant who truly knows the answer to all items, and knows that she knows (gives an average confidence rating of 100%), will not be impacted by correct guesses and thus will not show an underconfidence effect.
The guessing-induced underconfidence bias in calibration brings to mind a well-known mismatch between self-evaluations and skill: The Dunning-Kruger effect describes a phenomenon whereby, across a wide variety of tasks and contexts, individuals with poor task performance are prone to overestimating their skill (Kruger and Dunning 1999). The reasons underlying the Dunning-Kruger effect are still debated, and some researchers have suggested that statistical artefacts and scale effects may partly explain the tendency of poorer performers to have inflated self-assessments (Feld et al. 2017; Krajc and Ortmann 2008; McIntosh et al. 2019). However, when possible, guesses will lead to a bias in the opposite direction of the Dunning-Kruger effect. In studies on calibration and related phenomena, such as the Dunning-Kruger effect, researchers should be aware of the potentially biasing impact of lucky guesses on measures of calibration.
Summary of simulation study
In summary, our simulation study demonstrated that in studies of metacognition using multiple-choice testing, metrics of resolution will necessarily correlate with primary task performance.
One possible critique, though, is that we assumed a generative model of confidence that relied on random guessing in the primary task. One concern with this model is that such random guessing, while intuitively appealing, may not be empirically plausible (e.g. Higham 2007). In fact, one study using SAT (five alternative multiple-choice) materials found that a signal detection theoretic (SDT) model described performance better than did a high-threshold model (i.e. model with random guessing; Higham (2007)). Specifically, high-threshold theory (as implied in our simulations) predicts that accuracy at the lowest level of confidence should not drop below 1/K (K = number of response alternatives). In contrast, as found in that study and predicted by SDT, accuracy was below 20% for low confidence responses, thus discrediting the random guessing assumption (Higham 2007).
To begin to address this issue, we took the data of Experiments 1A-F, and asked if performance did indeed drop below 25% at the lowest level of confidence. We did this analysis separately for performance tertiles of participants, because good performing students should necessarily guess less than poor performers. In support of the guessing hypothesis, none of the performance tertiles had performance below 25% at the lowest level of confidence (Low performers: 24.6%, 95%CI = [20.9, 28.2], medium performers: 32.1%, 95%CI = [27, 37.3], high performers: 40%, 95%CI = [33.1, 47]). In fact, as can be seen, the lowest performers were almost exactly at 25% at the lowest level of confidence. Nevertheless, these analyses were preliminary, and a stronger test of our hypothesis would be to experimentally contrast tasks where guessing was possible and where it was not. Therefore, we put the idea that resolution metrics are related to domain knowledge in multiple-choice tasks, possibly due to guessing, to an experimental test. In Experiment 2, we directly compared indices of metacognitive resolution, and their relation to domain skill, between free-response trials and multiple-choice trials.
Experiment 2
Experiment 2 directly tested the hypothesis, suggested by Experiment 1 and the simulations described above, that measures of resolution in multiple-choice tasks would be i) smaller in magnitude than in free response tasks and ii) correlated to performance in the primary task (more strongly so than in free response tasks). Participants answered a series of general information questions, either by selecting from two alternatives (2 alternative forced choice; 2AFC) or by typing in an answer (free response). After each response, participants provided a rating of confidence in the accuracy of the response.
Method
Participants
We recruited 100 participants through the Prolific (https://prolific.ac) online platform. 57 participants were female, and age ranged from 18 to 72 years (median = 29.50). We recruited participants currently residing in the US, and 97 reported English as their first language. Participants were paid $3.64 for participating, in line with the platform guidelines. All participants provided informed consent. The sample size was determined with a power simulation based on the results of the simulation study described above.
Materials
We collected general knowledge questions from Tauber et al. (2013) and from previous experiments conducted in our laboratory. Based on those previous studies, we selected 120 questions of varying degrees of difficulty, and found the most frequently endorsed commission errors to be used as the false response options in the 2AFC condition. We also screened the questions (and response alternatives) for potentially offensive or outdated material, and replaced unsuitable false response options with new ones. As an example, one question was “What was the name of the clown on the ‘howdy doody’ television show?”. (Correct response: “Clarabell”, incorrect alternative: “Bozo”). In this Experiment, we used general information questions rather than mathematics problems in order to generalize the findings from Experiment 1.
Design and procedure
After providing informed consent, participants read the following instructions:
You will answer a number of general information questions. For some questions, you will type in your answer. For other questions, you will choose your answer from a list of alternatives. If you feel like you do not know the answer, please provide your best guess. After submitting your response, you will rate how confident you are that your answer was correct. There will be many questions, so don’t labor too much over any individual question. At the same time, please be careful and pay attention throughout. The study will take approximately 25 min. You can view all the questions and correct answers at the end of the study. During the study, please do not search for the answers online using Google or similar.
They then begun the experiment. Each trial consisted of the question printed in bold font on top of the browser window. In free response trials, an empty text box was displayed below the question. In 2AFC trials, two response options were displayed below the question, and participants chose their response by clicking a button next to their endorsed alternative. The response type was randomized for each trial, thus leading to a one-way within-participant design (Condition: 2AFC vs. free response). After providing the response, participants clicked a button labelled “Submit”, which revealed a horizontal slider scale with labels “Not confident” and “Completely confident” on the left and right ends, respectively. Participants then clicked a “Continue” button to proceed to the next trial.
The 120 questions were divided into five blocks, due to software limitations, but the blocking was not apparent to participants. The blocks were presented in pseudorandom orders. For each block, the order of questions was randomized for every participant. The mean time to complete the experiment was 38 min. The online experiment was programmed and run on the formr platform (Arslan et al. 2019).
Results
We quantified trivia performance as proportion correct, which was calculated for each subject, separately for the 2AFC and free response conditions. For free response answers, accuracy was determined as any response whose Jaro-Winkler distance to the correct answer was less than 0.2 (van der Loo 2014). Additionally, 54 two-word responses that contained the correct answer were labelled as false by this algorithm (e.g. correct answer was “Child”, and participant had answered “Julia Child”), but we manually labelled those as correct. No participants or trials were excluded.
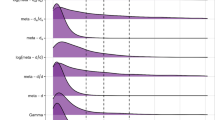
As in Experiment 1, metacognitive resolution was quantified with da, the ROC based gamma, and the concordant-discordant pairs gamma (Benjamin and Diaz 2008; Higham and Higham 2018; Nelson 1984). These measures, proportions correct, and mean confidence ratings are summarized in Table 3. First, this table shows that both proportion correct and mean confidence were significantly greater in the 2AFC condition. More importantly, all three resolution metrics were greater in the free response condition. This dramatic difference is surprising insofar as participants’ knowledge across the two conditions was presumably equal. These results supported hypothesis i: Resolution measures were lower in the 2AFC task.
We then turned to the second part of our hypothesis; that resolution would be spuriously correlated to performance in a 2AFC task. To answer, we correlated the three resolution metrics to performance, separately in the two conditions, again using the nonparametric tau correlation. The correlation was significant for each of the three resolution metrics in the 2AFC condition. However, it was much smaller in the free response condition, where it was only significant for the concordant-discordant pairs based gamma (Table 4). These scatterplots are shown in Fig. 4.
To quantify whether the correlations were significantly different between the two conditions, we fit a mixed effects regression model separately for each resolution metric. The model predicted resolution from performance, condition, and their interaction. Performance was used as a linear predictor, and condition was dummy coded with free response = 0, and 2AFC = 1. Thus, a significant positive interaction term would indicate a stronger correlation in the 2AFC condition. This prediction was supported in all three models (da: b = 1.28 (SE = 0.62), p = 0.042; gamma (pairs): b = 0.67 (SE = 0.24), p = 0.006; gamma (ROC): b = 0.61 (SE = 0.25), p = 0.018).
Together, the results from Experiment 2 supported our main hypotheses: i) resolution appears artificially smaller in 2AFC testing; and ii) resolution is confounded with performance in 2AFC testing. Additionally, using free response methodology, we found little support that performance and resolution are correlated above and beyond the confound illustrated by our simulations, at least in the general information domain.
Conclusions
The applied implications of metacognitive accuracy are often discussed in the context of self-regulated learning (Flavell 1979): Knowing that you don’t know, often construed as a low judgment of learning, feeling of knowing, or confidence rating, should prompt learners to further investigate the topic or question. Thus, learners who are metacognitively more sensitive to the accuracy of their answers should be able to better use this information to enhance study, leading to a hypothesized positive relationship between metacognitive resolution and domain skill. To accurately test this hypothesis, it is important that measures of the two abilities are not inherently related. In the current work, we showed that in multiple-choice testing, performance level and metrics of metacognitive resolution are inherently related.
In six multiple-choice mathematics testing experiments, we found a positive relation between mathematics performance and metacognitive resolution. Following Schwartz and Metcalfe (1994), we suspected that an underlying reason for the correlation was that some correct responses resulted from lucky guesses, rather than true knowledge, and that such lucky guesses—which decrease observed resolution—necessarily occur more when performance is low than high. We conducted simulations based on the assumption that the response alternative to unknown items is randomly guessed. This assumption led to a strong correlation between resolution and domain skill, even when the two abilities were truly uncorrelated. However, the random guessing hypothesis implies a high threshold model of performance on the primary task, which has been shown to be a poorer fit to data than is signal detection theory (Higham 2007). However, signal detection theoretic analyses of multiple-choice tasks with more than two alternatives are rare, and researchers commonly use proportion correct as a measure of performance instead (see DeCarlo 2012). Therefore, we then experimentally verified that i) resolution metrics were smaller in 2AFC than in free-response testing, and that ii) there was a strong positive correlation between resolution metrics and performance in 2AFC, but not in free-response testing, as predicted by the guessing assumption.
Related to the current work, Maniscalco and Lau (2012) suggested a measure of relative metacognitive accuracy that explicitly models the relation between primary task performance and metacognition. Based on an analysis showing that sensitivity and response bias in the primary task impact measures of metacognitive performance when studied in a signal detection task (Galvin et al. 2003), this new measure has the attractive quality that it is measured in the same units as the primary task performance (i.e. d’). This metric, meta-d’, allows normalizing metacognitive performance with primary task performance, leading to a measure of metacognitive “efficiency” (\( \frac{\mathrm{meta}-{d}^{\prime }}{d^{\prime }} \)), that is not inherently constrained by primary task performance or bias. While otherwise an attractive measure of metacognition, meta-d’ requires that the primary task be conducted in a manner analogous to a signal detection task (e.g. 2AFC). Thus, it is not suitable as a measure of metacognition in free-response tasks, or, in its current implementation, multiple-choice tasks where the number of choice alternatives exceed 2. Nevertheless, the general implication of that approach is the same as elucidated by our results: In certain tasks, metrics of resolution are inherently related to performance on the primary task.
The results of our findings have important consequences to many studies of metacognition. It is sometimes said that the relationship between performance and resolution “seems obvious” (Schwartz and Metcalfe 1994, p. 110). Perhaps so—although our results suggest otherwise—but because the two appear necessarily correlated if guesses are possible, studying this relationship may prove more difficult than previously thought (see also Fleming and Lau 2014; Galvin et al. 2003; Maniscalco and Lau 2012). The handful of studies that have investigated the performance-resolution relationship have reported mixed results (Griffin et al. 2009; Griffin et al. 2008; Kelly and Metcalfe 2011; Kelly et al. 1976; Thiede 1999). Our results highlighted one reason for observed positive correlations between the two, and therefore suggests caution in interpreting them, at least when the criterion test can involve guessing.
Notes
These tests can be downloaded from http://www.nysedregents.org/algebraone/. Some tests included a free-response problem but we excluded them from the current analysis (not enough free-response problems were included for a meaningful analysis).
Here, ‘perfect metacognition’ means a complete separation between the confidence rating distributions for unknown and known items. Consequently, the variance in these gammas stems from the variation in which specific confidence ratings, from the low 1–3 distribution, are assigned to the correct guesses. If all correct guesses receive the highest low confidence rating (3), gamma will still be 1.0.
Although the assumption of equal variances may not hold in real data, varying this parameter would be inconsequential to the current question. Further, Higham (2007) found that the equal variances model provided a good description of metacognitive ROCs. Therefore, for simplicity, we chose equal variances.
References
Arslan, R. C., Walther, M. P., & Tata, C. S. (2019). Formr: A study framework allowing for automated feedback generation and complex longitudinal experience-sampling studies using R. Behavior Research Methods, 52, 376–387. https://doi.org/10.3758/s13428-019-01236-y.
Baars, M., van Gog, T., de Bruin, A., & Paas, F. (2014a). Effects of problem solving after worked example study on primary school Children’s monitoring accuracy. Applied Cognitive Psychology, 28(3), 382–391. https://doi.org/10.1002/acp.3008.
Baars, M., Vink, S., van Gog, T., de Bruin, A., & Paas, F. (2014b). Effects of training self-assessment and using assessment standards on retrospective and prospective monitoring of problem solving. Learning and Instruction, 33, 92–107. https://doi.org/10.1016/j.learninstruc.2014.04.004.
Benjamin, A. S., & Diaz, M. (2008). Measurement of relative metamnemonic accuracy. In J. Dunlosky & R. A. Bjork (Eds.), Handbook of memory and metamemory (pp. 73–94). New York: Taylor & Francis.
Bjork, R. A. (1994). Memory and Metamemory considerations in the training of human beings. In J. Metcalfe & A. P. Shimamura (Eds.), Metacognition: Knowing about knowing. Cambridge: MIT Press.
Bürkner, P.-C., & Vuorre, M. (2019). Ordinal regression models in psychology: A tutorial. Advances in Methods and Practices in Psychological Science, 77–101. https://doi.org/10.1177/2515245918823199.
Butterfield, B., & Metcalfe, J. (2001). Errors committed with high confidence are hypercorrected. Journal of Experimental Psychology: Learning, Memory, and Cognition, 27(6), 1491–1494. https://doi.org/10.1037/0278-7393.27.6.1491.
Butterfield, B., & Metcalfe, J. (2006). The correction of errors committed with high confidence. Metacognition and Learning, 1(1), 69–84. https://doi.org/10.1007/s11409-006-6894-z.
DeCarlo, L. T. (2012). On a signal detection approach to m-alternative forced choice with bias, with maximum likelihood and Bayesian approaches to estimation. Journal of Mathematical Psychology, 56(3), 196–207. https://doi.org/10.1016/j.jmp.2012.02.004.
Desender, K., Boldt, A., & Yeung, N. (2018). Subjective confidence predicts information seeking in decision making. Psychological Science, 29(5), 761–778. https://doi.org/10.1177/0956797617744771.
Dunlosky, J., & Metcalfe, J. (2009). Metacognition. Thousand Oaks: SAGE Publications.
Dunlosky, J., Mueller, M. L., Morehead, K., Tauber, S. K., Thiede, K. W., & Metcalfe, J. (2020). Why does excellent monitoring accuracy not always produce gains in memory performance? (in press).
Feld, J., Sauermann, J., & de Grip, A. (2017). Estimating the relationship between skill and overconfidence. Journal of Behavioral and Experimental Economics, 68, 18–24. https://doi.org/10.1016/j.socec.2017.03.002.
Finn, B., & Metcalfe, J. (2007). The role of memory for past test in the underconfidence with practice effect. Journal of Experimental Psychology: Learning, Memory, and Cognition, 33(1), 238–244. https://doi.org/10.1037/0278-7393.33.1.238.
Flavell, J. H. (1979). Metacognition and cognitive monitoring: A new area of cognitive developmental inquiry. American Psychologist, 34(10), 906–911. https://doi.org/10.1037/0003-066X.34.10.906.
Fleming, S. M., & Lau, H. (2014). How to measure metacognition. Frontiers in Human Neuroscience, 8, 443. https://doi.org/10.3389/fnhum.2014.00443.
Fleming, S. M., Weil, R. S., Nagy, Z., Dolan, R. J., & Rees, G. (2010). Relating introspective accuracy to individual differences in brain structure. Science, 329(5998), 1541–1543. https://doi.org/10.1126/science.1191883.
Galvin, S. J., Podd, J. V., Drga, V., & Whitmore, J. (2003). Type 2 tasks in the theory of signal detectability: Discrimination between correct and incorrect decisions. Psychonomic Bulletin & Review, 10(4), 843–876.
Glenberg, A. M., & Epstein, W. (1987). Inexpert calibration of comprehension. Memory & Cognition, 15(1), 84–93. https://doi.org/10.3758/BF03197714.
Glenberg, A. M., Sanocki, T., Epstein, W., & Morris, C. (1987). Enhancing calibration of comprehension. Journal of Experimental Psychology: General, 116(2), 119–136. https://doi.org/10.1037/0096-3445.116.2.119.
Gonzalez, R., & Nelson, T. O. (1996). Measuring ordinal association in situations that contain tied scores. Psychological Bulletin, 119(1), 159–165. https://doi.org/10.1037/0033-2909.119.1.159.
Goodman, L. A., & Kruskal, W. H. (1954). Measures of Association for Cross Classifications. Journal of the American Statistical Association, 49(268), 732–764. https://doi.org/10.1080/01621459.1954.10501231.
Griffin, T. D., Wiley, J., & Thiede, K. W. (2008). Individual differences, rereading, and self-explanation: Concurrent processing and cue validity as constraints on metacomprehension accuracy. Memory & Cognition, 36(1), 93–103. https://doi.org/10.3758/MC.36.1.93.
Griffin, T. D., Jee, B. D., & Wiley, J. (2009). The effects of domain knowledge on metacomprehension accuracy. Memory & Cognition, 37(7), 1001–1013. https://doi.org/10.3758/MC.37.7.1001.
Hart, J. T. (1965). Memory and the feeling-of-knowing experience. Journal of Educational Psychology, 56(4), 208–216. https://doi.org/10.1037/h0022263.
Hart, J. T. (1967). Memory and the memory-monitoring process. Journal of Verbal Learning and Verbal Behavior, 6(5), 685–691. https://doi.org/10.1016/S0022-5371(67)80072-0.
Hautus, M. J. (1995). Corrections for extreme proportions and their biasing effects on estimated values ofd′. Behavior Research Methods, Instruments, & Computers, 27(1), 46–51. https://doi.org/10.3758/BF03203619.
Higham, P. A. (2007). No special K! A signal detection framework for the strategic regulation of memory accuracy. Journal of Experimental Psychology: General, 136(1), 1–22. https://doi.org/10.1037/0096-3445.136.1.1.
Higham, P. A., & Higham, D. P. (2018). New improved gamma: Enhancing the accuracy of GoodmanKruskal’s gamma using ROC curves. Behavior Research Methods, 51, 108–125. https://doi.org/10.3758/s13428-018-1125-5.
Janowsky, J. S., Shimamura, A. P., & Squire, L. R. (1989). Memory and metamemory: Comparisons between patients with frontal lobe lesions and amnesic patients. Psychobiology, 17(1), 3–11. https://doi.org/10.3758/BF03337811.
Kelley, C. M., & Lindsay, D. S. (1993). Remembering mistaken for knowing: Ease of retrieval as a basis for confidence in answers to general knowledge questions. Journal of Memory and Language, 32(1), 1–24. https://doi.org/10.1006/jmla.1993.1001.
Kelley, C. M., & Sahakyan, L. (2003). Memory, monitoring, and control in the attainment of memory accuracy. Journal of Memory and Language, 48(4), 704–721. https://doi.org/10.1016/S0749-596X(02)00504-1.
Kelly, K. J., & Metcalfe, J. (2011). Metacognition of emotional face recognition. Emotion, 11(4), 896–906. https://doi.org/10.1037/a0023746.
Kelly, M., Scholnick, E. K., Travers, S. H., & Johnson, J. W. (1976). Relations among memory, memory appraisal, and memory strategies. Child Development, 47(3), 648–659. https://doi.org/10.2307/1128179.
Knoblauch, K., & Maloney, L. T. (2012). Modeling psychophysical data in R. New York: Springer.
Koriat, A. (1997). Monitoring one’s own knowledge during study: A cue-utilization approach to judgments of learning. Journal of Experimental Psychology: General, 126(4), 349–370. https://doi.org/10.1037/0096-3445.126.4.349.
Koriat, A. (2008). Subjective confidence in one’s answers: The consensuality principle. Journal of Experimental Psychology: Learning, Memory, and Cognition, 34(4), 945–959. https://doi.org/10.1037/0278-7393.34.4.945.
Koriat, A. (2011). Subjective confidence in perceptual judgments: A test of the self-consistency model. Journal of Experimental Psychology: General, 140(1), 117–139. https://doi.org/10.1037/a0022171.
Koriat, A. (2012). The self-consistency model of subjective confidence. Psychological Review, 119(1), 80–113. https://doi.org/10.1037/a0025648.
Koriat, A., Sheffer, L., & Ma’ayan, H. (2002). Comparing objective and subjective learning curves: Judgments of learning exhibit increased underconfidence with practice. Journal of Experimental Psychology: General, 131(2), 147–162. https://doi.org/10.1037/0096-3445.131.2.147.
Kornell, N., Son, L. K., & Terrace, H. S. (2007). Transfer of metacognitive skills and hint seeking in monkeys. Psychological Science, 18(1), 64–71. https://doi.org/10.1111/j.1467-9280.2007.01850.x.
Krajc, M., & Ortmann, A. (2008). Are the unskilled really that unaware? An alternative explanation. Journal of Economic Psychology, 29(5), 724–738. https://doi.org/10.1016/j.joep.2007.12.006.
Kruger, J., & Dunning, D. (1999). Unskilled and unaware of it: How difficulties in recognizing One’s own incompetence Lead to inflated self-assessments. Journal of Personality and Social Psychology, 77(6), 14.
Lichtenstein, S., & Fischhoff, B. (1977). Do those who know more also know more about how much they know? Organizational Behavior and Human Performance, 20(2), 159–183. https://doi.org/10.1016/0030-5073(77)90001-0.
Maki, R. H., & Berry, S. L. (1984). Metacomprehension of text material. Journal of Experimental Psychology: Learning, Memory, and Cognition, 10(4), 663–679. https://doi.org/10.1037/0278-7393.10.4.663.
Maniscalco, B., & Lau, H. (2012). A signal detection theoretic approach for estimating metacognitive sensitivity from confidence ratings. Consciousness and Cognition, 21(1), 422–430. https://doi.org/10.1016/j.concog.2011.09.021.
Masson, M. E. J., & Rotello, C. M. (2009). Sources of bias in the GoodmanKruskal gamma coefficient measure of association: Implications for studies of metacognitive processes. Journal of Experimental Psychology: Learning, Memory, and Cognition, 35(2), 509–527. https://doi.org/10.1037/a0014876.
McIntosh, R. D., Fowler, E. A., Lyu, T., & Della Sala, S. (2019). Wise up: Clarifying the role of metacognition in the Dunning-Kruger effect. Journal of Experimental Psychology: General. No Pagination Specified–No Pagination Specified. https://doi.org/10.1037/xge0000579.
Metcalfe, J. (2009). Metacognitive judgments and control of study. Current Directions in Psychological Science, 18(3), 159–163. https://doi.org/10.1111/j.1467-8721.2009.01628.x.
Metcalfe, J., & Finn, B. (2008). Evidence that judgments of learning are causally related to study choice. Psychonomic Bulletin & Review, 15(1), 174–179. https://doi.org/10.3758/PBR.15.1.174.
Metcalfe, J., Schwartz, B. L., & Joaquim, S. G. (1993). The cue-familiarity heuristic in metacognition. Journal of Experimental Psychology: Learning, Memory, and Cognition, 19(4), 851–861. https://doi.org/10.1037/0278-7393.19.4.851.
Morales, J., Lau, H., & Fleming, S. M. (2018). Domain-general and domain-specific patterns of activity supporting metacognition in human prefrontal cortex. Journal of Neuroscience, 38(14), 3534–3546. https://doi.org/10.1523/JNEUROSCI.2360-17.2018.
Nelson, T. O. (1984). A comparison of current measures of the accuracy of feeling-of-knowing predictions. Psychological Bulletin, 95(1), 109–133. https://doi.org/10.1037/0033-2909.95.1.109.
Nelson, T. O., & Dunlosky, J. (1991). When People’s judgments of learning (JOLs) are extremely accurate at predicting subsequent recall: The “delayed-JOL effect”. Psychological Science, 2(4), 267–271. https://doi.org/10.1111/j.1467-9280.1991.tb00147.x.
Nelson, T. O., & Narens, L. (1980). Norms of 300 general-information questions: Accuracy of recall, latency of recall, and feeling-of-knowing ratings. Journal of Verbal Learning and Verbal Behavior, 19(3), 338–368. https://doi.org/10.1016/S0022-5371(80)90266-2.
Nelson, T. O., & Narens, L. (1990). Metamemory: A theoretical framework and new findings. In G. H. Bower (Ed.), Psychology of learning and motivation (Vol. 26, pp. 125–173). San Diego: Academic Press. https://doi.org/10.1016/S0079-7421(08)60053-5.
Nelson, T. O., & Narens, L. (1994). Why investigate metacognition. In Metacognition: Knowing about knowing, 13, 1–25. Cambridge: The MIT Press.
Nelson, T. O., Dunlosky, J., Graf, A., & Narens, L. (1994). Utilization of metacognitive judgments in the allocation of study during multitrial learning. Psychological Science, 5(4), 207–213. https://doi.org/10.1111/j.1467-9280.1994.tb00502.x.
O’Leary, A. P., & Sloutsky, V. M. (2017). Carving metacognition at its joints: Protracted development of component processes. Child Development, 88(3), 1015–1032. https://doi.org/10.1111/cdev.12644.
R Core Team. (2019). R: A language and environment for statistical computing. Vienna: R Foundation for Statistical Computing.
Rawson, K. A., Dunlosky, J., & Thiede, K. W. (2000). The rereading effect: Metacomprehension accuracy improves across reading trials. Memory & Cognition, 28(6), 1004–1010. https://doi.org/10.3758/BF03209348.
Schraw, G. (1996). The effect of generalized metacognitive knowledge on test performance and confidence judgments. The Journal of Experimental Education, 65(2), 135–146. https://doi.org/10.1080/00220973.1997.9943788.
Schwartz, B. L., & Metcalfe, J. (1994). Methodological problems and pitfalls in the study of human metacognition. In J. Metcalfe & A. P. Shimamura (Eds.), Metacognition: Knowing about knowing. Cambridge: MIT Press.
Shimamura, A. P., & Squire, L. R. (1986). Memory and metamemory: A study of the feeling-of-knowing phenomenon in amnesic patients. Journal of Experimental Psychology: Learning, Memory, and Cognition, 12(3), 452–460. https://doi.org/10.1037/0278-7393.12.3.452.
Siegler, R. S., & Pyke, A. A. (2013). Developmental and individual differences in understanding of fractions. Developmental Psychology, 49(10), 1994–2004. https://doi.org/10.1037/a0031200.
Son, L. K., & Metcalfe, J. (2000). Metacognitive and control strategies in study-time allocation. Journal of Experimental Psychology: Learning, Memory, and Cognition, 26(1), 204–221. https://doi.org/10.1037/0278-7393.26.1.204.
Tauber, S., & Dunlosky, J. (2016). A brief history of metamemory research and handbook overview. In The Oxford handbook of metamemory (pp. 7–21). Oxford: Oxford University Press.
Tauber, S. K., Dunlosky, J., Rawson, K. A., Rhodes, M. G., & Sitzman, D. M. (2013). General knowledge norms: Updated and expanded from the Nelson and Narens (1980) norms. Behavior Research Methods, 45(4), 1115–1143. https://doi.org/10.3758/s13428-012-0307-9.
Thiede, K. W. (1999). The importance of monitoring and self-regulation during multitrial learning. Psychonomic Bulletin & Review, 6(4), 662–667. https://doi.org/10.3758/BF03212976.
Thiede, K. W., & Anderson, M. C. M. (2003). Summarizing can improve metacomprehension accuracy. Contemporary Educational Psychology, 28(2), 129–160. https://doi.org/10.1016/S0361-476X(02)00011-5.
Thiede, K. W., & Dunlosky, J. (1994). Delaying students’ metacognitive monitoring improves their accuracy in predicting their recognition performance. Journal of Educational Psychology, 86(2), 13.
Thiede, K. W., Redford, J. S., Wiley, J., & Griffin, T. D. (2012). Elementary school experience with comprehension testing may influence metacomprehension accuracy among seventh and eighth graders. Journal of Educational Psychology, 104(3), 554–564. https://doi.org/10.1037/a0028660.
van der Loo, M. P. J. (2014). The stringdist package for approximate string matching. The R Journal, 6(1), 111–122.
Wall, J. L., Thompson, C. A., Dunlosky, J., & Merriman, W. E. (2016). Children can accurately monitor and control their number-line estimation performance. Developmental Psychology, 52(10), 1493–1502. https://doi.org/10.1037/dev0000180.
Wiley, J., Griffin, T. D., Jaeger, A. J., Jarosz, A. F., Cushen, P. J., & Thiede, K. W. (2016). Improving metacomprehension accuracy in an undergraduate course context. Journal of Experimental Psychology: Applied, 22(4), 393–405. https://doi.org/10.1037/xap0000096.
Funding
This research was supported, in part, by Institute of Education Science grant (R305A150467) awarded to JM.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Informed consent
All participants provided informed consent.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Vuorre, M., Metcalfe, J. Measures of relative metacognitive accuracy are confounded with task performance in tasks that permit guessing. Metacognition Learning 17, 269–291 (2022). https://doi.org/10.1007/s11409-020-09257-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11409-020-09257-1