Rebalancing with transaction costs: theory, simulations, and actual data

Abstract

In the absence of transaction costs and the presence of independent returns, a buy-and-hold strategy theoretically generates higher expected returns than a fixed-weight strategy, where the portfolio weights are regularly readjusted/rebalanced to some initial level. This higher expected return comes with higher volatility. The resulting trade-off leads to different rankings of the Sharpe ratio depending on the statistical moments of the assets. We also focus on Maximum Drawdown. We theoretically discuss causes affecting the ranking of the Sharpe ratio, and we introduce an easy-to-implement methodology to deal with proportional transaction costs. Under transaction costs, the buy-and-hold strategy as the cheaper approach should be the winner. In various simulation experiments, we investigate the relevance of transaction costs on rebalancing strategies. Eventually, we consider several realistic portfolios with a risk-free asset, bonds, stock indices, commodities and real estate that allow us to demonstrate that in practice rebalancing has value.

1 Introduction

Investment portfolios contain risky assets whose value fluctuates over time. Therefore, the proportions of these assets also change over time and can substantially deviate from the initial allocation. A common practice to counter these changes is called portfolio rebalancing, also known as a fixed-weight strategy (FW). It is a contrarian strategy consisting of selling successful assets and buying losers, thereby restoring a predetermined set of portfolio weights. The main objective of rebalancing is to maintain a given (strategic) asset allocation and therefore maintain the risk profile of the portfolio in line with the risk tolerance of the investor. However, since rebalancing strategies involve selling a fraction of the best-performing assets and investing in the worst, if certain asset categories have momentum, it is difficult a priori to determine whether rebalancing generates an outperformance compared to buy and hold (BH), where a given initial portfolio is just held over time. Furthermore, this is particularly true in the presence of transaction costs.

A large and important stream of literature has focused on the comparison between FW and BH, but the conclusions substantially differ depending on, inter alia, the horizon and universe of investment as well as the transaction costs.

Early empirical studies demonstrate that with transaction costs, the rebalancing strategy leads to lower volatilities and, thus, better risk-adjusted returns. For example, an early paper by Perold and Sharpe (1988) shows that rebalancing strategies perform best in volatile markets. Arnott and Lovell (1993) demonstrate that nine of ten rebalancing strategies have a higher Treynor ratio than the BH strategy. The historical simulations conducted by Dichtl et al. (2012) show that a rebalancing strategy outperforms in terms of Sharpe ratios, Sortino ratios, and Omega measures in all the markets investigated. Zilbering et al. (2015) examined the value added by rebalancing strategies over the longest period ever tested (from 1926 to 2015) and found that the reduction in volatilities is approximately 3.5%. The outperformance is often linked to some characteristic: Plaxco and Arnott (2002) find that rebalancing strategies consistently outperform drifting mix strategies when the major asset classes have similar levels of return. Tokat and Wicas (2007) conclude that the risk is minimized in both mean-reversion markets and random walks, and Hilliard and Hilliard (2018) report that the risk is minimized when the momentum factor is low. In contrast Dayanandan and Lam (2015) advise for US stocks against active portfolio management.

Many studies focused on the comparison of different rebalancing strategies such as the calendar-based and constant-mix method. However, it is very difficult to draw a clear and precise conclusion. For example, Plaxco and Arnott (2002) recommend a monthly rebalancing strategy to investors with a long investment horizon, while Buetow et al. (2002) recommend a daily monitoring frequency together with a 5% inaction region within which asset prices may drift. Sun et al. (2006) developed a unique strategy of rebalancing that minimizes cost using stochastic programming.

For the empirical investigation of allocations we rely on selected benchmark portfolios as might be held by institutional investors. Such a choice has also been made by Leland (2000). Using benchmark portfolios instead of explicit portfolio optimization eschews the issue of estimating expected returns, which is a known difficulty. In practice small pension funds must by law choose long-term portfolio allocations where the weights allocated to different asset categories are given. Similarly for the amount of foreign currency exposure. Large pension funds may decide on broader asset categories and will still give themselves strategic allocations determined by ‘experts’ instead of relying on quantitative models. Deviations from those strategic allocations yield tactical allocations, typically allowed to fluctuate within certain boundaries around the strategic allocation.

The goal of this paper is to provide pension fund managers with a tool to understand the consequences of rebalancing their portfolio while dealing with transactions costs, predictability of assets and regions of inaction. Obviously, there exists a large body of sophisticated models dealing with all those aspects. Noticeable contributions are Constantinides (1976b), Constantinides (1976a), Magill and Constantinides (1976), Davis and Norman (1990), Dumas and Luciano (1991), Cvitanić and Karatzas (1992), Edirisinghe et al. (1993), Gennotte and Jung (1994), Shreve and Soner (1994), Kim and Omberg (1996), Leland (2000), Longstaff (2001), Bouchard (2002), Liu and Loewenstein (2002), Jang et al. (2007), Obizhaeva and Wang (2013), Ekren et al. (2018), Buss and Dumas (2019).

In this paper, we determine under which condition the Sharpe ratio of an FW strategy is higher than the BH strategy when transaction costs are incorporated. We also emphasize the consequence of rebalancing on Maximum Drawdown (MDD). Our first contribution is to introduce a methodology to deal with proportional transaction costs. This methodology is easy to implement and can be extended to portfolios with multiple assets. Obviously, we are not the first to consider transaction costs. An early study by Davis and Norman (1990) demonstrates that transaction costs imply a no-trade region of asset prices, where it is not optimal to trade. An important body of literature studies how to choose this inaction band. Dumas and Luciano (1991) determined the exact solution of the optimization problem in the form of two control barriers. In general, with only variable costs, any trading is to the boundary of the nontrading region, while fixed cost induces trading to the interior; see also Dybvig and Pezzo (2019). In this type of literature, the portfolio allocation should be as close to a given strategic allocation. The weighting of allocation discrepancies is done with a variance-covariance matrix, which is something we wish to avoid since it involves some form of optimization. Optimal rebalancing with no-trade bands can provide both higher returns and lower risk than other common rebalancing strategies (see Donohue and Yip (2003)). It is shown in Gârleanu and Pedersen (2013) how to introduce predictability of assets in addition to transactions costs.

Our second contribution is to present a numerical methodology to generate univariate or multivariate autocorrelated series so that the geometric mean of returns has a given expected value and a given standard deviation. This contribution allows us to account for the autocorrelation terms among returns that play a role in realistic portfolio allocations involving simple returns. As shown by Qian (2019), neglecting this aspect may lead to an erroneous classification of FW and BH allocations. The results of our algorithm reveal that the consequences are of first order and not of second order.

A third methodological contribution is that we develop a simple methodology, in the context of predictable asset returns, to construct a window of inaction that evolves dynamically as a function of the return-predictor. This method allows, for instance, enlarging the window in the case of low price-dividend ratios since low price-dividend ratios tend to be followed by price increases (assuming that returns can be predicted). Even though we present the window-of-inaction methodology in the context of predictability, it may be applied to other contexts. Again, we are not the first to deal with windows of inaction. They emerged already in Davis and Norman (1990). Other contributions in this setting are by Martin and Schöneborn (2011), contributions that consider momentum are Balduzzi and Lynch (1999), Lynch and Balduzzi (2000), Lynch and Tan (2011), Martin (2014), Lynch and Tan (2010), In the context of option hedging one finds: Whalley and Wilmott (1997), De Lataillade et al. (2012), Kallsen and Muhle-Karbe (2015).

Having all those ingredients, we investigate in various simulation experiments the relevance of asset characteristics, window of inaction, and transaction costs. In a two-asset setting, we show that the BH strategy dominates the rebalancing strategy except for situations where the autocorrelation of assets is strong and negative and when the correlation between assets is also negative. Those simulations, therefore, corroborate in a quantitative manner the theoretical results.

Subsequently, we apply our method to several portfolios representative of what a Swiss pension fund may manage. The portfolio consists of a risk-free asset, bonds, and several equity indices, commodities, real estate over a period from January 1st, 1999, to June 30th, 2021. The manager reallocates the portfolio every month. We demonstrate that for this practical exercise rebalancing matters economically even though it is not statistically different from a buy and hold allocation.

In Sect. 2, we develop a methodology for taking into account transaction costs in a rebalancing strategy, and then, in a second step, we build on Qian (2019) and present theoretical results that guide our later simulation exercises. Section 3 presents the different simulation experiments. The choice of simulations is based on the theoretical aspects discussed in Sect. 2, which provides us with some guidance on how to choose parameters. We test several portfolios, namely portfolios with and without risk-free assets and multi-asset portfolios, and we investigate the consequence of transaction costs within portfolio insurance. Finally, Sect. 4 discusses the results of actual allocations as one may find in a representative Swiss pension fund.

2 Theory

2.1 Rebalancing under transaction costs

We denote the price of asset $i=1,\ldots ,M$ at time t by $S_{i,t}.$ One of those assets may be the risk-free asset (cash), denoted by $B_t.$ Let $\theta _{i,t}$ be the number of units of asset i at time t in a trading strategy or portfolio. The portfolio is set up at time $t=0$ and may be rebalanced at times 1,2,$\cdots .$ The value of a portfolio at time t is denoted by $V_t.$ We let $\tau _i$ for $i=1,\ldots ,M$ be the transaction costs that we assume to be proportional to the value of shares traded. The investor will rebalance the portfolio at dates t. An instant before rebalancing, which we denote by $t-$, the prices are all assumed known, and the modification of the portfolio will take place instantaneously and without price impact so that just after rebalancing, for example, at time t, the weights are adjusted and the value of the portfolio has evolved according to

$$\begin{aligned} V_t=V_{t-}-\text {transaction costs.} \end{aligned}$$

The value of the portfolio before rebalancing is

$$\begin{aligned} V_{t-}=\sum _{i=1}^M \theta _{i,t-1}\, S_{i,t}. \end{aligned}$$

The transaction cost for asset i is given by $|\theta _{i,t}-\theta _{i,t-1}|S_{i,t}\tau _i.$ Hence,

$$\begin{aligned} V_t=V_{t-}-\sum _{i=1}^M |\theta _{i,t}-\theta _{i,t-1}|S_{i,t}\tau _i. \end{aligned}$$

After rebalancing, asset i should have a portfolio weight denoted by $a_{i,t}$ that is given exogenously. This allocation $a_{i,t}$ can be a fixed weight or can vary over time, which would be the case, for instance, in an optional duplicating strategy. The question is as follows: how must $\theta _{i,t}$ be modified for $i=1,\ldots ,M$ so that the proportion $a_{i,t}$ will be achieved after the transaction cost has been paid?

By definition

$$\begin{aligned} a_{i,t}=\frac{\theta _{i,t}S_{i,t}}{V_t}. \end{aligned}$$

Hence,

$$\begin{aligned} \theta _{i,t}\,S_{i,t}=a_{i,t}\,V_t=a_{i,t}\left[ V_{t-}-\sum _{i=1}^M |\theta _{i,t}-\theta _{i,t-1}|S_{i,t}\tau _i.\right] , \quad \text {for } i=1,\ldots ,M.\nonumber \\ \end{aligned}$$

(1)

In the absence of the absolute value, this set of equations would yield a system of M equations of M unknowns and would be trivial to solve. In the two-asset case, the discussion of the signs of the weight changes is trivial; in the general case, the discussion is more evolved. Since

$$\begin{aligned} |x|=\left\{ \begin{array}{cc} x &{} \text { if } x>0,\\ -x&{}\text {else}, \end{array}\right. \end{aligned}$$

one can rewrite the absolute value of x after introduction of some auxiliary variable denoted by e as $|x|=e\,x$, where $e=1$ if $x>0$ and $e=-1$ if $x\le 0.$ We therefore introduce at each period of time, when the portfolio should be rebalanced, a set of M variables $e_i\in \{+1,-1\}.$ We solve the system for such a set of $e_i,$ resulting in a set of $\theta _{i,t}.$ The resulting weight changes $\theta _{i,t}-\theta _{i,t-1}$ will then have either a positive or a negative sign. If the $e_i$ cover the full range of possible permutations, one obtains a set of potential allocations. One needs then to retain the solution that is compatible with the given $e_i,$ for all i. In other words, for all the assets, the signs of the weight changes should be of the same sign as the $e_i.$ Before presenting the general solution, let us discuss the pedagogical case with 2 assets that will illustrate the workings of our method. Equation (1) can then be written as

$$\begin{aligned} \theta _{1,t}\,S_{1,t}= & {} a_{1,t}\left[ V_{t-}-|\theta _{1,t}-\theta _{1,t-}|S_{1,t}\tau _1- |\theta _{2,t}-\theta _{2,t-}|S_{2,t}\tau _2\right] ,\\ \theta _{2,t}\,S_{2,t}= & {} a_{2,t}\left[ V_{t-}-|\theta _{1,t}-\theta _{1,t-}|S_{1,t}\tau _1- |\theta _{2,t}-\theta _{2,t-}|S_{2,t}\tau _2\right] . \end{aligned}$$

There are 4 cases given by the 2 possible signs of $\theta _{i,t}-\theta _{i,t-},$ and this is true for both assets. Introduce $e_1$ and $e_2$, and assume that all assets are included in the portfolio, $a_{i,t}\ne 0,$ yielding the system

$$\begin{aligned} \theta _{1,t}\,S_{1,t}/a_{1,t}= & {} V_{t-}-(\theta _{1,t}-\theta _{1,t-})S_{1,t}\tau _1e_1- (\theta _{2,t}-\theta _{2,t-})S_{2,t}\tau _2e_2,\\ \theta _{2,t}\,S_{2,t}/a_{2,t}= & {} V_{t-}-(\theta _{1,t}-\theta _{1,t-})S_{1,t}\tau _1e_1- (\theta _{2,t}-\theta _{2,t-})S_{2,t}\tau _2e_2. \end{aligned}$$

This system can be rewritten with matrices

$$\begin{aligned}&\left( \begin{array}{cc} S_{1,t}/a_{1,t}+S_{1,t}\tau _1e_1&{} S_{2,t}\tau _2 e_2\\ S_{1,t}\tau _1 e_1&{}S_{2,t}/a_{2,t}+S_{2,t}\tau _2e_2. \end{array}\right) \left( \begin{array}{c} \theta _{1,t}\\ \theta _{2,t} \end{array}\right) \\&\quad \qquad =(V_{t-}-\theta _{1,t-}S_{1,t}\tau _1e_1- \theta _{2,t-}S_{2,t}\tau _2e_2) \left( \begin{array}{c} 1\\ 1 \end{array}\right) . \end{aligned}$$

This system has generically a solution in $\theta _{1,t}$ and $\theta _{2,t}$ if the determinant of the LHS matrix is different from 0. This determinant is given by

$$\begin{aligned} \text {det}\left| \begin{array}{cc} S_{1,t}/a_{1,t}+S_{1,t}\tau _1e_1&{} S_{2,t}\tau _2 e_2\\ S_{1,t}\tau _1 e_1&{}S_{2,t}/a_{2,t}+S_{2,t}\tau _2e_2 \end{array} \right|= & {} S_{1,t}S_{2,t}\left( \frac{1}{a_{1,t}}+\tau _1e_1 \right) \left( \frac{1}{a_{2,t}}+\tau _2e_2 \right) \\&-S_{1,t}S_{2,t}\tau _1\tau _2e_1e_2. \end{aligned}$$

Since we may assume that the prices of the assets are different from 0, this determinant is different from 0 if

$$\begin{aligned} \left( \frac{1}{a_{1,t}}+\tau _1e_1 \right) \left( \frac{1}{a_{2,t}}+\tau _2e_2 \right) -\tau _1\tau _2e_1e_2\ne 0. \end{aligned}$$

However, this will be the case if $1+a_{1,t}\tau _1e_1+a_{2,t}\tau _2e_2\ne 0.$ This condition can be easily checked for given $e_1$ and $e_2.$ Once a solution has been found for the system yielding $\theta _{1,t}$ and $\theta _{2,t}$, it is possible to determine the signs of $\theta _{1,t}-\theta _{1,t-}$ and of $\theta _{2,t}-\theta _{2,t-}.$ If the signs coincide with the values of $e_1$ and $e_2$, the solution may be kept. Formally, introduce the sign function defined by

$$\begin{aligned} \text {sign}(x)=\left\{ \begin{array}{cc} 1 &{} \text { if } x>0,\\ 0 &{} \text { if } x=0,\\ -1&{}\text { if } x<0. \end{array}\right. \end{aligned}$$

Thus, if

$$\begin{aligned} |\text {sign}(\theta _{1,t}-\theta _{1,t-})-e_1|+ |\text {sign}(\theta _{2,t}-\theta _{2,t-})-e_2|=0, \end{aligned}$$

then the solution can be accepted. Indeed, it is easy to verify that only if $\text {sign}(\theta _{1,t}-\theta _{1,t-})=e_1$ and $\text {sign}(\theta _{2,t}-\theta _{2,t-})=e_2$ does the above sum equal 0.

To obtain all possible choices of signs in e, one may notice that the rows of the following matrix represent all possible choices of signs

$$\begin{aligned} E=\left[ \begin{array}{rr} 1&{}\quad 1\\ 1&{}\quad -1\\ -1&{}\quad 1\\ -1&{}\quad -1 \end{array}\right] . \end{aligned}$$

Such a matrix is, however, easy to construct from a matrix:

$$\begin{aligned} E'=\left[ \begin{array}{rr} 0&{}\quad 0\\ 0&{}\quad 1\\ 1&{}\quad 0\\ 1&{}\quad 1 \end{array}\right] . \end{aligned}$$

simply by mapping all 1 values of $E'$ into -1 and all 0 values of $E'$ into 1.

In turn, we recognize in $E'$, row-wise, the binary representation of the numbers $0,1,2,3=2^{M-1}.$ Thus, by transforming the integers 0, 1, 2, and 3 into their binary representation, by associating the various bits with the elements in a row in $E'$ and by performing the above described mapping, one generates the matrix E instantaneously.¹

In the general case, the matrix will be depicted as follows, where the last column represents the number required for the binary representation and the map

We can presently extend the resolution technique to the general case with $M>2$ assets. Denote by e a given row of E. Let $e=(e_1,e_2,\cdots e_M).$ Equation (1) generalizes into

$$\begin{aligned} a_{i,t}=\frac{\theta _{i,t}S_{i,t}}{V_t}. \end{aligned}$$

Hence,

$$\begin{aligned} \theta _{i,t}\,S_{i,t}/a_{i,t}= V_{t-}-\sum _{j=1}^M (\theta _{j,t}-\theta _{j,t-})S_{j,t}\tau _je_j, \text { for } i=1,\ldots , M, \end{aligned}$$

yielding the system:

$$\begin{aligned} \theta _{i,t}\,S_{i,t}/a_{i,t}+\sum _{j=1}^M \theta _{j,t}S_{j,t}\tau _je_j = V_{t-}+\sum _{j=1}^M \theta _{j,t-}S_{j,t}\tau _je_j, \end{aligned}$$

where we notice that the RHS does not depend on i and is therefore a constant. This system can be rewritten with matrices as

$$\begin{aligned}&\left[ \text {diag}(S_{1,t}/a_{1,t},S_{2,t}/a_{2,t},\cdots S_{M,t}/a_{M,t}) +(S_{1,t}\tau _1e_1,S_{2,t}\tau _2e_2,\ldots ,S_{M,t}\tau _Me_M)\otimes {\mathbb {I}}_{M} \right] \theta _t\nonumber \\&\qquad =\left( V_{t-}+\sum _{j=1}^M \theta _{j,t-}S_{j,t}\tau _je_j\right) \otimes {\mathbb {I}}_{M}), \end{aligned}$$

(2)

where diag(x) is a diagonal matrix with the elements of a vector x on the diagonal and 0 elsewhere. $\otimes$ denotes the Kronecker symbol. Additionally, ${\mathbb {I}}_{M}$ represents an $M\times 1$ vector of 1.

For each element of E, one computes the vector $\theta _t$ by solving the multivariate system (2). Eventually, for the rebalancing at time t, one retains the couple of allocations $\theta _t$, and vector of signs e satisfying

$$\begin{aligned} \sum _{j=1}^M |\text {sign}(\theta _{j,t}-\theta _{j,t-})-e_j|=0. \end{aligned}$$

It turns out that for all the simulations considered, there is always only one unique solution in $\theta _t$ satisfying this condition. We therefore conjecture that it ought to be a general property, even though we have not been able to demonstrate this point explicitly.

2.2 Optimization under transactions costs

In this section, we wish to show how the traditional Markowitz portfolio allocation can be extended to incorporate transactions costs. The traditional Markowitz optimization is given by

$$\begin{aligned} \begin{array}{cl} \max _a &{}\quad E[r^p(a)]\\ \text {s.t.} &{}\quad Risk(r^p(a))\le d,\\ &{}\quad \sum \limits _{i=1}^M a_{i}=1, \end{array} \end{aligned}$$

where a is the vector of portfolio allocations, given as percentages, to be allocated to the various assets whose returns are given by a vector $r^p$. The second equation specifies that risk should be limited and the third equation states that the weights on the assets should sum to one. Inspection of this program shows that the generic measure called ‘Risk’ can be a variance or another measure of risk. As long as the constraints can be written as functions an optimizer will be able to handle this problem even though the solution may no longer be expressed as linear functions.

We would like to emphasize that the methodology developed earlier is perfectly compatible with an optimization logic. The methodology generates a number, the transactions cost TC(a) per unit of time given an initial wealth $W_0$, and this for a given vector of portfolio weights a. The ratio $TC(a)/W_0$ represents the performance reduction in percent of a portfolio and if one considers the extended Markowitz optimization

$$\begin{aligned} \begin{array}{cl} \max _a &{}\quad E[r^p(a)]-TC(a)/W_0\\ \text {s.t.} &{}\quad Risk(r^p(a))\le d,\\ &{}\quad \sum \limits _{i=1}^M a_{i}=1, \end{array} \end{aligned}$$

then one can perform an optimization using variance or any other risk measure such as VaR, CVaR and Mean Absolute Deviation (MAD).

In our empirical work we wish to remain agnostic concerning the expected returns and we will take popular allocations. We introduce nonetheless as a measure of risk Maximum Drawdown (MDD) defined for instance in Chekhlov et al. (2005). For some stochastic process $X_t$, obtained by cumulating returns, the MDD at time T is defined as

$$\begin{aligned} MDD(T)=\max _{\tau \in (0,T)}\left[ \max _{t \in (0,\tau )} X_t-X_\tau \right] . \end{aligned}$$

The contribution by Chekhlov et al. (2005) shows how linear programming tools can be used to optimize a portfolio with respect to MDD. Their approach does not allow optimization under transactions costs however.

2.3 Theoretical aspects concerning fixed-weight and buy-and-hold strategies

In the previous section, we presented a method to rebalance a portfolio by incorporating transaction costs. In this section, we investigate the consequences of incorporating transaction costs into various trading strategies. The considered cases are the rebalancing of a portfolio as well as optional trading strategies.

2.3.1 Portfolio rebalancing without transaction costs

It is well-known that in a buy-and-hold (BH) strategy, certain assets see their value drift over time. This has as a consequence of modifying the riskiness of a portfolio. Before describing a simulation framework within which one can investigate the consequences of rebalancing, that is, reallocating a portfolio to some given weights, it is useful to understand why rebalancing may lead to better performance than a BH strategy. Much of our development directly follows the remarkable work by Qian (2019).

Let $r_{i,t}$ denote the simple return of an asset i between time $t-1$ and t. Typically, in the context of portfolio allocation, $r_{i,t}=S_{i,t}/S_{i,t-1}-1.$ In Fig. 1, we consider 2 assets at 2 different times. In the first case, the investor follows a buy-and-hold strategy, and in the second, she follows a fixed-weight (FW) strategy. Denote by $a_1,a_2$ the allocations, that is, the weight, for assets 1 and 2. Obviously, $a_1+a_2=1.$

Fig. 1

This picture illustrates the difference between a buy-and-hold strategy, presented in the upper part of the figure, and a fixed-weight strategy, also called a rebalancing strategy. In a buy-and-hold strategy, the initial wealth is attributed to the two assets that evolve in value over time driven by their returns. In a rebalancing strategy, the value of the portfolio is reallocated at each period of time. The final wealth for the fixed-weight strategy is given by $W_0[a_1(1+r_{1,1})+a_2(1+r_{2,1})][a_1(1+r_{1,2}) +a_2(1+r_{2,2})]$

Hence, for the BH strategy, the terminal wealth is

$$\begin{aligned} W_2^{BH}=W_0\left[ a_1(1+r_{1,1})(1+r_{1,2})+a_2(1+r_{2,1})(1+r_{2,2})\right] . \end{aligned}$$

Similarly, for the fixed-weight strategy, after one period, the portfolio value is $W_1=W_0\left[ a_1(1+r_{1,1})+ a_2(1+r_{2,1}) \right]$ and after the second period if becomes

$$\begin{aligned} W_2^{FW}= & {} W_1\left[ a_1(1+r_{1,2})+a_2(1+r_{2,2})\right] \\= & {} W_0\left[ a_1(1+r_{1,1})+a_2(1+r_{2,1})\right] \left[ a_1(1+r_{1,2})+a_2(1+r_{2,2})\right] . \end{aligned}$$

The expressions for $W_2^{BH}$ and $W_2^{FW}$ can be easily generalized to any number of assets and any number of time periods.

In the case of M assets, let $a=(a_1,a_2,\ldots ,a_M)$ be the vector of allocations. In addition, let $r_1=(r_{1,1},r_{2,1},,\ldots ,r_{M,1})$ and $r_2=(r_{1,2},r_{2,2},,\ldots ,r_{M,2})$ be the cross-sectional return vectors for time 1 and time 2, respectively. Denote by $\odot$ the element by element multiplication.²

We obtain that

$$\begin{aligned} W_2^{BH}= & {} W_0[a'(1+r_1)\odot (1+r_2)],\\ W_2^{FW}= & {} W_0[a'(1+r_1)\cdot a'(1+r_2)]. \end{aligned}$$

After developing, one obtains that

$$\begin{aligned} W_2^{FW}-W_2^{BH}=-W_0[a'(r_1\odot r_2) -(a'\,r_1)( a'\,r_2)]. \end{aligned}$$

We recognize an expression similar to a covariance where the weights a act as probabilities of the return realizations.³ The buy-and-hold strategy will generate higher wealth than the fixed-weight strategy if the cross-sectional covariance of the assets is positive. According to Qian (2019), we obtain after development of the various terms that

$$\begin{aligned} D=W_2^{FW}-W_2^{BH}=-a_1\,a_2\,W_0\,(r_{11}-r_{21})\,(r_{12}-r_{22}). \end{aligned}$$

(3)

This theoretical formula demonstrates that, in the case where both assets are long, the FW strategy outperforms the BH one when the spread differentials, that is, the difference in the cross section between two assets, have a negative product. The difference between the two allocations is known as rebalancing alpha. To get an idea of the order of magnitude of this difference, assume an equally weighted portfolio, and let $W_0=100.$ Assume asset one is a stock with a return in one month of 3% and of -3% in the next month. Assume that the second asset is a bond with a return of 0. Then $D=0.25*0.03^2=0.000225$. If this game goes on for an entire year, the final difference is of the magnitude of 1.35bp, a very small difference in practice.

There are various properties of the FW and BH strategies that can be discussed with Equation (3).

Proposition 1

The differential $W_2^{FW}-W_2^{BH}$ is largest for the equally weighted portfolio, i.e., when $a_1=a_2=1/2.$

Proof

$a_2=1-a_1.$ Hence, $a_1a_2=a_1-a_1^2.$ Maximization yields $a_1=1/2$. $\square$

Proposition 2

Suppose that the first asset is the risk-free asset, that is, an asset with 0 volatility, and define $r_1=r_f.$ Let the second asset be some risky asset. It is convenient to change notation and denote by r the random return of the risky asset with realizations for times 1 and 2 of $r_1,r_2.$ If the autocorrelation of r is zero, then the BH strategy has a higher expected value than the FW strategy. Denote by $\mu =E[r],$ and $\sigma ^2=V[r]$ the expected return and its variance. Denote by $\rho _{1,2}$ the autocorrelation of the risky asset; then,

$$\begin{aligned} E[D]=-a_1a_2\{\rho _{1,2}\sigma ^2+(\mu -r_f)^2\}. \end{aligned}$$

(4)

Proof

Let $D=(W_2^{FW}-W_2^{BH})/W_0=-a_1a_2(r_1-r_f)(r_2-r_f).$ Then,

$$\begin{aligned} E[D]= & {} -a_1a_2E[(r_1-r_f)(r_2-r_f)]\\= & {} -a_1a_2 \{E[r_1r_2]-r_fE[r_1+r_2]+r_f^2\}\\= & {} -a_1a_2\{\rho _{1,2}\sigma ^2+(\mu -r_f)^2\}. \end{aligned}$$

$\square$

It follows that if $\rho _{1,2}=0$, then $E[D]<0,$ and $E[W_2^{FW}]< E[W_2^{BH}].$

In practice, stock returns exhibit short-term price reversals over weeks or a few months leading to negative autocorrelation, and in the long run, over several months, they exhibit momentum where past winners continue to outperform.⁴ This observation suggests that, in the longer run, a buy-and-hold strategy should yield higher wealth than the rebalancing strategy. The intuition for this result is that if price increases are followed by further price increases, rebalancing prevents successful assets from taking full advantage of the subsequent price increase. Symmetrically, after a price drop, rebalancing increases the part of the risky asset in the portfolio that will lead to a subsequent drop in value if the price continues to drop. A portfolio that would have been left alone would have performed better.

Corollary 1

As long as $\rho _{1,2}>-(SR)^2$, meaning that the autocorrelation is larger than minus the square of the Sharpe ratio, then $E[W_2^{FW}]< E[W_2^{BH}].$

Proof

It follows immediately from the formula of the previous property. $\square$

Proposition 3

The price of risk (PR) of the wealth-return differential D does not depend on the portfolio weights.

Proof

Take the expectation and variance of D to immediately obtain the result. $\square$

The implication of this is that to change the characteristics of the portfolio, a change in the weights is not enough. The asset manager should consider different assets than the ones currently used.

There does not appear to exist a simplification of the ratio E[D]/Std[D] in the case where the first asset equals the risk-free rate and the second asset equals the risky asset.

The expression for the expected wealth differential is given in (4). The variance is given by

$$\begin{aligned} V[D]= & {} Cov(r_1^2,r_2^2)+E[r_1^2]E[r_2^2]-2r_fE[r_1^2r_2]+r_f^2E[r_1^2]-2r_fE[r_1r_2^2]\\&+4r_f^2[Cov(r_1,r_2)+\mu ^2]-2\mu r_f^3+r_f^2E[r_2^2]-E[D]^2. \end{aligned}$$

This expression can be implemented numerically and be readily used.

2.3.2 Two random assets

In this section, we wish to discuss the possible ranking between the buy-and-hold strategy and the fixed-weight one if one has two random assets. We follow again Qian (2019), in this general discussion, where both assets are random.

Proposition 4

Suppose that the return differentials $r_{1,t}-r_{2,t}\sim N(\mu ,\sigma ^2)$ for $t=1,2$ and are autocorrelated with magnitude $\rho _{1,2}.$ Then,

$$\begin{aligned} E[W_2^{FW}]<E[W_2^{BH}]\text { as long as } \rho _{1,2}> -(\mu /\sigma )^2. \end{aligned}$$

The proof may be found in Qian (2019) but is repeated here for convenience.

Proof

$$\begin{aligned}&E[(W_2^{FW}-W_2^{BH})/W_0]\\&\quad =-a_1a_2E[(r_{1,1}-r_{2,1})(r_{1,2}-r_{2,2})]\\&\quad =-a_1a_2\left[ Cov[r_{1,1}-r_{2,1},r_{1,2}-r_{2,2}]+E[r_{1,1}-r_{2,1}]E[r_{1,2}-r_{2,2}]\right] \\&\quad =-a_1a_2[\rho _{1,2}\sigma ^2+\mu ^2]. \end{aligned}$$

Hence, $E[W_2^{FW}] < E[W_2^{BH}]$ if $\rho _{1,2}>-\mu ^2/\sigma ^2$. $\square$

We conclude that as long as the reversal of spreads is not too negative (that is, the autocorrelation is more negative than the squared price of the risk of the return differentials), the BH strategy yields higher expected value than the FW strategy.

At this stage, it would seem that there is a strong case to adhere to a BH strategy. If one adheres to a BH strategy, as mentioned, the risk of the portfolio may, however, significantly increase over time. Assets that had good performance will dominate the portfolio, leading to a concentration of assets, that is, less diversification. Moreover, since the weights of the portfolio are random in a BH strategy, there is added risk. To consider the expected return alone is not sufficient. One needs to consider the return-risk reward defined as the expected value of terminal wealth to its standard deviation. We will recall the results of Qian (2019) in the next section. The conclusion of that section will be that, given that no closed form for the return-risk reward exists, simulation experiments are required to understand the consequences of changes in the parameters of the assets.

2.3.3 Many assets and many time periods

Here, we wish to consider the case of many assets denoted by $i=1,\ldots ,M$ and many time periods denoted by $t=1,\ldots ,T.$ The generalization of the value of the terminal wealth for the BH and FW strategies follows directly from Fig. 1. Let $a_1,a_2,\ldots ,a_M$ be the allocations associated with the different assets. The terminal wealth for the FW portfolio and the BH portfolio is given by

$$\begin{aligned} W_T^{FW}= & {} W_0\prod _{t=1}^T\left( 1+\sum _{i=1}^Ma_i r_{i,t}\right) ,\\ W_T^{BH}= & {} W_0\sum _{i=1}^Ma_i\left[ \prod _{t=1}^T(1+ r_{i,t})\right] . \end{aligned}$$

To obtain further results, it is useful to assume independence across time of the return vectors. If the vectors of expected returns are the same for each period, then

$$\begin{aligned} E[W_T^{FW}]= & {} W_0\prod _{t=1}^T\left( 1+a'\mu \right) =W_0(1+a' \mu )^T,\\ E[W_T^{BH}]= & {} W_0a'(1+ \mu )^T. \end{aligned}$$

Using Jensen’s inequality, it follows that $E[W_T^{FW}]\le E[W_T^{BH}],$ with equality if the individual expected returns are not only the same over time but also identical among themselves, $\mu _i=\mu$, for all i.

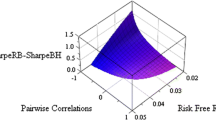
Qian (2019) shows that when pairwise correlations are positive, which is the case in practice, if one considers assets among a similar asset class and if one considers a long-only portfolio, then $V[W_T^{FW}]\le V[W_T^{BH}].$ The risk of the fixed-weight strategy is lower than the one of the buy-and-hold strategy, confirming our earlier intuition. This implies, however, that the ranking of the prices of risk $PR[W_T]=E[W_T]/\sqrt{V[W_T]}$ for the two strategies is ambiguous and similarly for the Sharpe ratio.

We may conclude this section by noticing that in the simplifying case of pairwise positive correlations and long-only portfolios, the relative performance of the BH and FW strategies is ambiguous. This ambiguity becomes worse in the case where the simplifying assumptions are relaxed. Such is the case when the pairwise correlation of assets is not positive, which could be the case in practice if one considers different asset classes or structured products and, similarly, if assets are time dependent and even more so if one has to deal with transaction costs. This observation hints at some sort of uncertainty principle, somehow analogous to Heisenberg’s principle from physics, meaning that there is no general rule on which to base a recommendation. This observation could explain the abundant literature discussing the relative benefits of the BH versus the FW strategy for various assets classes under various scenarios of rebalancing already mentioned in an earlier section.

In the next section, we will discuss various simulations to investigate the consequences of relaxing one assumption or the other.

3 Simulation experiments

As we started implementing our simulations it occurred to us that much of the literature deals with log-returns. If $r_1$ and $r_2$ are log-returns, computed from an asset with price $S_t$, say $r_1=\ln S_1/S_0,$ $r_2=\ln S_2/S_1,$ then clearly $\ln S_2/S_0=r_1+r_2$ showing that long-term log-returns can be conveniently obtained as the sum of short-term log-returns. In the actual practice of portfolio allocation, given the relevance of rebalancing alpha, which is a relatively small number of the order of basis points (bps), one needs to be as precise and realistic as possible and use simple returns. In our simulation experiments, with autocorrelated returns, we came to realize that because of the autocovariances of various orders, the passage of average log-returns to geometric means of simple returns is not a trivial step. To see this, let $r_1^{(n)},r_2^{(n)},r_3^{(n)}$ be dependent simulated returns for three consecutive months. The (n) exponent indicates the number of the simulation, with $n=1,\ldots ,N$. It is easy to show that due to the Law of Large Numbers, if one estimates average quarterly geometric returns assuming identical distributed returns that:

$$\begin{aligned} \frac{1}{N}\sum _{i=1}^N(1+r_1^{(n)})(1+r_2^{(n)})(1+r_3^{(n)})\xrightarrow [n\rightarrow \infty ]{} 1+3E[r_j]+3E[r_jr_{j+1}]+E[r_jr_{j+1}r_{j+2}], \end{aligned}$$

where j is some dummy index for a given month. For an asset with autocorrelation $\gamma (1)\equiv Cov(r_j,r_{j+1})/Var[r_j]$ we obtain that:

$$\begin{aligned} E[r_jr_{j+1}]=Var[r_j]\gamma (1)+E[r_j]E[r_{j+1}]. \end{aligned}$$

To get an idea of the magnitude of this number assume an annual volatility of 25% and an average return of 5%. Assume a first order autocorrelation term of 0.1. In an empirical section below, we show that the Swiss stock index has an autocorrelation of 0.14 and a commodity like sugar has an autocorrelation of 0.11. Then our estimate becomes for monthly frequency:

$$\begin{aligned} E[r_jr_{j+1}]=\frac{(0.25) ^2}{12}\times 0.1+\left( \frac{0.05}{12}\right) ^2 =5\cdot 10^{-4}+0.17\cdot 10^{-4}. \end{aligned}$$

The first term involving the autocorrelation contributes for about 5bps dominating the return product of 0.17bp! For a small market index such as for the Swiss market, this autocorrelation term therefore matters and is not only a matter of second order. So far, we dealt with quarterly returns where the interaction term $E[r_jr_{j+1}]$ appears 3 times. For annual returns, this term would appear 12 times. One can therefore expect a contribution to the annual return of about $12\times E[r_jr_{j+1}]$ that is about 60bps. If one counts additional co-moments of higher order, say $E[r_jr_{j+1}r_{j+2}]$ this nonlinear contribution could become even larger. We conclude that in the presence of autocorrelation in returns there will be a significant difference between the long-term return computed as a sum of short-term returns and a long-term return obtained as a geometric return.

3.1 Simulations from monthly data with correct annual moments

In several simulations below, we deal with autocorrelated returns. Because of the insights of the previous section, we understood that in order to correctly capture the rebalancing alpha, it is necessary to compute geometric returns to obtain the correct annual returns. As a solution to this problem, we propose a new algorithm whereby the parameters are empirically adjusted in such a way that the simulated returns have exactly the true moments. We propose to call this technique the TAR calibration since it yields True Aggregate Returns.

3.1.1 The TAR calibration

Let $r_t$ be a monthly return. We assume that the unconditional distribution of $r_t$ is Gaussian with annual parameters $\mu$ and variance $\sigma ^2.$ This asset may be autocorrelated with autoregressive parameter $\rho _{1,2}.$ We simulate the risky asset as an AR(1):

$$\begin{aligned} r_{t+1}=m+\rho _{1,2} r_t+s\,\varepsilon _{t+1}, \quad \text { with } \varepsilon _{t+1}\sim {\mathcal {N}}(0,1). \end{aligned}$$

(5)

An initial wealth $V_0$ at time $t=0$ would have evolved 12 months later into $V_{12}.$

$$\begin{aligned} V_{12}=V_0(1+r_1)(1+r_2)\cdots (1+r_{12}). \end{aligned}$$

(6)

The difficulty in obtaining the parameters m and s,  for given $\rho _{1,2}$ so that the annual returns match desired values, that is the given annual values $\mu =E[V_{12}/V_0]-1$ and $\sigma ^2=Var[V_{12}/V_0]$, comes from all the interaction terms in the development of the products in (6). These interaction terms start with the combination $r_1r_2$ and end with the joint product $r_1r_2\cdots r_{12}.$

We seek an approximation of the true parameters m and s. For an AR(1) process, it is known that the steady-state distribution has expectation $E[r_t]=m/(1-\rho _{1,2})$ and variance $V[r_t]=s^2/(1-\rho _{1,2}^2).$ By setting $m=(1-\rho _{1,2})\mu \Delta$ and $s^2=\sigma ^2(1-\rho _{1,2}^2)\Delta ,$ with $\Delta =1/12$, we obtain an approximation of the parameters for monthly returns. As mentioned above, the geometric product (6) will in general not have the desired true annual moments $\mu$ and $\sigma ^2$. For this reason, we perform simulations and adjust the level and scale of the $r_t$ until the annual moments match.

Therefore, we simulate a large number of $\varepsilon _{t}$ values and store them in memory.⁵ We consider a draw of some initial return $r_0$ in the approximate steady-state distribution ${\mathcal {N}}(m,s^2).$ We then use a minimization algorithm to minimize a distance function obtained as follows:

• 1. Using the $\varepsilon _{t}$ and candidate parameters $(m',s')$, generate a long series, a multiple of 12, of monthly returns $r_t.$

• 2. Compute the geometric average return over one year, i.e., that by using 12 returns $(1+r_1)\cdots (1+r_{12})-1.$

• 3. Compute the mean, namely $\hat{\mu }$, and the standard deviation, namely $\hat{\sigma }$, of the annual returns.

• 4. Present to the minimizer: $d(m',s')=(\hat{\mu }(m',s')-\mu )^2+(\hat{\sigma }(m',s')-\sigma )^2.$

In practice, for all the cases we considered, using the MATLAB minimizer fmincon, we obtained convergence in less than 10 steps. Notice that the last series produced in the optimization can be used immediately for a portfolio evaluation. In the case, a very long time series is required, then the method outlined above can be iterated. A generalization to many assets is trivial. Generate multivariate correlated $\varepsilon .$ Store them, and after constructing AR(1) processes as above, iterate on each of them till the required moments are obtained.

To investigate the relevance of this algorithm, we decided to perform a simulation exercise involving one million annual drawings each involving 12 monthly returns and apply the algorithm. The results are reported in Table 1. We consider annual returns that are distributed as a $N(m,\sigma ^2).$ We set m to 5% and volatility $\sigma$ to 25%. This corresponds to parameters of a typical stock. We allow for various autocorrelations $\rho _{1,2}$ ranging from 0 to 0.3 with an increment of 0.05. The columns m and s represent the monthly estimates of mean and standard deviation drawn from the steady-state distribution. We then generate $m^{\mathrm{est}}$ and $s^{\mathrm{est}}$ by applying the algorithm described above. We briefly verify that the method generates correct measures for the average and the standard deviation of annual geometric returns presented in columns $m^{\mathrm{geom}}$ and $s^{\mathrm{geom}}$. We also compare with the usual mean and standard deviation. The results are in columns $m^{\mathrm{arith}}$ and $s^{\mathrm{arith}}.$ As one can observe, our algorithm produces perfectly sized returns that yield annual moments correct up to 2 decimals. Obviously using geometric returns is important since the differences between the theoretical means and standard deviations with usual average returns and standard deviations are quite striking. For a correlation coefficient of 0.1 the mean is smaller by 50 bps and the standard deviation moves from 0.236 to 0.211. This figure matches the theory of the earlier section where we found a similar order of magnitude (actually 60bps). In the case of strong autocorrelations of 0.3 the standard deviation could even drop to 0.179 if one neglects the interaction terms between months. Such a high correlation is luckily unrealistic for stocks.

Table 1 We perform 1 million simulations of 12 months

3.2 Various simulation exercises

The theoretical Sect. 2.3 provides us with guidance regarding what kind of simulation may be of interest. We noticed the relevance of autocorrelation for an asset as well as pairwise correlation among assets. Little seems to be known about the introduction of a transaction cost, which matters fundamentally in practice. As a consequence, the FW strategy that requires rebalancing and therefore generates a cost will be particularly affected by the introduction of a transaction cost.

For these reasons, we presently wish to conduct various simulation experiments to understand the relevance of those features. Table 2 summarizes the various simulation experiments that we wish to perform with their focus. In the following sections, we will discuss the results of our simulations for those specifications.

Table 2 In this table, we summarize our various simulation scenarios

3.2.1 Basic investigations

Our simulation considers the following data-generating process (DGP): Asset 1 is a risk-free asset with annual return $r_f$, and asset 2 is a risky asset with monthly return $r_{t}.$

For $\rho _{1,2}=0,$ we can investigate the impact of varying basic parameters such as the allocation or transaction cost. In the case where $\rho _{1,2}<0$, our asset is mean-reverting. For an extensive discussion of reversals, see Bali et al. (2017). This is a short-term phenomenon. In the case where $\rho _{1,2}>0,$ our risky asset will display momentum, which is a long-term phenomenon and has been described in Jegadeesh and Titman (1993). Once we obtain returns for both the risk-free and the risky asset, we cumulate over time to generate asset prices and bond prices as in:

$$\begin{aligned} S_T=S_0(1+r_1)(1+r_2)\cdots (1+r_T),\quad B_T=B_0(1+r_f)^T. \end{aligned}$$

Table 3 presents the results of the benchmark simulations. The parameters of our simulation are as follows. We run all the simulations 50,000 times, and this also the approach in the subsequent experiments unless otherwise specified. In all cases, our time horizon is one year. The initial amount invested is 100 and $S_0=B_0=100.$ In fact, any amounts may be used here; however, by using an initial amount of 100 and inspecting the value of the end of the year, the return is straightforward to obtain. We assume an annual interest rate of 2% and obtain the monthly rate using $r_f=1.02^{1/12}-1.$ For the risky asset, we assume $\mu =5\%.$ Table 3 describes the choice of additional parameters in the left part, and in the right part, it presents Sharpe ratios computed as

$$\begin{aligned} SR=\frac{ \frac{1}{N} \sum _{i=1}^N R_i-r_f }{ \sqrt{ \frac{1}{N-1} \sum _{i=1}^N (R_i-\bar{R})^2 } }, \end{aligned}$$

where $R_i$ denotes an annual return and $\bar{R}$ is the average annual return.

Table 3 In this table, we present the results of allocations where we use either a buy-and-hold strategy or a rebalancing fixed-weight one for monthly data over one-year horizons

We also consider the Maximum Drawdown (MDD) defined for instance in Chekhlov et al. (2005). For some stochastic process $X_t$, obtained by cumulating returns, the MDD at time T is defined as

$$\begin{aligned} MDD(T)=\max _{\tau \in (0,T)}\left[ \max _{t \in (0,\tau )} X_t-X_\tau \right] . \end{aligned}$$

The contribution by Chekhlov et al. (2005) shows how linear programming tools can be used to optimize a portfolio with respect to MDD. The traditional Markowitz optimization is given by

$$\begin{aligned} \begin{array}{cl} \max _a &{}\quad E[r^p(a)]\\ \text {s.t.} &{}\quad Risk(r^p(a))\le d,\\ &{}\quad \sum \limits _{i=1}^M a_{i}=1, \end{array} \end{aligned}$$

where a is the vector of portfolio allocations, given as percentages, to be allocated to the various assets whose returns are given by a vector $r^p$. The second equation specifies that risk should be limited and the third equation states that the weights on the assets should sum to one. Inspection of this program shows that the generic measure called ‘Risk’ can be a variance or a MDD. As long as the constraints can be written as functions an optimizer will be able to handle this problem even though the solution may no longer be expressed as linear functions.

We would like to emphasize that the methodology developed earlier is perfectly compatible with an optimization logic. The methodology generates a number, the transactions cost TC(a) per unit of time given an initial wealth $W_0$, and this for a given vector of portfolio weights a. The ratio $TC(a)/W_0$ will reduce the performance of a portfolio and if one considers the extended Markowitz optimization

$$\begin{aligned} \begin{array}{cl} \max _a &{}\quad E[r^p(a)]-TC(a)/W_0\\ \text {s.t.} &{}\quad Risk(r^p(a))\le d,\\ &{}\quad \sum \limits _{i=1}^M a_{i}=1, \end{array} \end{aligned}$$

then one can perform an optimization using variance, MDD or any other risk measure such as VaR, CVaR and Mean Absolute Deviation (MAD).

In the first exercise, we change the allocation in the risky asset from 0.2 to 0.9. As expected, as more money is put in the asset with higher returns, the BH strategy also generates higher returns. For the FW allocation, we assume a transaction cost of 2%. The FW allocation generates average returns that increase similar to the BH strategy. Since we have calibrated the parameters to given annual returns, by construction, it must be that the SR for the BH strategy does not change as the portfolio changes. We notice that the FW allocation has a SR that increases, such that it joins the SR of the BH strategy. This is expected, since in the extreme case when all the wealth is invested in a single asset, namely the risky one, BH and FW are identical.

The last columns indicate the evolution of the transaction costs, TC. We notice that the TC follows an inverted U-shape pattern. The maximal transaction cost is reached for an equally weighted portfolio. We know from Proposition 1 that the terminal wealth between a BH and an FW strategy is the most different for this case, meaning that the transaction costs must also be largest.

In our second exercise, we assume that the transaction cost increases to 3%, 4%, and 5%. As expected, the SR and MDD fall in this case. If one considers the 60/40 portfolio, the MDD more than doubles as the costs increase from 2% to 5%.

In our next simulation we allow for deviations from the given (strategic) allocation. Sometimes those non-intervention intervals are also called tactical allocations. This captures the practical feature that portfolio allocations are not necessarily rebalanced each month; the manager may allow for a deviation of the desired strategic allocation by some amount, which we denote by $\delta .$ We will also allow for this choice by assuming that the manager will only rebalance the portfolio if the deviation of the actual weight, $a'$, from the desired weight a is larger than an amount $\delta .$ The larger the $\delta$ is, the more lenient the manager is about deviation from the desired weight, and the strategy will approach a buy-and-hold strategy. From the point of view MDD, fewer rebalancing decrease transactions costs and therefore improve the MDD for the FW allocation. In comparison with the 60/40 benchmark allocation, MDD is halved as one moves to the 3% inaction region.

Our next simulation assumes that the volatility of the risky asset evolves from 10% to 40%. We observe that increasing volatility changes the Sharpe ratios of the BH and FW strategies but the difference between the SR values remains constant. For high volatility of the risky asset, as one would expect, this asset requires larger amounts to be reallocated, leading to higher transaction costs. In agitated years, the total transaction cost may climb as high as 2.6%. Also, as expected, an increase in volatility increases MDD, in particular so for the FW allocation.

In the last exercise, we consider autocorrelated assets. By construction, the mean and volatility of the BH strategy are set to be the same for all autocorrelation patterns which can be achieved with the TAR algorithm.

We observe, as indicated by Corollary 1, that for strong mean reversion of assets (acorr negative), the FW strategy dominates the BH one. While theory can provide guidance of the direction of matters, simulations or actual data are required for the assessment of the actual magnitude of the consequences. As the simulations demonstrate, this result holds even with relatively large transaction costs of 2%. The columns labeled MDD represent an annualized MDD. Inspection of those columns shows that if assets strongly revert to their mean, then it means for instance that a loser will subsequently catch up. If one readjusts the position of the loser, as it is the case in the FW strategy, then this reduces MDD. For strong negative correlation, this effect can be so strong that the difference of MDD between BH and FW becomes positive. Such a strong autocorrelation is, however, unrealistic in practice for stocks or bonds.

3.2.2 Two risky assets

As the theoretical part has shown, autocorrelation and cross-sectional correlation may affect the ranking between the BH and FW strategies. This is what we wish to study in the second experiment of Table 2. The DGP for the system of assets is given by:

$$\begin{aligned} r_{1,t+1}= & {} m_1+\rho _{1}\, r_{1,t}+s_1\,\varepsilon _{1,t+1}, \quad \varepsilon _{1,t+1}\sim {\mathcal {N}}(0,1),\\ r_{2,t+1}= & {} m_2+\rho _{2}\, r_{2,t}+s_2\,\varepsilon _{2,t+1}, \quad \varepsilon _{2,t+1}\sim {\mathcal {N}}(0,1). \end{aligned}$$

Furthermore, we assume that the two residuals $\varepsilon _{1,t+1}$ and $\varepsilon _{2,t+1}$ are correlated with parameter $\rho .$ From given annual parameters of expected returns $(\mu _1,\mu _2)$ and volatilities $(\sigma _1,\sigma _2)$, we infer the parameters $m_1,m_2,s_1,s_2$ required for the monthly simulations, proceeding in an analogous manner to the previous simulation by using the TAR calibration. The only addition is that one simulates correlated innovations $\varepsilon _{1,t}$ and $\varepsilon _{2,t}.$

For both assets, we assume identical $\mu$ of 5% and identical $\sigma$ of 25%.

Both assets face a transaction cost of 2%. Autocorrelations are also equal ranging over a grid of values. Next, we assume an equally weighted allocation $a_1=a_2=0.5.$ In Table 4, we present the results of this simulation. The first column presents the correlation between the two assets. This column will dictate if prices increase or decrease simultaneously. If both assets move in the same direction, little rebalancing will be required. When assets move in different directions, in contrast, this will modify more strongly the allocations, leading to more rebalancing and higher transaction costs. The second column, AC, dictates if assets are reverting or if they have positive momentum. We know already that for reverting assets, the FW strategy is most beneficial. The actual amount of benefit is, however, an empirical issue.

Table 4 In this table, we present the results of allocations resulting from two risky assets with various patterns of autocorrelation (AC) and cross-sectional correlation ($\rho$)

The BH strategy always has the same mean return. We notice that the FW strategy has the larger SR only when assets move strongly in opposite directions and are mean-reverting. Those findings are exactly in line with the propositions in the theoretical section. What this simulation allows to show is that the parameter values need to be rather extreme for the FW strategy to have higher SR than the BH strategy.

Concerning MDD, we observe that in general the difference between MDD for BH and FW remains negative, as in the previous table. As autocorrelation increases, the difference in MDD becomes more negative. Exactly, for the same reason for which the SR is better for the FW than the BH strategy the MDD will be smaller.

If we inspect the columns of the transaction costs (TC) on the right of the table, we notice that when assets are negatively correlated and tend to move in opposite directions, the TC are then the highest. It is also for this case that the BH strategy is much better than the FW strategy. The difference in performance can be quite substantial, as indicated by the various numbers in this table.

3.3 Predictability of stock returns

There is a large stream of literature that demonstrates that asset returns may be predicted; see Barberis (2000), Campbell and Thompson (2007), and Cochrane (2007), and even if this issue is controversial, see a discussion in Bali et al. (2017), it is interesting to empirically investigate if some advantage could be made out of this in the presence of transaction costs. This is the focus of the last experiment of Table 2.

3.3.1 Modeling the inaction region

If asset returns are partially predictable, e.g., by the dividend-price ratio, dp, then if a manager believes the next period’s returns to be positive, the manager has two possibilities to deal with this issue under the assumption that the portfolio is already at its predetermined threshold a. The manager may decide to let the allocation of the risky asset float. Therefore, instead of maintaining the allocation at a, she may decide to rebalance only at $a+\delta .$ This suggests modeling the $\delta$ as a function of the dp. As an alternative, the manager may assume a strategic allocation of a, but if the dp varies, then may modify the allocation. This implies that after an increase in the dp, the allocation is set at a higher level. It may initially seem that modifying the $\delta$ that is the threshold at which the portfolio is rebalanced and changing the allocation is the same, but it is not. In the first case, the assets may drift and will not be rebalanced unless the threshold has been hit. In the second case, the allocation is changed to some new threshold and a transaction cost will be paid as soon as a new deviation of this new allocation occurs.

At this stage, the manager is alerted to the possible need to modify the intervention threshold $\delta$ or the allocation (or both). To investigate the quantitative importance of this we render the boundary $\delta$ dependent on the previous month’s dp. We assume for this purpose, that $\delta$ ranges between $\delta _{\mathrm{min}}$ and $\delta _{\mathrm{max}}.$ A possible specification is:

$$\begin{aligned} \delta _t=\delta _{\mathrm{min}}+(\delta _{\mathrm{max}}-\delta _{\mathrm{min}}) \frac{\exp (a\, dp_t+b)}{1+\exp (a\, dp_t+b)}. \end{aligned}$$

In an appendix, we explain how to calibrate a and b.

To investigate the consequence of changing allocation as dp varies, we follow a similar approach, and we assume that the allocation a may evolve between some lower bound $a_{\mathrm{min}}$ and $a_{\mathrm{max}}.$ The functional specification of the relation between $a_t$ and dp is assumed to be given by:

$$\begin{aligned} a_t=a_{\mathrm{min}}+(a_{\mathrm{max}}-a_{\mathrm{min}})\frac{\exp (a\, dp_t+b)}{1+\exp (a\, dp_t+b)}. \end{aligned}$$

The methodology to determine a and b is identical to the case above. We will assume for the benchmark case that the allocation is 60% in equity. For the allocation where the allocation changes over the business cycle, we assume that $a_{\mathrm{min}}$ and $a_{\mathrm{max}}$ are 80% of a and 120% of a, respectively.

3.3.2 The DGP

We assume that the allocation is between a risk-free asset and a predictable stock return. Setting $\Delta =1/12$ for a monthly time increment we have:

$$\begin{aligned} r_{B,t}= & {} (1+r_f)^\Delta -1,\\ r_{S,t}= & {} \mu _{S,t}\Delta +\sigma _{S}\, \sqrt{\Delta }\varepsilon _{S,t},\\ \mu _{S,t}= & {} \alpha +\beta dp_t, \text { where }dp_t\equiv D_t/S_t,\\ dp_t= & {} \gamma +\phi \, dp_{t-1}+\sigma _{dp}\,\varepsilon _{dp,t} \end{aligned}$$

Here, $D_t$ is the amount of dividends generated in month $t-1$ and paid at time t. There is a strong negative correlation $\rho _{D,S}$ between $\varepsilon _{dp,t}$ and $\varepsilon _{S,t}.$ We assume here that this correlation is constant.⁶

For the calibration, we follow Barberis (2000) who uses monthly data covering January 1927 to December 1995, and set:

$$\begin{aligned} \mu _{S,t}= & {} -0.0056+0.2580\,dp_t,\\ dp_{t+1}= & {} 0.0008+0.9774\,dp_{t}+\sqrt{3.0E-6}\,\varepsilon _{dp,t},\\ \rho _{D,S}= & {} -0.9351. \end{aligned}$$

The implementation of this DGP is very simple.⁷ We turn now to the discussion of the implementation of the empirical simulation.

3.3.3 Discussion

In Table 5, we present the results from our simulations. We still simulate 50,000 experiments, and the time horizon of our allocation is a year. We still assume a 2% annual risk-free return. The risky asset has a 25% annual volatility. In the first line, we present the benchmark case with the dynamic of the asset mean given as above. In the subsequent lines, we find the parameters of the ceteris-paribus exercise, changing each time one parameter. The first of the various columns contains the SR for the buy-and-hold strategy, and the SR of the FW where the manager-econometrician ignores the predictability of the stock market. We denote with an index 1 the statistics obtained when the manager ignores predictability. In a second set of columns, indexed by 2, the reader finds the SR for the FW strategy where the inaction threshold $\delta _t$ is changed over the business cycle, and the comparison with the SR of the initial and the associated transaction cost. In the last set of columns, indexed by 3, the manager adjusts the portfolio allocation weight a over the business cycle as predicted by the dividend-price ratio.

Table 5 The risky asset is predictable

The column with $SR-FW_1$ demonstrates that for the benchmark allocation, the SR of the rebalancing strategy is 5%. If the transaction cost increases from 2 to 4%, the SR decreases. Additionally, if volatility increases, then in comparison with the benchmark, the SR decreases because the TC is also higher. Rendering $\alpha$ more negative means that expected returns of the risky asset decrease. Since volatility remains the same, this yields a negative SR. Increasing $\beta$ means that stocks become more predictable. Moreover, since the assets have positive $\varphi ,$ meaning persistence, this means that asset returns become more persistent.

In the next case, we decrease the persistence parameter $\varphi$ from 0.98 to 0.78. This implies that the asset returns are more random. In this case, rebalancing comes at a cost with respect to the benchmark.

We also increase $\sigma _{dp}$ from 0.0017 to 0.0021. This means that we render the system more uncertain. Indeed, the FW strategy leads to a slight decrease in the benchmark. As asset return correlation becomes less negative, which means that the dp is less related to the returns.

In the next group of statistics, we find $SR-FW_2$ corresponding to the situation in which the manager changes the intervention threshold $\delta$ as a function of dp. This means that if the weight of the risky asset moves in a segment $[a-\delta ,a+\delta ]$, the portfolio is not rebalanced. The comparison between SR-$FW_2$ and SR-$FW_1,$ which can be found in column 6, demonstrates that allowing a window of inaction is beneficial. For all the parameters of the comparative static exercise, the SR increases by 4 to 7 percent. As TC2 demonstrates, because there is less portfolio allocation, the transaction costs also decrease, which is beneficial.

In the last 3 columns, we investigate the consequences of willfully changing the allocations if one believes in the return predictability. The SR of the FW strategy is found in column 8, and the comparison with the benchmark in SR $FW_3-FW_1.$ We notice that all the signs are negative and the numbers vary between 1 and 10 percent in absolute value. This demonstrates that forcing a different allocation can come at a costly price. After all, the predictability is weak, and forcing a reallocation because of a believed change in the expected returns reveals dangerous consequences. As the column with the transaction costs demonstrates (TC3), the deterioration is particularly strong in the case when $\varphi$ decreases from 0.98 to 0.78. In this case, the expected returns are not so well predicted. As a result, the portfolio will be managed in a more erratic way, resulting in a large transaction cost.

4 Actual allocation

In this section, we discuss the results of an actual allocation representative of some Swiss pension funds. The pension fund manager has a relatively large set of instruments in which she can invest. Those instruments are a set of well-known stock indices that could be cheaply duplicated by ETFs. Then there are commodities and real estate as alternative assets. On the fixed income side, the manager may invest in short-term interest rates or in 10-year Swiss and 10-year German Government bonds.

In Table 6, we present the assets and their descriptive statistics.⁸ It should be noticed that all prices have been converted, if necessary, into CHF. Returns are simple returns. We converted the 10-year yields of the bonds into prices by assuming constant coupon bonds with terminal repayment. The bonds have constant maturity and coupons are set to have a constant duration of 8 years.⁹ One may notice the relatively low volatility of the Swiss stock market and of its 10-year Government bond. The Swiss real estate index distinguishes itself by relatively high historical returns and a volatility comparable to the one of the 10-year German Government bond. The 10-year German Government bond is riskier and less performing than the Swiss Government bond because of exchange rate fluctuations and the steady appreciation of the CHF in comparison to the EUR over the past years.

Table 6 This table presents annualized statistics for various assets

In Table 7, the reader may find the matrix of correlations. Autocorrelations are inserted in the diagonal of the matrix. We notice that interest rates and monthly stock returns are correlated among themselves. Interest rates and assets tend to be negatively correlated. When we inspect the diagonal of this matrix, one notices the high persistence of interest rates. Assets are slightly positively autocorrelated. The highest is the Swiss market with 0.12, which can be explained by the fact that in comparison with the other large indices, this market is a rather small and illiquid. A priori, with such a rich pattern of correlations and autocorrelations, the prediction of whether a buy-and-hold or a fixed-weight strategy dominates appears delicate.

Table 7 In this table, we present the correlations of asset classes and, on the diagonal, the first-order autocorrelation

In Table 8, the reader may find the actual results of a conservative allocation where the weights in the various assets are as follows: 5% in short-term risk-free, 5% in 3-month Swiss interest rates, 20% in 10-y German Bonds, 30% in 10-y Swiss Bonds, 10% in the French CAC, 5% in the German DAX, 10% in the Swiss SMI, 5% in the British FTSE, and finally 10% in the S &P 500.

Table 8 In this table, we present the terminal wealth for an actual portfolio allocation where either the strategy or the transaction costs change

It turns out that for actual assets, in the long run, the dynamic is sufficiently complex that the given BH strategy is dominated by a fixed-weight strategy as long as transaction costs are relatively small. We perform various estimations of the final wealth with a rebalancing strategy under various assumptions for the transaction cost. In the initial setting, there are no transaction costs. Starting with 100 CHF on January 1, 1999, an investor would have achieved a wealth by June 30, 2021 of 128.40 with a buy-and-hold strategy. With a fixed-weight strategy, the investor would have obtained 135.90. We then run the allocation with increasing transaction costs of 50 bps, 1%, and 2%. We notice that it is only with a relatively high transaction cost of 2% for each asset that the fixed-weight strategy no longer dominates the buy-and-hold strategy. In practice, the level of transaction cost is in the range of 0.5%, and therefore, a fixed-weight strategy is interesting.

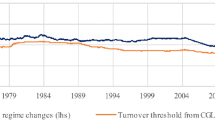
Next, we wish to investigate whether the dominance of the fixed-weight strategy is a permanent feature of the data or whether it changes over time. To do so, we reallocate our portfolio at the beginning of each year and then investigate at each end of the year which strategy performs best. Since realistic transaction costs are in the neighborhood of 0.5%, we compare the BH strategy with a FW strategy assuming 0.5% transaction costs. To ease the reading, we insert in Table 8 a star * in columns 2 and 5 to indicate the annual winner. In 3 years, the data are tied. In 15 years, when market performance was particularly good or particularly bad, we find that BH is best, as indicated by theory. In the remaining 6 years, the rebalancing strategy performs better. The finding that the rebalancing strategy is outperforming the buy-and-hold strategy in the long run, thus, results from exceptional results in certain years which are not undone in the losing years. We also tested from a formal statistical point if the Sharpe Ratios between the BH and FW allocations are equal. Jobson and Korkie (1981) derived the statistical properties of a single Sharpe Ratio under iidness. Lo (2002) extended those properties to a GMM setting allowing for autocorrelated returns. More recently, Ledoit and Wolf (2008) derive tests of equality between Sharpe Ratios allowing for dependency of returns and potentially non-Gaussian returns by introducing bootstrapped standard errors. It is this method that we apply to our setting.¹⁰ From a purely statistical point of view, it turns out that the null hypothesis of the SR of BH being equal to the SR of FW cannot be rejected in the long-run.

In Fig. 2, we find the trajectories over time for the BH and FW strategies. We notice that the relative performance of the BH versus the FW one is not due to a single outlier but rather due to a general force rendering it suboptimal. In this plot, we consider various transactions costs. It is only for the highest transaction costs that the FW allocation is dominated by the BH strategy. Even though the allocations are from a statistical point of view not different, most pension fund managers when confronted with this diagram would prefer a FW strategy.

Fig. 2

Trajectories of wealth depending on allocation strategy. The bold continuous curve in the center is the buy-and-hold strategy. The other curves are fixed-weight strategies with various transaction costs. The allocation is discussed in the text

We also tried to rationalize the success of the FW strategy by investigating the relation between volatility and performance. Unreported results of this investigation did not reveal a pattern such as that in volatile years one strategy outperforms the other. It is the overall constellation of temporal and cross-sectional characteristics that determines the success of the FW strategy even though based on our simulations, the BH strategy appears to be the winner. It is this complexity that may explain the plethora of papers written on the comparison between FW and BH strategies for all sorts of asset classes.

To investigate further the stability of the outperformance of the FW allocation over the BH one, we decided to consider a wider range of portfolio allocations. The results of this experiment as well as the allocations can be found in Table 9. In the upper part we represent the allocations in the various assets. In the second column of allocation weights, one finds the allocations used in the previous investigation. In the lower part, one finds the annualized average return, volatility Sharpe Ratios and for the FW allocations the p-values of a test between the SR of the given FW allocation and the one of the BH allocation. We consider for the FW allocation transactions costs of 0%, 0.05%, and 1%.

Table 9 In the upper part of the table we find for various assets various allocations that pension fund managers may follow

This table confirms that for all possible allocations, as long as the transaction cost remains below 1%, the SR of the FW allocation is larger than the one for the BH strategy. For instance, as can be seen from the first column, a BH allocation would yield an annualized SR of 0.24, whereas a FW one with no transaction cost would yield 0.27. The FW with a plausible transactions cost of 0.5% yields a SR of 0.25. As we move from the left to the right in the table, the portfolio becomes either more diversified in terms of assets or in terms of asset classes, since we introduce commodities and real estate. Then, for a BH allocation the SR is 0.40 and for a FW allocation the SR is 0.47% for a realistic transaction cost of 0.5%. Statistically, the two SR are the same. Again, if a portfolio manager had to choose between the two strategies, she is likely to pick the one with rebalancing yielding fixed weights.

In this table we also present the MDD for the various allocations. The MDD depends both on the allocations and on the BH/FW choice. Except for the first two allocations, a FW strategy generates smaller MDDs and this independently of the transactions costs. Those findings suggest that the improvement of the SRs tends to go hand in hand with improvements of MDDs.

5 Conclusion

This paper addresses questions of why and under which conditions a rebalancing strategy dominates a buy-and-hold strategy when there are transaction costs. We introduce a methodology to take into account transaction costs and perform various simulation experiments to quantify the relevance of transaction costs, as well as to verify our methodology. We also validate our methodology by applying it to actual data comprising a realistic portfolio.

Our method is useful for actual portfolio allocations where various transaction costs have to be taken into account and a portfolio needs to be optimized.

First, our paper demonstrates that a rebalancing strategy may be advocated for risk-averse investors because it reduces volatility in situations often encountered. This finding corroborates past studies. The main finding is the relevance of autocorrelation for an asset as well as pairwise correlation among assets. We observe that for a strong mean reversion of assets, the fixed-weight strategy dominates the buy-and-hold one. Concerning pairwise correlation, we show that when assets are negatively correlated, the transaction costs are the highest, and the buy-and-hold strategy is significantly better (except when the market exhibits strong mean reversion).

Generally, if a portfolio manager managing a well-diversified portfolio faces transaction costs of less than 2% and if she anticipates a future market with mean reversion, then she should rebalance her portfolio.

The predictability of asset returns can help in the choice of whether or not to rebalance the portfolio. If the investor believes future returns to be positive, she may decide not to rebalance immediately and let the weights deviate from their theoretical allocation. Our results indicate that in this case, it can be useful to introduce an interval of inaction and rebalance only if the weights deviate by some margin.

On the other hand, when we apply the portfolio allocation under transaction costs to actual data, we find that a fixed-weight strategy is better, in terms of return and risk, than a buy-and-hold strategy as long as the transaction costs remain reasonable. This last result can be explained by autocorrelations and cross-correlation of the portfolio during the chosen period of time that are sufficiently complex as to render an empirical simulation necessary to uncover which is better: the buy-and-hold or rebalancing strategy.

We also examine the performance of maximum drawdowns. We find that in general strategies where the SR is larger are also strategies where the maximum drawdowns is smaller.

Finally, even though this is not at the center of our research, we would like to note that rebalancing strategies, because of their deterministic character, exclude any emotions and subjective influences on buying and selling decisions and thus tend to limit behavioral biases.

Appendix

The objective of this appendix is to provide a functional specification of the inaction threshold as a function of some exogenous variable x. The objective is to cover the range $\delta _t\in [\delta _{\mathrm{min}},\delta _{\mathrm{max}}],$ as x describes the range $[x_{\mathrm{min}},x_{\mathrm{max}}].$

We model the evolution of $\delta$ by introducing the logistic transform as follows:

$$\begin{aligned} \delta _x=\delta _{\mathrm{min}}+(\delta _{\mathrm{max}} -\delta _{\mathrm{min}})\frac{\exp (ax+b)}{1+\exp (ax+b)} \end{aligned}$$

An obvious issue is how to choose a and b. Since we operate in a simulated environment, it is possible to generate many draws for x and to determine empirically its support. Denote by $x_{\mathrm{min}}$ and $x_{\mathrm{max}}$ the $k_{\min }=1\%$ and $k_{\max }=99\%$ percentiles, where the figures chosen are for illustrative purpose only. The value of each of those boundaries is obtained via simulation and depends on the DGP.

Define

$$\begin{aligned} y=\frac{\exp (ax+b)}{1+\exp (ax+b)}. \end{aligned}$$

Basic linear algebra yields

$$\begin{aligned} a\, x +b=\ln \frac{y}{1-y}. \end{aligned}$$

Define

$$\begin{aligned} Y_{\mathrm{min}}=\frac{y_{\mathrm{min}}}{1-y_{\mathrm{min}}}, \quad Y_{\mathrm{max}}=\frac{y_{\mathrm{max}}}{1-y_{\mathrm{max}}} . \end{aligned}$$

We want to select a and b so that $x_{\mathrm{min}}$ and $x_{\mathrm{max}}$ also correspond to $y_{\mathrm{min}}=1\%$ and $y_{\mathrm{max}}=99\%$ percentiles of the range of y. Since the total range of y is [0,1], it means that $y_{\mathrm{min}}=k_{\min }=0.01$ and $y_{\mathrm{max}}=k_{\max }=0.99.$ With the choice made above, one obtains $Y_{\mathrm{min}}=\ln (k_{\min }/k_{\max })$ and $Y_{\mathrm{max}}=\ln (k_{\max }/k_{\min }).$

Finally, one needs to set

$$\begin{aligned} a=\frac{Y_{\mathrm{max}}-Y_{\mathrm{min}}}{x_{\mathrm{max}}-x_{\mathrm{min}}}, \quad b=Y_{\mathrm{min}}-ax_{\mathrm{min}}. \end{aligned}$$