Slot Theory and Slotite Theory

Abstract

‘Instantiation-directed slot theorists’ believe that properties/relations have slots which are filled by their instances/relata e.g., where Abigail is taller than Bronia, there are two slots in the relation Taller Than such that Abigail fills the first slot and Bronia fills the second. This crude statement of the theory runs into ‘The Problem of Filling’, whereby a natural understanding of the relation between slots, filling, and instantiation leads to absurd results. This paper examines a variety of solutions to that problem, one of which is an extension of slot theory that adds an additional category of entities, ‘slotites’.

1 Introduction

1.1 Slot Theory

Slot theorists believe that, in addition to properties/relations existing, there exist ‘slots’ Dixon (2018b: 56n15) lists those who endorse it; (Dixon (2018a) and Gilmore (2013) defend it in-depth). As a, somewhat crass, first pass understanding, imagine the slot theorist says that every property/relation possesses a number of slots equal to its adicity e.g. Red has one slot and Married has two slots.

To progress this crass understanding, we have two alternatives. One is that slots are proposition-directed: a proposition is grounded in the slots of a property/relation being filled by entities ((Gilmore 2014); see also Williamson (1985: 257)) e.g. the (false) proposition 〈Nikk Effingham hates Barack Obama〉 is grounded in facts involving Hates having two slots, one being filled by myself and the other being filled by Obama. Grossman (1992: 57) thinks both actualised and unactualised states of affairs exist and result from filling slots of properties—this would be a variation on proposition-directed slots.) The second alternative way of understanding slots is instantiation-directed whereby slots are filled by the different relata of the relation (or instances of the property). For instance, Red’s slot could be filled by a red ball which instantiates Red whilst Married’s slots would be filled by pairs of spouses. In this paper, I focus solely on instantiation-directed slots, since they are the slots which I find most appeal to my metaphysical sensibilities. (Although I suspect that some of the issues discussed in this paper can be ported over to proposition-directed slots.)¹

Start by sketching a (somewhat crude) theory of instantiation-directed slots. It would have the following three pieces of (possibly primitive, possibly non-primitive) ideology:

• (CSs) ‘__ is a slot’ (which holds of slots).

• (CSp) ‘__ is possessed by __’ (the first relatum is a slot; the second relatum is a property/relation).

• (CSf) ‘__ fills __’ (the first relatum is a relatum/instance of a relation/property; the second relatum is a slot possessed by that relation/property).

For example, if some x fills the slot possessed by Red then x instantiates Red. And in the case of Taller Than—which has two slots, σ₁ and σ₂—we would end up with the following bi-conditional:

• ≡_Crude: For any x and y, x and y jointly instantiate Taller Than—and x is thereby taller than y—iff x fills σ₁ and y fills σ₂.

1.2 The Problem of Filling (POF)

≡_Crude is too crude (Dixon (2018a: 201–04) also notes the following problem). Imagine: Abigail is taller than Bronia and both are fully grown women of a tall stature; Clare is taller than Damaris, but both are young children who are both short comparable to Abigail and Bronia i.e. neither Clare nor Damaris are taller than Abigail or Bronia. Given filling is a dyadic relation between a relation’s relatum and one of its slots: Abigail fills σ₁ whilst Bronia fills σ₂ (for Abigail is taller than Bronia); Clare fills σ₁ and Damaris fills σ₂ (for Clare is taller than Damaris); but then, given ≡_Crude, Clare is thereby taller than Bronia. Since that’s false, we have a problem. Call this the Problem of Filling (POF for short).

This paper discusses how slot theorists can try to solve POF, using it as a chance to survey different slot theories. §§2–4 discuss slot theories which relativise filling to some further entity: instantiations (§2); sums, pluralities, or ordered tuples (§3); and spacetime regions (§4). I then discuss an extension which adds in an extra ontological category to help—‘slotites’ (§5). It not only solves POF but also solves a problem with symmetric relations. §§6–8 discuss different varieties of slotite theory.

Note that this paper does not argue for a specific theory; whilst some have clear downsides, the remainder all have their charms. Rather, this paper is an exploration of logical space, surveying the different theories available and seeing the different metaphysical itches which they can scratch.

2 Instantiation Relative Slot Theory

Roughly speaking, Dixon’s suggestion (2008a: 204) is to relativize filling to instantiations. Call that ‘Instantiation Relative Slot Theory’. Treating instantiations as states of affairs, we replace (CSf) with:

• (IRf) ‘__ fills __ relative to __’ (the first relatum is a relatum/instance of a relation/property; the second relatum is a slot possessed by that relation/property; the third relatum is the state of affairs of the relatum/instance of the relation/property instantiating the relation/property).

Thus, Abigail and Bronia fill σ₁ and σ₂ relative to their instantiation of the Taller Than relation, whilst Clare and Damaris fill those slots relative to their instantiation; there is also an instantiation involving Bronia and Clare, but relative to that instantiation Bronia fills σ₁ and it is Clare who fills σ₂. Problem solved. Instead of ≡_Crude, Instantiation Relative Slot Theorists endorse:

• ≡_InsRel For any x and y, x and y jointly instantiate Taller Than iff there exists an instantiation, ϑ, and both (i) x fills σ₁ relative to ϑ, and (ii) y fills σ₂ relative to ϑ.

Some might want to avoid Instantiation Relative Slot Theory. To see why, first we must better understand the relationship between filling and instantiation. Whilst slot theorists will agree that there is a bi-conditional connection between filling and instantiation (e.g. ≡_InsRel or ≡_Crude), they’ll vary over which side of the bi-conditional is more fundamental than the other. There are three types of fact: facts about which slots are filled (‘filling facts’); facts about which instances/relata instantiate which property/relation (‘instantiation facts’); facts about what the instances/relata are like (e.g. the ball being red or Jack and Jim being married; call them ‘predicational facts’). We then end up with three different views over how these facts relate to the bi-conditional: Filling First is the principle that filling facts ground instantiation and predicational facts; Instantiation First is the principle that instantiation facts ground filling and predicational facts; Predication First is the principle that predicational facts ground filling and instantiation facts.² (I ignore the prima facie implausible idea that these facts are independent of one another.) Which of Filling First, Instantiation First, and Predication First you opt for obviously determines which side of ≡_InsRel is more fundamental than the other.

Having assumed that instantiations are states of affairs/facts, instantiations are either predicational facts or instantiation facts. For instance, in the case of Abigail and Bronia, the relevant instantiation of Taller than would either be the fact that Abigail is taller than Bronia or the fact that Abigail and Bronia jointly instantiate Taller than. Whichever it is, represent it using T. Given Filling First, T ontologically depends upon filling facts about σ₁ and σ₂—only once we have those filling facts can we ‘build’ T. But if ≡_InsRel is true then filling must be relative to T. Since, Meinongianism aside, something can only bear a relation to an existent thing, we have a problem. Abigail can only fill σ₁ if T already exists (in order for her filling of σ₁ to be relativised to T) but T depends on the filling fact; thus T depends upon the filling fact, but the filling fact depends upon T. Given the standard assumption that dependence is asymmetric, instantiation relative slot theory can’t be combined with Filling First.

This is not a problem for all slot theorists. If a slot theorist endorses Predication First (and adds that the derivative instantiation facts further explain fillings facts) or endorses Instantiation First, then we don’t get this problem. In both cases, T would exist before the filling facts and would thus be a suitable relatum of the filling relation. (And note that Dixon explicitly endorses Predication First (Dixon 2018b) so he, at least, has no problem.)

So this is not an objection which will faze all slot theorists. However, there are things to be said for Filling First being true. A reason to be a slot theorist would be for slots to explain the order of relations. Return to Abigail and Bronia. They both instantiate Taller Than, but we need more than this; as is, their joint instantiation of Taller Than is compatible both with Abigail being taller than Bronia as well as Bronia being taller than Abigail. We must say that their instantiation is ordered in some way (e.g. such that Abigail comes first and then Bronia, or vice versa). Whilst we may take this ordering to be a primitive feature of instantiation, receiving no further metaphysical explanation, we might equally try and find some explanation for this ordering. And it’s natural for slots to be the answer to that search (cf (Fine 2000)): Abigail is taller than Bronia because she fills slot σ₁ whilst Bronia fills σ₂ (rather than vice versa). Were slots to play this role, instantiation facts must be explained by filling facts (elsewise the more fine-grained filling facts would be explained by the coarse-grained, unordered, instantiation facts, rallying against the principle that the more fundamental a fact is, the more fine grained it is). Thus, if you want to explain the order of instantiation (a laudable goal!) then you must favour Filling First over Instantiation First.³ Whilst this is not a reason to favour Filling First over Predication First (for we might think some predicational fact explains Abigail filling σ₁/Bronia filling σ₂, which in turn explains their joint instantiation of Taller Than), since Instantiation First is prima facie plausible, Filling First must be as well. So we have some reason to think Filling First is true. That said—and purely in the interests of metaphysical exploration—§§3–4 assume that Filling First is true and try to find alternative solutions to POF which salvage it.

3 Entity Relative Slot Theory

The next two sections consider theories that solve POF by relativizing to entities other than instantiations. The first such theory, suggested to me by Donnchadh O’Conaill, is to relativise filling to the respective entities involved. For single slot properties, this would be unproblematic. For instance, the red ball would fill Red’s single slot relative to the red ball, whilst a red pen fills Red’s slot relative to that red pen. But things become problematic when we try the same thing with relations for it’s then unclear what exactly do their relata fill their slots relative to? A natural answer would be the mereological sum of the relata. But imagine Rness is a two-place many-one relation corresponding to a relational predicate R. Rness has two slots, σ°₁ and σ°₂. Imagine a, b, and c exist, such that:

• (a) a and b stand in R to c;

• (b) b and c stand in R to a;

• (c) no other instances of R hold.

Having relativized filling to mereological sums, we should endorse:

• ≡_EnRel For any x (or xs) and y, xRy (or xsRy) iff (i) x (or the xs) fills σ°₁ relative to the mereological sum composed of the xs plus y; and (ii) y fills σ°₂ relative to that same sum.

Given (a) and ≡_EnRel c fills σ°₂ relative to the mereological sum a + b + c. Given (b) and ≡_EnRel the plurality of b and c fill σ°₁ relative to a + b + c. Therefore, given ≡_EnRel, the plurality of b and c are R-related to c which, given (c), is false. So mereological sums can’t play the relativizing role. (And we get the same problem if we relativized filling to pluralities of the relata instead of mereological sums of them e.g. if c filled σ°₂ relative to the plurality of a, b and c.)

The problem comes about because mereological sums are blind to the ‘order’ of their constituents (and pluralities are blind to the order of the things amongst them⁴). But some entities have a metaphysical structure better suited to capturing such order. States of affairs are an obvious example, but if we start using them we’ll end up back at Instantiation Relative Slot Theory (for what state of affairs could be salient if not the state of affairs of the objects instantiating the relevant relation?). But there is another alternative: Ordered tuples. In that case, given (a), a and b fill σ°₁ relative to 〈{a,b},c〉 and c fills σ°₂ relative to 〈{a,b},c〉. Given (b), b and c fill σ°₁ relative to 〈{b,c},a〉 and a fills σ°₂ relative to 〈{b,c},a〉. Unlike with mereological sums, the entities playing the relativizing role (i.e. 〈{a,b},c〉 and 〈{b,c},a〉) aren’t identical and thus we can’t generate the problem we had with sums and pluralities.

I don’t deny that relativizing to ordered tuples is an open option. However, having brought ordered tuples into the picture we might want to pause as to why we don’t go the whole hog and endorse class nominalism. What complaint could be raised against such an endorsement? It cannot be that class nominalism requires classes to exist, since that’s part-and-parcel of relativizing to tuples. Nor can the complaint be that class nominalism requires arbitrarily identifying tuples with sets (Benacerraf 1965) since that same problem faces Entity Relative Slot Theory. And so on for every complaint. Having already roped in ordered pairs, class nominalism should be a natural theory to endorse.

So if you are attracted to Entity Relative Slot Theory, I suggest you should be a class nominalist. One might think that class nominalism is incompatible with slot theory; after all, Gilmore explicitly ties slot theory to Platonic universals (Gilmore 2013: 187). But I see no reason to deny that non-Platonic universals (e.g. immanent universals, mereological fusions, or classes) could have slots. Just as the Platonist introduces slots as sui generis entities standing in a primitive ‘possession’ relationship to a property, we can say exactly the same for these other theories. With little said about what ‘possession’ amounts to (because the Platonist doesn’t offer even a rudimentary analysis of it!) there’s no impediment to saying that non-Platonic universals can ‘possess’ sui generis slots (see also Effingham (2020): 171).⁵

The problem is not that class nominalism is inconsistent with slot theory. Rather, the problem is that—at the stage in the dialectic we are in—we further need Filling First to be true. And that’s a step too far because stereotypical class nominalists (e.g. Lewis 1986: 50–69) endorse Predication First, not Filling First. And the closest alternative to a class nominalism accepting Predication First is a class nominalism which says that instances/relata instantiate properties/relations in virtue of being members of an ordered tuple that’s a member of that property/relation. But then, since facts about membership are grounded solely in facts about what exists in tandem with the axioms of set theory, there’d be no room for filling facts to play a role in explaining instantiation facts i.e. Filling First must be false even given this alternative understanding of class nominalism.

In summation: I don’t deny that there’s room in logical space for relativising filling to ordered tuples. But, as this section has explained, it does raise awkward questions about the motivation for such a theory: Given there are ordered tuples playing a crucial role in our metaphysical scheme, why not be a class nominalist? And if you’re a class nominalist, how do you square that with Filling First?

4 Spatiotemporal Relative Slot Theory

Spacetime is a dimension along which we commonly find variation of facts. I am tall now, but short then; the kilt is red in one place, green in another; it is raining in Birmingham, but not in Madrid. So it’s natural to relativise filling facts to regions of spacetime—a slot may be filled by something in one place but unfilled in another, just as whether ‘here’ is occupied by matter may vary as you move across space. Call this ‘Spatiotemporal Relative Slot Theory’. It’s natural to add that slots would themselves be spatiotemporally located, presumably occupying wherever the relevant relata are (and, equally, it’d be natural to assume that properties are likewise located, either being immanent universals or mereological fusions). We replace (CSf)/(IRf) with:

• (SRf) ‘__ fills __ relative to __’ (the first relatum is a relatum/instance of a relation/property; the second relatum is a slot possessed by that relation/property; the third relatum is a spacetime region).

And then endorse:

• ≡_STRel For any x and y, x and y jointly instantiate Taller Than iff there exists some spacetime region, α, and both (i) x fills σ₁ relative to α, and (ii) y fills σ₂ relative to α.

(Filling is region-relative, whilst instantiating the property is not; this is as it should be.)

Reconsider POF’s problematic example case in light of ≡_STRel. Imagine Abigail, Bronia, Clare, and Damaris respectively exactly occupy four regions, r_a, r_b, r_c, and r_d. Abigail fills σ₁ relative to r_a∪r_b; Bronia fills σ₂ relative to r_a∪r_b; Clare fills σ₁ relative to r_c∪r_d; Damaris fills σ₂ relative to r_c∪r_d; Bronia fills σ₁ relative to r_b∪r_c whilst Clare fills σ₂ relative to r_b∪r_c; and so on. Because the thing we relativize to is appropriately different each time, POF appears to have been solved.

But spacetime relativisations are always an awkward beast since it’s possible that there exist superposed entities e.g. superposed bosons, statues and lumps of clay, or ghosts and the walls they walk through. Imagine that four bosons exist, b₁-b₄; b₁ and b₄ spin whilst b₂ and b₃ do not; b₁ and b₂ are superposed (and exactly occupy r₁); b₃ and b₄ are superposed (and exactly occupy r₄). Bosons are spinlike, and jointly instantiate the relation Spinlike, iff they have the same spin. Thus b₁ and b₄ jointly instantiate Spinlike, as do b₂ and b₃. σ^′₁ and σ^′₂ are the two slots which Spinlike possesses. Thus: b₁ fills σ^′₁ relative to r₁∪r₄ (because b₁ has the same spin as b₄) whilst b₄ fills σ^′₂ relative to r₁∪r₄ (for similar reasons). The same thing is true of b₂ and b₃. Now the problem creeps back in: Relative to r₁∪r₄, b₁ (which spins) fills σ^′₁ and b₃ (which doesn’t spin) fills σ^′₂. Given ≡_STRel, b₁ and b₃ jointly instantiate Spinlike, which is ex hypothesi false.

One could deny the possibility of superposed objects. But for everyone who admits their possibility—which includes myself—some other alternative must be found if we want a slot theory that allows for Filling First.

5 Slotite Theory

5.1 Slotites

To get a different style of solution, we should compare POF to the problem of temporary intrinsics (Wasserman 2006). Roughly speaking, there are two styles of response to that problem: (i) endurantists relativise instantiation to times (or spacetime points, or utilise time-relativised adverbs etc.); (ii) perdurantists, rather than relativising instantiation, add in extra ontology (i.e. temporal parts) to do the work. When it comes to POF I’ve discussed options which relativise filling; those responses are analogous to endurantist responses to the problem of temporary intrinsics. It’s not hard, though, to imagine a response analogous to perdurantism. We add in extra ontology, ‘slotites’, to solve POF. Just as the perdurantist demands a plethora of temporal parts (one for every instant that an object exists at), slotite theorists commit to a plethora of slotites. For now, imagine that every property/relation has a number of slotites equal to its adicity multiplied by the number of its instantiations, such that each instantiation gets its own, distinct slotites. (I say assume this ‘for now’ because I’ll later suggest that the number of slotites may only be at least as many as this.) For example, returning to Abigail, Bronia, Clare, and Damaris, there are six instantiations of Taller than (Abigail being taller than Bronia, Bronia being taller than Clare, Abigail being taller than Damaris etc.). Since Taller than is dyadic, there must then be twelve slotites, τ₁, τ₂…τ₁₂. Having used ‘filling’ for the relation between slots and instances, use ‘plug’ for the similar relation between slotites and instances. One pair of slotites, τ₁ and τ₂, are plugged by Abigail and Bronia respectively; another pair, τ₃ and τ₄, are plugged by Clare and Damaris respectively; similarly, for Abigail and Clare, Abigail and Damaris, Bronia and Clare, and Bronia and Damaris. The slotite theorist then adds that these pairs are ‘yoked together’ so that we know which slotites ‘hook up’ with which other slotites. Thus τ₁ and τ₂ are yoked, τ₃ and τ₄ are yoked, τ₅ and τ₆ are yoked etc. and no other pairs are yoked i.e. τ₁ and τ₃ aren’t yoked, nor τ₁ and τ₄, nor τ₁ and τ₅ etc.

(Technically, things don’t plug slotites and it’s instead their temporal parts which do the plugging. For any two (possibly identical) times, t and t′, such that Abigail exists at t and Bronia at t′, there’s a pairing of Abigail’s t-temporal part, a_t, and Bronia’s t′-temporal part, b_t′. For each pairing: distinct slotites exist, τ_α and τ_β; a_t plugs τ_α; b_t′ plugs τ_β; τ_α and τ_β are yoked. For ease of presentation, I’ll ignore this complication about temporal parts.)

Slotite theory needs different ideology than slot theory:

• (STsl) ‘__ is a slotite’ (which holds of slotites).

• (STp) ‘__ is possessed by __’ (the first relatum is a slotite; the second relatum is a property/relation).

• (STf) ‘__ plugs __’ (the first relatum is a relatum/instance of a relation/property; the second relatum is a slotite possessed by that relation/property).

• (STy) ‘__ are yoked together’ (which holds of a plurality of slotites).

Regarding Taller than, slotite theorists say:

• ≡_Slotite For any x and y, x and y jointly instantiate Taller Than iff there exist two slotites, τ_x and τ_y, such that: (i) x plugs τ_x; (ii) y plugs τ_y; (iii) τ_x and τ_y are yoked; (iv) τ_x and τ_y are both possessed by Taller Than.

≡_Slotite, plus the facts about which slotites are yoked, solves POF. It can also avoid the problem of superposed objects. Since b₁ and b₄ are spinlike-related, they have their own pair of yoked slotites which they plug; b₂ and b₃ are likewise. When it comes to b₁ and b₂ the slotite theorist will either say that, because they aren’t spinlike-related, either there isn’t a pair of slotites or (if the slotite theorist is willing to add in more slotites) there is a pair of yoked slotites, but they go unplugged. Whichever is the case, ≡_Slotite entails that b₁ and b₄ are spinlike-related, as are b₂ and b₃. But b₁ and b₂ are not. Problem solved!

5.2 Objections to Slotite Theory

Objection One

Slotite theory demands an increase in one’s ontology, for now there are a lot of slotites. But, just as perdurantism’s extra ontological commitments aren’t normally thought to be a deal breaker, we should say the same of slotite theory.

Objection Two

One may complain that, whilst slots are an intuitive category of entity, slotites are weird, contrived, and/or otiose. But we should, again, compare the theory to perdurantism. Just as perdurantism ‘unearths’ a commitment to temporal parts that were originally thought to be a bizarre category of entity (Chisholm 1976: 143; Geach 1972: 311; van Inwagen 1981: 133), slotite theorists should treat their theory as having made an ontological discovery. Just as people came to grips with temporal parts, I’m sure that if we spent long enough trucking in slotites rather than slots they’d become quite natural items of one’s ontology.

Objection Three

Slotites must come in different ‘flavours’. Consider the pair of yoked slotites, τ₁ and τ₂, plugged by Abigail and Bronia respectively. There must be something about these slotites which means that Abigail plugging τ₁ and Bronia plugging τ₂ makes the former taller than the latter; τ₁ must be a ‘tall-flavoured’ slotite whilst τ₂ must be a ‘short-flavoured’ slotite. But what explains these flavours?

Such concerns are dialectically inappropriate, because we’re comparing slotite theory to slot theories and their variants. Even the most vanilla slot theorist will already have something to say about such ‘flavouring’, saying: Taller than possesses two slots; Abigail fills one slot; Bronia fills the other; something about these slots means that what fills the first slot is the thing which is tall compared to the shorter thing which fills the other slot. But in that case, slots also have ‘flavours’. (See also Fine's 2000: 10) diagrammatic representation of positionalism, which represents the slots differently—that is, as having different flavours—and purposefully captures exactly this idea (Fine 2000: 10). And if slots have flavours, why not slotites? Alternatively, the slot theorist may roll out some reason why they don’t need slots to have flavours—but then I expect that the same reasoning will apply to slotites!

It is doubly dialectically inappropriate if, as we’re currently assuming, we are realists who deny Predication First. Then a ball is red in virtue of it instantiating Red. So either something about Red explains why its instances are red (in which case properties come in different ‘flavours’—why not, then, slotites?) or nothing does (and, again, why can’t we then say slotites don’t need flavours either?).

Objection Four

We’ve stopped talking about slots and so slotite theory isn’t really a variant of slot theory. But slots can be easily recovered. Just as temporal parts compose objects, slotites could compose slots. Assuming that both slotites and slots come in flavours, slots would be fusions of all and only the slotites of the same flavour e.g. one slot of Taller than is composed of the first slotite of every pair of yoked slotites, whilst the other slot is composed of the remainder. (We can further analyse filling slots in terms of plugging slotites that are parts of the slot; similarly, we can say that a property possesses a slot iff it possesses the slotites composing the slot.)

Objection Five

Slotite theory threatens believing in properties in the first place. All of the heavy lifting in our metaphysical theory is being carried out by things plugging slotites of certain flavours. We need no longer explain why red things are red in terms of their instantiating Red when we can explain their being red in terms of plugging a certain flavour of slotite.

One option is to admit this and drop properties in favour of slotites. Another option is to recover properties in the same way that slots were recovered. Properties would be composed by the slotites that they possess.⁶ Properties would be derivative entities, much like a table is derivative of its atoms. And just as the derivative nature of tables is no slight against the existence of tables, the derivative nature of properties would be no slight against properties.

Objection Six

One may worry that slotites are just tropes in all but name. But this isn’t the case. Admittedly, in monadic cases they seem the same. Consider some red balls. The trope theorist says that, for each ball, there exists a distinct particular i.e. a distinct red trope. The slotite theorist says that, for each ball, there exists a distinct particular i.e. a distinct slotite. But in polyadic cases, the similarity ends. If the trope theorist admits of relational tropes, then two spinlike bosons are related by a single spinlike trope. But the slotite theorist says there are two things i.e. the two yoked slotites. Demonstrably, slotites and tropes are different.

What I don’t deny is that we might be able to build up connections between tropes and slotites. Just as properties and slots were identified with fusions of slotites, we can say the same of tropes—slotites are the distinct ‘legs’ of a relational trope and tropes are ‘built up’ out of slotites. An unyoked slotite, e.g. the slotite possessed by Red and plugged by a ball, is a trope. Similarly, a fusion of maximally yoked slotites is a trope. So tropes are ontologically reducible to slotites.

5.3 The Problem of Symmetric Relations

Slotite theory solves POF. It also solves Fine's (2000: 17–22) problem for slot theory when it comes to symmetric relations. Non-symmetric relations have slots with different flavours and it’s clear which relatum fills which slot. But with symmetric relations things are problematic. Spinlike has two slots, σ^′₁ and σ^′₂; spinlike-related bosons, like b₁ and b₄, fill those slots. But either slot is as good as the other when it comes to such filling. Perhaps (i) b₁ fills σ^′₁ and b₄ fills σ^′₂ but equally we might say (ii) b₁ fills σ^′₂ and b₄ fills σ^′₁. In (i) and (ii) different slots are being filled by different things, thus they’re distinct states of affairs. But clearly (i) and (ii) are the same state of affairs (namely, the state of affairs of b₁ and b₄ being spinlike). Since it’s contradictory for states of affairs to be both distinct and the same, slot theory has a problem.

Dixon’s solution (2008a) is that symmetrical relations have just a single slot filled by a plurality of entities e.g. Spinlike has a single slot filled by the plurality of b₁ and b₄ (where that filling would be relativised to an instantiation, or what have you). Given there’s a single slot, there’s only ever one state of affairs—the problem is solved. But Dixon’s solution is revisionary, making Spinlike monadic when it’s intuitively dyadic. This occludes the prima facie difference between (i) monadic properties instantiated by pluralities and (ii) symmetric polyadic relations. To better understand, first distinguish the two ways to understand ‘adicity’. We might mean the number of places a relation has or we might mean the number of things which can fill those places (cf Morton 1975: 309–10; Oliver and Smiley 2004: 615–18). For instance, the property Forming a circle—as in ‘Those points form a circle’—appears to have one place but that place can be filled by a varying number of points. This ambiguity in mind, I’ll stipulate that ‘adicity’ refers to places. So Forming a circle is a monadic collective property. And it’s intuitively different from Spinlike which appears to be dyadic (which relates two entities and has two places). Dixon’s theory makes Spinlike akin to Forming a circle; it ends up being monadic when, intuitively, it’s dyadic.

Slotites avoid Fine’s problem whilst keeping Spinlike dyadic. Assume that slotites are like tropes in that, just as a trope is necessarily had by whatever has it (and, e.g., my tropes can’t be shared with anyone else), slotites are only ever plugged by whatever actually plugs them.⁷ Constructing a Finean problem case is now impossible. There’s only one state of affairs, namely b₁ plugging slotite τ′₁ and b₄ plugging slotite τ′₂. And it’s now impossible for the reverse state of affairs to hold i.e. for b₁ to plug slotite τ′₂ and b₄ to plug slotite τ′₁.

We can now correctly capture the adicity of Spinlike:

• A property/relation, Fness, is n-adic = _df There are n slotites, the τs, such that (i) each is possessed by Fness and (ii) the τs are yoked together.

For example, a symmetrical relation like Spinlike is such that it possesses pairs of slotites i.e. always two slotites yoked together. Thus, Spinlike is dyadic.

5.4 Dimensions of Variation

The above move requires a necessary connection between slotites and those things which plug them. Necessary connections are usually thought to be mysterious. One way to resolve such mystery is to say that the connected entities stand in some sort of relation of ontological dependence; that is, either the things which plug the slotites depend upon the slotites or the slotites depend upon the things which plug them. That’s one dimension that slotite theories may differ along.

Another dimension of variation concerns one’s take on Filling First/Instantiation First/Predication First. We now get an additional position: Facts about what slotites are plugged explain the instantiation facts, predicational facts, and facts about which slots are filled. Call that Plugging First. Once you take on-board the existence of slotites it seems bizarre to now think that filling slots does the explaining—if you’re attracted to Filling First you should now instead be attracted to Plugging First. That leaves slotite theories varying over which of Instantiation First, Predication First, and Plugging First is true.

These two dimensions in mind, we can carve up the slotite theories into the following:

(There may be more dimensions of variation than these two. For instance, can there exist unplugged slotites i.e. that relation R has more slotites than merely its adicity multiplied by the number of its instantiations? Or is every slotite plugged? Or we could ask whether slotites depended upon properties or properties upon slotites? But I will limit my investigation only to these two dimensions.)

6 Nominalist and Grounded Slotite Theory

Just as slot theorists may think that instantiation facts are the explanatory base for both filling and predicational facts, slotite theorists might likewise think plugging facts are explained by instantiation facts. Call this ‘Grounded Slotite Theory’. You won’t be a grounded slotite theorist because of anything to do with POF. Having endorsed Instantiation First, Instantiation Relative Slot Theory will work fine in solving POF—no slotites required! But slotites will still be useful in solving the problem of symmetric relations. Moreover, one might be quite permissive about ontology (Schaffer 2009: 356–62) and so be committed to slotites anyhow. So there are reasons to think that those who endorse Instantiation First will nonetheless endorse slotite theory and be grounded slotite theorists.

Grounded slotite theory is worth noting. But, just as I’ve focussed on Filling First for most of the paper, I want to focus on its slotite-equivalent, Plugging First. So I’ll set aside grounded slotite theory. Similarly, a slotite theory that accepts Predication First (‘Nominalist slotite theory’, because the world is nominalistic at the fundamental level) may be deserving of a proper investigation, but in the context of this paper I will move on from it to discuss slotite theories accepting Plugging First.

7 Byzantine Slotite Theory

It is natural to pair (i) predicational facts being grounded in plugging facts with (ii) instances being grounded in their slotites. And it’s natural to pair (i) plugging facts being grounded in instantiation facts with (ii) slotites being grounded in their instances. ‘Byzantine slotite theory’ endorses a third, unnatural, option, pairing (i) instantiation facts being grounded in plugging facts with (ii) the slotites being grounded in their instances.

Byzantine slotite theory isn’t just weird in that respect—it’s pointlessly over-complicated. Assume that bosons are fundamental and return to considering b₁’s spinning. Some fundamental fact, U, is the ultimate explanans of that predicational fact. Since b₁ is fundamental, it’s natural to think it’ll be named in U and that it’s of the form Φb₁… (where Φ is some fundamental, joint-carving predicate). If Φ is other than monadic, U is a relational fact about b₁. It can’t be a relation to a slotite, since byzantine slotite theory says slotites are derivative and thus can’t feature in fundamental facts. Nor can it be a relation to a property for then—surely!— U would be a fact about b₁ instantiating the property; in that case, instantiation facts would be explaining predicational facts, not plugging facts (contrary to Plugging First). Nor is it reasonable to think that it’s a relation to some object, for b₁ could spin even if the cosmos were empty of all other objects. Thus Φ must be a monadic predicate i.e. U is of the form Φb₁. U explains the fact that the relevant slotite of Spin is plugged by b₁; call that fact ‘P’. Given plugging facts are the explanation of predicational facts, P explains H, where H is the predicational fact about ‘how b₁ is’ i.e. that b₁ spins. Here’s the rub: It’s weird for U to be a monadic fact about how b₁ is and not be the predicational fact that b₁ spins. If you’re going to have some monadic fact about b₁ be fundamental why not just make it the predicational fact you’re looking to explain in the first place? Why doesn’t U=H? Why are we going all around the houses drawing lines of explanation through plugging facts to get to H? Byzantine slotite theory is simply a pointless complexification of nominalist slotite theory. It should be ignored.

8 Slotite Bundle Theory

8.1 Constructions of co-Plugged Slotites

On the flip side, slotites could be more fundamental than instances, presumably grounding the instance’s existence by being constituents of them. Just as with standard bundle theory, where instances are constituted by properties, we would have a theory whereby instances are constituted by slotites. Call this ‘slotite bundle theory’.

A standard bundle theorist would say of our bosons, b₁ and b₂, that b₁ is a bundle of two co-instantiating properties e.g. 125GeV (being the property of having a mass of 125 GeV) and Spin. Similarly, b₂ is a bundle of a different pair e.g. 125GeV and Scalar (being the property of not spinning). There’s a primitive of ‘co-instantiation’ which these properties stand-in in order to bundle themselves together and make up the instance.

Slotite bundle theorists follow suit, but using a different primitive: ‘co-plugging’. Co-plugged slotites constitute an object. Slotite bundle theorists will think that a slotite possessed by 125GeV and another possessed by Spin are amongst b₁’s constituents. But they should also add that b₁ has amongst its constituents slotites possessed by relations. All slotite theorists hold that, for any n-adic relation R, such that Rx₁…x_n is true, there are yoked slotites τ₁…τ_n such that τ_m is plugged by x_m; the bundle slotite theorist adds that τ_m is amongst the slotites which co-plug to comprise x_m. Given slotite theory, τ^′₁ and τ^′₂ are yoked slotites possessed by Spinlike; b₁ plugs τ^′₁ whilst b₄ plugs τ^′₂. Given slotite bundle theory, τ^′₁ is a constituent of b₁ and τ^′₂ is a constituent of b₄. This has an interesting upshot, for now slotite bundle theory improves upon standard bundle theory. Standard bundle theorists analyse the instantiation of monadic properties by saying that such things are the constituents of instances, but bundle theorists are rather quieter when it comes to relations (cf Sider 2006: 395n4). If relations aren’t constituents of bundles, bundle theory doesn’t provide a wholly general analysis of instantiation, for it no longer says anything about the (joint) instantiation of relations. If relations are constituents of bundles (and, e.g., Spinlike is a constituent of b₁)—which is not what most bundle theorists believe—then, whilst we can now analyse b₁’s instantiating Spinlike, we can’t analyse its instantiating Spinlike alongside b₄. Making relations constituents of instances only tells you that they’re a relatum of some instantiation of the relation, rather than telling us anything about which relata they are related to. Again, we don’t have a general analysis of instantiation. Slotite bundle theory, taking a slotite analogue of the second approach, solves this problem (because the distinct slotites are possessed by distinct relata and there’s a primitive yoking relation to tell you which are the relata of one and the same instantiation).

8.2 Tangent: A Problematic Alternative

I’ve just argued that slotite bundle theory is better when it comes to analysing the instantiation of relations than standard bundle theory. Were the bundle theorist to have an alternative solution to that problem, this would undermine the motivation for slotite bundle theory. This section briefly discusses two alternatives, arguing that neither is suitable (and, thus, slotite bundle theory is still attractive in offering a general analysis of instantiation).

The first alternative is to exclude relations from our ontology entirely. If there aren’t any relations, the bundle theorist needn’t bother themselves explaining their instantiation. But throughout this paper I’ve assumed some version of slot theory is true and that’d be a pretty poor thing to assume if only monadic properties were possible (because slot theory only becomes useful/interesting once relations are introduced). So this response won’t work.

Hawthorne and Sider (2002: esp. 54–56) discuss a second alternative. Your bog standard bundle theorist treats co-instantiation as a plural predicate which pluralities of properties fall under e.g. the plurality of Spin and 125 MeV being co-instantiated to constitute b₁. Hawthorne and Sider take it up a notch: Co-instantiation relates a varying number of pluralities of properties. For example, b₁ and b₃ are spatiotemporally seperated, thus they instantiate the relation of spatiotemporal separation—call it Distant. Thus b₁ (itself a bundle of Spin and 125 MeV) and b₃ (being a bundle of Scalar and 125 MeV) jointly instantiate Distant. Hawthorne and Sider’s suggestion is that there’s a state of affairs, D, which is the state of affairs of: Distant being co-instantiated with (i) the plurality of Spin and 125 MeV and (ii) the plurality of Scalar and 125 MeV. D explains b₁ and b₃ instantiating Distant.

But this solution has problems that slotite bundle theory does not. Co-instantiation must now be understood in one of two ways. Either (i) co-instantiation is varigrade or (ii) co-instantiation involves superpluralities. Either option is problematic.

Consider the varigrade approach first. Standardly, we say that properties/relations have a fixed number of slots/places; perhaps the number of things which fill those slots varies, but not the number of slots themselves (e.g. Forming a circle has one slot, and that fact doesn’t vary, but it can vary over how many points collectively instantiate it). A relation is varigrade iff it instead can have a variable number of slots/places (Macbride 2005: 588). This first approach assumes that Hawthorne and Sider treat co-instantiation as a varigrade relation. For instance, in D, co-instantiation would have three slots (one for Distant, one for the plurality of Spin and 125 MeV, and one for the plurality of Scalar and 125 MeV), whilst in other states of affairs, co-instantiation has a different number of slots (e.g. in the case of b₁ co-instantiation has just a single slot, which is filled by the plurality of Spin and 125 MeV). So in some cases co-instantiation has three slots and in other cases it has one slot (and in yet more cases, it has a different number of slots). Co-instantiation is varigrade.

But varigrade relations come in for a hard time (Gilmore 2013: 229–31). Like some others (e.g. Macbride 2005) I’m more open to the idea of them, even at the fundamental level. For instance, a natural reading of endurantism makes parthood fundamentally varigrade. Mereological relations between spacetime regions, or between abstracta, are two-place e.g. one region is a part of another simpliciter and the number 2 is part of the real number series simpliciter. But when the mereological relation holds between enduring objects it is three-place e.g. the wheel is a part of the car at midday––it relates two objects and a time. If we think it’s the same relation in both cases, then the mereological relation will be varigrade. (Perdurantists will say the same, but add that the temporally relativised relation is derivative of the fundamental dyadic relation, thus mereological relations aren’t fundamentally varigrade.) And it’s not just mereological relations. For instance, the same thinking applies to location relations. In some spacetimes, e.g. relativistic spacetimes, location is a two-place relation, whilst in a world with enduring spatial regions and separate temporal instants, spatial location will be a three-place relation between objects, spatial regions, and instants. If we think the same location relation holds in both spacetimes, location is varigrade.

But whilst I’m open to the idea of varigrade relations at the fundamental level, co-instantiation seems nothing like these examples. In these examples, the adicity of the relation varies because it’s connecting things from wholly different ontological categories. Where the dyadic mereological relation relates spacetime regions or abstracta, the triadic relates objects and times (or spatial regions and times). Where the dyadic location relation relates objects to spacetime regions, the triadic location relation objects to enduring spatial regions and instants. If varigradicity is plausible, it’s plausible because in different cases there appears to be an entirely new ontological category of entities to be relating things too. And that’s not what’s going on with co-instantiation, where the extra places are added to make room for more of the same sort of thing (i.e. pluralities of properties). In the different cases where the adicity of co-instantiation varies it’s always relating properties, or pluralities of properties. It doesn’t seem like co-instantiation is similar to other candidates for varigrade relations.

The alternative to co-instantiation being varigrade was that co-instantiation instead involved ‘superpluralities’ (i.e. a plurality of pluralities (Rayo 2006)). On this view, co-instantiation is always a monadic predicate with a single slot/place. In the case of b₁, co-instantiation’s sole place is filled by 125 MeV and Spin. In the case of D, co-instantiation’s sole place is filled by a plurality of three things: (i) Distant; (ii) the plurality of 125 MeV and Spin; and (iii) the plurality of 125 MeV and Scalar. As this example makes clear, the co-instantiation predicate now holds of a superplurality. The problem is that facts about co-instantiation are fundamental facts, which would mean facts involving superplurals will be fundamental. And that’s the bit which I baulk at; I’m fine with superplural facts being derivatively true, but I’ve a hard time thinking that facts involving superplurals can be fundamentally true. (Indeed, we may have worries about whether facts involving just straightforward plurals can be fundamental, never mind superplurals (Sider 2011: 208–16).⁸

In short, Hawthorne and Sider’s theory is not without its challenges. Slotite bundle theory, then, is an interesting alternative to consider if you want a general analysis of instantiation.

8.3 Inter-Dependence

Slotite bundle theory builds everything—instances, properties, slots, tropes—out of slotites. However, this ends up reintroducing mysterious connections. According to slotite bundle theory, slotites won’t be able to ‘float free’ of instances any more than properties float free of bundles according to standard bundle theory. Thus if a slotite exists, it’s a constituent of something. Therefore, if one slotite of a relation exists, it’s a constituent of an instance and that instance must instantiate the relation. Necessarily, there must therefore be another (or many other) slotite(s) yoked to it. A mysterious connection has returned because the existence of some things is now necessitated by the existence of a distinct thing.

Above, I relieved necessary connections of their mystery by saying that one of the connected existents depended on the other. If relations have directions, e.g. if Taller than related the tall thing first and the shorter thing second (Grossman 1992: 57), we could say that slotites plugged by the ‘later’ things depend on the slotite plugged by the ‘first’ thing. But this has two difficulties. First, (Fine 2000) advances compelling reasons to deny that relations have directions. Second, we’re left in the dark when it comes to symmetric relations, which are clearly directionless—given that the prime candidates for fundamental relations include symmetric relations like spatiotemporal separation (Armstrong 1978: 90), that’s particularly problematic. So this approach is a possibility but probably unappealing.

The alternative is to say that no slotite is prior to a yoked compatriot. Instead, yoked slotites are inter-dependent: For any plurality of (maximally) yoked slotites, each slotite is wholly grounded in the remaining slotites. Not everything will inter-depend, since ‘unyoked’ slotites can still be fundamental, but this inter-dependence nevertheless extends to instances: if every instance is related to at least one other instance, every instance inter-depends upon some other instance (the view of Madhyamika Buddhism); if any two instances are related, all instances inter-depend (the view of Huayan Buddhism) Bliss and Priest 2017)).

Inter-dependence is contentious since it requires dependence (and/or grounding, ontological priority, or whatever relation your metametaphysics favours) to be non-symmetric. It’s not been popular in contemporary analytic metaphysics, which has inclined to thinking dependence is well-founded. But inter-dependence has not gone without defence (Barnes 2018; Thompson 2016; Thompson 2018). And whilst I’m in no rush to accept inter-dependent entities, I’m less hostile to them than other philosophers—after all, they didn’t seem unintuitive to Buddhist philosophers and that fact alone should give one pause to too fervently thinking that dependence is well-founded. Also, it’s particularly defensible in this case because, if you have any time whatsoever for the possibility of inter-dependent entities, yoked slotites are surely the best candidates for being inter-dependent. If you want to go inter-dependent about anything, go inter-dependent about these things!

However, it does undermine some of the dialectical force for slotite theory in the first place. If non-symmetric dependence relations are on the table then the original objection to Instantiation Relative Slot Theory (back in §2) loses its bite, for it played on the idea that dependence was asymmetric.

9 Summary

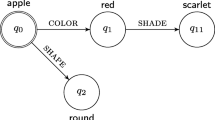
This paper hasn’t motivated slot theory, nor defended any particular brand of it. I’ve merely surveyed logical space, mapping out where one would find oneself were one motivated to become a slot theorist. Here’s a pictorial summary:

I leave with some parting comments on our options. For those who endorse Predication First, slot theory will work just fine—just endorse Instantiation Relative Slot Theory and be done with it. (And, if you want slotites too, endorse nominalist slotite theory.) And those slot theorists who believe Filling First are faced by POF. I followed through the solutions until I arrived at slotite theory, the most plausible version of which comes with a commitment to metaphysically inter-dependent entities. For those who are staunchly committed to the asymmetry of all dependence relations, I suspect that spells bad news for slotite bundle theory a fortiori bad news for Filling First—indeed, one possible conclusion you may draw from this paper is that (instantiation-directed) slot theorists are forced to believe Predication First.