Abstract
Purpose
An innovative way to define navigable fluid mud layers is to make use of their rheological properties, in particular their yield stress. In order to help the development of in situ measurement techniques, it is essential that the key rheological parameters are estimated beforehand. Is there only one yield stress? In which shear rate/shear stress range is yield expected to occur? How is yield stress dependent on depths and locations in the harbor? In order to answer these questions, we investigated the changes in the rheological properties of mud from along the river stream in the Port of Hamburg, Germany, using a recently developed laboratory protocol.
Materials and methods
In this study, a detailed rheological analysis was carried out on the mud samples collected from different locations and depths of the Port of Hamburg. A variety of rheological tests was performed including: stress sweep tests, flow curves, thixotropic tests, oscillatory amplitude, and frequency sweep tests.
Results and discussion
The yield stresses of sediments from different locations were significantly dissimilar from each other due to differences in densities and organic matter content. Two yield stresses (termed static and fluidic) were observed for every sample and linearly correlated to each other. The thixotropic studies showed that all mud samples, except from one location, displayed a combination of thixotropic and anti-thixotropic behaviors. The results of frequency sweep tests showed the solid-like character of the sediments within the linear viscoelastic limit. The yield stresses, thixotropy, and moduli of the mud samples increased by going deeper into the sediment bed due to the increase in density of the sediments.
Conclusions
This study confirmed the applicability of the recently developed protocol as a fast and reliable tool to measure the yield stresses of sediments from different locations and depths in the Port of Hamburg. The fluid mud layer, in all the locations it was observed, exhibited relatively small yield stress values and weak thixotropic behavior. This confirms that despite the fact that rheology of fluid mud is complex, this layer can be navigable.
Similar content being viewed by others
1 Introduction
Mud is a cohesive material which contains predominantly clay minerals, water, organic matter, and some amounts of silt and sand. The particles forming the fluid mud layer, to be found at the bottom of some harbor channels, are kept in suspension by the continuous effect of wave motion generated by climatic events, ship motion (Ross and Mehta 1989; Mehta 2013), human activities like dredging and fishing (Gordon 1974), or bioturbation (Harrison and Wass 1965; Ross and Mehta 1989). Fluid mud is usually defined as a fluid having a density within the range of 1030–1300 kg m−3, in which settling is considerably hindered by the presence of flocs (Inglis and Allen 1957; Whitehouse et al. 2000; McAnally et al. 2007a). Extensive research has been undertaken on the measurements of floc size and settling rates in the laboratory for muddy sediments (Manning and Dyer 2002; Gratiot and Manning 2004; Manning et al. 2007; Spencer et al. 2010; Soulsby et al. 2013; Mehta et al. 2014). The hindered settling behavior was also observed for the sand/mud mixtures (Whitehouse and Manning 2007; Manning et al. 2010; Manning et al. 2011; Spearman et al. 2011; Spearman and Manning 2017). The navigation in ports and waterways and the maintenance of dredging channels are highly dependent on the rheological properties of fluid mud (May 1973; Parker and Kirby 1982; Kirichek et al. 2018). Generally, natural mud has a complex rheological behavior, displaying viscoelasticity, shear thinning, thixotropy, and yield stress. It has been shown that rheological properties are dependent on the mud density, and that the presence of small amounts of organic matter is affecting the cohesion and rheological behavior significantly (Paterson et al. 1990; Paterson and Hagerthey 2001; Tolhurst et al. 2002; Wurpts 2005; Malarkey et al. 2015; Schindler et al. 2015; Parsons et al. 2016).
In the literature, extensive research is available on cohesion-less sediment rheology (Jorgen Fredsoe 1992; Houssais et al. 2016). In particular, steady and oscillatory rheological analysis of cohesive sediments have been reported (Jiang and Mehta 1995; Coussot 1997; Van Kessel and Blom 1998; Bai et al. 2002; Fass and Wartel 2006; Coussot 2007; Babatope et al. 2008; Huang and Aode 2009). Van Kessel and Blom (1998) reported the rheological analysis of estuarine mud and kaolinite clay samples. The results showed higher yield stress values for estuarine mud samples compared with the china clay due to the cohesive nature of the samples. Xu and Huhe (2016) presented the rheological studies of estuarine mud at Lianyungang (China) using both steady and dynamic measurements. They reported an exponential increase in the yield stress of mud samples by increasing the volume fraction of particles. From the oscillatory experiments, two regions were identified: elastic and viscous. Yang et al. (2014b) also investigated the rheological characteristics of three different cohesive sediments from the Yangtze River, and shoal of the Hangzhou Bay and Yangcheng Lake (China). The results revealed three different deformation regions in the flow curves obtained from shear rate sweep tests. Yang et al. (2014a) also discussed the comparative rheology of kaolin and natural mud samples using mechanical and shear vibrational loads. They observed a typical thixotropic and shear thinning behavior for cohesion-less sandy sediments, whereas a combination of thixotropy and anti-thixotropy, as a function of shear rate, was evident for cohesive sediments (kaolin and mud). Soltanpour and Samsami (2011) compared the rheology of kaolinite and Hendijan mud, northwest part of the Persian Gulf. The outcome of this study showed that the rheological parameters were strongly dependent on the water content of the samples.
Besides fluid mud, other mud layer types can be observed in a port, corresponding to mud in different stages of consolidation. All these layers can vary in thickness and rheological properties. As natural mud samples can exhibit various rheological behaviors like viscoelasticity, shear thinning, thixotropy, and yield stress, multiple rheological tests were performed on the samples to fully characterize them. In the literature, the rheological properties of natural sediments as a function of density are usually studied by diluting dense mud samples. In this study, however, the samples are not diluted and the dependence on density is done by studying the rheological properties of denser natural mud layers at the same location. Management of mud sediments (i.e., fluid mud) using the nautical bottom approach (McAnally et al. 2007b), based on the yield stress of the sediments, requires the knowledge of rheological properties particularly the yield stress of the sediments. The application of this navigable bottom approach may reduce operational and maintenance costs particularly in the areas where a significant layer of fluid mud exists. In order to help the development of in situ measurement techniques, it is essential that the key rheological parameters are estimated beforehand. Therefore, the following research questions are addressed in the present study: Is there only one yield stress? In which shear rate/shear stress range is yield expected to occur? How is yield stress dependent on depths and locations in the harbor? The aim of the present study is therefore to quantify the rheological characteristics of mud observed in different locations of the Port of Hamburg, particularly where significant amounts of fluid mud are found, using a recently developed protocol.
2 Experimental methods
In this study, natural mud samples were collected from different locations (Vorhafen (VH), Köhlbrand (KBZ), Rethe (RT) and Reiherstieg Vorhafen (RV), Köhlfleet mit Köhlfleethafen (KH) and Sedimentfang Wedel (SW)) of the Port of Hamburg, Germany, using a 1-m core sampler (Fig. 1a and b). These locations were chosen on the basis of a preliminary analysis, which showed that the selected locations have different densities and organic matter content with significantly different rheological fingerprints. The collected samples were divided into different layers based on the differences in their visual consistency. These layers were named fluid mud (FM), pre-consolidated (PS), pre-consolidated to consolidated (PS/CS), and consolidated (CS) sediments (Fig. S1, Electronic Supplementary Material (ESM)). The samples were packed in sealed containers and transported to the laboratory. The dry density of the minerals was considered to be about 2650 kg m−3. The bulk density of the mud samples was determined by the method reported in Coussot (1997). In short, the mass of the mud samples was determined before and after oven drying at 105 °C for 24 h. This gave the mass of the dry solids and water content in the mud samples. By using the densities of water and minerals, the corresponding volumes were then estimated. The final bulk density of mud samples was then calculated based on these masses and volumes. Particle size distributions within the different mud layers were measured using static light scattering (Malvern MasterSizer 2000MU). The organic matter content of the sediments was determined using an ISO standard 10694:1996-08 (ISO 1995). The characteristics of the selected mud samples are summarized in Table S1 (ESM). Before the rheological experiments, all the mud samples were homogenized by mild hand stirring. Rheological experiments were performed using a HAAKE MARS I rheometer (Thermo Scientific, Germany) with concentric cylinder (Couette) geometry. Couette geometry with grooves was also used to investigate the wall slip effects. The results revealed the absence of wall slip by displaying similar results as obtained with smooth Couette geometry (data not shown). A waiting time of 3–5 min was used to eliminate the disturbance created by the bob after attaining its measurement position. This time was estimated by performing the preliminary oscillatory time sweep experiments in linear viscoelastic regime. After this time interval, the increase in storage modulus as a function of time was not very significant, which showed the recovery of a structure disturbed by the bob. The temperature was maintained at 20 °C during each experiment using a Peltier controller system. Each experiment was carried out in duplicate to check the repeatability of the measurements.
Stress sweep tests were performed using the stress-controlled mode of the rheometer. An increasing stress was applied from 0 to 500 Pa at a rate of 1 Pa s−1, depending upon the consistency of the sample. The corresponding motor displacement was measured, and the shear rate and viscosity were then determined. The flow curve experiments were carried out using the shear rate–controlled mode of the rheometer by linearly increasing the shear rate from 0 to 25 s−1 in 170 s and from 25 to 300 s−1 in 100 s without giving enough time between each point of measurement to reach the steady state. Thixotropic experiments were performed by increasing the shear rate from 0 to 100 s−1, followed by shearing at 100 s−1 for 30 s and then decreasing from 100 to 0 s−1. These thixotropic loops were produced two times without giving any time between both loops to evaluate the effect of structural breakdown on the response of the material. The dynamic experiments were executed as a function of either oscillation amplitude or frequency. Preliminary amplitude sweep tests were carried out at a constant frequency of 1 Hz to estimate the linear viscoelastic regime. Frequency sweep tests were then performed from 0.1 to 100 Hz within the linear viscoelastic regime. The storage modulus (G′) and loss modulus (G″) were recorded as a function of frequency. The complex modulus (G∗) and phase angle (δ) can then be calculated as follows:
3 Results and discussion
3.1 Stress sweep and flow curves
Figure 1c shows the outcome of stress sweep tests for the PS mud layer. Two yield stresses (i.e., two-step yielding) were determined from the sharp decline in viscosity by an extrapolation method (Zhu et al. 2001). The stress values associated with the first decline are referred to as “static yield stress” (\( {\tau}_y^s \)); the second decline are termed “fluidic yield stress” (\( {\tau}_y^f \)). Increasing shear rate sweeps were performed to obtain the flow curves presented in Fig. 1d. At low shear rates, a minimum in flow curve was observed for all samples. This type of minimum in flow behavior has already been reported for similar systems (Van Kessel and Blom 1998) and is attributed to stick/slip phenomena at the cup’s wall. Below a shear rate of 20 s−1, an extensive structural breakdown is observed for all samples followed by the shear stress equilibrium above 20 s−1. This value can be referred to as the “critical shear rate” that was applied to destroy the structure of the sample as found by Xu and Huhe (2016). By comparing Fig. 1c and d, it can be seen that this critical shear rate is corresponding to the fluidic yield stress found by the stress sweep test. The same analysis has been done on the samples from different mud layers. For all layers, similar trends were obtained, and two yield stresses (static and fluidic) were defined. The comparisons of static and fluidic yield stresses, TOC, and density of the PS and CS layers for all locations are presented in Fig. 2a and b. The mud samples obtained from the RT location displayed higher values of yield stresses (57–312 Pa) with the comparatively lower values of densities (1154–1210 kg m−3) due to their higher organic matter content (4.1–4.3%).
Evolution of density, TOC, and static and fluidic yield stresses for different locations in the harbor for a PS layer and b CS layer. The right side of panels a and b represents upstream of the river and left side represents downstream. To plot all the parameters in one figure, some of them were multiplied with different factors indicated close to the curves in panels a and b. Yield stress as a function of density for c different layers (all locations) and d different locations (all layers). Filled symbols represent static yield stress values and empty symbols represent fluidic yield tress values (multiplied by 1/5)
It can be observed that for all layers (FM and PS/CS not shown), the ratio between fluidic and static yield stress is always of the order of 5 (KH, KBZ, RV). At VH (FM) and RT (PS/CS layer), it is of the order of 3, while it is nearly 7 for SW (PS layer). Both static and fluidic yield stresses are following the same trends in density: higher densities lead to higher yield stresses and vice versa. Even though the amount of organic matter and the values for density are rather constant between the PS and the CS layers, there is a significant increase in yield stresses between the layers. As expected, the organic matter content decreases in the seawards direction. For the locations VH and KH, the organic matter content is higher which may be attributed to harbor activities.
The increase in yield stress is generally fitted as an exponential function of density. In Fig. 2c and d, we give the relation between yield stress and density as a function of layers and as a function of locations. It is clear that the exponential relation holds for a given location only. This is consistent with the exponential increase in yield stress as a function of density found by diluting concentrated mud samples (Xu and Huhe 2016). Other parameters, such as particle size distribution, type of clay, and organic matter of the sample, must play a role to explain the differences observed between the layers of different locations (see Fig. 2c).
3.2 Thixotropy
The thixotropic character of the mud samples was investigated by ramping up and ramping down the shear rate between 0 and 100 s−1. Several factors such as the composition of the material, shear history, level, and rate of shearing can affect the shape of the thixotropic loop. Comprehensive reviews have been reported on the topic of thixotropy by Barnes (1997) and Mewis and Wagner (2009).
Thixotropic behavior (clockwise hysteresis loop) is typically observed when the rate of structure breakdown in increasing shear rate ramp (ramp up) is faster than the rate of structure buildup in decreasing shear ramp (ramp down). Anti-thixotropy or negative thixotropy, represented by a counterclockwise hysteresis loop, is the inverse case where the rate of structure reformation during ramp down is faster than the structure breakdown in ramping up the shear rate. The results showed that all the PS sediments, except from the RV location, behave like a typical flocculated suspension, where flocs are broken at higher shear rates and do not have time/possibility to reform during the ramp down (Fig. 3a). An anti-thixotropic behavior was however observed at lower shear rates, which suggests that at those shear rates the rate of forming bonds between particles is faster than the rate at which bonds were destroyed at ramp up. Nosrati et al. (2011) reported similar results with a combination of thixotropy and anti-thixotropy for muscovite dispersions. The combination of thixotropy and anti-thixotropy can be associated with the occurrence of shear thickening phenomenon, which was evident for these mud samples in stress weep tests particularly at higher stresses. Mud samples from the RV location were the only ones to display a typical thixotropic behavior (lower stresses in the whole ramp down curve) for the investigated shear rate range. The RV samples are (see Fig. 2a and b and Table S1, ESM) the samples having one of the lowest densities and the highest organic matter content. The flocs in the RV samples might therefore be much larger than the flocs in other samples, which implies that their restructuration at ramp down might require a longer time. The anti-thixotropic behavior of the sample from the SW location and the typical thixotropic behavior for the RV sample were also observed in the second thixotropic loop (Fig. 3b and c, respectively).
Thixotropic behavior was also investigated for the sediments from the same location (VH) having different consistencies. Figure 3d–f show the outcome of thixotropic experiments for different layers of sediments from the VH location. Two thixotropic loops were performed by increasing and decreasing shear rates without giving any time between each measurement loop. The fluid mud layer displayed quite a small thixotropic character (Fig. 3d) due to its very low density and liquid-like behavior. A minimum was also observed in the first ramp up for the fluid mud layer which was absent for other ramps. This may be associated with the structural collapse which was irrecoverable in subsequent ramps due to the very short shear rate times. A similar irrecoverable structure in thixotropic experiments was also observed for Caland channel mud (Van Kessel and Blom 1998). On the other hand, pre-consolidated and consolidated mud layers showed quite significant thixotropic behaviors with different shapes of hysteresis loops. For the pre-consolidated mud layer, a combination of thixotropy and anti-thixotropy was observed (Fig. 3e). The consolidated mud layer, contrary to the pre-consolidated layer, displayed typical thixotropic behavior over the entire range of shear rates (Fig. 3f). The area of second hysteresis loop was also smaller than that of the first hysteresis loop, in addition to the lower stress values, which also suggested the structural breakdown in the sediments which was irrecoverable in such small shear rate times.
3.3 Frequency sweep
In the oscillatory mode, amplitude sweep tests at a constant frequency were performed prior to the frequency sweep experiments in order to recognize the different transition regimes for selecting suitable stress values. Figure S2 (ESM) presents the storage and loss moduli as a function of applied amplitude at a constant frequency of 1 Hz for PS layer sediments. Three different regimes were identified for all the sediments: (i) a linear regime where sediments displayed solid-like behavior (G′ > G′′); (ii) a transition regime in which the transformation from solid-like to liquid-like state occurred; and (iii) a non-linear regime where a liquid-like behavior was evident for all the sediments (G′′ > G′). The sediments displayed different values of the stress at which the crossover between G′ and G′′ occurred, with the highest value (27 Pa) for SW sediments and the lowest value (11 Pa) for RV sediments which may be due to their different densities and organic matter content. Frequency sweep tests were then performed by selecting the stress values within the linear viscoelastic regime (i.e., intact structure), in order to evaluate the effect of frequency on the properties of the sediments.
Figure 4a and b show the outcome of these frequency sweep tests, performed in the linear regime, in the form of complex modulus and phase angle as a function of frequency for PS layer sediments. These tests are very useful for examining the mechanical properties of the samples without altering the structure of the samples. The complex modulus values with weak frequency dependency and very small phase angle values (no crossover) were observed, which points to a solid-like behavior of the samples. A similar solid-like behavior of natural sediments for frequency sweep tests, within the linear viscoelastic regime, has been reported in the literature (Van Kessel and Blom 1998; Soltanpour and Samsami 2011; Xu and Huhe 2016). The complex modulus of sediments from the SW location (3917 Pa) was one order of magnitude higher than the sediments from the RV location (417 Pa), which can be attributed to their very high density. At higher frequencies, an increase in complex modulus and a decrease in phase angle were observed, which was due to the rheometer head inertial effects. This experimental data obtained due to the head inertial effects was removed from the figures to avoid any misconception.
PS layer results: a complex modulus and b phase angle as a function of frequency for different locations within linear viscoelastic regime; c complex modulus and d phase angle as a function of frequency within linear viscoelastic regime for different mud samples having different visual consistencies. Bars represent standard deviation. The solid line is a guide for the eye
Frequency sweep tests were also carried out in linear regime for sediments from the same location but with different consistencies (i.e., densities), in order to evaluate their mechanical properties, and the results are shown in Fig. 4c and d. All the sediments displayed a solid-like behavior as evident from their weak frequency-dependent complex modulus (Fig. 4c) and very small values of phase angle (Fig. 4d). This solid-like character became more pronounced (the modulus increased from 13 to 8033 Pa and the phase angle decreased from 11° to 7°) with the increasing consistency of the samples (i.e., going deeper into the sediment bed). The similar increase in mechanical properties (i.e., increase in storage modulus) of natural sediments as a function of volume concentration of solids was also reported by Huang and Aode (2009). Furthermore, the rheometer head inertial effects were very substantial for the fluid mud layer at frequencies higher than 3 Hz due to their prominent liquid-like character.
3.3.1 Relation between storage modulus and volume fraction of solids
The following empirical model, similar to the one reported by Lupi et al. (2016, 2017), is proposed to fit the storage modulus of samples as a function of volume fraction of solids:
where G0 is a fitting parameter, ϕ is the volume fraction of solid, and ϕm is the maximum packing fraction. The volume fraction of solids is determined by using the expression given by Coussot (1997). Figure 5a shows the quite good fit of the model with the experimental data of the storage modulus at 1 Hz of the mud sediments. The values of the fitting parameters are presented in Table S2 (ESM).
3.3.2 Correlation between storage modulus and yield stresses
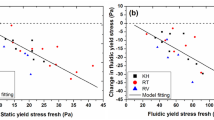
An empirical approach, similar to the one proposed by Chateau et al. (2008), was used to correlate the yield stresses with the storage modulus of the mud suspensions using the following relation:
where α2 is the fitting parameter and its value was 0.325 Pa for static yield stress, and 7.62 Pa in the case of fluidic yield stress. Figure 5b and c present the good agreement between the model and the experimental data of mud sediments for different locations.
The values of the rheological parameters obtained in this study were also compared with the values of rheological properties of the mud samples reported in the literature (Table 1). The comparison displayed similar values of rheological parameters for mud samples from the Port of Santos, the Port of Rotterdam, and the Port of Hamburg, for similar density ranges. However, the mud samples from Eckernförde Bay have significantly lower yield stress values for comparable density ranges. This might be due to the differences in measuring technique/geometry, organic matter content, or analysis of rheological data. The samples from other mentioned locations showed substantially higher values of rheological parameters because of their higher densities compared with those of the three other ports mentioned above.
Stress sweep tests were proven to be practical and time-efficient tests for measuring both static and fluidic yield stresses. The fluidic yield stress value of fluid mud is an important parameter for controllability and maneuverability of vessels because above this yield stress the fluid mud behaves as a liquid-like material. Static yield stress of fluid mud, on the other hand, can be a suitable parameter for characterizing the mud in the low-energy regions of the harbor. The fluid mud layer, in all locations it was observed, displayed small yield stresses with a weak thixotropic character. This result shows that vessels can pass through this layer without damage. This rheological analysis is a step forward for safe navigation and economic sediment management strategies at the Port of Hamburg.
4 Conclusions
A detailed rheological analysis was performed on the mud samples collected from different locations of the Port of Hamburg, Germany, representing different layers within the sediment bed. Stress sweep tests, flow curves, thixotropic tests, oscillatory amplitude, and frequency sweep tests were performed to assess the rheological fingerprint of the considered mud sediments. Two yield stresses (static and fluidic) were identified for all samples and their relative ratio was approximatively equal to 5. The mud samples obtained from RT location displayed higher values of yield stresses (57–312 Pa) with the comparatively lower values of densities (1154–1210 kg m−3) due to their higher organic matter content (4.1–4.3%). The yield stress analysis of the mud samples of a given location displayed an increase in the yield stress values (0.8 to 45 Pa in the case of static yield stress, and from 2.44 to 284 Pa for fluidic yield stress) by going deeper into the sediment bed attributed to the increase in density of these samples (i.e., from 1087 to 1230 kg m−3). The thixotropic studies revealed that all the sediments, except from the RV location, exhibit a combination of thixotropic and anti-thixotropic behaviors. The fluid mud layers showed a negligible thixotropic behavior due to their liquid-like character. The sediments from RV location displayed only a thixotropic behavior for the entire shear rate range. The results of frequency sweep tests, within the linear viscoelastic limit, showed that the complex moduli of all the sediments were fairly frequency independent and also the phase angle values were very small (no crossover) which can be linked to a solid-like behavior of the samples in that frequency range. Even though the results presented here are applicable to the Port of Hamburg, the same protocol and principles can be applied to investigate any other harbor mud samples.
References
Babatope B, Williams PR, Williams DJA (2008) Cohesive sediment characterization by combined sedimentation and rheological measurements. J Hydraul Eng 134:1333–1336
Bai YC, Ng CO, Shen HT, Wang SY (2002) Rheological properties and incipient motion of cohesive sediment in the Haihe Estuary of China. China Ocean Eng 16:483–498
Barnes HA (1997) Thixotropy—a review. J Non-Newton Fluid Mech 70:1–33
Chateau X, Ovarlez G, Trung KL (2008) Homogenization approach to the behavior of suspensions of noncolloidal particles in yield stress fluids. J Rheol 52:489–506
Coussot P (1997) Mudflow rheology and dynamics. CRC Press, Rotterdam, The Netherlands
Coussot P (2007) Rheophysics of pastes: a review of microscopic modelling approaches. Soft Matter 3:528–540
Fass RW, Wartel SI (2006) Rheological properties of sediment suspensions from Eckernforde and Kieler Forde Bays, Western Baltic Sea. Int J Sediment Res 21:24–41
Fonseca DL, Marroig PC, Carneiro JC, Gallo MN, Vinzón SB (2019) Assessing rheological properties of fluid mud samples through tuning fork data. Ocean Dyn 69:51–57
Gordon RB (1974) Dispersion of dredge spoil dumped in near-shore waters. Estuar Coast Mar Sci 2:349–358
Gratiot N, Manning AJ (2004) An experimental investigation of floc characteristics in a diffusive turbulent flow. J Coast Res 41:105–113
Harrison W, Wass ML (1965) Frequencies of infaunal invertebrates related to water content of Chesapeake Bay sediments. Southeast Geol 6:177–186
Houssais M, Ortiz CP, Durian DJ, Jerolmack DJ (2016) Rheology of sediment transported by a laminar flow. Phys Rev E 94:062609
Huang Z, Aode H (2009) A laboratory study of rheological properties of mudflows in Hangzhou Bay, China. Int J Sediment Res 24:410–424
Inglis C, Allen F (1957) The regimen of the Thames Estuary as affected by currents, salinities, and river flow. Proc Inst Civil Eng 7:827–868
ISO (1995) Soil quality: determination of organic and total carbon after dry combustion (elementary analysis). ISO, Geneva
Jiang F, Mehta AJ (1995) Mudbanks of the southwest coast of India IV: mud viscoelastic properties. J Coast Res 11:918–926
Jorgen Fredsoe RD (1992) Mechanics of coastal sediment transport. Advanced series on ocean engineering, vol 3. World Scientific Publishing, Singapore
Kirichek A, Chassagne C, Winterwerp H, Vellinga T (2018) How navigable are fluid mud layers? Terra et Aqua 151:6–18
Lupi FR, Shakeel A, Greco V, Rossi CO, Baldino N, Gabriele D (2016) A rheological and microstructural characterisation of bigels for cosmetic and pharmaceutical uses. Mat Sci Eng C 69:358–365
Lupi FR, De Santo MP, Ciuchi F, Baldino N, Gabriele D (2017) A rheological modelling and microscopic analysis of bigels. Rheol Acta 56:753–763
Malarkey J et al (2015) The pervasive role of biological cohesion in bedform development. Nat Commun 6:6257
Manning AJ, Dyer KR (2002) The use of optics for the in situ determination of flocculated mud characteristics. J Opt A Pure Appl Opt 4:S71–S81
Manning AJ, Friend PL, Prowse N, Amos CL (2007) Estuarine mud flocculation properties determined using an annular mini-flume and the LabSFLOC system. Cont Shelf Res 27:1080–1095
Manning AJ, Baugh JV, Spearman JR, Whitehouse RJS (2010) Flocculation settling characteristics of mud: sand mixtures. Ocean Dyn 60:237–253
Manning AJ, Baugh JV, Spearman JR, Pidduck EL, Whitehouse RJS (2011) The settling dynamics of flocculating mud-sand mixtures: part 1—empirical algorithm development. Ocean Dyn 61:311–350
May EB (1973) Environmental effects of hydraulic dredging in estuaries. Alabama Marine Resources Bulletin. Alabama Marine Resources Laboratory, Alabama
McAnally WH et al (2007a) Management of fluid mud in estuaries, bays, and lakes. I: present state of understanding on character and behavior. J Hydraul Eng 133:9–22
McAnally WH, Teeter A, Schoellhamer D, Friedrichs C, Hamilton D, Hayter E, Shrestha P, Rodriguez H, Sheremet A, Kirby R (2007b) Management of fluid mud in estuaries, bays, and lakes. II: measurement, modeling, and management. J Hydraul Eng 133:23–38
Mehta AJ (2013) An introduction to hydraulics of fine sediment transport, vol 38. World Scientific Publishing Company, Singapore
Mehta AJ, Manning AJ, Khare YP (2014) A note on the Krone deposition equation and significance of floc aggregation. Mar Geol 354:34–39
Mewis J, Wagner NJ (2009) Thixotropy. Adv Colloid Interfac Sci 147:214–227
Nosrati A, Addai-Mensah J, Skinner W (2011) Rheology of aging aqueous muscovite clay dispersions. Chem Eng Sci 66:119–127
Parker WR, Kirby R (1982) Time dependent properties of cohesive sediment relevant to sedimentation management-European experience. In: Lewis LR (ed) Estuarine comparisons. Academic Press, pp 573–589
Parsons DR, Schindler RJ, Hope JA, Malarkey J, Baas JH, Peakall J, Manning AJ, Ye L, Simmons S, Paterson DM, Aspden RJ, Bass SJ, Davies AG, Lichtman ID, Thorne PD (2016) The role of biophysical cohesion on subaqueous bed form size. Geophys Res Lett 43:1566–1573
Paterson DM, Hagerthey SE (2001) Microphytobenthos in constrasting coastal ecosystems: biology and dynamics. In: Reise K (ed) Ecological comparisons of sedimentary shores. Springer Berlin Heidelberg, Berlin, pp 105–125
Paterson DM, Crawford RM, Little C (1990) Subaerial exposure and changes in the stability of intertidal estuarine sediments. Estuar Coast Shelf Sci 30:541–556
Ross MA, Mehta AJ (1989) On the mechanics of lutoclines and fluid mud. J Coast Res 5:51–62
Schindler RJ, Parsons DR, Ye L, Hope JA, Baas JH, Peakall J, Manning AJ, Aspden RJ, Malarkey J, Simmons S, Paterson DM, Lichtman ID, Davies AG, Thorne PD, Bass SJ (2015) Sticky stuff: redefining bedform prediction in modern and ancient environments. Geol 43:399–402
Soltanpour M, Samsami F (2011) A comparative study on the rheology and wave dissipation of kaolinite and natural Hendijan Coast mud, the Persian Gulf. Ocean Dyn 61:295–309
Soulsby RL, Manning AJ, Spearman J, Whitehouse RJS (2013) Settling velocity and mass settling flux of flocculated estuarine sediments. Mar Geol 339:1–12
Spearman J, Manning AJ (2017) On the hindered settling of sand-mud suspensions. Ocean Dyn 67:465–483
Spearman JR, Manning AJ, Whitehouse RJS (2011) The settling dynamics of flocculating mud and sand mixtures: part 2—numerical modelling. Ocean Dyn 61:351–370
Spencer KL, Manning AJ, Droppo IG, Leppard GG, Benson T (2010) Dynamic interactions between cohesive sediment tracers and natural mud. J Soils Sediments 10:1401–1414
Tolhurst TJ, Gust G, Paterson DM (2002) The influence of an extracellular polymeric substance (EPS) on cohesive sediment stability. In: Winterwerp JC, Kranenburg C (eds) Proceedings in marine science, vol 5. Elsevier, The Netherlands, pp 409–425
Van Kessel T, Blom C (1998) Rheology of cohesive sediments: comparison between a natural and an artificial mud. J Hydraul Res 36:591–612
Whitehouse R, Manning A (2007) Mixing it: how marine mud and sand interact. Innovation & Research Focus, Institution of Civil Engineering, London, Thomas Telford Services Ltd, 71
Whitehouse R, Soulsby R, Roberts W, Mitchener H (2000) Dynamics of estuarine muds: a manual for practical applications. Thomas Telford, London
Wurpts R (2005) 15 years experience with fluid mud: definition of the nautical bottom with rheological parameters. Terra et Aqua 99:22–32
Xu J, Huhe A (2016) Rheological study of mudflows at Lianyungang in China. Int J Sed Res 31:71–78
Yang W, Tan SK, Wang H, Yu G (2014a) Rheological properties of bed sediments subjected to shear and vibration loads. J Waterway Port Coastal Ocean Eng 140:109–113
Yang W, Yu G-l, Tan S, Wang H-k (2014b) Rheological properties of dense natural cohesive sediments subject to shear loadings. Int J Sed Res 29:454–470
Zhu L, Sun N, Papadopoulos K, Kee DD (2001) A slotted plate device for measuring static yield stress. J Rheol 45:1105–1122
Acknowledgments
This study is carried out within the framework of the MUDNET academic network: https://www.tudelft.nl/mudnet/.
Funding
This study is funded by the Hamburg Port Authority.
Author information
Authors and Affiliations
Corresponding author
Additional information
Responsible editor: Marta Castellote
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
ESM 1
(DOCX 760 kb)
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Shakeel, A., Kirichek, A. & Chassagne, C. Rheological analysis of mud from Port of Hamburg, Germany. J Soils Sediments 20, 2553–2562 (2020). https://doi.org/10.1007/s11368-019-02448-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11368-019-02448-7