Abstract
Purpose
Several methods were developed to quantify the damage to mineral resources in LCA. Building on these and further expanding the concept of how to assess mineral resources in LCA, the authors developed in previous articles a method to account for dissipative resource flows in life cycle inventory (LCI). This article presents a price-based life cycle impact assessment method to quantify the potential impact of dissipative uses of resources.
Methods
This article firstly defines an impact pathway from resource use to resource dissipation and subsequent damage to the safeguard subject for “mineral resources”. It explores the quantification of this damage through the definition of characterization factors (CFs), for application to dissipative flows reported in LCI datasets. Market prices are used as a relevant proxy for the multiple, complex and varied functions and values held by mineral resources. Price data are collected considering a 50-year timeframe. Intervals of 10, 15, 20 and 30 years are considered for sensitivity analysis. Price-based CFs are tested on one cradle-to-gate case-study (copper production), in combination with accounted resources dissipated across the life-cycle. An approach to calculate the normalization factor (NF) is explored at the EU level.
Results and discussion
CFs are calculated for 66 mineral resources, considering copper as reference substance. Precious and specialty metals have the largest CFs. Minerals are instead ranked at the bottom of the hierarchy. New insights that this method brings in LCA are discussed for the copper production case-study. Losses due to final disposal of tailings are key (90% of total value loss), as opposed to e.g. emissions to environment. Relevance, robustness, completeness and consistency of the price-based CFs are discussed. This method in particular offers a relatively large coverage of elementary flows, with underlying data of good quality. Sensitivity of CFs to the chosen time interval is relatively limited. Initial analysis for a NF based on 14 key resources dissipated in the EU in 2016 is presented.
Conclusions
The developed CFs are relevant to address the issue of mineral resources value loss in LCA. They may be used in combination with dissipation-based methods at the LCI level, as tested in this study, or potentially (i) with classical extraction-based LCI datasets or (ii) as potential complements to existing life cycle impact assessment methods not capturing damage to resource value. Future refinements shall aim at extension to additional mineral resources and investigate the possibility of regionalisation of CFs and NF calculation.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Mineral resources are part of our daily lives and are key for our well-being and the majority of technological applications. They are also crucial for the competitiveness and growth of economies. In the European Union (EU), the publication of the Raw Material Initiative in 2008 (EC 2008) set the basis for growing focus on sustainable supply of raw materials from EU sourcing and from global markets, in addition to resource efficiency and recycling. A secure and sustainable supply of those raw materials considered “critical” is particularly crucial for the EU, and actions to increase EU resilience and open strategic autonomy are therefore underway (EC 2020).
Several methods, capturing diverse dimensions of the issue related to mineral resources, have been developed in the last two decades to quantify the damage to mineral resources in the LCA of a product or a system (Sonderegger et al. 2020). The “task force mineral resources” of the Life Cycle Initiative hosted by UN Environment classified these methods according to the questions they address, recommending existing life cycle impact assessment (LCIA) methods in relation to these questions (Berger et al. 2020). The abiotic depletion potential (ADP, ultimate reserve; Guinee et al. 2002; van Oers et al. 2002) is in particular recommended for use by practitioners when addressing the question of the relative contribution of a product system to the depletion of mineral resources (Berger et al. 2020). This recommendation is in line with that of the product and organization environmental footprint (PEF/OEF) methods, currently in its transition phase in the European Union (Zampori and Pant 2019; EC 2021). LIME2 (standing for life-cycle impact assessment method based on endpoint modelling) is moreover interim recommended to quantify the relative (economic) externalities of mineral resource use (Berger et al. 2020). It evaluates the effect of a hypothetical lack of investment of earnings from the sale of finite resources in terms of potential externality of lost future income (Berger et al. 2020; Itsubo and Inaba 2014). The future welfare loss, not published at the time of the “task force mineral resources” work and therefore not recommended (Berger et al. 2020), is a market-price-based method that aims at assessing the social cost of resource exhaustion (Huppertz et al. 2019). In these three methods (ADP, LIME2 and future welfare loss), and generally in other LCIA methods, characterization factors (CFs) are applied to resource extraction flows as classically reported in life cycle inventory (LCI) datasets.
During the development of the Organization Footprint Sector Rules (OEFSR) of the copper producing sector, the Technical Secretariat (TS) in charge of drafting the rules highlighted the shortcomings of depletion-based approaches, such as ADP in its various applications (EC 2018a, b). As a follow up, the Joint Research Centre (JRC) explored the possibility of implementing the concept of resource dissipation in an LCA, with a specific focus on the environmental footprint (EF) methods (Zampori and Sala 2017).
The “task force mineral resources” additionally called for the definition of the concept of dissipative resource use and for its integration in future method developments (Berger et al. 2020). Several authors have subsequently explored the concept of resource dissipation and its potential implementation in LCA. Beylot et al. (2020b) described the status of resource dissipation in the literature of life-cycle-based studies and suggested a comprehensive definition for this concept, in the absence of a common understanding (in literature) of what a dissipative flow is. In parallel, several authors have developed methods to operationalize the accounting of resource dissipation in LCI and/or LCIA (van Oers et al. 2020; Owsianiak et al. 2022; Charpentier Poncelet et al. 2021; Charpentier Poncelet et al. 2022; Beylot et al. 2020a; Beylot et al. 2021). In particular, the Joint Research Centre of the European Commission developed a life cycle inventory method (named as “JRC-LCI” method in the following) that relies on accounting for dissipative flows at the unit process level in LCI datasets, considering a short-term perspective (Beylot et al. 2020a, 2021). Tested on a case study, this method proved relevant to identify hotspots in terms of resource dissipation in supply chains, in mass units. Yet, so far, this method stands for a “fate model” enabling to distinguish between dissipative and non-dissipative resource flows at the unit process level, while the “effect” induced by these dissipative flows is not assessed.
The “task force mineral resources” stated that the damage to the safeguard subject for “mineral resources” is the reduction or loss of the "potential to make use of the value that mineral resources can hold for humans in the technosphere" (Berger et al. 2020). In this context, this article complements the JRC-LCI method, which so far enables to account for dissipative flows in a product system at the LCI level in mass units (Beylot et al. 2021), with an impact assessment method that further quantifies the damage induced by these dissipative flows. The combination of the JRC method, at the LCI level (Beylot et al. 2021) and at the impact assessment level (this article), overall enables to quantify reduced accessibility to mineral resources value in LCA.
This article is structured as follows: Sect. 2 describes the proposed method (including impact pathway description and computation of CFs); Sect. 3 presents the resulting CFs and impact assessment in a case-study; Sect. 4 discusses these results in terms of (i) the new insights this method brings as support to decision-making, (ii) sensitivity to the timeframe considered for CFs calculation, (iii) possible approach for defining normalization factor; and (iv) relevance, robustness, completeness and consistency of the method.
2 Method
2.1 Impact pathway description
2.1.1 “Value”: the key concept to be captured in the damage assessment
The “task force mineral resources” defined the safeguard subject for “mineral resources” with the intention to account for “humans as the most relevant stakeholders for mineral resources, i.e., the focus is on the instrumental value of resources for humans” (Berger et al. 2020). “Value”, or “utility” (i.e. by providing a certain function) for a certain subject (usually humans, in the common anthropogenic perspective) is more generally classically core in the definition of natural resources in the literature (Ardente et al. 2019). Value was moreover key in the intended consensus process as described for the SUPRIM project by Schulze et al. (2020), which concluded that the so-called type B perspective (“Abiotic resources are valued by humans for their functions used (by humans) in the technosphere”) best summarized their view on the role of abiotic resources. Still at this stage, there is no consensus on the way either the resource value (potentially “instrumental”) or the “potential to make use of the value that mineral resources can hold for humans in the technosphere” (Berger et al. 2020), shall be captured, in particular in LCA. Capturing value in the quantification of the damage to mineral resources in LCA is moreover also in line with principles of circular economy, as e.g. fostered in the EU action plan for the circular economy (EC 2015). In the latter, the instrumental value/function of the natural resources (extracted, harvested and overall transformed) are aimed to be maintained for the beneficial use by humans.
2.1.2 Accounting for mineral resource dissipation and induced value loss in LCA
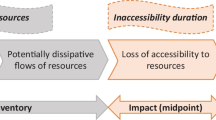
In this context, this study suggests the following impact pathway to account for the reduction or loss of the potential to make use of the value that mineral resources can hold for humans in the technosphere. A product system requires the use (“consumption”) of mineral resources. Part of these are extracted from ground (primary resources), while the remaining share stems from the life cycle of other product systems via recycling activities (secondary resources). It is noteworthy that:
-
The concept of “resources” as intended here matches the understanding by the “task force mineral resources”, which encompasses resources from both ecosphere and technosphere. It also aligns with the perspective promoted by Schulze et al. (2020), according to which “resources may originate from both primary and secondary production”;
-
“resources” here refers to the ones used by the product system, not to the geological stock of resources as sometimes implicitly considered when referring to “resource depletion”.
All along the life cycle of the product system under study, part of these resources are rendered not accessible to future users due to different constraints, which prevent humans to make use of the function(s) that these resources could have in the technosphere (e.g. mineral resources emitted to environment). Building on the definition of “resource dissipation” provided by Beylot et al. (2020b), the product system under study consumes/uses mineral resources as inputs, and delivers part of these mineral resources in a dissipated form. It is noteworthy that the level of accessibility of (potentially) dissipative mineral resources may depend on technological and economic factors, which can change over time (Beylot et al. 2020b). The temporal perspective is therefore key in the determination of dissipative flows and shall be specified in any method development building on this impact pathway.
Subsequently, these dissipative flows (or losses; Beylot et al. 2020b) of mineral resources further imply the loss of the value that these resources can hold for humans in the technosphere, as humans cannot access them anymore within the time horizon in the problem definition. These dissipative flows damage the safeguard subject for “mineral resources” in terms of a loss of value. Any method that is developed following this impact pathway is accordingly expected to address the question: “How can I quantify the consequences of temporal or permanent loss of the functional values of natural resources (as related to dissipation) caused by its use in a product system?”.
2.1.3 Resource “prices” as a representative proxy for resource “value”
Mineral resources hold a value regarding what they can be used for by humans, i.e. in terms of “services” they may provide to humans within a product (either alone or in combination with other mineral — and sometimes non-mineral — resources). This can reflect an anthropocentric perspective focused on the role of resources in the economy (Schulze et al. 2020). For example, the use of tungsten allows mobile phones to vibrate, while gallium and indium are part of light-emitting diode technology in lamps. This “value” is therefore highly connected to the function(s) that the mineral resources may provide to humans, so that the term functional (or instrumental) value may sometimes be used instead of “value”.
The market price of mineral resources represents the way that these resources are valued by the economic actors requiring their use for product manufacturing (e.g. electronics, automotive, building, etc. sectors). Higher priced metals (e.g. tungsten, gallium and indium) are generally used in more specialized applications than cheaper ones, for which their specific functionalities can be fully utilized. Despite these natural resources may also provide some more basic functions, their high production cost normally prevents their use in lower added-value applications for which they are substituted by lower priced resources.
Metal price variations and their consequences in terms of substitution highlight further the close connection between function, value and price of mineral resources. Resource prices also reflect their availability in the market (in a certain moment), as also affected by geopolitical tensions and social aspects: prices are affected by (and to some extent, reflect the) competition between different production processes. In case of higher prices of metals, the latter are used specifically for some of their higher-valued functionalities, e.g. copper substituted by aluminium for pipes or electrical applications when the price of copper increased in the 2000s. In that case, the increase in copper price led to its use preferentially in applications of higher value. We may conclude that market prices of resources may be influenced by a large number of factors (some of them as listed above), being, however, a discussion of how prices are determined beyond the scope of this article.
The use of economic relations is also not new in LCA: for instance, the use of allocation factors based on the economic value of different co-products can summarize complex attributes of products or services quality that cannot be easily measured by physical criteria (Ardente and Cellura 2012).
Overall, the general assumption and concept behind the proposed method for building CFs for resources is that price can be considered a proxy for the multiple, complex and varied functions and values that natural resources can have in highly interconnected socioeconomic systems. It is recognized that natural resources could have cultural, spiritual or emblematic “values” that could not be captured by the economic value (Dewulf et al. 2015); still, we consider that price-based CFs can be a good proxy of the overall resource functions and values,Footnote 1 especially for short-term evaluations,Footnote 2 with the additional benefit that these are easy to be calculated.
2.2 Impact assessment and associated characterization factors: operationalization
This section describes the operationalization of the above-presented general impact pathway. Dissipative flows of mineral resources are accounted at the LCI level through implementation of the JRC-LCI method (Sect. 2.2.1). The associated value lost is assessed through a market-price-based method as described in Sects. 2.2.2 and 2.2.3.
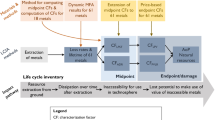
2.2.1 Resource dissipation in life cycle inventories
The JRC-LCI method consists in reporting dissipative flows of mineral resources at the unit process level, in mass units, considering a predefined list of dissipative mineral resource flows to a number of compartments (Beylot et al. 2020a, 2021). Beylot et al. (2020a; 2021) suggest to consider a short-term perspective (25 years). In this context, any flow of resources to (i) environment, (ii) final waste disposal facilities and (iii) products-in-use in the technosphere, without providing any significant function anymore (including due to non-functional recycling), is suggested to be reported as dissipative. The JRC-LCI method shall be implemented in two steps: (i) mapping the flows of mineral resources into and out of the unit processes under study (“resource flow analysis”, RFA, i.e. substance flow analysis of the resources), and (ii) identifying the dissipative flows and reporting them in the LCI at the unit process level. The JRC-LCI method focuses on dissipation, and therefore excludes “occupation-in-use” for which by definition the function(s) that the resources could hold in the technosphere is (are) exploited (Beylot et al. 2021). Yet, it is recalled that, despite not being a form of dissipation, “occupation-in-use could be considered as potentially affecting the accessibility of the resources for other users” (Beylot et al. 2021).
RFA consists in quantifying the flows entering the unit process as resources from ground and resources embodied in products from the technosphere, and coming out of the unit process. The outputs from the unit process are in one of the three following forms:
-
i)
Embodied in the output product. In that case, resources may be conserved (that is, holding a significant function in the product) or, by opposition, dissipated (if holding none or low function);
-
ii)
Directly dissipated as emissions to the environment;
-
iii)
Embodied in a waste for further treatment. In that case, the resources may be conserved (i.e. significant function conserved, through e.g. a recycling process) or dissipated (e.g. final disposal in a landfill, without valorisation of the function).
Moreover, regarding the definition of mineral resources, the same rules as the ones considered in Beylot et al. (2021) for the implementation of the JRC-LCI method have been followed in this study. In short:
-
Regarding primary mineral resources: “if the mineral or aggregate has a value as such (e.g., gypsum or sand), the mineral is considered the relevant elementary flow” (Berger et al. 2020), that is to say, it is the resource; instead if the value of a mineral ore is to host elements only, then the target elements in the ore are considered to be the resources (as in the ecoinvent 3 database; Weidema et al. 2013);
-
Regarding mineral resources in use in the technosphere: as long as the chemical elements, minerals and aggregates hold their value in the product system under study, they are resources.
As a basis, the list of mineral resource flows derives from the EF reference package (version 3.0; EC 2019), considering all minerals classified as “resources from ground”.
2.2.2 Damage assessment
The impact of resource dissipation in terms of value loss can be calculated as the sum of the mass of each individual resource dissipated multiplied by a CF that reflects its value with respect to a reference substance (Eq. 1):
where:
-
Value loss (VL) = impact related to dissipation of mineral resources value [kg Ref. sub. €eq]
-
mi = mass of the ith mineral resource dissipated [kg];
-
CFi = characterization factor of the ith resource, compared to a reference substance and calculated as in Eq. (2):
$${CF}_i=\frac{{Price}_{Av,i}}{{Price}_{Av,ref.sub.}}{\,}{\,}{\,}{\,}{\,}{\,}{\,}\left[\frac{\frac{\EUR}{{kg}_i}}{\frac{\EUR}{{kg} {\,}{Ref.Sub.}}}\right]$$(2)
where:
-
PriceAv,i = average price (over a certain timeframe) of the ith resource [€/kg];
-
PriceAv,ref. sub. = average price (over a certain timeframe) of a reference substance [€/kg].
This method delivers the impact of a product system on the safeguard subject “mineral resources” in terms of “Value Loss” (VL), i.e. in terms of the loss of value that mineral resources can hold for humans in the technosphere. The approach proposed in Eqs. 1 and 2 is relevant for assessment in a short-term perspective, although it might be relevant also for longer temporal scopes, especially in the absence of easy and suitable alternatives. Through this method, all the flows of different resources dissipated accounted for in the LCI phase (e.g. copper, aluminium and iron) are translated in the equivalent dissipated mass of a reference resource (e.g. copper, gold or antimony) based on their relative values. For example, assuming copper as reference substance, an hypothetical impact of VL equal to 2.5 kg Cu€eq would mean that, along the whole life cycle of the system under study, the overall amount of all the resources dissipated is equivalent, in value terms, to 2.5 kg of copper.
2.2.3 Price data for characterization factors determination
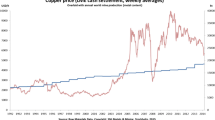
The Historical Statistics for Mineral and Material Commodities of the United States Geological Survey (USGS) are considered in this study for implementation of Eqs. 1 and 2 (USGS 2020). They represent a comprehensive database for resources’ prices, characterized by good data availability (relatively high completeness), precision, representativeness and with up-to-date information. Net present value (which is the economic function that allows to compare cash flows occurring in different times) is considered in order to account for the time value of money.
Prices of resources can be affected by variability, especially in short timeframes, induced by a multitude of aspects not necessarily related to the utility of the resource (e.g. political decisions, wars and tariffs), and beyond the scope and problem definition of this article. However, when considering longer periods (e.g. some decades), price fluctuations of many resources tend to be less important. One main temporal perspective (50 years) is considered, with four additional temporal perspectives (10, 15, 20 and 30 years) considered within a sensitivity analysis (see Supplementary Information—Online Resource).
2.2.4 Scope of the impact assessment method
The resource scope, temporal scope and geographical scope of this price-based impact assessment method may be reported with building on the framework developed by Schulze et al. (2020). In this study, price-based CFs are developed considering elements (e.g. copper and zinc) and configurations (e.g. clays and gypsum). They may be applied with LCI accounting for either dissipative flows or flows extracted from ground, at the elemental and configurations level as in the JRC-LCI method (for dissipative flows) or standard LCI databases (for resource flows extracted from ground). The five temporal perspectives (10, 15, 20, 30 and 50 years; with 50 years as the main reference) are all rather short-term perspectives. This temporal scope of the price-based CFs makes them particularly fit for combination with the JRC-LCI method in a short-term perspective (25 years) as developed by Beylot et al. (2020a, 2021). Still, the proposed price-based approach might be relevant to be used for longer perspectives, but this requiring additional investigation. Finally, the developed method enables to address the mineral resource issue on a global scale, yet with potentially some differences in values (prices) depending on the region of the world where losses actually occur (see the "Sect. 4" where potential need for regionalization is addressed).
2.3 Case study
This method to account for resource value loss in LCA is tested on one case study. It builds on the work of Beylot et al. (2021) who assessed direct dissipation of mineral resources along the cradle-to-gate primary production of copper, with 1 kg of copper cathode as the reference flow. Beylot et al. (2021) accounted for the mass of dissipative flows along the production process steps; in this article, the damage induced by these dissipative flows is further assessed. The system boundary first encompasses mining and concentration, which result in the production of copper concentrate (containing around 30% of copper) from sulfidic copper ore extraction and treatment. In this case study, tailings are considered to be disposed of in a tailings management facility. The copper concentrate is then further treated in pyrometallurgy, resulting in the production of copper cathodes from the treatment of copper concentrate. This case study mainly builds on the exploitation of two ecoinvent (version 3.5) datasets: "copper mine operation, sulphide ore, GLO" and "copper production, primary, GLO", respectively representing the process of copper concentrate production and copper production (from copper concentrate) at a global scale (ecoinvent 2019; Classen et al. 2009).
It is highlighted that this case-study has been discussed to analyse the applicability of the proposed method, although further testing of full cradle-to-grave examples would provide further relevant insights regarding dissipation in the use and product end-of-life phases of products and systems life-cycles.
3 Results
3.1 Characterization factors
The CFs are computed for 66 minerals and chemical elements based on their 50-year price-average, considering copper as the reference mineral resource. They are represented in Figs. 1 and 2 distinguishing four categories of metals as defined by the UNEP (2011; precious, specialty, ferrous and non-ferrous metals), in addition to one generic category of minerals. For sake of clarity, CFs have been represented in two separate figures, distinguishing resources with CFs > 1 from those with CFs < 1. CFs are available in the Supplementary Information (Online Resource) associated with this article, considering alternative timeframes (10, 15, 20 and 30 years, in addition to 50 years) and different reference substances (e.g. gold and antimony, in addition to copper). Highest CFs are observed for precious metals (gold, platinum group metals — PGMs — and to a slightly lower extent silver; Fig. 1). Precious metals have historically been prized for their relation to wealth and status, but they are increasingly used in technological applications (UNEP 2011). The CFs associated with gold and PGMs are more than three orders of magnitude larger than that of Cu, by definition set to 1 in this method as the reference chemical element. Moreover, specialty metals are also globally highly ranked in this classification (Fig. 1). They are classically used in industrial and consumer products in small amounts thanks to their specific chemical and physical properties. Rhenium, thallium, gallium, germanium, etc. in particular have CFs between 2 and 3 orders of magnitude larger than that of copper. Thirdly, ferrous and non-ferrous metals have CFs in-between one order of magnitude larger and one order of magnitude lower than that of copper. In particular, the basic metals lead, nickel, tin, aluminium and zinc are ranked relatively close to copper. Finally, minerals are globally ranked in the second part (and bottom) of this hierarchy. These minerals include in particular gypsum, feldspar, diatomite, salt, sand and gravel, etc.
3.2 Application to a case study
Dissipative flows of mineral resources are accounted at the LCI level, based on the JRC-LCI method, as already presented in Beylot et al. (2021), including the discussion on main assumptions and limitations. In order to produce 1 kg of copper cathode, 0.88 kg of direct dissipative resource flows is generated, mainly in the form of calcium carbonate (51% of the total mass) with copper additionally representing a significant contribution (30% in mass terms), while iron (8%), sulphur (5%), molybdenum and chromium (2%) overall represent more limited shares (Fig. 3). Tailings final disposal, and to a slightly lower extent pyrometallurgy and mining and concentration, all represent important contributions in mass terms (respectively 42%, 29% and 26%).
The further implementation of market price-based CFs as developed in this study, applied to the dissipative flows at the unit process level, enables to account for the associated resources value loss. Copper is the main contributing mineral and metal resource, representing 62% of the total impact. Mineral resource value loss is mainly associated with copper loss in tailings disposal facility (54%), and to a lower extent in slags used in construction (7%) and in environment (1%). Molybdenum is the second most contributing resource (25%, in tailings disposal facility). Other dissipative resource flows have more limited contributions (nickel, 5%; iron, 3%; calcium carbonate, 2%; etc.), as driven by smaller masses dissipated compared to copper and molybdenum (e.g. in the case of nickel) and/or due to lower CFs (e.g. regarding iron and calcium carbonate). Tailings final disposal is the hotspot process step, representing 90% of the damage to mineral resources value. Instead, dissipation as emissions to the environment (from mining and concentration and pyrometallurgy) only represents 3% of the total damage to mineral resources value.
4 Discussion
4.1 Comparison with depletion-based impact assessment method
Price-based CFs may be put in perspective with abiotic depletion potential (ADP) CFs, ultimate reserve, as recommended respectively by the "task force mineral resources" and by the European Commission in the PEF method, to calculate the contribution of mineral and metal resource use to depletion (EC 2021). Prices and ultimate reserves capture two distinct aspects of mineral resources, respectively value and scarcity, only poorly interconnected and eventually resulting in very different sets of CFs, as demonstrated by a poor correlation (R2 = 0.26; Fig. 4). For example, ADP CFs for gallium and germanium are very low (order of magnitude of 10−7) because they are not scarce in the Earth’s crust. Instead their CFs based on prices are relatively high (beyond 200): the amount of these resources available in the market for practical uses is relatively low compared to demand in several very specific, high-valued, applications. Actually, a resource may be largely present in the crust (as magnesium, one of the most abundant element in Earth’s crust and marine water), but still the resource can be scarce in forms that can be mined and made available for the production processes (e.g. magnesium listed among the EU Critical Raw Materials list; EC 2020). The proposed method therefore may be more relevant for assessment in a short-term perspective, focusing on the use of the resources in the technosphere (as currently known).
4.2 Timeframe and price variations
Metal prices are known to be relatively volatile. This is for example the case for rare earth elements, whose prices have significantly increased in 2011, e.g. by a factor 70 for neodymium considering its value in July 2011 compared to the period 2002–2003, in average (Bru et al. 2015). Despite their volatility, in a very common context of metal co-production (i.e. multi-functional) processes, metal prices have classically been considered in LCA as an allocation key to assess the impacts by co-produced metals. For example, in their LCA study applied to metal production, including rare earth oxides, Nuss and Eckelman (2014) consider average prices over the period 2006–2010. Arshi et al. (2018) instead consider prices for rare earths in 2016. The choice for different short-time intervals to calculate price averages as allocation keys, in particular in the context of rare-earths elements which showed very extreme price increase in 2011, may partly drive different impact assessment results as obtained in different studies.
Building on this observation, in this study, the timeframe for deriving average prices has been intentionally set to a relatively long period (50 years). Such time interval is particularly adapted to smooth out prices fluctuations and prevent that sudden, short-term, effects of volatility have large effects on the determination of the average price. It is also assumed that the relative differences in prices between resources may be considered a proxy for the price differences between resources in the short-term future.
The influence of the chosen timeframe set to calculate price-based CFs is further investigated in a sensitivity analysis considering average prices over 10, 15, 20 and 30 years, as compared to 50 years set as the reference in this study. Sixty mineral resources are covered in this sensitivity analysis, compared to 66 covered with a CF for the 50-year timeframe. This is due to lack of recent data which hampers to calculate reliable CFs for shorter timeframes. Despite differences between CFs of different resources calculated respectively for a 50-year timeframe and for 10, 15, 20 and 30 years, one observes a very good correlation, as demonstrated by R2 in the interval [0.96; 0.99] (Fig. 5 and Supplementary Information—Online Resource). Despite price evolution over time, both in the long-run and in the short-run (with sudden peaks), relative prices as captured by the developed price-based CFs are relatively similar regardless the timeframe considered. Detailed calculation of the different CFs for different timeframes, and different reference resources, is provided in the Supplementary Information (Online Resource).
4.3 Strengths and weaknesses
Strengths and weaknesses of the price-based characterization method are discussed, both in absolute terms (considering this method only) and in relative terms (comparison with other, widely-used, impact assessment methods), regarding the following criteria: relevance to the question to be addressed; robustness of underlying assumptions; completeness (coverage of elementary flows); data quality (including uncertainty and representativeness); consistency with other impact categories; operationalization and communication.
4.3.1 Relevance
The “task force mineral resources” of the Life Cycle Initiative hosted by UN Environment set the issue of “value” as of utmost importance regarding the safeguard subject for “mineral resources” (which is “the potential to make use of the value that mineral resources can hold for humans in the technosphere”; Berger et al. 2020). The price-based characterization method enables to capture “value” in the impact assessment step, especially to what concerns the functions that resources may have for humans in the technosphere. When combined with a method to account for dissipated resources at the LCI level, it enables to capture the loss of value of mineral resources as induced by a product-system over its life cycle, i.e. the damage to the safeguard subject as defined by the “task force mineral resources”.
Methods to account for dissipation in particular encompass the JRC-LCI method as considered in the case study of this article. Further combination of price-based CFs with other methods to account for dissipative flows at the inventory level is additionally conceivable, e.g. with the method developed by Owsianiak et al. (2022) that enables to distinguish the actual dissipative emissions of resources to environment, from the non-dissipative ones, in the LCI step in mass units. Yet in the latter case, the associated robustness of conceptual foundations for the combination between such LCI-based methods and price-based CFs (e.g. regarding consistency in temporal perspectives) and associated potential issues of operationalization (e.g. nomenclatures of elementary flows) still require to be assessed.
It is noteworthy that more generally, price-based CFs may be directly combined with (i) classical approach to resource accounting in LCIs, which consists in reporting resources extraction from ground, or even (ii) in combination with LCIA methods that apply to current LCI (e.g. average dissipation rate, ADR, and lost potential service time, LPST, methods developed by Charpentier Poncelet et al. 2021, for estimating the impacts of dissipative flows of metals). These possible combinations shall be further explored regarding a number of aspects, including actual complementarity (e.g. in terms of conceptual ground for these methods, and operationalization) and consistency in terms of assumptions, defined problem and scope.
4.3.2 Robustness
This method builds on a limited number of both hypotheses and layers of data, whose uncertainty would add in the derivation of CFs. Still, it builds on one fundamental hypothesis: historical market prices of mineral resources are assumed to represent a best available proxy for their “values” in the technosphere and representative for resource prices in the near future. At this stage, there is not only no consensus on the way resource value shall be captured in LCIA of mineral resource use; there is also still no consensus on what the concept of “value” covers and how it should be defined. We consider that market prices of mineral resources represent the way that these resources are valued by economic actors, using them for the specific functions they provide. It is true that on the production side, market price is driven by a number of parameters, like energy consumption and associated costs, scarcity, etc. Energy consumption, in particular, represents a relevant component of resource price. Anyway, value of resources should reflect also their accessibility and the difficulties to get the resource available for their use in a product system (including energy necessary to mine and refine). Therefore, we consider that costs for energy consumption should be considered in the impact assessment of resources. As future development of the method, the possibility to decouple the costs for energy from the resource value should be investigated.
It is also recommended to grant consistency between the inventoried dissipative flows and their corresponding CFs. This can be difficult in some cases, as for example dissipated metals in unrefined ores may have a value lower than that of refined metals. Still, we would recommend to use the price of refined metals as best proxy available (in the absence of more precise price figures). This is, however, a limitation needing further exploration.
Still, on the demand side, the price that is paid by economic actors is conditioned by the benefit that they will make from the use of these mineral resources. In terms of robustness of the underlying assumptions, it can be considered that the use of resources prices well fits as a proxy to determine their value as intended in this paper. The use of proxies has been adopted also by other impact assessment methods. For example ADP CFs are built considering that resource content of the continental crust (assuming 12 km depth) is a correct proxy for the ultimate reserve; which is further assumed to be a correct proxy for ultimately extractable reserve in the computation of CFs (van Oers et al. 2020). Similarly, Owsianiak et al. (2022) assume that average concentration in the continental crust is a good proxy threshold for mineral resources accessibility, and that all chemical elements in extracted mineral ores (even those in concentrations close to 0) are mineral resources. Therefore, we consider that (i) the price-based method developed in this article enables to account for the loss of value of mineral resources, which makes it fully relevant as this topic is core according to the "task force mineral resources" recommendations, and (ii) there is some trade-off regarding robustness of the underlying assumptions (here considering “price” as a good proxy for “value”), yet acceptable in view of assumptions made in other classically implemented LCIA methods for mineral resource use.
4.3.3 Data quality and completeness of coverage
CFs are based on mineral resources market price data which overall can be qualified of good quality. This encompasses (i) reliability, (ii) representativeness and (iii) completeness:
-
i)
Prices are by definition a quantified value agreed upon and communicated between stakeholders (sellers, buyers and potentially transparently available to market). In this study, data are drawn from the USGS. Therefore, both the nature of the data at stake and their source as used for CFs compilation make them reliable, in absolute terms (relatively low uncertainty) and in relative terms as compared to other types of data (in particular physical flows) classically implemented in LCA calculations;
-
ii)
Representativeness here refers to both temporal and geographical representativeness. Data over a 50-year interval are implemented in the CFs, so that temporal representativeness may be considered good. Shorter temporal scopes moreover show rather limited influence on differences in CFs, as discussed in Sect. 4.2. Moreover, geographical representativeness is also expected to be good, with many metal markets classically at a worldwide scale;
-
iii)
Finally, coverage of substances is rather large. CFs have been developed for 66 minerals and chemical elements, which is e.g. comparable to the good coverage in ADR/LPST methods and in the updated ADP method (respectively 61 metals covered, and 76 chemical elements covered; Charpentier Poncelet et al. 2022; van Oers et al. 2020). One asset of the price-based CFs relies in particular on the possibility to consider not only chemical elements but instead both chemical elements and minerals as “mineral resources”.
4.3.4 Consistency with other impact categories, operationalization and communication
The price-based method to account for resources value loss, as developed in this study with respect to mineral resources, may be further extended to other types of natural resources. This in particular includes fossil resources, while it is still to be explored and it may be questionable the applicability to other natural resources such as land or freshwater.
Price-based CFs as developed in this study are available in the Supplementary Information in Excel format (Online Resource). They are ready for use by practitioners, either directly combined with classical approach to account for mineral resources extracted from ground in LCI datasets, or with more recent method to account for dissipative flows, such as the JRC-LCI approach. Moreover, the concept of "value loss", that is captured by these CFs when combined with dissipative flows in LCI datasets, may be adequately understood by (and therefore communicated to) decision-makers or non-expert public audience. However, consistency with other impact categories requires careful evaluation, especially in respect to time frame and problem definition.
4.4 Improved CFs and developing normalization factor: a way forward
4.4.1 Improving CFs reliability and completeness
Despite overall good quality (including representativeness) of the CFs as computed in this study, they may be further improved in the future in a number of ways.
Firstly, CFs for chemical elements refer to metals in their refined form; whereas losses in the life cycle are not necessarily in such metal form, but rather e.g. in oxidized form and therefore of lower value. Moreover, in one case, the price of a material (steel) was used as a proxy for the price of the major metal it is composed of (iron). The CFs as listed in this study accordingly tend to overestimate the impact of dissipative losses in the production steps along the life cycle of products and systems. Secondly, it is noteworthy that some commodities (e.g. rare earths) are primarily traded on over-the-counter markets (i.e. directly between two parties and without a central exchange or broker). This implies less transparent data, and as a consequence potentially more uncertain reporting in databases such as that of the USGS.
These limits may be overcome by exploring further data sources. These include e.g. data published by the London Metal Exchange (LME 2022), Fastmarkets (Fastmarkets 2022), Oanda (Oanda 2022), etc. Exploring these other data sources is beyond the scope of this study, but may be relevant in further developments, as it will potentially open the door to:
-
More complete data, i.e. potentially integrating additional mineral resources beyond those covered in Figs. 1 and 2, including disaggregation of the CF associated with rare earth elements (REEs) into CFs for individual REEs;
-
Less uncertain data, including intervals of values to be integrated in sensitivity analysis;
-
Regionalisation of CFs and evaluation of associated relevance (or not), at a level of disaggregation (in terms of countries/regions) to be determined;
-
Evaluation of the relevance of regionalization of CFs, at a level of disaggregation (in terms of countries/regions) to be determined. “Relevance” could here be explored both in terms of (i) any actual, observable, difference in prices for each mineral resource (as a function of regions where these are sold); and (ii) conceptual validity of such potential regionalization (in a context where the developed impact assessment method intends to evaluate value loss for humans). This latter point would require exploring how far the LCIA method shall be approached either in one single global perspective (i.e. one single value of each mineral resource for humans, independently on any price difference by region), or shall instead account for potentially different (regional) valuations by humans, as might be reflected by different prices per region.
Moreover, while mineral resource elements may hold a value for humans, in some cases, they may reduce the accessibility of other mineral resource elements, and/or the functionality of these other elements, therefore negatively affecting the value of these other resources. This is e.g. the case of arsenic in copper concentrates, which is deleterious for downstream resources recovery though smelting and refining processes. Each smelter sets diverse limits for contaminants, reflected by diverse penalties potentially escalating with increasing concentration (Salomon-de-Friedberg and Robinson 2015). More generally, the content of impurities is sometimes used to reflect quality of recycling (Tonini et al. 2022). It is also considered that the presence of potential impurities is somehow factored in by the price paid by a smelter. However, these aspects are not addressed in the LCIA method presented in this article. Further developments both at the inventory level (within the JRC LCI method) and at the impact assessment level would be relevant to further reflect how far impurities affect the accessibility and value of other mineral resources in a material (whether a product or a waste).
Finally, it is noteworthy that CFs shall be updated in a sufficiently regular basis, at a frequency that depends on the temporal perspective considered for the CFs; that is, more frequent updates for CFs averaged over 10 years than regarding CFs averaged over 50 years. The use of a 50-year timeframe as a reference allows also to reduce the need of frequent updates due to the smoothing effect associated with such a long timeframe.
4.4.2 An approach to develop a normalization factor
In LCA, and in particular in EF, normalization factors (NFs) are developed as a useful step for a better interpretation of results. As an example, Crenna et al. (2019) developed global NFs for EF impact categories.Footnote 3
A way forward to develop a NF for the impact category on dissipated resources is presented here. Calculations have been based, however, on annual data of resource dissipation as available for the EU. Value loss is quantified considering 14 mineral resources, based on the data from material systems analysis (Matos et al. 2021, 2020; Passarini et al. 2018). These references adopted a common approach to flows accounting, despite showing some inconsistencies in geographical and temporal scopes, as (i) data have mainly been drawn for year 2016, yet also considering data for earlier or later years regarding some mineral resources; and (ii) they are not globally representative whereas generally referring to the EU-27 (i.e. without the UK), except for three substances (Al, Cu and Fe). We checked the correspondence in flows to ensure that dissipative flows as in these abovementioned references were equivalent to dissipative flows in JRC-LCI, including estimations for in-use dissipation.Footnote 4 Correspondence between nomenclatures and calculations is described in the Supplementary Information (Online Resource). In this context, the estimated normalization factor for the EU amounts to 1.63E + 07 tonnes Cu€eq, with large contribution of Fe (76%), and to a lower extent Al and Cu (9% each). This large contribution of Fe to the total value loss in the EU is primarily driven by its large contribution (93%) to the total mass of resources dissipated. The mass of Fe dissipated is more than 1 to 5 orders of magnitude larger than that of each of the 13 other resources accounted for in this analysis.
The approach here described represents a first attempt to estimate the NF based on the proposed method, and therefore the use of this NF by LCA practitioners for normalization should be implemented with caution. Additional research to develop a robust NF is, however, needed, especially concerning data availability of amounts dissipated so far for a limited number of resources. Moreover, the approach here described for NF for the EU should be also considered at global scale (especially to grant consistency with price series used for the calculation of the CF).
5 Conclusions and perspectives
This article presents a price-based characterization method to quantify the impact of mineral resource use in LCA and, in particular, the loss of value that abiotic resources (primary and secondary) may hold for humans in the technosphere (Schulze et al. 2020). The price of a given resource is used as a representative proxy for the functions that such resource has in the economy. The CFs of this LCIA method are calculated for 66 minerals considering configurations (e.g. clays and gypsum) and chemical elements (e.g. copper and zinc) based on their 50-year price-average, considering copper as the reference mineral resource. Alternative CFs are moreover made available regarding other temporal perspectives (10, 15, 20 and 30 years). General considerations on the method are not affected by changes in the chosen reference substance (e.g. copper, gold or antimony). The temporal scope of the method is rather oriented to short-term assessment, and geographical scope is global. The potential use for longer time frames and the relevance of regionalization should be further explored.
The 50-year-price-based CFs are tested in this article on one cradle-to-gate case study (copper production), in combination with the JRC-LCI method which accounts for dissipative mineral resource flows at the inventory level. This combined use of the JRC-LCI and the price-based CFs enables to capture the loss of value of mineral resources as induced by a product-system over its life cycle. The developed price-based CFs may alternatively be further combined with (i) other methods to account for resource dissipation in the LCI of products and systems, e.g. methods that consider only emissions of mineral resources to environment as dissipative flows; (ii) classical approach to accounting of resources extraction from ground; or (iii) some mineral resource LCIA methods that apply to current LCI datasets, yet without capturing the value of resources (e.g. ADR and LPST). Such combinations shall be further explored, in particular in terms of consistency (e.g. of underlying assumptions in each method) and operationalization.
The developed price-based characterization method is relevant to address the issue of mineral resources value loss in LCA. Associated CFs enable good coverage of elementary flows, with using as a basis underlying data of good quality. These CFs could be easily understood by LCA practitioners and non-expert public (including policy makers). They moreover offer relevant perspectives for coherently accounting for natural resources (including mineral resources) in LCA. Yet, despite this overall satisfying level of quality, the developed CFs offer in the meantime perspectives for short- and long-term improvements. In the short-term, these CFs may be further refined considering (i) higher disaggregation at the level of substances, including distinction between the form of metals (e.g. as metal at a high purity versus in oxidized form); (ii) extension to additional mineral resources, not covered yet; (iii) potential regionalisation of CFs (e.g. at the level of some regions of the World; e.g. the EU); and (iv) further development and testing of NFs following the approach proposed in the present article. Finally, it is noteworthy that the developed CFs have so far not been tested extensively to a broad number of case studies. Therefore, potential users of these CFs should be aware of this limitation. It is recommended that these CFs should be further tested before they are applied routinely in LCA studies.
Data availability
Main data analysed and generated in this article is provided in the Supplementary information (SI) (Online Resource). This includes the background data for the calculation of CFs (with Cu as reference substance); the background data for the calculation of CFs (with Au and Sb as reference substances); the background data for the calculation of NF; and the correspondence between the dissipative flows in the JRC-LCI method and in the background studies used to calculate the NF.
Notes
Different and better proxies could be used in long-term assessments, although the authors believe that, due to their simplicity, long historical series of market prices may be also considered for assessments referred to longer time frames.
EF impact categories include climate change, ozone depletion, human toxicity (cancer and non-cancer), ecotoxicity, particulate matter, ionizing radiation, photochemical ozone formation, acidification, eutrophication (terrestrial, marine, and freshwater), land use, water use and resource use.
In use dissipation refers, for example, to loss of zinc due to corrosion of zinc coating on steel and loss of copper due to spread of copper sulphate as a fungicide.
References
Ardente F, Beylot A, Zampori L (2019) Towards the accounting of resource dissipation in LCA. XIII Conference of Rete Italiana LCA, Rome, 14–15 June 2019. https://www.sipotra.it/wp-content/uploads/2020/01/Atti-del-XIII-Convegno-della-Rete-Italiana-LCA.pdf (Last access: June 2022)
Ardente F, Cellura M (2012) Economic allocation in life cycle assessment. J Ind Ecol 16:387–398. https://doi.org/10.1111/j.1530-9290.2011.00434.x (Last access: June 2022)
Arshi PS, Vahidi E, Zhao F (2018) Behind the scenes of clean energy: the environmental footprint of rare earth products. ACS Sustain Chem Eng 6:3311–3320. https://doi.org/10.1021/acssuschemeng.7b03484 (Last access: June 2022)
Berger M, Sonderegger T, Alvarenga R, Bach V, Cimprich A, Dewulf J, Frischknecht R, Guinée J, Helbig C, Huppertz T, Jolliet O, Motoshita M, Northey S, Peña CA, Rugani B, Sahnoune A, Schrijvers D, Schulze R, Sonnemann G, Valero A, Weidema BP, Young SB (2020) Mineral resources in life cycle impact assessment: part II– recommendations on application-dependent use of existing methods and on future method development needs. Int J Life Cycle Ass 25:798–813. https://doi.org/10.1007/s11367-020-01737-5 (Last access: June 2022)
Beylot A, Ardente F, Penedo De Sousa Marques A, Mathieux F, Pant R, Sala S, Zampori L (2020a) Abiotic and biotic resources impact categories in LCA: development of new approaches. EUR 30126 EN, Publications Office of the European Union, Luxembourg, 2020a, ISBN 978–92–76–17227–7, https://doi.org/10.2760/232839, JRC120170
Beylot A, Ardente F, Sala S, Zampori L (2021) Mineral resource dissipation in life cycle inventories. Int J Life Cycle Ass 26:497–510. https://doi.org/10.1007/s11367-021-01875-4 (Last access: June 2022)
Beylot A, Ardente F, Sala S, Zampori L (2020b) Accounting for the dissipation of abiotic resources in LCA: status, key challenges and potential way forward. Resour Conserv Recy 157:104748. https://doi.org/10.1016/j.resconrec.2020.104748 (Lastaccess:June2022)
Bru K, Christmann P, Labbé JF, Lefebvre G (2015) - Panorama mondial 2014 du marché des Terres Rares. Rapport public. BRGM/RP-65330-FR. 194 p., 58 fig. 32 tab
Charpentier Poncelet A, Helbig C, Loubet P, Beylot A, Muller S, Villeneuve J, Laratte B, Thorenz A, Tuma A, Sonnemann G (2021) Life cycle impact assessment methods for estimating the impacts of dissipative flows of metals. J Ind Ecol 25:1177–1193. https://doi.org/10.1111/jiec.13136 (Last access: June 2022)
Charpentier Poncelet A, Loubet P, Helbig C, Beylot A, Muller S, Villeneuve J, Laratte B, Thorenz A, Tuma A, Sonnemann G (2022) Midpoint and endpoint characterization factors for mineral resource dissipation: methods and application to 6000 data sets. Int J LIfe Cycle Ass. https://doi.org/10.1007/s11367-022-02093-2
Classen M, Althaus HJ, Blaser S, Tuchschmid M, Jungbluth N, Doka G, Faist Emmenegger M, Scharnhorst W (2009) Life cycle inventories of metals. Final report ecoinvent data v2.1 No.10. EMPA Dübendorf, Swiss Centre for Life Cycle Inventories, Dübendorf, CH
Crenna E, Secchi M, Benini L, Sala S (2019) Global environmental impacts: data sources and methodological choices for calculating normalization factors for LCA. Int J Life Cycle Ass 24:1851–1877. https://doi.org/10.1007/s11367-019-01604-y (Last access: June 2022)
Dewulf J, Benini L, Mancini L, Sala S, Blengini GA, Ardente F, Recchioni M, Maes J, Pant R, Pennington D (2015) Rethinking the Area of Protection “Natural Resources” in life cycle assessment. Environ Sci Technol 49:5310–5317. https://doi.org/10.1021/acs.est.5b00734 (Last Access: June 2022)
EC (2008) Communication from the Commission to the European Parliament and the Council. The raw materials initiative — meeting our critical needs for growth and jobs in Europe {SEC(2008) 2741}. Brussels 4.11.2008. COM(2008) 699 final
EC (2015) Communication from the Commission to the European Parliament, the Council, the European Economic and Social Committee and the Committee of the Regions. Closing the loop - An EU action plan for the Circular Economy. COM 614
EC (2018a) Website “The Environmental Footprint Pilots”. Available at: http://ec.europa.eu/environment/eussd/smgp/ef_pilots.htm (Last access: 22/06/2022)
EC (2018b) Organisation Environmental Footprint Sector rules – Copper Production, 2018b. Version Number 3.0. Available at: http://ec.europa.eu/environment/eussd/smgp/documents/OEFSR_Copper.pdf (Last access: 22/06/2022)
EC (2019) EF reference package 3.0 (transition phase). Available at: https://eplca.jrc.ec.europa.eu/LCDN/EF_archive.xhtml (Last access: 15/10/2022)
EC (2020) Communication from the Commission to the European Parliament, the Council, the European economic and social committee and the Committee of the regions. Critical Raw Materials Resilience: Charting a Path towards greater Security and Sustainability. COM/2020/474 final
EC (2021) Commission recommendation of 16.12.2021 on the use of the Environmental Footprint methods to measure and communicate the life cycle environmental performance of products and organisations. Brussels 16.12.2021 C(2021) 9332 final
ecoinvent (2019) The ecoinvent Database. Available at: https://ecoinvent.org/the-ecoinvent-database/ (Last access: May 2022)
Fastmarkets (2022) Website. https://www.fastmarkets.com/ (Accessed 13 June 2022), (Last access: June 2022)
Guinee JB (2002) Handbook on life cycle assessment operational guide to the ISO standards. Int J Life Cycle Ass 7:311. https://doi.org/10.1007/BF02978897 (Last access: June 2022)
Huppertz T, Weidema BP, Standaert S, De Caevel B, van Overbeke E (2019) The social cost of sub-soil resource use. Resour 8. https://doi.org/10.3390/resources8010019
Itsubo N, Inaba A (2014) LIME2 - chapter 2: characterization and damage evaluation methods. Tokyo
London Metal Exchange (LME) (2022) Website: https://www.lme.com/ (Accessed 13 June 2022) (Last access: June 2022)
Matos CT, Ciacci L, Godoy León MF, Lundhaug M, Dewulf J, Müller DB, Georgitzikis K, Wittmer D, Mathieux F (2020) Material system analysis of five battery-related raw materials: cobalt, lithium, manganese, natural graphite, nickel, EUR 30103 EN, Publication Office of the European Union, Luxembourg, 2020, ISBN 978–92–76–16411–1. https://doi.org/10.2760/519827, JRC119950
Matos CT, Devauze C, Planchon M, Ewers B, Auberger A, Dittrich M, Wittmer D, Latunussa C, Eynard U, Mathieux F (2021) Material system analysis of nine raw materials: barytes, bismuth, hafnium, helium, natural rubber, phosphorus, scandium, tantalum and vanadium. EUR 30704 EN, Publications Office of the European Union, Luxembourg, ISBN 978–92–76–37768–9. https://doi.org/10.2760/677981, JRC125101
Nuss P, Eckelman MJ (2014) Life cycle assessment of metals: a scientific synthesis. PLoS ONE 9(7):e101298. https://doi.org/10.1371/journal.pone.0101298 (Last Access: June 2022)
Oanda (2022) Website. www.oanda.com (Last access: June 2022)
Owsianiak M, van Oers L, Drielsma J, Laurent A, Hauschild MZ (2022) Identification of dissipative emissions for improved assessment of metal resources in life cycle assessment. J IND ECOL 26:406–420. https://doi.org/10.1111/jiec.13209 (Last access: June 2022)
Passarini F, Ciacci L, Nuss P, Manfredi S (2018) Material flow analysis of aluminium, copper, and iron in the EU-28, EUR 29220 EN. Publications Office of the European Union, Luxembourg 2018 ISBN 978–92–79–85744–7. https://doi.org/10.2760/1079, JRC 111643
Salomon-de-Friedberg H, Robinson T (2015) Tackling impurities in copper concentrates. Teck Resources Limited. https://www.teck.com/media/Tackling-Impurities-in-Copper-Concentrates.pdf (Accessed Sept 2022)
Sonderegger T, Berger M, Alvarenga R, Bach V, Cimprich A, Dewulf J, Frischknecht R, Guinée J, Helbig C, Huppertz T, Jolliet O, Motoshita M, Northey S, Rugani B, Schrijvers D, Schulze R, Sonnemann G, Valero A, Weidema BP, Young SB (2020) Mineral resources in life cycle impact assessment—part I: a critical review of existing methods. Int J Life Cycle as 25:784–797. https://doi.org/10.1007/s11367-020-01736-6 (Last access: June 2022)
Schulze R, Guinée J, van Oers L, Alvarenga R, Dewulf J, Drielsma J (2020) Abiotic resource use in life cycle impact assessment—part I- towards a common perspective. Resour Conserv Recy. https://doi.org/10.1016/j.resconrec.2019.104596
Tonini D, Albizzati PF, Caro D, De Meester S, Garbarino E, Blengini GA (2022) Quality of recycling. Waste Manage 146:11–19. https://doi.org/10.1016/j.wasman.2022.04.037 (Last access: September
UNEP (2011) Recycling rates of metals - a status report, A report of the Working Group on the Global Metal Flows to the International Resource Panel. Graedel, T. E.; Allwood, J.; Birat, J.-P.; Reck, B. K.; Sibley, S. F.; Sonnemann, G.; Buchert, M.; Hagelüken, C. 2011
USGS (2020) Historical statistics for mineral and material commodities in the United States. https://www.usgs.gov/centers/national-minerals-information-center/historical-statistics-mineral-and-material-commodities (Last access: May 2022)
van Oers L, de Koning A, Guinée JB, Huppes G (2002) Abiotic resource depletion in LCA. Road and Hydraulic Engineering Institute, Ministry of Transport and Water, Amsterdam
van Oers L, Guinée JB, Heijungs R (2020) Abiotic resource depletion potentials (ADPs) for elements revisited—updating ultimate reserve estimates and introducing time series for production data. Int J Life Cycle as 25:294–308. https://doi.org/10.1007/s11367-019-01683-x (Last access:June 2022)
Weidema BP, Bauer C, Hischier R, Mutel C, Nemecek T, Reinhard J, Vadenbo CO, Wernet G (2013) Overview and methodology. Data quality guideline for the ecoinvent database version 3. Ecoinvent Report 1(v3). St. Gallen: The ecoinvent Centre.
Zampori L, Pant R (2019) Suggestions for updating the Organisation Environmental Footprint (OEF) method, EUR 29681 EN. Publications Office of the European Union, Luxembourg, ISBN 978–92–76–00651–0. https://doi.org/10.2760/577225, JRC115960
Zampori L, Sala S (2017) Feasibility study to implement resource dissipation in LCA, EUR 28994 EN. Publications Office of the European Union, Luxembourg ISBN 978-92-79-77238-2. https://doi.org/10.2760/869503, JRC109396
Acknowledgements
This research was mainly supported by the European Commission — Directorate General for Environment “Technical support for the Environmental Footprint and the Life Cycle Data Network”. The authors would like also to thank Gian Andrea Blengini and Rana Pant for suggestions and discussions that helped in conceiving and framing the research.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no competing interests.
Disclaimer
The views expressed in the article are personal and do not necessarily reflect an official position of the European Commission.
Additional information
Communicated by Matthias Finkbeiner
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ardente, F., Beylot, A. & Zampori, L. A price-based life cycle impact assessment method to quantify the reduced accessibility to mineral resources value. Int J Life Cycle Assess 28, 95–109 (2023). https://doi.org/10.1007/s11367-022-02102-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11367-022-02102-4