Abstract
Purpose
Despite efforts to treat uncertainty due to methodological choices in life cycle assessment (LCA) such as standardization, one-at-a-time (OAT) sensitivity analysis, and analytical and statistical methods, no method exists that propagate this source of uncertainty for all relevant processes simultaneously with data uncertainty through LCA. This study aims to develop, implement, and test such a method, for the particular example of the choice of partitioning methods for allocation in LCA, to be used in LCA calculations and software.
Methods
Monte Carlo simulations were used jointly with the CMLCA software for propagating into distributions of LCA results, uncertainty due to the choice of allocation method together with uncertainty of unit process data. In this study, a methodological preference is assigned to each partitioning method, applicable to multi-functional processes in the system. The allocation methods are sampled per process according to these preferences. A case study on rapeseed oil focusing on three greenhouse gas (GHG) emissions and their global warming impacts is presented to illustrate the method developed. The results of the developed method are compared with those for the same case similarly quantifying uncertainty of unit process data but accompanied by separate scenarios for the different partitioning choices.
Results and discussion
The median of the inventory flows (emissions) for separate scenarios varies due to the partitioning choices and unit process data uncertainties. Inventory variations are reflected in the global warming results. Results for the approach of this study vary with the methodological preference assigned to the different allocation methods per multi-functional process and with the continuous distribution of unit process data. The method proved feasible and implementable. However, absolute uncertainties only further increased. Therefore, it should be further researched to reflect relative uncertainties, more relevant for comparative LCAs.
Conclusions
Propagation of uncertainties due to the choice of partitioning methods and to unit process data into LCA results is enabled by the proposed method, while capturing variability due to both sources. It is a practical proposal to tackle unresolved debates about partitioning choices increasing robustness and transparency of LCA results. Assigning a methodological preference to each allocation method of multi-functional processes in the system enables pseudo-statistical propagation of uncertainty due to allocation. Involving stakeholders in determining these methodological preferences allows for participatory approaches. Eventually, this method could be expanded to also cover other ways of dealing with allocation and to other methodological choices in LCA.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Methodological choices are unavoidable in all phases of life cycle assessment (LCA) and are a source of uncertainty (Björklund 2002). Methodological choices in LCA refer, among others, to choices about system boundaries (Tillman et al. 1994), functional units, characterization factors (Huijbregts 1998), and methods to solve multi-functionality of processes (allocation methods). The latter is one of the most debated topics in the field of LCA (Weidema 2000; Pelletier et al. 2014; Ardente and Cellura 2012). According to the International Standardization Organization (ISO) 14044 guidelines, the choice of allocation method involves a stepwise procedure (ISO 2006): (1a) avoid allocation by dividing multi-functional unit processes; (1b) avoid allocation by expanding the system; (2) divide the system (partitioning) using physical relations between products; or (3) divide the system (partitioning) by other relations of products. The application of this procedure to solve multi-functionality constitutes a source of variability in LCA results of many product systems (Ayer et al. 2007; Weidema and Schmidt 2010; van der Harst and Potting 2014; Luo et al. 2009; Svanes et al. 2011; Guinée and Heijungs 2007) and may pose problems in different decision-making situations (Wardenaar et al. 2012). Hence, the importance of this specific methodological choice in LCA is evident.
The ISO procedure aimed to create consensus and standardization (Björklund 2002) thus increasing the inter-comparability of LCAs dealing with the same topics. Despite the fact that ISO guidelines are widely applied by practitioners, the consensus reached in practice has been limited (Pelletier et al. 2014; Weidema 2014). Besides following standards and guidelines, LCA practitioners may opt to show the influence of different allocation methods on LCA results through sensitivity analysis. If more than one allocation method is applicable to a multi-functional process, one-at-a-time (OAT) local sensitivity analysis is mostly performed. The influence of the choice of allocation method on the LCA results is investigated by adopting different sets or combinations of allocation methods in scenarios (Björklund 2002). This approach is very common when partitioning methods are used to solve multi-functionality (Ayer et al. 2007; Weidema and Schmidt 2010; van der Harst and Potting 2014; Luo et al. 2009; Svanes et al. 2011; Guinée and Heijungs 2007).
Another approach to treat the choice between methods to solve multi-functionality is based on mathematical arguments. To provide a solution for the system of linear equations of an LCA (Heijungs and Suh 2002), the use of the least-squares technique has been investigated (Marvuglia et al. 2010; Cruze et al. 2014). In this sense, particularly Cruze et al. (2014) favor avoiding allocation over partitioning regardless of the principle arguing that, “since the number of solutions to choose from is infinite, even consensus… would not necessarily lend validity to an LCA study.”
More recently, the study by Hanes et al. (2015) developed an analytical approach dealing with the choice of allocation method: the Comprehensive Allocation Investigation Strategy (CAIS). This approach considers all possible combinations of partitioning methods in a comparative LCA; therefore, it systematically explores the allocation space of various systems. CAIS helps determine whether comparisons between various systems are robust as far as the allocation space is concerned.
In a similar line of research, Jung et al. (2013) developed a method for integrating uncertainty of allocation factors in matrix-based LCA calculations and propagating it to LCA results using an analytical approach (i.e., first-order approximations). This method considers the allocation factors themselves as uncertain input parameters that have a variation and therefore lead to variability in the LCA outputs. It is thus not a method for choosing between allocation methods.
Besides the analytical method of Hanes et al. (2015), there is the statistical approach of Andrianandraina et al. (2015). They apply local and global sensitivity analyses to determine the influence of uncertainty in unit process data and methodological and modeling parameters to the total uncertainty in LCA results. Technical, environmental, and methodological parameters are treated as variables, and using a detailed LCA model for the foreground system, they calculate scenarios dependent on the values of these parameters. Particularly, the partitioning method is treated as a qualitative methodological parameter with a uniform discrete distribution and two possible values that correspond to economic and mass partitioning. Moreover, of the available literature, only Andrianandraina et al. (2015) treat variability of LCA results due to unit process data uncertainty as well as due to the choice of allocation method.
Despite the cited references for addressing the uncertainty or variability introduced by the choice of allocation method, no method has yet been developed to simultaneously propagate uncertainty in unit process data and the sensitivity due to the choice of allocation methods of more than one process to LCA results, without requiring a detailed, parameterized foreground model and with the potential to be applied to other methodological choices. In this study, we develop such a method to be used in LCA calculations and software. Data uncertainty and sensitivity due to methodological choices together determine the total range of LCA results for a specific system. Only propagating their influence simultaneously will provide the full total range of results. As we strive toward circular economies, multi-functional processes will be encountered more often in LCA systems, increasing the importance of this simultaneous approach, the development of which is the aim of this article.
2 Methods
For the development of the method of this article, it is first important to place the method of this study in the space of methods that have a similar purpose (see Table 1). For each reviewed method, Table 1 also lists allocation methods considered, the result after applying each approach, and the sources of variability accounted for. The most sophisticated methods include uncertainty in unit process data, choice uncertainty, and other sources of uncertainty, leading to results that account for these sources of variability.
In this study, for propagation of the uncertainty of unit process data, we use Monte Carlo simulations as propagation method. Within this sampling-based approach, we now include the discrete choice of allocation method as another element. Of course, uncertainty of process data and uncertainty of allocation method are distinct. There is a wide natural variability for process data, and a probability distribution properly reflects this, so that a sampling method is appropriate. For the discrete choice of allocation method, this is different. There is no natural variability. Nevertheless, we treat it in a similar way, because the effect is similar: In a given situation, we are not sure of the precise process data and we are not sure of the precise choice of allocation method. Therefore, combining the uncertainty of data and the spectrum of choices in one probabilistic setup is defendable. Notice that the usual terms that are appropriate for data uncertainty (uncertainty, probability, statistical, etc.) are not entirely suitable for describing choices. We will therefore in some cases avoid using such words, in other cases add a qualifier (like in “pseudo-statistical”), and in some cases just use them, tacitly acknowledging the changed usage. A short reflection around the—admittedly debatable—terminology used in this study will be provided at the end of the Sect. 4.
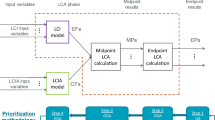
The application of this pseudo-statistical method poses an additional question: Is our method a local or global sensitivity analysis or rather an example of an uncertainty analysis? We argue that our method is closer to the realm of uncertainty analysis because the way we treat unit process data uncertainty is an example of a true uncertainty analysis propagating input uncertainties into output uncertainties (Fig. 1b). Moreover, contrary to common OAT practice (Fig. 1c), the choice of allocation method is also propagated using Monte Carlo simulations. The latter is clearly beyond an OAT sensitivity analysis and also constitutes the main reason why we consider this study to be more closely related to uncertainty analysis than to OAT sensitivity or scenario analysis. The aim of our method is to simultaneously propagate data and choice uncertainty to LCA results for all relevant processes of a product system (Fig. 1d).
a Schematic representation of a standard LCA using point values for unit process data as input as well as one allocation method per multi-functional process; the output corresponds with a point value for an environmental impact category or inventory flow. b Uncertainty analysis, using ranges, standard deviation, and distributions of unit process data instead of point values as inputs together with one allocation method per multi-functional process to calculate distributions of outcomes. c Local OAT sensitivity analysis varies a certain percentage of the inputs (one at a time) to see the influence in the outcomes. d This study propagates both data and allocation method choice uncertainty to the outputs. e Global sensitivity analysis starts with an uncertainty analysis and then calculates how much of the variability of the output is due to variability of each input
Finally, to illustrate the development and implementation of the method, we use the choice among partitioning methods as an example of methodological choice in LCA. This means that methods to avoid allocation will not be considered. In Sect. 4, the possibilities of broadening up the application of the method to other ways of dealing with allocation and to other methodological choices are addressed.
2.1 Implementation of a pseudo-statistical propagation method for uncertainty due to the choice of partitioning method
For a multi-functional unit process, one or several partitioning methods can be applied in order to solve multi-functionality. Partitioning factors are defined as the fraction that divides the non-functional economic (i.e., the input products and the output wastes) and environmental flows to the functional flows (i.e., the product of interest) of a multi-functional process (Guinée et al. 2004). For each multi-functional unit process in the system, partitioning factors are defined and applied to enable the calculation of the inventory table. Typically, the sum of all partitioning factors for each partitioning method is equal to 1 (Heijungs and Guinée 2007). This is, in very general terms, the working procedure for partitioning methods using different physical and non-physical principles such as mass, energy content, and economic value.
To be able to introduce pseudo-statistical propagation of the choice of partitioning method in an LCA system, the methodological preference (p) (as a percentage) is introduced for each applicable partitioning method per multi-functional process. This parameter corresponds to a discrete methodological parameter and has been set to a value between 0 and 100 %. The assignment of a methodological preference is a subjective choice offering a possibility to more actively account for different views by involved scientists and stakeholders or perhaps accounting for patterns in the partitioning choices already made by relevant literature. For instance, if only one partitioning method is applicable for a multi-functional process, then p equals 100 % for that method and process, and if for example, for another multi-functional process, three partitioning methods are applicable, then p 1, p 2, and p 3 should equal a value between 0 and 100 %, all together adding up to 100 %. These methodological preferences define the ranges of methodological preference such that for each range, one partitioning method takes place. The value of a random number from a uniform distribution between 0 and a 100 is then generated and evaluated for the ranges of preference, and in this way, a partitioning method is determined for each multi-functional process in the system.
In mathematical terms, every time a multi-functional process is encountered in a system, the following action takes place: A random deviate x is drawn uniformly between 0 and 100, and depending on its value, a certain allocation choice (partitioning in this case) is implemented.
After definition of the parameters introduced above, a method to propagate uncertainties to the LCA results is selected. For this, several methods exist and have been used in LCA (Groen et al. 2014; Heijungs and Lenzen 2014). Among the most widely used ones are sampling methods such as Monte Carlo (MC) simulations that rely on determining the probability distribution of the results by brute computing force progressively increasing in time (Heijungs and Huijbregts 2004). Other methods such as Latin hypercube simulation, which uses a more efficient random sampling, could be used for propagation too (Groen et al. 2014). However, given the aim of the paper, we focused on the most widely used and intuitively easiest approach: MC.
To propagate the uncertainty due to the choice of partitioning method using the described parameter definitions, MC simulations were adopted for the repeated random sampling. The larger the number of runs, the more combinations of partitioning choices could be taken into account in the results.
In case the same number of partitioning methods applies for all processes, the total number of partitioning scenarios for a system with multi-functional processes and several partitioning methods applicable to each process would be equal to the total amount of multi-functional processes to the power of the number of partitioning methods possible. For instance, Guinée and Heijungs (2007) found 54 “multi-output” processes linked to passenger car and diesel systems in the ecoinvent v1.1 database (Swiss Centre For Life Cycle Inventories 2004). From these, only seven were selected for the study by means of a contribution analysis. The study looked at the influence of economic partitioning, physical partitioning, and the ecoinvent default partitioning on the LCA results. A full scenario analysis for all partitioning methods would have implied 543, i.e., 157,464 possible partitioning scenarios, nonetheless only three were considered, i.e., the seven selected multi-output processes using either economic, physical, or ecoinvent v1.1 default partitioning.
With the method proposed here, the analysis of a system with a relative large number of multi-functional processes and/or partitioning methods, such as that of Guinée and Heijungs (2007), would become computationally feasible, by capturing most (if not all) possible partitioning scenarios by means of MC simulations without actually having to define scenarios.
2.2 Case study
The approach described in Sect. 2.1. has been implemented in the CMLCA software (CML 2014) version beta 5.2 and has been tested with a simple system: rapeseed oil production in Northern Europe, as shown in the flow diagram of the system in Fig. 2. The system is similar to the one implemented by Wardenaar et al. (2012); however, here it stops at rapeseed at mill in order to concentrate on the really important novel aspect. The focus of the case study is on the only two multi-functional processes: [P1] rapeseed cultivation and [P3] rapeseed oil extraction by cold pressing of rapeseed. Process [P1] produces straw and rapeseed, and process [P3] produces rapeseed oil and rapeseed cake at mill. Thus, both processes are multi-functional and require allocation. The functional unit is 1 kg of rapeseed oil at mill, and the system includes the production, storage, and transport of the main inputs to the three foreground processes shown in Fig. 2. The entire background system is specified using ecoinvent data version 2.2 (Swiss Centre For Life Cycle Inventories 2007) which is already allocated. The background system remains constant for all the scenarios analyzed in this study. Scenarios result from combinations of the partitioning methods selected for process [P1] and process [P3], as will be further specified. A detailed description of the implementation of the system is available in the Electronic Supplementary Material.
For the two multi-functional processes, two partitioning methods are identified as applicable. In the case of [P1] (rapeseed cultivation), 100 % partitioning, i.e., assuming that the straw is ploughed through the soil, and therefore all flows should be allocated to the rapeseed is the first option (Wardenaar et al. 2012b). The second partitioning principle identified is based on the mass of straw and rapeseed which is found for the typical production of rapeseed and straw in Northern Europe in van der Voet et al. (2008), and although in their study, they use 100 % partitioning, mass is another possibility for allocation. In the case of [P3] (rapeseed cold pressing), partitioning based on energy content and economic values of co-products could hold and the same partitioning factors as defined by Wardenaar et al. (2012) are used. Table 2 shows the partitioning factors per co-product for each of the partitioning methods and multi-functional processes described above.
The proposed method is tested by comparing two sets of LCA results. The first set corresponds to LCA results of the case study using an OAT sensitivity analysis to study the influence of different partitioning methods (i.e., without choice uncertainty) and process data uncertainty propagated with MC simulations. The second set corresponds to the LCA results for the case study using the method implemented in Sect. 2.1 to propagate the uncertainty due to the choice of partitioning method while also accounting for process data uncertainty and both sources of uncertainty propagated with MC simulations. The former LCA results are referred to as “allocation scenarios” or simply as “scenarios” (i.e., excluding choice uncertainty) and the latter as the results of “this study” (i.e., including choice uncertainty).
The scenario results are calculated for four scenarios defined by the combinations of two multi-functional processes in the system with two applicable partitioning methods in each process. To include unit process data uncertainty, the method of Henriksson et al. (2013) was used to determine the unit process data distributions where possible despite that there are other methods available (van der Harst and Potting 2014; Hong et al. 2010; Imbeault-Tétreault et al. 2013; Heijungs and Lenzen 2014). Moreover, for propagation, we used MC simulations with a sample size of 1000 simulations for each of the four allocation scenarios. Further, as shown in Table 2, the methodological preference assigned to one partitioning method per multi-functional process in each scenario corresponds to 100, because as stated in Sect. 2.1, choosing for one method corresponds to 100 % preference of that method.
For the calculation of the LCA results of this study, the unit process data uncertainty and the choice of partitioning are simultaneously propagated, using MC simulations based on unit process data distributions (same as in the allocation scenarios) and the methodological preference for the choice of partitioning method as defined in Table 2. A 50 % methodological preference has been arbitrarily chosen for all applicable partitioning methods in both multi-functional processes in the case study, but although arbitrary, this preference allows an equal representation for all the methods enabling one to propagate uncertainty due to the choice of method. A total of 4000 MC simulations are run to create a representative sample to cover all possible partitioning scenarios. One would expect to be able to do with fewer simulations in order to have a computational gain compared to the 1000MC simulations for the four scenarios. However, as the aim of case study is to test the method, it was decided to have the same amount of runs in order to increase the chance of covering all partitioning combinations. Besides, for a more complex system (with more than two multi-functional processes), the computational gain becomes more evident as the chance of reproducing all partitioning scenarios is low, while the feasibility of capturing them with the method of this study is higher. These results are expected to cover the full range of the scenario results without choice uncertainty.
Finally, as an example of inventory results, only the main greenhouse gases (GHG), i.e., carbon dioxide (CO2), methane (CH4), and di-nitrogen monoxide (N2O) will be presented, as well as the LCIA results for global warming using the IPCC (2007) global warming potentials for a 100-year time horizon.
3 Results
The median of the life cycle inventory (LCI) results for the allocation scenarios varies for carbon dioxide emissions from around 0.7 to 1.2 kg CO2/kg of rapeseed oil, for methane emissions from around 1.0 to 1.7 g CH4/kg of rapeseed oil, and for di-nitrogen monoxide emissions from around 1.8 to 4.0 g N2O/kg of rapeseed oil (Fig. 3, left panels). Thus, the differences between the median values of the scenarios only follow the choice of allocation methods for the two multi-functional processes in the case study.
Left panels: LCI results for the main GHG emissions to air of 1000 MC simulations for the four allocation scenarios and 4000 MC simulations for the method introduced in this study. The red line represents the median, the lower boundary of the blue box Q1, and the upper boundary Q3, so the height of the blue box is the interquartile range (IQR). The range of the whiskers (black horizontal lines) beyond the first and third quartiles is set to Q1(Q3)–(+) 1.5*IQR. The whiskers extend from the blue box to show the range of the data. The data points outside of this range represent the outliers beyond the whiskers and are plotted as blue crosses. Right panels: histograms with a bin size of 100 based on the same MC simulations as in the left panels
Figure 3 shows the absolute GHG emissions per kilogram of rapeseed oil at mill for the 1000 MC simulations (left panels) for each allocation scenario separately including a statistical propagation of unit process data uncertainty. As expected, for those allocation scenarios with higher allocation factors for rapeseed and rapeseed oil (scenarios 1 and 4), the GHG emissions for the system studied are higher. The range that results for each of the allocation scenarios is smaller than the range resulting from all together. This indicates that scenario analysis can be misleading if all possible scenarios are not taken into account in the results.
Moreover, Fig. 3 shows the absolute GHG emissions per kilogram of rapeseed oil at mill for the 4000MC simulations for the method introduced in this study (left panels column labeled “This study”). The results cover the full range of the four possible allocation scenarios but without separating between different scenarios as is seen in Fig. 3 (left panels, scenario 1, 2, 3 and 4 vs. This study).
The histograms displayed in Fig. 3 (right panels) show the distribution of the LCI results for the method of this study and the allocation scenarios.
For each allocation scenario, there is a peak around the median of the LCI results, and for the method of this study, an overlapping distribution is observed. For instance in the case of CO2 emissions, there are three observable peaks (not four as the peak of scenarios 1 and 3 overlap) which coincide with the medians of the allocation scenario. This outcome is also observable in the left panel graphs of Fig. 3, in the form of more dense clouds of points around certain values of emissions; however, it is not always so clear in the whisker plots and this is the main reason for presenting the same results also in histograms.
Figure 4 (left panel) shows the global warming results for the same four scenarios and for the method developed in this study. The contribution of emissions to the global warming results varies depending on the allocation scenario between 49 and 55 % for CO2, around 2 % for CH4, and between 43 and 49 % for N2O emissions. Moreover, the scenario results now show less overlap, which is reflected by the histograms that more clearly show four discernible peaks around the medians of the allocation scenarios.
Left panel: global warming in kg CO2 equivalents as an example of an impact category for the case study for 1000 MC simulations for the four allocation scenarios and 4000 MC simulations for the method introduced in this study. See the caption of Fig. 3 for an explanation of the blue boxes, red lines, and crosses. Right panel: histograms with a bin size of 100 based on the same MC simulations as in the left panels
4 Discussion
The method presented here to simultaneously propagate uncertainties in unit process data and due to the choice of partitioning methods is based on the introduction of the methodological preference of each applicable partitioning method for all multi-functional processes in a system.
In the case study presented, an equal methodological preference for all allocation methods applicable to the multi-functional processes in the systems was used. An equal methodological preference for all methods is of course an arbitrary choice, which can be made differently and in a more sophisticated way. One way to determine the methodological preferences of allocation methods could be to involve scientists, experts, and stakeholders of specific sectors whose preference for the different allocation methods could be taken as basis for determining these values. Another way could be to determine patterns in the allocation choices already made by means of a meta-analysis (van der Voet et al. 2010) of existing case studies preferably specific for rapeseed oil.
Moreover, the methodological preference may influence the case study’s results. We have investigated this influence by performing two distinct OAT sensitivity analyses. The two sensitivity analyses are variations of the two most extreme allocation scenarios, i.e., scenarios 2 and 4, arbitrarily changing the values of p as shown in Table 3 with the aim of exploring the effect of this parameter on the results.
Figure 5 illustrates the results of the sensitivity analyses compared to the equal methodological preference originally adopted for the case study.
Left panels: LCI results for the main GHG emissions to air of 4000 MC simulations for the method introduced in this study using three different sets of methodological preferences for the allocation methods as defined in Table 3. See the caption of Fig. 3 for an explanation of the blue boxes, red lines, and crosses. Right panels: histograms with a bin size of 100 based on the same MC simulations as in the left panels
The frequencies of the LCI results concentrate more around the median of a specific allocation scenario, as it is expected, once the methodological preference for one allocation method gets closer to 100 %. Therefore, the values of p affect the distribution of the results for the approach of this study. In Fig. 5 (left panels), the range of results for the second sensitivity case reduces compared to the original range of our case study. But also, the amount of data points beyond the whiskers (outliers) increase. This could indicate that the LCI data distributions have long tails that show up in the results only for seldom MC runs. For the first sensitivity, the total range increases slightly, and this is also an indication that the LCI data distributions are more sampled for values on the tails of the distributions.
As mentioned before, to calculate the uncertainty due to the choice of allocation method in separate scenarios and not integrated with the MC-based propagation of unit process data uncertainty, results have to be calculated for at least four scenarios for the simple case study (including only two multi-functional processes with two possible allocation methods each) and to run1000 MC simulations for each scenario in order to propagate LCI data uncertainty to the LCA results. This is a time consuming and a hardly ever performed work, and even less for more complex systems. In this context, the method proposed here accounts in a pseudo-statistical manner for a representative sample of possible combinations and shows a representative range of possible results for a system with its likelihood (i.e., distribution) demanding less time from the practitioner than a normal setup of an OAT sensitivity analysis but perhaps demanding more time for computation. The time spent in the case study for separate scenarios is the same as used by applying the method of this study, if the same number of MC simulations is adopted. However, we adopted more MC simulations for our method in order to ensure that all possible combinations of both data and allocation methods are sampled. For this reason, the time demand of our method is higher.
It can also be argued that this method could be intensive in terms of computing capacity requirements as it uses MC simulations as a propagating method. Nevertheless, analytical methods do not yet exist for propagation of the choice of allocation methods, and we doubt if this is possible at all. Relying on increasing computational capacity, we consider the proposed method as a good alternative to tackle two of the main sources of uncertainty in LCA in an integrated way. Possibilities for more efficient statistical propagation methods (e.g., Latin hypercube sampling) also remain a topic for further research.
Another point for discussion is the increased total uncertainties shown in the results of the method of this study, compared to those of the allocation scenarios. LCA studies are mostly relevant for comparing two or more alternative systems fulfilling the same functional unit. In the context of comparative LCA, relative uncertainties (Henriksson et al. 2015) play an important role for the application of this method. Therefore, the pseudo-statistical method becomes particularly relevant when comparing two or more alternative systems fulfilling the same functional unit.
Applying the method developed in this study for a comparison of two alternatives (A and B), fulfilling the same functional unit requires dependent MC sampling and comparison of the inventory and/or characterization results for each run, for example, by subtracting the results from alternative B from the results of alternative A (A − B). In this way, each alternative builds upon the same sampled parameters for those parts of the systems that are shared (similar) for both A and B (Henriksson et al. 2015). Similarly, we here argue that the same allocation scenarios should be sampled for multi-functional processes that are shared between the two systems A and B. In fact, comparing two or more alternative systems providing the same function could be misguided if different allocation methods are chosen for each system. The method of this study can provide comparable relative results simultaneously accounting for the same or varying allocation choices and LCI data uncertainties where pertinent, which would be more meaningful information than the full absolute range of uncertainty as shown, for example, in the case study.
One could think that information about the influence of the allocation choice is disguised as the range of absolute uncertainty only increases. However, a global sensitivity analysis (Fig. 1e) could reveal back the influence of the choice in the results. The contribution of uncertainty of the input parameters to the total uncertainty of the outputs can be identified. Therefore, one could prioritize the main contributors to the total uncertainty, and reduction of the overall uncertainty could be strived for, on the basis of which better data could be collected and/or consensus on allocation methods to be applied. This would never be possible with OAT sensitivity scenarios for allocation methods alone for a full-scale LCA. Exercises such as a comparative LCA and a global sensitivity analysis are, however, out of the scope of the present article and a topic for further research.
The method was presented for the example of dealing with the choice dilemma in solving multi-functionality by partitioning. The method could, however, also be applied to a higher level of choices for solving the multi-functionality problem. For instance, in the realm of consequential LCA, various scenarios of substitution or system expansion could also be assigned a methodological preference. In the realm of attributional LCA, as explored in the case study, various partitioning principles can be accounted for. As mentioned in other studies too, there is not one single way of solving multi-functionality in LCA (Guinée et al. 2004; Wardenaar et al. 2012), even when accepting that the solution should serve the purpose of the LCA (Pelletier et al. 2014).
The method could also be applied to other choices than only the one related to multi-functionality as long as the choice can be represented as a discrete choice. Then, a methodological preference can be assigned to each option, and the uncertainty introduced by the choice can be propagated into LCA results. For example, in the case study, the 100-year global warming potential (GWP100) was adopted to calculate the global warming results. We could also have adopted the GWP20 or GWP500. Assigning a methodological preference to the GWP20, GWP100, and GWP500 characterization factors and using the method developed in this study would lead to inclusion of the influence of characterization factors simultaneously with the choice of allocation method and LCI data uncertainty, if desired. For this example, the calculation works correctly as long as the characterization factors for the different time horizons lead to the same type of LCA results, i.e., in kg of CO2 equivalents. On the other hand, if for example characterization factors for different methods lead to different type of results such as different type of units and scales, the method presented here could not be directly applied because the units could not be comparable among the different choices. In summary, the method developed in this study is valid for all discrete choices leading to comparable results.
Finally, we would like to discuss the terminology used throughout the article. As explained in the methodology section, we believe that this pseudo-statistical method is closer to the domain of uncertainty analysis, given that not only unit process data is propagated but also the methodological preference of allocation methods are propagated too by means of a statistical method (in this case Monte Carlo), to the LCA results. We are aware though, that for example, Andrianandraina et al. (2015) account for the propagation of the uncertainty due to methodological preference of allocation methods to the LCA results as a way of sensitivity analysis, therefore placing their method in the realm of sensitivity analysis. Independent of the type of analysis and admitting the debate around the semantics used to refer to our method, we consider more important the fact that robustness is added to the results by explicitly accounting for various sources of variability.
5 Conclusions
Methodological choices are unavoidable in all phases of LCA and are a source of uncertainty. Among these choices, practitioners typically choose between different methods to solve multi-functionality, and within partitioning methods, different choices can be made again. Unresolved debates on these choices constitute a major source of uncertainty in LCA results. Ways to deal with this issue include standardization, OAT sensitivity analysis, and analytical and statistical methods for uncertainty analysis. Standardization reduces uncertainty, while OAT sensitivity analysis serve to analyze the system using specific combinations of allocation methods, in order to show a range of possible results. The full range of results given all possible choices for allocation methods and combinations in a system with several multi-functional unit processes is only shown by means of statistical and analytical methods, however. Not showing all (or very many) possible combinations can be misleading when evaluating the environmental impacts of a production system and when comparing two or more systems even more. In addition, so far, only one study showed all combinations of allocation methods, as well as accounting for unit process data uncertainty.
This study proposed, implemented, and tested a pseudo-statistical method (not statistical in the strict sense of the word) to enable the use of Monte Carlo simulations as a statistical approach to simultaneously propagate uncertainty in unit process data and uncertainty due to the choice of partitioning methods to LCA results. For this purpose, the methodological preference was introduced and assigned to each partitioning method for each multi-functional process in a system. The assignment of a methodological preference involves an arbitrary choice offering a possibility to more actively account for different views by involved scientists, experts, and stakeholders or patterns from meta-analysis of existing case studies.
The distribution of LCA results was analyzed for a very simple case study, with and without the previous approach and in both cases including LCI data uncertainty. We conclude that the proposed method enables in a relatively simple way, i.e., with a few additional parameters and computational calculation capacity dependent on the system, the propagation of uncertainty due to the choice of partitioning methods to solve multi-functional problems and data uncertainty into LCA results while not requiring a detailed foreground model for the foreground system.
It is concluded that this method can be particularly useful when comparing relative uncertainties of several alternative systems, as increased absolute uncertainty in the LCA results does not necessarily lead to more meaningful conclusions. Moreover, information about the contribution of choice and data uncertainty to the total uncertainty could be further provided by, for example, a global sensitivity analysis. However, these are topics for further research.
In addition, the results of the application of the method provides a more transparent and robust base for comparative LCAs than OAT sensitivity analyses or uncertainty analyses only accounting for uncertainty in unit process data or subsets of combinations between data and allocation methods. More sources of uncertainty are explicitly accounted in the results by making explicit the methodological preference of an allocation method per multi-functional process.
Moreover, exploring the implementation of the proposed method for higher levels of choices in LCA, such as methods to solve multi-functionality in a broader sense and other methodological choices in LCA is another topic for further research. We argue that the method will also be valid for these choices as long as they can be represented as discrete choices and lead to comparable results. Furthermore, implementation and testing of the method for more complex systems, i.e., higher numbers of multi-functional processes with various applicable allocation methods, is also required. We believe that a trade-off between time spend by the practitioner in setting the analysis and calculation time could take place for more complex systems.
References
Andrianandraina E, Ventura A, Senga Kiessé T, Cazacliu B, Idir R, van der Werf HMG (2015) Sensitivity Analysis of Environmental Process Modeling in a Life Cycle Context: A Case Study of Hemp Crop Production. J Ind Ecol. doi:10.1111/jiec.12228
Ardente F, Cellura M (2012) Economic allocation in life cycle assessment. J Ind Ecol 16(3):387–398
Ayer NW, Tyedmers PH, Pelletier NL, Sonesson U, Scholz A (2007) Co-product allocation in life cycle assessments of seafood production systems: review of problems and strategies. Int J Life Cycle Assess 12(7):480–487
Björklund AE (2002) Survey of approaches to improve reliability in LCA. Int J Life Cycle Assess 7(2):64–72
CML (2014) CMLCA. Available at: www.cmlca.eu
Cruze NB, Goel PK, Bakshi BR (2014) Allocation in life cycle inventory: partial set of solutions to an ill-posed problem. Int J Life Cycle Assess 19(11):1854–1865
Groen E, Heijungs R, Bokkers EAM, de Boer IJM (2014) Methods for uncertainty propagation in life cycle assessment. Environ Model Softw 62:316–325
Guinée J, Heijungs R (2007) Calculating the influence of alternative allocation scenarios in fossil fuel chains. Int J Life Cycle Assess 12(3):173–180
Guinée J, Heijungs R, Huppes G (2004) Economic allocation: examples and derived decision tree. Int J Life Cycle Assess 9(1):23–33
Hanes RJ, Cruze NB, Goel PK, Bakshi BR (2015) Allocation games: addressing the ill-posed nature of allocation in life-cycle inventories. Environ Sci Technol 49(13):7996–8003
Heijungs R, Guinée J (2007) Allocation and “what-if” scenarios in life cycle assessment of waste management systems. Waste Manag 27(8):997–1005
Heijungs R, Huijbregts MAJ (2004) A review of approaches to treat uncertainty in LCA. iEMSs 2004 International Congress. Available at: http://www.iemss.org/iemss2004/pdf/lca/heijarev.pdf [Accessed April 15, 2014].
Heijungs R, Lenzen M (2014) Error propagation methods for LCA—a comparison. Int J Life Cycle Assess 19(7):1445–1461
Heijungs R, Suh S (2002) The computational structure of life cycle assessment. Int J Life Cycle Assess 7(5):314–314
Henriksson PGJ et al (2013) A protocol for horizontal averaging of unit process data—including estimates for uncertainty. Int J Life Cycle Assess 19(2):429–436
Henriksson PJG et al (2015) Product carbon footprints and their uncertainties in comparative decision contexts. PLoS ONE 10(3):e0121221
Hong J, Shaked S, Rosenbaum RK, Jolliet O (2010) Analytical uncertainty propagation in life cycle inventory and impact assessment: application to an automobile front panel. Int J Life Cycle Assess 15(5):499–510
Huijbregts MAJ (1998) Application of uncertainty and variability in LCA part II: dealing with parameter uncertainty and uncertainty due to choices in life cycle assessment. Int J Life Cycle Assess 3(1):343–351
Imbeault-Tétreault H et al (2013) Analytical propagation of uncertainty in life cycle assessment using matrix formulation. J Ind Ecol 17(4):485–492
ISO (2006) Environmental management — Life cycle assessment — Requirements and guidelines. Environ Manag 3(1):54
Jung J, Assen N, Bardow A (2013) Sensitivity coefficient-based uncertainty analysis for multi-functionality in LCA. Int J Life Cycle Assess 19(3):661–676
Luo L, Van der Voet E, Huppes G, Udo de Haes H (2009) Allocation issues in LCA methodology: a case study of corn stover-based fuel ethanol. Int J Life Cycle Asses 14(6):529–539
Marvuglia A, Cellura M, Heijungs R (2010) Toward a solution of allocation in life cycle inventories: the use of least-squares techniques. Int J Life Cycle Assess 15(9):1020–1040
Pelletier N, Ardente F, Brandão M, De Camillis C, Pennington D (2014) Rationales for and limitations of preferred solutions for multi-functionality problems in LCA: is increased consistency possible? Int J Life Cycle Assess 20(1):74–86
Svanes E, Vold M, Hanssen OJ (2011) Effect of different allocation methods on LCA results of products from wild-caught fish and on the use of such results. Int J Life Cycle Assess 16(6):512–521
Swiss Centre For Life Cycle Inventories (2004) ecoinvent database V1.1. Available at: www.ecoinvent.ch
Swiss Centre For Life Cycle Inventories (2007) ecoinvent database v2.2. Available at: http://www.ecoinvent.org/database/
Tillman AM et al (1994) Choice of system boundaries in life cycle assessment. J Clean Prod 2(1):21–29
van der Harst E, Potting J (2014) Variation in LCA results for disposable polystyrene beverage cups due to multiple data sets and modelling choices. Environ Model Softw 51:123–135
Van der Voet E, van Oers L, Davis C, Nelis R, Cok B, Heijungs R, Chappin E (2008) Greenhouse gas calculator for electricity and heat from biomass, CML - Leiden University
van der Voet E, Lifset RJ, Luo L (2010) Life-cycle assessment of biofuels, convergence and divergence. Biofuels 1(3):435–449
Wardenaar T, Ruijven T, Mendoza Beltran A, Vad K, Guinée J, Heijungs R (2012) Differences between LCA for analysis and LCA for policy: a case study on the consequences of allocation choices in bio-energy policies. Int J Life Cycle Assess 17(8):1059–1067
Weidema BP (2000) Avoiding co-product allocation in life-cycle assessment. J Ind Ecol 4(3):11–33
Weidema BP (2014) Has ISO 14040/44 failed its role as a standard for life cycle assessment? J Ind Ecol 18(3):324–326
Weidema BP, Schmidt JH (2010) Avoiding allocation in life cycle assessment revisited. J Ind Ecol 14(2):192–195
Acknowledgments
This research has been done as part of the Increasing Industrial Resource Efficiency in European Mariculture project (IDREEM; www.idreem.eu) and has received funding from the European Union’s Seventh Framework Programme (FP7/2007-2013) under grant agreement no. 308571. The authors would also like to acknowledge the invaluable contribution by Ruben Huele to the data visualizations of this study and to Valentina Prado for her insightful comments.
Author information
Authors and Affiliations
Corresponding author
Additional information
Responsible editor: Andreas Ciroth
Electronic supplementary material
Below is the link to the electronic supplementary material.
ESM 1
(DOCX 29 kb)
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Mendoza Beltran, A., Heijungs, R., Guinée, J. et al. A pseudo-statistical approach to treat choice uncertainty: the example of partitioning allocation methods. Int J Life Cycle Assess 21, 252–264 (2016). https://doi.org/10.1007/s11367-015-0994-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11367-015-0994-4