Mathematical model of Boltzmann’s sigmoidal equation applicable to the spreading of the coronavirus (Covid-19) waves

Abstract

Currently, investigations are intensively conducted on modeling, forecasting, and studying the dynamic spread of coronavirus (Covid-19) new pandemic. In the present work, the sigmoidal-Boltzmann mathematical model was applied to study the Covid-19 spread in 15 different countries. The cumulative number of infected persons I has been accurately fitted by the sigmoidal-Boltzmann equation (SBE), giving rise to different epidemiological parameters such as the pandemic peak t_p, the maximum number of infected persons I_max, and the time of the epidemic stabilization t_∞. The time constant relative to the sigmoid Δt (called also the slope factor) was revealed to be the determining parameter which influences all the epidemiological parameters. Empirical laws between the different parameters allowed us to propose a modified sigmoidal-Boltzmann equation describing the spread of the pandemic. The expression of the spread speed V_p was further determined as a function of the sigmoid parameters. This made it possible to assess the maximum speed of spread of the virus V_pmax and to trace the speed profile in each country. In addition, for countries undergoing a second pandemic wave, the cumulative number of infected people I has been successfully adjusted by a double sigmoidal-Boltzmann equation (DSBE) allowing the comparison between the two waves. Finally, the comparison between the maximum virus spread of two waves V_p max 1 and V_p max 2 showed that the intensity of the second wave of Covid-19 is low compared to the first for all the countries studied.

Introduction

The emergence of the new infectious disease of coronavirus (Covid-19) is currently the most intriguing field of research for the entire scientific community around the world. Unlike other diseases, the gigantic effects of this pandemic go beyond the health dimension to have serious, even disastrous consequences on other areas, namely, the economic situation of the affected countries, the suspension of school and university activities, cultural, sporting events.... From a virological point of view, SarS-CoV-2 (Covid-19) is a new virus, not studied enough for virologists to give all the answers related to its spread mode. As a result, scientists from all disciplines such as biologists, physicists, chemists, mathematicians, and economists were intensively involved in the study of this pandemic in order to consolidate the epidemiologist’s efforts. The aim is to understand the spread dynamics of Covid-19 and predict the pandemic peak as well as the stabilization time of the epidemic in order to study the possible twists and turns of the epidemic and therefore the appearance of new waves. This can provide policymakers with efficient solutions to fight and control this pandemic. In this sense, several studies have been conducted based on typical epidemiologic models such as the susceptible infected recovered (SIR) model (Fanelli and Piazza (2020), Castro et al. (2020) Arima model (Chakraborty and Ghosh (2020)) to forecast and predict the spread dynamic. Others have used mathematical models such as the Poisson model (Zhang et al. (2020)), the Gauss error function (Ciufolini and Paolozzi (2020)) and power law model (Manchein et al. (2020)) to analyze data related to the evolution of the pandemic. In their report, Hao (2020) considered that the dynamics of virus infection are analogous to the dynamics of certain colloidal systems, and therefore developed a model based on the Eyring model to predict the evolution of Covid-19. In this context that our current study takes place. Indeed, by observing the evolution of the cumulative number of people infected with Covid-19 in each step, we can distinguish 3 consecutive growth modes: slow growth, exponential rapid growth, and slow growth. It is indeed a sigmoidal pattern. Typically, nonlinear models from the Richards family (Fekedulegn et al. (1999)) are the most indicated in the literature for the description of sigmoidal growth curves, namely Logistic, Gompertz, Brody, and von Bertalanffy. Usually, biologists of all specialties are used to apply this type of model to describe the growth of certain processes, namely, complex molecular processes and cellular properties, including interactions between molecules and cell proliferation as well as the development of the compactness of the grape clusters (Dubois et al. (2009)). Furthermore, Navarro-Verdugo et al. (2011) proposed a modified sigmoidal-Boltzmann model for the phase transition of smart gels. Also, Hait et al. (2002) proposed a refined method based on sigmoidal-Boltzmann equation (SBE) to estimate the parameters of physical’s process in micellar solutions like micellization process and percolation parameters. In certain physical, chemical, or biological processes, the sigmoidal pattern is reproduced consecutively with two points of inflection. In this regard, we can cite the work of Fernandes et al. (2017) who modeled the growth of coffee berries by double sigmoid function. In addition, Román-Román et al. (2019) proposed multi-sigmoidal Gompertz functions to describe growth at multiple inflection points.

The main objective of this study is to apply this sigmoidal model to the cumulative number of people infected with Covid-19 during a pandemic wave. In addition, we plan to adopt a double sigmoid model for countries where a second pandemic wave has been observed. Indeed, in this model, to describe the double sigmoid growth, two simple sigmoids are considered in the same model, each in order to explain a certain stage of growth. We will thus exploit the characteristics of the sigmoid model to derive epidemiological parameters relating to the spread of the pandemic. Our study is based on data of the cumulative number of infected people provided by the Johns Hopkins University Resource Center (COVID-19 Dashboard (2020)) until the date of 28 May 2020 for Lebanon, Jordan, South Korea, North Macedonia, and Malta. Otherwise, the data on cumulative number of infected people for the United States of America (USA), United Kingdom (UK), Chile, Brazil, Mexico, Saudi Arabia, India, Turkey, and Spain are collected until the date of 10 September 2020.

Theoretical background

Sigmoidal-Boltzmann equation

The application of mathematical models in the analysis of experimental data relating to transition phenomena revealed patterns of their physical and geometric behaviors. In the same phases, for example, sigmoidal patterns and inflection points are identified. Also, whether the transition from continuous to discontinuous at inflection point, the inflection point will lead to the critical phase. To model this pattern, Boltzmann have suggested equation (Reséndiz-Muñoz et al. (2017)) was based on the sigmoidal equation of logistics:

$$ y(x)=\frac{1}{1+\exp \left(-x\right)} $$

(1)

Typically, Eq. (1) has been used to describe observed behaviors where a given element causes a transition from one state to another of quite different significance. Therefore, the following sigmoidal-Boltzmann equation is formulated, where the original formula is modified, and includes the necessary geometric properties. In fact, to describe the evolution of a magnitude evolving as a function of a variable, the sigmoid-Boltzmann equation (SBE) has the following form:

$$ y(x)={y}_r\left[1+\left(\frac{y_i-{y}_r}{y_r}\right)\times {\left\{1+\exp \left(x-{x}_0\right)/\Delta x\right\}}^{-1}\right] $$

(2)

where y is the measured magnitude of the system which depends on x, y_i and y_r are the left and right asymptotes of y, x₀ is the center (where y returns the mean of y_i and y_r), and Δx is the constant period of the independent variable that determines the rise profile or decrease from y_i to y_r (for a high Δx, the increase is slow while for low Δx, increase is quick), and it was called also the slope factor. The equation therefore basically deals with the flipping of a parameter from an original state (state of y_i) to a final state (state of y_r) through a transition x₀.

In some cases, the independent variable, y, reproduces the sigmoidal pattern with a time offset; a double sigmoidal-equation (DSBE) takes the following form (Fernandes et al. (2017)):

$$ y={y}_0+{y}_{\mathrm{max}}\left[p{\left\{1+\exp \left(\frac{x-{x}_{01}}{\Delta {x}_1}\right)\right\}}^{-1}+\left(1-p\right){\left\{1+\exp \left(\frac{x-{x}_{02}}{\Delta {x}_2}\right)\right\}}^{-1}\right] $$

(3)

where y₀ and y_max are the minimum and the maximum values taken by y. P is the fraction of the curve comprising phase 1, 1 − p is the fraction of the curve comprising phase 2, Δx₁ and Δx₂ are the constant intervals that control the rise of phase 1 and phase 2 (called also slope factors).

A modified sigmoidal-Boltzmann equation for the number of infected persons I

By applying the sigmoidal growth equation for the cumulative number of infected people, I evolving over the time, t the equation therefore deals with the flipping of numbers, I from an original state, I_i, to a final state, I_max, through the transition, t_p. At this point, the transition, t_p corresponds therefore to what is called the pandemic peak or the turning point.

$$ I(t)={I}_{\mathrm{max}}\left[1+\left(\frac{I_i-{I}_{\mathrm{max}}}{I_{\mathrm{max}}}\right)\times {\left\{1+\exp \left(t-{t}_p\right)/\Delta t\right\}}^{-1}\right] $$

(4)

Δt is a time constant.

Knowing that I_max ≻  ≻  ≻ I_i Eq. (4) becomes:

$$ I(t)={I}_{\mathrm{max}}\left[1-{\left\{1+\exp \left(t-{t}_p\right)/\Delta t\right\}}^{-1}\right] $$

(5)

Therefore, we can derive from Eq. (5) two essential epidemiological parameters, namely the maximum number of infectious individuals reached I_max from which the disease starts to stabilize. The pandemic peak time t_p, often called the turning stage, is the time which marks the transition from a dangerous epidemic state marked by a high speed of virus transmission to a declining epidemic with a speed of the virus spread in decrease.

Generally, the epidemic state stabilizes when the number of infected cases I reaches almost the maximum number of infected cases I = 0.99I_max which corresponds to infinite time, t_∞ of pandemic spread:

Considering Eq. (5), the t_∞ value can be calculated from the following equation:

$$ {t}_{\infty }=2.19\Delta t+{t}_p $$

(6)

Generalized sigmoidal-Boltzmann equation for the number of infected persons I

In cases where the spread of the virus in some countries undergoes a rebound, thus, the speed of virus spread accelerates again and the number of people infected increases exponentially again. This is manifested by the appearance of a new sigmoidal portion in the cumulative case curves. Epidemiologists call this trend a second wave pandemic wave. The Boltzmann sigmoid equation takes the following form in this case:

$$ I(t)={I}_i+{I}_{\mathrm{max}}\left[p{\left\{1+\exp \left(\frac{t-{t}_{p1}}{\Delta {t}_1}\right)\right\}}^{-1}+\left(1-p\right){\left\{1+\exp \left(\frac{t-{t}_{p2}}{\Delta {t}_2}\right)\right\}}^{-1}\right] $$

(7)

where I_i ≈ 1 and I_max are the initial and the maximum values taken by I. p is the fraction of the first curve (first wave intensity) 1, 1 − p is the fraction of the second wave 2 (second wave intensity), and Δt₁ and Δt₂ are the time constant intervals (slope factors) that control the rise of the first and the second waves. t_p1 and t_p2 are the pandemic peaks of the two waves.

Knowing that I_max ≻  ≻  ≻ I_i Eq. (7) becomes:

$$ I(t)\approx {I}_{\mathrm{max}}\left[p{\left\{1+\exp \left(\frac{t-{t}_{p1}}{\varDelta {t}_1}\right)\right\}}^{-1}+\left(1-p\right){\left\{1+\exp \left(\frac{t-{t}_{p2}}{\varDelta {t}_2}\right)\right\}}^{-1}\right] $$

(8)

Expression of speed of the virus spread

Case of one wave spread

Knowing that the variation in the number of infected people over time defines the speed of spread of virus, V_p, in a given population, the speed of propagation can therefore be determined from I expression (Eq. (5)) by the following equation:

$$ {V}_p=\frac{\partial I(t)}{\partial t} $$

(9)

So,

$$ {V}_p(t)=\frac{I_{\mathrm{max}}\exp \left(t-{t}_p/\Delta t\right)}{\Delta t{\left(1+\exp \left(t-{t}_p/\Delta t\right)\right)}^2} $$

(10)

Since the speed of virus spread is maximized during the pandemic peak, i.e., at t = t_p, the maximum speed of virus spread V_{p, max} is expressed as follows:

$$ {V}_{p,\max }=\frac{I_{\mathrm{max}}}{4\Delta t} $$

(11)

By rearranging Eq. (11), we can express the modified Boltzmann sigmoid spread equation (Eq. (5)) as a function of V_{p, max}, I_max, and t_p:

$$ I(t)={I}_{\mathrm{max}}\left[1-{\left\{1+\exp \left(4\left(t-{t}_p\right){V}_{p,\max }/{I}_{\mathrm{max}}\right)\right\}}^{-1}\right] $$

(12)

Case of one two spread

For countries where a second wave appears, the expression of the spread speed V_p is obtained from the derivative of Eq. (8) as follows:

$$ {V}_p\approx {I}_{\mathrm{max}}\left[-p\exp \left(\frac{t-{t}_{p1}}{\Delta {t}_1}\right){\left\{\Delta {t}_1{\left(1+\exp \left(\frac{t-{t}_{p1}}{\Delta {t}_1}\right)\right)}^2\right\}}^{-1}-\left(1-p\right)\exp \left(\frac{t-{t}_{p2}}{\Delta {t}_2}\right){\left\{\Delta {t}_2{\left(1+\exp \left(\frac{t-{t}_{p2}}{\Delta {t}_2}\right)\right)}^2\right\}}^{-1}\right] $$

(13)

Analysis of the spread of Covid-19 in 15 different countries using the Boltzmann sigmoid model

In our study, we collected the data relating to the cumulative number of people infected I by Covid-19 since the first detected case. Provided by the Johns Hopkins University resource center (COVID-19 Dashboard (2020)), the data concern 15 countries affected by the pandemic differently.

Case of countries undergoing one pandemic wave

Epidemiological parameters describing the pandemic spread

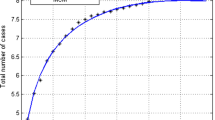
By plotting the variation in the cumulative number of infected persons with respect to time from the day of the first detected case, we noted a sigmoidal growth for 10 of the 15 countries studied (USA, UK, India, Brazil, Mexico, Saudi Arabia, Turkey, Spain, Chile, and Russia). The adjustment of these curves by the modified sigmoidal-Boltzmann equation (SBE) (Eq. 5) has been carried out successfully using nonlinear least squares method (very high values of the adjusted R squared).

The results are reported in Figs. 1 and 2. It is clear that the USA (Fig. 1) recorded the highest number of people infected with Covid-19 compared to other countries. However, it appears that the UK is the country least affected by the pandemic. We have reported in Table 1 the different epidemiological parameters from the fit associated with the infinite time of the pandemic spread t_∞ estimated from Eq. (6). It is important to note that the country currently most affected is the USA with I_max = 9.633 10⁶ and t_∞ = 299.943, and the fit results predict also that India is the second country where the pandemic has spread on a large scale with respectively I_max = 8.877.10⁶ and t_∞ = 291.567. Obviously, the infinite time for the pandemic spread t_∞ is a reliable indicator of the effectiveness of the precautionary measures taken by each country (general quarantine, isolation, etc.). In fact, the lower this parameter, the more effective the measures, and vice versa. From Table 1, we can observe that this parameter takes minimum values for Turkey and the UK and maximum values for the USA and India.

Fig. 1

Variation in the cumulative number of infected people I in the 4 countries most affected by the pandemic since the day of first detected case

Fig. 2

Variation in the cumulative number of infected people I in 6 studied countries since the day of first detected case

Table 1 Sigmoid-Boltzmann (SBE) fit parameters for countries undergoing 1 pandemic wave

A novel expression of the sigmoidal-Boltzmann equation

In Fig. 3, we plot the variation of the pandemic infinite time t_∞ as a function of the pandemic peak t_p. According to the curve, a linear relationship between these two parameters was highlighted.

Fig. 3

t_∞ versus t_p for the 10 countries studied (with 1 wave)

So t_∞ is connected to t_p by the following equation:

$$ {t}_{\infty }=19.35+1.07{t}_p $$

(14)

Given Eq. (6), the constant time can be connected to the pandemic peak as follows:

$$ \Delta t=8.83+0.03{t}_p $$

(15)

By replacing in Eq. (5), the modified sigmoidal-Boltzmann equation can be expressed only as function of t_p and I_max as follows:

$$ I={I}_{\mathrm{max}}\left[1-{\left\{1+{\mathrm{e}}^{\left(t-{t}_p/8.83+0.03{t}_p\right)}\right\}}^{-1}\right] $$

(16)

Speed profile of virus spread

Using Eq. (10), we have calculated the speed of the virus spread for the 10 studied countries since the first detected case. Results are depicted in Fig. 4 as function of$\frac{t}{t_p}$. With a maximum spread speed V_pmax more than 80.000 cases/day, India far exceeds other countries. It was succeeded by the USA and Brazil which recorded considerably high maximum spread speeds. However, the lowest maximum propagation speed was recorded for Spain (nearly V_pmax = 3000 cases/day). From an epidemiological point of view, we consider that the maximum speed of pandemic spread is a key factor reflecting the intensity of the pandemic affecting each country.

Fig. 4

Speed of the pandemic spread V_p profile in 10 studied countries since the day of first detected case

Case of countries undergoing two pandemic waves

Epidemiological parameters describing the pandemic spread

By plotting the variation in the cumulative number of infected persons with respect to time from the day of the first detected case, we noted a double sigmoidal growth for the 5 countries studied (Jordan, Lebanon, Malta, North Macedonia, and South Korea). The reproduction of the same sigmoid pattern is considered the sign of a second pandemic wave. The fit of these curves by the double sigmoidal-Boltzmann equation (DSBE) (Eq. 8) has been carried out accurately (Fig. 5). The fit results are listed in Table 2.

Fig. 5

Variation in the cumulative number of infected people I in 5 studied countries undergoing 2 pandemic waves

Table 2 Double sigmoid-Boltzmann (DSBE) fit parameters for countries undergoing 2 pandemic waves

The difference (t_p2 − t_p1) allows us to estimate the time difference between the two peaks relating to each wave. Ranging from 22.4 in South Korea to 53.6 in Jordan, this difference can give us an idea of the speed of governments’ response to the pandemic rebound. On the other hand, the ratio between two time constants $\frac{\Delta {t}_1}{\Delta {t}_2}$ allows to compare the rhythms of exponential growth between the two waves and therefore the intensity of two waves.

We have reported in Fig. 6 the infinite time (time of the epidemic stabilization) t_{∞1, 2} variation of each of the waves versus the pandemic peaks t_{p1, 2} of two waves. Similar to the case of countries with a single wave, a linear relationship was also observed:

$$ {t}_{\infty 1,2}=13.53+1.007{t}_{p1,2} $$

(17)

Fig. 6

t_{∞1, 2} versus t_{p1, 2} for the 5 countries studied (with 2 waves)

The time constant Δt_{1, 2} can be therefore expressed:

$$ \Delta {t}_{1,2}=6.17+0.03{t}_{p1,2} $$

(18)

Thus, the modified sigmoidal-Boltzmann equation can be expressed according to Eq. (19):

$$ I(t)\approx {I}_{\mathrm{max}}\left[p{\left\{1+{\mathrm{e}}^{\left(t-{t}_{p1}/6.17+0.03{t}_{p1}\right)}\right\}}^{-1}+\left(1-p\right){\left\{1+{\mathrm{e}}^{\left(t-{t}_{p2}/6.17+0.03{t}_{p2}\right)}\right\}}^{-1}\right] $$

(19)

Speed profile of virus spread

Using Eq. (13), we have determined the profile of the virus speed spread in countries undergoing 2 pandemic waves (Fig. 7). We clearly observe the existence of two maximums in the speed curve corresponding respectively to the speeds V_p max 1 and V_p max 2 recorded during the two pandemic peaks t_p1 and t_p2.

Fig. 7

Speed of the pandemic spread V_p profile in 5 studied countries undergoing 2 waves

The values found (Table 3) show that for all countries the maximum speed of the second V_p max 2 wave is lower than that of the first wave V_p max 1.

Table 3 Maximum speed of pandemic spread V_pmax for the 15 countries studied

To quantify this decrease, we have calculated the relative decay rate ε of maximum speed spread according to the following equation:

$$ \varepsilon =100\left|\frac{V_{p\max 1}-{V}_{p\max 2}}{V_{p\max 1}}\right| $$

(20)

The found values are reported in Table 3.

By following the evolution of relative decay rate ε as a function of the $\frac{\Delta {t}_1}{\Delta {t}_2}$ ratio, we noted a parabolic dependence (Fig. 8) between these two parameters described by the following equation:

$$ \varepsilon ={\lambda}_1+{\lambda}_1\left(\frac{\Delta {t}_1}{\Delta {t}_2}\right)+{\lambda}_2{\left(\frac{\Delta {t}_1}{\Delta {t}_2}\right)}^2,{\lambda}_1=114.15,{\lambda}_2=-104.9,{\lambda}_3=30.35 $$

(21)

Fig. 8

Variation of relative decay rate ε as a function of $\frac{\Delta {t}_1}{\Delta {t}_2}$ ratio for the 5 studied countries undergoing 2 waves

Conclusions

In this report, investigation was carried out on the spread dynamic of Covid-19 in 15 different countries. The work was based on the use of a mathematical model, the Boltzmann sigmoid model (SBE), strongly used in different fields, namely, biology, chemistry, physics, and economics, to model the Covid-19 spread.

Initially, a modified sigmoidal-Boltzmann equation was introduced following the application of the model on the cumulative number of infected people I in 10 countries (UK, USA, Brazil, Mexico, Russia, India, Spain, Turkey, Saudi Arabia, and Chile). In addition, 3 major epidemiological parameters were drawn, the time for epidemic stabilization since the first day t_∞, the pandemic peak t_p, and the maximum number of people infected N_max.

Then, the adjustment of I with a double sigmoidal-Boltzmann equation (DSBE) in 5 other countries (North Macedonia, Jordan, Lebanon, Malta, and South Korea) undergoing a second pandemic wave made it possible to characterize the second wave and the comparison with the first. Furthermore, a spread speed equation was given in both cases, countries with one wave and countries with two waves. This allowed us to estimate the values of the maximum spread speeds V_pmax for each country. In the countries undergoing a second wave, the comparison of two maximum speeds revealed that the epidemic intensity of the second wave is lower than that of the first for all the countries studied. This finding proves that the possible rebound of the Covid-19 wave remains relatively low. It is necessary to note that whether for countries undergoing a single pandemic wave or those undergoing two pandemic waves, the parameter having the most influence on all the epidemiological parameters is the time constant of the sigmoid Δt. Even for the start of a second wave, we only need to compare this parameter Δt₂ to that of the first wave Δt₁ to predict the intensity of a second wave.

It seems crucial to mention that in the present study we have focused on the cumulative number of cases infected with Covid-19, based on data provided by various government health sources, and gathered by the Johns Hopkins University Resource Center. As a result, our modeling represents a quantitative analysis of the Covid-19 spread rate aimed at approaching reality independently of various factors that may influence the reliability of the results such as the effectiveness of the testing strategy adopted by each country studied, the different procedures taken by each country in relation to general containment and targeted containment, the financial resources dedicated to Covid-19 which differs from one country to another, and the strength of the health system in each country. We believe that these deficiencies have a definite effect on the accuracy of the results found in all current studies aimed at modeling the spread of the virus. However, we see that obtaining results close to reality, especially with regard to the first wave, can give us a rough picture of the dynamics of the spread of the Covid-19. At present, virologists and epidemiologists are intensifying their efforts to fully understand the intrinsic characteristics of this new virus Sars-Cov-2 (Covid-19) in order to have clear answers on its mode of contamination as soon as possible. In parallel, clinical trials are underway to identify an effective treatment to neutralize the virus. For this, at the moment, only mathematical models can shed light on the dynamics of propagation of Covid-19. This can provide policymakers to adopt precautionary and preventive measures to mitigate the damage and fight against this pandemic.