Introduction

Thermoelastic stress analysis (TSA) is a thermography-based, contactless, full-field, experimental technique adopted to evaluate the surface stress (first stress invariant) of a body undergoing a cyclic load under linear elastic conditions [1,2,3].

In recent years, TSA has been adopted for different applications ranging from damage monitoring of components [4, 5] to non-destructive evaluations to detect and quantify the damage phenomena, especially in composites [6, 7]. Moreover, TSA has been adopted for assessing changes in material behaviour under fatigue regimes by exploiting the loss of adiabaticity [5,6,7] of the process and the consequent thermal signal variation. Furthermore, TSA has showed capability in fatigue limit estimation [8].

In the field of stress analysis, TSA shows a great capacity for validating numerical models or for characterising the mechanical behaviour of components/prototypes obtained by, for example, 3D printing [9]. Referring to this latter application, the role of stress analysis is significant. In fact, to quantitatively assess the stresses from thermographic data, it is necessary to carry out a specific calibration procedure [3, 10], and the more accurate and precise the procedure is in assessing stresses, the more the technique is suitable for the validation of finite element numerical models.

TSA is also useful in the field of fatigue behaviour assessments for any kind of material (metals and composites). In effect, one can use the loss of adiabaticity [11] in the material, due to fatigue damage, to indirectly study the beginning of significant damage and possibly estimate the endurance/fatigue limit [11].

As demonstrated by several studies [5, 6, 11, 12], TSA can also provide damage parameters, which are useful in the field of damage analysis on composite materials. In this way, as shown in the pioneering work of Emery et al. [12], and in the continuing work by [12, 13], it is possible to directly link thermoelastic material response to the degradation of mechanical properties (usually in terms of stiffness loss in the longitudinal load direction) in order to carry out structural health monitoring during a material’s lifespan.

In classic thermoelastic theory [3], variations in Young’s (E) and Poisson’s (v) moduli with temperature can be neglected; hence, the thermoelastic data calibration methodology performed to obtain a stress map involves simply the thermoelastic constant. In this case, the thermoelastic temperature variations are directly and linearly related to the first stress invariant [10, 14].

In the literature, three main procedures for data calibration have been proposed, all focused on directly or indirectly assessing the thermoelastic constant [10]. However, for materials such as titanium, the variations in mechanical properties which depend on temperature are significant, and, in some circumstances, cannot be neglected in the classic thermoelastic formulation [15,16,17,18,19].

This led to the consideration of an extended formulation accounting for the mean stress effect that results from this dependence of mechanical properties (E,v) on temperature [15,16,17,18,19].

In the works of Palumbo et al. [20,21,22], it was demonstrated that neglecting the mean stress effect can lead to errors in the calibration procedure of 20% and more. In particular, in [22], the revised form of the thermoelastic stress analysis theory for a uniaxial stress state was presented on a titanium alloy showing a significant sensitivity to mean stress effect. If the influence of mean stress is neglected, the traditional calibration procedure of TSA data may result in errors of more than 20% in areas characterized by high stresses. Errors in classic TSA calibration can lead to incorrect estimation of the material stress state. This would negatively affect the stress evaluation of the designed mechanical components. Furthermore, [22] refer to the simple case of uniaxial loading.

Under a more complex stress state of material (i.e., biaxial), the neglection of the mean stress can lead to high errors, as demonstrated in the work of Di Carolo et al. [23] and Palumbo et al. [20, 24], in which errors in estimating the stress intensity factor range under mode I were presented with respect to the classic theory. In [20], the thermoelastic equation was rewritten with the aim of describing the stress distribution around a crack by using more robust formulations: Westergaard’s and Williams’s solutions including high-order terms such as T-stress. In that research, the authors demonstrated that using a less accurate formulation and without correcting the thermoelastic data, errors can range from 10 to 30% in the evaluation of the stress intensity factor range.

In the present work, starting from the general theory of thermoelastic stress analysis, where the mean stress effect is considered, the classic formulation has been extended to the case of biaxial stresses changing with a sinusoidal loading. In particular, it will be shown that the new formulation for thermoelastic temperature variations includes a second harmonic component running at twice the mechanical frequency, which is a well-established feature of higher order thermoelastic theory [18]; therefore, in this regard, this formulation is consistent.

Another interesting finding resulting from the proposed formulation is the presence in the formula of principal stresses, both separately and combined, in the first stress invariant, which differs from what happens in classic thermoelastic theory [3, 10, 14] where just the first stress invariant appears.

The natural consequence of this finding is that the calibration of thermoelastic temperature variations to obtain stresses cannot be possible via typical calibration methods [3].

In view of this, another outcome of the present work derives from the development of an analytic formulation of the error made in the first stress invariant amplitude evaluation in the presence of a biaxial stress state, when neglecting the mean stress effect. The presented error formulation can be defined as the error made in using the traditional calibration methods instead of the new formulation.

Finally, to validate the new formulation, experimental tests were carried out on a titanium holed plate and the Comsol® software was used to model the specimen and then as a reference for the analysis.

A holed sample is an example of a biaxial stress state that is of practical interest as they can be found in different machine members or components. Accounting for the second order effects for materials such as titanium is fundamental to correctly calibrating the thermoelastic signal in order to obtain stress maps as close as possible to real experienced stresses. Even if it is limited to the specific application case, the approach is useful, not only for its potential for application to out-of-laboratory case studies but also for the verification of the mechanical design.

The approach has the potential to provide an analytical formula to estimate the error in stress evaluation that occurs when titanium components are investigated with the TSA technique vs. the classical formulation. In this way, it can result in improvements in the verification of the quality of the design. However, since the presented research focuses only on a specific case, further works will be focused on extending this approach to other materials and stress states to prove the validity of the analytical function in the other cases.

Theory: Classical Thermoelastic Theory

It was since the second half of the last century, that in some pioneer works Belgen [25], Machin et al. [15], and Dunn et al. [16] demonstrated, for some materials, a linear dependence of the thermoelastic signal on the mean stress value. The works of Wong et al. [17,18,19] provided a physical interpretation of this effect and a review of thermoelastic theory where a thermoelastic equation was derived for an isotropic material, imposing the conservative laws that govern the mechanics of small quasi-static deformations [3] and the second law of thermodynamics for a reversible process. In particular, according to Wong et al. [17,18,19], the constitutive law derived with respect to the temperature is:

$$T\left[\left(-\eta -\frac{\partial \eta }{\partial T}\Delta T+\frac{\partial \lambda }{\partial T}{\varepsilon }_{kk}\right){\delta }_{ij}+2\frac{\partial \mu }{\partial T}{\varepsilon }_{ij}\right]\dot{{\varepsilon }_{ij}}-{\rho }_{0}{C}_{\epsilon }\dot{T}={Q}_{i,i}$$
(1)

where T is the temperature and \(\dot{T}\) its rate of variation, δij is the Kronecker delta, εij \({\dot{\varepsilon }}_{ij}\) are the strain tensor and its rate of variation, respectively (summing over i, j with i, j = 1–3), α is the coefficient of linear thermal expansion, λ and μ are the Lamé constants and εkk is the first strain invariant.

In particular, η can be defined as:

$$\eta =\left(3\lambda +2\mu \right)\alpha$$
(2)

while Lamé constants are defined through the mechanical properties of material in terms of Young’ and Poisson’ moduli:

$$\mu =\frac{E}{2(1+\nu )},\quad\quad \lambda =\frac{\nu E}{(1+\nu )(1-2\nu )}$$
(3)

The stress can be finally described by:

$${\sigma }_{ij}=2\mu {\varepsilon }_{ij}+\left(\lambda {\varepsilon }_{kk}-\eta\Delta T\right){\delta }_{ij}$$
(4)

where \(\Delta T\)=T-T0. By considering adiabatic conditions and expressing the strain as principal ones, it leads:

$${\rho }_{0}{C}_{\epsilon }\frac{\dot{T}}{T}=-\left(\eta +\frac{\partial \eta }{\partial T}\Delta T-\frac{\partial \lambda }{\partial T}{\varepsilon }_{kk}\right)\dot{{\varepsilon }_{kk}}+2\frac{\partial \mu }{\partial T}{\varepsilon }_{i}\dot{{\varepsilon }_{i}}$$
(5)

Substituting equations (2–3) into equation (5), and neglecting the high-order terms and the term (∂η/∂T)ΔT, and expressing it in terms of the principal stresses s [18, 19], it is possible to obtain the following equation:

$$\rho {C}_{\varepsilon }\frac{\dot{T}}{T}=-\left[\alpha +\left(\frac{\upsilon }{{E}^{2}}\frac{\partial E}{\partial T}-\frac{1}{E}\frac{\partial \upsilon }{\partial T}\right)s\right]\dot{s}+\left[\frac{\left(1+\upsilon \right)}{{E}^{2}}\frac{\partial E}{\partial T}-\frac{1 }{E}\frac{\partial \upsilon }{\partial T}\right]{\sigma }_{i}{\dot{\sigma }}_{i}$$
(6)

where s and \(\dot{s}\) correspond respectively to the principal stresses and their rates of variation:

$${s=\sigma }_{1}+{\sigma }_{2}, \dot{s}=\dot{\left({\sigma }_{1}+{\sigma }_{2}\right)}$$
(7)

Thermoelastic Equation in Presence of Biaxial Stresses

In order to obtain a general formulation valid also in the case of biaxial stresses, the starting point is put in a more compact form equation (6) by considering the two material constants a, b as discussed in previous works [20,21,22]:

$$a=\frac{\alpha }{\rho {C}_{\varepsilon }}, b=\frac{1}{{E}^{2}}\frac{\partial E}{\partial T}\frac{1}{\rho {C}_{\varepsilon }}$$
(8)

By substituting the equation (8) in equation (6) and neglecting the term \(\partial v/\partial T\), it leads:

$$\frac{\dot{T}}{T}=-\left(a+\upsilon bs\right)\dot{s}+b\left(1+\upsilon \right){\sum }_{i}{\sigma }_{i}{\dot{\sigma }}_{i}\, i=1, 2$$
(9)

Considering now a generic sinusoidal loading in which the load changes between maximum and minimum values, Pmin and Pmax, the loading ratio R can be defined as follows:

$$R=\frac{{P}_{min}}{{P}_{max}}=\frac{{\sigma }_{i,min}}{{\sigma }_{i,max}}, {\sigma }_{mi}={\sigma }_{ai}\frac{1+R}{1-R}={\sigma }_{ai}{R}_{f}, i=1, 2$$
(10)

From equation (10), the quantity Rf can be defined as:

$${R}_{f}=\frac{{\sigma }_{mi}}{{\sigma }_{ai}}$$
(11)

The variations of the generic principal stress and first stress invariants can be expressed as:

$$\begin{aligned}&{\sigma }_{i}=\sigma_{im}+\sigma_{ia}sin\omega t=\sigma{ia}(R_{f}+sin\omega t),\\&s=s_{m}+s_{a}sin\omega t=s_{a}(R_{f}+sin\omega t)\end{aligned}$$
(12)

The related time-derivatives are then obtained:

$${\dot{\sigma }}_{i} \omega {\sigma }_{ia}cos\omega t, \dot{s}=\omega {s}_{a}cos\omega t$$
(13)

By simply substituting equations (11, 12, 13) in equation (9) via simple mathematical operations and after integrating the temperature from T0 to T and through the time from 0 to t instants, it is possible to obtain the following general form describing thermoelastic temperature variations:

$$\begin{aligned}\frac{\Delta T}{{T}_{0}}=&\ \left\{-\left(a+\upsilon b{s}_{a}{R}_{f}\right){s}_{a}+b(1+\upsilon ){R}_{f}{\sum }_{i}{\sigma }_{ia}^{2}\right\}sin\,(\omega t)\\&+\left\{\frac{1}{4}\left(\upsilon b{s}_{a}^{2}+b(1+\upsilon ){\sum }_{i}{\sigma }_{ia}^{2}\right)\right\}sin\,(2\omega t)\end{aligned}$$
(14)

where ΔT is the temperature variation associated to the stress amplitude variation.

Equation (14) shows as the thermoelastic material response is characterised by the sum of two components: the first one varying at the same frequency of imposed mechanical loading while the second one varying at twice the mechanical frequency. Moreover, a stress-ratio (Rf) dependence is observed in the first left term of equation (14), it translates into a mean-stress dependence of the first component of the thermoelastic signal.

Another interesting point to be highlighted for the biaxial case is that, unlike uniaxial case, the components of principal stresses appear both as the first invariant and separately. Hence, in this case, the well-known calibration procedures useful to assess the first invariant based on the assessment of the thermoelastic constant are no longer useful [3, 10].

Equation (14) can be presented in a more compact form:

$$\frac{\Delta T}{{T}_{0}}={f}_{1}sin\,(\omega t)+{f}_{2}sin\,(2\omega t)$$
(15)

where the amplitude of the first right term is

$${f}_{1}=\left\{-\left(a+\upsilon b{s}_{a}{R}_{f}\right){s}_{a}+b(1+\upsilon ){R}_{f}{\sum }_{i}{\sigma }_{ia}^{2}\right\}$$
(16a)

and the second component is represented by:

$${f}_{2}=\left\{\frac{1}{4}\left(\upsilon b{s}_{a}^{2}+b(1+\upsilon ){\sum }_{i}{\sigma }_{ia}^{2}\right)\right\}$$
(16b)

Analytical Formulation of the Error

The formulation of the absolute error made in assessing the first stress invariant during calibration procedures when mean stress effect is neglected, starts by considering the classic thermoelastic equations [1,2,3]:

$$\frac{\Delta T}{{T}_{0}}=-a{s}_{a},$$
(17)

where sa is the first stress invariant amplitude.

On the other hand, considering the first term of the revised formulation equation (14) and, in particular, referring to the f1 term, the corrected form of the thermoelastic temperature variations is

$$\frac{\Delta T}{{T}_{0}}=-\left(a+\upsilon b{s}_{a}{R}_{f}\right){s}_{a}+b\left(1+\upsilon \right){R}_{f}{\sum }_{i}{\sigma }_{ia}^{2}.$$
(18)

The systematic error (εsa) made in evaluating \({s}_{a}\) using the wrong formulation (equation (17)) can be obtained by making equation (17) equal to equation (18):

$$\frac{\Delta T}{{T}_{0}}=-a\left({s}_{a}+{\varepsilon }_{sa}\right)=-\left(a+\upsilon b{s}_{a}{R}_{f}\right){s}_{a}+b\left(1+\upsilon \right){R}_{f}{\sum }_{i}{\sigma }_{ia}^{2},$$
(19)

and solving for \({\varepsilon }_{sa}\). The general formulation of the systematic error made in evaluating \({s}_{a}\) when the mean stress effect is neglected is shown as

$${\varepsilon }_{sa}={R}_{f}\frac{b}{a}\left({\upsilon s}_{a}^{2}-(1+\upsilon ){\sum }_{i}{\sigma }_{ia}^{2}\right).$$
(20)

Equation (20) shows that the error depends on the following:

  • Material properties (b/a e υ);

  • Loading conditions (Rf);

  • Square of the stress amplitudes in terms of principal stress and first invariant (sa, σia).

The error is zero in the case of fully reversed loading conditions (R = -1, Rf = 0). However, it is worth noting that it is not always possible to test components under these latter conditions due to the following:

  • The presence of a preload even if the macroscopic loading condition is fully reversed;

  • Buckling problems that could arise, so that R = -1 is usually not adopted for laboratory tests or in-service components under operating conditions.

Explicating the principal stress amplitude in the first stress invariant and rearranging the terms of the ratio between principal stresses β leads to the following:

$$\beta =\frac{{\sigma }_{2a}}{{\sigma }_{1a}}$$
(21)

and

$${\varepsilon }_{sa}={R}_{f}\frac{b}{a}{\sigma }_{1a}^{2}\left(2v\beta -1-{\beta }^{2}\right).$$
(22)

Also, the relative error in the first invariant determination can be estimated by dividing the absolute error \({\varepsilon }_{sa}\) by the first stress invariant amplitude:

$${\varepsilon }_{sa\_r}=\frac{{\varepsilon }_{sa}}{{s}_{a}}.$$
(23)

Putting equations (21) and (23) in equation (22), the general formula for relative error turns into

$${\varepsilon }_{sa\_r}={R}_{f}\frac{b}{a}\frac{{\sigma }_{1a}}{(1+\beta )}\left(2v\beta -1-{\beta }^{2}\right).$$
(24)

Depending on the \(\beta\) values, different loading cases can be analysed:

  • Case I: σ2 = 0 → β = 0;

  • Case II: σ1 ≥ σ2 > 0 → β > 0;

  • Case III: σ1 > σ2, σ2 < 0 → β < 0.

Figure 1 shows graphically the relative error (in terms of absolute values of \({\varepsilon }_{sa\_r}\)) made on the first stress invariant amplitude depending on different loading conditions (case studies I, II, and III). In Table 1, the thermos-physical and mechanical properties are reported for the considered titanium alloy. These data have been provided by the supplier of the material.

Fig. 1
figure 1

|\({\varepsilon }_{sa\_r}\)| values for (a) Case I (equation 25), (b) Case II (\({\sigma }_{1a}\)=100 MPa) (equation 24), and (c) Case III (\({\sigma }_{1a}\)=100 MPa), (equation 24). \({\varepsilon }_{sa\_r}\) is the relative errors made in evaluating sa,

Full size image

Considering equations (22) and (24) for absolute and relative errors respectively, in case I, the absolute error depends only on \({R}_{f}\), the material properties, and the square of the amplitude of the first principal stress, while the relative error depends on the same quantities and just the amplitude of first principal stress:

$${\varepsilon }_{sa\_r}={R}_{f}\frac{b}{a}{\sigma }_{1a}.$$
(25)

Figure 1(a) shows the percent errors that can be made in the case β = 0. In this case, the error has been evaluated depending on principal stress amplitude, and it is possible to observe that, for a specific stress value, the amount of error increases with increasing Rf. Instead, for a fixed Rf value, the error increases as the principal stress amplitude increases. Therefore, low errors (below 5%) in the calibration procedure are possible only if the imposed loading stress is very low.

Obviously, the loads the component or structure withstands while remaining in the elastic range are not always so low; hence, the error made in the calibration could be unacceptable.

In the case of a biaxial stress state (case II), and for \({\sigma }_{1a}\)=100 MPa, the error formulations are a little more complex. In particular, for case II (\(\beta >0\)), both the absolute and relative errors also depend on the Poisson ratio.

The |\({\varepsilon }_{sa\_r}\)| curves are represented in Fig. 1(b) and depend on the stress ratios R and Rf.

The value of |\({\varepsilon }_{sa\_r}\)| ranges between less than 5% in the case of a fully reversed load to 15–25% for higher stress ratios. This error value is due to the mean stress effect: the higher the mean stress, the higher the error. By observing Fig. 1(b), it can be seen that each curve presents a minimum, while |\({\varepsilon }_{sa\_r}\)| is the highest in each condition when β = 0.

Case II, where a biaxial stress state is present in the material (due, as an example, to the presence of a hole), is of practical interest as it can be found in different machine members or components. Accounting for the second order effects for those materials such as titanium is fundamental to correctly calibrating the thermoelastic signal in order to obtain stress maps as close as possible to real experienced stresses. In this way, according to Fig. 1(b), tolerable errors (under 5%) are possible only if β is higher than 0.1 and R is in the range 0–0.2.

For negative β-values (case III, \({\sigma }_{1a}\)=100 MPa, Fig. 1(c)), relative error could theoretically tend to \(-\infty\) for β = 1. Of course, β close to -1 or 1 is theoretically impractical (being outside the conditions of applicability of the thermoelastic technique) or difficult to realise under an operating point of view. In fact, the maximum and minimum values represented in Fig. 1(b), (c) are respectively 0.9 and -0.9, for the two case studies.

Also, for case III, the |\({\varepsilon }_{sa\_r}\)| dependence on β can also be investigated. In particular, the higher the stress ratio, the higher the error will be. At a fixed R value, the |\({\varepsilon }_{sa\_r}\)| increases as the second principal component increases (higher | \(\beta\) | values). A maximum |\({\varepsilon }_{sa\_r}\)| of 60% is theoretically achievable when β = -0.9 and R = 0.7, when neglecting the mean stress effect.

The curves of Fig. 1 demonstrate the potential of the proposed formulation (particularly for the case of a biaxial stress state) to assess the error that could arise in the first stress invariant estimation.

A smaller error would mean a more reliable calibration procedure and, therefore, less uncertainty in the estimation of the stresses. This information will, in turn, be useful in the validation of the FEA (finite element analysis) of the component or more complex structures made from the same material and undergoing operating loads. In this sense, the presented approach can be a tool to support the verification of the mechanical design.

Materials and Methods

In the present section, the numerical analysis and experimental campaign are shown. An overview of the methods and workflow of the activities is depicted in Fig. 2. In particular, material geometry, stress components, and mechanical properties are defined together with the mesh properties of the model as input to set the numerical model. Two approaches are implemented in this research:

  1. 1.

    Numerical analysis by finite element method to estimate the stress behaviour of the material.

  2. 2.

    Experimental tests to validate the theoretical formulation and numerical model. Experimental tests were carried out both on a unnotched sample under uniaxial stress state in order to assess material constants (a,b) and on a sample with a hole to reproduce bi-axial stress state.

Fig. 2
figure 2

Adopted approaches and workflow of the research

Full size image

The outputs have been represented by stress maps from FEA (finite element analysis) that were compared to those experimentally obtained, and the error theoretically estimated that was compared to the error estimated using experimental data.

Finite Element Analysis

The material investigated in the present study is a titanium alloy: Ti6Al4V. Titanium mixed with other metals (e.g., aluminium) exhibits relatively high sensitivity to the mean stress [15, 20, 22]. It is worth highlighting that, even if the inputted load values or the properties of the selected material are not very precise, these ‘mismatches’ would introduce small errors in the evaluation of stresses if compared with ones we expect to arise from using a wrong formulation (around 20–30%) [22].

It is also worth noting that the model could be affected by typical errors related to the following:

  • The convergence of the solution;

  • The material properties (that could not match those in the software database);

  • The adopted mesh.

However, considering that this is a very simple case study involving the application of a mechanical load that monotonically varies from zero to a pre-set value in linear elastic conditions, it can be considered a valid tool for obtaining an indication of the state of stress, since there are no closed solutions for the case of 'holed plate on a finite half-plane’ in the literature.

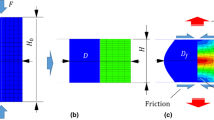
In Fig. 3(a), the geometry of the holed specimen is represented. The geometry was used to build the 2D numerical model in the Comsol Multiphysics® software.

Fig. 3
figure 3

(a) Holed Sample geometry. Dimensions expressed in mm, (b) mesh in Comsol

Full size image

To check the validity of the model from a geometric point of view, the stress concentration factor (Kt) was calculated according to the Peterson’ analytical formula for the case of a finite-width element having an eccentrically located circular hole under tension [26]. This resulted in a stress concentration factor with the nominal stress based on gross area Ktg = 3.18, and we compared such a value with the one obtained from the analysis of stress maps from FEM analysis (imposed load 5kN): Ktg = 142 MPa/45 MPa = 3.16. Therefore, it is possible to conclude that the model is geometrically consistent.

To model the material behaviour, linear elastic conditions have been assumed. For the mesh, the elements geometry was triangular (specifically, free tetrahedral), and it consisted of pyramids to match the tetrahedral mesh to any existing quadrilateral mesh on adjacent faces. In total, 293,682 elements were used.

The generated mesh was finer in the regions close to the hole and coarser in the more distant areas (Fig. 3(b)).

In fact, each element presented a generic dimension of 0.4 mm (far away from the hole) and 0.01 mm in proximity to the hole. In particular, the maximum–minimum dimension of elements of the coarser mesh was 3.4–0.034 mm with a growth factor of 1.3 and a curvature factor of 0.2. Referring to the refined mesh in the hole region, the element’s dimension ranged from 1 to 0,01 mm, with a growth factor of 1 and a curvature factor of 0.15.

The presented model is a simple, static structural FE analysis where the stress is imposed, statically ranging from 0 to the value of ΔP (Table 2). It only simulates mechanical effects, and the aim of carrying out the model was only to have a reference of the expected stress state (in particular, the first scalar stress invariant) in the holed specimen. We used this latter value as a reference for evaluating the error obtained when adopting the classical calibration procedure with experimental data.

Experimental Campaign

The material investigated in the present study was Ti6Al4V, as already discussed in "Finite Element Analysis".

The use of only one material (the titanium alloy Ti6Al4V) was mainly due to two motivations. The first one was the availability of material, and on the other hand, the possibility to investigate higher errors than Aluminum (which exhibits the same sensitivity to average stress) as already demonstrated elsewhere [23].

The experimental campaign was carried out on an unnotched sample (Fig. 4) that underwent an annealing thermal process to eliminate residual stresses, and on a holed sample (Fig. 3) that was also annealed after the hole was made [22].

Fig. 4
figure 4

Unnotched sample. Dimensions expressed in [mm]

Full size image

The unnotched sample was tested to obtain thermoelastic constants, while the holed sample was tested to validate the proposed novel formulation.

The tests consisted of the application of a cyclic load with a sine wave in an elastic regime. Table 2 reports the assigned loadings for both types of samples. For the unnotched sample, the loading program involved four loading levels of mean stress with a fixed imposed amplitude. Table 2 reports both loads and stresses in terms of mean values and amplitudes. These values have been selected to achieve a significant thermoelastic signal variation to detect the mean stress effect.

Three loading levels were adopted for the holed sample, characterized by a fixed amplitude and a variable mean load, in order to obtain three different conditions: Rf value equal to 9, 11, and 13, respectively.

The mechanical frequency was 10 Hz to ensure adiabatic test conditions. The adopted loading frame was an Instron Schenck with a capacity of 250 kN.

In order to obtain the stress maps from the thermoelastic stress analysis, the tests were monitored by a Deltatherm 1560 infrared camera with a focal plane array of 320*256 pixels, and a noise equivalent temperature difference (NETD) less than 18 mK. Thermal sequences were acquired at a frame rate of 153 frames per second for 2 min, setting the value of the “pixel integration time” equal to 75% [22]. The setup allowed a geometrical resolution of 0.27 mm/pixel.

In order to improve the surface emissivity, the surface of the samples was painted matt black (Dupli-color, Special Thermo 800 °C), while a first surface mirror with an enhanced aluminium coating was adopted to investigate the signal of the opposite sides of the specimens in order to detect and possibly compensate for spurious bending due to grips misalignment [22]. In effect, as described in [22], to assess out-of-plane bending due to a possible imperfect alignment of the clamps of the loading machine, or to a non-perfectly planar specimen, data from the front and rear surfaces of the specimen were simultaneously acquired using a mirror. Two symmetric regions of interest were considered to evaluate the average signal in each area. Finally, the averaged value of the signal was calculated using these two signals.

The overall setup is represented in Fig. 5.

Fig. 5
figure 5

Setup and equipment

Full size image

Data Processing

The thermal signal analysis was performed by acquiring the thermal response coming from the samples.

undergoing dynamical loads. The application of a sinusoidal load with a sufficiently high frequency made the heat transfer negligible. In particular, thermoelastic data were acquired according to the classic procedure [3, 22] involving the acquisition of a load reference signal from the load cell of the loading frame.

Thanks to a lock-in amplifier, the software DeltaVision [27] was able to process the data in real-time and to provide the thermoelastic temperature variation that can be described by the following [5, 8, 14]:

$${T}_{the}(t)={\Delta T}_{1}\mathrm{sin}(\omega t+\varphi )$$
(26)

where the right-hand-side term represents the first harmonic component temperature variation induced by the thermoelastic effect and varying at the same angular frequency as the imposed load. It is characterized by the amplitude ΔT1 and the phase φ that represents the delay between the load and the thermal response that is assumed to be constant throughout the sample, under adiabatic conditions. If the adiabatic condition is no longer respected, φ changes. This could be the case for high stress gradients, which lead to conduction effects [2, 3] or heat generation due to local plasticity [24, 28].

The software also provides a map of the mean temperature of the sample T0.

In this paper, we were interested in studying ΔT1, which is the amplitude, and T0 as a reference for the normalisation of the thermoelastic temperature values (ΔT1/T0). Once the ΔT1 maps of each frame of the sequence were acquired, the parameter (ΔT1/T0) was processed according to the following Fig. 6.

Fig. 6
figure 6

Flowchart of the procedure used for data processing

Full size image

The analysis of tests on unnotched samples provided the assessment of the two thermoelastic constants (a, b) according to the procedure described in [22], while the analysis of the holed sample provided the first stress invariant maps via thermoelastic data calibration equation (19).

In this work, the tests carried out in [22] were adopted for evaluating the proposed approach. In particular, the TSA data acquired in [22] were used for obtaining the thermoelastic constants on the unnotched sample and the stress maps on the holed sample. In this regard, the authors refer to [22] for a more detailed description of the processing procedure.

A 2D spatial smoothing was used to filter out noise from raw ΔT1 signals from the front and backside (reflected in the mirror) of the unnotched specimen and holed specimen. The data smoothing was necessary to reduce the signal noise by producing slow changes in value so that it would be easier to observe trends in the processed data [29]. It was adopting a 3 × 3 gaussian kernel that ensured a good quality in the resulting signal without affecting the signal behaviour. Therefore, while errors from the mathematical filtering procedure might have occurred, these were surely negligible compared to the benefit in the analysis [29].

Further, a selection of a region of interest in the ΔT1 maps was performed to focus the investigation on an area coinciding with the gauge length of both unnotched and holed specimens.

The signals from manually selected regions of interest (ROIs), on both the front and reflected surfaces, respectively ΔT1_front and ΔT1_back, were manually assessed to verify the presence of spurious bending [22]. Finally, each pixel of the ΔT1_front map was normalised by T0 in order to obtain the ratio ΔT1_front /T0, which was the ‘parameter’ considered for the analysis. For the sake of simplicity, the subscript ‘front’ in the previous formula expression is hereafter neglected.

The calibration procedure to obtain stresses was carried out using equation (20).

Results and Discussion

Assessment of Thermoelastic Constants for Signal Calibration

In this work, the thermoelastic parameters a and b were evaluated by applying the experimental approach proposed by Palumbo et al. [22], briefly described in the present section.

The procedure required cyclic tests on an unnotched sample (geometry reported in Fig. 3) made of the same material as the holed test sample, with uniaxial and known stress distribution in the gauge length.

In this case, for the considered unnotched plate, σa2 is null and the first harmonic amplitude of the thermoelastic signal becomes

$$\frac{{\Delta T}_{1}}{{T}_{0}}=-a{\sigma }_{a1}+b{R}_{f}{{\sigma }_{a1}}^{2}$$
(27)

Dividing by σa1, and expressing in terms of σm1 gives

$${S}_{norm}=\frac{{\Delta T}_{1}}{{T}_{0}{\sigma }_{a1}}=-a+b{\sigma }_{m1}$$
(28)

where Snorm is the normalized temperature signal to the amplitude stress.

The outputs of the calibration procedure are the parameters a and b that represent the intercept and slope of the linear relation expressed by equation (28) and that can be evaluated by linearly fitting the experimental data.

The considered values [22] are reported in Table 3 and Fig. 7 where it is also possible to see the 95% confidence bounds of the coefficients of the linear fitting. In particular, in Fig. 7, the markers represent the experimental data according to the loading conditions reported in Table 2, the solid red lines are confidence bounds while the dashed black line is for the linear regression).

Fig. 7
figure 7

Assessment of thermoelastic constants (black circled markers represent the experimental data, while confidence bounds are in red and linear fitting line is the black dashed one)

Full size image

The coefficients experimentally obtained are consistent with previously published values for Ti6Al4V, i.e. the b/a ratio is very close to the value reported by Machin et al. [15].

Stress Assessments Via Classic TSA Formulation, Error Estimation and Validation

In the present section, the results obtained by the finite element analysis were used as a reference for evaluating the error in the first invariant estimation that can be committed if the classic thermoelastic formulation and calibration methods are used.

As it is well-known, the classic approach for calibrating the thermoelastic data is based on the assessment of the thermoelastic constant (constant a in this work) and it can be performed by adopting three different approaches [3, 8, 22]:

  1. 1.

    Direct evaluation of a using radiometric properties of the detector, the system setting, the surface emissivity, and the thermoelastic constant of the material,

  2. 2.

    evaluation of a against a measured stress,

  3. 3.

    evaluation of a against a calculated stress.

As already explained in the previous sub-section, the first invariant was assessed by adopting the third method.

Figure 8a shows the map of the first stress invariant obtained by the numerical model, compared with the experimental maps obtained by imposing the three loading conditions in Table 2. Figure 8a proves under a qualitative point of view the acceptability of the model; in fact, it is possible to see that the first stress invariant maps from TSA data calibration and FEM analysis coincide up to the edge of the hole. The main differences between numerical and experimental data can be observed in the proximity of the hole due to the well-known [30, 31] edge effects and other effects related to the experimental measurement, such as the presence of a slight in-plane bending due to imperfect alignment in the loading machine and/or a non-perfect alignment of the IR camera.

Fig. 8
figure 8

(a) First stress invariant map from FEA corresponding a specific loading case (σm = 253 [MPa] and Δσ = 46 [MPa], Table 2) and related (b) values of stresses and \(\beta\) \((\beta =\frac{{\sigma }_{2a}}{{\sigma }_{1a}} )\) from the black dashed profile

Full size image

In Fig. 8b, the behaviour of principal stresses and the first invariant, together with β for the black dashed profile of Fig. 8a, is reported. As expected, the first principal stress and the first invariant were maxima near the hole edge while the second principal stress reached the zero value.

Before showing the quantitative comparison between the FEM analysis and experimental results, it is worth noting that the comparison between the data has been limited to an area in proximity to the hole edges avoiding the well-known edge effects affecting the acquired thermal signal in the presence of motion effects and/or material plasticization [30, 31]. The adopted test conditions (Table 2) involved an applied stress that laid in the elastic regime, while in correspondence with the hole the stress state could obviously be higher, and as such, it could determine a local plastic behaviour. That, of course, is not the case in the present research.

In Fig. 9, experimental data obtained using the classical formulation and calibration method given by equation (17), and after the signal processing procedure explained in "Materials and Methods", have been compared to numerical data considering a profile along a transverse direction through the centre of the sample (black dashed line, Fig. 8a). To perform a point-by-point comparison between experimental and numerical data, the latter were interpolated by means of a second-order polynomial function to obtain the missing points. Figures 9(a)–(c) refer to three different loading conditions, Rf = 9, 11, and 13, respectively.

Fig. 9
figure 9

(a), (c) and (e) values of stresses and \(\beta\) from black dashed profile (the data refer to the profile depicted in Fig. 8(a)). (b), (d) and (f) comparison between εexp and εsa_r for three loading conditions, Rf = 9, 11 and 13

Full size image

As expected, the experimental data of the first stress invariant amplitude obtained using the classic thermoelastic formulation were affected by the mean stress, and a difference is observed between the experimental and FEM data, that the difference is likely due to the mean stress effect. In particular, the effect of the mean stress produced an overestimation of the measured stresses that was more evident in the proximity of the hole edges and increased as the Rf value increased.

Finally, in order to validate the proposed analytical formulation, for case study II (loading condition indicated in Table 3 for holed specimen), the measured error εexp estimated using data from experimental analysis and data from the numerical model, has been compared to the theoretically predicted error εsa_r, equation (24).

Table 1 Thermophysical and mechanical properties of investigated Titanium alloy
Full size table
Table 2 Loading table
Full size table
Table 3 Thermoelastic constants obtained by fitting the thermoelastic data
Full size table

The measured relative error has been calculated as follows:

$${\varepsilon }_{exp}=\frac{{s}_{a\_exp}-{s}_{a\_FEM}}{{s}_{a\_FEM}}$$
(29)

where sa_exp is the amplitude of the first invariant assessed with the classical TSA approach and sa_FEM refers to the value assessed by FEM simulation and considered as a reference for the expected stress data.

The results are reported in Fig. 9(a)–(c) and show a good correlation between the two errors for each loading condition, Rf = 9, 11 and 13. Of course, red squared markers representing εexp are noisier than εsa_r due to the characteristic noise that characterises the TSA measurement, but the error values are roughly similar, confirming the validity of the formulation for the specific case study.

Again, it is worth noting that both εexp and εsa_r data start some millimetres far away from the hole edges, due to disregarding plastic and boundary effects, in error comparison.

It is worth noting that the field of validity of the present approach is limited to those materials whose thermoelastic response is sensitive to the mean stress effect. In this work, titanium in its largely used alloy (Ti6Al4V) has been considered since it presents a significant “mean stress” effect. However, the proposed approach can be extended to aluminium alloys even if these experience less sensitivity to the mean stress [3, 23]. In other words, the ratio between the thermoelastic constants (b/a) is less in aluminium than in titanium and this means that the error committed in stresses evaluation in aluminium alloys, for a given loading condition, will be less as well.

Moreover, it is important to highlight that the proposed equation has been verified only for case II (case I has already been investigated [22]). It is interesting to point out that for the biaxial stress state, unlike with the uniaxial case, the components of principal stresses appear both as the first invariant and separately. Hence, in this case, the well-known calibration procedure used to assess the first invariant based only on the assessment of material constants (a, b) is no longer useful. In this regard, further work will be dedicated to covering other cases involving both the stress state and the material, with the intention to export this approach to out-of-laboratory applications on components undergoing operating loads.

It is worth noting that the application of the proposed approach requires the following:

  • The possibility to record the thermal signal by placing the detector in situ;

  • The thermoelastic constants of the material (a, b) having been previously assessed.

Finally, it is important to remark that the knowledge of the error that could be committed represents an important guideline to understanding whether or not the classic calibration procedure can provide a good estimation of the stresses, depending on the loading conditions, and whether or not this estimation can be retained as acceptable.

Conclusions

In the present study, the effect of the mean stress on titanium in the presence of uniaxial and biaxial stress states was studied using an analytical approach accounting for the general theory of thermoelastic stress analysis.

The first result was a formulation to model thermoelastic temperature variations accounting for the mean stress effect in the presence of a biaxial stress state.

Second, an error analysis provided an analytical formulation for the error made in case the mean stress effect is neglected for different case studies (involving uni- and biaxial stress states).

The analytical formulation of the error shows that neglecting the mean stress effect for titanium involves significant errors in stress evaluation, depending on the material properties, loading conditions, and the square of the first principal stress and first invariant amplitude.

Another interesting point to be highlighted for the biaxial stress state is that unlike with the uniaxial case, the components of principal stresses appear both as the first invariant and separately. Hence, in this case, the well-known calibration procedure used to assess the first invariant based only on the assessment of material constants (a, b) is no longer useful.

Finally, the error equation was validated using experimental data in terms of thermoelastic temperature variations acquired during an experimental test on a holed sample. As expected, the experimental data of the first stress invariant amplitude obtained using the classic thermoelastic formulation were affected by the mean stress, and a difference is observed between the experimental and FEM data, which is likely due to the mean stress effect. In particular, the effect of the mean stress produced an overestimation of the measured stresses that was more evident in the proximity of the hole edges and increased as the Rf value increased.

However, since the presented research focuses only on a specific case, further studies will be focused on extending this approach to other materials and stress states to prove the validity of the analytical function in other cases.