Design of a Biaxial Cruciform Specimen with a High Degree of Plastic Deformation and Yield Locus Evolution

Abstract

Background

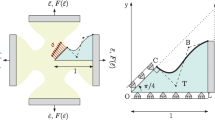
Evaluation of material properties under biaxial loading is a cumbersome process. Biaxial mechanical properties using the planar biaxial testing technique is a very accurate method compared to other out-of-plane biaxial testing techniques. Though the planar biaxial tests predict the deformation behavior of the material precisely, their applicability is limited to the design of the cruciform specimens. Improper cruciform specimen design induces inhomogeneous strain distribution, which leads to failure at a very low strain level or out of the gauge region.

Objective

The present study aims to design a novel cruciform specimen to achieve homogenous and maximum strain distribution at the gauge region.

Methods

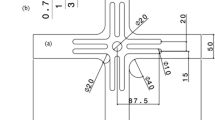
Initially, an optimized cruciform biaxial specimen was designed using a commercial finite element method. 1050 Aluminum alloy sheet with 2.5 mm thickness was used for the experimental validation. Strain evolution during planar biaxial testing was captured with the help of the Digital Image Correlation method.

Results

It was found that a cruciform sample with 60% thickness reduction at the gauge region is capable of achieving 87.5% of the fracture strain achieved during uniaxial tensile testing before breaking. It was observed that the optimized cruciform specimen was deformed uniformly with a fracture at the gauge region.

Conclusions

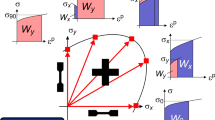
The optimized design was used for the measurement of yield locus up to higher plastic strain values. The experimental yield loci were compared to the yield criteria of von Mises, Hill’48, Hill’93, and Barlat. The Barlat yield criteria is the most accurate for AA1050 yield loci evaluation.

Appendix

Von Mises Yield Criteria [31]

The von Mises yield criteria is one of the most widely used plasticity models. Assuming the sheet material behaves isotopically, the 3D yield function is represented by all 6 components of the stress tensor as follows:

$$\overline{\upsigma }=\sqrt{\frac{1}{2}\left[{\left({\upsigma }_{\mathrm{xx}}-{\upsigma }_{\mathrm{yy}}\right)}^{2}+{\left({\upsigma }_{\mathrm{yy}}-{\upsigma }_{\mathrm{zz}}\right)}^{2}+{\left({\upsigma }_{\mathrm{zz}}-{\upsigma }_{\mathrm{xx}}\right)}^{2}\right]+3\left({\uptau }_{\mathrm{xy}}^{2}+{\uptau }_{\mathrm{yz}}^{2}+{\uptau }_{\mathrm{zx}}^{2}\right)}$$

(A.1)

For plane stress condition von Mises yield criteria can be written as (${\upsigma }_{\mathrm{zz}}={\upsigma }_{\mathrm{zx}}={\upsigma }_{\mathrm{yz}}$=0)

$$\overline{\upsigma }=\sqrt{{\upsigma }_{\mathrm{xx}}^{2}+{\upsigma }_{\mathrm{yy}}^{2}-{\upsigma }_{\mathrm{xx}}{\upsigma }_{\mathrm{yy}}+3{\uptau }_{\mathrm{xy}}^{2}}$$

where $\overline{\upsigma }$ is effective stress

Hill'48 Yield Criteria [26]

One of the most commonly used yield criteria for anisotropic materials is the Hill48 yield criteria. The yield criteria is written as a quadratic function of the following form:

$$\begin{aligned}2{\overline{\upsigma } }^{2}=&\;\mathrm{F}{\left({\upsigma }_{\mathrm{yy}}-{\upsigma }_{\mathrm{zz}}\right)}^{2}+\mathrm{G}{\left({\upsigma }_{\mathrm{zz}}-{\upsigma }_{\mathrm{xx}}\right)}^{2}+\mathrm{H}{\left({\upsigma }_{\mathrm{xx}}-{\upsigma }_{\mathrm{yy}}\right)}^{2}\\&+2\mathrm{L}{\upsigma }_{\mathrm{yz}}^{2}+2\mathrm{M}{\upsigma }_{\mathrm{zx}}^{2}+2\mathrm{N}{\upsigma }_{\mathrm{xy}}^{2}\end{aligned}$$

(A.2)

where $\tilde{\sigma }$ is effective stress and F, G, H, L, M and N are material parameters. Here x, y, and z represent rolling, transverse and thickness direction of sheet.

For plane stress conditions, the Hill'48 quadratic yield criteria is given by (${\upsigma }_{\mathrm{zz}}={\upsigma }_{\mathrm{zx}}={\upsigma }_{\mathrm{yz}}$=0)

$$(\mathrm{G}+\mathrm{H}){\upsigma }_{\mathrm{xx}}^{2}-2\mathrm{H}{\upsigma }_{\mathrm{xx}}{\upsigma }_{\mathrm{yy}}+(\mathrm{F}+\mathrm{H}){\upsigma }_{\mathrm{yy}}^{2}+2\mathrm{N}{\upsigma }_{\mathrm{xy}}^{2}=1$$

where

$${\mathrm{r}}_{0}=\frac{\mathrm{H}}{\mathrm{G}}, {\mathrm{r}}_{45}=\frac{2\mathrm{N}-\mathrm{F}-\mathrm{GH}}{2(\mathrm{F}+\mathrm{G})}\text{ and }{\mathrm{r}}_{90}=\frac{\mathrm{H}}{\mathrm{F}}.$$

Hill'93 Yield Criteria [32]

In 1993 Hill proposed an improved yield criteria for plastic behaviour of sheet metals given by following quadratic equation:

$$f(\sigma )=\frac{{\sigma }_{1}^{2}}{{\sigma }_{0}^{2}}-\frac{c{\sigma }_{1}{\sigma }_{2}}{{\sigma }_{0}{\sigma }_{90}}+\frac{{\sigma }_{2}^{2}}{{\sigma }_{90}^{2}}+\left[(p+q)-\frac{\left(p{\sigma }_{1}+q{\sigma }_{2}\right)}{{\sigma }_{b}}\right]\frac{{\sigma }_{1}{\sigma }_{2}}{{\sigma }_{0}{\sigma }_{90}}=1$$

(A.3)

where ${\upsigma }_{1}$ and ${\upsigma }_{2}$ are the principal stresses, $\mathrm{c},\mathrm{p}$ and $\mathrm{q}$ are material parameters which can be determined by using the following expressions:

$$\mathrm{c}={\upsigma }_{0}{\upsigma }_{90}\left(\frac{1}{{\upsigma }_{0}^{2}}+\frac{1}{{\upsigma }_{90}^{2}}-\frac{1}{{\upsigma }_{\mathrm{b}}^{2}}\right)$$

$$\mathrm{p}=\left[\frac{2{\mathrm{R}}_{0}\left({\upsigma }_{\mathrm{b}}-{\upsigma }_{90}\right)}{\left(1+{\mathrm{R}}_{0}\right){\upsigma }_{0}^{2}}-\frac{2{\mathrm{R}}_{90}{\upsigma }_{\mathrm{b}}}{\left(1+{\mathrm{R}}_{90}\right){\upsigma }_{90}^{2}}+\frac{\mathrm{c}}{{\upsigma }_{0}}\right]{\left(\frac{1}{{\upsigma }_{0}}+\frac{1}{{\upsigma }_{90}}-\frac{1}{{\upsigma }_{\mathrm{b}}}\right)}^{-1}$$

$$\mathrm{q}=\left[\frac{2{\mathrm{R}}_{90}\left({\upsigma }_{\mathrm{b}}-{\upsigma }_{90}\right)}{\left(1+{\mathrm{R}}_{0}\right){\upsigma }_{90}^{2}}-\frac{2{\mathrm{R}}_{0}{\upsigma }_{\mathrm{b}}}{\left(1+{\mathrm{R}}_{0}\right){\upsigma }_{0}^{2}}+\frac{\mathrm{c}}{{\upsigma }_{0}}\right]{\left(\frac{1}{{\upsigma }_{0}}+\frac{1}{{\upsigma }_{90}}-\frac{1}{{\upsigma }_{\mathrm{b}}}\right)}^{-1}$$

where ${\upsigma }_{0}{,\upsigma }_{90}$ are ${\mathrm{R}}_{0}, {\mathrm{R}}_{90}$ are the yield strength and R-values along 0 and 90 to the rolling direction respectively and ${\upsigma }_{\mathrm{b}}$ is biaxial yield strength.

Barlet Yield Criteria [33]

All the above mentioned yield criteria are the quadratic yield criteria, whereas in 1989 Barlat proposed a non-quadratic yield criteria of the following form:

$$\mathrm{f}(\upsigma )=\mathrm{a}{\left|{\mathrm{K}}_{1}+{\mathrm{K}}_{2}\right|}^{\mathrm{M}}+\mathrm{a}{\left|{\mathrm{K}}_{1}-{\mathrm{K}}_{2}\right|}^{\mathrm{M}}+\mathrm{c}{\left|2{\mathrm{K}}_{2}\right|}^{\mathrm{M}}=2{\overline{\upsigma } }^{\mathrm{M}}$$

(A.4)

where ${\mathrm{K}}_{1}=\frac{{\upsigma }_{\mathrm{xx}}+\mathrm{h}{\upsigma }_{\mathrm{yy}}}{2},{\mathrm{K}}_{2}=\sqrt{{\left(\frac{{\upsigma }_{\mathrm{xx}}-\mathrm{h}{\upsigma }_{\mathrm{yy}}}{2}\right)}^{2}+{\left(\mathrm{p}{\upsigma }_{\mathrm{xy}}\right)}^{2}},\mathrm{M},\mathrm{a},\mathrm{c},\mathrm{p}$ and $\mathrm{h}$ are material parameters which can be calculated by using the following expressions:

$$\mathrm{h}=\frac{{\upsigma }_{0}}{{\upsigma }_{90}}$$

$$\mathrm{a}=\frac{2{\left({\upsigma }_{0}/{\upsigma }_{\mathrm{b}}\right)}^{\mathrm{MA}}-2|1-\mathrm{h}{|}^{\mathrm{M}}}{1+{\mathrm{h}}^{\mathrm{M}}-|1-\mathrm{h}{|}^{\mathrm{M}}}$$

$$\mathrm{c}=2-\mathrm{a}$$

$$\mathrm{M}=8\ \mathrm{for\ FCC\ materials}$$

$$\mathrm{p}={\left(\frac{2}{2\mathrm{a}+{2}^{\mathrm{M}}\mathrm{c}}\right)}^{1/\mathrm{M}}\frac{{\upsigma }_{0}}{\uptau }$$

where ${\upsigma }_{0}$ tensile yield strength and  $\uptau$  is the yield strength in shear.