Comparison Between Surface and Near-Surface Residual Stress Measurement Techniques Using a Standard Four-Point-Bend Specimen

Abstract

Background

Determination of near-surface residual stresses is challenging for the available measurement techniques due to their limitations. These are often either beyond reach or associated with significant uncertainties.

Objective

This study describes a critical comparison between three methods of surface and near-surface residual stress measurements, including x-ray diffraction (XRD) and two incremental central hole-drilling techniques one based on strain-gauge rosette and the other based on electronic speckle pattern interferometry (ESPI).

Methods

These measurements were performed on standard four-point-bend beams of steel loaded to known nominal stresses, according to the ASTM standard. These were to evaluate the sensitivity of different techniques to the variation in the nominal stress, and their associated uncertainties.

Results

The XRD data showed very good correlations with the surface nominal stress, and with superb repeatability and small uncertainties. The results of the ESPI based hole-drilling technique were also in a good agreement with the XRD data and the expected nominal stress. However, those obtained by the strain gauge rosette based hole-drilling technique were not matching well with the data obtained by the other techniques nor with the nominal stress. This was found to be due to the generation of extensive compressive residual stress during surface preparation for strain gauge installation.

Conclusion

The ESPI method is proven to be the most suitable hole-drilling technique for measuring near-surface residual stresses within distances close to the surface that are beyond the penetration depth of x-ray and below the resolution of the strain gauge rosette based hole-drilling method.

Introduction

Residual stress, a tensor quantity, are locked-in stresses within a component without external loading, generated as a result of complex non-linear thermal–mechanical processing during manufacturing. Most manufacturing processes introduce residual stress that has a direct bearing on manufacturing (e.g., undesirable distortion) and on the resilience of products in service and their design life [1,2,3,4,5,6]. Historically, residual stresses have primarily been incorporated into structure critical component design through a significant safety factor because they are challenging to characterise and control, and there is little design guidance in codes and standards. Consequently, components have thicker sections than needed, increasing the resource use and entry cost of the product as well as the cost of ownership through extra weight. Management of residual stress has the potential to radically improve the sustainability of high value products not only from the perspective of the level of resources used, but also in terms of their through-life impact on the environment. Residual stresses are rather challenging to accurately model in an engineering component, compared to in-service applied stresses [7]. Despite of all the advances made in modelling and simulations, characterisations and measurements of residual stress are still the corner stone of these developments. This increases a need for appropriate measurement techniques as they are the main means of validation to enhance the confidence of the industrial end users in the predictive models.

Depending on their characteristic domain of influence, which is a length over which the stresses reach an equilibrium with their surroundings, residual stresses can be categorised into three types. These are type I long range residual stress that equilibrate over distances comparable to the dimensions of the component, type II medium range residual stress that equilibrate over few grains, and type III short range residual stress that equilibrate over distances with atomic dimensions. Examples of type II and III residual stresses are the stresses arisen from grain boundary misorientation, thermal stresses in metal matrix composites, and stress fields generated by dislocations and point defects [8]. The type I residual stress can be estimated to a reasonable accuracy by continuum models using finite element analyses in which the materials’ inherent microscopic natures such as polycrystalline and multiphase are ignored [8]. Accordingly, several measurements techniques have been developed, matured and nowadays readily available for the characterisation of residual stresses depending on their characteristic length scale (i.e., types I, II or III) [9].

The most common methods of residual stress measurement by usage, are the mechanical-based and diffraction-based techniques. The former techniques are typically destructive or semi-destructive in nature and rely on tracking changes in dimensions following successive material removal that results in stress relaxation [9, 10]. On the other hand, the latter techniques measure the changes in the atomic interplanar spacing ‘d’, induced by the presence of residual stresses that can be used to detect elastic strain ‘ε’ according to the Bragg relationship by having a knowledge of the incident wavelength ‘λ’ and the variation in the Bragg scattering angle ‘Δθ’ [9].

Hole-drilling is a mechanical-based residual stress measurement technique in which undamaged and intact regions of a part is subjected to step-by-step incremental drilling (i.e., successive material removal) while the changes in shape and dimension induced by the stress relaxation, caused by the material removal, are measured. These measured changes can then be converted to strains and subsequently used for inverse calculation of the stresses required to cause the measured dimensional changes [11, 12]. The material removal usually consists of drilling a hole around which the displacement caused by drilling is measured by either strain gauge rosettes [13, 14], or optical methods such as electronic speckle pattern interferometry (ESPI) [15, 16] or digital image correlation (DIC) [17]. The measurements covers a confined area of the sample up to 5 times of the dimeter of the drilled hole, typically between 0.1–3.2 mm, and provides information about the stress profile down to a depth approximately equivalent to 60% of the hole diameter [11, 18, 19]. While this technique is capable of providing useful information about the near-surface residual stress profile down to a limited depth from the surface, it is not useful for measurement on samples with complex surface geometry and where information about bulk residual stresses is needed. Other techniques such as deep hole-drilling and the contour method have been developed for the measurements of bulk residual stresses that are discussed in more details elsewhere [20, 21].

From engineering perspective, measurements of displacement by the aid of optical means are of considerable importance for two main reasons of (i) being fast, and (ii) has no additional damage and intrusion into the measurements. Measurements at the speed of light enables the acquisition of data during highly dynamic events (e.g., drilling) at a very short time. Additionally, light does not usually introduce any unwanted damages such as scratches, wears, and deformation on the surface of most engineering materials and alloys that are critical for residual stress measurements [8, 9]. This is in fact the major advantage of the optical methods compared to the traditional strain gauge rosette based methods, as for most metallic materials and alloys surface preparation is not required which means no additional mechanical damage will be introduced to the surface. However, light can be influenced by environmental factors such as temperature, moisture, vibration, dust, or pressure, which make the design of an optical measurement system challenging, especially if the measurement needs to be conducted in harsh environments.

Digital speckle pattern interferometry (DSPI) and electronic speckle pattern interferometry (ESPI) are the two basic approaches of illuminating the surface either through a single illumination beam or double illumination beams [15, 22, 23]. Typically, single illumination is mainly suitable for measurements of out-of-plane displacements where the interference is constructed by superimposing a reference illumination on the surface illumination, which can be directed to the camera sensor or to an auxiliary surface. The double illumination configuration on the other hand, is a preferable option for in-plane displacement measurements where the coherent lights, originating from the same source, are illuminating the surface of interest from two different directions and the interference is produced by the mutual interaction between the two light components. The surface of the area of interest should usually be optically rough to enable the formation of speckle patterns upon interaction with the diffused incident laser beam [24, 25]. The light directed to the surface is scattered from a finite interaction zone where its physical characteristics including phase, amplitude and intensity that are directly related to the surface property and microstructure of the reflection zone are measured. The interference of the light reflected from the surface of the sample with the reference beam results in a light filed with random intensity, phase and amplitude that is also a speckle pattern. The occurrence of any displacement on the surface such as those caused by material removal (i.e., hole-drilling) leads to a change in the distance between an object on the surface and the image which results in a change in the phase of the speckle pattern; this will be used for the measurements of surface displacement field [24, 25].

For most diffraction-based techniques, a value is required for the stress free interplanar spacing ‘d₀’, which is usually measured from an annealed sample, to benchmark the lattice strain in a stressed material that can then be used for the calculation of residual stress by using a relevant stiffness value, according to Hooke’s elastic law [26]. Due to its selective nature, diffraction is skewed towards a certain group of grains with a particular orientation in which the shift in diffraction peak will provide information on both type I and the averaged type II residual stresses of that grain family. The type III residual stresses leads to peak broadening in the diffraction profile. This diffraction behaviour can be applied to investigate the stress status of individual microstructural phases in multi-phase materials. In single phase materials the type II intergranular residual stress may compromise the measured elastic strain as this may not be a good representative of the bulk residual stresses. Hence, corrections are required to be carried out on the recorded type II stress to deduce representative bulk residual stresses [27].

The main objective of this study is to conduct a cross comparison between three different methods of surface and near-surface residual stress measurements using a standard four-point-bend specimen for the generation of residual stress. These are XRD (i.e., diffraction-based) and two different hole-drilling methods (mechanical-based) one based on strain gauge rosettes and the other based on ESPI. The effect of surface preparation for strain gauge installation, required for hole-drilling method has been investigated to understand the extent of the mechanical damage and consequently the impact on the residual stress profile. The novelty of the current study is in the use of a standard sample, based on ASTM, for the generation of known magnitudes of residual stress to benchmark these measurement techniques. Otherwise, cross comparisons between diffraction and hole-drilling methods have been carried out previously and reported through numerous studies (e.g., [20, 21]). However, none of these studies have performed these cross comparisons on a standard setup with a pre-defined nominal stress magnitude.

Experimental Procedures

Material and Method

A type 304 high carbon austenitic stainless steel (UNS S30400) in the form of plate with a known rolling direction (RD) was selected for these investigations, which was in the mill annealed condition. The chemical composition of the material, supplied by the manufacturer, along with a standard composition for type 304 stainless steel [20] are provided in Table 1. A set of strips with 260 × 28 × 6 mm (L × W × T) dimensions were machined from the as-received plate with their length along the RD.

Table 1 Nominal chemical composition of the 304 stainless steel used in this study [wt%]

Microstructure of the as-received material was characterised by optical microscopy (OM) and electron backscatter diffraction (EBSD) across both cross-sections parallel and perpendicular to the RD. Sufficient number of samples were ground and polished to a mirror finished condition using standard metallographic preparation methods. For the OM analysis, the samples were electro-etched for approximately 45 s at 13 V in 10% Oxalic acid. For the EBSD analysis, the additional samples were subjected to a final electro-polishing step in an electrolyte made from a mixture of acetic acid (92% vol.) and perchloric acid (8% vol.) with a stainless steel cathode. EBSD maps were collected from both cross-sections using a automated Nordlys II EBSD system interfaced to a FEI Quanta-250 field-emission gun scanning electron microscope, with an accelerating voltage of 20 kV and a 100 µm dia. aperture. The acquisition time was set to 40 ms, collecting at least 1 frame for each point. For each sample, an area of 500 µm × 500 µm was scanned with 0.5 µm step size, and at least 90% of the scanned area was indexed.

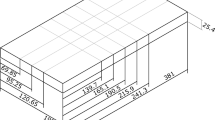
The four-point loaded specimen design was chosen from ASTM standard, to apply nominal tensile elastic stress on the strip surface for residual stress measurements [28]. The four-point bend beam assembly is designed in a way where a strip is bent by pushing two internal rollers against two outer rollers located at both ends of the strip on the opposite side. An image of the four-point bend geometry with all the associated dimensions are shown in Fig. 1. The two inner supports are located symmetrically around the midpoint between the outer supports. The magnitude of tensile stress in the outer fibre of the four-point loaded specimen depends on the dimension of the strip. The maximum stress occurs between the contact points with the inner support. In this area, theoretically the stress is constant for a slender beam [28]. From the contact point with the inner support the stress decreases linearly towards zero at the ends of specimens. The elastic stress in the middle portion of the specimens is calculated by using the relationship in (equation (1)) [28].

$$\sigma = \;\frac{12Ety}{{3{H^2} - 4{A^2}}}$$

(1)

Fig. 1

(a) Schematic illustration of four-point bend specimen and top view of the sample with all dimensions, and (b) a photograph of one of the four-point bend samples

where σ is the maximum tensile stress, E is the modulus of elasticity of the material, t is the thickness of the strip, H is the length of specimen strip, A = H/4 is the distance between inner and outer support, and y is the maximum deflection, i.e. distance between the contact point with the outer supports and middle of the strip in loaded condition (see Fig. 1).

The strips were loaded to different magnitudes of nominal stress by applying various deflections (y) to the four-point-bend loaded sample assembly. Depending on the uniformity of the specimen thickness (t) and the accuracy in the applied deflection (y) and other dimensional measurements, the nominal stress can vary. The uncertainties in the nominal stress caused by the maximum thickness non-uniformity and the inaccuracy in deflection measurements have been calculated. Table 2 provides the calculated nominal stress along with the range of uncertainties for the deflections applied throughout this study. The uncertainty for each nominal stress magnitude was evaluated by taking into consideration the uncertainties associated with the dimensional measurements (0.001 mm) and Young’s modulus (± 5%) (i.e., E, t, H, and A in (equation (1)), as the second root of sum of the squares of all uncertainties. It can be seen in Table 2 that the maximum uncertainties associated with the dimensional measurement errors and the sample’s thickness unevenness for all deflections is negligible.

Table 2 Nominal applied stresses at different deflections of four-point loaded sample assembly calculated by (equation (1)) 

Residual Stress Measurements

The residual stress measurements were carried out on the samples in the as-received condition and after applying different nominal loads. These measurements were done by XRD and hole-drilling using the two different methods of strain measurement; one based on strain gauge rosette known as the incremental central hole-drilling (ICHD), and the other using ESPI. The measurements by the XRD were performed first for all conditions, and then the measurements by the hole-drilling methods were conducted under different nominal loads and at various locations.

XRD stress measurement

XRD stress measurements were carried out on the strips in the as-received condition and also in the four-point-bend loaded form under different levels of nominal stress (see Table 2). This was by using a Proto-LXRD stress diffractometer and the sin²ψ method in accordance to the NPL’s good practice guide [29], certified to UKAS’s ISO17025 accreditation. A Mn K-α target tube was utilised with a wavelength of 2.1031 A°, and a round collimator with 2 mm diameter. Measurements were performed along the middle fibre of the strips, within 130 mm gauge lengths at 10 mm intervals, to determine the stress magnitudes in both the longitudinal and the transverse directions (see Fig. 1) under all the nominal stresses described in Table 2. The stresses were calculated from the measured strains of (311) crystallographic planes at 152.8° Bragg angle, assuming x-ray elastic constants -S1(hkl) (MPa) and ½S2(hkl) (MPa) of 1.20 × 10^–6 and 7.18 × 10^–6, respectively. The x-ray elastic constants were measured for the same material by the same XRD machine according to ASTM standard [30]. These are approximately equivalent to the material’s elastic properties of E = 190 GPa and Poisson’s ratio of v = 0.305. For each point in both directions, measurements were performed at eleven ψ off-set angles in the range of ± 33° where 10 acquisitions with 1 s exposure time were carried out at each angle. The uncertainty of the stress measurements was calculated from the best fit to the sin² plot.

ESPI-based hole-drilling method

The hole-drilling measurements based on ESPI was carried out using a StressTech Prism® system manufactured by Stresstech. This system is composed of a monochromatic laser source, an illuminator, a CCD camera equipped with a beam combiner, and an automatic high speed drill. A coherent laser beam is directed from the laser source through an fibre optic cable to the illuminator which diffuses the beam on the surface to be measured. A separate laser beam, originating from the same source, is directed through an additional fibre optic cable to the beam combiner in the CCD camera. The reference beam and the surface reflection of the illumination beam are then combined in the CCD camera to form speckle patterns. The dim surface of the as-received material with low reflectivity along with its smooth surface provided an optimised condition for drilling and image acquisition by ESPI.

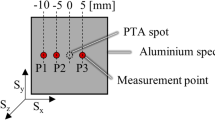
For the purpose of comparison with the XRD and the strain gauge rosette-based hole-drilling data, carbon coated endmills with 1.8 mm diameter was used for drilling. Images were recorded during each step of incremental hole-drilling and subsequently the surface displacement (i.e. strain) induced by material removal during drilling were evaluated. The measured strains were then used for inverse calculation of residual stresses using the integral method, assuming the Young’s Modulus and Poisson’s ratio of 190 GPa and 0.305, respectively (i.e., as similar as to those used in XRD stress measurements). Measurements were carried out on the same sample as that used for XRD and strain gauge rosette-based hole-drilling techniques at two deflection conditions of y = 1 mm and y = 2.4 mm, nominal stresses of 81.8 ± 7.4 MPa and 179.9 ± 7.6 MPa, respectively (see Table 2). Two measurements were conducted for the former and three measurements for the latter at locations highlighted in Fig. 2(a). Additionally, a separate four-point-bend sample, loaded to 179.9 ± 7.6 MPa nominal stress (i.e., y = 2.4 mm deflection) was used for residual stress measurements by ESPI using endmills with different diameters including 0.79 mm, 1.25 mm, and 1.80 mm. The location of these measurements are highlighted in Fig. 2(b).

Fig. 2

Schematic illustration of the locations of residual stress measurements on the sample used for (a) comparison between different techniques, and (b) comparison between ESPI hole-drilling with endmills of different diameters. Note that distance between the centre of the measurement points is 10 mm from either side

ICHD method

Residual stress measurement by ICHD was performed using an MTS3000 system manufactured by SINT technology. These measurements were carried out in accordance to ASTM standard [31], and similarly to the XRD, certified to UKAS’s ISO17025 accreditation. For these measurements the surface of the four-point loaded sample that was already subjected to XRD and ESPI stress measurements, was ground and prepared for strain gauge installation in loaded conditions. Prior to the installation of strain gauge rosettes, the ground surface residual stress was measured by the XRD to explore the effect of surface preparation and grinding on the status of residual stress. Then the strain gauge rosettes were installed on the spots that underwent residual stress measurements before and after surface preparation by the XRD. The strain gauge rosettes used for these investigations were pre-wired rosette consisting of three quarter-bridges arranged at 45° angles around the hole, manufactured by HBM. The endmills used for drilling were 1.8 mm TiN coated drills made by the same manufacturer as the hole-drilling system. The distortions induced by drilling were measured at each incremental steps of drilling, and then the residual stresses were calculated by using integral method and the same mechanical properties as those used for ESPI based method (i.e. Young’s Modulus and Poisson’s ratio of 190 GPa and 0.305, respectively). Similarly to the ESPI method, measurements were carried out at two deflection conditions of y = 1 mm and y = 2.4 mm, generating nominal stresses of 81.8 ± 7.4 MPa and 179.9 ± 7.6 MPa, respectively. The locations of the measurements are highlighted schematically in Fig. 2(a). The uncertainties were calculated by an in-house developed software in MATLAB using the information (e.g., compliance coefficients) provided in ASTM standard [31].

Results

Materials Microstructure

Figure 3(a) and (b) show EBSD maps of the as-received material using inverse pole figure (IPF) colouring with respect to the RD, for two cross-sections of parallel and perpendicular to the RD, respectively. The as-received microstructure contains equiaxed austenite grains with an average grain size of 11 µm, and ẟ-ferrite stringers parallel to the RD. The material does not have a homogeneous microstructure since grains as large as 75 µm has been observed in the microstructure. There is no strong preferred texture, as shown in Fig. 3(c) in forms of {100}, {110} and {111} polefigures. There is a weak tendency of < 110 > poles to be at 45° to the RD with heterogeneous distribution that might have resulted from the final hot-band rolling of the manufacturing process.

Fig. 3

Microstructure characteristics of the as-received material, (a), (b) EBSD maps with IPF colouring with respect to the RD from the cross-sections parallel and perpendicular to the RD, respectively, and (c) {001}, {011} and {111} polefigures showing weak textures in the as-received material. The intensity of the texture is quantified in the unit of the multiple of uniform density (MUD)

Residual Stress Measurements

Figure 4 shows the plot of measured residual stresses on the surface of one of the as-received strips by XRD in both longitudinal and transverse directions. These were measured in the middle of the strip in the area that was located between the inner supports of the four-point loaded samples during loading (see Fig. 1). The measured longitudinal stress show negligible magnitudes of tensile stress indicating that the as-received material is almost stress free along the RD. This makes the material suitable for the purpose of these investigations as the longitudinal component of stress is expected to change during loading with a four-point bend fixture according to equation 1. On the other hand, the measured residual stress in the transverse direction of the as-received material ranges between 130 and 150 MPa compressive, consistently. Based on (equation (1)) (i.e., ASTM standard [28]) the transverse component of stress does not change during loading in the four-point bend fixture [28].

Fig. 4

Measured residual stress by XRD on the surface of the as-received material in both longitudinal and transverse directions. The horizontal axis is corresponding to the 130 mm middle fibre of the four-point-bend specimen (i.e., h in Fig. 1) and the distance is calculated from the left to the right whereby the XRD stress measurements have taken place at each 10 mm

The results of XRD residual stress measurements in the four-point-bend loaded strip used for the comparison between measurement techniques at various levels of deflections, corresponding to different nominal stress magnitudes, are shown in Fig. 5(a) and (b) for both longitudinal and transverse directions, respectively. From Fig. 5(a), it can be seen that at each deflection condition the measured longitudinal stress is in a very good agreement with the calculated nominal stress (see Table 1). An increase of ≈ 30–40 MPa nominal stress at each deflection step has nicely been resolved by the XRD. This shows the superb sensitivity of the XRD system in resolving relatively low magnitudes of stress. The measured residual stresses in the transverse direction at different deflections, shown in Fig. 5(b), are almost the same for all nominal stresses. This agrees with the standard [28] which suggests that the deflection only produces tensile stress in the longitudinal direction. Although the as-received material was not stress free in the transverse direction (i.e., ~ -130–150 MPa), this does not have a significant bearing on the generated stress in the longitudinal direction when loaded to different levels of nominal stress in the four-point-bend fixture (see Fig. 5(a)). Meanwhile, the transverse stress component might have small effects on residual stress at micro-scales (i.e., Type III), especially close to the outer surface of the loaded sample, but these do not compromise the nominal stresses for the purpose of this study. As shown in Fig. 5(a), the measured stresses at all levels of deflections are close to the nominal stresses, confirming the suitability of the samples for the purpose of these comparisons.

Fig. 5

Measured residual stress by XRD in the as-received condition and in four-point-bend fixture loaded to different levels of nominal stresses under different deflections, (a) in the longitudinal, and (b) in the transverse directions. The ranges of nominal stresses calculated for each deflection condition (see Table 1) is provided as the transparent strips in (a) for the aid of comparison. The horizontal axis is corresponding to the 130 mm middle fibre of the four-point-bend specimen (i.e., h in Fig. 1) and the distance is calculated from the left to the right whereby the XRD stress measurements have taken place at each 10 mm

The results of residual stress measurements by XRD and two different hole-drilling techniques a four-point-bend strip at two nominal stresses are shown in Fig. 6(a) and (b), respectively for the longitudinal and transverse directions. The nominal stresses and the range of their uncertainties (see Table 2) in the longitudinal direction are also provided for the aid of comparison. It can be seen from Fig. 6(a) that the results of XRD and ESPI agree well with the expected nominal stresses. One of the important observations is the sensitivity of the ESPI based hole-drilling method to small variations in stress magnitude. For instance, at 81.8 ± 7.4 MPa nominal stress, the stresses measured by XRD at two locations are varied by approximately 10 MPa and this variation has been resolved also by the ESPI. At 179.9 ± 7.6 MPa the results of both XRD and ESPI at three different locations are all similar and comparable with the expected nominal stress.

Fig. 6

Comparison between the measured residual stresses on a standard four-point-bend loaded sample at various nominal stresses by different techniques, including XRD, ESPI and ICHD, (a) longitudinal, and (b) transverse. The corresponding XRD stress data for each measurement point is provided in similar marker shape and colour

The result of stress measurement by ICHD at 81.8 ± 7.4 MPa nominal stress is comparable to the expected stress and also to the results of XRD and ESPI. However, at higher value of nominal stress (i.e. 179.9 ± 7.6 MPa) the result of the ICHD was significantly different (≈ 50 MPa) from the expected stress, though it appeared to be converged towards the result of ESPI at depth of 0.3 mm.

The transverse stress component measured by different techniques (Fig. 6(b)) are all consistent with each other implying that all techniques provide relatively the same reading, despite of the fact that their measurement criteria are based on completely different principles. In both Fig. 6(a) and (b), it can be seen that the measured stress profiles obtained by the ICHD method are not originating from the surface; but at a depth of approximately 0.15 mm. This is the amount of material removed by grinding during surface preparation for strain gauge installation.

To quantitatively characterise the effect of grinding, during surface preparation for strain gauge installation, on the surface residual stress status, the surface of the four-point-bend sample used for comparison between different techniques were subjected to XRD stress measurements at a nominal stress condition of 81.8 ± 7.4 MPa. Figure 7 shows the results of these measurements for both longitudinal and transverse directions. As can be seen in Fig. 7(a), the measured longitudinal residual stress profile by XRD at the loaded condition before grinding was very close to the expected nominal stress, however, the results of stress measurements at the same positions after grinding shows significant magnitudes of compressive residual stress. This implies that the grinding process introduces mechanical damage into the surface. Similar trend can be seen for the measured stress in the transverse direction (Fig. 7(b)) showing that the stresses introduced by grinding are of similar magnitudes in both longitudinal and transverse directions.

Fig. 7

Comparison between surface residual stresses measured by XRD at y = 1 mm deflection, corresponding to 81.8 ± 7.4 MPa nominal stress before and after grinding for strain gauge installation, (a) longitudinal stress, and (b) transverse stress. The range of nominal stress calculated for y = 1 deflection condition (see Table 1) is provided as the transparent strip in (a) for the aid of comparison. The horizontal axis is corresponding to the 130 mm middle fibre of the four-point-bend specimen (i.e., h in Fig. 1) and the distance is calculated from the left to the right whereby the XRD stress measurements have taken place at each 10 mm

Figure 8 shows the plot of surface residual stress in the longitudinal direction for the additional sample in the as-received and four-point-bend loaded conditions. Similarly to the previous sample (Fig. 5(a)), the measured longitudinal residual stress in unloaded condition is very small, with some small local variations from point to point. Loading the strip to various nominal stresses has increased the measured surface residual stress, albeit with some local discrepancies at higher stress magnitudes. The slight scattering of the measured stresses at higher nominal loads could be due to non-uniformity in the thickness of the as-received sample. Since the measured residual stress magnitudes and distributions for the transverse direction were similar to those presented in Fig. 5(b), the data for this direction is not provided to prevent repetition. This sample was used to investigate the effect of drill diameter on the measured residual stress by ESPI.

Fig. 8

Measured longitudinal residual stress by XRD in the as-received condition and in four-point-bend fixture loaded to different levels of nominal stresses under different deflections. The ranges of nominal stresses calculated for each deflection condition (see Table 1) is provided as the transparent strips for the aid of comparison. The horizontal axis is corresponding to the 130 mm middle fibre of the four-point-bend specimen (i.e., h in Fig. 1) and the distance is calculated from the left to the right whereby the XRD stress measurements have taken place at each 10 mm

Figure 9(a), and (b) show the results of these comparisons respectively for the longitudinal and transverse directions at a nominal stress of 171.7 ± 7.5 MPa. Following the stress measurements by XRD, the ESPI stress measurements were carried out at the same locations (see Fig. 2(b)) using three drill diameters of 0.79 mm, 1.25 mm and 1.8 mm. The results show that the stresses measured by XRD are closely comparable with those measured by ESPI, disregarding the size of the drill. At positions where 0.79 mm and 1.25 mm drills were used, the residual stresses measured on the surface by both the XRD and ESPI are lower than the nominal stress by about 50 MPa. The reason for the discrepancy between the results of both measurement techniques with the nominal stress can be due to the initial state of stress in the material itself. As can be seen in Fig. 8, the initial residual stresses at these points measured by XRD were below the nominal stress prior to ESPI hole-drilling. Therefore, comparison between the results of ESPI with those of XRD shows that both measurement techniques are closely related.

Fig. 9

Comparison between the residual stresses on a standard four-point-bend sample loaded to a constant nominal stress of 171.7 ± 7.5 MPa, measured by XRD and ESPI based hole-drilling using drills of different diameters, (a) longitudinal stress, and (b) transverse stress. Note that the ESPI measurements are conducted to a depth of 60% of the drill diameter in each case

Discussion

The four-point-bend assembly has previously been used for loading specimens to specified levels of constant elastic stress for stress corrosion cracking experiments [4, 5, 32]. Previous studies showed the effectiveness of this assembly for applying stress with minimised uncertainties. The material used in this study was in a mill annealed condition and as such there was negligible level of stress in its longitudinal direction, making it ideal for the purpose of this study. The uncertainties of the measured strains for the as-received material in both directions were less than 10 MPa for all the XRD measurements. This is due to the relatively small grain size of the material (≈ 11 µm) as well as the low level of cold work in the as-received plate (i.e., mill annealed condition) in shown in Fig. 3. Usually the higher uncertainties are related to the smaller sampling population of the measured crystallographic planes in the coarser grain size microstructure. The EBSD maps collected from two orthogonal cross-sections, parallel and perpendicular to the RD (see Fig. 3(a) and (b)), do not show intragranular disorientations and sub-structures which are evidence of type II residual stress and cold work (i.e., strain) [8, 9]. Also, the IPF EBSD maps and the polefigures presented in Fig. 3 show no strong texture in the material, implying that there is no mechanical anisotropy and directional effect on the materials elastic properties.

The data obtained by XRD on different samples under various nominal loading conditions (see Figs. 5 and 8) prove that the XRD is sensitive enough to capture small changes in the nominal stress. For both samples the measured stresses have consistently increased with higher nominal stress. The small local variations that have been observed from point to point may be due to the existence of type II intergranular residual stresses. This suggests that there remain some residual stresses in the microstructure that are sufficient to cause variation in the measured strain from point to point; such residual stresses arise from strain incompatibilities with grain orientation and should be expected to exist throughout the microstructure [4, 5].

The ESPI based hole-drilling technique has been found to be a very accurate method of residual stress measurement, particularly to resolve near-surface stresses that are beyond the penetration depth of XRD and also become mechanically damaged for conventional strain gauge based hole-drilling method (i.e., ICHD). In fact, the results obtained by ESPI for the surface are all close to those of XRD and fall within the expected ranges of the applied nominal stresses (see Figs. 6 and 9). The ESPI technique is capable of capturing small changes in the nominal stress as similar as to the XRD. It can bridge the gap between the XRD technique, which is typically penetrating to 10–50 µm, depending on material, and ICHD method that is not able to provide information from the initial 200—300 µm distance from the surface. Additionally, the measurement time is typically only 25% of the time required for the conventional methods such as ICHD. Further, as opposed to the ICHD method, the ESPI based hold-drilling technique can easily be adjusted for measurements with drills of different sizes, ranging from 0.1 to 3.2 mm, by zooming-in or -out the objective camera. This means that for smaller drill diameters, the objective camera needs to be zoomed-in, which results in higher magnification images (i.e., smaller area for surface displacement measurements), and vice versa for larger drill diameters. Figure 9 showed that the stresses measured on a sample loaded to ≈ 170 MPa nominal stress using drills with different diameters are almost the same with the only difference that the smaller drills can provide measurements for shallower depth (i.e., 60% of the drill diameter). This flexibility is obviously not the case for ICHD since each drill diameter requires a certain type of strain gauge rosette which is not readily available. Moreover, the residual stress measurements by ICHD requires a certain flat area of the sample from which the measurement needs to be taken available for strain gauge installation which depending on the strain gauge size cannot typically be smaller than ≈ 1 cm². On the other hand, hole-drilling with ESPI is not as limited and measurements can be conducted on small areas and features such as weld ripples [20] that cannot be measured by strain gauge rosette hole-drilling otherwise.

The main reason behind the variation of the data measured by ICHD from the applied nominal stress on the surface (see Fig. 6) can be the mechanical damage caused by the grinding process during surface preparation for strain gauge installation (see Fig. 7). In addition to the mechanical damage, the grinding process typically removes approximately 100–200 µm material from the surface. This means that the information from the first 200 µm distance from the surface will be completely lost. Thereafter, the results obtained at the first few points of measurement (≈ 200 µm) are biased toward high magnitudes of compressive stresses that are induced into the surface during surface preparation, as can be clearly seen in Fig. 7. These observations imply that the ICHD method provides reasonable reading of the existing stress only from about ≈ 400 µm from the surface onward, although the measured values can be compromised by the mechanical damage.

To further evaluate the authenticity of the measured stresses with both hole-drilling methods as functions of depth, the generated through thickness stresses under different levels of deflection (i.e., nominal stress) in four-point-bend fixture, were analytically calculated using the relationship in (equation(2)).

$${\sigma_t} = \left( {\frac{t}{2} - \;{\Delta t}} \right)\frac{24Ey}{{3{H^2} - 4{A^2}}}$$

(2)

where ${\sigma_t}$ is the calculated stress at each depth, t is the strip’s thickness, ${\Delta t}$ is an arbitrary depth, E is the Young’s modulus of the material, y is the applied deflection in the four-point-bend fixture, H and A are the length of the strip and the distance between the inner and the outer support, respectively, similarly to those in (equation (1)). The calculated through thickness stresses at two deflection levels of y = 1 mm and y = 2.4 mm, equivalent to nominal stresses of 72.4 ± 7.4 MPa and 173.7 ± 7.6 MPa respectively (see Table 2), are shown in Fig. 10 along with the results of XRD and both hole-drilling stress measurement techniques in the longitudinal direction. Note that (equation (2)) evaluates the through thickness stresses in the longitudinal direction. Similarly, Fig. 11 shows the evaluated through thickness stress at y = 2.4 mm, equivalent to nominal stress of 173.7 ± 7.6 MPa, together with the results of XRD and ESPI hole-drilling stress measurements using drills of different diameters.

Fig. 10

Comparison between the results of XRD and two hole-drilling stress measurement techniques, in a four-point-bend beam sample loaded to 72.4 ± 7.4 MPa and 173.7 ± 7.6 MPa nominal stress (i.e., y = 1 mm and y = 2.4 mm, respectively), and the analytically evaluated through thickness stresses. The corresponding XRD stress data for each measurement point is provided in similar marker shape and colour

Fig. 11

Comparison between the results of XRD and ESPI hole-drilling stress measurements, using drills of different diameter, in a four-point-bend fixture loaded to 173.7 ± 7.6 MPa nominal stress (i.e., y = 2.4 mm deflection), and the analytically evaluated through thickness stress

At first sight, it ca be seen that the results of XRD at both nominal stresses are very close to those evaluated analytically based on (equation (2)) (see Fig. 10). The results of the ESPI based hole-drilling method is also very close to the calculated stresses with the exception of a small region just under the surface up to a depth of 200 µm. This can be due to the work-hardening and plastic deformation caused by hot rolling during manufacturing of the plate, which can also result in microstructural changes (e.g., work-induced martensite) leading to a different elastic property at or just below the surface. This depth damage is also evident from the stress measured for the transverse direction shown in Figs. 6(b) and 9(b). The results of ICHD method however, are not close to the analytically evaluated stress and nor to the results of other techniques (i.e., XRD and ESPI). Figure 11 further confirms the validity of XRD and ESPI based hole-drilling, using different drill diameters, and their tight proximity with the calculated stress. Accordingly, it can be concluded that both XRD and ESPI based hole-drilling techniques are very sensitive and accurate methods of surface and near surface residual stress measurements that can provide readings of stress with minimum uncertainty. However, the ICHD residual stress measurement method is associated with significant uncertainties resulting mainly from the surface preparation required for strain gauge installation, and care must be taken on the interpretation of the data especially when sensitive readings are necessary.

Conclusion

In this study, a standard four-point-bend fixture has been used to load samples to pre-defined levels of elastic stress. Three different techniques of surface and near-surface residual stress measurements, including XRD and two hold-drilling methods one based on ESPI and the other strain gauges rosette, were used for stress measurements. A comparison has been made between these techniques and the pre-defined nominal stresses applied by the standard fixture. The major findings of these measurements are concluded as follows:

• The XRD is capable of measuring stresses on standard samples with negligible uncertainties, and high sensitivity to small changes in the nominal stress.

• The ESPI based hole-drilling technique has been found to be a very sensitive and accurate method of residual stress measurements, capable of measuring near-surface residual strains that are beyond the penetration depth of XRD and cannot be measured by conventional strain gauges rosette based hole-drilling method.

• The strain gauges rosette based hole-drilling method is able to measure stresses comparable to the expected nominal stress on a standard sample; however, it is not able to obtain a reliable strain from the first ≈ 400 µm distance from the surface.

• The surface preparation procedure for strain gauge installation introduces significant damage into the surface, in form of compressive stress, whereby the introduced stresses make the results of the strain gauge based hole-drilling method biased with increased uncertainties from the actual existing stress profile.