Introduction

Coating, welding and additive manufacturing are key manufacturing processes in modern production lines and can be found across a wide field of technical applications. Especially the processing of metallic components is often followed by an inhomogeneous thermal heat input leading to the formation of residual stresses. The distribution and magnitude of the residual stresses play an important role for the correct design of the product and its manufacturing processes as residual stresses can have either a positive or a negative effect on the load-bearing capabilities (Ref 1). The formation of residual stresses during coating processes may result in cracks or even the delamination of the coating (Ref 2). Welding is mainly characterized by thermal distortion. Residual stresses can have a negative impact on the alternating load resistance. Similarly, additive manufacturing processes combine both aspects: a negative influence in form of thermal distortion as well as an unexpected component failure due to multiaxial stress formation (Ref 3, 4). There are various destructive and non-destructive methods for measuring residual stresses (Ref 5). Destructive methods are based on measuring the surface deformation of a workpiece after the removal of material, while non-destructive methods estimate the amount of residual stresses via the distortion of the crystal structure using diffraction methods. Endeavors for a cross-comparison between various methods have been made (Ref 6, 7). The used materials and the process technology have a great influence.

The materials used in this study were AlCu6Mn bulk material as well as an AlZn5.5MgCu coating on an S355J2 + N substrate. AlCu6Mn represents a high-strength aluminum alloy that is predominantly used in the aerospace industry (Ref 8, 9). Strengthening effects are achieved by segregating Al2Cu. AlCu6Mn is the focus of current research, particularly in additive manufacturing (Ref 9). One disadvantage is its tendency to form hot cracks during welding, which can also be caused by residual stress fields. AlZn5.5MgCu is another high-strength aluminum alloy. Current research is being conducted to produce hybrid materials by joining aluminum and steel for a lightweight design using pressure casting (Ref 10). In an approach to facilitate metallurgical bonding between aluminum and steel during pressure casting, AlZn5.5MgCu is deposited on steel by means of cold spraying.

There are several fundamental differences between the microstructure of the bulk material and the thermally sprayed coatings contains. The influences of these differences on the comparability of various residual stress measurement methods are one major aspect that needs to be examined. Therefore, the aim of this study is to investigate the requirements for a qualitative or quantitative comparison of various methods. Since components are exposed to various types of heat inputs during manufacturing, the effects of a unilateral as well as a uniform heat input on the residual stress state in the components are of interest.

Methods and Materials

Residual stresses in solid materials are quantified through calculation rather than direct measurement (Ref 11). In most cases, this calculation is based on measurable strains. Some methods, however, use different variables such as magnetic permeability (Ref 12). In general, residual stresses are divided into three orders (Ref 13). The residual stresses of the first order are macro-stresses. They are homogeneous over multiple grains. The residual stresses of the second and third orders, on the other hand, classify as micro-stresses. While the residual stresses of the second order are homogeneous over single grains, the residual stresses of the third order are inhomogeneous over smallest areas such as unit cells. For an appropriate assessment of the measured strain, knowledge of the measured volume and its microstructure are necessary. Therefore, the grain size of the investigated specimens was determined as the equivalent circular diameter using the area counting method described in ISO 643 (Ref 14). Next, the arithmetic average of the equivalent circular diameter was calculated from three independent micrographs per specimen. It was furthermore necessary to verify the reliability of the experimental data. This was done by comparing the results obtained from different methods. Two common methods to collect data on residual strain in metallic specimens are x-ray diffraction (XRD) and incremental hole-drilling (IHD).

Specimen Preparation

The bulk specimens B1 to B3 are made of AlCu6Mn. They were milled from one block of raw material and subsequently cut to an equal shape of 27 × 27 × 6 mm3. The milling of the surface on which the following measurements were conducted was performed in a single pass with the tool centre point outside of the specimen dimension. After milling, a local heat input was introduced in the centre of B2 using a plasma transferred arc (PTA) welding torch of the type Tetrix 350AC/DC from EWM AG (Germany). B3, on the other hand, was heat-treated for 2 h at T = 250 °C and cooled down slowly. The temperature–time parameter was chosen to achieve a stress relieving effect and simultaneously prevent annealing effects. For the local heat input, the plasma arc was focused on the centre of the specimen and burned for 5 s with a welding current of 10 A. For the coated specimen, an S355J2 + N substrate was cold sprayed with a coating of AlZn5.5MgCu using the Kinetics 8000 cold spray system from Oerlikon Metco (Switzerland). The process parameters are given in Table 1. AlZn5.5MgCu was used as a substitute for AlCu6Mn, which was not readily available as thermal spray powder. Both materials exhibit a similar strength and because the main phase of both alloys is aluminum, the general assertions of the comparison between the results of the two residual stress measurement methods are unaffected. The total dimensions of the coated specimen were 25 × 22 × 2.5 mm3, while the average thickness of the AlZn5.5MgCu coating was s = 140 µm. The differing dimensions used for the bulk and the coated specimens may lead to a quantitative deviation of the measured stress values, though there is no impact on the applicability of the residual stress measurement methods. In further residual stress calculations, the coating properties were assumed to be those of the bulk material, as more accurate data was not available.

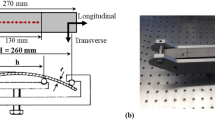
Table 1 Process parameters for cold spraying
Full size table

The position of the welding spot in B2 was projected to all specimens. Per specimen, three measurement points were allocated in one line with that projected welding spot perpendicular to the initial milling direction. First, XRD measurements were conducted as a non-destructive method. Afterward, IHD was conducted at the same measurement points. For the specimen C2, this procedure was carried out 18 months after the coating was produced in order to observe time-related change. Moreover, additional data were available. For one thing, there were data available from XRD measurements conducted immediately after cold spraying. These results will be referred to as C1. Additionally, there were stress values for C1 determined by IHD. Even though the drill step size for C1 was larger than for the IHD conducted in this study, the data were used to evaluate the effect of the natural aging of AlZn5.5MgCu on the residual stress state. In addition to a simplified description of the specimens, Fig. 1 shows the direction of the final milling step on the surface as well as the specimen coordinates Sx, Sy and Sz, which will be referred to in further explanations.

Fig. 1
figure 1

Schematic of the used specimen with specimen coordinate system S

Full size image

In the following, the specimens from the bulk material will be referred to as B1, B2 and B3, while the coated specimen will be referred to as C1 and C2. An overview of the specimens and their respective treatments is given in Table 2.

Table 2 Specimen overview
Full size table

X-ray Diffraction

X-ray diffraction patterns correlate directly with the lattice structure of the examined material. Bragg’s law defines the relation between the measured diffraction angle θ and the lattice spacing. Thus, a residual stress-induced increase or decrease in lattice spacing can be determined from shifts of the diffraction peak. The lattice strain εφ,ψ (Ref 15) is defined as:

$$\varepsilon_{\varphi ,\psi } = - \frac{1}{2}\cot \theta_{0} (2\theta_{\varphi ,\psi } - 2\theta_{0} )$$
(1)

with θ0 being the Bragg angle and θφ,ψ the measured diffraction angle at the specimen orientation φ and ψ.

For the residual stress analysis, the established sin2 ψ method was used. The coordinate systems necessary for the calculation of the residual stresses are shown in Fig. 2. The directions of the stresses σxx, σyy and σzz follow the specimen coordinates Sx, Sy and Sz, respectively. The coordinates Lx through Lz correspond to the diffracting lattice plane in which Lz is normal to that lattice plane. According to the theory of elasticity, when considering a general triaxial stress state, the lattice strain in Eq 1 can alternatively be described as

$$\varepsilon_{\varphi ,\psi } = \frac{1}{2}s_{2}^{{\{ hkl\} }} \left[ {\sigma_{\varphi } - \sigma_{zz} } \right]\sin^{2} \psi + \frac{1}{2}s_{2}^{{\{ hkl\} }} \tau_{\varphi } \sin (2\varphi ) + \left( {\frac{1}{2}s_{2}^{{\{ hkl\} }} + s_{1}^{{\{ hkl\} }} } \right)\sigma_{zz} + s_{1}^{{\{ hkl\} }} [\sigma_{xx} + \sigma_{yy} ]$$
(2)

with \(s_{2}^{{\{ hkl\} }}\) and \(s_{1}^{{\{ hkl\} }}\) being the x-ray elastic constants (XEC) of the diffracting lattice plane {hkl}. The stress components σφ and τφ along the direction Sφ are, respectively, defined as

$$\sigma_{\varphi } = \sigma_{xx} \cos^{2} \varphi + \sigma_{xy} \sin \left( {2\varphi } \right) + \sigma_{yy} \sin^{2} \varphi$$
(3)

and

$$\tau_{\varphi } = \sigma_{xz} \cos \varphi + \sigma_{yz} \sin \varphi$$
(4)
Fig. 2
figure 2

Coordinate systems on the specimen surface used for residual stress determination (Ref 16)

Full size image

To identify the general stress state within the measured volume, the specimen is rotated along the φR and ψR axes for a total of 91 independent specimen orientations. The positioning of the specimen in the goniometer is depicted in Fig. 3. The specimen is the only component that is moved during a measurement. The x-ray tube and the detector are stationary, thus ω is constant. When φ is kept constant and the specimen is rotated along the ψR axis, εφ,ψ can be plotted over sin2 ψ. An elliptical curve is formed for all stress states except a biaxial one, in which case a linear correlation is observed. The width of the ellipse is proportional to the value of τφ. A more detailed description of the sin2 ψ method is given in the literature (Ref 15,16,17). The stress state of a specimen is indicated by three normal stresses as well as three shear stresses. Those six stress values correlate with each other. Moreover, their values vary depending on the underlying coordinate system. By rotating the coordinate system the shear stresses can be set to 0 MPa. Here, the stress state is described by only three normal stresses σ1, σ2 and σ3, in this case called principal stresses. As the specimen coordinate system shown in Fig. 2 depends on the physical orientation of each specimen during the measurement, the principal stresses were used for a better comparison between the residual stress values determined by the XRD and IHD methods.

Fig. 3
figure 3

Goniometer for sin2 ψ method (Ref 16)

Full size image

Hauk (Ref 17) established an equation to calculate the penetration depth of x-rays using a material-specific mass attenuation coefficient determined by Thinh (Ref 18). The penetration depth is defined as the depth at which an intensity of 63% = 1 − 1/e of the signal is perceived. As the measurements were conducted within only a few micrometres from the surface, micro-stress in normal direction to the surface can usually be neglected. Only if the grain size is much smaller than the penetration depth, micro-stresses in normal direction need to be considered (Ref 16).

In this study, the XRD measurements were conducted using an XRD 3000 (GE Inspection Technologies GmbH, Hürth, Germany) with a Cu anode emitting a Kα1 wavelength of λKα1 = 0.15405 nm. The emitted radiation is parallelised in a point collimator with a diameter of 1 mm. A line detector was used to record the signal in an angle range of up to 7° with a resolution of 0.05°, which is adequate for a single peak. For the results to be meaningful, a sufficient number of counts per measurement needs to be taken above the background noise. For the current investigation, at least 1000 counts per measurement are suggested according to EN 15205 (Ref 16), which took a time of t = 300 s. The calibration of the system was performed using stress-free Ag powder with a grain fraction of − 53 µm and a purity of 99.99 wt.%. The calibration is classified as successful when all principal stresses are below 10 MPa, resulting in a measurement error of the XRD method of ± 10 MPa. The experimental setup is adopted from a previous XRD study (Ref 19). As aluminum is the main component of the investigated alloys, the aluminum phase was evaluated for all specimens. The used XEC for aluminum are given in Table 3 (Ref 20). The mean penetration depth according to Hauk (Ref 17) and Thinh (Ref 18) is 26.7 µm. The {331} plane was chosen to avoid a possible confusion of aluminum-induced reflections with copper-induced ones in AlCu6Mn. As recommended by the standard EN 15305 (Ref 16), multiple filters were used for signal post-processing. The filters used are Lorentz, polarization, absorption, background and Rachinger filters. The peak was fitted with a parabolic curve through 11 points.

Table 3 X-ray elastic constants (XEC) s1 and s2 for aluminum (Ref 20)
Full size table

Incremental Hole-Drilling

The implementation of the incremental hole-drilling method is based on measuring the elastic material relaxation by removing material through stepwise drilling (Ref 21). When material is removed from a stress field, the remaining material performs an elastic deformation to rearrange the residual stress field and achieve a new equilibrium. Measuring the deformation around the drilled hole allows the calculation of the underlying stresses before the removal of the material. In contrast to the XRD method, a greater measurement depth can be achieved (Ref 1).

While a common method is to measure the deformation via strain gauges arranged in a circle around the measuring point, the method applied in this article was based on the electronic speckle pattern interferometry (ESPI). Here, the displacement is captured by illuminating the measurement area with coherent laser light and analyzing the movement of a speckle pattern, using a digital high-resolution camera. The speckle pattern is generated by interferences, which result from the rough sample surface. This implies that the surface of the test specimen requires certain reflective properties for a proper speckle pattern to form. As the aluminum specimens B1 through B3 showed a highly reflective surface, a thin layer of varnish was applied to reduce the reflectivity.

All measurements were performed using a PRISM hole drilling system by Stresstech GmbH (Germany). The diameter of the TiN-coated drill was ddrill = 0.8 mm, which enables a measurement depth of up to 0.64 mm. The size of the digital measurement field is 640 × 480 px. The hole radius for the calculations was adjusted manually after performing pixel displacement measurements. The position of the circle in which calculations were conducted was always at the centre of the image at approximately 320 and 240 px. The hole radii varied between 59.4 and 72.4 px. To keep a constant zero-position, the running drill was moved to the sample surface in small increments until it lightly scratched the varnish. This drill position was then defined as zero position. Therefore, all measurements were performed without zero-depth-offset. The surface displacement is proportional to the phase change of the reference beam, which is shifted by 90°. A comparison of pixels with their neighboring pixels leads to a displacement information.

For the stress calculation a Young’s modulus of 73 GPa and a shear modulus of 27 GPa were estimated. The actual calculation of the residual stresses was performed through a measurement software by fitting the measured displacement map to displacement maps, generated by FEM simulations for a planar stress distribution. The mathematical equations for the FEM simulations as well as a detailed description of the calculation procedure, can be found in Ref 22. In general, the displacement data D(r, φ) from the ESPI measurement is first reduced to a smaller number of representative quantities by a Fourier transformation and subsequently weighted. The stress calculations follow the integration over an inner and outer integration radius. These two radii represent the areas most significant for surface displacement (Ref 22). The inner and outer integration radii were 2 × rdrill and 4 × rdrill while rdrill is the radius of the drill. The measurements were performed in 15 steps down to a depth of 0.15 mm. The reason for this was to gain information about the stress propagation along a certain depth and identify possible outliers, as a repetition of the measurements for statistical validation was not feasible at the same measurement point. The stress calculations were performed without regularisation. Outliers are caused by optical disturbance during the measurement. Furthermore, the measurement result may be affected, if the drill is worn-out or the measurement angles of the camera and the laser were calculated incorrectly. To prevent it from wearing out, the drill was replaced for every sample.

Results and Discussion

In Fig. 4, light microscope and SEM pictures of the investigated specimens are shown. All bulk specimens show a coarse-grained microstructure with Al2Cu segregations, which is typical for AlCu6Mn. The grains are oriented in the rolling direction of the raw material. The grain size of the bulk specimens can easily be detected using light microscopy. However, the grain size of the cold-sprayed coating C2 could only be determined via SEM. The average equivalent circular diameter of B1 was determined to 172 µm, while the values for B2 and B3 were determined to 195 and 202 µm respectively. The observed increase in the grain size in B2 and B3 compared to B1 is related to grain growth induced by heat input via PTA or heat treatment. The average equivalent circular diameter of C2 was determined to 1.8 µm.

Fig. 4
figure 4

Light microscope pictures of B1, B2, B3 and C2 (top, middle) and SEM pictures of B2 and C2 (bottom)

Full size image

The preferential direction of the grains in B1, B2 and B3 is a result of the rolled base material that was used in the production. This moreover led to the significantly different peak intensities that were measured by XRD within a single measuring point. For the bulk specimens, the values of the peak intensities depend on the specimen orientations ψ and φ. For the coating, on the other hand, all peak intensities have the same value at all ψ and φ orientations, as is depicted in Fig. 5. Since the grain size of the used bulk specimens is larger than 100 µm and the mean penetration depth of Cu radiation in aluminum-based materials is 26.7 µm, a biaxial state of micro-stress is assumed in the evaluation of the lattice distortion measured by XRD (Ref 16, 17). In the coating, however, a triaxial state of micro-stress must be considered, as the grain size of 1.8 µm is much smaller than the penetration depth of Cu radiation in aluminum-based materials. Using IHD, only biaxial distortions can be detected. For the stress calculation, the stress normal to the sample surface is therefore assumed to be σzz = 0 MPa, regardless of the grain size.

Fig. 5
figure 5

XRD graph of measurement point P3 of B1 (top) and C2 (bottom) at φ = 308.6°

Full size image

As von Mises principal stresses (σv,M) simplify a multiaxial stress state into an equivalent uniaxial stress state, they were used to compare XRD results among each other, see Fig. 6. The highest von Mises principal stresses were measured in B1 with decreased stress levels in B2 and even lower stress levels in B3. The thermal conductivity of aluminum-based materials is very high. Therefore, the plasma arc-induced heat in B2 is distributed rapidly throughout the entire specimen, leading to a specimen state resembling a homogenous heat treatment. Thus, the crucial difference between B2 and B3 is the total amount of induced heat. Both samples show stress relaxation. However, it is more prominent in the heat-treated specimen B3 as a larger amount of heat was induced in this specimen. In each of the bulk samples, the von Mises principal stresses show a trend from measurements P1 through P3 within each of the bulk samples. This is explained by the location of each of those measurement points relative to the initial milling direction during specimen preparation. The residual stress state at the specimen surface is determined by a superposition of cutting forces during milling (Ref 23). The cutting force components along all three spatial coordinates change for each new tool revolution and are repeated periodically. This leads to different residual stress states perpendicular to the milling direction at the specimen surface. Additionally, the residual stresses on the surface are asymmetrical to the PTA spot as during milling the tool centre point during milling was placed outside of the final specimen dimensions.

Fig. 6
figure 6

Calculated von Mises principal stresses σv,M of bulk specimens measured by XRD

Full size image

The total residual stress state in thermally sprayed coatings is a superposition of two stress components (Ref 24,25,26). The first stress component results from the deposition stress occurring during the spraying process. Because of the low temperature and high kinetic energy of particles during cold spraying, this stress component is compressive. This mechanism is referred to as shot peening. The second stress component originates from the cooling of the specimen after cold spraying to room temperature. The magnitude of this stress component depends on the thermal misfit of coating and substrate material (Ref 27). The thermal misfit is characterized by the difference of the coefficients of thermal expansion (CTE) of the used materials. Construction steel has a CTE of 12 × 10−6 K−1, while AlZn alloys have a CTE of 21 × 10−6 to 24 × 10−6 K−1 (Ref 28). As shown in Fig. 7, in the cold-sprayed coating the total residual stresses of all three spatial directions σ1, σ2 and σ3 are tensile stresses. Thus, the tensile stress component induced by the thermal misfit of the used materials is much larger than the compressive stress component induced during the spraying process. A similar observation was made by Suhonen et al. (Ref 29), who used cold spraying to deposit an aluminum-based powder on construction steel. The thermal contraction movement of each grain is constricted by adjacent grains in all three spatial directions. Against common expectation, the shot peening effect is weak for the used material and process temperature. The process temperature of Tprocess = 450 °C is relatively high compared to the solidus temperature of AlZn5.5MgCu of Tsolidus = 477 °C (Ref 30). This leads to a high plasticity of the particles during cold spraying. In addition, the impact of shot peening is less significant in the top layer of the coating, where the XRD measurements were conducted, as compared to the first layer. Further, over a period of 18 months of natural aging a stress relaxation by the factor of 5 was observed.

Fig. 7
figure 7

Stress relaxation in AlZn5.5MgCu from as-sprayed (C1) state to 18 months of natural aging (C2) measured by XRD

Full size image

The results of the residual stress measurements via IHD are presented in Fig. 8. B1 shows a similar stress distribution for all points up to a measurement depth of 50 µm. The residual stress level starts between 70 and 190 MPa, while it drops to about − 100 MPa at 50 µm for all three curves. From there, the level increases again to 150 MPa at the centre at P2 and remains stable at about 50 MPa at the edges in P1 and P3. The tensile stress on the surface is induced by thermal effects due to milling (Ref 31) during the specimen preparation. At higher depths, the tensile stress is superposed by compressive stress due to machining forces (Ref 31). Any stresses measured deeper than 80 µm are assumed to be related to the process history prior to this study. This assumption is in compliance with the depth profiles of residual stresses in milled aluminum workpieces reported in the literature (Ref 31).

Fig. 8
figure 8

Residual stress depth profiles of bulk specimens B1 through B3 for σ1 and σ2 by IHD

Full size image

During measurement P3, execution errors occurred in B2. The respective measurement data will not be considered in the further evaluation. For the measuring points P1 and P2 the distribution is similar. The variance, however, is slightly higher for the measurement at P2. The partially significant differences of measured residual stress values at the same depths at varying measurement points or per drilling step at a single measurement point suggests the detection of micro-stresses with IHD. This is contrary to the previous assumption that only macro-stresses can be detected using the hole-drilling method (Ref 6). In this study, the IHD depth resolution is defined as the ratio between drill steps dstep = 10 µm and average grain size dgrain. The lateral resolution is defined as the ratio between drill diameter ddrill = 800 µm and average grain size dgrain. These ratios are seen as a measure for the amount of analyzed grains per drill step as lower resolution values result in fewer grains in the measuring volume. Using the average equivalent circular diameters, which are determined in the micrographs in Fig. 4, the IHD depth resolution dstep/dgrain equals 0.058 in B1, 0.051 in B2 and 0.049 in B3. The lateral resolution ddrill/dgrain for B1, B2 and B3 equals 4.65, 4.10 and 3.96, respectively. Both resolutions decrease with an increasing grain size from B1 through B3. With just a few grains in the measured volume the stress state of each single grain has a significant impact on the total stress state of that measured volume. The correlation between depth resolution and micro-stress detection via IHD is further supported by the measurements in C1 and C2. The ratio for those measurements is larger than 5. Thus, a higher amount of grains is examined per drill step, resulting in smoother depth profiles of the macro-stresses. The graph of C2 in Fig. 9 shows a deviation from the relatively smooth depth profiles at depths of 110 µm at P1 and 140 µm at P2 and P3. This is assumed to be related to the interface between the coating and the substrate. The difference between those three measurements can be explained by a fluctuating coating thickness. In the graph of C1 in Fig. 9, however, there is no significant change in the residual stress when reaching the interface between the coating and the substrate. The deeper the tensile stress reaches into the surface, the lower it is. Eventually, it transitions into compressive stress in the lower layers of the coating. This progression of the residual stress is in accordance with the development of residual stresses during thermal spraying discussed elsewhere (Ref 24,25,26).

Fig. 9
figure 9

Residual stress depth profiles of coated specimens C1 and C2 for σ1 and σ2 by IHD. The dotted lines show the detected interface between the coating and the substrate. *Exact measurement position undefined

Full size image

In Fig. 10, values of the principal stress σ1 determined by IHD and XRD are shown for direct comparison. For the XRD results, a biaxial stress state is assumed for B1, B2 and B3, while for C1 and C2, a triaxial stress state has to be considered. The depicted depth of the XRD results is the mean penetration depth of 26.7 µm. In the IHD depth profile of B1, there is a considerable difference in the stress values for depths of 20 and 30 µm. The stresses by XRD show a similar magnitude. With a lower difference of stress values by IHD between the depths of 20 and 30 µm, XRD is able to replicate the stress value quantitatively as is observed in B2. While B3 is almost stress-free according to XRD, IHD measurements show low residual tensile stresses after heat treatment. Considering small differences in actual stress values between XRD and IHD, those methods can be compared quantitatively when micro-stresses are measured by IHD, which is the case in specimens B1, B2 and B3. This conclusion is not valid for C1 and C2, as a triaxial state of micro-stresses has to be considered (Ref 16, 17). Within the theoretical framework of biaxial state of micro-stresses, stress calculation from XRD measurement results in similar stress values to those determined by IHD. As, due to their low grain size, this framework is not applicable for C1 and C2, IHD is not suitable for a quantitative analysis of small-grained coatings produced by cold spraying. However, a qualitative analysis of the stress profile along the coating thickness can be conducted using IHD.

Fig. 10
figure 10

Comparison of determined values for σ1 in biaxial stress state by IHD and XRD. For C2, values of triaxial stress state are added. *Exact measurement position undefined

Full size image

Conclusion

Residual stress measurements have been successfully conducted using both the x-ray diffraction method and the incremental hole-drilling method combined with electronic speckle pattern interferometry. An aluminum-based bulk material as well as an aluminum-based coating deposited on construction steel via cold spraying were examined in this study. The effect that various heat inputs into bulk material have on the residual stress was investigated. Furthermore, the comparability of both methods was evaluated. The conclusions of this study are summarized as follows:

  • Residual micro-stresses determined by the XRD method and the hole-drilling method are comparable for a coarse-grained bulk material within the framework of a biaxial stress state.

  • IHD is not suited for a quantitative analysis of residual micro-stresses in fine-grained coatings deposited by means of cold spraying if the grain size is much lower than a single drill step. It is, however, possible to conduct a qualitative analysis of the stress development in depth direction.

  • Heat treatment has a relaxing effect on residual stress levels. A unidirectional heat input, e.g., in welding or additive manufacturing, into an aluminum-based material has a similar, but weaker effect compared to a homogeneous heat treatment.

  • Micro-stresses in coarse-grained materials can be measured via IHD using drilling steps smaller than the average grain size.

Further investigations will need to be conducted to figure out additional conditions for the comparability of XRD and IHD. Another commonly used method for measuring residual stress in thermally sprayed coatings is the curvature method, determining residual stresses by measuring substrate curvature change during the spray process. Thus, for thermally sprayed coatings, comparative investigations of the curvature method and XRD or IHD should be addressed as well.