Introduction

Manufacturing of metal components often involves changing stress and strain states in the material during the forming process (e.g., shear and plane strain tension at deep-drawing). Changes in the stress states lead to non-linear strain-paths in the material and their effects need to be considered in manufacturing. The non-linear strain-path not only affects the failure of the material [1], but also affects its yield strength. Depending on the type of strain-path change, the yield stress might decrease (load reversal) or increase (orthogonal strain-path change) [2]. The effect of reduced yield stress after load reversal is known as Bauschinger effect and an increased yield stress after orthogonal strain-path change is often referred to as cross-hardening.

Different theories for the explanation of cross-hardening on the microstructural level exist. A widely accepted explanation is based on the fact that a given monotonic strain-path causes a characteristic pattern of dislocation accumulations, called dense dislocation walls [3]. An orthogonal strain-path change then activates new glide systems. The dense dislocation walls from previous monotonic loading are then a barrier which results in a stress overshoot on the macroscopic scale [2]. This is referred to as cross-hardening. With further loading the previous dislocation accumulations are dissolved and a new pattern of dislocation accumulation, specific for the new loading path, establishes. The cross-hardening effect has been observed for sheet metals with body-centered cubic (bcc) crystal lattice [4] and face-centered cubic (fcc) crystal lattice [5]. However, not all metals with such lattice show cross-hardening. For example, dual-phase steels with their ferritic and martensite phases, both bcc, have been reported to show no cross-hardening at all [6]. Based on these reports one could conclude, that an ideal condition for cross-hardening is the initially unhindered mobility of dislocations within the grain. This means, a) that within a grain, which experienced deformation, a change of the active glide systems is to occur with subsequent deformation and, b) that dislocation glide within a grain is not hindered by imperfections like carbides or grain boundaries. The latter could be achieved if the microstructure:

  • is single-phase

  • has large average grain size

  • small amount of carbon or other alloying elements, which might lead to additional phases or precipitates

Yet, other works have questioned the importance of dense dislocation walls on cross-hardening effect and claim a greater importance of texture evolution [7].

The cross-hardening may be interpreted as a special form of anisotropic hardening, which leads to a modification of the yield stress. The first model of that kind was introduced by Teodosiu and Hu [8]. Later different variants have been presented by Choi et al. [9] and Mánik et al. [10]. Another admissible interpretation postulates instead a distortion of the yield surface, due to the evolution of a Hill-type anisotropy tensor. Exemplary models have been introduced by Levkovitch and Svendsen [11] and Feigenbaum and Dafalias [12]. Recently, Barlat et al. [13] proposed a modification of the homogenous anisotropic hardening model (HAH) to capture cross-hardening effects. In subsequent work a more general modification was suggested to enhance the HAH model [14].

The occurrence of cross-hardening is characterized by a stress overshoot \(\Delta \sigma\) Fig. 1(a), which is typically maximum directly after the strain-path change [10]. A transient region follows afterwards, where the work hardening is either reduced, stagnating or even negative (i.e., softening occurs). Figure 1(b) illustrates the different behavior for a sequence of simple shear experiments in different orientations with respect to the initial loading direction for mild steel [2].

Fig. 1
figure 1

(a) Definition of stress overshoot ∆σ [10]. (b) Exemplary stress overshoot for a mild steel [2]

Full size image

It is sometimes observed for continued strain after the orthogonal strain-path change that the flow curve after strain-path changes becomes parallel to or coincides with the monotonic curve [15]. The amount of the stress overshoot and the length of the transient zone depend on the amount of prestrain [2].

While the choice of material is critical, whether cross-hardening may occur at all, the realization of the orthogonal strain-path change has significant influence as well. The magnitude of cross-hardening is maximum, when the strain-path change is abrupt (i.e. no gradual changes in the strain-path) [16] and when the subsequent strain states are perfectly orthogonal [2]. Schmitt et al. [17] proposed to measure the strain-path change of two subsequent and discrete load steps by

$$\kappa = \frac{{\Delta{\varvec{\varepsilon}}}_{1}^{\mathrm{pl}}:\Delta {{\varvec{\varepsilon}}}_{2}^{\mathrm{pl}}}{\Vert {\Delta{\varvec{\varepsilon}}}_{1}^{\mathrm{pl}}\Vert \Vert {\Delta{\varvec{\varepsilon}}}_{2}^{\mathrm{pl}}\Vert } .$$
(1)

Here, \({\Delta{\varvec{\varepsilon}}}_{i}^{\mathrm{pl}}\) is the tensor corresponding to the plastic strain increment of load step i. Thus, \(\kappa =1\) represents the monotonic case (i.e., linear strain-path). Values of 0 and -1 represent orthogonal strain-path change and a reversed strain-path, respectively.

For the experimental characterization of the cross-hardening in sheet metals, various two-step setups have been investigated to achieve an orthogonal strain-path change (Table 1). In general, one of the first observations of cross-hardening has been reported for a sequence of biaxial tension and uniaxial tension [18]. For the investigated steel the biaxial prestrain was below 0.2. Later setups mostly used uniaxial tensile or plane strain tensile tests. The prestrain in such approaches is limited to approximately 0.2 or less, as the strain field must be homogeneous to ensure the uniformity of the deformation in the second stage. Shear tests allow much higher uniform strains, but at high strains the shear deformation causes significant change of texture anisotropy. To minimize the influence of changing texture Bouvier et al. [24] recommend to limit the shear strain to 0.4, which roughly corresponds to an equivalent strain of 0.2. A common approach is to test a large specimen in the first step and mechanically separate miniaturized specimens under various angles for the second step. The existing tests have some disadvantages, which are namely:

  • trimming operations (e.g., machining, cutting) in the examination surface for subsequent specimens

  • limited to (equivalent) prestrain of approximately 0.2 when using shear, plane-strain or uniaxial tension in the first step

Material removal between subsequent tests might release residual stresses (both on the micro scale and the macro scale), or even change the material at the edge (e.g. laser-cutting). As these influences on cross-hardening are not quantified yet, it is advisable to avoid material removal. Larger strains are of interest for forming technologies, where significantly larger strains occur. Typically strains are as large as 1.0 true plastic strain in sheet metal forming and even 2.5 true plastic strain in sheet-bulk metal forming [26].

In general, two classes of tests can be distinguished. Setups combining different types of loading e.g., tension and shear (cf. Fig. 2(a)), require a suitable measure to compare the different type of strains. A frequent choice for the equivalent strain is the use of the isotropic von Mises model [27], or the simplified Hill model with a single \({r}_{n}\) value, assuming transversal isotropy [28]. Another physically motivated solution is to compare the dissipated plastic work [29]. The other class of tests are setups maintaining the loading type e.g., shear followed by shear, but changing the angle of loading (Fig. 2(b)). The necessary angle for an orthogonal strain-path change between tensile tests depends on the anisotropy [24]. As the sheet’s anisotropy varies with the orientation in the sheet plane and with the amount of plastic strain, a perfect orthogonal strain-path change, i.e. \(\kappa =0\), is cumbersome to obtain with this approach. In this regard it is noteworthy that the orthogonality of subsequent strains and not necessarily the orthogonality of the outer loads is relevant. E.g., loading of an isotropic sheet in uniaxial tension in rolling direction and subsequently in transverse direction would result in \(\kappa = -0.5\).

Fig. 2
figure 2

Tests for orthogonal strain-path changes. (a) Sequence of plane-strain tension and simple shear, [16]. (b) Sequence of simple shear in 0° and 45° rolling direction, [24]

Full size image

Besides the setup for the orthogonal strain-path change an additional monotonic test, the reference test, is required to determine any macroscopic cross-hardening effect. The reference test needs to enable large monotonic strain, such that the sum of prestrain and subsequent loading are covered.

This short review of existing tests and the demand of forming applications help to postulate requirements for an ideal characterization test for cross-hardening:

  1. 1.

    The change of strain path should be abrupt.

  2. 2.

    The change of strain path should be purely orthogonal.

  3. 3.

    The orthogonality should be accomplished independently of a material’s anisotropy.

  4. 4.

    Uniform strain distribution after the first test sequence is required.

  5. 5.

    The first load step should enable large strains.

  6. 6.

    A suitable measure to compare the subsequent testing stages is used.

  7. 7.

    Mechanical manipulation of the material should be avoided.

To the best knowledge of the authors there exists no test in the literature, which fulfills all the above listed requirements. This is especially the case for the large prestrains. But even for smaller prestrains there are only a few tests left, which can ensure purely orthogonal strain-path changes or do not require mechanical manipulation. The proposed setup aims to provide a test, which fulfills all the above requirements. The test is used to compare different steel grades directly to check the hypothesis on ideal conditions in the microstructure for occurrence of cross-hardening and explicitly quantify the amount of cross-hardening.

In the next section details of the investigated steel grades and the used conventional tests are introduced. Subsequently, the design of the new test setup with analyses justifying that the ideal conditions aimed at are met is presented. Afterwards the stress over-shoot and cross-hardening are presented and discussed.

Materials and Basic Test Setups

Initially the investigated materials and their most relevant characteristics are presented. This is followed by a brief presentation of used conventional experiments, the hydraulic bulge test and the in-plane torsion test.

Materials Tested

To clarify which materials are likely to show cross-hardening, different steel grades from different suppliers have been selected. The carbon content and the average grain size are determined as shown in Table 2. For better comparability the material specification according to VDA 239–100 [30] is provided. The mechanical properties have been determined by tensile tests (Table 3). The determination of the initial yield stress \({R}_{\mathrm{p}0.2}\) and the ultimate strength \({R}_{\mathrm{m}}\) are defined in EN-ISO standard 6892 [31]. The strain hardening exponent \(n\) is defined in EN-ISO standard 10275 [32] and describes the increase of true stress \(\sigma\) with the increase of true plastic strain \(\varepsilon\) between the initial yield stress \({R}_{\mathrm{p}0.2}\) and the end of uniform strain in the uniaxial tensile test by the equation \(\sigma =C\cdot {\varepsilon }^{n}\), where \(C\) is the so-called strength coefficient. The parameter \({r}_{i}\) relates the amount of strain in width and thickness direction in uniaxial tensile test with angle i with respect to the rolling direction. The normal anisotropy \({r}_{\mathrm{n}}=\frac{{r}_{0}+2{r}_{45}+{r}_{90}}{4}\) yields the average anisotropy, according to EN-ISO 10113 [33]. DC06, DC04 and DX56 are mild steels with an interstitial-free (IF) microstructure. All three grades are cold rolled and exhibit significant hardening (\(n\approx 0.25\)) as well as normal anisotropy (\({r}_{\mathrm{n}}\approx 2\)). They differ by the amount of carbon and their average grain sizes. DX56 has 0.16 weight percent carbon, which is the most among all investigated grades, while DC06 has the lowest amount of carbon content (0.02%). Cross-hardening has been reported for the latter by [6, 24, 34] (Fig. 13). The mechanical behavior of DC04 and DX56 have not been tested for orthogonal strain-path changes previously. Due to the same metallurgical concept as DC06 they are expected to exhibit cross-hardening. The larger grain sizes might cause a more severe stress overshoot especially for large prestrain, as larger grains allow the dislocations to form more pronounced dense dislocation walls. Yet, the increased carbon content might cause more intragranular imperfections which obstruct mobility of dislocations. Therefore, the magnitude of cross-hardening (compared to DC06) is of special interest.

Table 1 Selected setups for orthogonal strain-path change in sheet metals
Full size table
Table 2 Microstructural information and estimation of cross-hardening tendency
Full size table
Table 3 Mechanical properties from tensile tests
Full size table
Table 4 Summary of characterized cross-hardening ratio \({C}_{R}\) and key microstructure parameter of investigate steel grades (*DP600 evaluated at \({\varepsilon }_{\mathrm{p}}=0.3\) instead of \({\varepsilon }_{\mathrm{p}}=0.4\))
Full size table

In the class of modern high strength steels different candidates are considered. BS600 is a virtually single-phase bainitic steel, according to the supplier. It has a large grain size and moderate carbon content compared to mild steels. Differing from the other mild and high strength grades, the steel is hot rolled. Its potential for cross-hardening is unknown, but some cross-hardening might be expected, due to its large single-phase grains and moderate carbon content.

DP600 is an example of a dual-phase steel with ferritic and martensite phases. Deformation occurs mostly in the ferritic phase. Due to the dual-phase concept the average ferritic grain size is quite small (9 µm). Principally, a cross-hardening effect might be possible. Yet, no cross-hardening effect has been reported in literature, up to equivalent strain levels of 0.2. The novel setup enables characterization for larger prestrain. ZE800 is a micro-alloyed grade which has been recovery annealed. The moderate content of carbon (0.1%) and the largest grain-size of all investigated grades should enable occurrence of cross-hardening. Yet, its potential for cross-hardening is unknow so far. Microsections of the investigated grades are presented in Appendix A.

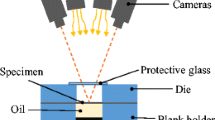
Prestrain Test: Hydraulic Bulge Test

The hydraulic bulge test is performed on a Zwick BUP1000 hydraulic testing machine. The strain field is measured optically during the test with a GOM Aramis 4 M digital imaging correlation (DIC) system. The DIC system uses discrete local fields, so-called facets which incorporate a finite number of pixels (here: 19 × 19 pixels) and a defined regular distance to each other (here: 16 pixels). Together with the resolution of the camera (here: 2358 × 1728 pixels) and the size of the measuring area (here: 155 mm × 115 mm) an equivalent strain gauge length can be determined which is approximately two times the distance of the facets [35]. The equivalent strain gauge length is 2 mm for the bulge test. The inner die diameter is \({D}_{\mathrm{Die}}=120\) mm. The velocity of the punch, which pushes the hydraulic oil into the test chamber is set 0.1 mm/s to ensure quasi-static loading of the sheet. The equivalent strain rate varies during the process, but remains below 0.01 1/s (Fig. 10). At the pole meridional stress \({\sigma }_{\theta }\) and circumferential stress \({\sigma }_{\varphi }\) are identical and referred to as biaxial stress \({\sigma }_{\mathrm{B}}\). The thickness strain \({\varepsilon }_{\mathrm{p}}\) and biaxial Cauchy stress \({\sigma }_{\mathrm{B}}\) are determined according to the EN-ISO 16808 standard [36]. Both, stress and strain are required to compute the specific work

$$w={\int }_{0}^{{t}_{\mathrm{Experiment}}}{\varvec{\sigma}}:{\varvec{D}}dt={\int }_{0}^{{\varepsilon }_{\mathrm{p}}}{\sigma }_{\mathrm{B}}d\varepsilon ,$$
(2)

where \({\varvec{D}}\) is the plastic rate of deformation tensor. The measured curvature radius \(R\) of the sheet and calculated work for all tests are given in Appendix B.

One requirement for an ideal characterization test to determine cross-hardening, is that the deformation in the gauge area after the first test is homogeneous. In fact, the gradient of strain in meridional direction (Fig. 3) does not influence the evaluation of the shear stress, which is always calculated for a specific radius. Thus, for the concept of bulge-torsion the requirement reduces to homogeneity of the strain in circumferential direction.

Fig. 3
figure 3

Major principal strains in meridional direction after bulge test for DC04

Full size image

The subsequent torsion after the bulge test is evaluated at \(r=10.5\) mm. At this radius the major principal strain is \({\varepsilon }_{1}=0.2895\pm 0.0019\) for DC04, which is considered as sufficiently homogenous.

In-Plane Torsion Test for Plane and Curved Sheets

The setup for testing of plane sheets is given in [38] and illustrated in (Fig. 4(a)). For testing of bulged specimen an analogous setup is used (Fig. 5). The clamping radii for the bulged specimen are \({r}_{\mathrm{I}}=10\) mm and \({r}_{\mathrm{O}}=91\) mm for the inner clamping and outer clamping, respectively.

Fig. 4
figure 4

(a) Principle of the in-plane torsion test [37]. (b) Stress computation for inclined sheets

Full size image
Fig. 5
figure 5

Scheme of proposed bulge-torsion test

Full size image

In the current experiments the shear strain \({\gamma }_{\mathrm{Torsion}}\) is measured using the Aramis 5M DIC system from GOM, with an equivalent strain gauge length of 0.2 mm. Details of the equipment and the post-processing parameters are presented in [35]. Typical strain fields are presented in Appendix D. For inclined sheets the shear stress at the torsion test is constant in the normal of the sheet direction [39]. Therefore, the radius of the point where the strain is measured and the radius of the corresponding cross-section for stress evaluation are no longer identical in the torsion test (Fig. 4(b)). The shear stress \({\tau }_{\varphi r}\) depends on the effective radius \({r}_{\mathrm{eff}}\)

$${\tau }_{\varphi r}= \frac{T}{2\cdot \pi \cdot {r}_{\mathrm{eff}}^{2}\cdot {t}_{\mathrm{eff}}} ,$$
(3)

where \(T\) is the measured torque on the inner clamping, while the effective radius and the sheet thickness in vertical direction are given as:

$${r}_{\mathrm{eff}}=r-\frac{1}{2}\cdot t\cdot \mathrm{sin}\left(\theta \right) \; \; {t}_{\mathrm{eff}}=\frac{t}{\mathrm{cos}(\theta )}$$
(4)

In both equations the sheet thickness t after the bulge test is calculated from the measured sheet thickness before the bulge test and the obtained strain by DIC in the bulge test. For the largest evaluation radius \(r=10.5\) mm and the smallest curvature radius of the sheet \(R=65\) mm the corresponding angle \(\theta =9.4^\circ\). The above equations have been validated for angles up to at least 35°.

$$w={\int }_{0}^{{t}_{\mathrm{Experiment}}}{\varvec{\sigma}}:{\varvec{D}} \; dt={\int }_{0}^{{\gamma }_{\mathrm{Torsion}}}{\tau }_{\varphi r}d\gamma$$
(5)

The torsion of the curved sheets is usually evaluated at \(r=10.5\) mm, only for prestrains above 0.4 the evaluation radius is changed to \(r=10.4\) mm. With increasing distance from the inner clamping, the detection quality of DIC pattern is improved. Yet, the amount of deformation decreases. Both distances have a sufficient quality for evaluation. The influence of different evaluation radii on the stress–strain curve is given in Appendix C. The uncertainty in the shear stress calculation is below 0.35% for all investigated cases [40]. From the Cauchy shear stress \({\tau }_{\varphi r}\) and the shear strain \({\gamma }_{\mathrm{Torsion}}\) the specific work \(w\) is determined.

Design of New Test

First, the concept of the new proposed bulge-torsion test (BTT) is introduced. Then, orthogonality of the strain sequence is analyzed and modifications for the in-plane torsion of curved sheets are presented. Afterwards the procedure for cross-hardening analysis is described. Finally, influences on the determination of stress and strain are investigated and the advantages and limitations of the test are discussed.

Concept of the Bulge-Torsion Test

The proposed experiment involves two steps (Fig. 5). In the first step a conventional bulge test is conducted until a given pole height is reached. In the second step the pre-bulged specimen is loaded with coaxial torsion with respect to the rotational axis of the specimen, analogous to the classic in-plane torsion test in the previous section. The general idea was presented in [41] by the authors.

For the analysis of the proposed experiment, a spherical coordinate system with the unit vectors \({{\varvec{e}}}_{r},{{\varvec{e}}}_{\theta }, {{\varvec{e}}}_{\varphi }\) is used. Here, \(r\) is the radial distance from the center. For an ideal sphere, the thickness direction of the sphere is parallel to \({e}_{r}\). During the hydraulic bulge test. Only \({\sigma }_{\theta }\) and \({\sigma }_{\varphi }\) differ from zero. According to the Levy–Mises flow rule the deviatoric Cauchy stress \({\sigma }_{ij}^{^{\prime}}\) is directly proportional to the rate of plastic strain. Thus:

$${D}_{\theta \theta }\ne 0; \; {D}_{\varphi \varphi }\ne 0; \; {D}_{rr}\ne 0$$
(6)

where \({D}_{ij}\) is the rate of deformation tensor. In the subsequent step, the semi-hemispherical sheet is loaded in torsion. For the given setup the shear strain is constant in normal direction to the surface [39]. Thus, the only non-zero stresses are \({\tau }_{\theta \varphi }={\tau }_{\varphi \theta }\). The resulting directions of plastic strain rates are:

$${D}_{\theta \varphi }={D}_{\varphi \theta }\ne 0$$
(7)

Consequently, the scalar product of \({D}_{ij, \mathrm{bulge}}\) with \({D}_{ij,\mathrm{ torsion}}\) is zero, independent of the sheet’s plastic anisotropy. Due to the proportional loading in the bulge test and the torsion test, also the strain increments \({\Delta{\varvec{\varepsilon}}}_{\mathrm{bulge}}^{\mathrm{pl}}\) and \({\Delta{\varvec{\varepsilon}}}_{\mathrm{torsion}}^{\mathrm{pl}}\) are parallel to \({D}_{ij, \mathrm{bulge}}\) with \({D}_{ij,\mathrm{ torsion}}\), respectively. Hence, according to (equation (1)) it is expected to achieve ideal orthogonal loading (\(\kappa =0\)).

The bulge test is performed as described in the previous section without any modification of the conventional setup. The subsequent torsion test is implemented in the setup of the classic in-plane torsion test for plane sheets, with the following modifications for the curved sheets. The outer clamps are replaced by guides (Fig. 6). The upper and lower inner clamps are replaced by sets of adjusted inlays for the upper and lower clamps to transmit the torque through the pre-bulged sheet (Fig. 7(a)). Ideally, the radius of the inner clamp matches exactly the radius of the bulged sheet.

Fig. 6
figure 6

Integration of curved specimen at the in-plane torsion test

Full size image
Fig. 7
figure 7

(a) Concept of clamp design and definition of maximum height deviation between two curvatures. (b) Set of clamping inlays with respective curvature radius. (c) Exemplary topography of upper and lower clamp determined by confocal microscopy

Full size image

However, this would require an infinite number of clamps. Therefore, a finite number of clamps with discrete levels of curvature are chosen, such that the vertical difference \(\Delta h\) at the outermost point of the clamps surface to the next larger/smaller curvature radius is lower than 0.08 mm. Consequently, six clamping sets have been designed. In order to compensate the sheet thickness, the lower clamps have been designed with 1 mm less curvature radius than the corresponding upper clamp (Fig. 7(b)). The curved clamp surfaces are designed with grooves to increase the transmissible torque (Fig. 7(c)).

The strains on the sheets are measured via DIC. After the bulge test and before the torsion test the sprayed DIC pattern is removed and re-applied. This is necessary due to the different measuring volumes.

Analysis Procedure

The determination of a cross-hardening effect requires the comparison of the stress after the orthogonal strain-path change with a monotonic reference stress. Both, the bulge-torsion test (after bulge test) and the in-plane torsion test (monotonic torsion) are simple shear tests. Therefore, the absolute shear stress of both can be directly compared. For the shear strain this is not permissible, as the biaxial tension has caused some (intended) prestrain. Both loads can be compared by the specific work \(w\) (equation (2) and (5)) Thus, the shear-stress of the bulge-torsion test is shifted by the specific work applied during the hydraulic bulge test and can then be compared to the monotonic shear test (Fig. 8(a)). Differing from the previous definition of \(\Delta \sigma\) (cf. Fig. 1(a)) the positive difference between the shear stress of bulge-torsion test and in-plane torsion test at the same specific work \({w}^{*}\) defines the amount of shear stress overshoot

Fig. 8
figure 8

Determination of orthogonal strain-path change effects. (a) Stress overshoot, (b) cross-hardening (CH)

Full size image
$${\sigma }_{\mathrm{CH}}({w}^{*})={\sigma }_{\mathrm{bulge}-\mathrm{torsion}}({w}^{*})-{\sigma }_{\mathrm{in}-\mathrm{plane torsion}}({w}^{*}).$$
(8)

In general, the hardening rate after an orthogonal strain-path change is reduced, compared to the monotonic hardening rate. Therefore, \({\sigma }_{\mathrm{CH}}\) tends to decrease with further deformation. The stress overshoot for a given specific work \({\sigma }_{\mathrm{CH}}({w}^{*})\) may be normalized by the reference stress of the in-plane torsion test at identical specific work \({w}^{*}\) (Fig. 8(b)), which gives the cross-hardening ratio

$${C}_{\mathrm{R}}\left({w}^{*}\right)=\frac{{\sigma }_{\mathrm{CH}}\left({w}^{*}\right)}{{\sigma }_{\mathrm{in}-\mathrm{plane torsion}}\left({w}^{*}\right)}\cdot 100\mathrm{\%}.$$
(9)

In case of no cross-hardening the \({C}_{\mathrm{R}}\) is 0. The black curve in (Fig. 8(b)) represents the evolution of \({C}_{R}\) after the strain-path change and is calculated as the average of all tests for specific prestrain. The maximum value of that evolution is indicated by a red diamond. The corresponding specific work \({w}_{\mathrm{MaxCH}}\) is indicated in Fig. 8. The grey horizontal bar represents the variation of specific work for a specific prestrain, while the vertical bar represents the scatter of the maximum cross-hardening of the tests for specific prestrain.

With further deformation the stress overshoot \({\sigma }_{\mathrm{CH}}\) and hence the cross-hardening ratio \({C}_{R}\) decreases after a single strain-path change has occurred. A possible way to characterize the transient characteristic is to evaluate the change of \({C}_{R}\) after a certain amount of deformation. The amount should be large enough to cover significant deformation, but also small enough that it is also applicable to large prestrains, where only little formability is left. Thus, 20% of the specific work at maximum cross-hardening \({w}_{\mathrm{MaxCH}}\) is chosen (i.e., 1.2 \({w}_{\mathrm{MaxCH}}\)). The corresponding \({C}_{R}\) at 1.2 \({w}_{\mathrm{MaxCH}}\) is marked with a red dot (Fig. 8(b)).

Analysis of the New Setup

As the bulge-torsion test setup aims to identify isolated changes of yield stress due to an orthogonal strain-path change, appropriate care must be taken to exclude changes in the yield stress by other reasons. Therefore, the influence on the yield stress by imperfect clamping conditions, strain rates and hydrostatic pressure in the tests is investigated. Finally, the overall advantages and limitations of the proposed setup are discussed.

Clamping of Curved Sheets

In practice, a curved sheet may not be tested with clamps of identical curvature. The deviation of the curvature between clamps and sheet might induce additional stress and strain, compared to the torsion of plane sheets. The superposed stress might affect the yield stress and thus, the necessary torque for in-plane shearing, compared to the torsion of plane sheets. This scenario has been investigated with an implicit 3D Finite-Element (FE) analysis. A 2.0 mm thick sheet with elastic–plastic behavior similar to DC04 has been modelled with 0.2 mm large elements. The sheet was chosen to have a curvature of \({R}_{\mathrm{Sheet}}=140\) mm on the upper surface (Fig. 9(a)). The tools have been modelled with the same curvature (\({R}_{\mathrm{Tool}}=140\) mm) and the next larger curvature of the manufactured clamps (\({R}_{\mathrm{Tool}}=110\) mm). In both cases the clamping force has been set to 100 kN (as in the experiments). After the clamping force is applied, the sheet is rotated by the same amount for both configurations.

Fig. 9
figure 9

(a) Setup for investigation of curvature deviations at clamping on the shear stress. (b) Torque at rotation for different clamping curvatures

Full size image

The evolution of torque shows a deviation of less than 0.16% (Fig. 9(b)). Thus, it is reasonable to assume, that a mismatch of the curvature radii between sheet and clamping tools has a negligible influence on the stress calculation. It is concluded from this analysis that the influence of the inner clamping on the torque is negligible for all clamps because the change of height to the next larger/smaller curvature \(\Delta h\) is constant and less than 0.08 mm (cf. Fig. 7).

Strain Rate and Viscous Effects

Although all torsion tests have been performed at the constant rotation speed of 3.3°/min, the effective strain rate is varying. The strain rate depends on the angular velocity, but also on the radial position r on the specimen and the hardening rate of the material. As the hardening rate is expected to vary in the tests, the strain rate has been analyzed for DC04 for the monotonic torsion and the torsion after bulge for different prestrains from the bulge test (Fig. 10). All strain rates have been calculated as the ratio of von Mises strain increment and the time increment. For the monotonic torsion the strain rate starts at 0.005 1/s and then mildly increases to 0.006 1/s at a plastic strain of 0.6. For the bulge-torsion the strain rate starts between 0.004 1/s and 0.006 1/s and decreases with continued deformation. Thus, both torsion tests have approximately the same strain rate at the beginning of deformation. The strain rate of the bulge test has an almost linear increase up to 0.005 1/s (Fig. 10(b)). Due to the chosen test parameters the differences in the strain rates are approximately the same (until hardening stagnation). According to the work of Larour et al. [42] a factor of 2 in the strainrate would increase the yield stress less than 3% after 0.1 prestrain in mild steel and significantly less for the high strength steels. The EN-ISO 6892–1 standard [31] allows strain rates up to 0.008 1/s for the determination of the tensile strength under quasi-static conditions. Therefore, it is also concluded that the tests are quasi-static.

Fig. 10
figure 10

Strain rate investigation for (a) in-plane torsions tests and (b) hydraulic bulge test

Full size image

The dense dislocation walls created during the prestrain test may partially recover afterwards. Experiments by Manik et al. [10] with commercially pure aluminum for intervals from several minutes to an entire year demonstrate that the stress overshoot decreases by approximately 20%. However, this decrease seems to follow an exponential function. Thus, the decrease in overshoot is strongest during the first minutes after the prestrain test. The interval of the tests for the proposed setup has been between at least 2 h and 3 weeks.

Hydrostatic Pressure Analysis

Although, it is very common to assume that the hydrostatic pressure has no influence on the yield stress, a minor influence for steels has been reported [43]. However, the yield stress in shear tests of plane and curved sheets is not affected by the pressure dependency because there is no hydrostatic pressure in shear. In the current case the stress overshoot is evaluated based on the comparison of tests involving a strain-path change in shear with a monotonic shear test. Yet, during the bulge test significant hydrostatic pressure \({\sigma }_{\mathrm{h}}=\frac{2}{3}{\sigma }_{\mathrm{B}}\) occurs. This might have an effect on the yield stress in bulge. Experimental work by Bridgman [44] has shown that the yield stress is only affected instantaneously by the hydrostatic pressure. After the forming operation the effect is no longer detectable.

Advantages of the New Bulge-Torsion Test

The reference test for the proposed setup is the conventional in-plane torsion test. The proposed bulge-torsion test combines biaxial tension applied by hydraulic bulge test and shear applied by in-plane torsion test at the curved sheet. Thus, large plastic strain can be applied in the first step. Equivalent prestrains up to 0.6 have been realized for the investigated grades with the current setups. In circumferential direction the strain is almost uniform. The concept of the bulge-torsion test does not require a mechanical trimming of the specimen between the loading steps. Therefore, the stress state after the application of the prestrain is not modified and no plastic strain or additional work-hardening is introduced due to machining operations. For comparison of shear and biaxial load the specific work is calculated, thus no constitutive assumption is required. The strain sequence from biaxial tension to simple shear ensures always an exactly orthogonal strain-path change. Due to the discrete steps the strain-path change is also abrupt. Finally, in the hydraulic bulge test and the in-plane torsion test stress and strain are averaged over the circumference. Therefore, integral measures are obtained. Consequently, the determined cross-hardening is isolated from the influence of anisotropic yield stresses.

Disadvantages and Limitations

Beside the advantages, the design of the setup has also some drawbacks.

Although mentioned previously as an advantage (from the forming technology point of view), one could argue that averaging material anisotropy in the torsion test is a disadvantage. Anisotropic materials may exhibit different amount of plastic work over the circumference. However, the reproducibility of the results is not affected due to the averaging over the circumference.

The determination of the biaxial stress in the bulge test following the ISO standard introduces some error. Min et al. [45] have shown that the error in the stress is as large as 3%. This is a considerable uncertainty for the determination of the cross-hardening effect. Yet, this approach has been chosen, as it is a well-established procedure.

The high gradient of strain at the inner clamping of torsion test is a challenge for the DIC evaluation. Traphöner et al. [35] revealed that the strain will be overestimated. For DC04 the error is less than 0.5%. However, this considers only the strain and not the stress. Therefore, the amount of cross-hardening is not affected.

It is not possible to determine the strain rate a priori in the in-plane torsion test for a specific test. Thus, an iterative approach was chosen to obtain a pre-defined value of the strain rate. Another aspect to consider is to obtain the desired curvature in the bulge test. A scatter up to \(\Delta \varepsilon =0.05\) was observed for different test aiming at identical prestrains. A better accuracy cannot be obtained because the starting pressure in the hydraulic bulge test is determined by the oil level before the test, which is adjusted by the operator manually.

Results and Discussion

The results of the bulge-torsion test (i.e., the stress overshoot and cross-hardening) are presented for the DC06 steel grade first. On the basis of these results, possible uncertainties and scatter are discussed. This is followed by a comparison with results for cross-hardening obtained for this grade in previous works. Afterwards the results of bulge-torsion test are presented for the remaining grades.

Stress Overshoot and Cross-Hardening for DC06

The bulge-torsion test produces the typical instantaneous stress overshoot which was expected for DC06 (Fig. 11(a)). After further work the shear stress approaches the monotonic yield stress. For the large prestrain of 0.4 the specimen failed before the yield stress reached the monotonic curve again. The absolute value of the stress overshoot \({\sigma }_{\mathrm{CH}}\) increases with the amount of prestrain. Not only the absolute stress difference increases (Fig. 11(b)), but also the cross-hardening ratio \({C}_{R}\) defined in (equation (9)). Small scatter in the determination of the shear stress has a large impact on the determined level of cross-hardening ratio. While the shear stress of bulge-torsion test curves has only a scatter of 2% (5 MPa/248 MPa) at \({\varepsilon }_{\mathrm{p}}=0.2\), the cross-hardening ratio \({C}_{R}\) varies relatively by 29% (between 7% and 9.5%). The analysis is based on 5 repetitions at \({\varepsilon }_{\mathrm{p}}=0.2\) and \({\varepsilon }_{\mathrm{p}}=0.4\), and 4 repetitions at \({\varepsilon }_{\mathrm{p}}=0.1\). The cross-hardening ratio \({C}_{R}\) decreases monotonically with further deformation. The amount of cross-hardening after an additional 20% of specific work based on the previously performed work during the bulge test reveals that the rate is constant. The cross-hardening ratio \({C}_{R}\) reduces to 85% and 86% of the initial, maximum cross-hardening for \({\varepsilon }_{\mathrm{p}}=0.1\) and \({\varepsilon }_{\mathrm{p}}=0.4\), respectively. Due to the increase of yield stress at larger strains, the amount of specific work also increases, thus the rate of decrease decreases in (Fig. 11(b)).

Fig. 11
figure 11

Results of novel bulge-torsion Test for DC06. (a) Stress overshoot after orthogonal strain-path change. The parameter \({n}_{\mathrm{s}}\) specifies the number of samples. (b) Cross-hardening evolution

Full size image

Comparison with Literature

The evaluation of stress overshoot and cross-hardening ratio by the performed specific work is not an intuitive measure. This is true especially, if the results should be used in forming operations with significant hardening. Therefore, it is desirable to evaluate the test in terms of an equivalent strain. Another reason is the ability to compare the results to other tests in the literature with different stress states.

The choice of von Mises equivalent strain shows a similar behavior for the stress overshoot (Fig. 12(a)) as the evaluation with the specific work. Yet, the analysis of cross-hardening ratio reveals differences (Fig. 12(b)). The cross-hardening ratios evaluated with the equivalent strain are between 5% larger (for \({\varepsilon }_{\mathrm{p}}=0.1\)) and 31% larger (for \({\varepsilon }_{\mathrm{p}}=0.4\)). Therefore, the evaluation with equivalent strain is feasible for a rough estimation of cross-hardening, but not for its exact determination.

Fig. 12
figure 12

Results of novel bulge-torsion Test evaluated with equivalent measures. (a) Stress overshoot of DC06 after orthogonal strain-path change. (b) Cross-hardening evolution of DC06

Full size image

In previous works focusing on the mechanical response of DC06 after an orthogonal strain-path change (Fig. 13) the amount of stress overshoot or cross-hardening was not quantified. Therefore, the published stress–strain curves have been re-evaluated. Due to the different stress states and the unknown amount of specific work for prestrain-step the evaluation is done with equivalent von Mises strain. Bouvier et al. [24] performed simple shear tests in the rolling direction (0°) and subsequent orthogonal tests at 45° with respect to the rolling direction for a FeP06 steel grade, which is very similar to DC06. The prestrain in 0° was applied up to 0.09 and 0.17 equivalent strain. The shear stress in 45° direction was about 5% and 4% higher than for the monotonic shear stress. Haddadi et al. [6] have tested DC06 in uniaxial tension up to 0.1 and 0.2 true strain and subsequently cut shear specimen for shear tests. The \({C}_{R}\) has been identified to almost 10% and 7%, respectively. Wang et al. [34] loaded DC06 in plane-strain tension up to an equivalent strain of 0.12. Subsequent shear stress was about 13% higher than for the monotonic case.

Fig. 13
figure 13

Comparison of bulge-torsion test results for DC06 with experiments from literature. All tests evaluated with equivalent von Mises strain

Full size image

The results from literature reveal a \({C}_{R}\) between 5 and 13% at 0.1 prestrain for specific directions. For the same prestrain the bulge-torsion test evaluated with von Mises strain yields a \({C}_{R}\) of about 8%. The cross-hardening determined with the new proposed bulge-torsion test is in the range of observed cross-hardening in literature. But as shown previously in this section, the evaluation with equivalent strain causes significant deviation from the evaluation with specific work. For DC06 the \({C}_{R}\) determined based on the equivalent strain is up to 1/3 different from the \({C}_{R}\) determined based on the specific work.

The proposed bulge-torsion test reveals an increasing maximum \({C}_{R}\) with increasing prestrain, which is in accordance to experimental observations and microstructural explanations of Rauch and Schmitt [2].

Results for Other Steels

For DC04 (Fig. 14) prestrains up to 0.6 have been realized. In case the remaining formability after the prestrain and strain-path change is sufficiently large, the yield curves of most experiments meet the monotonic curve (Fig. 14(a)). For the prestrain of 0.4 the subsequent yield curve converges to the monotonic curve. For the strain-path change after 0.6 prestrain the tests were stopped, when the torque had decreased significantly, as this indicates failure of the specimen. The cross-hardening increases from about 6% for small prestrains up to about 11% for large prestrains (Fig. 14(b)). After an additional 20% specific work the \({C}_{R}\) reduces to 85% and 86% of its initial, maximum \({C}_{R}\) for \({\varepsilon }_{\mathrm{p}}=0.1\) and \({\varepsilon }_{\mathrm{p}}=0.4\), respectively (cf. red dots in Fig. 14(b)). This is identical to the values for DC06.

Fig. 14
figure 14

Results of novel bulge-torsion Test for DC04. (a) Stress overshoot after orthogonal strain-path change. The parameter \({n}_{\mathrm{s}}\) specifies the number of samples. (b) Cross-hardening evolution

Full size image

For the DX56 steel grade (Fig. 15) the stress overshoot seems to look similar to the previous DC grades (Fig. 15(a)), but analysis of cross-hardening reveals that the maximum \({C}_{R}\) is about 7% for prestrain of 0.1 and 0.4 (Fig. 15(b)). Thus, it seems that the cross-hardening might be independent of the amount of prestrain. After additional 20% specific work the \({C}_{R}\) reduces to 78% of its initial, maximum value for \({\varepsilon }_{\mathrm{p}}=0.1\), which is significantly lower than for the DC grades. The determination of the reduction at \({\varepsilon }_{\mathrm{p}}=0.4\) was not possible, due to prior failure of the specimens in the bulge-torsion test.

Fig. 15
figure 15

Results of novel bulge-torsion Test for DX56. (a) Stress overshoot of after orthogonal strain-path change. The parameter \({n}_{\mathrm{s}}\) specifies the number of samples. (b) Cross-hardening evolution

Full size image

For the high strength grades BS600 and ZE800 (Fig. 16) no stress overshoot is observed. Thus, no cross-hardening is determined. The absence of the stress overshoot for the BS600 may be explained with its special constitutive phase. The bainite phase is a composite of ferrite and cementite. The distribution of cementite might impede the formation of necessary characteristic patterns of dense dislocation walls during the monotonic deformation (cf. Appendix A).

Fig. 16
figure 16

Results of novel bulge-torsion Test for (a) BS600 and (b) ZE800. The parameter \({n}_{\mathrm{s}}\) specifies the number of samples

Full size image

For DP600 (Fig. 17(a)) the stress overshoot is atypical. The stress exceeds the monotonic reference stress and shows regular hardening behavior as in the monotonic case. Thus, the absolute stress overshoot \({\sigma }_{\mathrm{CH}}\) seems to be constant with further deformation. The absence of the typical softening after the stress overshoot is explained by a modified disintegration of the characteristic dense dislocation walls without micro shear-bands [46]. Analysis of the cross-hardening reveals that the \({C}_{R}\) increases with prestrain from 3 to 6% at \({\varepsilon }_{\mathrm{p}}=0.1\) and \({\varepsilon }_{\mathrm{p}}=0.3\), respectively (Fig. 17(b)). Alternative evaluation by equivalent von Mises strain confirms the presented results qualitatively (Fig. 18). Yet, the amount of \({C}_{R}\) is 26% and less than 1% lower at \({\varepsilon }_{\mathrm{p}}=0.1\) and \({\varepsilon }_{\mathrm{p}}=0.3\). This corresponds to the alternative evaluation for DC06, which also confirmed the qualitative results, but quantitatively had significant differences.

Fig. 17
figure 17

Results of novel bulge-torsion Test for DP600. (a) Stress overshoot after orthogonal strain-path change. The parameter \({n}_{\mathrm{s}}\) specifies the number of samples. (b) Cross-hardening evolution

Full size image
Fig. 18
figure 18

Alternative evaluation of novel bulge-torsion Test by von Mises strain for DP600. (a) Stress overshoot after orthogonal strain-path change. (b) Cross-hardening evolution

Full size image

The work of Haddadi et al. [6] reports no deviation from monotonic strain-path for DP600 at prestrains of 0.1 and 0.2 true plastic strain. The authors had used a sequence of uniaxial tension and simple shear. The applied method for shifting the prestrained test data by the uniaxial prestrain is not explicitly stated.

In summary, the hypothesis concerning characterization of the material cannot be confirmed. The mild steels (DC06, DC04 and DX56) with significant cross-hardening have carbon contents between 0.02% and 0.16% and grain-sizes between 10 µm and 28 µm. Yet the single-phase high-strength steels do not show any cross-hardening, although ZE800 and BS600 have carbon content below 0.11% and large grain-sizes of 35 µm and 27 µm, respectively. Thus, there have to be additional parameters that influence the mobility of dislocations to form the typical pattern, which are supposed to cause the cross-hardening effect.

Conclusions

Different mild steels (DC06, DC04 and DX56) and high strength steels (DP600, BS600, ZE800) have been tested for cross-hardening in a novel setup. It is demonstrated that the bulge-torsion test is suited to determine cross-hardening. The proposed setup enables the characterization of cross-hardening at prestrains up to 0.6 for the first time. The analysis reveals that the normalized cross-hardening ratio \({C}_{R}\) of DC grades increases mildly with increasing prestrain, while it seems to be constant at 6% for the DX56 (Table 4). Thus, it can be concluded that the absolute stress of cross-hardening always increases, even at large strains. The reduced maximum \({C}_{R}\) for the DX56 grade may be caused by the higher amount of carbon in the microstructure which impedes the formation of more pronounced dense dislocation walls. The decrease of cross-hardening with further deformation has been quantified by the reduction of \({C}_{R}\) after additional 20% work. The DC grades had a constant reduction of \({C}_{R}\) to about 85%, while the DX grade reduced to 78%.

Surprisingly, the dual-phase steel DP600 revealed also some mild cross-hardening for prestrains of 0.1 and 0.3. BS600 and ZE800 have been investigated the first time for the cross-hardening effect and are not sensitive for cross-hardening. A cross-hardening effect might have been possible, due to their virtually single-phase microstructure and moderate amount of carbon and large grain-size. It is supposed that other parameters impede the mobility of the dislocations to form the necessary patterns.

It has been demonstrated that the method to compare different load types has a significant influence on the determined cross-hardening.