Introduction

The shrink-fit is a routinely used method for attaching gearwheels and other components, collectively referred to here as hubs, onto shafts [1]. The standard calculation of the necessary interference for the shrink-fit to support given torsional and axial loads uses the Lamé thick walled cylinder equations combined with the assumption of Coulomb friction. However, detailed analysis shows a region of slip may develop between the hub and shaft close to the surface of the hub. Slip under cyclic loading may lead to fretting fatigue [2] but the standard approach to shrink-fit design is unable to determine whether such slip will occur.

Semi-analytical results are available for a rectangular cross section peg shrink-fitted into a cavity in a half-space where an extraction force, normal to the surface of the plane is applied to the peg [3]. The peg was assumed to be sufficiently long that the conditions at the end of the peg did not affect the behaviour. Results were presented for the opening and slip of the contact as the load is increased. This work accounts for the coupling between the extraction force and the interface pressure: the extraction force reduces the magnitude of the interface pressure up to the point where the surfaces separate. No such results have been obtained for the axisymmetric case where an extraction load is applied to a shaft shrink-fitted into a circular cavity in a half space. However, the case of torsion applied to a shaft shrink-fitted into a cavity has been addressed [4]. As the torsion is increased a slip region initiates at the surface of the half-space and then propagates along the interface between the shaft and circular cavity. Results are obtained for the depth to which the slip region propagates. In this work there is no coupling between the torsion and interface pressure such as would exist if an extraction load was applied to the shaft.

Finite element analysis may be combined with analytical solutions to aid the design of shrink-fits so that failure can be avoided in service [5,6,7]. These approaches can include complicating factors such as the geometry at the edge of the shrink-fit [8] and the influence of surface roughness at the interface [9]. These approaches however rely on the knowledge of the frictional conditions at the interface between the shrink-fitted components. For the high interface pressures typically encountered in shrink-fits, these frictional conditions are difficult to measure [10]. In cases where cyclic loading occurs, common in practice, the frictional behaviour becomes much more complex [11, 12].

There is limited previous experimental work where the interface conditions in a shrink-fit under applied load have been measured. An ultrasound technique has been used to determine the interface pressure by measuring the ratio of transmitted to reflected waves [13]. Photo-elastic measurements have also been made of the interface stress between a shaft and hub manufactured from an epoxy material [14]. Results were obtained for the interface pressure and the interface shear when the shaft was subjected to torsion. Measurements were also made of the residual shear stress after a cycle of torsion. Another study used neutron diffraction to measure the interface stress between a steel shaft and hub, although the low magnitude of the stress made accurate measurements difficult [15]. However, no work appears to have been carried out to measure the slip at the interface as increasing applied load is applied to the shrink-fit.

In the work described here experimental measurements are made of the slip between a hub and shaft in a shrink-fit assembly subjected to axial load. These measurements are then compared with the results of finite element analysis. The case of axial load is of particular interest because, just like the rectangular peg [3], Poisson contraction of the shaft resulting from the axial load reduces the interface pressure between the shaft and hub, increasing the likelihood of slip.

The technique for the measurement of slip that will be described here may be combined with measurements of the stress components at the interface to improve the understanding of the frictional conditions between shrink-fit components.

Nominal Expressions

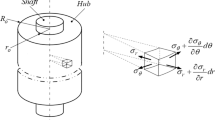
The geometry of a shrink fit assembly of a shaft in a hub is shown in Fig. 1. The shaft has radius r i while the hub an outer radius r o and length of engagement l . The shaft and hub are assembled with a radial interference δ. The nominal pressure p developed at the interface between the shaft and hub is

$$ p=\frac{E\delta}{r_i\left(1-{\nu}^2\right)}\left[\frac{k^2-1}{2{k}^2}\right] $$
(1)

where E is Young’s modulus and ν Poisson’s ratio for the hub and shaft, and k = r o /r i . Equation (1) assumes that the shaft and hub remain elastic and that conditions of plane strain apply. It also ignores end effects and any influence of a tensile load applied to the end of the shaft. Such a tensile load will tend to reduce the interface pressure due to Poisson contraction of the shaft, hence the interface pressure calculated by equation (1) can only be considered to give a nominal value.

Fig. 1
figure 1

Geometry of a shrink-fit assembly of a shaft and hub

Full size image

If a sufficiently high axial load is applied to the shaft so that slip between shaft and hub occurs, the nominal shear stress τ at the interface is

$$ \tau =\mu p $$
(2)

assuming Coulomb friction where μ is the coefficient of friction. The nominal axial load to cause complete extraction of the shaft, called the nominal extraction load in the remainder of the paper, is

$$ {P}_X=2\pi {r}_i l\tau $$
(3)

The actual extraction load will be lower than the nominal extraction load because axial load causes a Poisson contraction of the shaft and hence a reduction of the interface pressure leading to a reduced limiting shear stress. Slip initiates at the point where the shaft enters the hub and as the axial load increases a region of slip of axial length d forms between the shaft and hub, as shown in Fig. 1. With increasing load the slip region will eventually reach the end of the hub and extraction will occur.

Experimental Measurements of Slip

An experimental approach will be described in this section to measure the interfacial slip in a shrink-fit shaft and hub assembly as a progressively increasing axial load is applied to the shaft. Following an exploration of alternative methods to measure slip, the technique shown in Fig. 2 was identified as the most accurate and reliable method. After assembly of the shaft and hub a series of cross holes were drilled through the hub into the shaft. These holes were just large enough to enable the probe of a Talysurf Intra profilometer to enter and then measure the profile of the hole at the interface between the shaft and hub. Although not reported in detail here, three dimensional finite element analyses were carried out to determine the effect of the presence of the hole on the measurement of slip. These analyses showed the effect was small provided the diameter of the hole was less than 0.1 times the diameter of the shaft.

Fig. 2
figure 2

Technique used to measure interfacial slip

Full size image

The complete shrink-fit assembly used in these tests is shown in Fig. 3. The shaft and hub were manufactured from low carbon steel (070 M20) with Young’s modulus of 210 GPa and Poisson’s ratio of 0.29 [16]. The assembly was more complex than a shrink-fit between a shaft and hub because it was designed so that axial load could be applied in a test machine, then the load could be locked in, the assembly removed from the test machine and finally the slip measured remote from the test machine. The requirement to allow the loaded assembly to be removed from the test machine was due to the concern that the Talysurf could be damaged accidentally if the measurements were made in the test machine, but also so that the Talysurf could be aligned precisely with the cross holes. The location of these cross holes is shown in Fig. 4. Four cross holes were used at depths of 20, 40, 60 and 80 mm, distributed radially around the axis of the shaft.

Fig. 3
figure 3

Dimensions of the experimental shrink-fit specimens

Full size image
Fig. 4
figure 4

Locations of the cross holes used for measurement of slip

Full size image

Three shrink-fit assemblies were manufactured, referred to as Hub A, Hub B and Hub C. The shafts and hubs were machined roughly to size and then the shaft and the bore of the hub accurately ground. The diameter of the shaft and hub were measured at a number of axial and radial positions to ensure they were parallel and circular. The measurements for all 3 assemblies are shown in Table 1. Diametral interferences of between 30 and 33 μm were achieved. The assembly of the shrink fits was carried out by first immersing the shafts in liquid nitrogen and heating the hubs to 150 °C in an oven. A short tapered section was machined onto the end of the shaft, shown in Fig. 3, to allow the shrink-fit procedure to be carried out easily. Once the shrink fit has been made the hub was fixed to the lower loading attachment using 6 equally spaced M6 bolts as shown in Fig. 3. These bolts were lightly preloaded.

Table 1 Dimensions of test specimens
Full size table

The shrink-fit assemblies were loaded in steps in a 250 kN servo-hydraulic test machine. The procedure was first to locate the upper and lower loading attachments of the shrink-fit assembly (Fig. 3) in the wedge grips of the test machine. Load was then applied to the assembly in steps. After each step in load had been applied the assembly was removed from the test machine so that the profiles of each of the holes could be measured. Removing the assembly from the test machine was achieved by tightening the locking nut and then slowly reducing the load. As the load was reduced the reading of the strain gauges attached to the shaft was monitored; the locking nut was tightened further to keep the strain gauge reading constant.

Once the shrink-fit assembly had been removed from the test machine the assembly was disassembled to leave the shaft and hub. The shaft and hub were then located on a special fixture, Fig. 5, so that the alignment of the profilometer with the holes in the specimen could be maintained. Figure 6 shows a series of example profiles measured for one hole at a number of different load levels. The step in the profiles due to slip at the interface between the shaft and hub is clearly evident. The slip at the interface was evaluated by using a least squares linear fit through the profiles measured in the shaft and hub, and calculating the step between them at the interface.

Fig. 5
figure 5

Measurement jig to ensure alignment of the profilometer with the specimen

Full size image
Fig. 6
figure 6

Typical data showing the profile of one hole measured at a number of different load levels

Full size image

Measurements were made for all 3 shaft and hub assemblies, but not for all holes. For Hub A, only hole 1 was measured and for Hub B only holes 1 and 2 were measured. Measurements were made for all holes for Hub 3, but no slip was observed at hole 4 for any of the load levels. Measurements of slip versus hole depth for tensile loads of 20, 40, 60 and 80 kN are shown in Fig. 7. For a load of 20 kN slip is limited to hole 1, closest to the top of the hub. As the load is increased, slip is measured at holes at greater depth. The maximum magnitude of slip measured in the tests was about 20 μm. A maximum difference of about 5 μm was observed for measurements made on different shaft and hub assemblies but for the same hole location and load level. The same experimental data are re-plotted later as slip versus load for each hole position and compared with the results of finite element analysis. The full set of experimental results are provided in Tables 2, 3 and 4.

Fig. 7
figure 7

Experimental measurements of the slip versus depth at different loads

Full size image
Table 2 Experimental results of slip versus load for Hub A
Full size table
Table 3 Experimental results of slip versus load for Hub B
Full size table
Table 4 Experimental results of slip versus load for Hub C
Full size table

Slip was measured for loads up to 120 kN. All three hub assemblies were then loaded beyond this load until the extraction load was achieved. The extraction load for all three hubs was similar, about 180 kN. Table 1 lists the extraction load measured for the hubs.

Finite Element Analysis

An axisymmetric finite element simulation was carried using ABAQUS 6.12 of the effect of axial load applied to a shrink fit assembly to provide a comparison with the experimental results. The geometry of the finite element model is shown in Fig. 8. The dimensions of the model matched the dimension of the experimental shrink fit assembly shown in Fig. 3. A structured mesh using 2D 4 node axisymmetric elements of type CAX4R were used for the shaft and hub near the interface. A more coarse mesh was used away from the area of interest in the outer part of the hub consisting of CAX4R and CAX3 elements. Approximately 200 matched elements of size 0.5mm2 were used along the length of the contact interface. A detail of a small part of the mesh is shown in Fig. 9. The shrink fit was simulated by modelling the shaft and hub interference in the geometry and using the interference fit option in ABAQUS. An interference value of 31.5 μm was taken to represent the range of measured interferences provided in Table 1. The contact conditions at the interface were enforced using the penalty formulation. Load was applied to one node at the end of the shaft and the other nodes constrained so that the axial displacement was the same as the loaded node. The axial but not the radial displacements of nodes on the upper end of the hub were constrained to be zero, as shown in Fig. 8. Since the bolts attaching the hub to the lower loading attachment (Fig. 3) were only lightly preloaded and had a total axial stiffness much less than that of the hub, the constraints in the finite element model were chosen to represent the assumption that these bolts carried all the load applied to the shaft.

Fig. 8
figure 8

Geometry of the finite element mesh

Full size image
Fig. 9
figure 9

Details of the finite element mesh for a portion of the mesh

Full size image

Before attempting to compare the finite element predictions with the experimental results, a series of analyses were conducted for a coefficient of friction equal to 0.15. This value is lower than that used to provide finite element predictions for the experimentally measured values.

Figure 10 shows the variation of pressure along the interface measured from the loaded end for various end loads. Also shown in the figure is the nominal interface pressure calculated using equation (1) of 73 MPa. For no applied end load, the pressure is constant along a central portion of the interface. Increasing axial load reduces the pressure at the interface, particularly near the loaded end, due to the Poisson contraction. The maximum end load of 120 kN in the figure was equal to the extraction load predicted by the finite element analysis. A value of 100 mm was used for the length of engagement, 110 mm for the length of the hub minus 10 mm for the length of the taper on the shaft.

Fig. 10
figure 10

Finite element prediction of the interface pressure versus distance for varying applied end loads

Full size image

The variation of shear stress at the interface for varying end loads can be seen in Fig. 11. The shear stresses for no applied axial load are not zero since axial stresses are generated in the shaft and hub by the shrink fit procedure. These axial stresses must be balanced by a shear stress at the interface. As the axial load is increased, slip occurs over a portion of the interface. For example, for a load of 40 kN the slip occurs up to a point roughly 40 mm from the loaded end of the interface. The shear stress over the portion of the interface where slip occurs is roughly equivalent to the nominal value calculated by equation (2). The extent of the slip region versus the axial load is shown in Fig. 12. The slope of the curve is almost constant except for small axial loads and axial loads close to the extraction load.

Fig. 11
figure 11

Finite element prediction of the shear stress at the interface versus distance for varying applied end loads

Full size image
Fig. 12
figure 12

Finite element prediction of the extent of the slip region versus applied end load

Full size image

A series of analyses were performed to investigate the predicted extraction load versus the axial length of engagement of the shrink fit for the same interference, shaft and hub diameters. The results are presented in Fig. 13 and compared with the nominal extraction load calculated using equation (3). This equation suggests the extraction load increases linearly with the axial length of engagement but the finite element analysis shows that this only occurs when the axial length is small.

Fig. 13
figure 13

Extraction load versus length of engagement predicted by finite element analysis

Full size image

Figure 14 shows the results of another series of analyses to predict the extraction load, this time where the geometry of the shrink fit was kept the same but the coefficient of friction was varied. Again, the finite element predictions are compared with the nominal extraction load calculated using equation (3) using a length of engagement, l = 100 mm. Equation (3) suggests the extraction load increases linearly with the coefficient of friction but the finite element analysis demonstrates that this is only valid for small coefficients of friction.

Fig. 14
figure 14

Extraction load versus coefficient of friction predicted by finite element analysis

Full size image

The finite element model was now used to provide predictions of slip that could be compared with the experimental measurements. Representative values for the coefficient of friction were taken from test results where a shaft was clamped between two test pads and then an axial extraction load was applied to the shaft [10]. Two series of tests each with sample sizes of 16 were carried out for two different interface pressures representative of those in a shrink-fit assembly. The results of one of these series for interface pressures of 44 MPa resulted in measured coefficients of friction of between 0.17 and 0.22. This range of values was used in the finite element model to produce the results shown in Fig. 15. The Figure shows the magnitude of slip predicted by the finite element analysis at the 4 hole locations versus the applied end load, compared with the experimental results. The slip measured in the experiments shows acceptable agreement with that predicted by the finite element analysis. The same range of coefficients of friction was then used to predict extraction loads of between 117 and 147 kN. These predicted values are rather lower than the extraction loads measured in the experiments of around 180 kN (Table 1).

Fig. 15
figure 15

Comparison of finite element predictions of slip versus load at the positions of the 4 holes with experimental measurements

Full size image

Discussion

Both experimental measurements and finite element predictions of slip versus axial load show slip occurring at small loads compared to the ultimate extraction load. For example, at an axial position 20 mm along the interface from the loaded end of the shaft, a slip of the order of 4 μm was measured at a load of 40 kN, much smaller that the extraction load of 180 kN. It would seem that to ensure fretting fatigue does not occur in axially loaded shrink fits, the level of the loading should be much smaller that the extraction load. However, no measurements of slip have been made under conditions of cyclic loading and it is possible that in practice shakedown would occur, reducing the likelihood of fretting fatigue.

The interaction of axial load and interface pressure ensures some nonlinearity in the behaviour of the shrink fit. As the length of engagement increases, the additional increase in the load carrying ability of the shrink fit reduces, as seen in Fig. 13. However, typical shrink fit designs have a length of engagement similar to the shaft diameter and for such designs the effect of the nonlinearity appears to be small. A similar nonlinearity is evident for variations of the coefficient of friction. Figure 14 shows that doubling the coefficient of friction does not quite double the extraction load. Again though, for typical levels of friction encountered between dry metallic surfaces, such nonlinearities are probably negligible.

The experimental measurements of slip in Fig. 15 show a maximum variation of the order of 5 μm between the three hub assemblies for the same load. This variation compares with a maximum measured slip of about 20 μm while the Talysurf data of Fig. 6 suggests the experimental error is less than 1 μm. Some of the variation may be attributed to dimensional differences between the three hubs, although the measurements in Table 1 show these differences are only of the order of 5%. Another potential cause of variation is due to axial stress: the shrink fit procedure generates axial stress as well as radial stress as indicated by the finite element results of Fig. 11 showing shear stress at the interface for the case of zero applied load. The precise distribution of these axial stresses will depend on the way the hub first comes into contact with the shaft as it cools down. These axial stresses will influence the behaviour of the hub assembly under superimposed axial load. We are not aware of any work that has been carried out to measure axial stress in a shrink fit assembly or assess its effect on the behaviour under load.

The finite element predictions of slip shown in Fig. 15 show differences compared to the experimental measurements of the order of the variability in these measurements. The finite element results assume an axial stress distribution that would exist if the contact between hub and shaft occurs uniformly along the length whereas in practice a different axial stress distribution may exist. In addition, the finite element analysis has assumed Coulomb friction using a range of coefficients of friction taken from existing experimental data [10]. Although these coefficients of friction led to adequate agreement between the finite element predictions and the experimental results for slip, the predictions of extraction load were significantly lower than the experimental results. A possible mechanism to explain this discrepancy is that the effective friction between two surface increases as slip accumulates and there is some experimental evidence that such an effect does occur [12].

Detailed measurements of the friction conditions between contacting surfaces at the microscopic scale are being made [17], allowing models of friction for such contacts to be generated. The work described in this paper to measure slip in a shrink fit component could be combined with measurement of the pressure and shear stress at the interface to enable friction models to be developed for accurate assessment of the behaviour of shrink-fit components.

Conclusions

Experimental measurements have been made of the slip at the interface in a shrink fit assembly of a shaft and hub subjected to axial load. The measurements show that slip occurs near the loaded end of the shrink fit at levels of axial load much smaller that the ultimate extraction load. Finite element analysis has also been carried out to predict the slip under axial load with adequate agreement with the experimental results. The finite element analysis suggests that extraction loads for shrink fit components do not vary linearly with length of engagement or the coefficient of friction. However, for lengths of engagement similar to the diameter of the shrink fit and for typical levels of friction the estimates using the standard shrink fit analysis appears to be adequate.

The technique for measurement of slip that has been described offers the opportunity to carry out in situ measurements of frictional behaviour in a shrink-fit assembly when the measurement of slip is combined with a measurement of the pressure and shear stress at the interface.