Multi-Axial Deformation Setup for Microscopic Testing of Sheet Metal to Fracture

Abstract

While the industrial interest in sheet metal with improved specific-properties led to the design of new alloys with complex microstructures, predicting their safe forming limits and understanding their microstructural deformation mechanisms remain as significant challenges largely due to the inadequacy of the existing experimental tools. The investigation of the strain-path dependent failure mechanisms requires miniaturized testing equipment, which can be placed in a scanning electron microscope for in situ experiments. So far, such tests could only be carried out for a single strain path (uniaxial tension). In this work, in order to fill this gap, a miniaturized Marciniak test setup is designed, built and tested. With this setup real-time, multi-axial tests of industrial sheet metal can be carried out to the point of fracture within a scanning electron microscope. Proof-of-principle experiments demonstrate that a realm of information can be obtained, crucial for the understanding of the mechanical behavior of new alloys.

Introduction

There is a growing scientific and industrial interest in the development of sheet metal with improved specific-properties, governed primarily by the weight-reduction motivations in the automotive industry [1]. Whereas related metallurgical research has lead to new alloys with complex microstructures (e.g. transformation induced plasticity steels, twinning induced plasticity steels, dual-phase (DP) steels, magnesium alloys, aluminium alloys, etc.), it also triggered two main challenges regarding the proper character of the mechanical behavior of these alloys:

• (i) Experimental or numerical determination of the forming and fracture limits (e.g. tensile instability, ductile fracture, shear fracture) of these new alloys in different stress and strain states,

• (ii) Understanding the underlying micromechanisms that dictate the observed global material behavior and its accompanying failure mechanisms.

Although the literature has seen an extensive amount of research on both aspects separately, the connection between them is only rarely established, e.g., to link the strain path dependent forming limits to the underlying microstructural deformation mechanisms [2, 3]. The major cause of this gap in the literature is the limitations of the commonly available experimental methodologies, i.e. macro-scale mechanical deformation tests for measuring forming limits and post-mortem fractography analyses for revealing microstructural-deformation mechanisms. Although these techniques have provided clear insight in the behavior of metal microstructures over the past century, thorough understanding of the deformation mechanisms in the complex microstructures of the aforementioned new alloys requires real-time analysis of microstructural deformation mechanisms. Therefore, recent studies employ miniaturized tensile testing equipment inside scanning electron microscopes, e.g., to investigate the influence of tempering [4] or segregation-induced banding [5] in DP steels. These studies clearly demonstrate the benefits of real-time microstructural analysis. In fact, a mechanical-microscopical approach makes it possible to address both challenges stated above simultaneously, by high-resolution real-time imaging enabling the investigation of the underlying deformation mechanisms and subsequent micrographic digital image correlation to enable determination of deformation limits even locally.

On the other hand, commonly used sheet metal forming processes almost always impose complex strain paths to the sheet being formed, making it unrealistic to analyze the strain path dependent behavior and failure of the sheet through tests along a single strain path only (i.e. the standard uniaxial tension test). Realistically, a full understanding of this path dependency requires in situ examination of the deformation-induced microstructure evolution in all relevant strain paths. However, this was so far not possible due to the absence of a setup that allows in situ multi-axial testing of sheet metal up to the point of failure. This paper presents a miniaturized Marciniak test setup that is dedicated for this purpose. In the following sections, first the choice for the Marciniak deformation concept is motivated through a critical comparison between possible candidates. Next, the challenges related to the miniaturization of the Marciniak setup to enable real-time in situ scanning electron microscope (SEM) visualization are explained, and the resulting final design is presented. The paper is finalized with results from proof-of-principle experiments.

Critical Comparison of Potential Testing Methodologies for Miniaturized Multi-Axial Loading

Several multi-axial testings setups have been developed to study deformation of sheet metal, e.g. bulge pressure tests [6, 7], hemi-spherical punch (i.e. Nakazima) tests [2, 8], cruciform tests [9–11], flat punch (i.e. Marciniak) tests [12, 13], multiaxial compression tests

[14, 15], electromagnetic forming tests [16, 17] (Fig. 1). Each of these techniques have specific strengths and weaknesses regarding the degree of the control of the stress state, the quality of information provided, practicality, etc. The minimum requirement for any methodology for real-time mechanical-microstructural characterization of multi-axial deformation in a miniaturized configuration, is to:

• avoid constraining the physical deformation and failure mechanisms of the sheet being tested to allow characterization of “true” microstructural mechanisms,

• operate safely within the vacuum chamber of a SEM to allow for in situ visualization and local strain mapping,

• produce the required level of load and displacement to reach sheet metal failure.

Fig. 1

Commonly used methodologies for applying multi-axial loading, illustrated here for the case of biaxial tension testing: (a) bulge test, (b) Nakazima test, (c) cruciform test, (d) Marciniak test, (e) compression test, and (f) electro-magnetic test

In this section, these methods are comparatively analyzed for their potential as a miniaturized setup. Where required, results from finite element simulations are presented. Note that all simulations mentioned in this work are modeled with an isotropic elasto-plastic material model of high-quality deep-drawing steel, for which the elastic and plastic material properties are determined from tensile tests (Fig. 2). The sheet is modeled using solid axisymmetric elements, a four node quadrilateral element with bilinear interpolation, while the punch and the two clamps are modeled as rigid bodies. For friction the coulomb model is used, and the coefficients of friction are varied between 0 and 1.

Fig. 2

Material properties for the finite element simulations are obtained from the shown tensile test data of deep-drawing steel

Commonly used methodologies such as the compression test and the hemi-sphere punch test exert the required force through direct contact with the test piece. This makes the observed material behavior heavily dependent on the degree of friction, the level of influence of which is difficult to assess in small-scale tests. For instance, finite element simulations show that the location of fracture in the hemi-sphere punch test is directly related to the level of friction between the punch and the sheet metal being pressed (Fig. 3(a)). Similar concerns hold for the compression test, for which a direct view of observation in SEM is also not possible. For the hemi-sphere punch test the imposed strain path is further complicated due to the existence of a bending component, which increases with the miniaturization of the punch (Fig. 3(b)). As a result of these complications, characterization of the microstructural mechanisms using the hemi-sphere punch test and the compression test is not trivially possible.

Fig. 3

Finite element simulations of the hemi-sphere punch tests demonstrate the challenges in miniaturization: (a) friction strongly influences the stress distribution and failure, such that increasing friction causes the highest stresses to occur away from the top of the punch, as shown here for the equivalent Von Mises stress distribution. (b) Miniaturization of the punch decreases Von Mises stress and plastic strain homogeneity along the thickness direction. Note that the punch, which has been omitted from the graphs for clarity, comes in from left to right. Only half of the sheet is simulated

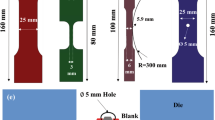
Contact related problems are not an issue for bulge tests, electromagnetic forming tests or cruciform tests. However, for the former two cases, operation within SEM is not possible, due to the required fluid pressure (that is released upon sheet metal fracture) and strong magnetic field, respectively. The cruciform test, on the other hand, is an interesting candidate for miniaturization, and upon initial consideration there seems to be no direct influence of boundary conditions on the region of interest (i.e. center of the cruciform). However, finite element simulations carried out with the same material model used in Fig. 3 revealed that reaching high levels of deformation in the center of the cruciform is not possible, unless the thickness in the center is significantly reduced to a bowl-profile with the central thickness approximately ~20% of that of the as-received sheet (Fig. 4(a–c)). It was reported earlier that such a thickness reduced geometry may be manufactured by electro-discharge machining or electro-chemical machining, ensuring that the failure is forced to occur at the center (Fig. 4(b)) [11]. Unfortunately, it is well-known that industrial sheet metals have a non-homogeneous microstructure distribution along the thickness direction. Removing layers from top and bottom of the sheet render the probed microstructure not representative anymore for the as-received sheet metal. Furthermore, it is questionable whether the real material failure behavior is properly probed, since the center of the bowl, with the smallest thickness, is forced to fracture first (Note that in case of a bowl with a flat base, the fracture always occurs at the edge of the flat base, see Fig. 4(b)). Due to these reasons, the cruciform test is also regarded as unsuited for investigating large deformation induced macro and microstructural phenomena in sheet metal.

Fig. 4

Finite element simulations of the cruciform samples with (a) original thickness, (b) homogeneously-reduced thickness and (c) bowl-shaped profile. (d) Experiments carried out using a home-built biaxial deformation setup showing that the thickness reduced cruciforms fail in their center

Finally, in the Marciniak test, the load is transferred from a flat punch to the specimen via a so-called ‘washer’ plate, which has an opening window in the middle under the region of interest. Hence, there are no friction effects in this gauge region of the specimen. Both the specimen and the washer are drawn simultaneously, the latter at a larger velocity due to the opening in the center. This creates the main difference from a typical deep drawing experiment, as the resulting relative velocity between the specimen and the washer in the Marciniak test creates friction forces on the specimen in the opposite direction of those that occur in a normal deep-drawing experiment without a washer (Fig. 5).

Fig. 5

Sheet displacement and friction directions in (a) deep drawing and (b) the Marciniak test

This reversed friction force in the Marciniak test limits the level of deformation of the regions where there is contact between the washer and the sheet and, as shown by the finite element simulation in Fig. 6, allows the largest deformation and failure to occur at the center, where there is no contact, making the test fundamentally different from a standard punch test. As a result of the absence of contact a true in-plane deformation occurs and inhomogeneous material deformation is not artificially enforced. Accordingly, this test is perfectly suitable for characterizing microstructural mechanisms and, therefore, regained a lot of interest recently [18–21]. Furthermore, the Marciniak tests can be carried out safely in SEM since there is no influence on the working principles of electron microscopy. All these considerations qualify the Marciniak test as the most suitable candidate for a in situ miniaturized multi-axial deformation test, however, the challenge lies in miniaturization of the Marciniak setup.

Fig. 6

Finite element simulation of the Marciniak tests reveal that the highest level of deformation occurs at the center of the tested specimen, if the experimental parameters shown in the figure (punch radius (r _p), punch edge radius (r _pe), washer hole radius (r _wh), die edge radius (r _de), distance from die to punch (d _dp)) and friction (i.e. between the punch and the washer (μ _pw) and between the washer and the sheet (μ _ws)) are optimized. Note that the material model is the same as in the previous figures, and that the punch comes from below

Challenges in the Design of a Miniaturized Marciniak Test Setup

It was observed in preliminary macro-scale Marciniak tests that unwanted failure modes (see Fig. 7, and also [21]) may be triggered under certain experimental settings (e.g. too small punch radius, too small punch corner radius, too small or too large washer opening radius, too large friction, etc.), all affecting the relative drawing velocity of the washer compared to the tested sheet. Of specific concern for miniaturization is a deep drawing type of failure (Fig. 7(b)), which occurs when the reverse friction effect is insufficient, thereby causing a stress concentration, σ _e, at the corner of the flat punch, that exceeds the stress level, σ _c, at the contactless region at the specimen center. In order to evaluate the sensitivity of the stress ratio σ _e/σ _c to miniaturization of the setup and to provide specifications for the miniaturized Marciniak setup, finite element simulations of the Marciniak test are carried out, with a range of different geometries (0 < r _wh < 16 mm; 0 < r _pe < 25 mm; 0 < r _p < 30 mm) and friction settings (i.e. μ _pw and μ _ws between 0 and 1) (Fig. 6). These simulations incorporate the same material model, finite elements and material parameters (Fig. 2) as the hemi-sphere punch test explained above, but with a flat punch and an additional washer sheet with an opening in the center, both of which are modeled with the same material properties.

Fig. 7

Different failure modes in the Marciniak test investigated on IF steel (for r _p = 50 mm, r _pe = 10 mm): (a) washer hole initiated failure (washer hole too large) (b) deep drawing failure (i.e. the reverse friction effect not sufficiently strong) and (c) successful failure triggering a random crack in the center region

The simulation results revealed that r _pe should be above ~5 mm and that the friction between the punch and the washer should be as low as possible (μ _pw < 0.2) to keep σ _e/σ _c to a minimum, while the friction between the washer and the specimen should be maximized (μ _ws > 0.8). Furthermore, the washer hole radius, r _wh, also has a strong influence on the stress ratio, and has to be chosen < ~13 mm (to avoid “cutting” the tested sheet at the corner (Fig. 7(a)) yet larger than ~5 mm (to avoid deep drawing failure at the cup (Fig. 7(b))).

The most important choice from a miniaturization perspective is the size of the punch, r _p, since it directly affects the mode of failure, as well as the required force and total stroke to reach failure. In general, an increase in the punch size ensures failure at the specimen center, however, it also quickly increases the required force level to reach failure. As the design is limited by the available small SEM sample chamber volume, the punch size should be kept at a minimum to have a force specification that can still be realized, while having a low enough ratio of σ _e/σ _c. Finite element simulations show that for r _p < ~20 mm the stress ratio rises significantly, which should be avoided in the miniaturized setup. Determining design specifications for the required force level and total stroke is not trivially possible through finite element simulations due to the complexity of the deformation in the Marciniak test concept. Therefore, preliminary macro-scale Marciniak experiments were carried out with two steels at different extremes of formability, a 1 mm thick advanced high strength steel DP steel (σ _UTS = 600 MPa) and a 0.7 mm thick high formability deep-drawing steel (Fig. 2), to determine force and stroke specifications that would allow testing of sheet metal with a wide range of properties.

Experiments with the critical punch radius of r _p = 20 mm on the DP steel sample and the washer revealed that a maximum force of 100 kN is sufficient to reach failure, and the failure indeed occurred in the specimen center (Fig. 7(c)). In order to take into a factor of safety and the possibility to test even higher strength sheet material when needed, a maximum force specification of 150 kN is set for the miniaturized Marciniak setup. Experiments with a slightly larger punch of r _p = 25 mm of the deep drawing steel sample and the washer revealed that a maximum stroke of 15 mm is required to reach failure. This value is taken as the specification for the total stroke of the miniaturized Marciniak setup.

Design of the Miniaturized Marciniak Test Setup

To manufacture a Marciniak apparatus with a 15 mm stroke and a load range of 150 kN, a hydraulic press would be the most logical way for the small working volume available. However, this is obviously not possible in the vacuum environment of a SEM chamber. An alternative idea consists in using a spindle with a nut, driving the nut with an electric motor. Yet, the amount of friction consumes too much torque, making it impossible to select a gearbox-motor combination within the maximum working volume. Even going to 16 small spindle-nut combinations around the sample does not match up the design specifications within the working volume of the SEM.

Therefore, an alternative solution is pursued, consisting in the use of a long strong string between two thick plates (Fig. 8). The sample and the washer are clamped in the top plate, and a punch is fixed in the bottom plate. During a test, the top plate is drawn towards the bottom plate, pulling the sample onto the stationary punch.

Fig. 8

A schematic drawing of the miniaturized Marciniak test concept: specimen (yellow); top plate (brown); bottom plate (dark green); punch (light green); long string (red; only one of the three strings is shown); pulleys (blue); and winch (grey)

With this concept, the force on the string is amplified by a factor of 72 towards the sample in the final setup, because the string is wrapped around 36 pulleys in the top plate and 36 pulleys in the bottom plate, mounted around the sample (Fig. 9). In fact not one string, but three separate strings are used, driving three equally sized segments with (2×12) rolls around the sample, in order to provide a linear vertical displacement without rotation between bottom and top plate (and thus between top plate and punch). The three strings are reeled on a winch with a 22 mm brushless motor combined with a harmonic drive gearbox (component 6 in Fig. 9). The force can be accurately measured with strain gauges placed on the bottom plate, due to the relatively high bending strains on the lower central part of the elastically deforming bottom plate. The displacement is measured at the two sides with contactless Eddy current displacement sensors (component 7 in Fig. 9). Depending on the sheet metal to be tested, the force level, stroke and stress ratio can be modified by the use of different punches that are manufactured within the specifications determined with the numerical analysis explained above. For the experiments that are presented here two punches are used, the first one having r _p = 20 mm and r _pe = 12.5 mm and the second having r _p = 25 mm and r _pe = 12.5 mm.

Fig. 9

The components of the miniaturized Marciniak apparatus: the sample and washer (depicted in yellow) are clamped with the clamping ring (1) to the top plate (2), and are deformed by the punch (3) which is mounted on the bottom plate (4). The punch force is supplied by pulling three cables (depicted in red) over 72 pulleys (5) (i.e. 36 pulleys in the top plate and 36 in the bottom plate, all journalled in needle bearings for low friction), and the excess cable is reeled in using a winch mechanism (6). The punch displacement is measured using a contactless Eddy current sensor (7); the punch force is measured using strain gauges on the bottom plate (not shown). A picture of the finalized setup is also shown below

Proof-of-Principle Experiments

The capabilities of the miniaturized Marciniak apparatus are demonstrated by in situ testing of two industrial alloys: an aluminium 6016 alloy and a DP600 alloy. The use of the larger punch (r _p = 25 mm) is most suitable experiments for the former whereas the use of the smaller punch (r _p = 20 mm) is more suitable for the DP steel. Experiments are carried out in three different strain paths (i.e. uniaxial tension (Fig. 10(a), plane strain tension (Fig. 10(b)) and biaxial tension (Fig. 10(c)) through the use of specimens of different geometries, although for the DP600 steel we present only the results of the biaxial sample (Fig. 10(d)), for which the highest force level is required. The difference in the strain path is achieved by imposing different level of deformation constraint in the minor axis as a result of the changes in specimen width or notch geometry. For the presented experiments the full sample (i.e. the biaxial strain path sample) had the diameter of 94.5 mm, the plane strain sample had a reduced width of 20 mm with a small notch radius of 2 mm, and the uniaxial tension sample had a reduced width of 20 mm with a large notch radius of 40 mm. The washer material is chosen as the deep drawing steel for the aluminium samples and an extra DP steel sheet for the DP steel samples. Note that the washer material needs to withstand the rising force level, while deforming together with the tested material. Due to these requirements the best candidate for the washer material is typically the tested material itself. Before mounting the sample and the washer, the facing sides of the washer and the samples are ground for enhanced friction, except for the center of the sample. The bottom side of the washer, on the other hand, is polished to reduce the friction between the washer and the punch. Alternating layers of teflon and vacuum grease is used to further reduce friction.

Fig. 10

Results of the proof-of-principle experiments for aluminium samples in (a) uniaxial tension, (b) plane strain tension and (c) biaxial tension strain paths and (d) the DP sample in biaxial tension strain path. Strain fields at the macro-level (using images from an optical camera), strain fields at the micro-level (using images from in situ SEM testing), and captured damage nucleation mechanisms (shown with the red arrows before and after deformation) are also shown for each of these samples. The micron-bar at the bottom right corner represents the scale in all microscope images. For the scale of the optical camera images please refer to Fig. 9

In all the tests, the setup operated within the determined working principles, verifying the success of the original design concept. Furthermore, fracture is reached in the flat central region of the punch, even for the most difficult case of the biaxial tension path, proving that the choice for the critical experimental parameters (i.e. r _p, r _pe, r _wh, r _de, d _dp, μ _pw and μ _ws) is effective, and the miniaturization related challenges in the Marciniak test have successfully been overcome.

Obtained results from these proof-of-principle experiments clearly underline the benefits of in situ testing: high resolution SEM images captured during deformation allow (i) carrying out micrographic digital image correlation to measure strains at the microstructure level, and (ii) studying deformation-induced microstructural mechanisms (e.g. damage evolution) from the obtained SEM image sequences (Fig. 10). For the two materials investigated here, for example, different strain partitioning behaviors (i.e. more pronounced strain partitioning in the DP steel due to the soft ferritic grains and hard martensitic islands) and different damage mechanisms (i.e. martensite cracking or martensite-ferrite decohesion in DP steel vs. damage from inclusions in aluminium alloy) are clearly captured.

Conclusions

In this work a miniaturized test setup was designed, built and tested, that allows real-time, multi-axial testing of industrial sheet metal within a scanning electron microscope. A prior numerical-experimental comparison of the existing (macro-scale) multi-axial testing setups revealed that the Marciniak test concept suits perfectly to the requirements of miniaturized in situ testing (e.g. avoiding manipulation of material behavior, operating (safely) within a scanning electron microscope, etc.). Next, miniaturization induced challenges in the Marciniak concept were investigated through finite element simulations, which led to a number of design guidelines to avoid unwanted failure modes for the miniaturized setup. An original design concept was developed to meet the determined guidelines within the limited volume of a scanning electron microscope. Proof-of-principle experiments revealed that the developed miniaturized Marciniak setup operates successfully within the design specifications, allowing a realm of information (e.g. high resolution SEM images of different stages of deformation, strain field at microstructure level, etc.) to be obtained.