Elastic Constants Determination and Deformation Observation Using Brazilian Disk Geometry

Abstract

Brazilian disk compression has been proposed as an alternative for measuring elastic constants of brittle solids with very low tensile strength (Hondros, Aust J Appl Sci 10:243–268, 1959). Subsequently however, the Brazilian disk geometry was mainly used for measuring fracture toughness and tensile strength of brittle materials, like rocks and concretes. In this study, we revisit the Brazilian disk specimen as a tool for determining elastic constants and for observing the deformation process up to failure. We used the optical digital image correlation (DIC) technique to obtain the displacement field on the specimen surface and proposed a scheme for determining the elastic constants from the measured displacement field and the applied load. Details of the elastic constant determination of a homogeneous material, epoxy resin, were presented. Comparison of the elastic constant measured using Brazilian disk with those obtained through more conventional means was carried out. We also present observations of the deformation evolution of the epoxy resin disk subjected to large nonlinear deformation up to failure and subjected to compressive loading and unloading.

Appendix: Elastic Solution of a Circular Disk

For planar deformation, either plane strain or plane stress, in a given Cartesian coordinate system (x, y), the in-plane stress components are denoted by σ _x , σ _y , and τ _xy , and the displacement components by u and v, respectively. By introducing a complex variable z = x + iy in the region ℝ, there exist two functions, ϕ(z) and ψ(z), which are analytic for z, such that the stress can be related to ϕ(z) and ψ(z) through

$$\label{eq:stress-potentials} \begin{array}{rcl} \sigma_{x}\! +\! \sigma_{y} &\!=\!& 4{\rm{Re}}\{\phi'(z)\}, \\ \sigma_{y}\! -\! \sigma_{x}\! +\! 2i\,\tau_{xy} &\!=\!& 2 \bigl\{\overline{z}\phi''(z)\! +\! \psi'(z)\bigr\}, \end{array} $$

(2)

and the displacement be represented by

$$\label{eq:displacement-potentials} 2\mu\,(u + i\emph{v}) = \kappa\,\phi(z) - z\,\overline{\phi'(z)} - \overline{\psi(z)}, $$

(3)

where the constant κ = (3 − ν)/(1 + ν) for plane stress and κ = 3 − 4 ν for plane strain, respectively, and μ is the shear modulus, ν the Poisson’s ratio. In equations (2) and (3), the bar over a symbol stands for the complex conjugate.

Let ℝ be a circular region with radius R, i.e., ℝ, and the boundary of the region, $\partial\mathbb{R}$, be described by $\lvert{z}\rvert = R$, or by points $\xi = R\exp(i\,\theta)$ ($0 \leqslant \theta \leqslant 2\pi$). Along $\partial\mathbb{R}$ and measuring from θ = 0, let the resultant force over the arc, $0 \leqslant \eta \leqslant \theta$, be denoted by f(ξ). The distribution of f(ξ) over $\partial\mathbb{R}$ is in self-equilibrium, i.e., the resultant force and the resultant moment over the entire $\partial\mathbb{R}$ vanish. The two analytic functions, ϕ(z) and ψ(z), can be obtained to be [12]:

$$ \begin{array}{rcl} \label{eq:potential-solutions-general} \phi(z) &=& \frac{1}{2\pi i} \oint_{\partial\mathbb{R}} \frac{f(\xi)}{\xi - z}d\xi - \alpha_{1}z, \\ \psi(z) &=& \frac{1}{2\pi i} \oint_{\partial\mathbb{R}} \frac{\overline{f(\xi)}}{\xi - z}d\xi - \frac{R^{2}\{\phi'(z) - \alpha_{1}\}}{z}, \end{array} $$

(4)

where

$$\label{eq:constant-alpha-1} \alpha_{1} + \overline{\alpha}_{1} = \frac{1}{2\pi i} \oint_{\partial\mathbb{R}} \frac{f(\xi)}{\xi^{2}}d\xi. $$

(5)

From equation (5), we see that for existence of a solution for the problem, the right-hand side of equation (5) must be real. This is equivalent to the requirement that the resultant moment of the applied force over the boundary $\partial\mathbb{R}$ must vanish. We also know that the imaginary part of α ₁ can be arbitrarily chosen without affecting the stress. Therefore, we may choose that ${\rm{Im}}\{\alpha_{1}\} = 0$, and hence

$$\label{eq:constant-alpha-1-final} \alpha_{1} = \frac{1}{4\pi i} \oint_{\partial\mathbb{R}} \frac{f(\xi)}{\xi^{2}}d\xi. $$

(6)

Now consider that a pair of concentrated forces represented by P = F _x  + i F _y , where F _x and F _y are both real, acting on the circular boundary $\partial\mathbb{R}$ at two locations

$$ \xi_{1} = R\,e^{i\delta_{1}}, \quad \xi_{2} = R\,e^{i\delta_{2}}, \quad 0 \leqslant \delta_{1} < \delta_{2} < 2\pi. $$

The resultant force function f(ξ) is thus

$$\label{eq:resultant-force-concentrated} f(\xi) = \begin{cases} 0, & 0 \leqslant \theta < \delta_{1}, \\ iP, & \delta_{1} \leqslant \theta < \delta_{2}, \\ 0, & \delta_{2} \leqslant \theta < 2\pi. \end{cases} $$

(7)

As a result,

$$ \begin{array}{rcl} \oint_{\partial\mathbb{R}}\frac{f(\xi)}{\xi^{2}}d\xi &=& \frac{P}{2\pi} \ln \left(\frac{\xi_{2} - z}{\xi_{1} - z}\right), \\ \oint_{\partial\mathbb{R}}\frac{\overline{f(\xi)}}{\xi^{2}}d\xi &=& -\frac{\overline{P}}{2\pi} \ln \left(\frac{\xi_{2} - z}{\xi_{1} - z}\right), \end{array} $$

and

$$ \alpha_{1} = \frac{P}{4\pi} \left(\frac{\overline{\xi}_{1} - \overline{\xi}_{2}}{R^{2}}\right). $$

where we have used the relation $\overline{\xi} = R\exp(-i\,\theta) = R/\exp(i\,\theta) = R^{2}/\xi$ along the boundary $\partial\mathbb{R}$. Also note that α ₁ should be a real number.

From equation (4), the analytic functions ϕ(z) and ψ(z) are given by

$$ \begin{array}{rcl} \label{eq:analytic-function-results} \phi(z) &=& \frac{P}{2\pi} \ln \left(\frac{\xi_{2} - z}{\xi_{1} - z}\right) - \frac{P}{4\pi} \left(\frac{\overline{\xi}_{1} - \overline{\xi}_{2}}{R^{2}}\right)z, \\ \psi(z) &=& -\frac{\overline{P}}{2\pi} \ln \left(\frac{\xi_{2} - z}{\xi_{1} - z}\right) - \frac{P}{2\pi} \left(\frac{\overline{\xi}_{1}}{\xi_{1} - z} - \frac{\overline{\xi}_{2}}{\xi_{2} - z}\right). \end{array} $$

(8)

By using equations (2) and (3), the stresses and the displacements within the circular disk are

$$ \begin{array}{rcl} \label{eq:stress-concentrated-force} \par \sigma_{x} + \sigma_{y} &=& {\rm{Re}} \left\{ \frac{2 P}{\pi} \left( \frac{1}{\xi_{1} - z} - \frac{1}{\xi_{2} - z} \right)\right.\\[6pt]&&\left.{\kern16pt} - \frac{P \bigl(\overline{\xi}_{1} - \overline{\xi}_{2}\bigr)} {\pi R^2} \right\}, \\[8pt] \sigma_{y} - \sigma_{x} + 2i\,\tau_{xy} &=& -\frac{P}{\pi} \left\{ \frac{\overline{\xi}_{1} - \overline{z}}{(\xi_{1} - z)^2} - \frac{\overline{\xi}_{2} - \overline{z}}{(\xi_{2} - z)^2} \right\}\\[6pt] &&- \frac{\overline{P}}{\pi} \left( \frac{1}{\xi_{1} - z} - \frac{1}{\xi_{2} - z} \right), \par \end{array}$$

(9)

and

$$ \begin{array}{rcl} \label{eq:displacement-concentrated-force} 2\mu\,(u + i\emph{v}) &=& \frac{P}{2\pi} \left\{ \kappa\, \ln\left(\frac{\xi_{2} - z}{\xi_{1} - z}\right) + \ln\left(\frac{\overline{\xi}_{2} - \overline{z}} {\overline{\xi}_{1} - \overline{z}} \right)\right.\\[6pt] &&\left.{\kern20pt}- \kappa\, \left( \frac{\overline{\xi}_{1} - \overline{\xi}_{2}}{2R^{2}} \right) z \right\} \\[1ex] &&+ \frac{\overline{P}}{2\pi} \left\{ \left(\frac{\xi_{1} - \xi_{2}}{2R^{2}}\right) z + \frac{\xi_{1} - z}{\overline{\xi}_{1} - \overline{z}} - \frac{\xi_{2} - z}{\overline{\xi}_{2} - \overline{z}} \right\}. \end{array} $$

(10)

Finally, let us consider the special case, where a pair of concentrated compressive forces with the magnitude F, acting across the diameter of the circular disk along the y direction. The locations, where the forces are applied, are ξ ₁ = i R and ξ ₂ = − i R, respectively, and P = − i F, where F represents the compressive force per unit thickness of the two-dimensional disk. In the Cartesian system (x, y) with origin located at the center of the disk, the stresses and the displacements can be expressed as

$$ \begin{array}{rcl} \label{eq:stress-concentrated-force-diameter} \sigma_{x}&=& -\!\dfrac{2F}{\pi} \left\{ \dfrac{x^{2}(R\!-\!y)}{\left[x^{2}\!+\!(R\!-\!y)^{2}\right]^{2}}\!+\! \dfrac{x^{2}(R\!+\!y)}{\left[x^{2}\!+\!(R\!+\!y)^{2}\right]^{2}} \right\}\!+\! \dfrac{F}{\pi R}, \\[6pt] \sigma_{y} &=& -\!\dfrac{2F}{\pi} \left\{ \dfrac{(R\!-\!y)^{3}}{\left[x^{2}\!+\!(R\!-\!y)^{2}\right]^{2}}\!+\! \dfrac{(R\!+\!y)^{3}}{\left[x^{2}\!+\!(R\!+\!y)^{2}\right]^{2}} \right\}\!+\! \dfrac{F}{\pi R}, \\[6pt] \tau_{xy} &=& \dfrac{2 F}{\pi} \left\{ \dfrac{x(R\!-\!y)^{2}}{\left[x^{2}\!+\!(R\!-\!y)^{2}\right]^{2}}\!-\! \dfrac{x(R\!+\!y)^{2}}{\left[x^{2}\!+\!(R\!+\!y)^{2}\right]^{2}} \right\}, \end{array} $$

(11)

and

$$ \begin{array}{rcl} \label{eq:displacement-concentrated-force-diameter} u &=& -\frac{F}{4\pi\!\mu} \left\{ (\kappa - 1) \tan^{-1} \left( \frac{2 R x}{R^{2} - x^{2} - y^{2}} \right) - \frac{(\kappa - 1) x}{R}\right. \\[6pt] && \left. - \frac{2 x (R - y)}{x^{2} + (R - y)^{2}} - \frac{2 x (R + y)}{x^{2} + (R + y)^{2}} \right\}, \\[10pt] \emph{v} &=& -\frac{F}{4\pi\!\mu} \left\{ \left(\frac{\kappa + 1}{2}\right) \ln \left( \frac{x^{2} + (R + y)^{2}}{x^{2} + (R - y)^{2}} \right) - \frac{(\kappa - 1)y}{R}\right. \\[6pt] &&\left. - \frac{x^{2} - (R - y)^{2}}{x^{2} + (R - y)^{2}} + \frac{x^{2} - (R + y)^{2}}{x^{2} + (R + y)^{2}} \right\}. \end{array} $$

(12)

Note that for the boundary condition of prescribed traction and for elastic deformation, the stress distribution within the circular disk does not depend on the elastic constants of the body. This property holds for any elastic problem of a two-dimensional simply-connected region composed of homogeneous and isotropic elastic solid.

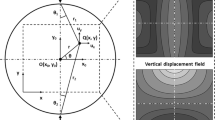
For the case where the compressive force is distributed over a finite region, we first consider the problem as shown in Fig. 9. The stresses and the displacements within the disk sample can be calculated using the Green’s functions given below. Let δ ₁ = π/2 − α and δ ₂ = 2π − (π/2 − α), where α represents the variable angle shown in Fig. 9. Thus, the two complex variables ξ ₁ and ξ ₂ in equation (8), are $\xi_{1} = R \exp(i(\pi/2 - \alpha))$ and $\xi_{2} = R \exp(-i(\pi/2 - \alpha))$. Also, let the concentrated force P = − i(δF), where δF is real. Then from equations (9) and (10), we have

$$ \begin{array}{rcl} \label{eq:stress-distributed-force} \delta\sigma_{x} && \frac{1}{\pi} \left\{ \frac{2 (y R\cos\alpha)(x R\sin\alpha)^{2}} {\left[(y R\cos\alpha)^{2} (x R\sin\alpha)^{2}\right]^{2}}\right. \\[-1pt] &&{\kern14pt} \left.- \frac{2 (y R\cos\alpha)(x R\sin\alpha)^{2}} {\left[(y R\cos\alpha)^{2} (x R\sin\alpha)^{2}\right]^{2}} + \frac{\cos\alpha}{R} \right\}\\[-1pt] &&{\kern14pt} \times\! \left(\frac{\delta{F}}{\delta{\eta}}\right)\delta{\eta}, \\[-1pt] \delta\sigma_{y} && \frac{1}{\pi} \left\{ \frac{2 (y R\cos\alpha)^{3}} {\left[(y R\cos\alpha)^{2} (xR\sin\alpha)^{2}\right]^{2}}\right. \\[-1pt] &&{\kern14pt} \left.- \frac{2 (y R\cos\alpha)^{3}} {\left[(y R\cos\alpha)^{2} (x R\sin\alpha)^{2}\right]^{2}} + \frac{\cos\alpha}{R} \right\}\\[-1pt] &&{\kern14pt} \times\! \left(\frac{\delta{F}}{\delta{\eta}}\right)\delta{\eta},\\ \delta\tau_{xy} && \frac{1}{\pi} \left\{ \frac{2 (y R\cos\alpha)^{2}(x R\sin\alpha)} {\left[(y - R\cos\alpha)^{2} + (x R\sin\alpha)^{2}\right]^{2}}\right. \\[-1pt] &&{\kern14pt} \left.- \frac{2 (y R\cos\alpha)^{2}(x R\sin\alpha)} {\left[(y R\cos\alpha)^{2} (x R\sin\alpha)^{2}\right]^{2}} \right\}\\[-1pt] &&{\kern14pt} \times\! \left(\frac{\delta{F}}{\delta{\eta}}\right)\delta{\eta}, \end{array} $$

(13)

and

$$ \begin{array}{rcl}\label{eq:displacement-distributed-force} \delta{u}&\!=\!& \frac{1}{4\pi\!\mu} \left\{ (\kappa\!-\!1) \tan^{-1}\! \left( \frac{2 R\cos\alpha (x\!-\!R\sin\alpha)} {y^{2}\!-\!R^{2}\cos^{2}\alpha\!+\!(x\!-\!R\sin\alpha)^{2}} \right)\right. \\[0.5ex] &&+ \frac{(\kappa\!-\!1) x\cos\alpha}{R}\!-\! \frac{2(y\!-\!R\cos\alpha)(x\!-\!R\sin\alpha)} {(y\!-\!R\cos\alpha)^{2}\!+\!(x\!-\!R\sin\alpha)^{2}} \\[0.5ex] &&\left. + \frac{2(y\!+\!R\cos\alpha)(x\!-\!R\sin\alpha)} {(y\!+\!R\cos\alpha)^{2}\!+\!(x\!-\!R\sin\alpha)^{2}} \right\} \left(\frac{\delta{F}}{\delta{\eta}}\right)\delta{\eta}, \\[1.0ex] \delta{\emph{v}}&\!=\!& \frac{1}{4\pi\!\mu} \left\{ \left(\frac{\kappa\!+\!1}{2}\right) \ln \left( \frac{(y\!-\!R\cos\alpha)^{2}\!+\!(x \!-\! R\sin\alpha)^{2}} {(y\!+\!R\cos\alpha)^{2}\!+\!(x \!-\! R\sin\alpha)^{2}} \right)\right. \\[0.5ex] &&+ \frac{(\kappa\!-\!1)y\cos\alpha}{R}\!-\! \frac{(y\!-\!R\cos\alpha)^{2}\!-\!(x\!-\!R\sin\alpha)^{2}} {(y\!-\!R\cos\alpha)^{2}\!+\!(x\!-\!R\sin\alpha)^{2}} \\[0.5ex] &&\left. + \frac{(y\!+\!R\cos\alpha)^{2}\!-\!(x\!-\!R\sin\alpha)^{2}} {(y\!+\!R\cos\alpha)^{2}\!+\!(x\!-\!R\sin\alpha)^{2}} \right\} \left(\frac{\delta{F}}{\delta{\eta}}\right)\delta{\eta}. \end{array} $$

(14)

One may check that by setting α = 0 and δF = F in equations (13) and (14), equations (11) and (12) are recovered. For the contact of an elastic circular disk with a rigid flat surface, as depicted in Fig. 2(a), the variation of the distributed traction, δF/δη, is given by

$$\label{eq:contact-traction-variation} \frac{\delta{F}}{\delta{\eta}} = \frac{\sigma_{0}}{b} \sqrt{b^{2} - \eta^{2}}, $$

(15)

where b is the half width of the contact region shown in Fig. 9, and the constant σ ₀ and the length b are related to the total applied compressive force F by

$$\label{eq:contact-constants} \sigma_{0} = \sqrt{\frac{8\mu F}{(\kappa + 1)\pi R}}, \quad b = \sqrt{\frac{(\kappa + 1) R F}{2\pi\!\mu}}. $$

(16)

Finally, the stresses and the displacements within the disk sample can be obtained by

$$ \begin{array}{rcl} \sigma_{x} &=& \int_{-b}^{b} \left(\frac{\delta\sigma_{x}}{\delta{\eta}}\right)d{\eta}, \quad \sigma_{y} = \int_{-b}^{b} \left(\frac{\delta\sigma_{y}}{\delta{\eta}}\right)d{\eta}, \quad\\ \tau_{xy} &=& \int_{-b}^{b} \left(\frac{\delta\tau_{xy}}{\delta{\eta}}\right)d{\eta}, \end{array} $$

(17)

and

$$ u = \int_{-b}^{b} \left(\frac{\delta{u}}{\delta{\eta}}\right)d{\eta}, \quad \emph{v} = \int_{-b}^{b} \left(\frac{\delta{\emph{v}}}{\delta{\eta}}\right)d{\eta}. $$

(18)

We need to point out that although contact loading is considered here, the formulation is still based upon the assumption of infinitesimal deformation, i.e., b ≪ R. Some of the numerical results are shown in Fig. 2.

Fig. 9

Fundamental problem for constructing solutions of distributed load across portion of the circular disk boundary