Skip to main content
SpringerLink
Log in

What Can We Learn from a Semiparametric Factor Analysis of Item Responses and Response Time? An Illustration with the PISA 2015 Data

  • Application Reviews and Case Studies
  • Published:
Psychometrika Aims and scope Submit manuscript

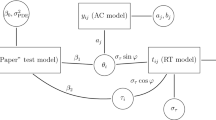
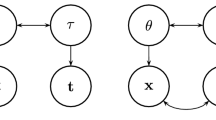
Abstract

It is widely believed that a joint factor analysis of item responses and response time (RT) may yield more precise ability scores that are conventionally predicted from responses only. For this purpose, a simple-structure factor model is often preferred as it only requires specifying an additional measurement model for item-level RT while leaving the original item response theory (IRT) model for responses intact. The added speed factor indicated by item-level RT correlates with the ability factor in the IRT model, allowing RT data to carry additional information about respondents’ ability. However, parametric simple-structure factor models are often restrictive and fit poorly to empirical data, which prompts under-confidence in the suitablity of a simple factor structure. In the present paper, we analyze the 2015 Programme for International Student Assessment mathematics data using a semiparametric simple-structure model. We conclude that a simple factor structure attains a decent fit after further parametric assumptions in the measurement model are sufficiently relaxed. Furthermore, our semiparametric model implies that the association between latent ability and speed/slowness is strong in the population, but the form of association is nonlinear. It follows that scoring based on the fitted model can substantially improve the precision of ability scores.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Notes

  1. With a slight abuse of terminology, both probability density functions for continuous random variables and probability mass functions for discrete random variables are referred to as densities.

  2. Slowness is the reversal of speed. We abide by the convention that the LV is positively associated with the MV.

  3. For simplicity, the same set of basis functions is used for the LVs in Eqs. 6, 9, and 14.

  4. Zhan et al. (2018) did not delete any extreme RT entries in their analysis. They performed Bayesian estimation with a somewhat informative prior configuration, which is presumably more stable in the presence of outlying observations.

  5. Note that this scoring function was also applied before computing the item-total correlation statistics in Table 2.

References

  • Abrahamowicz, M., & Ramsay, J. O. (1992). Multicategorical spline model for item response theory. Psychometrika, 57(1), 5–27.

    Article  Google Scholar 

  • Barton, M. A., & Lord, F. M. (1981). An upper asymptote for the three-parameter logistic item-response model. ETS Research Report Series, 1981(1), 1–8.

    Article  Google Scholar 

  • Bauer, D. J. (2005). A semiparametric approach to modeling nonlinear relations among latent variables. Structural Equation Modeling, 12(4), 513–535.

    Article  Google Scholar 

  • Birnbaum, A. (1968). Some latent trait models and their use in inferring an examinee’s ability. Statistical theories of mental test scores.

  • Bock, R. D., & Aitkin, M. (1981). Marginal maximum likelihood estimation of item parameters: Application of an EM algorithm. Psychometrika, 46(4), 443–459.

    Article  Google Scholar 

  • Bolsinova, M., De Boeck, P., & Tijmstra, J. (2017). Modelling conditional dependence between response time and accuracy. Psychometrika, 82(4), 1126–1148.

    Article  PubMed  Google Scholar 

  • Bolsinova, M., & Maris, G. (2016). A test for conditional independence between response time and accuracy. British Journal of Mathematical and Statistical Psychology, 69(1), 62–79.

    Article  PubMed  Google Scholar 

  • Bolsinova, M., & Molenaar, D. (2018). Modeling nonlinear conditional dependence between response time and accuracy. Frontiers in Psychology, 9, 1525.

    Article  PubMed  PubMed Central  Google Scholar 

  • Bolsinova, M., & Tijmstra, J. (2016). Posterior predictive checks for conditional independence between response time and accuracy. Journal of Educational and Behavioral Statistics, 41(2), 123–145.

    Article  Google Scholar 

  • Bolsinova, M., & Tijmstra, J. (2018). Improving precision of ability estimation: Getting more from response times. British Journal of Mathematical and Statistical Psychology, 71(1), 13–38.

    Article  PubMed  Google Scholar 

  • Bolsinova, M., Tijmstra, J., & Molenaar, D. (2017). Response moderation models for conditional dependence between response time and response accuracy. British Journal of Mathematical and Statistical Psychology, 70(2), 257–279.

    Article  PubMed  Google Scholar 

  • Borst, G., Kievit, R. A., Thompson, W. L., & Kosslyn, S. M. (2011). Mental rotation is not easily cognitively penetrable. Journal of Cognitive Psychology, 23(1), 60–75.

    Article  Google Scholar 

  • Cai, L. (2010). High-dimensional exploratory item factor analysis by a Metropolis–Hastings Robbins–Monro algorithm. Psychometrika, 75(1), 33–57.

    Article  Google Scholar 

  • Cai, L. (2010). Metropolis–Hastings Robbins–Monro algorithm for confirmatory item factor analysis. Journal of Educational and Behavioral Statistics, 35(3), 307–335.

    Article  Google Scholar 

  • Carroll, J. B. (1993). Human cognitive abilities: A survey of factor-analytic studies. Cambridge University Press.

  • Chatterjee, S. (2022). A survey of some recent developments in measures of association. arXiv preprint arXiv:2211.04702 .

  • Chen, Y., & Yang, Y. (2021). The one standard error rule for model selection: Does it work? Stats, 4(4), 868–892.

    Article  Google Scholar 

  • Cohen, J. (1988). Statistical power analysis for the behavioral sciences. Lawrence Erlbaum Associates.

  • Currie, I. D., Durban, M., & Eilers, P. H. (2006). Generalized linear array models with applications to multidimensional smoothing. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 68(2), 259–280.

    Article  Google Scholar 

  • Dagum, L., & Menon, R. (1998). OpenMP: An industry standard API for shared-memory programming. IEEE Computational Science and Engineering, 5(1), 46–55.

    Article  Google Scholar 

  • De Boeck, P., & Jeon, M. (2019). An overview of models for response times and processes in cognitive tests. Frontiers in Psychology, 10, 102.

    Article  PubMed  PubMed Central  Google Scholar 

  • De Boor, C. (1978). A practical guide to splines. Berlin: Springer.

    Book  Google Scholar 

  • Dempster, A. P., Laird, N. M., & Rubin, D. B. (1977). Maximum likelihood from incomplete data via the EM algorithm. Journal of the Royal Statistical Society: Series B, 39(1), 1–22.

    Google Scholar 

  • Deribo, T., Kroehne, U., & Goldhammer, F. (2021). Model-based treatment of rapid guessing. Journal of Educational Measurement, 58(2), 281–303.

    Article  Google Scholar 

  • Dou, X., Kuriki, S., Lin, G. D., & Richards, D. (2021). Dependence properties of b-spline copulas. Sankhya A, 83(1), 283–311.

    Article  Google Scholar 

  • Efron, B., & Tibshirani, R. (1994). An introduction to the bootstrap. Taylor & Francis.

  • Eilers, P. H., & Marx, B. D. (1996). Flexible smoothing with B-splines and penalties. Statistical science, 89–102.

  • Falk, C. F., & Cai, L. (2016). Maximum marginal likelihood estimation of a monotonic polynomial generalized partial credit model with applications to multiple group analysis. Psychometrika, 81(2), 434–460.

    Article  PubMed  Google Scholar 

  • Falk, C. F., & Cai, L. (2016). Semiparametric item response functions in the context of guessing. Journal of Educational Measurement, 53(2), 229–247.

    Article  Google Scholar 

  • Finn, B. (2015). Measuring motivation in low-stakes assessments. ETS Research Report Series, 2015(2), 1–17.

    Article  Google Scholar 

  • Geenens, G., & Lafaye de Micheaux, P. (2022). The hellinger correlation. Journal of the American Statistical Association, 117(538), 639–653.

    Article  Google Scholar 

  • Glas, C. A., & van der Linden, W. J. (2010). Marginal likelihood inference for a model for item responses and response times. British Journal of Mathematical and Statistical Psychology, 63(3), 603–626.

    Article  PubMed  Google Scholar 

  • Goldhammer, F. (2015). Measuring ability, speed, or both? challenges, psychometric solutions, and what can be gained from experimental control. Measurement: Interdisciplinary Research and Perspectives, 13(3–4), 133–164.

  • Gu, C. (1992). Cross-validating non-Gaussian data. Journal of Computational and Graphical Statistics, 1(2), 169–179.

    Google Scholar 

  • Gu, C. (1995). Smoothing spline density estimation: Conditional distribution. Statistica Sinica, 709–726.

  • Gu, C. (2013). Smoothing spline ANOVA models. Springer.

  • Gu, M. G., & Kong, F. H. (1998). A stochastic approximation algorithm with Markov chain Monte-Carlo method for incomplete data estimation problems. Proceedings of the National Academy of Sciences, 95(13), 7270–7274.

    Article  Google Scholar 

  • Gulliksen, H. (1950). Theory of mental tests. London: Wiley.

    Book  Google Scholar 

  • Hastie, T., Tibshirani, R., & Friedman, J. (2009). The elements of statistical learning: Data mining, inference, and prediction (2nd ed.). Berlin: Springer.

    Book  Google Scholar 

  • Jöreskog, K. G. (1969). A general approach to confirmatory maximum likelihood factor analysis. Psychometrika, 34(2), 183–202.

    Article  Google Scholar 

  • Kang, H.-A. (2017). Penalized partial likelihood inference of proportional hazards latent trait models. British Journal of Mathematical and Statistical Psychology, 70(2), 187–208.

    Article  PubMed  Google Scholar 

  • Kang, I., De Boeck, P., & Ratcliff, R. (2022). Modeling conditional dependence of response accuracy and response time with the diffusion item response theory model. Psychometrika, 1–24.

  • Kang, I., Jeon, M., & Partchev, I. (2023). A latent space diffusion item response theory model to explore conditional dependence between responses and response times. Psychometrika, 1–35.

  • Kang, I., Molenaar, D., & Ratcliff, R. (2023). A modeling framework to examine psychological processes underlying ordinal responses and response times of psychometric data. Psychometrika, 1–35.

  • Kauermann, G., Schellhase, C., & Ruppert, D. (2013). Flexible copula density estimation with penalized hierarchical b-splines. Scandinavian Journal of Statistics, 40(4), 685–705.

    Article  Google Scholar 

  • Kyllonen, P. C., & Zu, J. (2016). Use of response time for measuring cognitive ability. Journal of Intelligence, 4(4), 14.

    Article  Google Scholar 

  • Lee, Y.-H., & Chen, H. (2011). A review of recent response-time analyses in educational testing. Psychological Test and Assessment Modeling, 53(3), 359.

    Google Scholar 

  • Lee, Y.-H., & Jia, Y. (2014). Using response time to investigate students’ test-taking behaviors in a NAEP computer-based study. Large-Scale Assessments in Education, 2(1), 1–24.

  • Liu, Y., Magnus, B. E., & Thissen, D. (2016). Modeling and testing differential item functioning in unidimensional binary item response models with a single continuous covariate: A functional data analysis approach. Psychometrika, 81, 371–398.

    Article  PubMed  Google Scholar 

  • Liu, Y., & Wang, W. (2022). Semiparametric factor analysis for item-level response time data. Psychometrika, 87(2), 666–692.

    Article  PubMed  Google Scholar 

  • Liu, Y., & Yang, J. S. (2018a). Bootstrap-calibrated interval estimates for latent variable scores in item response theory. Psychometrika, 83(2), 333–354.

  • Liu, Y., & Yang, J. S. (2018). Interval estimation of latent variable scores in item response theory. Journal of Educational and Behavioral Statistics, 43(3), 259–285.

  • Luce, R. D. (1986). Response times: Their role in inferring elementary mental organization. Oxford University Press.

  • McDonald, R. P. (1982). Linear versus models in item response theory. Applied Psychological Measurement, 6(4), 379–396.

    Article  Google Scholar 

  • Meng, X.-B., Tao, J., & Chang, H.-H. (2015). A conditional joint modeling approach for locally dependent item responses and response times. Journal of Educational Measurement, 52(1), 1–27.

    Article  Google Scholar 

  • Molenaar, D., Tuerlinckx, F., & van der Maas, H. L. (2015). A bivariate generalized linear item response theory modeling framework to the analysis of responses and response times. Multivariate Behavioral Research, 50(1), 56–74.

    Article  PubMed  Google Scholar 

  • Molenaar, D., Tuerlinckx, F., & van der Maas, H. L. (2015). A generalized linear factor model approach to the hierarchical framework for responses and response times. British Journal of Mathematical and Statistical Psychology, 68(2), 197–219.

    Article  PubMed  Google Scholar 

  • Mordant, G., & Segers, J. (2022). Measuring dependence between random vectors via optimal transport. Journal of Multivariate Analysis, 189, 104912.

    Article  Google Scholar 

  • Nelsen, R. B. (2006). An introduction to copulas. Berlin: Springer.

    Google Scholar 

  • Nocedal, J., & Wright, S. (2006). Numerical optimization. New York: Springer.

    Google Scholar 

  • OECD. (2016). PISA 2015 assessment and analytical framework: Science, reading, mathematic and financial literacy. Paris: PISA, OECD Publishing.

  • Pek, J., Sterba, S. K., Kok, B. E., & Bauer, D. J. (2009). Estimating and visualizing nonlinear relations among latent variables: A semiparametric approach. Multivariate Behavioral Research, 44(4), 407–436.

    Article  PubMed  Google Scholar 

  • Qian, H., Staniewska, D., Reckase, M., & Woo, A. (2016). Using response time to detect item preknowledge in computer-based licensure examinations. Educational Measurement: Issues and Practice, 35(1), 38–47.

    Article  Google Scholar 

  • Ramsay, J. O., & Winsberg, S. (1991). Maximum marginal likelihood estimation for semiparametric item analysis. Psychometrika, 56(3), 365–379.

    Article  Google Scholar 

  • Ranger, J., & Kuhn, J.-T. (2012). A flexible latent trait model for response times in tests. Psychometrika, 77, 31–47.

    Article  Google Scholar 

  • Ranger, J., & Ortner, T. (2012). The case of dependency of responses and response times: A modeling approach based on standard latent trait models. Psychological Test and Assessment Modeling, 54(2), 128.

    Google Scholar 

  • Rossi, N., Wang, X., & Ramsay, J. O. (2002). Nonparametric item response function estimates with the EM algorithm. Journal of Educational and Behavioral Statistics, 27(3), 291–317.

    Article  Google Scholar 

  • Sinharay, S. (2020). Detection of item preknowledge using response times. Applied Psychological Measurement, 44(5), 376–392.

    Article  PubMed  PubMed Central  Google Scholar 

  • Sinharay, S., & Johnson, M. S. (2020). The use of item scores and response times to detect examinees who may have benefited from item preknowledge. British Journal of Mathematical and Statistical Psychology, 73(3), 397–419.

    Article  PubMed  Google Scholar 

  • Sklar, M. (1959). Fonctions de répartition àn dimensions et leurs marges. Publications de l’Institut de statistique de l’Université de Paris, 8, 229–231.

    Google Scholar 

  • Thissen, D., & Wainer, H. (2001). Test scoring. Taylor & Francis.

  • Thorndike, E. L., Bregman, E. O., Cobb, M. V., & Woodyard, E. (1926). The measurement of intelligence. Teachers College Bureau of Publications.

  • Thurstone, L. L. (1937). Ability, motivation, and speed. Psychometrika, 2(4), 249–254.

    Article  Google Scholar 

  • van der Linden, W. J. (2007). A hierarchical framework for modeling speed and accuracy on test items. Psychometrika, 72(3), 287–308.

    Article  Google Scholar 

  • van der Linden, W. J., & Glas, C. A. (2010). Statistical tests of conditional independence between responses and/or response times on test items. Psychometrika, 75(1), 120–139.

    Article  Google Scholar 

  • van der Linden, W. J., Klein Entink, R. H., & Fox, J.-P. (2010). IRT parameter estimation with response times as collateral information. Applied Psychological Measurement, 34(5), 327–347.

    Article  Google Scholar 

  • van der Linden, W. J., Scrams, D. J., & Schnipke, D. L. (1999). Using response-time constraints to control for differential speededness in computerized adaptive testing. Applied Psychological Measurement, 23(3), 195–210.

    Article  Google Scholar 

  • von Davier, M., Khorramdel, L., He, Q., Shin, H. J., & Chen, H. (2019). Developments in psychometric population models for technology-based large-scale assessments: An overview of challenges and opportunities. Journal of Educational and Behavioral Statistics, 44(6), 671–705.

    Article  Google Scholar 

  • Wang, C., Chang, H.-H., & Douglas, J. A. (2013). The linear transformation model with frailties for the analysis of item response times. British Journal of Mathematical and Statistical Psychology, 66(1), 144–168.

    Article  PubMed  Google Scholar 

  • Wang, C., Fan, Z., Chang, H.-H., & Douglas, J. A. (2013). A semiparametric model for jointly analyzing response times and accuracy in computerized testing. Journal of Educational and Behavioral Statistics, 38(4), 381–417.

    Article  Google Scholar 

  • Wise, S. L. (2017). Rapid-guessing behavior: Its identification, interpretation, and implications. Educational Measurement: Issues and Practice, 36(4), 52–61.

    Article  Google Scholar 

  • Wise, S. L., & Kong, X. (2005). Response time effort: A new measure of examinee motivation in computer-based tests. Applied Measurement in Education, 18(2), 163–183.

    Article  Google Scholar 

  • Woods, C. M., & Lin, N. (2009). Item response theory with estimation of the latent density using Davidian curves. Applied Psychological Measurement, 33(2), 102–117.

    Article  Google Scholar 

  • Yang, J. S., Hansen, M., & Cai, L. (2012). Characterizing sources of uncertainty in item response theory scale scores. Educational and Psychological Measurement, 72(2), 264–290.

    Article  PubMed  Google Scholar 

  • Zhan, P., Liao, M., & Bian, Y. (2018). Joint testlet cognitive diagnosis modeling for paired local item dependence in response times and response accuracy. Frontiers in Psychology, 9, 607.

    Article  PubMed  PubMed Central  Google Scholar 

  • Zhang, D., & Davidian, M. (2001). Linear mixed models with flexible distributions of random effects for longitudinal data. Biometrics, 57(3), 795–802.

  • Zhang, X., Wang, C., Weiss, D. J., & Tao, J. (2021). Bayesian inference for IRT models with non-normal latent trait distributions. Multivariate Behavioral Research, 56(5), 703–723.

    Article  PubMed  Google Scholar 

Download references

Funding

The work is sponsored by the National Science Foundation under grant No. 1826535.

Author information

Authors and Affiliations

  1. Department of Human Development and Quantitative Methodology, University of Maryland, 3304R Benjamin Bldg, 3942 Campus Dr, College Park, MD,  20742, USA

    Yang Liu & Weimeng Wang

Authors
  1. Yang Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Weimeng Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yang Liu.

Ethics declarations

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Data availability

The dataset analyzed during the current study is available in the OECD PISA Database (https://www.oecd.org/pisa/data/).

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

The manuscript was handled by the ARCS Editor Dr. Nidhi Kohli.

Supplementary Information

Below is the link to the electronic supplementary material.

Supplementary file 1 (pdf 1224 KB)

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liu, Y., Wang, W. What Can We Learn from a Semiparametric Factor Analysis of Item Responses and Response Time? An Illustration with the PISA 2015 Data. Psychometrika (2023). https://doi.org/10.1007/s11336-023-09936-3

Download citation

  • Received:

  • Published:

  • DOI: https://doi.org/10.1007/s11336-023-09936-3

Keywords

Search

Navigation