1 Introduction

As a consequence of the rapidly increasing demand for high-speed wireless communication networks, wide bandwidth, huge data transfer, infinite capacity, wide-ranging applications, and a high degree of security, the emerging technology of visible light communication (VLC) has become a promising solution for such requirements of wireless communication networks [1,2,3]. Indoor VLC systems use common household light sources, especially white LEDs, as transmitters, while photo detectors are used as receivers [1,2,3,4].

The early research of indoor VLC issues was primarily concerned with the physical layer of the optical wireless network including light transmitters, photodetector receivers, and optical channel modeling. Non-cellular VLC systems provide good wireless network for small indoor areas [1,2,3,4]. On the other side, cellular VLC is recommended for satisfactory signal coverage and user mobility in large indoor areas [5,6,7,8,9]. Recent research work in the field of indoor VLC has become more focused on the communication system level by employing cellular arrangements of multi-access and multi-user communication with highlights on the issues of dynamic resource allocation, mobility, and handover. This needs the utilization of multiple access points (APs) that are distributed over the indoor area for full coverage. Such investigations has introduced the problem of intercell interference (ICI) caused by signals transmitted by the APs of adjacent cells that are simultaneously received by all the users in the VLC domain. The problem of cancelling or mitigating the ICI in indoor cellular VLC has become a top priority for research work in this field. For example, the work of [10] proposes a scheme for indoor cellular VLC to mitigate the ICI by making use of optimized angle diversity receiver (ADR). Such a receiver is constructed by a horizontal top detector and number of inclined side detectors. This scheme succeeds to improve the ICI by \(18.6\,{\text{dB}}\). In [11], the concept of intelligent transport system (ITS) is applied for the outdoor VLC employing multiple-input–single-output (MISO) system to improve its performance by mitigating the effect of interference in general. The ON–OFF keying (OOK) is employed as a modulation technique for light signaling to achieve signal-to-interference-plus-noise-ratio (SINR) of \(18\,{\text{dB}}\) and BER of \(1\, \times \,10^{ - 4}\). The work of [12] proposes future design and implementation of power-domain (PD) optical non-orthogonal multiple access (O-NOMA) in VLC systems. It is shown that integrating such emerging technology in indoor VLC will improve the SINR and an example of achieving BER of \(1\, \times \,10^{ - 4}\) is demonstrated. The work of [13] proposes an indoor VLC system that employs a hexagonal array arrangement with either soft frequency reuse (SFR) or Fractional frequency reuse (FFR) with OFDMA to improve the BER. It uses two modulation techniques for light signaling, the OOK and the 16-quadrature amplitude modulation (16-QAM). When the OOK is used, the achieved BER is \(2\, \times \,10^{ - 5}\). When the 16-QAM is used the achieved BER is \(8\, \times \,10^{ - 6}\). In [13], the pulse amplitude modulation (PAM) technique with a Hadamard code (HC) is proposed to build an algorithm that removes the ICI in indoor VLC. The application of this algorithm results in BER of \(1\, \times \,10^{ - 8}\). The method presented in [5] is based on the optimization of the optical attocell positions in indoor VLC to increase the minimum received power from \(- 1.29\) to \(- 0.225\,{\text{dBm}}\). Consequently, the employment of the OOK for light signaling leads to BER of \(4.4\, \times \,10^{ - 8}\), whereas the employment of the BPSK modulation leads to BER of \(6.6 \times 10^{ - 14}\).

Theoretically, the data rate of the VLC system can reach several Tera-bits-per-second (\({\text{Tbps}}\)) as it operates in a very wideband of the frequency (\(385 - 790\,{\text{THz}}\)). However, the practical VLC systems are limited to much lower data rates [14]. To the best of our knowledge, the highest data rates of the experimental VLC systems recorded recently range from 10 up to 100 Gbps [15,16,17,18]. In [15], data rate of 10 Gbps is accomplished by a VLC system employing blue series-biased \(\mu\) LED array. In [16], data rate of 15.73 Gbps is demonstrated by a VLC system employing four single color low-cost LEDs. In [17], data rate of 20.231 Gbps is realized by a VLC system using tricolor R/G/B LD as the source of light. In [19], data rate of 35 Gbps is achieved by a four-color multiplexed VLC system using laser diode (LD) emitting white ligh with micro-electro-mechanical (MEMS) mirror-based beam-steering system. In [18], data rate of 100 Gbps is realized by an indoor VLC system employing optical code division multiplexing and polarization division multiplexing.

The present work introduces an indoor cellular-based VLC system with hexagonal-shaped cells that are arranged to cover every point in a wide rectangular indoor area. A novel scheme is proposed for this VLC system by employing the optical wavelength division multiple access (WDMA) to establish optical wireless connections with the multiple users in the covered area. The total width of the visible light spectrum utilized for VLC is divided into a number of the wavelength divisions. Each wavelength division channel (WDC) can be assigned to an individual user in the shared medium. For enhancing the proposed system capacity, the optical spectrum is efficiently utilized by employing wavelength reuse with the appropriate shape and size of the wavelength reuse pattern. As a result of applying optical wavelength reuse, the intercell interference (ICI) is encountered in the VLC system and may affect its performance. A novel model is established for the communication channel of the proposed scheme for cellular indoor VLC. In this model, the received optical power (signal strength) and the ICI at every point in the indoor are evaluated. The ICI resulting in a given cell from employing wavelength reuse are accurately assessed by considering the interfering signals caused by all the multiple APs of the surrounding cells having the same wavelength divisions as the cell under investigation. The resulting distribution of the signal-to-ICI ratio (SICIR) is assessed at every point over the indoor area. Also, the distribution of the BER is evaluated under the assumption that the OOK modulation technique is used for optical signaling in the proposed VLC scheme.

After the introduction section, this work is presented as follows. The design of the indoor VLC system based on hexagonal-cell arrangement is explained in Sect. 2. A novel method for the assessment and analysis of the ICI encountered in the cells of the indoor area is explained in Sect. 3. The procedure applied to get the VLC system operating with satisfactory performance under the dynamic conditions is described in Sect. 4. The results of simulation using a Matlab® program developed for performance assessment of the VLC are presented and discussed in Sect. 5. A comparative performance analysis is summarized in Sect. 5 with reference to other designs presented in the literature. Section 6 outlines the most important conclusions.

2 Design of the Proposed Cellular VLC System

Cellular VLC system is deployed to enable seamless communication over large indoor areas. In this system, the entire area is uniformly divided to take the form of a grid with either rectangular or hexagonal cells [7]. In a VLC system with hexagonal-cell arrangement inside a rectangular room, the area over which the users move is divided into hexagonal cells as shown in Fig. 1. Within the boundaries of each cell, the moving users can be connected to an AP dedicated to this cell and placed on the room ceiling just above the cell center as shown in Fig. 2.

Fig. 1
figure 1

The room floor is divided using hexagonal-cell arrangement for indoor cellular VLC

Full size image
Fig. 2
figure 2

Indoor cellular VLC with hexagonal-cell arrangement and utilizing wavelength reuse

Full size image

The hexagonal-cell arrangement is considered in the proposed VLC system to cover the large indoor areas as described above. The area, \({A}_{C}\) of the hexagonal cell is expressed in terms of the cell radius, \(R\), as follows.

$$A_{C} = \frac{3\sqrt 3 }{2}R^{2}$$
(1)

The area of the rectangular room shown in Fig. 2 can be calculated as \({A}_{R}={L}_{x}{L}_{y}\). Thus, the total number of hexagonal cells in this room can be calculated as follows.

$$N_{C} = \frac{{A_{R} }}{{A_{C} }} = \frac{{2 L_{x} L_{y} }}{{3\sqrt 3 R^{2} }}$$
(2)

In the proposed cellular-based VLC system, the wavelength division multiple access (WDMA) [20] is used to enable multiple users to communicate through the network of APs that cover the large indoor area. In this scheme, each active user can be assigned a unique wavelength division for connection to the wireless network. To avoid high level of interference, different wavelength ranges of the visible light spectrum can be utilized in the adjacent cells. However, to enhance the spectral efficiency and thereby enhancing the entire system capacity, the wavelength reuse is employed in this system with the appropriate pattern size [9]. For hexagonal-cell arrangement the applicable wavelength reuse pattern size, \(k\), is constrained by the following rule.

$$k = i^{2} + ij + j^{2} ,\quad i = 0,1,2,..,\quad j = 1,2,..$$
(3)

Three possible hexagonal-cell arrangement of indoor VLC using three different sizes of the wavelength reuse patterns calculated using the rule (3) are presented in Fig. 3: \(k=3 (i=1, j=1)\), \(k=4 (i=0, j=2)\) and \(k=7 (i=1, j=2)\). The cells of the same color use the same range of the visible light wavelength for WDMA. It is shown in all the three patterns that no contiguous cells have the same wavelength range.

Fig. 3
figure 3

Hexagonal-cell arrangement of the VLC system showing wavelength reuse patterns of size a \(k=3\), b \(k=4\), and c \(k=7\), in indoor cellular VLC system

Full size image

The distance between the cell center and the center of the nearest cell employing the same wavelength range is known as the wavelength reuse distance, \(D\). It can be shown that the distance, \(D\), can be expressed in terms of the cell radius, \(R\), and the wavelength reuse pattern size, \(k\), as follows.

$$D = \sqrt {3k} ,\quad k = 1,3,4,7,9,12, \ldots$$
(4)

3 Channel Model and Evaluation of the Intercell Interference

Each hexagonal cell is covered by an AP that is small LED (point source) mounted on the room ceiling at a height \(h\) above the horizontal plane of the moving users. The LED source is placed just above the center of the hexagonal cell to produces uniform illumination and signal coverage. This LED emits a luminous flux intensity that can be expressed as follows [1].

$$I\left( \theta \right) = I_{0} \cos \theta$$
(5)

where the \(\theta\) is the angle between the line-of-sight (LOS) and the normal to the plane of the room ceiling as at the corresponding AP shown in Fig. 2 and the amplitude \({I}_{0}\) has the following dependence on the visible light power, \({P}_{Tx}\), transmitted by each this AP [1].

$$I_{0} = \frac{{P_{Tx} }}{\pi }$$
(6)

The received power density at the location of the receiver is the horizontal illuminance caused by the light emitted from the LED source at the user location. Thus, the received power density can be expressed as follows [2].

$$E\left( \theta \right) = \frac{{I_{0} \left( {\cos \theta } \right)^{4} }}{{h^{2} }}$$
(7)

3.1 Dependence of the ICI on the Cell Radius and the Frequency Reuse Pattern Size

In the proposed cellular-based VLC system, the WDMA is used to enable multi-user wireless communication through the network of APs that cover the entire indoor area. The wavelength reuse is employed in this system with the appropriate pattern size to enhance the spectral efficiency and thereby enhancing the entire system capacity. The drawback of employing wavelength reuse is the intercell interference (ICI) encountered in the cells due the signals from different APs employing the same wavelength range.

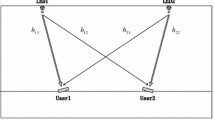
The method of calculating the illuminance caused by the ICI is described in this section. Let a mobile receiver be existing within the boundaries of cell 1 as shown in Fig. 4. The desired signal at the location of the mobile unit is the illuminance (power density) received from AP1 (covering cell 1). The undesired (interfering) signal is the illuminance received from AP \(n\) that utilizes the same wavelength to cover cell \(n\).

Fig. 4
figure 4

Evaluation of the ICI in a cell caused by an AP of a different cell utilizing the same wavelength

Full size image

From the geometry shown in Fig. 4 and by making use of (6) and (7), the signal level, which is the illuminance received by the mobile unit from AP1 is given as follows [1,2,3,4].

$$E = \frac{{P_{Tx} \left( {\cos \theta } \right)^{4} }}{{\pi { }h^{2} }}$$
(8)

The ICI, which is the illuminance received by the same user from AP \(n\), is given as follows.

$$E_{{F_{n} }} = \frac{{P_{Tx} \left( {\cos \theta_{{F_{n} }} } \right)^{4} }}{{\pi { }h^{2} }}$$
(9)

Making use of (8) and (9), the signal-to-ICI ratio (SICIR), which is the ratio of (\(E/{{E}_{F}}_{n}\)) can be evaluated as follows.

$${\text{SICIR}}_{n} = \frac{E}{{E_{{F_{n} }} }} = \left( {\frac{\cos \theta }{{\cos \theta_{{F_{n} }} }}} \right)^{4}$$
(10)

From the geometry shown in Fig. 4, \(\mathrm{cos}\theta\) is given as follows.

$$\cos \theta = \frac{h}{D} = \frac{h}{{\sqrt {h^{2} + r^{2} } }}$$
(11)

Also, \(\mathrm{cos}{\theta }_{F}\) is given as follows.

$$\cos \theta_{{F_{n} }} = \frac{h}{{D_{{F_{n} }} }} = \frac{h}{{\sqrt {h^{2} + r_{{F_{n} }}^{2} } }}$$
(12)

Thus, by substitution from (11) and (12) into (10), the SICIR due to the ICI caused by only AP \(n\) at the location of the mobile receiver indicated in Fig. 4 can be evaluated as follows.

$${\text{SICIR}}_{n} = \left( {\frac{{h^{2} + r_{{F_{n} }}^{2} }}{{h^{2} + r^{2} }}} \right)^{2}$$
(13)

From the geometry shown in Fig. 4 and making use of (4), the distance \({r}_{{F}_{n}}\) can be expressed in terms of the distance \(r\) and the cell radius, \(R\), and the wavelength reuse pattern size as follows.

$$r_{{F_{n} }} = r + D = r + \sqrt {3k} R$$
(14)

Substituting from (14) into (13), the SICIR due to one of the APs employing the same wavelength range for VLC can be expressed as follows.

$${\text{SICIR}}_{n} = \left[ {\frac{{h^{2} + \left( {r + \sqrt {3k} R} \right)^{2} }}{{h^{2} + r^{2} }}} \right]^{2}$$
(15)

The expression (15) can be rewritten as follows.

$${\text{SICIR}}_{n} = \left[ {1 + \frac{{2r\sqrt {3k} R + 3kR^{2} }}{{h^{2} + r^{2} }}} \right]^{2}$$
(16)

It is clear from (16) that increasing \(k\) and/or \(R\) results in increasing the SICIR. Also, it is clear that increasing the height \(h\) of the APs above the room floor results in decreasing the SICIR. Thus, it may be concluded that increasing \(R\) and \(k\) and decreasing \(h\) results in mitigating the ICI resulting from the wavelength reuse in the VLC system at every point in the indoor area.

Considering the total ICI caused by all the APs utilizing the same wavelength as the cell of the mobile receiver, the overall SICIR ratio at this receiver can be calculated as follows.

$${\text{SICIR}} = \frac{E}{{\mathop \sum \nolimits_{n = 1}^{N} E_{{F_{n} }} }} = \left( {\frac{\cos \theta }{{\mathop \sum \nolimits_{n = 1}^{N} \cos \theta_{{F_{n} }} }}} \right)^{4} = \left[ {\left( {h^{2} + r^{2} } \right)\mathop \sum \limits_{n = 1}^{N} \frac{1}{{h^{2} + r_{{F_{n} }}^{2} }}} \right]^{ - 2}$$
(17)

where \(N\) is the total number of APs utilizing the same wavelength as the cell of the mobile receiver.

3.2 Dependence of the VLC System Capacity on the Cell Radius and the Frequency Reuse Pattern Size

The communication system capacity is defined as the maximum of the product of multiplying the number of users by the user spectral efficiency. Thus, the evaluation of the VLC system capacity requires the calculation of the maximum number of users in the system and its dependence on the cell radius, \(R\) and the wavelength reuse pattern size, \(k\).

3.2.1 Maximum Number of Users in the VLC System

Let the total width of the visible light spectrum utilized for VLC be \(\Lambda ={\uplambda }_{max}-{\uplambda }_{min}\), where \({\uplambda }_{max}\) and \({\uplambda }_{min}\) are the longest and shortest wavelengths used for communication. Also, let the spectral width of the wavelength division channel (WDC) assigned to the individual users be \(\delta\Lambda\). Thus, the total number of wavelength divisions, \(N\), can be determined as follows.

$$N = \frac{{\Lambda }}{{\delta {\Lambda }}}$$
(18)

The bandwidth, \(B\), of the light spectrum utilized for communication is evaluated as follows.

$$B = {\text{c}}\left( {\frac{1}{{\lambda_{min} }} - \frac{1}{{\lambda_{max} }}} \right)$$
(19)

where \(c\) is the velocity of light in free space.

In a VLC system employing wavelength reuse pattern of size \(k\), the number of WDCs,\({n}_{W}\), per cell can be calculated as follows.

$$\overline{n}_{W} = \frac{1}{{N_{C} }}\mathop \sum \limits_{m}^{{N_{C} }} n_{{W_{m} }} = \frac{N}{k}$$
(20)

Thus, the maximum number of users that can be served simultaneously in the cell number \(m\) is equal to \({{n}_{W}}_{m}\). This means the maximum number of users that can be simultaneously served in the entire area covered by the VLC (i.e. the total number of WDCs in the system) is given as follows.

$$N_{u} = \mathop \sum \limits_{m}^{{N_{C} }} n_{{W_{m} }}$$
(21)

The average number of WDCs per cell, \({\overline{n} }_{W}\), is given as follows.

$$\overline{n}_{W} = \frac{1}{{N_{C} }}\mathop \sum \limits_{m}^{{N_{C} }} n_{{W_{m} }}$$
(22)

Making use of (22), the maximum of served users in the VLC system can be calculated as follows.

$$N_{u} = N_{C} \overline{n}_{W}$$
(23)

Substituting from (2) and (20) into (23), the following expression gives maximum number of users that can be served simultaneously in the entire indoor VLC system.

$$N_{u} = \frac{{2 N L_{x} L_{y} }}{{3\sqrt 3 k R^{2} }}$$
(24)

3.2.2 VLC System Capacity

Under the assumption of employing the WDMA in the shared medium of the VLC, each active user is assigned a unique WDC. The maximum number of users per cell is equal to the WDCs in each cell. Thus, the capacities of the cells are equal and, hence, the capacity of the cell number \(m\) can be evaluated as follows.

$$C_{{{\text{cell}}_{m} }} = n_{W} \frac{{r_{b} }}{B}$$
(25)

The overall VLC system capacity can be evaluated as the summation of the capacity of each cell.

$$C = \mathop \sum \limits_{m = 1}^{{N_{C} }} C_{{{\text{cell}}_{m} }} = \frac{{r_{b} }}{B}\mathop \sum \limits_{m = 1}^{{N_{C} }} n_{W}$$
(26)

Making use of (21) into (26), the following expression is obtained for the overall VLC system capacity.

$$C = N_{u} \frac{{r_{b} }}{B}$$
(27)

where \({r}_{b}\) is the bit rate in bps assigned to the individual users.

Substituting from (24) into (27), the following expression is obtained for the VCL system capacity.

$$C = \frac{{2 r_{b} N L_{x} L_{y} }}{{3\sqrt 3 B k R^{2} }}$$
(28)

It is clear from (28) that the VLC system capacity is inversely proportional to the square of (\(\sqrt{k} R\)). On the other hand, the expression (16) shows that the SICIR is a growing fourth-order polynomial in the same quantity (\(\sqrt{k} R\)). Thus, a compromise should be made regarding the optimum values of \(R\) and \(k\) to get satisfactory performance regarding the VLC system capacity together with the SICIR.

4 Procedure of Dynamic Optimization of the Indoor Cellular VLC

The system dynamics under consideration in the present context involve the continuous changes of the locations and number of the mobile units in each cell, the continuous change of the mobile units in the entire indoor area covered by the VLC, and the movements of the mobile units leaving on cell and moving to a neighboring one. Under these dynamics the VLC system performance changes with time and thereby requiring continuous optimization to continuously improve the performance. Under these considerations of system dynamics, the algorithm described by the flowchart presented in Fig. 5 runs repeatedly (as a continuous loop) to calculate the values of \(R\) and \(k\) that give the satisfactory performance regarding the compromise of the BER averaged over the active users (connected mobile units) and the overall VLC system capacity. The objectives of this procedure are to minimize the average BER and to maximize the system capacity. At least, it is required to satisfy some preset threshold values regarding the maximum allowable BER (\({B}_{th}\)) and the minimum acceptable system capacity (\({C}_{th}\)), i.e. it is required to get the \(BER<{B}_{th}\) and \(C>{C}_{th}\). It is assumed that the numbers and locations of the Aps (that act as the light sources at the same time) can be controlled over the horizontal plane of the room ceiling.

Fig. 5
figure 5

Flowchart of the procedure applied to select the appropriate cell radius, \(R\), and wavelength reuse pattern size, \(k\), to achieve the optimum performance of the proposed VLC scheme

Full size image

5 Numerical Results and Discussions

The numerical results presented in this section are concerned with studying the effects of the cell radius (ranging from \(R = 0.8 \,{\text{m}}\) to \(R = 2\,{\text{m}}\)) and the size of the wavelength reuse pattern (ranging from \(k = 3\) to \(k = 12\)) on the VLC system performance regarding the system capacity and the BER caused by the ICI. In the following presentation of numerical results the indoor region under consideration is a closed rectangular room with the dimensions \(16 \,{\text{m}} \times 12 \,{\text{m}} \times 4\,{\text{m}}\). The APs are assumed to be white LED sources that are uniformly arranged over the room area at a height of \(3.8\,{\text{m}}\) above the floor. Also, it is considered that the receivers are moving horizontally at height of \(0.8\,{\text{m}}\) over the room floor. In the proposed VLC system, the multiple users are connected to the VLC wireless network by employing WDMA. For light signaling, the OOK is employed in which the dependence of the BER depends on the ratio \(E_{b} /N_{0}\) (i.e. the SICIR) as shown in Fig. 6 [21], where \(E_{b}\) is the bit energy and \(N_{0}\) is the noise power spectral density.

Fig. 6
figure 6

Relation between the BER and the ratio \({E}_{b}/{N}_{0}\) for OOK modulation technique

Full size image

5.1 Intercell Interference in VLC System with Small Cell Size and Small Wavelength Reuse Pattern

A cellular indoor VLC system with hexagonal-shaped cells has the arrangement presented in Fig. 7. This system has a cell radius \(R = 0.8\,{\text{m}}\) and wavelength reuse pattern size \(k = 3\). The range of the wavelength divisions assigned to users in each cell for WDMA is indicated in color code.

Fig. 7
figure 7

Arrangement of indoor cellular VLC system with hexagonal-shaped cells in a rectangular room of dimensions \(12\,{\text{m}}\, \times \,16\,{\text{m}}\). The cell radius \(R = 0.8\,{\text{m}}\) and wavelength reuse pattern size \(k = 3\). The cell color indicates the wavelength range assigned to the cell for WDMA

Full size image

The distribution of the signal strength (received power density or, equivalently, the horizontal illuminance) over the indoor coverage area is illustrated in Fig. 8. It is shown that the signal strength ranges between \(33.4\) and \(33.9\,{\text{dBm}}/{\text{m}}^{2}\), which means that the distribution of the received power is almost uniform over the room area with some slight increase at the cell centers relative to the cell edges. Such range of the signal strength is quite acceptable provided that the level of interference and noise are well controlled not to exceed the levels that deteriorate the resulting system performance regarding the SINR and the resulting BER.

Fig. 8
figure 8

Signal strength (received power density) distribution over the indoor coverage area in a VLC system with \(R = 0.8\,{\text{m}}\) and \(k = 3\)

Full size image

In this case, the distribution of the ICI strength (horizontal illuminance caused by the ICI) over the indoor area is presented in Fig. 9. It is shown that the ICI ha its maximum value in the region at the center of the room and has its minimum value in the regions near the room corners. In the regions near the room edges the ICI has intermediate values. This can be attributed to that the number of APs causing interference in the cells near the room center is larger than the number of APs causing interference in the cells near the room edges and corners.

Fig. 9
figure 9

ICI distribution over the indoor coverage area in a VLC system with for \(R = 0.8\,{\text{m}}\) and \(k = 3\)

Full size image

The signal strength and ICI distributions presented in Figs. 8 and 9, respectively, result in the SICIR distribution presented in Fig. 10. It is clear that the SICIR has its minimum values in the region around the room center and has its maximum values in the regions near the room corners. At the room edges, the SICIR has intermediate values. This comes in correspondence with the ICI distribution shown in Fig. 9.

Fig. 10
figure 10

SICIR distribution over the indoor coverage area in a VLC system with \(R = 0.8\,{\text{m}}\) and \(k = 3\)

Full size image

Figure 11 presents the distribution of the BER over the room area that corresponds to the SICIR distribution shown in Fig. 10. The curve shown in Fig. 6 is used to get the value of the BER from the corresponding SICIR assuming that the OOK is used for light signaling. It is shown that the lowest BER is \(1\times {10}^{-4}\) and is achieved in the regions near the room corners. Also, it shown that maximum BER exceeds \(1\times {10}^{-2}\) in the region around the room center, which indicates unacceptable performance of the VLC with these values of \(R\) and \(k\).

Fig. 11
figure 11

BER distribution over the indoor coverage area in a VLC system with \(R = 0.8\,{\text{m}}\) and \(k = 3\)

Full size image

5.2 Intercell Interference in VLC System with Large Cell Size and Small Wavelength Reuse Pattern

A cellular indoor VLC system with hexagonal-shaped cells has the arrangement presented in Fig. 11. This system has a cell radius \(R = 2\,{\text{m}}\) and wavelength reuse pattern size \(k = 3\). The range of the wavelength divisions assigned to users in each cell for WDMA is indicated in color code (Fig. 12).

Fig. 12
figure 12

Arrangement of indoor cellular VLC system with hexagonal-shaped cells in a rectangular room of dimensions \(12\,{\text{m}}\, \times \,16\,{\text{m}}\). The cell radius \(R = 2\,{\text{m}}\) and wavelength reuse pattern size \(k = 3\). The cell color indicates the wavelength range assigned to the cell for WDMA

Full size image

The distribution of the signal strength over the indoor coverage area is illustrated in Fig. 13. It is shown that the signal strength ranges between \(31\) and \(34\,{\text{dBm}}/{\text{m}}^{2}\). The received signal strength at the cell center is greater than that at the cell edges by about \(3\,{\text{dB}}\). When the received signal strength distribution shown in Fig. 13 is compared to the signal distribution presented in Fig. 8 for cell radius of \(0.8\,{\text{m}}\), it becomes clear that decreasing the cell radius results in more uniform distribution of the signal strength over the indoor coverage area. However, the range of the signal strength, in this case, is still acceptable provided that the level of interference and noise are well controlled not to exceed the levels that deteriorate the resulting system performance regarding the SINR and the resulting BER.

Fig. 13
figure 13

Signal strength (received power density) distribution over the indoor coverage area in a VLC system with \(R = 2\,{\text{m}}\) and \(k = 3\)

Full size image

In this case, the distribution of the ICI strength over the indoor area is presented in Fig. 14. It is shown that the ICI ha its maximum value in the region at the center of the room and has its minimum value in the regions near the room corners. In the regions near the room edges the ICI has intermediate values. By comparing the ICI distribution shown in Fig. 14 to that shown in Fig. 9 for a VLC system with the same value of \(k\) but with \(R = 0.8\,{\text{m}}\), it becomes evident that the ICI is decreased with increasing the cell radius. This can explained as that the APs causing interference with a cell become farther from this cell with increasing the cell radius.

Fig. 14
figure 14

ICI distribution over the indoor coverage area in a VLC system with \(R = 2\,{\text{m}}\) and \(k = 3\)

Full size image

The signal strength and ICI distributions presented in Figs. 13 and 14, respectively, result in the SICIR distribution presented in Fig. 15. It is clear that the SICIR has its minimum values in the region around the room center and has its maximum values in the regions near the room corners. At the room edges, the SICIR has intermediate values. This comes in correspondence with the ICI distribution shown in Fig. 14. When the SICIR distribution presented in Fig. 15 is compared to that presented in Fig. 10 for a VLC system with the same value of \(k\) but with \(R = 3\,{\text{m}}\), it becomes clear that increasing \(R\) has the effect of increasing the SICIR at every point in the room.

Fig. 15
figure 15

SICIR distribution over the indoor coverage area in a VLC system with \(R = 2\,{\text{m}}\) and \(k = 3\)

Full size image

Figure 16 shows the distribution of the BER over the room area that corresponds to the SICIR distribution presented in Fig. 15. The curve shown in Fig. 6 is used to get the value of the BER from the corresponding SICIR assuming that the OOK is used for light signaling. It is shown that the BER is maintained below \(1\, \times \,10^{ - 7}\) over most of the room area showing high performance of the VLC system. By comparing the BER distribution obtained in this case to that presented in Fig. 11 for a VLC system with the same value of \(k\) but with \(R = 0.8\), it becomes clear that increasing \(R\) results in a lower BER even for small value of \(k\). Such levels of the BER over the entire room area are quite acceptable for high performance VLC system.

Fig. 16
figure 16

BER distribution over the indoor coverage area in a VLC system with \(R = 2 {\text{m}}\) and \(k = 3\)

Full size image

5.3 Intercell Interference in VLC System with Small Cell Size and Large Wavelength Reuse Pattern

A cellular indoor VLC system with hexagonal-shaped cells has the arrangement presented in Fig. 17. This system has a cell radius \(R = 2\,{\text{m}}\) and wavelength reuse pattern size \(k = 12\). The range of the wavelength divisions assigned to users in each cell for WDMA is indicated in color code.

Fig. 17
figure 17

Arrangement of indoor cellular VLC system with hexagonal-shaped cells in a rectangular room of dimensions \(12\,{\text{m}}\, \times \,16\,{\text{m}}\). The cell radius \(R = 0.8\,{\text{m}}\) and wavelength reuse pattern size \(k = 12\). The cell color indicates the wavelength range assigned to the cell for WDMA

Full size image

The distribution of the received optical power density over the indoor coverage area is illustrated in Fig. 18. It is shown that the signal strength ranges between \(33.4\) and \(33.9\,{\text{dBm}}/{\text{m}}^{2}\), which means that the distribution of the received power is almost uniform over the room area with some slight increase at the cell centers relative to the cell edges. The range of the signal strength, in this case, is quite acceptable provided that the level of interference and noise are well controlled not to exceed the levels that deteriorate the resulting system performance regarding the SINR and the resulting BER. Comparing the signal distribution presented in Fig. 18 to that presented in Fig. 7, it is become clear that the signal strength distribution depends only on \(R\) and is independent of \(k.\)

Fig. 18
figure 18

Signal strength (received power density) distribution over the indoor coverage area in a VLC system with \(R = 0.8\,{\text{m}}\) and \(k = 12\)

Full size image

In this case, the distribution of the ICI strength over the indoor area is presented in Fig. 19. It is shown that the ICI ha its maximum value in the region at the center of the room and has its minimum value in the regions near the room corners. Like the previously investigated cases, the ICI has intermediate values in the regions near the room edges. By comparing the ICI distribution shown in Fig. 19 to that shown in Fig. 9 for a VLC system with the same value of \(R\) but with \(k=3\), it becomes evident that the ICI is decreased with increasing \(k\). This can explained as that the APs causing interference with a cell become farther from this cell with increasing the size of the wavelength reuse pattern.

Fig. 19
figure 19

ICI distribution over the indoor coverage area in a VLC system with \(R = 0.8\,{\text{m}}\) and \(k = 12\)

Full size image

The signal strength and ICI distributions presented in Figs. 18 and 19, respectively, result in the SICIR distribution presented in Fig. 20. It is clear that the SICIR has its minimum values in the region around the room center and has its maximum values in the regions near the room corners. At the room edges, the SICIR has intermediate values. This comes in correspondence with the ICI distribution shown in Fig. 19. When the SICIR distribution presented in Fig. 20 is compared to that presented in Fig. 10 for a VLC system with the same value of \(R\) but with \(k=3\), it becomes clear that increasing \(k\) has the effect of increasing the SICIR at every point in the room.

Fig. 20
figure 20

SICIR distribution over the indoor coverage area in a VLC system with \(R = 0.8\,{\text{m}}\) and \(k = 12\)

Full size image

Figure 21 shows the distribution of the BER over the room area that corresponds to the SICIR distribution presented in Fig. 20. The curve shown in Fig. 6 is used to get the value of the BER from the corresponding SICIR assuming that the OOK is used for light signaling. It is shown that the BER is maintained below \(1\times {10}^{-8}\) over most of the room area. Such levels of the BER over the entire room area are quite acceptable for high performance VLC system. By comparing the BER distribution obtained in this case to that presented in Fig. 11 for a VLC system with the same value of \(R\) but with \(k=3\), it becomes clear that increasing \(k\) results in a lower BER even for small cell radius. Also, By comparing the BER distribution obtained in this case to that shown in Fig. 16 for a VLC system with the same \(k\) but with \(R = 2\,{\text{m}}\), it can be concluded that a VLC system with large \(R\) and small \(k\) has similar performance to that of a VLC system with small \(R\) and large \(k\).

Fig. 21
figure 21

BER distribution over the indoor coverage area in a VLC system with \(R = 0.8\,{\text{m}}\) and \(k = 12\)

Full size image

5.4 Investigation of the Parameters Affecting the ICI in the VLC System

The dependence of the average level of the illuminance caused by ICI over the indoor coverage area \(R\) is presented in Fig. 22 for different values of \(k\). It is shown that increasing \(R\) while keeping constant value of \(k\) results in global mitigation of the ICI over the entire indoor area. In the same analogy, the ICI can be mitigated by increasing \(k\) and keeping \(R\) constant.

Fig. 22
figure 22

Dependence of the average ICI strength over the indoor area on \(R\) for different values of \(k\)

Full size image

The averaged SICIR over the indoor area corresponding to the distribution of the signal strength (\(E\)) and the ICI strength (\({E}_{F}\)) is obtained by averaging the ratio (\(E/{E}_{F})\) over the room area. The dependence of the average SICIR on \(R\) is presented in Fig. 23 for different values of \(k\). It is shown that the SICIR can be increasing by increasing the cell radius and the size of the wavelength reuse pattern.

Fig. 23
figure 23

Dependence of the average SICIR over the room area on \(R\) for different values of \(k\)

Full size image

5.5 Investigation of the Parameters Affecting the VLC System Capacity

The VLC channels are subject to the non-negativity of the signal and the average optical power [22]. Therefore, the classic Shannon channel rules are not applicable to calculate the optical channel capacity of the VLC system. The present work is concerned only with investigation of the effect of the ICI on the VLC system performance. The additive white Gaussian noise (AWGN) is not considered in this context. The present study is concerned with evaluating the VLC system capacity that is averaged over all the channels existing within this system. Thus, for evaluating the system capacity, it is considered that the user data rates are already determined.

As mentioned in the introduction of the present work, the highest data rates of the experimental VLC systems recorded in the recent publications range from \(10\) up to \(100\,{\text{Gbps}}\) [15,16,17,18]. For this reason, the numerical results for the VLC system capacity presented in this section are calculated using (28) considering that the user bit rate is limited as \(r_{b} \le 100\,{\text{Gbps}}\).

The dependence of the cellular VLC system capacity, \(C\), on the user bit rate, \(r_{b}\) is presented in Fig. 24 for different values of \(R\). A log scale is used for the vertical axis to be able to clearly demonstrate the dependence of \(C\) on \(r_{B}\) for large values of \(R\). The wavelength reuse pattern size is fixed at \(k = 3\). It is shown that the VLC system capacity, \(C\), increases linearly with increasing the user bit rate, \(r_{b}\). Also, it is shown that \(C\) considerably decreases with increasing \(R\).

Fig. 24
figure 24

Dependence of the VLC system capacity, \(C\) (log scale), on the user bit rate, \(r_{b}\) for different values of the cell radius, \(R\) (for \(k = 3)\)

Full size image

The dependence of the system capacity, \(C\), on the user bit rate, \(r_{b}\) is presented in Fig. 25 for different values of \(k\). A log scale is used for the vertical axis to be able to clearly demonstrate the dependence of \(C\) on \(r_{B}\) for large values of \(k\). The cell radius is fixed at \(R = 1.2\,{\text{m}}\). It is shown that the VLC system capacity, \(C\), increases linearly with increasing the user bit rate, \(r_{b}\). Also, it is shown that \(C\) considerably decreases with increasing \(k\).

Fig. 25
figure 25

Dependence of the VLC system capacity, \(C\) (log scale), on the user bit rate, \(r_{b}\) for different values of the wavelength reuse pattern size, \(k\) (for \(R\)\(= 1.2\,{\text{m}}\))

Full size image

5.6 Design Procedure of the Proposed Indoor VLC System

The design of hexagonal-cell-based indoor VLC utilizing WDMA to provide wireless network for multiple users and to satisfy a target performance measure is a complex and challenging task. The design procedure that provides continuous dynamic optimizations is described in Sect. 4 with the aid of the flowchart presented in Fig. 5. Nevertheless, in this section some curves are provided to help the VLC system designer to arrive at the appropriate start-up design parameters that can then be subjected to the continuous optimizations described in Sect. 4.

Let a designer be assigned the task of determining the appropriate design parameters (\(R, k\)) of an indoor VLC system in a room of dimensions \(12\,{\text{m}} \times 16\,{\text{m}} \times 4\,{\text{m}}\), given that the user data rate is \(r_{b} = 100\,{\text{Gbps}}\). The average BER over the room area shall satisfy the condition \({\text{BER}}_{av} \le 10^{ - 6}\) and the maximum BER over the room area shall satisfy the condition \({\text{BER}}_{max} \le 10^{ - 5}\). The VLC system capacity shall satisfy the condition \(C \ge 0.8\,{\text{bps}}/{\text{Hz}}\). The design constraints on the cell radius and the size of the wavelength reuse pattern are limited to the sets \(R \in \left\{ {0.8,{ }1.0,{ }1.2,{ }1.4,{ }1.6,{ }1.8,{ }2.0\,{\text{m}}} \right\}\) and \(k \in \left\{ {3,{ }4,{ }7,{ }9,{ }12} \right\}\), respectively. Also, the spectrum of the visible light is limited to the wavelength range \(448\) nm \(\le \lambda \le 700\,{\text{nm}}\). The OOK is used as a modulation technique for communication and the WDMA technique with wavelength division \(\delta {\Lambda } = 1 {\text{nm}}\) is used for multiple access in the wireless network.

The procedure applied to establish the VLC system that satisfies the above design goals within the given constraints is based on the flowchart shown in Fig. 5 with the aid of the design curves presented in Figs. 26, 27 and 28. In the following, the design procedure to achieve the system requirements is briefly described.

Fig. 26
figure 26

Dependence of the cellular VLC system capacity, \(C\) (log scale), on the cell radius, \(R\), for different values of the wavelength reuse pattern size, \(k\). The user data rate is \(r_{b} = 100 \,{\text{Gbps}}\)

Full size image
Fig. 27
figure 27

Dependence of the average BER (log scale) over the indoor area on \(R\) for different values of \(k\)

Full size image
Fig. 28
figure 28

Dependence of the maximum BER (log scale) over the indoor area on \(R\) for different values of \(k\)

Full size image

Figure 26 presents the dependence of the system capacity, \(C\), on \(R\), for different values of \(k\) when the user data rate is \(r_{b} = 100\,{\text{Gbps}}\). From this figure, the combinations of the values of \(R\) and \(k\) that satisfy a system capacity \(C \ge 0.8\,{\text{bps}}/{\text{Hz}}\) are presented in Table 1. Figure 27 presents the dependence of \({\text{BER}}_{av}\) on \(R\), for different values of \(k\). From this figure, the combinations of \(R\) and \(k\) that satisfy a system capacity \({\text{BER}}_{av} \le 10^{ - 6}\) are presented in Table 2. Figure 28 presents the dependence of \({\text{BER}}_{max}\) on \(R\), for different values of \(k\). From this figure, the combinations of \(R\) and \(k\) that satisfy a system capacity \({\text{BER}}_{max} \le 10^{ - 5}\) are presented in Table 3. From the three tables: 1, 2, and 3, it is shown that the conditions that can be satisfied together are those on the first and second rows (with bold) of each table.

Table 1 Values of \(R\) and \(k\) to satisfy the condition: \(C \ge 0.8\,{\text{bps}}/{\text{Hz}}\)
Full size table
Table 2 Values of R and \(k\) to satisfy the condition: BERav ≤ 10−6
Full size table
Table 3 Values of R and \(k\) to satisfy the condition: BERmax ≤ 10−5
Full size table

Thus, the design goals can be achieved using the four different pairs of \(R\) and \(k\) values listed in Table 4 with the corresponding performance measures. If it is required to solve the VLC system design problem with bias to maximize the system capacity then the best choice is \(R = 0.8\,{\text{m}}\) and \(k = 12\), which gives \(C = 1.257\,{\text{bps}}/{\text{Hz}}\), \({\text{BER}}_{av} = 1 \times 10^{ - 6}\), and \({\text{BER}}_{max} = 1 \times 10^{ - 5}\). On the other side, if it is required to solve design problem with bias to minimize BER then the best choice is \(R = 1.0\,{\text{m}}\) and \(k = 9\), which gives \(C = 0.805\,{\text{bps}}/{\text{Hz}}\), \({\text{BER}}_{av} = 1 \times 10^{ - 10}\), and \({\text{BER}}_{max} = 1 \times 10^{ - 9}\).

Table 4 Values of R and \(k\) that satisfy the design goals of the indoor VLC system
Full size table

6 Comparative Performance

For assessment of the VLC performance improvement achieved by the proposed design, the performance parameters (SICIR and BER) achieved in the present work are compared to those achieved by different designs presented in other related publications. It should be noted that the descriptions of the VLC systems proposed in the publications cited in Table 5 are briefly outlined in the introduction of the present paper.

Table 5 Comparison between the performance parameters (SICIR and BER) achieved using different designs of VLC systems presented in other publications and the performance achieved in the present work
Full size table

According to the summary presented in Table 1, it is clear that the indoor cellular VLC system design introduced in the present work has the best achievement regarding the SICIR and BER that are averaged over the room area. It is shown that the present work is the unique work that proposes the employment of the WDMA as multiple access technique for indoor VLC among those listed in Table 5. It may be worthwhile to mention that the WDMA enable the most efficient utilization of the wavelength reuse patterns relative to the other multiple access techniques. Also, as clear from the values of the BER achieved by the various modulation techniques listed in Table 5 that the PSK results in much lower BER than that achieved by the OOK. However, the OOK is preferred and, hence, recommended in the present work, to be used for light signaling because the PSK, QAM, and other modulation techniques that depend on the phase modulation require that the receivers are able to measures the phase shifts of the received light signal. The optical phase measurement is a complicated process that cannot be achieved by the currently available photodetectors and requires more complicated expensive devices to be added to the receiver system.

7 Conclusion

A high-performance multi-user indoor VLC of hexagonal-cell arrangement has been. In this system, the WDMA is employed to enable multi-user communication by assigning a unique WDC to each user. A wavelength reuse scheme is utilized to increase the maximum number of users in the system and to enhance the VLC system capacity. The ICI caused by the wavelength reuse has been evaluated and its dependence on the cell radius and the wavelength reuse pattern size has been numerically investigated. Both the received power density and the ICI at the location of the moving user have been evaluated and the resulting SICIR has been calculated at every point over the indoor area. The system capacity has been evaluated and its dependence on the design parameters including the cell radius, the size of the wavelength reuse pattern, and the user data rate has been numerically investigated. A design procedure has been proposed to minimize the BER resulting from the ICI and to maximize the system capacity and the maximum allowable number of users in the system by selecting the optimal radius of the hexagonal cells and the most appropriate size of the frequency reuse pattern. The effect of the data rate per user on the system capacity has been numerically investigated. It is shown numerically that the signal strength over the indoor area ranges between 31 and \(34\,{\text{dBm}}/{\text{m}}^{2}\) whereas the ICI level ranges between \(10\) and \(27\,{\text{dBm}}/{\text{m}}^{2}\). Thus, the corresponding SICIR ranges between 4 to \(24\,{\text{dB}}\) according to the design parameters. Also, it has been shown that a SICIR of greater than \(24\,{\text{dB}}\) and BER of less than \(1\, \times \,10^{ - 15}\) can be achieved. A system capacity of more than \(4\,{\text{bps}}/{\text{Hz}}\) has been achieved by the application of the proposed VLC design optimization procedure.