1 Introduction

VLC is a new technology in optical communications and is a green power to use. It is now required in this era for smart cities and smart homes in case of implementation in indoor and outdoor environments. In this paper, the focus is on the indoor only. VLC has numerous features. It prevents damage to the human body unlike the wireless communication. The Radio Frequency (RF) is harmful on the human body, where the RF radiation is absorbed by the body in a large enough amount. It can produce heat that leads to burn and causes a body tissue damage. Also, it can cause cancer due to magnetic wave radiation. On the other hand, the VLC uses LEDs, where their light radiation is a non-harmful source for the human body, yielding no human risk. VLC also provides the security needed to be implemented indoor (Haas et al. 2016).

Using VLC is the main purpose of this paper to avoid frequency overlapping, where the user having own phone and is moving between two cells, he can find an interruption for the established communication (Haas et al. 2016).

To mitigate the interference between users, it is a main objective to decrease the BER while the handover technique is presented, in this paper, by using the FR concept which is divided into two types: SFR and FFR. Both of these techniques make the frequency overlapping too low and beside the proposed LED distribution array for the hexagon array it makes it efficient without frequency overlapping and to get the higher signal to noise ratio (SNR) (Mahfouz et al. 2018; Khadr et al. 2019).

In this paper, we propose a four techniques: OOK, QAM, SFR and FFR to improve the BER by using a hexagonal array. Each cell has two FoVs and has four frequencies: F1, F2, F3 and F4. We will use it, in each cell, to reduce the overlapping between two cells while the user is moving between two cells or more as shown in Fig. 1 (Mahfouz et al. 2018; El-Garhy et al. 2019).

Fig. 1
figure 1

Hexagonal array for indoor VLC using two field of views

Full size image

In addition, adequate communication and illumination to multiple roaming devices must be achieved using VLC technology for a large indoor environment. Multiple LEDs need to be installed which act as access points (APs) in the ceiling of a room. The existence of the interference inside the cell, especially in adjacent cells, degrades SNR available to a cell-edge user. This significantly affects seamless wireless service and leads to high outage probability consequently; illumination is required in the cell (Khadr et al. 2019; El-Garhy et al. 2019).

However, inside the two, cells there is the inner side and the outer side. The main priority is to give the maximum coverage for the edge of the cell if the user is moving, and they need a soft handover to avoid the interruption.

The block diagram, in Fig. 2, illustrates each process with VLC system (El-Garhy et al. 2019).

Fig. 2
figure 2

VLC system block diagram (El-Garhy et al. 2019)

Full size image

In Fig. 2, a typical single-user VLC system is shown, where the transmitter typically consists of the channel encoder and a modulator followed by the optical front end. The electrical signal modulates the intensity of the optical carrier to send the information over the optical channel. At the receiver, a photodiode receives the optical signal and converts into an electrical signal followed by the recovery of data (Shinwasusin 2015; Chowdhury et al. 2018). However, in VLC, this is achieved by fast turning of light on and off (also called OOK) by using 0 bit is OFF and 1 bit is ON (Shinwasusin 2015). The BER issue in VLC is solved by creating a circular cell only with a four frequency reuse and it causes an interruption for transferring data been the sender and receiver (Huynh et al. 2012).

The remainder of the paper is organized as follows. In Sect. 2, the VLC communication system is illustrated using a new distribution array with a hexagonal shape by using the FR concept. Then, in Sect. 3, the simulation results are displayed and discussed for the BER in case of LoS and Non-LoS using MATLAB. Finally, we concluded the paper in Sect. 4.

2 System model

The system of interest is constructed for the indoor environment to have satisfactory coverage for this model. The entire coverage area depends on the model presented which depends on the design for the LED lighting. This area is divided into seven cells forming a hexagonal shape for the array of lightning in the celling. The proposed hexagonal shape is implemented, in this paper, to achieve the best results for BER with different techniques.

In Fig. 3, there are three cells, and they use one frequency in the center of each circular cell. There is also a gap between the three cells represented by a triangle with a red color, which may cause interruption to transfer the data if the user moves between all these cells from the ground. This operation is called the handover frequency (Melikov 2011). Cells represented by a triangle with a red color, which may cause interruption to transfer the data if the user moves between all these cells from the ground. This operation is called the handover frequency (Melikov 2011).

Fig. 3
figure 3

Circular cell using one frequency

Full size image

The handover frequency is used to implement a hexagonal shape for the LED array as illustrated in Fig. 4 (Sharma 2014, 2011). This shape helps in obtaining the best result for transferring data including BER and the SNR.

Fig. 4
figure 4

Hexagonal cell using one frequency (Sharma 2010, 2014)

Full size image

In Fig. 4, there are three cells. They use one frequency in the center of each hexagonal cell. There is no gap between the three cells. It enhances the data transfer if the user moves between all these three cells from the ground (Novlan et al. 2010). This hexagonal cell enhances the BER in order to avoid the data interruption (Sharma 2014).

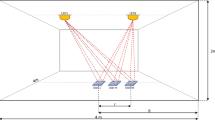
As shown in Fig. 1, we have developed an indoor VLC simulation model in a (5 × 5 × 3 \({\mathrm{m}}^{3})\) room as in Nguyen et al. (2010) and Yang et al. 2009). The hexagonal array has seven cells. Each cell has two FoVs. The outer shape is the hexagonal shape and the inner FoV inside the hexagonal shape is a circular cell in the center. Four frequencies are implemented in each cell. The outer side contains F1, F2, F3, and F4. The inner FoV as a circular array has F0 (Mahfouz et al. 2018; Khadr et al. 2019). By creating all these frequencies in all these cells, FR is implemented to achieve the best result possible by using the SFR and FFR using the array of hexagon shape (Sharma and Dewangan 2014). The modulation techniques implemented with this array using: OOK, QAM, and FR concept. Our proposed model aims to enhance the BER with the higher SNR in the designed room compared to the model in Huynh et al. (2012). The simulation parameters are listed in Table 1. The number of LEDs per array is 60 × 60 for the outer FoV hexagonal array and is 5 × 5 inner FoV as illustrated in Fig. 4. The FoV for the cell center reaches up to 60° and up to 70° for the cell edge to cover all users in the cell edge. The area of photodetector (PD) is 1 \({\mathrm{cm}}^{2}\) and the proposed number of users in the room is 35 users divided into: 28 users in the cell edge in the designed room dimension and 7 users dealing with cell center with a carrier frequency of 700 THZ. The concentrator of FoV is 60° and the thermal noise is − 160 dBm/Hz (Huynh et al. 2012).

Table 1 Simulation parameters for the VLC system
Full size table

In Fig. 5, the VLC channel has two different types of paths: LoS and Non-LoS. The mathematical derivation of the LoS and Non-LoS channel links with reflected path and total receive power calculation is explained briefly as follows.

Fig. 5
figure 5

VLC model for LoS and Non-LoS

Full size image

The received signal, Y(t), from the PD is represented by Huynh et al. (2012), Yang et al. 2009)

$$ {\text{Y}}\left( {\text{t}} \right) = {\text{R }}\cdot{\text{X}}\left( {\text{t}} \right){\text{*h}}\left( {\text{t}} \right) + {\text{N}}\left( {\text{t}} \right) $$
(1)

where R is the photo-detector sensitivity, * is the convolution sign while h(t) is the impulse response, X(t) is the input optical power from the LED to the PD while X (t) ≥ 0 and N (t) is the additive white Gaussian noise (AWGN). The optical transmitted power, Pt, is calculated as (Huynh et al. 2012)

$$ {\text{P}}_{{\text{t}}} = \mathop {{\text{lim}}}\limits_{{{\text{T}} \to \infty }} \frac{1}{{2{\text{T}}}}\mathop \int \limits_{{ - {\text{T}}}}^{{\text{T}}} {\text{X}}\left( {\text{t}} \right){\text{dt}} $$
(2)

By definition, the received optical, power \({\mathrm{P}}_{\mathrm{r}}\), from the PD is:

$$ {\text{P}}_{{\text{r}}} = {\text{H}}\left( 0 \right) \times {\text{P}}_{{\text{t}}} $$
(3)

where H (0) = \({\int }_{-\infty }^{\infty }h\left(t\right)d\left(t\right)\) is the channel direct current (DC) gain (Novlan et al. 2011).

$$ H\left( 0 \right) = \left\{ {\begin{array}{*{20}l} {\frac{{\left( {m + 1} \right)A}}{{2\pi D^{2} }}\cos^{m} \left( \phi \right)T_{s} \left( \psi \right)g\left( \psi \right)\cos \left( \psi \right), } \hfill & {0 \le \psi \le \psi_{c} } \hfill \\ {0,} \hfill & {{\text{elsewhere}}} \hfill \\ \end{array} } \right. $$

where A is the PD area, D is the distance between transmitter and receiver (Huynh et al. 2012).

The order of Lambertian emission, m, is

$$ {\text{m}} = - \frac{{\ln 2}}{{\ln \left( {\cos \phi _{{1/2}} } \right)}} $$
(4)

where \({\upphi }_1/2\) is the transmitter of FoV, \(\upphi \) is the angle of irradiance, ψ is the angle of incidence, \({\mathrm{T}}_{\mathrm{s}}\left(\Psi \right)\) is the signal transmission coefficient for the optical filter, g (ψ) is the gain for the optical concentrator of the PD, and the \({\uppsi }_{\mathrm{C}}\) is the receiver for the FoV (Huynh et al. 2012; Ghassemblooy et al. 2013).

While the g (ψ), is given by

$$ g\left( \psi \right) = {\text{ }}\left\{ {\begin{array}{*{20}l} {\frac{{{\text{n}}^{2} }}{{\sin ^{2} \Psi _{{\text{C}}} }},} \hfill & {0 \le \Psi \le \Psi _{C} } \hfill \\ {0,} \hfill & {elsewhere} \hfill \\ \end{array} } \right. $$
(5)

where n is the refractive index that achieves the gain of the medium as shown in Eq. (5). To calculate the SNR, we will put in our consideration the received power is given by Huynh et al. (2012) and Ghassemblooy et al. 2013)

$$ P_{rsignal} = \mathop \int \limits_{0}^{{\text{T}}} \left( {\sum {\text{h}}_{{\text{i}}} \left( {\text{t}} \right){\text{*x}}\left( {\text{t}} \right)} \right){\text{dt}} $$
(6)

and SNR is expressed as

$$ {\text{S}} = {\text{R}}^{2} {\text{P}}_{{{\text{rsignal}}}}^{2} $$
(7)

In addition, we have the variance of Gaussian noise \({\sigma }^{2}\), which it is the sum of the thermal noise, shot noise and the intersymbol interference from the optical path difference (Huynh et al. 2012), i.e.

$$ {\upsigma }_{{\text{total }}}^{2} = {\upsigma }_{{\text{shot }}}^{2} + {\upsigma }_{{{\text{thermal}}}}^{2} + {\text{R}}^{2} {\text{P}}_{{{\text{rISI}}}}^{2} $$
(8)
$$ {\upsigma }_{{\text{shot }}}^{2} = 2{\text{qR}}\left( {{\text{P}}_{{\text{signal }}} + {\text{P}}_{{{\text{rISI}}}} } \right){\text{B}}_{{{\text{en}}}} + 2{\text{qI}}_{{{\text{bg}}}} {\text{I}}_{2} {\text{B}}_{{{\text{cn}}}} $$
(9)
$$ {\upsigma }_{{\text{thermal }}}^{2} = \frac{{8\pi {\text{kT}}_{{\text{k}}} }}{{\text{G}}}{\text{C}}_{{{\text{pd}}}} {\text{AI}}_{2} {\text{B}}_{{{\text{en}}}}^{2} + \frac{{16\pi^{2} {\text{kT}}_{{\text{k}}} {\text{E}}}}{{{\text{g}}_{{\text{m}}} }}{\text{C}}_{{{\text{pd}}}}^{2} {\text{A}}^{2} {\text{I}}_{3} $$
(10)

where \(q\) is the electronic charge, \({B}_{en}\) is equivalent noise bandwidth, \({I}_{bg}\) is background current, \({I}_{2}\) is the noise bandwidth factor, \(k\) is Bolzmann's constant, \({T}_{k}\) is the absolute temperature, \(G\) is the open-loop voltage gain, \({\text{C}}_{\text{pd}}\) is the fixed capacitance of photo-detector per unit area, \(E\) is the field effect transistor (FET) channel noise factor, \({g}_{m}\) is the FET transconductance, \({I}_{3}=0.868\), and \({P}_{rsI}\) is the received power by intersymbol interference(Huynh et al. 2012; Ghassemblooy et al. 2013). The received power by intersymbol interference is, \({\mathrm{P}}_{\mathrm{rISI}}\), in the total Gaussian noise, is

$$ {\text{P}}_{{{\text{rISI}}}} = \mathop \int \limits_{{\text{T}}}^{\infty } \left( {\sum {\text{h}}_{{\text{i}}} \left( {\text{t}} \right){\text{*x}}\left( {\text{t}} \right)} \right){\text{d}}\left( {\text{t}} \right) $$
(11)

Then, the SNR in the final image is (Huynh et al. 2012)

$$ {\text{SNR}} = \frac{{{\text{R}}^{2} {\text{H}}^{2} \left( 0 \right){\text{p}}_{{\text{t}}}^{2} }}{{{\upsigma }_{{{\text{totaL}}}}^{2} }} $$
(12)

Accordingly, the BER is (Chowdhury et al. 2018)

$$ {\text{BER}} = {\text{Q}}\left( {\sqrt {{\text{SNR}}} } \right) $$
(13)

where

$$ {\text{Q}}\left( {\text{x}} \right) = \frac{1}{{2{\uppi }}}\mathop \int \limits_{{\text{x}}}^{\infty } {\text{e}}^{{ - {\text{y}}{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} {\text{dy}} $$
(14)

From Eq. (14), we will add our modulation techniques to the input channel DC gain to get the BER by using the hexagonal shape.

Considering power due to the Non-LoS paths, the DC channel gain of the reflected path is given by Chowdhury et al. (2018)

$$ H_{Non - LoS} \left( 0 \right) = \left\{ {\begin{array}{*{20}l} {\frac{{\left( {m + 1} \right){\text{A}}}}{{2\pi D_{1}^{2} D_{2} ^{2} }}dA_{{\text{wall }}} \cos^{m} \left( \phi \right)\cos \left( \alpha \right)\cos \left( \beta \right)T_{s} \left( \psi \right)g\left( \psi \right)\cos \left( \psi \right),} \hfill & {0 \le \psi \le \psi_{c} } \hfill \\ {0,} \hfill & {{\text{elsewhere}}} \hfill \\ \end{array} } \right. $$
(15)

where \(\beta \) represents the angle of irradiance from the reflective area of the wall, \(\alpha \) is the angle of irradiance to the wall, \({D}_{1}\) is the distances between the transmitter and the wall, and \({D}_{2}\) is the distance between the wall and a point on the receiving surface, and \(d{A}_{\text{wall}}\) is the size of the reflective area.

Now, if we consider both multipath propagation and the LoS component, for the more general case, the total received power \(,{P}_{r}\), is given by Chowdhury et al. (2018)

$$ {\text{P}}_{{\text{r}}} = {\text{P}}_{{\text{t}}} \cdot{\text{H}}_{{{\text{LoS}}}} \left( 0 \right) + \int\limits_{{\text{walls }}} {{\text{P}}_{{\text{t}}} \cdot {\text{H}}_{{\text{Non - LoS }}} } (0) $$
(16)

Finally, the SNR is given by

$$ SN{\text{R}} = \frac{{\left( {R\cdot H\left( 0 \right)P_{r} } \right)^{2} }}{{\sigma_{total}^{2} }} $$
(17)

2.1 BER with M-QAM

The M-QAM Orthogonal Frequency Division Multiplexing (OFDM) could be employed to enhance the transmission capacity. This subsection discusses the spectral efficiency of a single user VLC system employing M-QAM OFDM. Figure 6 is a block diagram for a VLC system with adaptive M-QAM OFDM, where the value of \(\mathrm{M}\) represents the number of points in the signal constellation and can be varied in accordance with the SNR (Haitham et al. 2018; Játiva 2019).

Fig. 6
figure 6

VLC system employing M-QAM OFDM

Full size image

The original data are firstly processed by serial-to-parallel (S/P) and mapped onto M-level QAM constellation before being transformed by the Hadamard block which operates in Hadamard transform and reduces the correlation of the input data sequences (Haitham et al. 2018).

Hermitian symmetry is imposed with the Inverse Fast Fourier Transform to obtain real value signal (Haitham et al. 2018). When applying IFFT, we do oversampling to make the distribution of the amplitude of the discrete IFFT output signals close to that of continuous signals. After the parallel to-serial (P/S) operation, the cyclic prefix (CP) is added to eliminate the intersymbol interference. The OFDM time domain signal must be both real and positive, the DC bias is introduced. Intensity Modulation (IM) is employed at the transmitter. The forward signal Y(t) drives the LED, which, in turn, converts the magnitude of the input electric signals Y(t) into optical intensity. At the receiver side, direct detection (DD) is employed. The PIN PD converts the incoming optical power into the amplitude of an electrical signal. The CP is then removed. The Inverse Hadamard transform is performed after the FFT and the M-QAM demodulation is performed (Haitham et al. 2018; Játiva 2019).

Applying a gray coding for the mapping of the M- QAM signal, the BER of the M-QAM OFDM signal is given by Haitham et al. (2018)

$$ {\text{BER}} \approx \frac{4}{{\log_{2} \left( {\text{M}} \right)}}\left( {{\text{I}} - \frac{1}{{\sqrt {\text{M}} }}} \right){\text{Q}}\left( {\sqrt {\frac{{3\log_{2} \left( {\text{M}} \right){\text{Eb}}}}{{{\text{M}} - {\text{N}}_{0} }}} } \right) $$
(18)

where \(Q\left(\cdot \right)\) is the Q-function.

$$ {\text{SNR}}\;{\text{per}}\;{\text{bit}} = \left( {{\text{E}}_{{\text{b}}} /{\text{N}}_{0} } \right) $$
(19)

The value of M in M-QAM is 8, 16, 64 and 256 because while increasing the M-QAM values the higher data rate can be offered but the BER will be high due to increasing the M values and we need to enhance the BER while increasing at M-QAM values.

3 BER in FR concept

3.1 Fractional frequency reuse (FFR)

The FFR is based on the inter-cell interference (ICI) in OFDMA based wireless networks. But, we are using this technique in optical networks especially in our proposed model for the indoor VLC, where the major frequencies in the cell center region are founded a partitioned frequencies in the cell edge. This reduces the ICI because cell border regions use orthogonal frequency to uplink (Novlan et al. 2010; Svahn et al. 2019).

The use of FFR in optical networks leads to improve the data rate and coverage for cell-edge users and overall network throughput and spectral efficiency (Melikov 2011; Novlan 2011).

In the proposed model, for a user served by the LED light as a source, the associated signal to interference noise ratio SNR as the following equation (Nguyen et al. 2010).

$$ SNR = \frac{{P_{t} h_{{ty}} D_{{ty}} }}{{\sum\limits_{{x \in X}} {P_{x} h_{{xy}} D_{{xy}} } }} $$
(20)

where y Is a user, x is LED source, \({P}_{t}\) is the transmitted power from the source, \({h}_{ty}\) is the channel fading power, \( {D}_{ty}\) is the path loss between the user and the LED source, \({\sigma }^{2}\mathrm{total}\) is the total noise power, X represents all the interference from the LED arrays. Then, the BER is given by Eq. (13).

3.2 Soft frequency reuse (FFR)

The SFR is used in the proposed model to get the accurate data while transmitted and received in the indoor VLC. It depends on a cell which is partitioned into center zone and edge zone for the seven cells per cluster. The frequency band is divided into four sub-bands. The edge zone of the cells in a cluster is allocated to different sub-bands and the center zone uses the sub-band selected for the neighboring cell’s edge zone (Novlan 2010).

While SFR is more bandwidth efficient than FFR, it results in more interference to both cell center and edge user, and the SNR is given by Novlan (2010).

$$ {\text{SNR = }}\frac{{\beta {\text{Ph}}_{{{\text{ty}}}} {\text{D}}_{{{\text{ty}}}} }}{{{\text{P}}\sum\limits_{{{\text{q}}_{{\text{i}}} \in {\text{Q}}_{{\text{i}}} }} {{\text{h}}_{{{\text{q}}_{{\text{i}}} {\text{y}}}} {\text{D}}_{{{\text{q}}_{{\text{i}}} {\text{y}}}} + \beta {\text{P}}\sum\limits_{{{\text{q}}_{{\text{e}}} \varepsilon {\text{Q}}_{{\text{e}}} }} {{\text{h}}_{{{\text{q}}_{{{\text{ey}}}} }} } + {\text{Dq}}_{{{\text{ey}}}} } }} $$
(21)

where \({Q}_{i}\) consists of all interfering base stations transmitting to cell interior users on the same sub-band as user y, \({Q}_{e}\) consists of all interfering base stations transmitting to cell-edge users on the same sub-band, \(\beta \) is a power control factor \(\ge 1\) and is introduced to the transmit power, \({P}_{t}\), to create different classes \({\mathrm{P}}_{\mathrm{interior}}\) = P for cell center and \({\mathrm{P}}_{\mathrm{exterior}}\) = \(\beta P\) for the cell-edge user, where \({Q}_{i}\) consists of all interfering base stations transmitting to cell interior users on the same sub-band as user y, \({Q}_{e}\) consists of all interfering base stations transmitting to cell-edge users on the same sub-band, \(\beta \) is a power control factor \(\ge 1\) and is introduced to the transmit power, \({P}_{t}\), to create different classes \({\mathrm{P}}_{\mathrm{interior}}\) = P for cell center and \({\mathrm{P}}_{\mathrm{exterior}}\) = \(\beta P\) for the cell-edge user.

Similar and detailed analysis are performed in literature concerning phase distribution of a hexagonal array at fractional Talbot planes (Guo et al. 2007), LED diffused transmission freeform surface design for uniform illumination (Zhu 2019), and software design of SMD LEDs for homogeneous distribution of irradiation in the model of dark room (Liner et al. 2014).

4 Simulation results

Our proposed model was presented by a new LED distribution with a hexagonal shape by dividing it into seven cells in Fig. 4.

Figure 7 displays the SNR per single LED for the designed room dimension (5 × 5 × 3 \({\mathrm{m}}^{3}\)) showing an improved SNR distribution. The maximum SNR at the maximum peak is 38.9 dB, which is good for our proposed model to apply, to get an improved BER. Figure 8 displays the luminance of the proposed model for the hexagonal array shown in Fig. 1 to get the good coverage to the end user.

Fig. 7
figure 7

SNR distribution for the VLC system in a room with one LED

Full size image
Fig. 8
figure 8

Luminance distribution for the hexagonal array

Full size image

Figure 8 displays the luminance of the proposed model for the hexagonal array shown in Fig. 1 to get the good coverage to the end user.

We apply the OOK for the proposed model in two scenarios: LoS and Non-LoS to check the BER after applying the LED distribution for a hexagonal shape of Fig. 1. In Fig. 9, we present the BER for our proposed model in case of LoS using OOK. In Fig. 9, while the SNR is increased, the BER is getting lower. Figure 10 shows the BER for our proposed model in case of Non-LoS using OOK. In Fig. 10, while the SNR is increased, the BER is getting lower. The BER at different values of SNR is summarized in Table 2, showing also a comparison between LoS and Non-LoS scenarios. As expected, the LoS case achieves better (lower) BER.

Fig. 9
figure 9

BER in case of LoS using OOK

Full size image
Fig. 10
figure 10

BER in case of Non-LoS using OOK

Full size image
Table 2 BER for OOK in both LoS and non-LoS scenarios
Full size table

After applying the OOK, we applied the M-QAM technique with M values = 8, 16, 64 and 256 to obtain the BER in case of LoS and Non-LoS. In Fig. 11, the BER is plotted in case of LoS at different M-QAM values to show the enhancement.

Fig. 11
figure 11

BER in case of LoS using M-QAM

Full size image

In Fig. 11, while increasing the M values, one higher BER can get. The BER with different values of M-QAM at standard values in SNR is summarized in Table 3.

Table 3 BER for M-QAM in LoS state
Full size table

In Fig. 12, the BER is shown in case of Non-LoS at different M-QAM values.

Fig. 12
figure 12

BER in case of Non-LoS using M-QAM

Full size image

In Fig. 12, at different values of M-QAM technique, while increasing the M values, we can see the effective performance for the proposed scheme for Non-LoS. The BER at different values of M-QAM at standard values in SNR is summarized in Table 4.

Table 4 BER for M-QAM in Non-LoS state
Full size table

Due to the reflections, we can see the performance of BER in case of LoS is better than Non-LoS, when comparing Tables 3 and 4. After applying OOK and M-QAM techniques in LoS and Non-LoS, the final proposed schemes for SFR and FFR are presented in Figs. 13 and 14, respectively.

Fig. 13
figure 13

Performance of BER for SFR and FFR in LoS state

Full size image
Fig. 14
figure 14

Performance of BER for SFR and FFR in Non-LoS State

Full size image

In Fig. 13, we have BER for the LoS scenario for the FR concept (for SFR and FFR). The result is enhanced after applying the hexagonal array using FR as compared to the previous work (Huynh et al. 2012). Table 5 shows the difference between the SFR and FFR at the same values of SNR.

Table 5 BER for SFR and FFR in LoS state
Full size table

Figure 14 shows the FR concept for SFR and FFR BER for the Non-LoS scenario under reflection and is summarized in Table 6.

Table 6 BER for SFR and FFR in Non-LoS state
Full size table

Finally, one can conclude that this paper presents the best results shown in the following Table 7. for BER performance for all techniques compared to the previous work (Huynh et al. 2012).

Table 7 Total BER performance for all techniques compared to the previous work
Full size table

5 Conclusions

VLC is a promising technology for the near future that uses LEDs for illumination and communication simultaneously. In order to achieve the best results for BER, the higher SNR is required.

In this paper, the performance of BER was evaluated with different techniques in two scenarios LoS and Non-LoS using hexagonal array to mitigate the interference between cells. The optimal results in this proposed model were found in SFR specifically in LoS unlike the Non-LoS and the BER in case of LoS was decreased by 47% compared in case of Non-LoS due to a reflections. The BER performance for SFR in case of LoS for the proposed model and comparing it to the previous work (Huynh et al. 2012) the BER is enhanced by 90%.

OOK modulation technique in the proposed model was measured in LoS and Non-LoS and the BER is enhanced by 70% compared to the Non-LoS state. For M-QAM modulation technique in the proposed model was measured at different values of M and at different SNR values in the previous scenarios: LoS and Non-LoS. The BER in case of LoS is enhanced by 60% compared to the Non-LoS state.

To conclude the optimal result is found in SFR specifically in case of LoS due to applying the hexagonal shape and using FR concept to have a good result for BER. It is recommended for the future work to implement it in a practical way.