1 Introduction

Drought management plans usually include operational components that contemplate the implementation of water saving measures in situations where there is a risk of failure to meet the required supply within a decision horizon. The so-called "hedging rules" for reservoir management are an example of this type of measure (You and Cai 2008; Peng et al. 2015; Adeloye et al. 2016). By means of this technique, storage thresholds are established in reservoirs to trigger water saving measures. If storage reserves become depleted beyond the threshold, the supply of certain types of demand is partially restricted to avoid total resource exhaustion. The rationale for this practice is that a succession of moderate deficits over a certain period is preferable to having to face unacceptable deficits, even if the duration of this situation is much shorter (Rossi et al. 2012). The formulation of an optimal operating policy for a reservoir under hedging rules requires the definition of thresholds to activate the rules and the identification of the appropriate supply restrictions to overcome the deficit periods with minimum damage (Draper and Lund 2004). Many methods have been proposed in the literature to formulate and optimize hedging rules. A recent review was published by Neelakantan and Sasireka (2015). The work presented in this paper is based on the model of Spiliotis et al. (2016). They presented a methodology based on particle swarm optimization (PSO) to identify optimal hedging rules for the operation of a reservoir under drought conditions.

Hedging rules are preferred by practitioners over more sophisticated approaches to reservoir operation due to their simplicity and effectiveness. They are easily understood and accepted by stakeholders, who can in turn formulate their drought management strategies based on the foreseen shortages. For example, most drought management plans in Spain adopted hedging rules for operating reservoir systems under drought conditions (Estrela and Vargas 2012, Garrote et al. 2007). However, most hedging rule schemes do not have adaptive capabilities. Once the optimal policy has been identified, it is applied regardless of the system condition. This is acceptable in case of within-the-year reservoir systems because the importance of carryover storage is small, and the system practically resets every year. However, in the case of over-the-year reservoir systems, carryover storage plays a significant role because the conditions at the beginning of each hydrological year may vary over time. For these systems, it could be beneficial to consider the state of the system to define a new set of hedging rules every hydrological year. Adaptive schemes have been proposed for reservoir management under uncertain conditions. The most frequent source of uncertainty is on reservoir inflows. Several adaptive schemes have been proposed to cope with inflow uncertainty. Yang and Ng (2017) proposed reservoir operating rules under nonstationary inflows based on a fuzzy inference system, with emphasis on achieving robustness in operation. Xu et al. (2015) defined rules for multistage optimal hedging operations for the Miyun reservoir in China, where a statistically significant decline in reservoir inflow trend has been observed. Ahmadi et al. 2015 applied a meta-heuristic multi-objective optimization algorithm in conjunction with climate projections to propose adaptive operation of the Karoon-4 reservoir in Iran. Feng et al. (2017) focused on identifying changing patterns of reservoir operating rules under various inflow alteration scenarios. Leta et al. (2022) examined the effect of land use land cover change on the watershed’s hydrological processes and the corresponding patterns of reservoir operation. All these studies acknowledge the difficulty of defining operating rules under changing conditions.

The objective of this work is to formulate adaptive hedging rules for reservoir drought operation and compare their performance with static hedging rules. The adaptive hedging rules are based on the available reservoir storage at the beginning of the decision period, as in the model presented by Jin and Lee (2019) and on the availability of a mid-term streamflow forecast, as in the works of Zhang et al. (2017) and Mostaghimzadeh et al. (2022). The model proposed by Spiliotis et al. (2016) is extended to incorporate an adaptive scheme in which a different set of rules is defined every hydrological year. Rather than optimizing system performance over the long-term historic time series of reservoir inflows, it is optimized over an ensemble of short-term reservoir inflows, either representing climatological conditions or adopting an available short-term forecast.

2 Methodology

The analysis methodology is presented in this section. First, the problem data and the simulation tool are described. Then, the developed adaptive optimization procedure is described.

2.1 Problem Formulation

The methodology is formulated for a water resource management system that must jointly meet a series of demands sorted by priority. Water demand may vary from month to month but remain constant from year to year in all simulations. The topology of the system consists of inflow points, river reaches, reservoir nodes, and demands. Data are structured according to a network topology consisting of nodes and arcs. The nodes may be associated with inflows, reservoirs, or demands. The arcs are associated with river stretches.

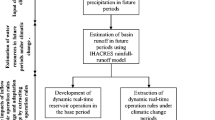
Problem formulation is described in the supplementary material. Full details of the mathematical formulation can be found in Spiliotis et al. (2016). Operating rules may be static or adaptive. Under the static approach, the optimization problem is solved by running the simulation model over the full time series of historical flows. The identified rules are assumed to be valid for any system condition, and therefore they are fixed over the entire operation period. The adaptive approach is illustrated in Fig. 1. The problem is solved cyclically: a new set of operating rules is defined periodically. In each decision horizon \({H}_{d}\), the current situation is analysed, and the optimal rules are defined contemplating the horizon of analysis \({H}_{a}\). The new rules are applied during the next decision horizon. Once the end of the decision horizon is reached, the problem is solved again starting from the configuration of the system at the beginning of the new cycle.

Fig. 1
figure 1

Schematic representation of the operation of the adaptive model

Full size image

2.2 Resolution Algorithm

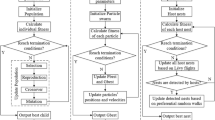
An optimization algorithm based on dynamic optimization, was developed to solve the optimization problem. The algorithm is described in detail in Spiliotis et al. (2016). A summary of the main steps is presented here. The following describes the initial step and an intermediate generic step. The presentation is illustrated in Fig. 2.

Fig. 2
figure 2

Schematic representation of the methodology

Full size image

The starting point is the set of possible drought thresholds deduced from the system risk analysis (Fig. 2a). Risk analysis is conducted by performing a simulation of system operation over a period of a certain length starting with a given reservoir storage on a given month (for instance, 18 months starting with 75% capacity in March). The model is run for all subseries of inflows that begin in the selected month and have a duration equal to the period of analysis. For each starting volume, a probability distribution of deficits may be estimated by analysing the simulation results. Risk levels are associated with specific probability values of having a deficit that exceeds a certain fraction of the demand (Fig. 2b). Storage values that lead to the same probability of deficits over the year configure the drought activation thresholds (for instance: 60% probability of having a deficit equal or larger than 10% of the demand).

For each of these possible drought thresholds, the optimal combination of restriction coefficients is selected for each type of demand. This combination minimizes the objective function over the set of expected flows. Figure 2c presents an example in which two types of demand, urban supply and irrigation are considered. The value of the objective function is represented as both coefficients are modified. The minimum value is obtained for a restriction coefficient of 0.7 for irrigation demand and no restriction for urban demand. Once the optimal coefficients have been identified in each drought threshold, the curve that achieves the minimum value of the objective function is selected as the drought activation threshold. Figure 2d presents the values of the objective function for the different activation curves analysed. The coefficients adopted are those that correspond to the optimal management of each curve. The minimum value is obtained for the curve that corresponds to monthly storage values that lead to a probability of 60% of having a deficit of 10% over the period of analysis. The management rule is defined by the activation threshold that leads to the minimum value of the objective function and the corresponding restriction coefficients (Fig. 2e). This basic procedure is repeated for each operation cycle throughout the historical series. The result of the process is a sequence of optimal operating rules that change over time because they adapt to the volumes stored in the reservoirs and to the expected flows in each operation cycle.

3 Case Study

The proposed methodology has been applied to the Pisuerga-Carrión water resources system, in the Duero-Douro basin. The Pisuerga-Carrión system comprises the basin of the Pisuerga River up to its mouth in the Duero-Douro River, with a total area of 12,007 km2. The map of the area and the schematic topology of the model are presented in Fig. 3. The Pisuerga-Carrión System is in the north of the Iberian Peninsula. The headwaters of the Pisuerga and Carrión rivers are in the Cantabrian Mountain range at elevations over 2000 m and the rivers flow in a north–south direction through a plateau with an altitude between 800 and 600 m. The climate of the headwaters is Atlantic or Euro-Siberian, with high rainfall, exceeding 1,400 mm/year. The runoff is mainly concentrated in the headwaters of the basins, which is where the regulation reservoirs are located. On the plateau, the climate is continental. Winters are long and cold, and summers are hot and dry, with annual rainfall between 400 and 600 mm/year. An important irrigated agriculture has been developed in this plateau area.

Fig. 3
figure 3

Representation of the Pisuerga-Carrión water supply system and the simplified topology adopted in the model

Full size image

The data for the model were obtained from the draft of the ‘River Basin Plan for the Spanish Part of the Duero River Basin District’ for the cycle 2022–2027 (Confederación Hidrográfica del Duero 2022). The main demands of the system correspond to the urban water supply for the cities of Valladolid (44.9 hm3/a) and Palencia (10.4 hm3/a) and the irrigated areas of Carrión-Saldaña (99 hm3/yr), Canal de Castilla North (62 hm3/yr), Canal de Castilla Centre-South (117 hm3/yr) and Pisuerga (80 hm3/a). Total demand in the system amounts to 55.3 hm3/yr for urban supply and 357 hm3/yr for irrigation. The weighting coefficients adopted for the objective function were \({\beta }_{1}=1\) for urban supply and \({\beta }_{2}=0.1\) for irrigation. The hydraulic infrastructure of the basin consists of several irrigation canals that serve irrigation districts and five large reservoirs. Camporredondo and Compuerto on the Carrión River and Requejada, Cervera and Aguilar on the Pisuerga River. The model considers an equivalent reservoir on the Carrión River (169 hm3) and another on the Pisuerga River (342 hm3), each of them integrating the storage volume available in its basin. The total reservoir capacity considered in the model is 511 hm3. Streamflow for the model was taken from the results of the SIMPA model (Estrela and Quintas 1996; Alvarez et al. 2004). A total of 55 years of monthly time series were available, running from the hydrological year 1960–61 to 2015–16. Total mean annual flow from the Carrión-Pisuerga basin is 967 hm3/s, but only 558 hm3/yr are regulated in the reservoirs: 262 hm3/yr in the Carrión River and 296 hm3/yr in the Pisuerga River.

3.1 Simulation with No Rules

An initial simulation was carried out to evaluate the current ability to meet demands without drought operating rules. The results of the simulation are shown in Fig. 4a. It represents the evolution of storage in the system as a function of time and the deficits of the demands for urban supply and irrigation. There are 13 episodes where the reservoirs become empty, thus producing important supply deficits that reach 100% of the monthly demand, both for urban supply and irrigation. The cumulative contribution of urban and irrigation demands to the objective function is shown as a black line in the corresponding plots of urban and irrigation deficits. The total value of the objective function for this simulation is 0.2479 hm3/m. The contribution of urban demand to the objective function is 0.1835 hm3/m while the contribution of irrigation demand is 0.0644 hm3/m.

Fig. 4
figure 4

Results of the simulation of the Pisuerga-Carrión system. a) Simulation without rules. b) Simulation with static rules. c) Simulation with adaptive rules without forecast. d) Simulation with adaptive rules with forecast

Full size image

3.2 Static Operating Rules

The results of the simulation with static operating rules are shown in Fig. 4b. The algorithm was run with one activation threshold and one set of restriction coefficients. The activation threshold is shown as a dark blue line in the storage plot. The optimal values of the restriction coefficients were found to be 1 for urban demand and 0.55 for irrigation demand. Therefore, no restrictions were applied to urban supply. Drought control rules manage to reduce the number of episodes where the reservoirs become empty to just three. There is one three-month event in which the reservoirs become empty and produces deficits in the urban supply. There are two one-month events with empty reservoirs, but they do not produce deficits in urban demand. On the other hand, irrigation deficits are more frequent but less intense compared to simulation without rules. The total value of the objective function for this simulation is 0.0703 hm3/m. The contribution of urban demand to the objective function is reduced to 0.0218 hm3/m while the contribution of irrigation demand is 0.0485 hm3/m.

3.3 Adaptive Operating Rules without Forecast

Adaptive operating rules were first applied without forecast. The algorithm was run with an annual operation cycle starting in October, with a decision horizon of 12 months. The analysis horizon was also set to 12 months. In this case, the ensemble of hydrological flows considered in the analysis was the same in each cycle of operation. It was constructed by extracting from the historical series all the subseries that begin in the current month and have a duration equal to the analysis horizon, \({H}_{a}\). The values of the activation thresholds and restriction coefficients were determined for each operation cycle, taking advantage of knowing the volume of water available in the reservoirs at the beginning of the operation cycle. An optimization problem was solved in each cycle, selecting the activation thresholds and restriction coefficients that minimize the expected value of the objective function in the analysis horizon, \({H}_{a}\). In each period, a single operating rule was defined (one activation threshold and one set of restriction coefficients), due to the limitations of computing time, since it is necessary to perform as many optimizations as operating cycles are defined (55 in total). Operating rules were required for 53 of the 55 years. Restrictions coefficients for urban demand ranged from 0.90 to 1.00. The restrictions coefficients for irrigation demand ranged from 0.10 to 0.95. The operating rules thus defined are applied during the following decision horizon, \({H}_{d}\).

The results of the simulation with adaptive operating rules without forecast are shown in Fig. 4c. The selected activation threshold, shown as a dark blue line in the storage plot, changes every operation cycle. The total value of the objective function for this simulation is 0.0943 hm3/m. The contribution of urban demand to the objective function is 0.0381 hm3/m while the contribution of irrigation demand is 0.0563 hm3/m. There are nine episodes with empty reservoirs and in three of them the duration is longer than a month, thus producing deficits in urban demands.

3.4 Adaptive Operating Rules with Forecast

Adaptive operating rules were also applied assuming that a streamflow forecast is available over the analysis horizon. Since no actual forecast is operationally available for the Pisuerga-Carrión system, the forecast was emulated with a stochastic model built from the historical series. In each optimization cycle, the historical series was disturbed on the analysis horizon. A random error term was added to the observed values. The error term increases over time, to represent the greater uncertainty of longer-term forecasts. The following describes the process used to simulate the availability of a forecast.

An increasing error structure is generated from an initial error \({\varepsilon }_{0}\) and an increment factor \(\phi\), with \(\phi >1\). The error at instant \(j\), \({\varepsilon }_{j}\), will be:

$${\varepsilon }_{j}={\varepsilon }_{j-1}\phi ={\varepsilon }_{0}{\phi }^{j}$$
(1)

From there, the standard deviation of the error, \({\delta }_{j}\), is modeled as:

$${\delta }_{j}=\sqrt{{\varepsilon }_{j}^{2}-{\varepsilon }_{j-1}^{2}}$$
(2)

With this error structure, a stochastic process is generated, starting from a sequence of uncorrelated of random numbers \({\varphi }_{j}\) of normal distribution with zero mean and standard deviation \({\delta }_{j}\). The error \({\vartheta }_{j}\) is obtained by accumulating the sum of the sequence of random numbers:

$${\vartheta }_{j}=\sum_{1}^{j}{\varphi }_{j}$$
(3)

The monthly series of streamflow throughout the period is \({Y}_{i}^{k}\), where \(k\) corresponds to the year and \(i\) corresponds to the month. First, the standardized series of streamflow, \({x}_{i}^{k}\), is determined:

$${x}_{i}^{k}=\frac{{Y}_{i}^{k}-{\mu }_{i}}{{\sigma }_{i}}$$
(4)

where \({\mu }_{i}\) is the mean of month \(i\) and \({\sigma }_{i}\) is the standard deviation of month \(i\).

The reference series, \({x}_{j}^{k}\), is the normalized series of values that correspond to the analysis period. The uncertain forecast, \({Z}_{i}^{k}\), is generated by applying the error to the reference series and reconstructing the original values.

$${Z}_{i}^{k}=\left({x}_{i}^{k}+{\vartheta }_{j}\right){\sigma }_{i}^{k}+{\mu }_{i}^{k}$$
(5)

A forecast ensemble is generated by repeating this procedure with a certain number of random series. This forecast can approximate the actual series depending on the chosen values of the initial error \({\varepsilon }_{0}\) and the increment factor, \(\phi\).

The algorithm was run with the same settings as in the case without forecast, but substituting the climatological ensemble by an uncertain forecast consisting of 20 series generated with an initial error of \({\varepsilon }_{0}=0.2\) and an increase factor of \(\phi =1.15\). In this case, the algorithm not only has information on the storage available at the beginning of the operation cycle; it also has some information on the inflows that can be expected into the reservoirs. This information allows for a reduction in the number of cycles where operating rules were required to 18 years. The restriction coefficients for urban demand ranged from 0.95 to 1.00. The restriction coefficients for irrigation demand ranged from 0.20 to 0.95.

The results of the simulation with adaptive operating rules with forecast are shown in Fig. 4d. The activation thresholds, shown as a black line in the storage plot, are very different from the values obtained in the case without forecast. In wet years, restrictions are not required, and no activation thresholds are set. However, in dry years, the algorithm adjusts the activation thresholds according to the expected flows. The total value of the objective function for this simulation is 0.0846 hm3/m. The contribution of urban demand to the objective function is 0.0365 hm3/m while the contribution of irrigation demand is 0.0481 hm3/m. The reservoirs become empty ten times. Three of these episodes produce deficits in urban demands.

4 Discussion

The results obtained in the simulations performed for the Pisuerga-Carrión system in the four alternatives considered are summarized in Table 1 and in Figs. 5 and 6. The application of adaptive rules reduces the duration of the restrictions. According to static rules, the system enters drought condition in 105 months, 15.9% of the period under analysis. This figure is reduced to 63 months under adaptive rules (9.5% of the time) and to 70 months under adaptive rules with forecast (10.6% of the time). As seen in the upper row of Fig. 5, the application of drought operating rules leads to higher storage values, although the differences are not very significant. The increase in reservoir storage is greater for static rules than for adaptive rules, because static rules lead to larger restrictions overall. The differences between adaptive rules with and without forecast were found to be small. This emphasis on water conservation is relevant to reduce the number of episodes where the reservoirs become empty. The activation thresholds established by adaptive rules are variable. In the case of adaptive rules without forecast, the activation thresholds may be above or below the thresholds established for static rules, following the wet and dry cycles of streamflow. In general, higher values of reservoir storage led to thresholds above, and lower values of reservoir storage led to thresholds below those established for static rules. When established, the thresholds for adaptive rules with forecast were higher than the thresholds established in the same year for adaptive rules without forecast.

Table 1 Simulation results for the Pisuerga-Carrión system in the four alternatives considered
Full size table
Fig. 5
figure 5

Time evolution of storage variables for the simulation of the Pisuerga-Carrión system. Upper row: reservoir storage (a: actual values; b: changes with respect to the simulation with no rules; c: cumulative values of changes). Lower row: activation thresholds (d: actual values; e: changes with respect to the simulation with static rules; f: cumulative values of changes)

Full size image
Fig. 6
figure 6

Time evolution of demand variables for the simulation of the Pisuerga-Carrión system. a) Simulation without rules. b) Simulation with static rules. c) Simulation with adaptive rules without forecast. d) Simulation with adaptive rules with forecast. Upper row: supply restriction coefficients. Centre row: cumulative value of the supply deficit. Lower row: cumulative value of the objective function

Full size image

The intensity of the restrictions applied under drought conditions can be seen in the upper row of Fig. 6. Under static rules, the same restrictions are applied every drought year. Under adaptive rules, the intensity of restrictions is variable depending on the conditions. There are no restrictions for urban demand under static rules. Under adaptive rules, the restrictions amount to 0.54 hm3. Restrictions for irrigation are stricter under adaptive rules, but the duration of the periods under restriction is shorter than in the case of static rules and the global value of restricted supply turns out to be lower, as shown in Table 1. Under static rules, the restricted supply amounts to 27.50 hm3. The uncontrolled deficit, produced when there is no remaining storage in the reservoirs, is 4.18 hm3. The total irrigation deficit is 31.68 hm3. According to adaptive rules, restricted irrigation supply is 20.57 hm3. This value is further reduced to 16.34 hm3 when a forecast is available. The uncontrolled deficits are higher than in the case of static rules: 5.87 hm3 and 7.50 hm3, respectively. However, adaptive rules manage to reduce total irrigation deficit with respect to that of static rules: 26.44 hm3 without forecast (a 16.5% reduction) and 24.14 hm3 with forecast (a 23.8% reduction).

The lower row of Fig. 6 shows the evolution of the objective function during the simulation. In the option without rules, deficits are not very frequent, but they imply significant jumps in the objective function because the deficits are usually a large fraction of the monthly demand. There are 13 episodes of deficit, of which 10 affect urban demand. The average urban deficit is 0.37 hm3 per period and the average irrigation deficit is 1.76 hm3 per period. Under static rules, there is only one episode of urban deficit, spanning a three-month period and totalling 0.49 hm3. However, the number of periods of irrigation deficit increases to 19, with an average value of 1.67 hm3 per period. This suggests that restrictions were applied when they were not really needed, given the actual inflow received in the period. The restrictions imposed by static rules led to deficits that were harmful. However, the application of rules is beneficial throughout the analysis period because the total accumulated value of the objective function is less than in the option without rules. The application of adaptive rules leads to even more frequent deficits. There are 20 periods of deficit for urban demand and 22 for irrigation demand for adaptive rules without forecast. The frequent deficits due to restrictions in urban supply have very little effect on the objective function, because deficits due to restrictions are a small fraction of the monthly demand. However, there are three episodes where urban deficit is not due to water conservation measures but to lack of water availability. These three episodes produce a much larger impact on the objective function. The application of adaptive rules leads to more frequent restrictions, but it has the beneficial effect of reducing the total deficit.

The best overall behaviour of the objective function is presented by the option of static rules. Without rules, the total value of the objective function was 0.2479 hm3/m. With static rules, this value was reduced to 0.0703 hm3/m. Adaptive rules lead to a final value of 0.0943 hm3/m, that was reduced to 0.0846 hm3/m assuming an adequate inflow forecast. At first glance, this may be surprising, since the option of static rules does not consider the state of the reservoir at the beginning of each cycle. However, there are two circumstances that explain this behaviour. First, the algorithm that was used to define the static rules optimized the same objective function that was used for the evaluation. Adaptive options, however, perform a partial optimization in each cycle and are later evaluated on their performance over the entire period of analysis. Second, and more important, the static option was able to define the operating rules knowing exactly the series of inflows that enter the reservoirs of the system. The validation of the rules thus defined was done with the same inflow series that were used in rule definition, which constitutes a situation of comparative advantage for static rules.

A numerical experiment was carried out to analyse this point. The system was simulated without rules and with static rules, but with a set of 10,000 random series of inflows. Random inflows were generated from the historical series, but changing the actual sequence of the hydrological years. Under the hypothesis of stationarity, these random series can be considered representative of future inflows because the autocorrelation of annual series is very low. Figure 7 shows the results of these simulations. The plots of the cumulative values of the objective function are shown in the upper row. Plot a corresponds to the simulation without rules and plot b corresponds to the simulation with static rules. In the lower row, plot c shows the comparison of the empirical probability distribution of the final value of the objective function for the simulations without rules and with static rules. The cumulative values of the objective function corresponding to the historical time series have been highlighted in all three plots, together with the average value of the 10,000 series. As can be seen in the plots, the objective value obtained for the historical time series (0.2479) is close to the average value for the simulation without rules (0.2732). However, for the simulation with static rules, the objective value obtained for the historical time series (0.0703) is much lower than the average value (0.1290). The value obtained for the simulation with the historical time series is less than 86% of the 10,000 random series analysed.

Fig. 7
figure 7

Results of the simulation of the Pisuerga-Carrión System with random streamflow series. Upper row: Evolution of the objective function for the 10,000 random series (a: no rules; b: static rules). Lower row, c: probability distribution of the final value of the objective function; d: evolution of the objective function for all alternatives

Full size image

The reference for comparison with adaptive rules should be the average value of the objective function with random time series. This comparison is shown in plot d of Fig. 7. It shows the cumulative value of the objective function obtained for the four cases analysed with historical series (no rules, static rules, adaptive rules, and adaptive rules with forecast) and the average values of the cumulative function in the two cases analysed with random series (no rules, static rules). The behaviour of adaptive rules with the historical series (0.0943 hm3/m without forecast and 0.0846 hm3/m with forecast) is clearly better than the expected value of the static rules for random series (0.1290 hm3/m). The reduction in objective function is 26.9% for adaptive rules without forecast and 34.4% for adaptive rules with forecast.

The above analyses were carried out assuming constant demand values over time. In practice, demand values are known to vary over time. They may increase, in response to population growth in cities or the development of new irrigated areas, or they may decrease, because of the implementation of water saving measures. The possibility of changing demands makes adaptive models more attractive. If demands are expected to change, adaptive rules can react to the evolution of demands and help maximize system performance. The methodology presented in this work may be easily modified to accommodate time variant demands. In each rule definition cycle, the simulations could be performed with the expected values of urban supply and irrigation demands for the near future. The case where future demands are uncertain could be treated in a similar way as streamflow forecasts. The simulations could be performed with an ensemble of forecasted demands to obtain the rule parameters that minimize the expected value of the objective function over the ensemble of forecasted demands. The performance of the system under the derived rules would, obviously, depend on the accuracy of the demand forecast.

5 Conclusions

In this work, a methodology has been proposed for the determination of optimal rules for the operation of reservoir systems from a given initial state. These rules can be applied in a system to support decisions for managing the reservoir system under drought conditions. The methodology consists of simulating the behaviour of the reservoir system during a period of analysis from its initial state, subjected to random hydrological forcing. An objective function is used to compare and select alternatives. The optimal rules consist of a set of thresholds to trigger management actions and coefficients to restrict supply to the demands present in the system.

The main result of the research is the development of a general methodology for the definition of adaptive rules that provides a satisfactory solution in an acceptable computing time. With the proposed methodology, the optimal operating rules of reservoir systems can be obtained for any system with available data.

The methodology was applied to the Pisuerga-Carrión system, in the Duero-Douro basin. Adaptive rules were defined on an annual cycle stating on the month of October, at the beginning of the hydrological year. The specific operating rules for each cycle were determined in two working hypotheses: with no hydrological forecast and assuming that a hydrological forecast is available. Different activation thresholds and restriction coefficients are produced for each year. The values obtained depend mainly on the initial state of the reservoir at the beginning of the cycle and the availability of forecasts.

The results obtained were compared with the operation without rules and with the application of static rules valid for the entire analysis period. Adaptive rules were found to not improve the behaviour of static rules when applied to the same historical series that was used to determine them. However, if random inflow series were considered, the adaptive rules would lead to lower values of the objective function compared to the expected value obtained with static rules. The application of dynamic rules was also found to reduce the duration of periods under restrictions and the overall supply deficit.