1 Introduction

The problems related to managing drinking water distribution networks (WDN), together with their interdependence with other technological infrastructures, require in-depth analysis, mainly when sensitive aspects affect their functioning. Furthermore, the interest related to the management of WDNs depends on the status of Critical Infrastructures (Adedoja et al. 2018) because the alteration of the correct functioning determines considerable impacts on the population's well-being (Johansen and Tien 2018), not only in terms of distributed resource but mainly on the quality of the same. Therefore, it is a priority to have tools capable of estimating the level of exposure to the risks associated with their optimal management to make it sustainable.

In this context, sustainable management models must be based on accurate planning of the entire life cycle of the network, with a short and long-term vision and considering the possible objectives to be achieved (Maiolo et al. 2020). These aspects, linked to quantitative and qualitative assessments, represent the input data for the management models. Expressly, the quality of the water resource assumes a priority role, ensuring compliance with internationally regulated qualitative parameters (e.g., 2000/60/EC) and sustainability requirements and protecting against the risk of contamination.

Identifying sources of contamination in a WDN represents a literary trend that has developed over time. The literature offers different models for estimating quality, prediction, and monitoring (Capano et al. 2019). Generally, it is impossible to disregard the analysis of the context related to modeling the movement and reactions of contaminants within a WDN. The studies of particle transport in computational fluid dynamics mainly show two approaches, the Lagrangian and the Eulerian, respectively (Zhang and Chen 2007). The Lagrangian approach describes the phenomena focusing on the particles that are chased in motion. The Eulerian approach describes phenomena from a specific point in space through which the particles transit. Both methods presuppose the previous knowledge of the WDN hydraulic operating (pipe flow direction and value) throughout the simulated period.

In general, modeling the quality of the resource in a drinking water network requires the calculation of three primary parameters: the position of the source, the concentration, and the intrusion time of the contaminant. The literature identifies different modeling and problem-solving approaches. Sun et al. (2019) analyzes the spatial–temporal characteristics of user alerts during a contaminant intrusion event, proposing a new analysis methodology aimed at reducing the arrival times of reports based on the Convolution Neural Network (CNN). Capano et al. (2019) presented a quick procedure for identifying one or more sensitive nodes in a network using a mainly topological approach called Identification of Contamination Potential Source (ICPS). Benamar et al. (2020) presented a study to obtain detailed information on global changes in Physico-chemical parameters at different sampling points. Ortega et al. (2020) use a Bayesian approach for the source of contamination determination, using an algorithm that reports the probability that each node is the source to explain the correlations between the sampling positions, defining a classification. Grbčić et al. (2021) present a complete framework for identifying the source of contamination (with a machine learning algorithm), the contamination times (with a stochastic fireworks optimization algorithm), and the injected contaminant concentration (through optimization and Random Forest algorithm).

However, the modeling and technological advancement required using forecast analyses point out that traditional models appear unsuitable for the scope. For example, in many cases present in the literature, the analysis of water systems is based only on optimization models of hydraulic properties (velocity, pressure, length of pipelines) (Hassanvand et al. 2021). These represent the input of models with different analytical characteristics, including the Neural Network and the Fuzzy approach, which, through Artificial Intelligence (Salimi et al. 2020), increase the complexity of traditional modeling approaches. This aspect is a priority for the frequent use of management tools, such as the Decision Support System (DSS) (Grimaldi et al. 2020; Pagano et al. 2021), which require accurate and reliable estimates of the parameters.

In his attempt to understand the fundamental mechanisms behind self-reproduction, the Cellular Automata (CA) (Neumann and Burks 1966) are considered a new approach to treating some complex systems whose behavior may be expressed in terms of local laws. The system's complexity emerges from the interactions of its elementary (cellular) units by applying relatively simple local rules. Hence, it can be considered an alternative approach to differential equations and a general formalism that can represent and solve numerical methods. CA has been used to simulate many natural complex phenomena. In particular, Extended Cellular Automata (XCA), which is an extension of the original CA computational paradigm, have proven to be suitable for simulating complex natural phenomena like unsaturated water flow (Mendicino et al. 2006; De Rango et al. 2021), lava flows (Spataro et al. 2017), forest fires (Avolio et al. 2014).

Moreover, another type of CA exists, the Graph-based CA (Wu and Rosenfeld 1979), which has been widely used (Małecki et al. 2019). The principal difference from the classical CA is the definition of the neighborhood modeled as a directed graph.

CA-based models provide other opportunities besides their natural predisposition to parallel computing, which can exploit to improve further computational speed. Specifically, asynchronous functionality optimization can be developed, allowing additional computation speed.

In this paper, the definition of asynchronous functionality is similar to that of Furnari et al. (2021), where a rule is imposed to allow only a part of the domain (called active cells or automata) to evolve step by step to the next state and keep quiescent (i.e., remaining in the same state) the residual part (called non-active cells or automata). From a computational point of view, this functionality avoids unnecessary calculations related to non-active parts of the domain which does not change their state during the simulation execution.

For WDNs the use of classical CA-based models is limited. This aspect is mainly related to the not fixed neighborhood since a WDN is not a classical regular grid. In Keedwell and Khu (2006), one of the first applications of CA to a WDN is proposed. This study introduces the CA approach in the context of optimal design in WDN, developing a direct performance comparison with genetic algorithms (GA). Guo et al. (2007), following the comparative approach between CA and GA, present a structured model with CA, which guarantees better performance than multi-objective genetic algorithms in terms of optimization efficiency. From a qualitative point of view, interest in the combination of CA and water quality modeling has been developing in recent years. Afshar and Hajiabadi (2018) propose a CA approach based on Parallel Cellular Automata (PCA) for multi-objective reservoir operation optimization. In Abhijith and Mohan (2020), the CA approach is used to predict chlorine's temporal and spatial variations in a WDN, using stochastic Lagrangian techniques to represent advection and dispersion processes. Abhijith and Mohan (2021) use a CA approach to model microbial growth and trihalomethane formation in chlorinated water distribution systems.

In this paper, we propose an Eulerian Water quAlity Modeling—Cellular Automata (EWAM-CA), based on a finite volume forecasting model formalized in the Graph-based XCA approach in the water resource quality modeling proposed in Rossman et al. (1993). EWAM-CA enables the modeling of the transport and reaction of a chemical substance mixed with water within pipelines of a drinking water network. The model's potential is evaluated in the application by simulating chlorine injection in a medium-sized network with a steady-state hydraulic simulation. The model is structured to adapt to unsteady-state hydraulic simulations and model different reaction mechanisms of the transported substances. In detail, the EWAM-CA model performs a discretization of volumes, according to Rossman et al. (1994). Each pipeline is divided into a defined number of sub-volumes compatible with the hydraulic operating regime of the network. The chemical substance in each sub-volume is routed downstream, updating the states of the automata representing the network nodes.

The parallel implementation of the EWAM-CA model, together with the application of a new asynchronism rule, is applied on a Fossolo network (Bragalli et al. 2008; Meirelles et al. 2018). This network, single source, includes 36 nodes, 58 pipes that extend for about 8.4 km. For quality simulation a sodium hypochlorite is chosen as input substance, with a constant and an impulsive input, useful to comparing the result compared with the Epanet software. The main aim is to evaluate the potential of the EWAM-CA parallel implementation coupled with the asynchronous functionality in terms of computational efficiency.

Then, in Sect. 2 the criteria relating to the hydraulic modeling of the water network and the modeling with CA are detailed, including a case study presentation. In the Sect. 3 the results of the EWAN-CA application and the relative computational performances are presented. The conclusions are explained in Sect. 4.

2 Materials and Methods

2.1 Water Quality Modeling in an Urban Network

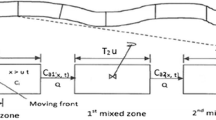
The hydraulic simulation aims to model the WDN operating regime starting from known data. On the other hand, the quality simulation goal is the knowledge of how chemical substances move and react in the network. Quality models use as input the hydraulic operating regime of and the characteristics of the introduced substances (diffusivity, solubility, concentration). Rossman et al. (1993) present a solution approach using a finite volume Eulerian scheme. The method assumes that the pipes are divided into equally sized volume segments once a temporal discretization is defined. The volumes composing each pipe are considered thoroughly mixed, limiting the numerical diffusion.

The authors, in this paper, propose a computation method based on the Eulerian finite volume method presented in Rossman et al. (1993). The model uses the operator splitting technique on the advective flow equation.

The tubes are divided into sub-volumes depending on the quality time step chosen. For each quality time interval, each volume element undergoes the reaction and dispersion (Eq. (1)) and is subsequently transported (Eq. (2)) following the hydraulic operating regime.

$$\frac{\partial C}{\partial t}-D\frac{{\partial }^{2}C}{{\partial }^{2}x}+{k}_{b}C=0$$
(1)
$$\frac{\partial C}{\partial t}+u\frac{\partial C}{\partial x}=0$$
(2)

In which: \(\mathrm{C}\) is the concentration of the chemical substance along the pipe, \(u\) is the flow average velocity, \(x\) represent the position in the i-st pipe (\(x=0\) pipe start, \(x={L}_{i}\) pipe end, \({L}_{i}\) is the i-st pipe length), \(D\) is the diffusion, \({k}_{b}\) represent the reaction rate coefficient.

Rossman et al. (1993) use a criterion for dividing pipes into elements based on the pipe travel time:

$$\tau =min\left(\frac{{V}_{i}}{{Q}_{i}}\right)$$
(3)
$${\eta }_{i}^{*}=\left(\frac{{V}_{i}}{{\tau Q}_{i}}\right)$$
(4)
$${v}_{i}=\frac{{V}_{i}}{nearest\;integer({\eta }_{i}^{*})}$$
(5)

where \(\tau\) is the quality simulation time interval, \(i\) is the index pipes, \({V}_{i}\) is the total volume, \({Q}_{i}\) is the flow rate, \({\eta }_{i}^{*}\) is the non-integer number of finite sub-elements, \({v}_{i}\) is the volume of the \({\eta }_{i}\) sub-elements. To assess the effectiveness of the EWAM-CA to model the introduction and transport of a chemical substance model, we compare the results obtained with the Epanet software, characterized by a Lagrangian solution approach (Liou and Kroon 1987). Epanet (Rossman 2000) is a software developed by the USEPA (the United States Environmental Protection Agency). It is one of the most known software for WDN hydraulic simulation. It allows performing hydraulic simulations of chemicals within a WDN.

Herein we chose sodium hypochlorite as the input chemical substance. This substance is commonly used for water disinfection because the reaction kinetics are well known. This substance, used for water disinfection, undergoes a decay process in the network. The sodium hypochlorite decay process releases free chlorine, which functions well in water quality control. In additions, its systematic determination allows recognizing degradative processes in progress in the network, providing important information on the disinfection process.

There are many chlorine decay analysis models. Most of these models refer to the one proposed by Rossman et al. (1994), which laid the content foundations for the quality simulation criteria setting in Epanet 2 (Rossman 2000). EWAM-CA simulates chlorine concentration decay using the one-dimensional conservation of mass equation for a dilute concentration of total free chlorine in water flowing through a section, proposed in Rossman et al. (1994) to use the Eq. (1):

$$\frac{\partial C}{\partial t}=-u\frac{\partial C}{\partial x}-{k}_{b}C-\frac{{k}_{w}\left(C-{C}_{w}\right)}{r}$$
(6)

where \(C\) is the chlorine concentration in the bulk flow, \(u\) is the flow average velocity, \({k}_{b}\) is the bulk flow decay rate, \({C}_{w}\) chlorine concentration at pipe wall and \(r\) is the hydraulic radius.

Equation (6) excludes the dispersion term, considered negligible compared to the others. The decision to neglect \({k}_{w}\) depends on the variability of this parameter, linked to the temperature of the water, and the actual conditions of the pipe material. It is usually determined during the calibration phase of the model. According to Eq. (6) the concentration depends on three terms. The first term considers the advection due to the water flow, while the second and third represent the decay in the bulk flow and on the pipe wall, respectively. In the often recurring hypothesis of considering the total chlorine decay mechanism within the bulk flow, Eqs. (1) and (2) can be rewritten as follows:

$$\frac{\partial C}{\partial t}=-{k}_{B}C$$
(7)
$$\frac{\partial C}{\partial t}+u\frac{\partial C}{\partial x}=0$$
(8)

in which

$$C(t)=C(t-\Delta t){e}^{-{k}_{B}\Delta t}$$
(9)

where \({k}_{B}\) represents the total bulk decay rate.

2.2 Cellular Automata Water Quality Modeling

CA can be considered a time/space discrete model where space is represented by a d-dimensional (i.e., 1D, 2D, 3D, …) structured grid of cells. At the beginning of the simulation, cells are in an arbitrary state, and the CA evolves by changing the states of the cells in discrete time steps by applying the same evolution law to each of them simultaneously. The evolution law can also consider the states of neighboring cells, defined by neighoborhood conditions, a geometrical pattern invariant in time and space. Despite their simple definition, CA may give rise to highly complex behavior at a macroscopic level. Even if the local laws that regulate the system's dynamics are known, the system's global behavior can be tough to predict. In general, CA is formally identified by a quadruple which describes its fundamental characteristics. The quadruple is composed of: cellular space, in which the automata can evolve (e.g., one-, two-, three-dimensional); the pattern of the neighborhood, which identifies the spatial correlation between the cells in the computational domain and cannot change over time (e.g., Von Neumann or Moore neighborhood); the finite set of the cells states; the deterministic transition function, which allows evolving the cellular automata over time. It is simultaneously applied to each cell of the CA, and according to the neighborhood pattern, the cell changes its state. Moreover, the keys properties of the CA are: parallelism the state of each cell is updated independently from the others; locality, the new state of the cell depends only on its old state and the state of the neighborhood; homogeneity, the same deterministic transition function is applied to each cell of the domain.

Many different CA-based methods can be found in the literature to simulate many natural phenomena. XCA (Di Gregorio and Serra 1999) represent an extension of the original CA computational paradigm. The XCA formalism introduces some extensions concerning the classical CA. Major novelties regard the possibility of decomposing the state of the cells in substates (i.e., chemical concentration, total water volume, etc.) related to the phenomenon to be modeled. The cell state thus belongs to the Cartesian product of the considered substates. Phenomenon parameter behaviors, such as total bulk decay rate, can also be considered. In addition, the state transition function is divided into elementary processes, describing particular aspects of the supposed phenomenon.

A Graph-based XCA has been here considered as an explicit solver. The Graph-based XCA preserves all fundamental characteristics of the XCA. Nevertheless, the condition of the neighborhood has been relaxed to be considered as a directed graph. The choice of the Graph-based XCA was dictated by the context of WDN in which a topological position describes the relationship between the various nodes of the network.

The formal definition of the Graph-based XCA is described by the following formulation:

$$\text{EWAM-CA} =\, <D, G, S, P, \sigma >$$
(10)

where:

\(D= \left[0, n-1\right]\subset {\mathbb{Z}}\) is the one-dimensional discrete computational domain, with \(n\) representing the number of cells.

\(G\) is a directed graph \(G=\left(V, E\right),\) which is defined by a set of nodes \(V\left(G\right)\), set of edges \(E\left(G\right)\). Each vertex \({v}_{i}\) corresponds to one automaton cell and identifies a set of elements such as tanks, reservoirs, and junctions, while the edge represents the longitudinal elements such as pipes and valves. The neighborhood of the vertex \({v}_{i} \in V\left(G\right)\) is the set of vertices \(X\left({v}_{i}\right)={X}_{in }\left({v}_{i}\right)\cup {X}_{out }\left({v}_{i}\right)\), in which \({X}_{in }\left({v}_{i}\right)=\{{v}_{j }| {v}_{j }{v}_{i }\in E\left(G\right)\}\) and \({X}_{out }\left({v}_{i}\right)=\{{v}_{j }| {v}_{i }{v}_{j }\in E\left(G\right)\}\).

In particular, the edge between a generic node \({v}_{i}\) and node \({v}_{j}\) is modeled to be subdivided into \({\eta }_{ij}\) equal size volume elements, which identify the discrete mass value over the pipe, and are calculated by Eqs. (3) and (4).

\(S\) is the set of finite states of the cell that is defined as:

$${S}_{{v}_{i}}= {S}_{c}\times {S}_{f}^{\left|X\left({v}_{i}\right)\right|}\times {S}_{m}^{{\eta }_{i1}}\times ... \times {S}_{m}^{{\eta }_{i\left|X\left({v}_{i}\right)\right|}}\times {S}_{c}^{{\eta }_{i1}}\times ... \times {S}_{c}^{{\eta }_{i\left|X\left({v}_{i}\right)\right|}}$$
(11)

where \({S}_{c} [Mg/l]\) identifies the chemical concentration of the node, while the states \({S}_{f} [l/s]\)  represent the neighborhood relationship with the other automata, \({S}_{f}^{\left|X\left({v}_{i}\right)\right|}\) is the flow referring to the pipes connecting to the vertex \({v}_{i}\), \({S}_{m}^{{\eta }_{i1}}\times ... \times {S}_{m}^{{\eta }_{i\left|X\left({v}_{i}\right)\right|}}\) and \({S}_{c}^{{\eta }_{i1}}\times ... \times {S}_{c}^{{\eta }_{i\left|X\left({v}_{i}\right)\right|}}\) are the mass of the chemical and the concentration referring to pipes connecting the vertex \({v}_{i}\) and the vertex \({v}_{j }\) and subdivided into \({\eta }_{ij}\) sections.

\(P=\{{k}_{b}\}\) is the set of parameters identified, where \({k}_{b}\) is the total bulk decay rate.

\(\sigma =\{{\sigma }_{1 },{\sigma }_{2 }, {\sigma }_{3 }, {\sigma }_{4 }\}\) is the deterministic transition function. It is composed of the following elementary processes, listed below in the same order as they are applied.

It allows to define the state of the automaton at time \(t+1\) and depends on the state of its neighborhood at time \(t\):

$${\sigma }_{1} : {S}_{m}^{{\eta }_{i1}}\times ... \times {S}_{m}^{{\eta }_{i\left|X\left({v}_{i}\right)\right|}} \to {S}_{m}^{{\eta }_{i1}}\times ... \times {S}_{m}^{{\eta }_{i\left|X\left({v}_{i}\right)\right|}}$$
(12)

\({\sigma }_{1}\) allows calculating the mass of chemicals by considering the elements inside the edge between node \({v}_{i}\) and node \({v}_{j}\) by applying the following equation:

$${m}_{ij}^{\mathrm{^{\prime}} k}={m}_{ij}^{k}{e}^{{k}_{b}\tau}\;\forall k \in \left\{1,..,{\eta }_{ij}\right\}$$
(13)

where \({m}_{ij}^{k}\) is the chemical mass in the k-st element in the pipe between a generic node \({v}_{i}\) and node \({v}_{j}\) before reaction and \(m_{ij}^{\prime k}\) is the new value after the reaction.

$${\sigma }_{2} : {S}_{m}^{{\eta }_{i1}}\times ... \times {S}_{m}^{{\eta }_{i\left|X\left({v}_{i}\right)\right|}} \times {S}_{f}^{\left|X\left({v}_{i}\right)\right|} \to {S}_{c}$$
(14)

\({\sigma }_{2}\) updates the chemical concentration within the cell as:

$${M}_{{v}_{i}}= \sum_{j}^{\left|{X}_{in}\left({v}_{i}\right)\right|}{m}_{ji}^{{n}_{ji}-1}$$
(15)
$${V}_{{v}_{i}}= \sum_{j}^{\left|{X}_{in}\left({v}_{i}\right)\right|}\tau {Q}_{{v}_{j}}$$
(16)
$${C}_{{v}_{i}}^{{{\prime}}}= \frac{{M}_{{v}_{i}}}{{V}_{{v}_{i}}}$$
(17)

where \({M}_{{v}_{i}}\) is the total mass of the chemical entering the \(i\)-st vertex, \({m}_{ji}^{ {\eta }_{ij}}\) is the mass of the chemical in the last sub-element (\({\eta }_{ji}\)) in the pipe between a generic node \({v}_{i}\) and node \({v}_{j}\), \({V}_{{v}_{i}}\) is the total water volume entering the \(i\)-st node, and \({C}_{j}^{in}\) is the chemical concentration in the \(i\)-st node.

$${\sigma }_{3} : {S}_{m}^{{\eta }_{i1}}\times ... \times {S}_{m}^{{\eta }_{i\left|X\left({v}_{i}\right)\right|}} \to {S}_{m}^{{\eta }_{i1}}\times ... \times {S}_{m}^{{\eta }_{i\left|X\left({v}_{i}\right)\right|}}$$
(18)

\({\sigma }_{3}\) defines the update the mass and the concentration using the following equation:

$${m}_{ij}^{k+1}={m}_{ij}^{k}\;\forall k \in \left\{1,..,{\eta }_{ij}-1\right\}$$
(19)

where \({m}_{ij}^{k}\) identifies the \({k}^{th}\) mass element in the pipe between the generic node \({v}_{i}\) and \({v}_{j}\).

$${\sigma }_{4} : {S}_{m}^{{\eta }_{i1}}\times ... \times {S}_{m}^{{\eta }_{i\left|X\left({v}_{i}\right)\right|}}\times {S}_{f}^{\left|X\left({v}_{i}\right)\right|} \to {S}_{m}^{{\eta }_{i1}}\times ... \times {S}_{m}^{{\eta }_{i\left|X\left({v}_{i}\right)\right|}}$$
(20)

\({\sigma }_{4}\) allows to calculate the mass by using the following equation:

$${m}_{ij}^{1}= {C}_{{v}_{i}} {Q}_{{v}_{i}} \tau$$
(21)

Where \({m}_{ij}^{1}\) identifies the first mass element in the pipe between a generic node \({v}_{i}\) and node \({v}_{j}\) and \({C}_{{v}_{i}} , {Q}_{{v}_{i}}\) and \(\tau\) correspond to the concentration, the discharge, and the time interval, respectively.

Figure 1 illustrates, as pseudo-code, the primary simulation process of the EWAM-CA. The EWAM-CA was developed in C++. At the beginning of the process, the init() function allows the loading the computational domain by defining the relation between the cells of the Graph-based XCA. The main cycle, lines 7–14, permits the evolution of the EWAM-CA model by applying at each cell the set of the transition function. Finally, lines 11–12 allow updating the set of the state of the cellular space.

Fig. 1
figure 1

EWAM-CA pseudo-code to describe the main simulation process

Full size image

2.3 Making Cellular Automata Parallel and Asynchronous

The OpenMP API was considered to exploit the CA intrinsic parallelism property, supporting multi-platform shared-memory parallel programming in C/C++. This choice is mainly related to OpenMP portability, a simple and flexible interface that can exploit parallel computation from a workstation to supercomputer architectures.

The asynchronous functionality permits narrowing the computation only to the set of active nodes, allowing to skip the not active nodes, meaning that not only the transition function is not computed, but also that the not active cells are entirely skipped. At the beginning of the computation, all the node state is set to non-active unless for the source node. During the simulation, a node can set to active one of the neighborhood nodes by considering the following rule:

$$active\;\,if\;\exists\;i\in [1, ..., \left| {X}_{in}\left({v}_{c}\right)\right| ] |\;{m}_{ic}^{{\eta }_{ic}-1} > 0$$
(22)

A node can change its state to non-active using the following rule:

$$\begin{aligned}nonactive\;\,if\;{C}_{{v}_{c}}&= 0\,\wedge\,\forall\,i\;[1, ..., \left| {X}_{out}\left({v}_{c}\right)\right| ] | \sum\limits_{k=0}^{{\eta }_{ci}}{m}_{ci}^{k}\\&=0\,\wedge\,\forall\,i\;[1, ..., \left| {X}_{in}\left({v}_{c}\right)\right| ] | \sum\limits_{k=0}^{{\eta }_{ic}}{m}_{ic}^{k} =0\end{aligned}$$
(23)

More in detail, a node activates a neighborhood node if the chemical mass of the last element of the pipe is greater than zero. Instead, a node deactivates itself if its concentration is zero, the sum of all chemical mass in its outgoing pipe is zero, and the sum of all chemical mass in its incoming pipe is zero.

Applying the above rules allows skipping the non-active node's \({\sigma }_{1}, {\sigma }_{2}, {\sigma }_{3},\,\mathrm{and}\;{\sigma }_{4}\) deterministic transition functions computation altogether. Since the transport of a chemical substance does not necessarily and immediately involve all the network nodes, an asynchronous implementation deactivates the automata that do not participate in the chemical transport, leading to an increase in computational performance.

2.4 Case Study

The chosen case study is a network presented in Bragalli et al. (2008) and Meirelles et al. (2018) (Fig. 2). The network supplies water to a District Metered Area (DMA) in the city of Bologna. The DMA extends over 0.5 square kilometers.

Fig. 2
figure 2

Fossolo plan view. Google “Satellite” background

Full size image

The WDN counts 36 nodes, an average altitude of 64.3 a.s.l., and 58 pipes extending for about 8.4 km. The network has a single source modelled by a reservoir (tank of infinite volume) with a fixed hydraulic head of 121 a.s.l., which provides a flow of 33.9 l/s to the served area.

3 Results

The comparison between the Epanet solution model and the EWAM-CA concerns a steady flow hydraulic simulation. The simulation duration covers a total period of 1 h. The limited simulation duration is due to the small size of the network. The topologically farthest node from the reservoir has a water age of 18.6 min. The quality simulation models two scenarios. The first considers as input a constant amount of chlorine for the whole simulation period. The second one considers as inputs the same chemical concentration for a shorter period (10 min).

The chemical input affects node "1", located immediately downstream of the reservoir the chemical input is modeled by setting the concentration of each flow, leaving the node to the chosen value (500 µg/l). This chemical input corresponds to the setpoint booster source in the Epanet quality simulation module.

The limited simulation duration imposes short time-steps. Epanet hydraulic simulation is set to 5 min. Fossolo network is characterized by variable travel times ranging from 18.5 s to more than 40 min. According to what is reported in Rossman et al. (1993), the quality time-step must be at most equal to the shortest pipe time travel in the network (Eqs. (3), (4), and (5)) to ensure that water is not transported beyond its downstream boundary node. Therefore, for both the presented scenarios a time-steps of 10 s is used.

Figures 3 and 4 show a comparison between the results of the models for both scenarios. As seen from the figures, the behavior of the applied model is very similar to that of Epanet. The EWAM-CA model is characterized by the arrival times of the contaminant slightly lower than those of Epanet. This is due to the time shift error that characterizes EWAM-CA. As shown, the model is suscetible to choosing the quality timestep.

Fig. 3
figure 3

Comparison between the simulation results with the \(\Delta t\) = 10 s and a constant input

Full size image
Fig. 4
figure 4

Comparison between the simulation results with the \(\Delta t\) = 10 s and an impulsive input

Full size image

3.1 Computational Performance

The performance of EWAM-CA implementation is evaluated by considering the execution on a cluster node equipped with Intel(R) Xeon(R) Gold 6128 CPU @ 3.40 GHz with 64 GB of RAM. Two variants of the algorithm were tested for the above mentioned scenarios. The first former is based only on the Parallel Implementation, called hereafter PI. The second one is based on the Parallel and the Asynchronism Implementation, called hereafter PAI. The automata in the PAI are initially inactive and activated when the movement involves the automata connected to them. The automata are kept deactivated if they do not participate in the transport.

To evaluate the performance improvement of the PA and PAI with respect to the serial algorithm (i.e., Not parallelized), the use of the speedup is introduced. The speedup allows to characterize the performance improvement of a parallelized algorithm. The speedup is the ratio of the running time of the serial algorithm of its parallelized variant. The higher the speedup value, the better the performance gain due to parallelization.

The first series of experiments are shown in Fig. 5. The PAI version achieved the best speedup, approximately 3.2, with eight cores. The PAI demonstrated higher computational performance in all experiments than the PI implementation. Figure 5b shows the number of active nodes during the simulation. Since a constant injection rate is considered, the number of active nodes never decreases and reaches the total number of nodes approximately after 1000 s.

Fig. 5
figure 5

a shows the speedup achieved by the PI and PAI versions. b illustrates the number of the active nodes in the system during the simulation for the PAI implementation

Full size image

The second series of experiments are shown in Fig. 6. Again, the PAI version achieved the best speedup, approximately 4.2, with eight cores. The PAI demonstrated higher computational performance in all experiments than the PI implementation. Figure 5b shows the number of active nodes during the simulation. Since an impulsive input is considered, the number of active nodes increases and decreases, reaching a peak approximately at the 500 s. Moreover, the gap between the two implementations is more noticeable in the first series of experiments. This trend is related to the asynchronous functionality, which can significantly improve the performance when only some of the nodes are involved in the contaminant propagation.

Fig. 6
figure 6

a shows the speedup achieved by the PI and PAI versions. b illustrates the number of the active nodes in the system during the simulation for the PAI implementation

Full size image

The PAI version achieved better speedup in all experiments, mainly concerning the impulsive injection scenario. While the performance gain is reduced, considering a constant input. This latter scenario is configured as the worst case since the input reaches all the network nodes, and being constant prevents the cells from changing their state to non-active. Otherwise, considering an impulsive injection, the performance gain is mainly due to the deactivation of the cells, which are not involved in the propagation process, as seen in Fig. 6.

Further remarkable optimization can be achieved considering a constant source rate injection not located in the upper part of the network. The pollutant propagation process will probably not affect some network nodes that will never be activated by the model. Injecting a substance in a network-internal node reduces the maximum number of cells activated during a simulation.

4 Conclusions

Identifying a criterion to define the level of contamination risk in a water network requires increasingly sophisticated models and novel and performing computational tools. The proposed EWAM-CA interprets this need and declines it by integrating the CA paradigm in a non-continuous domain, such as a drinking water network, requiring the formalization of a Graph-based XCA approach.

The EWAM-CA simulation results have shown very similar behavior to the Epanet ones, confirming the reliability of the proposed model. Furthermore, the EWAM-CA computational efficiency has been improved by considering parallelization and asynchronous functionality. In particular, the introduction of the new asynchronous rules, which allows for locally managing the activation/deactivation of the automata, together with an efficient parallel implementation of the EWAM-CA, increased the computational simulation performance significantly. This aspect is crucial, especially when hundreds or thousands of simulations are in demand for real-time problems, such as contaminant-source detection.

Future developments are oriented to employ EWAM-CA model as an efficient simulation tool for a contaminant-source identification system. This latter will use a large batch of simulations over the domain by changing the source input for each network node with different source types and characteristics. Furthermore, the use of CA allows for building local rules that can be used to describe specific phenomena regarding the chemical transport and reactions within the networks, which is also suitable for emergency management.