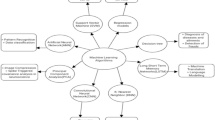
Abstract
Hydrological data provide valuable information for the decision-making process in water resources management, where long and complete time series are always desired. However, it is common to deal with missing data when working on streamflow time series. Rainfall-streamflow modeling is an alternative to overcome such a difficulty. In this paper, self-organizing maps (SOM) were developed to simulate monthly inflows to a reservoir based on satellite-estimated gridded precipitation time series. Three different calibration datasets from Três Marias Reservoir, composed of inflows (targets) and 91 TRMM-estimated rainfall data (inputs), from 1998 to 2019, were used. The results showed that the inflow data homogeneity pattern influenced the rainfall-streamflow modeling. The models generally showed superior performance during the calibration phase, whereas the outcomes varied depending on the data homogeneity pattern and the chosen SOM structure in the testing phase. Regardless of the input data homogeneity, the SOM networks showed excellent results for the rainfall-runoff modeling, presenting Nash–Sutcliffe coefficients greater than 0.90.
Graphical Abstract

Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
There are several uses for water resources, such as human supply, irrigation, animal watering, electricity generation, navigation, dilution of effluents, fishing, recreation, and landscaping (Collischonn and Dornelles 2015). Therefore, the effective management of water resources is essential to social and economic development. Moreover, the proper administration may mitigate the impacts of various natural phenomena, such as droughts that directly affect water disposal and the energy sector (Santos et al. 2019). Better water resources management includes understanding and analyzing water-related problems, such as inadequate supplies to meet water demands (e.g., drinking, sanitation, and power needs), flood damages, and water pollution (Loucks and Beek 2017). Thus, learning about the environmental variables that affect streamflow processes, especially rainfall, is a primary activity (Muhammad et al. 2018). The rainfall-streamflow relationship is a complex and non-stationary process, presenting non-linear spatiotemporal characteristics (Lettenmaier and Wood 1993). The mentioned complexity can be associated with the hydrological systems’ uncertainties.
A rainfall-streamflow model uses rainfall data as input to simulate the streamflow in a specific section of a river. Examples of rainfall-streamflow models commonly used are Soil Moisture Accounting Program – SMAP (Lopes et al. 1981); Tank Model (Sugawara 1961); self-calibrating hydrological model – MODHAC (Lanna and Schwarzbach 1989); and Soil and Water Assessment Tool – SWAT (Arnold et al. 2012). Lately, models based on artificial neural networks (ANN) have already been used to model the rainfall-streamflow relationship (Hsu et al. 1995; Jain et al. 2004; Farias et al. 2013; Da Silva Filho and Farias 2018; Santos et al. 2019); for river inflow prediction (Campolo et al. 1999; Kisi 2004; Kumar et al. 2004; Ciğizoğlu and Kisi 2005; Honorato et al. 2018; Santos et al. 2019); for precipitation forecast (Hall et al. 1999; Silverman and Dracup 2000; Freiwan and Cigizoglu 2005; Mirabbasi et al. 2018); for groundwater modeling (Coulibaly et al. 2001; Nayak et al. 2006; Mohanty et al. 2010); for water quality modeling (Singh et al. 2009; Gazzaz et al. 2012); for evapotranspiration estimation (Kumar et al. 2002; Trajkovic et al. 2003; Zanetti et al. 2007; Adeloye et al. 2011); and for sediment transport (Nagy et al. 2002; Ciğizoğlu and Alp 2006; Melesse et al. 2011; Farias and Santos 2014).
Self-organizing maps (SOM) are artificial neural networks (ANN) that cluster input data according to their similarities (Kohonen 1982; Haykin 1999; Farias and Santos 2014). Composed by a set of neurons, SOM networks use unsupervised machine learning techniques to organize data to preserve neighboring relationships. Also known as Kohonen neural networks, they are a cluster analysis and prediction method.
Several studies reported the successful application of SOM for modeling environmental and water resources systems. Garcı́a and González (2004), for instance, applied SOM to understand the behavior of input variables in the operation processes of a wastewater treatment plant. Novarini et al. (2019a, b) used the clustering capacity of SOM networks in the modeling stages of optimal pressure management in water supply systems. Voutilainen and Arvola (2017) employed SOM to cluster complex environmental data from a small boreal lake. Yotova et al. (2021) used SOM to water quality assessment on a river catchment scale. Adeloye et al. (2011) used SOM to predict the reference evapotranspiration. Farias and Santos (2014) and Farias et al. (2015) used SOM networks for runoff-erosion modeling.
Gao et al. (2021), Mannan et al. (2018), Nourani et al. (2013), and Ismail et al. (2012) employed SOM to identify spatially homogeneous clusters of precipitation. Zhang et al. (2022) also used SOM to cluster homogeneous regions for flash floods in China. Wang and Sun (2022) successfully analyzed the applicability of SOM for the statistical downscaling of regional daily precipitation in China. Li et al. (2020), Gholami et al. (2022), Wu et al. (2021), and Lee et al. (2021) characterized and analyzed groundwater quality based on SOM networks. Lastly, Adeloye and Rustum (2012), Farias et al. (2012, 2013), and Da Silva Filho and Farias (2018) are examples of the application of SOM for rainfall-streamflow modeling.
Responsible management of water systems depends on parsimonious models that use accessible and reliable input variables. Therefore, satellite rainfall products may be interesting for filling missing data and hydrological analysis. The lack of continuous and long rainfall time series is common in developing countries. According to Gadelha et al. (2019), the Brazilian rain monitoring network has approximately 11,820 rain gauges, resulting in a density of about one rain gauge per 720 km2, lower than that recommended by WMO (1994), i.e., one rain gauge per 575 km2.
Studies using SOM networks to simulate streamflow based on gridded satellite-estimated rainfall data and naturalized inflows for calibration are scarce worldwide. In this study, we simulated streamflow using Tropical Rainfall Measuring Mission (TRMM) rainfall for a reservoir in the São Francisco River basin, Brazil.
2 Materials and Method
2.1 Study Area
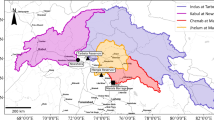
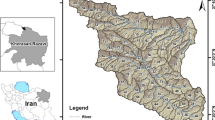
The Upper São Francisco River basin, located in the northeast central part of Brazil, lies between latitudes 18.125°S and 20.875°S and longitudes 43.875°W and 46.625°W (Fig. 1). It is a sub-basin of the São Francisco River, considered the third most relevant Brazilian river basin (Santos and Morais 2013). The Upper São Francisco River basin has about 49,574 km2 and, for example, is larger than the Netherlands, Denmark, and Switzerland. As for the relief, it is noteworthy that it has a wavy topography, with elevations ranging from 600 to 1600 m, as observed in Fig. 1.
The region has two seasons: a rainy summer (October–March) and a dry winter (April–September). According to Köppen’s classification (Alvares et al. 2013), the local climate types of the region vary from Cwa (dry winter and hot summer) to Cwb (dry winter and temperate summer) and Aw (tropical zone with dry winter). The average annual rainfall varies from around 2,000 mm in the central-western part to about 1,000 mm in the north-eastern part (Santos et al. 2018, 2019). About 85% of the annual rainfalls occur in the rainy season, and the average temperature is around 22 °C, with the evaporation around 1,000 mm per year (MMA 2017).
The local biome is the Cerrado, a seasonal ecosystem characterized by dry and wet seasons. Land use and cover include savanna vegetation, agriculture and pasture fields, urban areas, barren land, and forests (Silva et al. 2018). According to Klink and Machado (2005), tall and dense evergreen gallery forests form the vegetation, ranging from closed to open canopy deciduous and semi-deciduous with a maximum height of 15 m.
2.2 Streamflow Data
The streamflow records used in this work were the naturalized monthly inflows to Três Marias Reservoir, located in the upper part of the São Francisco River basin (Fig. 1a). Naturalized inflow means the quantity of water that would have entered the reservoir for which there have been no effects caused by diversion, storage, import, export, return flow, or changes in consumptive use. The Brazilian National System Operator (ONS; Operador Nacional do Sistema, available at: http://www.ons.org.br), responsible for the operation of the Brazilian Interconnected System, provided such naturalized monthly inflow data, composed of 264 values from January 1998 to December 2019 (Fig. 2b). The obtained streamflow time series presented maximum and minimum values of 3,016.0 m3/s and 6.8 m3/s, respectively. It is worth noting the inhomogeneity of the streamflow time series. According to the Pettitt test (Pettitt 1979), there was an abrupt change in the time series in April 2013. Table 1 shows the main statistics of these data for the first and second hydrological period, i.e., 01/1998–04/2013 and 05/2013–12/2019, and for the entire time series, i.e., 01/1998–12/2019. The first period presents an average inflow of 638.4 m3/s, while the second period presents an average of 269.4 m3/s. Severe water shortages impacted the basin during the intense austral summer drought of 2013–2015 (Abatan et al. 2022), generating several impacts on the flows and, consequently, on freshwater availability. The magnitude of the impact of this drought event had severe impacts on human consumption, energy production, and other socioeconomic activities (Paiva et al. 2020).
2.3 TRMM Rainfall Data
The TRMM was a joint mission between the National Aeronautics and Space Administration (NASA) and the Japan Aerospace Exploration Agency (JAXA), which provided critical precipitation measurements in the tropical and subtropical regions of the Earth (Plouffe et al. 2015; Teng et al. 2016; Santos et al. 2019). The monthly rainfall data were obtained at each 0.25° from 46.625°W to 43.875°W and 20.875°S to 18.125°S, considering only the grid-cell inside the study area’s boundary, in a total of 91 time series (Fig. 1b). Each time series had 264 monthly records, referring to the monthly period between January 1998 and December 2019. Figure 2a also depicts the hyetograph based on TRMM-estimated rainfall data, considering the Thiessen-weighted average over the river basin (Fig. 1a). At the same time, Table 1 shows the descriptive statistics for the inflow and average rainfall data.
3 Methodology
3.1 Self-Organizing Maps
A SOM network is a competitive learning ANN model that performs a kind of vector quantization that captures the topology of the input space (Kohonen 1982). The main objective of a SOM is to transform an arbitrary-sized input signal pattern into a discrete one-or-two-dimensional map. SOM models cluster the standard input data to represent similar patterns by the same output neurons or one of their neighbors. They consist of two layers: the input and the SOM or output layers. It is important to note that the grouping and mapping performed by the SOM network preserve the original topology of data, keeping essential information during the process. In this sense, each output neuron connects every input unit, and the weights of such links define a prototype vector (i.e., codebook vector) in the input space.
Initially, the input data is normalized (i.e., the mean value is zero, and the variance is one). This stage is necessary to permit all the features to move in roughly the same ranges and, possibly, be treated by the SOM in the same way. The weights represent the link strength \({w}_{ij}\) between input neuron j and output neuron i. For training, the model computes the Euclidean distances EDi between the input vector xj and weights wij connected to each output neuron j via:
where xj is the j-th component of the input vector x; n is the dimension of the input vector x; I ranges from 1 to M, with M being the total number of output neurons of SOM layer; and mj is the function mask, usually assumed as one. Values of mj may be zero to exclude the contribution of the element xj in the calculation of the Euclidean distance, widely used when the input variable has missing values.
The batch training algorithm was chosen between the two existing training types (incremental and batch modes) because it is generally much faster than the incremental one. The algorithm presents input vectors to the network using the whole dataset before updating any weight. In this sense, the search for the winning neuron is done for each input vector, and then the weight vector is moved to the average position of all input vectors for which there is a winner (best matching unit – BMU) or a neighbor of a winner.
The winner neuron and its neighbors are selected after the Euclidean distance is computed for all input vectors. In this method, the weights tend to stabilize after several presentations of the dataset. It is worth noting that this network training is unsupervised since there is no target outputs. In this training phase, the output neuron whose weight vector most closely matches the input data vector (i.e., the Euclidean distance is the lowest value) is selected as the winning neuron. In the present study, the Kohonen rule (Beale et al. 2012) updates the weights connected to each winner and neighbor neurons in a particular neighborhood radius.
The network training usually occurs in two distinct phases: ordering and tuning. In the first phase, training is limited by a given number of presentations of the complete dataset. The radius of the neighborhood starts with a given distance that decreases to the unit value. This measure allows the neuron weights to consistently organize themselves in the input space with neuron positions in the dimensional grid. The tuning phase uses the remaining number of presentations established for training. At this stage, the radius of the neighborhood is below unity, meaning that only the winner neuron weight is updated. Weights are expected to be modified relatively evenly in input space during this phase, maintaining the topology defined in the ordering phase (Beale et al. 2012).
Finally, it can be summarized that once the SOM network is trained, it is possible to use the model as a tool for forecasting or calculating variables. For this purpose, (i) the Euclidean distances between the input vectors and weights attached to the output neurons are calculated, disregarding the element j to be supplied, which is done by including a Boolean variable mj, as shown by Eq. (1). The variable mj is used to include (mj = 1) or exclude (mj = 0) the contribution of a given element j from the input vector to the calculation of Euclidean distances; (ii) the winning neuron is determined based on the shortest Euclidean distance; and (iii) the weight of the winning neuron connected to the missing element j of the input vector is used as the predicted value.
3.2 Datasets and Models
Three datasets were used, and three models were established for each dataset. The datasets correspond to three different study periods chosen due to the inhomogeneity of the complete streamflow time series, as discussed in Sect. 2.2. Dataset #1 was chosen to comprise the 1998–2019 period, dataset #2 related to the 1998–2014 period, whereas dataset #3 corresponded to the 2014–2019 period. Each of the three datasets was sub-divided into two sub-sets with 70% for calibration and 30% for testing. However, a hydrological time series may not be stationary, which difficulties the calibration of models and their future applications. Therefore, the division of the streamflow time series for calibration (70%) and testing (30%) was carried out in three different ways, as follows: (i) the calibration dataset comprising the first 70% of the time series (A), (ii) the calibration dataset comprising the last 70% of the time series (B), and (iii) the calibration dataset comprising the first and the last 35% of the time series (C), as schematically represented in Fig. 3. Table 2 summarizes each dataset and model used in this study, providing details about the dataset ID, inputs, model acronyms, and date ranges for the calibration and testing phases.
3.3 SOM Architecture
The number of neurons M was determined based on García and González (2004) according to the following equation:
where N is the total number of samples used in the calibration phase.
The optimum number of neurons M for each dataset, i.e., input vectors, was calculated as ∼67 for dataset #1, ~56 for dataset #2, and ~36 for dataset #3. A square structure was chosen to represent the SOM grids. Thus, the 9 × 9, 8 × 8, and 6 × 6 grids were chosen with a hexagonal structure to be used in this work. The input data were scaled to improve the training efficiency of the SOM model. The scaling process normalizes the inputs to have a zero mean and unitary standard deviation (Beale et al. 2012). The batch mode algorithm was used during the calibration phase, and the datasets were presented to the SOM structure 3,000 times to ensure consistent learning. For the ordering phase, 100 presentations of the dataset, an initial neighborhood radius equal to three steps, and a learning rate of 0.90 were used. The tuning phase lasted the 2,900 remaining presentations, using a neighborhood distance inferior to one and a learning rate of 0.02. The SOM models were implemented using the Neural Network Toolbox of MATLAB R2020b.
3.4 Evaluation Metrics
The estimation accuracy of the models was quantified using the coefficient of determination (R2), Nash–Sutcliffe efficiency (NSE) (Nash and Sutcliffe 1970), percent bias (RBIAS), and Normalized Root Mean Square Error (NRMSE), as shown in Eqs. (3)–(6). Such statistical metrics were chosen because they are widely used in hydrological analyses (Moriasi et al. 2015). In this study, the normalized version of the RMSE was chosen to compare the results from the different models due to the different orders of magnitude of the data in the time series (Viljanen et al. 2018).
where Oi are the observed values, Ci are the values generated by the SOM models, \(\overline{O }\) is the mean of observed values, \(\overline{C }\) is the mean of the values generated by the SOM models, and s is the sample size.
The coefficient of determination R2 evaluates the model performance, with its values varying from 0 to 1, where the optimal value is 1. The NSE assesses the adjustment between observed and estimated data, ranging from −∞ to 1 with an optimal value equal to 1. RBIAS determines how well the model simulates the average magnitudes for the calculated data, varying from −∞ to ∞ with an optimal value equal to 0. Positive values indicate that the model is generally overestimating the measured data, and negative values indicate the opposite (the model is underestimating the values). NRMSE is the normalized version of the root mean square error, where lower NRMSE values would indicate higher accuracy, i.e., the best value is 0.
4 Results and Discussion
4.1 Calibration Phase
The performance of the SOM rainfall-streamflow models was evaluated using the four described metrics, i.e., R2, NSE, RBIAS, and NRMSE, for both calibration and testing phases. For the calibration phase, the metrics results are shown in Table 3, while the observed and calculated inflows are plotted in Fig. 4. In general, satisfactory results can be seen in this calibration phase, showing excellent correspondences between the maximum and minimum values for the analyzed time series. All models presented R2 and NSE indices above 0.90, RBIAS absolute values less than 0.015, and relatively low values of NRMSE during the calibration phase.
Hydrographs for the observed and calculated streamflow for the three datasets and the three different models applied during the calibration, i.e., dataset #1 (1998–2019), dataset #2 (1998–2014), and dataset #3 (2014–2019). Three models developed for each dataset: A = initial 70% for calibration; B = final 70% for calibration and C = divided 70% for calibration
The best values of the obtained metrics are related to the D1C, D2C, and D3C models, which are the approaches that used the calibration dataset formed by the first and last 35% of the original time series. Dataset #3 also presented excellent results for R2 and NSE indices with values close to 1 concerning D3C during the calibration phase. Then, it seems that when the data for calibration includes different hydrological patterns, they do not interfere with the results but rather improve the model performance. It is also worth highlighting that SOM performed well even using short time series (i.e., D3A, D3B, and D3C), presenting, in this case, the best metrics results. Dataset #3 has only 56 months for the calibration phase.
Figure 5 shows the component planes for all models considering streamflow and rainfall from grid-cell #39. According to Beale et al. (2012) and Farias and Santos (2014), the component planes – which represent the weights associated with each input variable – allow the detection of similarities among variables. Lighter (yellow) and darker (black) colors respectively describe larger and smaller weights. The color gradient on each component plane appoints a direct (parallel gradients) or inverse (antiparallel gradients) correlation between two variables (García and González 2004). In Fig. 5, all models show that higher and lower flows are more directly related to current rainfall P(t) than any other input variables.
4.2 Testing Phase
The metrics related to the testing phase are shown in Table 4. Figure 6 shows a graphical comparison between the observed streamflow values and those calculated by the SOM models. In general, unlike for the calibration phase, the results of the metrics vary and, therefore, are thoroughly discussed. For dataset #1 (1998–2019), the worst metric values were observed during the calibration using the first 70% of the streamflow time series (D1A). The R2 and NSE coefficients presented values of 0.126, the RBIAS was 0.507, and the NRMSE was 0.87 (close to 1). As dataset #1 comprises the entire original streamflow time series, which has two different hydrological patterns (638.4 m3/s and 269.4 m3/s), such a pattern interferes with the simulation results. The performance of D1A, for example, can be classified as not satisfactory, according to Moriasi et al. (2015). However, when analyzing the same dataset #1, considering the last 70% of the time series for calibration (D1B) or considering the first and last 35% of the time series for calibration (D1C), the models’ performances can be classified as good in general, with D1C presenting the following values: R2 and NSE = 0.720, RBIAS = 0.047, and NRMSE = 0.561. Such an outcome shows that, although two patterns exist within the time series, models D1B and D1C could interpret such a difference and provide good simulation results.
Hydrographs for the observed and calculated streamflow for the three datasets and the three different models applied, i.e., dataset #1 (1998–2019), dataset #2 (1998–2014), and dataset #3 (2014–2019) for the testing phase. Three models are performed for each dataset: A = 70% initial for calibration; B = 70% final for calibration, and C = 70% divided for calibration
Even though the evaluation of SOM networks on dataset D1A provided poor metrics, according to Fig. 6a, the calculated series presents, in general, the same order of magnitude and patterns of increases/decreases exhibited by the observed data. In water resources management analysis, where only the magnitude order or the expected behavior of increase/decrease is necessary, the model can still be effective. For cases that require a more precise value, the model may not be adequate. For dataset #2, which uses data referring to the period of the first hydrological pattern identified in the complete series, i.e., 1998–2013, the results show a particular variation in the derived metrics. The metrics obtained for the model D2A were considered appropriate, with R2 and NSE equal to 0.689, RBIAS of −0.118, and NRMSE of 0.492. The values of R2 and NSE are reasonable, as is the RBIAS, which is only slightly greater than 0.10; however, the NRMSE has a relatively high value, indicating a sensible difference between the observed and calculated streamflows.
Regarding the D2B model, the metrics are mostly better than those found for the D2A approach, with R2 and the NSE showing values of 0.749, which indicate a good correlation and correspondence between observed and calculated flows, respectively. The D2C model can be highlighted with R2 and NSE equal to 0.805, revealing a high correlation and similarity between calculated and observed values. It is worth noting that the generated RBIAS of −0.060 by model D2C, which is close to 0, corroborates with the previous metrics, indicating that the calculated values, in general, neither underestimated nor significantly overestimated the observed results. In addition, the NRMSE decreased to 0.417.
Finally, for dataset #3, which comprises the period from 2013 to 2019, it is possible to highlight satisfactory results. For the D3A model, the metrics revealed increased values of R2 and NSE (0.821), showing excellent correlation and equivalence between calculated and observed flows; an RBIAS of −0.165, which is relatively low; and a not too high value of NRMSE (around 0.335). In the D3B model, the R2 and NSE decreased to 0.757; RBIAS reduced, in absolute terms, to 0.082; and the NRMSE slightly increased to 0.472. The D3C model also presented high-performance results in this testing phase, with R2 and NSE equal to 0.720, showing a high correlation between observed and calculated values. The RBIAS close to zero (0.047) suggests that, in general terms, the simulated flows by the D3C model presented correspondence to observed values. In addition, the NRMSE showed a value close to 0.50.
Figure 7 displays the SOM hit maps for the testing phase. The hit maps are plots of the SOM layer, in which the output neurons reveal the number of input vectors classified by them. Except for model D1A, the networks activated output neurons with even distribution and explicit separation of clusters. This outcome indicates that the methodology used to define the SOM’s size was efficient.
4.3 Discussion
Moriasi et al. (2015) provide a classification for the values of R2, NSE, and RBIAS metrics, widely used in the water resources area. In such ranking, considering a monthly scale, R2 values are considered “very good” above 0.85, “good” between 0.75 and 0.85, “satisfactory” between 0.60 and 0.75, and “unsatisfactory” when it is less than 0.60. For the NSE, the values are considered “very good” when above 0.80, “good” between 0.70 and 0.80, “satisfactory” between 0.50 and 0.70, and “unsatisfactory” if less than 0.50. Finally, for RBIAS, the absolute values are considered “very good” when below 0.05, “good” between 0.05 and 0.10, “satisfactory” between 0.10 and 0.15, and “unsatisfactory” if greater than 0.15. When comparing the classification provided by Moriasi et al. (2015) with the performance of the SOM networks, it is noteworthy that the results generally concentrated between the ranges of “good” to “very good”. Only the D1A model showed “unsatisfactory” values for the three metrics (R2, NSE, and RBIAS), probably due to the inhomogeneity of the time series.
For the three studied cases, all subsets that used the first and last 35% of the data for calibration (D1C, D2C, and D3C) presented "satisfactory" to "very good" results of R2 and NSE for the testing phase, and "very good" outcomes for all metrics considering calibration. Since neural networks learn from examples, they usually present low extrapolation performance. On the other hand, they are well suited for interpolation. The found metrics show high R2 and NSE values and low RBIAS and NRMSE, confirming the good agreement between observed and simulated streamflows. The outstanding performance of the SOM models using satellite-based rainfalls confirms that this technique is a feasible option for rainfall-streamflow modeling and hydrological analyses, especially in regions with ungauged catchments.
5 Conclusions
This study demonstrated the efficiency and practicality of using TRMM rainfall products and Self-Organizing Maps for modeling monthly streamflow. The methodology was applied and validated over three datasets of inflows to a reservoir in the São Francisco River basin, Brazil. From the nine models proposed, eight presented statistical metrics that could be ranked from “good” to “very good” in the classification suggested by Moriasi et al. (2015). In general, the SOM networks trained with the first and the last 35% of the dataset (models D1C, D2C, and D3C) derived better outcomes, confirming their abilities to predict missing values, mainly for hydrological regions with precarious instrumentation. The results also showed that predictions were accurate even when using short time series, as observed in models D3A, D3B, and D3C.
The SOM’s easiness for analysis and understanding of data (via maps of plane components) and the possibility of using incomplete input data for prediction purposes proved valuable for managing water resources. The presented models can also be tools for handling missing data in poorly monitored catchments, enabling studies and projects to be better developed.
The use of satellite-estimated rainfall data, which are promptly available, showed to be a viable alternative to rain gauge stations, which are especially limited in remote areas. In conclusion, this methodology could be a successful option for other catchments, allowing the hydrological modeling of different variables at several time scales.
Availability of Data and Materials
The data and materials that support the findings of this study are available from the corresponding author, CAGS, upon reasonable request.
Change history
18 May 2022
A Correction to this paper has been published: https://doi.org/10.1007/s11269-022-03172-7
References
Abatan AA, Tett SFB, Dong B et al (2022) Drivers and physical processes of drought events over the State of São Paulo, Brazil. Clim Dyn. https://doi.org/10.1007/s00382-021-06091-2
Adeloye AJ, Rustum R (2012) SOM and rainfall-runoff modelling in inadequately gauged basins. Hydrol Res 43(5):603–617. https://doi.org/10.2166/nh.2012.017
Adeloye AJ, Rustum R, Kariyama D (2011) Kohonen self-organizing map estimator for the reference crop evapotranspiration. Water Resour Res 47(W08523):1–19. https://doi.org/10.1029/2011WR010690
Alvares CA, Stape JL, Sentelhas PC, de Moraes Gonçalves JL, Sparovek G (2013) Köppen’s climate classification map for Brazil. Meteorol Z 22(6):711–728. https://doi.org/10.1127/0941-2948/2013/0507
Arnold JG et al (2012) SWAT: Model use, calibration, and validation. Trans ASABE 55(4):1491–1508
Beale M, Hagan M, Demuth H (2012) Neural network toolbox 7.0.3: User’s Guide. The MathWorks Inc, Natick, USA, p 404
Campolo M, Andreussi P, Soldati A (1999) River flood forecasting with a neural network model. Water Resour Res 35(4):1191–1197. https://doi.org/10.1029/1998WR900086
Ciğizoğlu HK, Alp M (2006) Generalized regression neural network in modelling river sediment yield. Adv Eng Softw 37(2):63–68. https://doi.org/10.1016/j.advengsoft.2005.05.002
Ciğizoğlu HK, Kisi Ö (2005) Flow prediction by three back propagation techniques using k-fold partitioning of neural network training data. Nord Hydrol 36(1):1–16
Collischonn W, Dornelles F (2015) Hidrologia para engenharias e ciências ambientais. Associação Brasileira de Recursos Hídricos – ABRH. 2nd Edition. Porto Alegre, Brazil, p 350
Coulibaly P, Anctil F, Aravena R, Bobde B (2001) Artificial neural network modeling of water table depth fluctuations. Water Resour Res 37(4):885–896. https://doi.org/10.1029/2000WR900368
Da Silva Filho JS, Farias C (2018) Stochastic modeling of monthly river flows by Self-Organizing Maps. J Urban Environ Eng 12(2):219–230. https://doi.org/10.4090/juee.2018.v12n2.219230
Farias CAS, Bezerra UA, Da Silva Filho JA (2015) Runoff-erosion modeling at micro-watershed scale: a comparison of self-organizing maps structures. Geoenviron Disasters 2:14. https://doi.org/10.1186/s40677-015-0022-9
Farias CAS, Carneiro, TC, Lourenço, AMG (2012) Mapas auto-organizáveis para modelagem chuva-vazão. Proceedings of the XI Simpósio de Recursos Hídricos do Nordeste, João Pessoa, Brazil, 1–14
Farias CAS, Santos CAG (2014) The use of Kohonen neural networks for runoff-erosion modeling. J Soils Sediments 14:1242–1250. https://doi.org/10.1007/s11368-013-0841-9
Farias CAS, Santos CAG, Lourenço AMG, Carneiro TC (2013) Kohonen neural networks for rainfall-runoff modeling: Case study of Piancó River Basin. J Urban Environ Eng 7(1):176–182. https://doi.org/10.4090/juee.2013.v7n1.176182
Freiwan M, Cigizoglu HK (2005) Prediction of total monthly rainfall in Jordan using feed forward backpropagation method. Fresenius Environ Bull 14(2):142–151
Gadelha AN, Coelho VHR, Xavier AC, Barbosa LR, Melo DCD, Xuan Y, Huffman GJ, Petersen WA, Almeida CD (2019) Grid box-level evaluation of IMERG over Brazil at various space and time scales. Atmos Res 218:231–244. https://doi.org/10.1016/j.atmosres.2018.12.001
Gao Q, Li G, Bao J, Wang J (2021) Regional frequency analysis based on precipitation regionalization accounting for temporal variability and a nonstationary index flood model. Water Resour Manage 35:4435–4456. https://doi.org/10.1007/s11269-021-02959-4
García HL, González IM (2004) Self-organizing map and clustering for wastewater treatment monitoring. Eng Appl Artif Intell 17(3):215–225. https://doi.org/10.1016/j.engappai.2004.03.004
Gazzaz NM, Yusoff MK, Aris AZ, Juahir H, Ramli MF (2012) Artificial neural network modeling of the water quality index for Kinta River (Malaysia) using water quality variables as predictors. Mar Pollut Bull 64(11):2409–2420. https://doi.org/10.1016/j.marpolbul.2012.08.005
Gholami V, Khaleghi MR, Pirasteh S, Booij MJ (2022) Comparison of self-organizing map, artificial neural network, and co-active neuro-fuzzy inference system methods in simulating groundwater quality: Geospatial artificial intelligence. Water Resour Manage 36:451–469. https://doi.org/10.1007/s11269-021-02969-2
Hall T, Brooks HE, Doswell CA III (1999) Precipitation forecasting using a neural network. Weather Forecast 14(3):338–345. https://doi.org/10.1175/1520-0434(1999)014%3c0338:PFUANN%3e2.0.CO;2
Haykin S (1999) Neural networks: a comprehensive foundation. Prentice Hall, Upper Saddle River, USA, p 842
Honorato AGSM, Silva GBL, Santos CAG (2018) Monthly streamflow forecasting using neuro-wavelet techniques and input analysis. Hydrol Sci J 63:15–16. https://doi.org/10.1080/02626667.2018.1552788
Hsu K, Gupta HV, Sorooshian S (1995) Artificial neural network modelling of the rainfall runoff process. Water Resour Res 31(10):2517–2530. https://doi.org/10.1029/95WR01955
Ismail S, Shabri A, Samsudin R (2012) A hybrid model of self organizing maps and least square support vector machine for river flow forecasting. Hydrol Earth Syst Sci 16:4417–4433. https://doi.org/10.5194/hess-16-4417-2012
Jain A, Sudheer KP, Srinivasulu S (2004) Identification of physical processes inherent in artificial neural network rainfall runoff models. Hydrol Process 18(3):571–581. https://doi.org/10.1002/hyp.5502
Kisi Ö (2004) River flow modeling using artificial neural networks. J Hydrol Eng 9(1):60–63. https://doi.org/10.1061/(ASCE)1084-0699(2004)9:1(60)
Klink CA, Machado RB (2005) Conservation of the Brazilian Cerrado. Conserv Biol 19:707–713. https://doi.org/10.1111/j.1523-1739.2005.00702.x
Kohonen T (1982) Self-organized formation of topologically correct feature maps. Biol Cybern 43:59–69. https://doi.org/10.1007/BF00337288
Kumar DN, Raju KS, Sathish T (2004) River flow forecasting using recurrent neural network. Water Resour Manage 18(2):143–161. https://doi.org/10.1023/B:WARM.0000024727.94701.12
Kumar M, Raghuwanshi NS, Singh R, Wallender WW, Pruitt WO (2002) Estimating evapotranspiration using artificial neural network. J Irrig Drain Eng 128(4):224–233. https://doi.org/10.1061/(ASCE)0733-9437(2002)128:4(224)
Lanna AE, Schwarzbach M (1989) MODHAC - Modelo Hidrológico Auto-Calibrável. Recursos Hídricos, Publicação 21. Pós-Graduação em Recursos Hídricos e Saneamento, Universidade Federal do Rio Grande do Sul, Rio Grande do Sul, Brazil
Lee CM, Choi H, Kim Y, Kim M, Kim H, Hamm S (2021) Characterizing land use effect on shallow groundwater contamination by using self-organizing map and buffer zone. Sci Total Environ 800:1–13. https://doi.org/10.1016/j.scitotenv.2021.149632
Lettenmaier DP, Wood EF (1993) Hydrologic Forecasting. In: Maidment DR (ed) Handbook of Hydrology (pp. 26.1–26.30). New York: McGraw-Hill Inc
Li J, Shi Z, Wang G, Liu F (2020) Evaluating spatiotemporal variations of groundwater quality in northeast Beijing by self-organizing map. Water 12(5):1–15. https://doi.org/10.3390/w12051382
Lopes JEJ, Braga Jr BPF, Conejo JGL (1981) Simulação hidrológica: Aplicações de um modelo simplificado. Proceedings of the III Simpósio Brasileiro de Recursos Hídricos, Fortaleza, Brazil, p 42–62
Loucks DP, Beek E (2017) Water resource systems planning and management. Water Resour Syst Plan Manage Ebook: Deltares and UNESCO-IHE. https://doi.org/10.1007/978-3-319-44234-7
Mannan A, Chaudhary S, Dhanya CT, Swamy AK (2018) Regionalization of rainfall characteristics in India incorporating climatic variables and using self-organizing maps. ISH J Hydraul Eng 24(2):147–156. https://doi.org/10.1080/09715010.2017.1400409
Melesse AM, Ahmad S, McClaina ME, Wang X, Lim YH (2011) Suspended sediment load prediction of river systems: an artificial neural network approach. Agric Water Manag 98(5):855–866. https://doi.org/10.1016/j.agwat.2010.12.012
Mirabbasi R, Kisi O, Sanikhani H, Gajbhiye Meshram S (2018) Monthly long-term rainfall estimation in Central India using M5Tree, MARS, LSSVR, ANN and GEP models. Neural Comput Appl 31:6843–6862. https://doi.org/10.1007/s00521-018-3519-9
MMA (2017) Programa de revitalização da bacia hidrográfica do Rio São Francisco. Disponível em: www.mma.gov.br. Accessed in 31 December 2019
Mohanty S, Jha MK, Kumar A, Sudheer KP (2010) Artificial neural network modeling for groundwater level forecasting in a river island of eastern India. Water Resour Manage 24(9):1845–1865. https://doi.org/10.1007/s11269-009-9527-x
Moriasi DN, Gitau MW, Pai N, Daggupati P (2015) Hydrologic and water quality models: Performance measures and evaluation criteria. Trans ASABE (am Soc Agric Biol Eng) 58(6):1763–1785. https://doi.org/10.13031/trans.58.10715
Muhammad W, Yang H, Lei H, Muhammad A, Yang D (2018) Improving the regional applicability of satellite precipitation products by ensemble algorithm. Remote Sens 10:577. https://doi.org/10.3390/rs10040577
Nagy HM, Watanabe KAND, Hirano M (2002) Prediction of sediment load concentration in rivers using artificial neural network model. J Hydraul Eng 128(6):588–595. https://doi.org/10.1061/(ASCE)0733-9429(2002)128:6(588)
Nash JE, Sutcliffe JV (1970) River flow forecasting through conceptual models I: a discussion of principles. J Hydrol 10(1):282–290. https://doi.org/10.1016/0022-1694(70)90255-6
Nayak PC, Rao YRS, Sudheer KP (2006) Groundwater level forecasting in a shallow aquifer using artificial neural network approach. Water Resour Manage 20(1):77–90. https://doi.org/10.1007/s11269-006-4007-z
Nourani V, Baghanam AH, Adamowski J, Gebremichael M (2013) Using self-organizing maps and wavelet transforms for space–time pre-processing of satellite precipitation and runoff data in neural network based rainfall–runoff modeling. J Hydrol 476:228–243. https://doi.org/10.1016/j.jhydrol.2012.10.054
Novarini B, Brentan BM, Meirelles G, Junior EL (2019a) Optimal pressure management in water distribution networks through district metered area creation based on machine learning. Brazil J Water Resour 24:e37. https://doi.org/10.1590/2318-0331.241920180165
Novarini B, Brentan BM, Meirelles G, Junior EL (2019b) Optimal pressure management in water distribution networks through district metered area creation based on machine learning. Brazil J Water Resour 24(37):1–11. https://doi.org/10.1590/2318-0331.241920180165
Paiva LFG, Montenegro SM, Cataldi M (2020) Prediction of monthly flows for Três Marias reservoir (São Francisco river basin) using the CFS climate forecast model. Brazil J Water Resour 25(16):1–18. https://doi.org/10.1590/2318-0331.252020190067
Pettitt ANA (1979) Non-parametric approach to the change-point problem. Appl Stat 28(2):126–135. https://doi.org/10.2307/2346729
Plouffe CCF, Robertson C, Chandrapala L (2015) Comparing interpolation techniques for monthly rainfall mapping using multiple evaluation criteria and auxiliary data sources: a case study of Sri Lanka. Environ Model Softw 67:57–71. https://doi.org/10.1016/j.envsoft.2015.01.011
Santos CAG, Brasil Neto RM, Silva RM, Passos JSA (2018) Integrated spatiotemporal trends using TRMM 3B42 data for the Upper São Francisco River basin. Brazil Environ Monit Assess 190:175. https://doi.org/10.1007/s10661-018-6536-3
Santos CAG, Freire PKMM, Silva RM, Akrami SA (2019) Hybrid wavelet neural network approach for daily inflow forecasting using tropical rainfall measuring mission data. J Hydrol Eng 24:04018062. https://doi.org/10.1061/(ASCE)HE.1943-5584.0001725
Santos CAG, Morais BS (2013) Identification of precipitation zones within São Francisco River basin (Brazil) by global wavelet power spectra. Hydrol Sci J 58(4):789–796. https://doi.org/10.1080/02626667.2013.778412
Silva RM, Dantas JC, Beltrão JA, Santos CAG (2018) Hydrological simulation in a tropical humid basin in the Cerrado biome using the SWAT model. Hydrol Res 49(3):908–923. https://doi.org/10.2166/nh.2018.222
Silverman D, Dracup JA (2000) Artificial neural networks and long-range precipitation prediction in California. J Appl Meteorol 39(1):57–66. https://doi.org/10.1175/15200450(2000)039%3c0057:ANNALR%3e2.0.CO;2
Singh KP, Basant A, Malik A, Jain G (2009) Artificial neural network modeling of the river water quality – a case study. Ecol Model 220(6):888–895. https://doi.org/10.1016/j.ecolmodel.2009.01.004
Sugawara M (1961) Automatic calibration of the Tank-Model. Hydrol Sci J 24(3):375–388. https://doi.org/10.1080/02626667909491876
Teng H, Rossel RAV, Shi Z, Behrens T, Chappell A, Bui E (2016) Assimilating satellite imagery and visible–near infrared spectroscopy to model and map soil loss by water erosion in Australia. Environ Model Softw 77:156–167. https://doi.org/10.1016/j.envsoft.2015.11.024
Trajkovic S, Todorovic B, Stankovic M (2003) Forecasting of reference evapotranspiration by artificial neural networks. J Irrig Drain Eng 129(6):454–457. https://doi.org/10.1061/(ASCE)0733-9437(2003)129:6(454)
Viljanen N, Honkavaara E, Näsi R, Hakala T, Niemeläinen O, Kaivosoja J (2018) A novel machine learning method for estimating biomass of grass swards using a photogrammetric canopy height model, images and vegetation indices captured by a drone. Agriculture 8(70):2018. https://doi.org/10.3390/agriculture8050070
Voutilainen A, Arvola LMJ (2017) SOM clustering of 21-year data of a small pristine boreal lake. Knowl Manag Aquat Ecosyst 418:36. https://doi.org/10.1051/kmae/2017027
Wang Y, Sun X (2022) Simulation and evaluation of statistical downscaling of regional daily precipitation over North China based on self-organizing maps. Atmosphere 13(86):1–23. https://doi.org/10.3390/atmos13010086
WMO (1994) Guide to Hydrological Practices: Data Acquisition and Processing, Analysis, Forecasting and Other Applications, WMO 168. Geneva: World Meteorological Organization
Wu C, Wu X, Lu C, Sun Q, He X, Yan L, Qin T (2021) Hydrogeochemical characterization and its seasonal changes of groundwater based on self-organizing maps. Water 13:1–23. https://doi.org/10.3390/w13213065
Yotova G, Varbanov M, Tcherkezova E, Tsakovskia S (2021) Water quality assessment of a river catchment by the composite water quality index and self-organizing maps. Ecol Ind 120:1–10. https://doi.org/10.1016/j.ecolind.2020.106872
Zanetti SS, Sousa EF, Oliveira VP, Almeida FT, Bernardo S (2007) Estimating evapotranspiration using artificial neural network and minimum climatological data. J Irrig Drain Eng 133(2):83–89. https://doi.org/10.1061/(ASCE)0733-9437(2007)133:2(83)
Zhang R, Chen Y, Zhang X, Ma Q, Ren L (2022) Mapping homogeneous regions for flash floods using machine learning: a case study in Jiangxi province, China. Int J Appl Earth Obs Geoinf 108:1–12. https://doi.org/10.1016/j.jag.2022.102717
Funding
This study was financed in part by the Brazilian Federal Agency for the Support and Evaluation of Graduate Education (Coordenação de Aperfeiçoamento de Pessoal de Nível Superior—CAPES) – Fund Code 001, the National Council for Scientific and Technological Development, Brazil – CNPq (Grant No. 313358/2021–4 and 309330/2021–1), Federal University of Campina Grande, and Federal University of Paraíba.
Author information
Authors and Affiliations
Contributions
CAGS designed the research; TVMN, CAGS and CASF wrote the original draft; TVMN, CAGS and CASF performed the manuscript review and editing; CAGS provided funding acquisition, project administration and resources; and TVMN, CAGS, CASF, and RMS wrote the final paper.
Corresponding author
Ethics declarations
Ethics Approval
Not applicable.
Consent to Participate
Not applicable.
Consent to Publish
Authors have agreed to submit the article in this Journal.
Competing Interests
The authors have no relevant financial or non-financial interests to disclose.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The original online version of this article was revised due to a retrospective Open Access order.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
do Nascimento, T.V.M., Santos, C.A.G., de Farias, C.A.S. et al. Monthly Streamflow Modeling Based on Self-Organizing Maps and Satellite-Estimated Rainfall Data. Water Resour Manage 36, 2359–2377 (2022). https://doi.org/10.1007/s11269-022-03147-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11269-022-03147-8