Abstract
Resilience of a water resource system in terms of water supply meeting future demand under climate change and other uncertainties is a prominent issue worldwide. This paper presents an alternative methodology to the conventional engineering practice in the UK for identifying long-term adaptation planning strategies in the context of resilience. More specifically, a resilience-based multi-objective optimization method is proposed that identifies Pareto optimal future adaptation strategies by maximizing a water supply system’s resilience (calculated as the maximum recorded duration of a water deficit period over a given planning horizon) and minimizing total associated costs, subject to meeting target system robustness to uncertain projections (scenarios) of future supply and demand. The method is applied to a real-world case study for Bristol Water’s water resource zone and the results are compared with those derived using a more conventional engineering practice in the UK, utilizing a least-cost optimization analysis constrained to a target reliability level. The results obtained reveal that the strategy solution derived using the current practice methodology produce a less resilient system than the similar costing solutions identified using the proposed resilience driven methodology. At the same time, resilience driven strategies are only slightly less reliable suggesting that trade-off exists between the two. Further examination of intervention strategies selected shows that the conventional methodology encourages implementation of more lower cost intervention options early in the planning horizon (to achieve higher system reliability) whereas the resilience-based methodology encourages more uniform intervention options sequenced over the planning horizon (to achieve higher system resilience).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
One of the greatest challenges facing decision makers in the water industry in the UK and worldwide are the increasing influences of “deep” climate change, population growth and urbanization uncertainties affecting the long-term balance of supply and demand and necessitating the need for adaptive action (Environment Agency 2013). Walker et al. (2013) defines the circumstances at which uncertainties can be classified as “deep” as when “one is able to enumerate multiple plausible alternatives without being able to rank the alternatives in terms of perceived likelihood”. Under this definition, which is utilized in this paper, uncertainties are often categorized by the generation of multiple future scenarios to represent a range of “alternative plausible conditions under different assumptions” (Mahmoud et al. 2009). Combining these scenarios with a suitable metric to measure system sensitivity to changing conditions (i.e., robustness) can then facilitate the examination of the potential benefits of alternative system configurations (i.e., adaptation strategies) across a range of deep uncertainties. The interaction of deep uncertainty, scenarios, robustness and adaptation is discussed in detail by Maier et al. (2016).
The complexity of these interactions brings into question the ability of current UK and international engineering planning approaches to deal with deep uncertainties. For example, the current water supply planning approach in the UK is to ensure a regional water system maintains a designated ‘level of service’ to its customers (NERA 2002; Environment Agency et al. 2012). This is essentially an agreement between a water company and its customers describing the average frequency that a company will implement temporary restrictions on water use. However, this ‘level of service’ calculation lacks transparency and is often presented as a general target (e.g., a target system performance of no more than 1 in 10 or 1 in 15 years enforced restrictions (Bristol Water 2014)). It is also calculated irrespective of the duration of each projected restriction. Further to this it relies on an assumption that a drought event can be assigned a probability of occurrence and associated return period despite the long acknowledged liabilities of event frequency estimation techniques (Turner et al. 2014). Especially in light of increasing climate change effects where the impacts on hydrology are likely to be non-linear and felt most at the extremes (Allen and Ingram 2002).
In response to the rising uncertainties a range of experimental frameworks and approaches are currently being developed and tested for potential use in the water industry. Recent international water resources management (WRM) literature includes a wide array of contrasting approaches for planning under “deep” uncertainty, such as: Robust Decision Making (Matrosov et al. 2013; Groves et al. 2015), Info-Gap decision theory (Korteling et al. 2013; Roach et al. 2016), Decision Scaling (Brown et al. 2012; Turner et al. 2014) and Robust Optimization (Ray et al. 2013; Kwakkel et al. 2015). Most of these approaches have been developed to evaluate the performance of a decision or strategy by calculating system robustness, which is the term commonly used to describe the degree, or percentage of plausible future conditions, under which a water supply system maintains a satisfactory level of performance. Alternative approaches incorporating flexibility analysis within the adaptive planning process are also being examined for WRM application, such as the use of Dynamic Adaptive Policy Pathways (Kwakkel et al. 2015). However, despite the widening range of approaches under development, the outputs from these methods remain highly dependent on how the water resource system performance itself is evaluated. It is within these more practical engineering features that a wider knowledge gap is often over looked.
The more well-known performance criteria often cited within WRM literature are those of Hashimoto et al. (1982) who were among the first to purpose the use of the terms reliability, vulnerability and resilience for water resource system performance evaluation. These performance criteria, in general, refer to how likely a system is to fail (its reliability), how severe the consequences of failure might be (its vulnerability) and how quickly it can bounce back, which is the recovery from a failure (its resilience). The EBSD ‘levels of service’ method used in current UK engineering practice can be most closely equated to a performance criterion of reliability and does not explicitly consider the resilience of the system. However, the latest investigation by the EA into WRM planning methods of the future (Environment Agency 2013), called for a review of the EBSD ‘levels of service’ method and for the advancement of incorporating more resilience into water resource system planning, indicating it will support adaptation strategies that are aimed at improving system resilience. Recent UK government reports have also emphasized resilience (Defra 2016); however, there is still no standard quantitative definition of resilience (Environment Agency 2013) and resilience remains generally poorly defined in practice to date.
The application of resilience as a criterion for measuring performance in WRM problems has been explored (Jung 2013; Linkov et al. 2014). Matrosov et al. (2012) and Paton et al. (2014) calculated resilience as the average duration of time a system is under a temporary restriction. Fowler et al. (2003) calculated it as a fraction of the total future time a system is under an unsatisfactory state. Loucks (1997) calculated it as the probability of a system recovering once it enters an unsatisfactory state. Kjeldsen and Rosbjerg (2004) calculated resilience in three alternative ways: the inverse of the mean value of the time the system spends in an unsatisfactory state, the maximum duration of an unsatisfactory state and the duration of the 90th fractile of observed unsatisfactory periods. They concluded that the maximum duration metric provided the most accurate and comprehensible estimation of performance. A direct maximum duration calculation was also the resilience metric of choice by Moy et al. (1986) who selected it to enable and simplify the quantification of resilience and its incorporation into a mathematical programming model. Kundzewicz and Kindler (1995) argued that a resilience definition based on a maximum value is more useful than one based on a mean, as the presence of small inconsequential events can lower the mean value and present an inaccurate picture of actual overall system performance. Using resilience as a performance criterion has also been investigated within several other areas of human, social and ecological systems science, from natural resource investigations (Tompkins and Adger 2004) to coral reef surveys (Hughes et al. 2003), with a detailed review of cross sector resilience measures conducted by Hosseini et al. (2016). It has generally been concluded that building resilience into systems (i.e. the ability to recover quickly from detrimental periods) can be an active and effective way to cope with environmental change characterized by future uncertainties and unknowable risks.
Despite several investigations involving resilience criteria (see above), few to date have applied the metric to a complex real-world WRM adaptation case study under deep uncertainty to identify optimal adaptation strategies from a wide range of potential supply and demand intervention options. Nor has a comparative analysis been conducted with results from current engineering practice. The novelty of this study lies in the assessment of whether incorporating a duration-based metric of resilience as a quantified objective in WRM assessments, in addition to appraisals of scenario-based robustness and total costs, can improve the identification of optimal adaptation strategies, when compared with the standard UK practice of performing a single least-cost linear optimization analysis constrained to a single reliability metric. To accomplish this, a novel resilience-based top-down multi-objective optimization method for the selection of optimal water resources adaptation strategies has been developed, validated and demonstrated.
The general WRM problem addressed is first defined followed by the definitions and concepts of resilience, reliability, robustness, adaptation strategies and costs. A description of the resilience-based methodology and the water resources simulation model developed for this study are then given. The quantitative case study of Bristol Water (BW) is then presented, followed by results and discussion.
2 Methodology
2.1 WRM Problem Definition
The WRM problem is defined here as the regional long-term water resources planning problem of maintaining adequate water supply to meet future demand over a pre-specified planning horizon under uncertain future conditions of climate change and population growth. The aim is to determine the best adaptation strategy(ies) (i.e., set of intervention options scheduled across a given planning horizon) that can upgrade an existing WRM system to maximize the resilience of the future regional water supply whilst minimizing the total cost of intervention options required subject to target levels of desired robustness. Note here that resilience is a primary planning objective being optimized for within the methodology, while target robustness is set as a changeable constraint.
2.2 Resilience of Water System
In this study, resilience is defined and calculated as the maximum recorded duration of time taken for the water supply system to enter, and then recover from a water deficit period. A water deficit period is defined as a consecutive time-period where a temporary water restriction must be put in place (e.g., a temporary water use ban). Extended water restrictions have potentially severe economic, environmental, societal and reputational impacts, particularly in large conurbation areas (Environment Agency 2015).
The conditions that elicit a water deficit period to occur are highly dependent on the water system under study. In the case study analysed in this paper (see section 3) a water deficit period is registered when the water level in the primary combined network reservoir system falls below an unacceptable pre-specified (threshold) level. The rationale behind this is that a water deficit period defined this way may be allowed to occur occasionally, to manage the water supply system during periods of drought, but an empty reservoir causing an unfulfilled water demand is deemed unacceptable. The threshold which defines a water deficit (the vulnerability of the system (Hashimoto et al. 1982)) is pre-specified by setting the water deficit threshold level to an appropriate magnitude. However, the frequency of deficit periods (the reliability of the system) is left unconstrained in this methodology to examine the effect of driving strategy optimization by resilience alone.
For comparison with the resilience-based methodology a ‘current practice’ methodology is also tested, which represents conventional water company practice of using ‘levels of service’. This defines the target frequency that customer water restrictions would be implemented. Rather than using a resilience metric this approach involves setting a target reliability for the system (here taken as a maximum allowable frequency of water deficit periods recorded over a planning horizon) and then optimizing with the same definition of system robustness, calculation of total strategy costs and utilizing the dynamic water resources simulation model as outlined below.
2.3 Robustness of Water Supply
Robustness is most commonly described in water resources literature as the degree to which a water supply system can maintain performance at a satisfactory level across a broad range of plausible future scenarios or conditions (Moody and Brown 2013; Matrosov et al. 2013). A global robustness measure of satisficing performance utilizing pre-defined domain criterions has been selected for this study, as it elicits a transparent quantified calculation of robustness that is suitable when examining a wide range of highly variable discrete future scenarios and has been successfully employed in numerous recent WRM studies (Paton et al. 2014; Beh et al. 2015; Roach et al. 2016). Robustness of long-term water supply is specifically defined here as in Roach et al. (2016) as the fraction (i.e., percentage) of future supply and demand scenarios that result in an acceptable system performance (here in terms of resilience), as shown in Eq. (3). For example, if 90 out of 100 scenarios maintain a given resilience (e.g., maximum duration of water deficit equal to 1 month) then the robustness, of the water supply to maintain this level of resilience is 0.9, i.e., 90%.
2.4 Adaptation Strategies and Water Resources Simulation Model
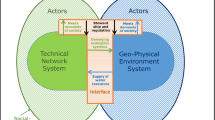
A range of different adaptation strategies can be generated by employing different combinations of new water resources and/or techniques to reduce water losses/consumption (intervention options) sequenced over a given long-term planning horizon (see examples in Table 2). The total cost of an adaptation strategy is expressed in terms of Present Value (PV), as shown in Eq. (2). Different adaptation strategies are evaluated using a dynamic water resources network model (see Fig. 1) that is designed to simulate the supply and demand balance of a regional water supply system/network, using a monthly time step, over a pre-established time horizon. Different adaptation strategies and future scenarios of supply and demand can be input to the system, analysing the performance of each system combination via system resilience results. The dynamic water resources simulation model is written in the Python programming language (Python Software Foundation 2013), and scenarios and strategies are selected and input automatically using an optimization algorithm routine constructed in the R programming language (R Core Team 2013).
2.5 Optimization Methodology
A resilience-based two-objective optimization method is presented that identifies Pareto optimal solutions by maximizing system resilience to water deficits and minimizing the total cost of interventions subject to target levels of robustness, i.e., as follows. The resilience of an adaptation strategy x to a discrete individual scenario combination of supply and demand u is calculated as:
where p(j) is the duration of the jth water deficit period. The total cost of adaptation strategy x is expressed in terms of Present Value (PV) using a standard discounting equation applied to both the estimated capital costs C y (£M) and operational costs O y (£M/yr) of each selected intervention option y, as follows:
where r = the annual discount rate, i = the time step of the planning horizon (in years), i y = the year in the planning horizon option y is implemented, Y = the total number of intervention options in the (adaptation) strategy, and I = the total number of years in the planning horizon. The robustness of long-term water supply is then derived as follows:
where A = the number of scenario combinations (of supply and demand) under which the system maintains a given level of resilience and U = total number of scenario combinations considered. Every time an adaptation strategy is evaluated during the optimization process all potential combinations of supply and demand are generated and assessed using full enumeration sampling of all potential scenarios. This ensures all viable futures are explored in the robustness calculation.
A discrete target level of robustness R is selected and set as a constraint in the optimization process and the highest level of resilience that can be maintained by a system at or above this target robustness level is recorded. For example, if target robustness is set at 80% and the highest level of resilience maintained by a given adaptation strategy system is 5 months, then the systems resilience is designated as 5 months. Note that if multiple optimization problems (for varying target levels of robustness) are solved this will enable the production of a 3D trade-off surface between resilience, cost and robustness.
The optimizing algorithm selected for this study is the NSGA-II (Deb and Pratap 2002), as its high performance and capabilities in handling multi-objective water related optimization problems is well documented (Nicklow et al. 2010; Zheng et al. 2016) and it is recognized as an industry standard and freely available algorithm (Wang et al. 2014). Alternative evolutionary algorithms, such as BORG or epsilon-NSGA2, have proven superior in certain criteria in recent studies (Reed et al. 2013; Zheng et al. 2016). However, the NSGA-II is still a reliable MOEA and proved suitably adequate to handle the complexity of this study following extensive test runs.
The selected NSGA-II uses integer values to select from the decision variables (options) and is modified to run using multi-processor parallel programming to increase run time efficiency. The dynamic, monthly-time step water resources simulation model and resilience-based methodology set-up is combined with the NSGA-II algorithm (see Fig. 1). The model then requires three data field inputs; a pool of plausible potential new intervention options being considered by a water company (see section 3.3) to form new adaptation strategy combinations, and a credible range of potential supply and demand scenarios for a region (see section 3.2). The selected NSGA-II parameters used in the case study optimization runs are fully listed in section 3.6 and further explanation of the NSGA-II operation can be found in Deb and Pratap (2002).
3 Case Study
3.1 Description
The methodology detailed in section 2 is applied to a case study of the Bristol Water (BW) water resource zone. Bristol Water manage a region in the south-west of the UK (see Fig. 2) supplying approx. 1.2 million customers (as of 2015). The current water supply/demand balance (i.e. as of 2015) is fine but this region is expected to experience increasing pressures on local water resources from rising populations (with a 15% projected increase in demand by 2045) and reductions in the availability of existing water resources as a consequence of climate change leading to a supply-demand deficit by the 2030s (Bristol Water 2014). This imbalance is anticipated to continue and worsen through to the end of the twenty-first century (HR Wallingford 2015). The existing primary water resources are shown in Fig. 2 and listed in Table 1.
The BW water resource zone, introduced in Roach et al. (2015), is designed to operate as a single resource zone across the whole company area. Under this set-up, no part of the BW resource zone is remaining solely dependent upon the consistent yield of a single water resource. The main river and groundwater sources (resources 1 and 2 in Table 1) are designated reliable and sustainable over the next planning period (2015–2039); whereas the resource available from the Mendip Reservoirs is anticipated to be impacted by climate change. For the Mendip Reservoirs there are three main input components to the combined reservoir system to be modelled when projecting climate scenarios. These are: the direct reservoir inflows to the Mendip reservoirs; the lake at Chew Magna and the river Axe at Cheddar (see Fig. 2 and section 3.2).
The aim of the real-life WRM problem analysed here is to determine the best adaptation strategy(ies) to upgrade/implement within the existing water resource system/network that will maximize the resilience of future regional water supply whilst minimizing the total cost of intervention options required subject to different target levels of robustness. The dynamic water resources simulation model (described in section 2.4) is developed for the BW resource zone to realistically simulate the monthly supply-demand balance of the system over a 25-year planning horizon (from year 2015 to year 2039 inclusive). A 25-year planning horizon is selected to imitate the time frame used in a typical UK water company WRMP planning horizon.
3.2 Scenarios of Supply and Demand
In this case study, two types of scenarios are generated, supply scenarios to model the impact of climate change on water availability at sources and demand scenarios, to model the impact of future population growth and urbanization changes.
The supply scenarios for the BW resource zone have been generated using the Future Flows climate/hydrology scenarios. These were used to generate future flow projections for the region’s major contributing rivers and reservoirs (Roach et al. 2015). The Future Flows project (Prudhomme et al. 2012) utilises the projections derived from the UKCP09 regional climate models (RCMs) from the Met Office Hadley Centre. They provide 11 plausible realisations (all assumed equally likely) of river flows at various river gauging stations across the UK accounting for the impact of climate change to 2100 under a Medium emission scenario. The key advantage of the Future Flow scenarios is that they are transient flow projections, so they do not require additional rainfall-runoff modelling and so can be directly utilized to continuously simulate the supply-demand balance over a given planning horizon and analyse the associated timing of interventions. The limitation of the current Future Flow projections is their utilization of only a medium global emission scenario; however, once resampled multiple times, the Future Flow projections provide an adequate range of uncertainty for this specific metric evaluation. Resampling of the flow projections (as outlined in Roach et al. (2016)) eliminates any bias in the selection of adaptation strategies due to the timing and duration of future drought conditions exhibited, and enables a sufficient investigation into the role of climate variability on the region’s resources.
The 11 Future Flow projections from the nearest gauging site to the Mendip region (Midford Brook) are each imposed on 30 resampled flow sequences (derived for each of the three input components to the combined reservoir system detailed in section 3.1) to create 330 discrete future supply scenarios. Using transient sequences of flows differs to the standard engineering practice (the EBSD method), which utilises a singular linear interpolation of future available supply projected from the baseline to the 2030s (Environment Agency et al. 2012).
The demand scenarios for the BW resource zone have been generated using the Office for National Statistics (ONS) population projections (ONS 2014). These consist of 3 scenarios of Low, Principal and High population growth used to perturb historic demand values that are then calculated subject to 3 alternative levels of population/urbanization uncertainty; based on the 80%, 90% and 100% risk and uncertainty calculations (Bristol Water 2014). This forms 9 discrete scenarios of demand, which combined with the 330 supply scenarios, creates 2970 potential future supply and demand scenario combinations to model.
3.3 Adaptation Strategies
An investigation into potential new intervention options for the BW region was carried out in Roach et al. (2015) using the BW WRMP 2014 data surveys (Bristol Water 2014). This created a list (or pool) of 31 potential new small to large water supply resources and options to reduce water consumption or losses. From this list a range of different adaptation strategies can then be formed by implementing different combinations of the new options, sequenced over the 25-year strategic planning horizon (2015–2039) in varying arrangements. The total Present Value (PV) costs of strategies are then calculated using the approach shown in Eq. (2), with an assigned annual discount rate of 4.5%, as utilised by Bristol Water (2014). Table 2 shows the 19 intervention options, out of the total 31, that feature in the final results (section 4).
3.4 The Resilience and Robustness of the Water System
As detailed in section 2.2, the resilience of an adaptation strategy under a given discrete future scenario of supply and demand is calculated as the maximum recorded duration (in months) that the system remains in a water deficit period (Eq. (1)), due to the remaining water volume in the combined reservoir network falling below a threshold level. The threshold levels vary depending on the month in the year as specified in BW’s drought plan (Bristol Water 2012). As there are 2970 scenario combinations examined, this results in 2970 resilience result for each adaptation strategy tested. A discrete target level of robustness is selected, and the maximum resilience level maintained by each adaptation strategy at or above this selected target robustness is recorded; or alternatively for the ‘current practice’ methodology under which a target level of reliability is maintained.
3.5 Current Practice Methodology Application
The target level of reliability for Bristol Water is currently set to maintain a 1 in 15 year maximum occurrence of temporary restrictions being put in place (Bristol Water 2014). Using reliability Eq. (4) the relative frequency/probability of a system not being in deficit is calculated (Kjeldsen and Rosbjerg 2004):
where j h = a value equal to 1 if a year contains a water deficit period, otherwise equal to 0; h = the year index and H = the total number of years in the planning horizon. For BW to meet its target ‘level of service’, this translates as maintaining approximately 93% reliability. Over the selected 25-year planning horizon this corresponds to a maximum allowable frequency of 2 water deficit periods occurring over the planning horizon. This ‘level of service’ must also be maintained over a specified level of a system’s supply/demand balance uncertainty known as target headroom (Environment Agency et al. 2012).
BW has selected to maintain a target headroom level of 90% over the next 25 year planning horizon to significantly reduce the risk of failing to maintain their agreed ‘level of service’ (Bristol Water 2014). The headroom percentage distributions are calculated either side of the median supply-demand balance forecasts and encompass the plausible range of uncertainty. It should be noted that BW’s headroom value is applied to an aggregate supply-demand balance, not directly within a simulation model, and includes factors that are not considered in this study (e.g. risk of outage events of assets). However, these are typically smaller components and this study considers a wider range of uncertainty in the supply and demand scenarios which are directly simulated. Therefore, BW’s target headroom level, reflecting an attitude to risk, is used by selecting a 90% target robustness of the supply/demand scenarios considered in the resilience-based methodology.
3.6 Application of Optimization Model
The dynamic, monthly-time step water resources supply and demand simulation model linked to the NSGA-II optimization method (as described in sections 2.4 and 2.5) has been used here. The NSGA-II parameters (derived as optimal from the testing of numerous parameter combinations) are as follows: population size: 400; number of generations: 2000; selection bit tournament size: 2; mutation probability (per gene): 0.2; crossover probability (single point): 0.7.
The generation of adaptation strategies, subsequent testing, ranking, crossover/mutation and ultimate Pareto optimal strategy set identification is automatically carried out by the NSGA-II algorithm during the optimization process after 2000 generation assessments. Ten separate runs (with different random seeds, i.e. randomly generated initial populations of solutions) are carried out to ensure that the true Pareto optimal strategies are being identified by the optimisation process.
A range of target levels of robustness are selected and input to the optimization model as constraints to derive a Pareto set of results. The Pareto sets obtained from multiple optimization model runs are then combined to produce a 3D–surface of Pareto optimal solutions. The discrete target levels of robustness selected for the optimization analysis are 50, 60, 70, 80, 90 and 100%. A ‘current practice’ (CP) problem was also solved to derive a single optimal solution under the constraints listed in section 3.5.
4 Results
The optimal solution derived by the ‘current practice’ (CP) methodology is presented first, including calculations of the respective resilience exhibited by this strategy over varying target levels of robustness. The resilience-based methodology results are presented afterwards. Selected Pareto optimal adaptation strategies from the resilience driven optimization methodology are then compared with the CP derived solution and engineering aspects discussed.
The CP methodology derives a single optimal adaptation strategy following low-cost optimization to a target reliability of ≥92% and target robustness of 90% (see section 3.5). The adaptation strategy derived has a PV of total cost of £199 M and consists of several low-cost options to reduce water consumption and water losses and several water transfer schemes scheduled from 2015 to 2017, before construction of a large reservoir at Chew Stoke (option R18 in Table 2) in 2021. Only few options are scheduled for post 2021. The full strategy details are shown in Fig. 6.
The strategy solution derived by the CP methodology is compared with the resilience driven optimization model by calculating the resilience of this strategy solution for the same target levels of robustness applied in the resilience-based methodology. Fig. 3 displays the maximum resilience maintained by the strategy under target levels of robustness of 50, 60, 70, 80, 90 and 100% respectively. It shows that this ‘reliability’ driven strategy solution can maintain a resilience as high as 3 months for at least 80% of future supply and demand scenarios, but this resilience worsens to 10 and 22 months respectively for 90% and 100% robustness respectively.
Pareto adaptation strategies were identified by the resilience driven methodology optimized by maximizing the system resilience and minimizing the PV of the total cost of adaptation strategies. Six separate optimization runs were conducted for the following target system robustness’s: 50, 60, 70, 80, 90 and 100%. Fig. 4 presents the 3D Pareto set derived from these optimizations runs as three 2D graphs displaying: (a) resilience vs cost for varying target levels of robustness, (b) robustness vs cost for varying levels of resilience and (c) resilience vs robustness for varying strategy cost groups, before being combined as a 3D–surface in Fig. 5.
A 3D–surface of Pareto adaptation strategies identified over performance indicators of resilience (0–24 months), robustness (50–100%) and PV of total cost (0–600 £M); for discrete target levels of robustness of 50, 60, 70, 80, 90 and 100%. Including individual strategies selected for further analysis (R1-R6, A1-A4, and B1-B3)
The selection of a preferable adaptation strategy can be made from Fig. 4; however, the 3D–surface provides a clearer overview of the various trade-off options and affords a decision maker more perspective about how best to satisfy the various performance criteria. An ideally located individual strategy can then be selected or a specific, more desirable, region of the surface selected for further examination of individual strategies. More specifically, the decision makers can select exactly how robust and resilient they want their system to be as well as being able to discern how moderate increases or decreases in expenditure will alter the performance of the water system. Optimization to individual target levels of performance, as is undertaken in current UK engineering practice using a cost only optimization (the EBSD approach (NERA 2002)), does not allow these observations to be made. Typically, only singular optimal solutions are derived (equivalent to identifying a single point in Fig. 4(a-c)).
The CP derived optimal strategy is compared with selected strategy solutions derived by the resilience-based methodology that exhibit similar levels of resilience / total costs in order to contrast and compare the solutions derived by each method. The strategies selected are shown on Fig. 5. They consist of: strategies R1-R6, which are selected as they exhibit the same resilience to target levels of robustness as the CP solution (i.e., from Fig. 3), and strategies A1-A4 and B1-B3 as they offer increased resilience at a high level of robustness (90% for strategies A1-A4 and 80% for strategies B1-B3) for a similar PV of total cost as the CP solution. Table 3 lists the PV of total cost of each strategy examined as well as the resilience and reliability exhibited, the respective levels of robustness and the average resilience and average reliability recorded across all future scenarios examined.
Comparing the CP optimal strategy with the R1-R6 strategies in Table 3 shows that, for a lower PV of total cost, solutions are generated with the same resilience as the CP strategy for the varying target levels of robustness. For example, strategy R3 has the matching resilience of 3 months over 80% of future scenarios whilst costing approximately £25 M less than the CP strategy. The trade-off is a slight decrease in reliability of water supply, with strategy R3 maintaining a reliability of 88% over 90% of future supply/demand scenarios as opposed to 92% in the case of the CP strategy. Strategy A1, the solution of most similar total cost to the CP solution produced a more resilient system, with 90% of future scenarios now maintaining a resilience of 6 months, in contrast to the 10 months exhibited by the CP solution. The trade-off again is a moderate reduction in reliability, with a reliability of 92% being maintained over 81% of future scenarios, which falls to 88% over the remaining 9% of future scenarios within the 90% target robustness region. This demonstrates that the resilience driven methodology has identified an adaptation strategy that provides a much more resilient, but marginally less reliable system. Strategy solutions A2, A3 and B1 can further increase the resilience of the system for around 5% increase in overall total costs. Strategy solutions A4, B2 and B3 increase both the resilience and reliability of the system but for increased overall costs. These trade-offs can only be identified from the resilience-based methodology as opposed to current practice, whereby singular optimal solutions to fewer objectives are derived. If the priority design criterion for a water supply system is to maintain high reliability then this could be set as a constraint and still maintained at a high robustness. However, the benefit of the resilience-based methodology is it allows a more resilient system to then be identified in addition to high reliability, albeit at a potentially increased PV of total cost.
Fig. 6 lists the individual intervention components for each analysed strategy and their time of implementation within the 25-year planning horizon (codes for individual intervention options located in Table 2). It shows that the CP reliability driven strategy solution includes a greater number of low cost intervention options early in the planning horizon (2015) with the costliest intervention option (R18 – a new reservoir at Chew stoke) not implemented until 2021. This strategy also includes no interventions later in the planning horizon (2029–2039), implying that a number of interventions selected early on in the horizon greatly improves system reliability. Opposite of this, the alternative strategies derived by the resilience driven methodology recommend a high cost intervention early in the planning horizon (either R4 – a reservoir at Cheddar, R18 or, for the most resilient strategy (B3), R3 – a small desalination plant), before distributing a number of lower cost interventions over the remaining planning horizon, right up to 2039. This suggests larger investment early in the planning horizon as well as regular smaller water resource additions to the system increases overall system resilience, as the duration as well as frequency of severe drought periods are projected to increase over time due to climate change.
Table of intervention option components and their year of implementation for selected strategies (option codes listed in Table 2)
Fig. 7 demonstrates the system capacity increases (water supply capacity added to the system) provided by the CP strategy and two similarly priced strategies A1 and B1, over the 25-year planning horizon. It highlights how the outputs from the ‘levels of service’ method and the resilience driven method differ considerably in the size and timing of intervention options recommended.
5 Discussion
The results obtained here demonstrate how simplifying a planning approach to optimize to a single criterion (i.e., reliability of supply) does not provide solutions that perform optimally across alternative criteria. The methodology proposed here produced a wide range of Pareto optimal strategies to the performance indicators of resilience, robustness and cost and allows a decision maker to select a strategy based on their final preferred trade-off across these criteria.
The variation in strategy solutions derived in this study highlights that resilience and reliability lead to differently designed systems and therefore by considering both performance indicators it may be possible to derive a solution that performs well across both metrics (see Fig. 7). Assessing resilience also increases the capability to attach economic value to the cost of water restriction periods, as a duration of deficit is more easily quantifiable than a frequency-based approach. Water planners and policy makers can more easily attach specific social, environmental and economic costs/risks, to a known duration of time rather than to a more abstract frequency of unknown events.
The detailed analysis into the sequencing of intervention options over the planning horizon and the direct effect the sequencing has on the resilience/reliability of the water system was only possible due to the utilization of the dynamic model developed in this study to simulate the monthly supply-demand balance. This highlights the additional information provided by a simulation-based approach to water resources adaptation assessments and adds further research fuel to the growing international support to move to more simulation-based assessments when dealing with deep uncertainties in water resources management.
6 Conclusions
This paper has presented a comparative assessment of a new resilience-based methodology for WRM planning that optimizes for resilience and cost for a given target level of robustness, with that of a more conventional engineering approach used in the UK.
The results obtained in the Bristol Water case study demonstrate that the new resilience-based approach for WRM planning improves on current key UK industry planning issues by: (a) increasing the transparency of adaptation strategy assessment processes and (b) improving the output information available to decision makers. The resilience-based methodology generated a 3D surface of Pareto-optimal strategies providing decision makers with a more complete trade-off picture of what different planning strategies can achieve in terms of system performance benefits and related costs thus enabling them to make better informed decisions.
In addition to above observations, a comparison of the new methodology with the current UK planning practice on the same case study resulted in further observations as follows:
-
1.
Trade-off exists between the measured resilience and reliability of the system, with optimisation to the one metric not necessarily optimising the system to the other.
-
2.
Analysing the time sequencing of interventions in the optimal strategies suggests that, at least in the case study analysed here, more low-cost interventions early in the planning horizon achieve higher system reliability whereas regular intervention options spread over the planning horizon achieve higher system resilience when planning to an uncertain future.
-
3.
Optimizing for a single objective in the current practice methodology yields only a single solution that is highly dependent on the initial target robustness (defined by headroom) and target reliability selected and does not provide alternative solutions that may achieve benefits for small trade-offs.
References
Allen MR, Ingram WJ (2002) Constraints on future changes in climate and the hydrologic cycle. Nature 419:224–232. https://doi.org/10.1038/nature01092
Beh, EHY, Maier HR, Dandy GC (2015) Adaptive, multiobjective optimal sequencing approach for urban water supply augmentation under deep uncertainty. Water Resour Res 51:1529–1551, DOI: https://doi.org/10.1002/2014WR016254
Bristol Water (2012) Bristol water plc drought plan. Available from http://www.bristolwater.co.uk/
Bristol Water (2014) Water resources management plan 2014. Bristol, UK. Available from http://www.bristolwater.co.uk/
Brown C, Ghile Y, Laverty M, Li K (2012) Decision scaling: linking bottom-up vulnerability analysis with climate projections in the water sector. Water Resour Res 48:W09537
Deb K, Pratap A (2002) A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE T Evol Comput 6:182–197. https://doi.org/10.1109/4235.996017
Defra (2016) Creating a great place for living: Enabling resilience in the water sector. Available from https://www.gov.uk/government/publications/water-sector-improving-long-term-resilience
Environment Agency (2013) Water resources management plans 2019 – preparing for the future (main report). Halcrow Group Ltd, Swindon, UK
Environment Agency (2015) Water supply and resilience and infrastructure: Environment Agency advice to Defra. Available from https://www.gov.uk
Environment Agency, OFWAT, DEFRA, the Welsh Government (2012) Water resources planning guideline - the technical methods and instructions. Bristol, UK
Fowler HJ, Kilsby CG, O’Connell PE (2003) Modeling the impacts of climatic change and variability on the reliability, resilience, and vulnerability of a water resource system. Water Resour Res 39:1222
Groves DG, Bloom E, Lempert R et al (2015) Developing key indicators for adaptive water planning. J Water Resour Plan Manag 141:5014008. https://doi.org/10.1061/(ASCE)WR.1943-5452.0000471
Hashimoto T, Stedinger JR, Loucks DP (1982) Reliability, resiliency, and vulnerability criteria for water resource system performance evaluation. Water Resour Res 18:14–20, DOI: https://doi.org/10.1029/WR018i001p00014
Hosseini S, Barker K, Ramirez-Marquez JE (2016) A review of definitions and measures of system resilience. Reliab Eng Syst Safe 145:47–61. https://doi.org/10.1016/j.ress.2015.08.006
HR Wallingford (2015) for the ASC. Update of UK-wide projections of water avaialability. Report to the Adaptation Sub-Committee as part of the 2nd UK Climate Change Risk Assessment
Hughes TP, Baird AH, Bellwood DR et al (2003) Climate change, human impacts, and the resilience of coral reefs. Science 301:929–933. https://doi.org/10.1126/science.1085046
Jung D (2013) Robust and resilient water distribution systems. PhD thesis. University of Arizona, USA
Kjeldsen TR, Rosbjerg D (2004) Choice of reliability, resilience and vulnerability estimators for risk assessments of water resources systems. Hydrol Sci J 49:755–767
Korteling B, Dessai S, Kapelan Z (2013) Using information-gap decision theory for water resources planning under severe uncertainty. Water Resour Manag 27:1149–1172. https://doi.org/10.1007/s11269-012-0164-4
Kundzewicz ZW, Kindler J (1995) Multiple criteria for evaluation of reliability aspects of water resource systems. Modelling and management of sustainable basin-scale water resources systems. IAHS Press, Wallingford pp 217–224
Kwakkel J, Haasnoot M, Walker W (2015) Developing dynamic adaptive policy pathways: a computer-assisted approach for developing adaptive strategies for a deeply uncertain world. Clim Chang 132:373–386, DOI: https://doi.org/10.1007/s10584-014-1210-4
Linkov I, Bridges T, Creutzig F et al (2014) Changing the resilience paradigm. Nat Clim Chang 4:407–409. https://doi.org/10.1038/nclimate2227
Loucks DP (1997) Quantifying trends in system sustainability. Hydrol Sci J 42:513–530, DOI: https://doi.org/10.1080/02626669709492051
Mahmoud M, Liu Y, Hartmann H et al (2009) A formal framework for scenario development in support of environmental decision-making. Environ Model Softw 24:798–808. https://doi.org/10.1016/j.envsoft.2008.11.010
Maier HR, Guillaume JH a., van Delden H, et al (2016) An uncertain future, deep uncertainty, scenarios, robustness and adaptation: how do they fit together? Environ Model Softw 81:154–164, DOI: https://doi.org/10.1016/j.envsoft.2016.03.014
Matrosov ES, Padula S, Harou JJ (2012) Selecting portfolios of water supply and demand management strategies under uncertainty—contrasting economic optimisation and “robust decision making” approaches. Water Resour Manag 27:1123–1148
Matrosov ES, Woods AM, Harou JJ (2013) Robust decision making and info-gap decision theory for water resource system planning. J Hydrol 494:43–58. https://doi.org/10.1016/j.jhydrol.2013.03.006
Moody P, Brown C (2013) Robustness indicators for evaluation under climate change: application to the upper Great Lakes. Water Resour Res 49:3576–3588. https://doi.org/10.1002/wrcr.20228
Moy W-S, Cohon JL, ReVelle CS (1986) A programming model for analysis of the reliability, resilience, and vulnerability of a water supply reservoir. Water Resour Res 22:489–498. https://doi.org/10.1029/WR022i004p00489
NERA (2002) The economics of balancing supply and demand (EBSD) main report. London, UK. 02/WR/27/3
Nicklow J, Reed P, Savic D et al (2010) State of the art for genetic algorithms and beyond in water resources planning and management. J Water Resour Plann Manag 136(412–432):4. https://doi.org/10.1061/(ASCE)WR.1943-5452.0000053
ONS (2014) 2012-based Subnational Population Projections for England. Available from http://www.ons.gov.uk/ons/dcp171778_363912.pdf
Paton FL, Maier HR, Dandy GC (2014) Including adaptation and mitigation responses to climate change in a multiobjective evolutionary algorithm framework for urban water supply systems incorporating GHG emissions. Water Resour Res 50:6285–6304. https://doi.org/10.1002/2013WR015195
Prudhomme C, Dadson S, Morris D et al (2012) Future flows climate. https://doi.org/10.5285/bad1514f-119e-44a4-8e1e-442735bb9797
Python Software Foundation (2013) Python language reference. Version 2.7. Amsterdam. Available at http://www.python.org. Released (03–07-2013)
R Core Team (2013) R: A language and environment for statistical computing. R Foundation for Statistical Computing. Vienna, Austria. ISBN 3–900051–07-0, Available at http://www.R-project.org/. R version 3.0.2, Released (2013–09-25)
Ray PA, Watkins DW, Vogel RM, Kirshen PH (2013) Performance-based evaluation of an improved robust optimization formulation. J Water Resour Plan Manag 140(6). https://doi.org/10.1061/(ASCE)WR.1943-5452.0000389
Reed PM, Hadka D, Herman JD et al (2013) Evolutionary multiobjective optimization in water resources: the past, present, and future. Adv Water Resour 51:438–456. https://doi.org/10.1016/j.advwatres.2012.01.005
Roach T, Kapelan Z, Ledbetter R (2015) Comparison of info-gap and robust optimisation methods for integrated water resource management under severe uncertainty. Procedia Eng 119:874–883. https://doi.org/10.1016/j.proeng.2015.08.955
Roach T, Kapelan Z, Ledbetter R, Ledbetter M (2016) Comparison of robust optimization and info-gap methods for water resource management under deep uncertainty. J Water Resour Plann Manag 04016028
Tompkins EL, Adger WN (2004) Does adaptive management of natural resources enhance resilience to climate change?. Ecology and Society 9(2):10. URL: http://www.ecologyandsociety.org/vol9/iss2/art10/
Turner SWD, Marlow D, Ekström M et al (2014) Linking climate projections to performance: a yield-based decision scaling assessment of a large urban water resources system. Water Resour Res 50:3553–3567. https://doi.org/10.1002/2013WR015156
Walker WE, Lempert RJ, Kwakkel JH (2013) Deep uncertainty. In: Gass S, Fu M (eds) Encyclopedia of Oper. Res. and management science, 3rd edn. Springer, Berlin, pp 395–402
Wang Q, Guidolin M, Savic D, Kapelan Z (2014) Two-objective design of benchmark problems of a water distribution system via MOEAs: towards the best-known approximation of the true Pareto front. J Water Resour Plann Manag 141:04014060
Zheng F, Zecchin AC, Maier HR, Simpson AR (2016) (Comparison of the searching behavior of NSGA-II, SAMODE, and Borg MOEAs applied to water distribution system design problems. J Water Res Plann Manage. https://doi.org/10.1061/(ASCE)WR.1943-5452.0000650
Acknowledgements
This work was financially supported by the UK Engineering and Physical Sciences Research Council, HR Wallingford and The University of Exeter through the STREAM Industrial Doctorate Centre (Grant EP/G037094/1). We thank Bristol Water for allowing the use of their data and information, which is available from their publicly available water resources management plan.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Roach, T., Kapelan, Z. & Ledbetter, R. A Resilience-Based Methodology for Improved Water Resources Adaptation Planning under Deep Uncertainty with Real World Application. Water Resour Manage 32, 2013–2031 (2018). https://doi.org/10.1007/s11269-018-1914-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11269-018-1914-8