1 Introduction

In the recent decades the problem of water scarcity and inappropriate distribution of water resources have made many scholars to put a great effort into extending some new integrated and sustainable approaches of watershed and water resources management (Loucks et al. 1988). Water resource planners and managers work in an environment of change and uncertainty (Guo et al. 2009). Stochastic variables, and insufficient information in the most general sense, may lead to water loss and reduction of net benefits if ignored (Ganji et al. 2006a, 2008). Uncertainty, mainly due to rainfall variability, is usually incorporated when developing a crop water allocation strategy (Villalobos and Fereres 1989).

Optimal policies of crop water allocation can be divided into two states of static and dynamic (Loucks et al. 1981). Static and dynamic models can be outlined in states of stochastic and deterministic and also continuous and discrete (Hung et al. 2002; Karamouz et al. 2003). Because of independency to time and local solutions, static models are more suitable (Loucks et al. 1981). Discrete dynamic models have two problems of time and memory requirement in computations (curse of dimensionality). Among the discrete dynamic models DP (Dynamic Programming) and SDP (Stochastic Dynamic Programming) are more popular. These models have been used by some researchers for crop water allocation (Dudley and Burt 1973; Rhenals and Bras 1981).

Against the discrete models, there are continuous dynamic models that do not suffer from the curse of dimensionality. Among the continuous dynamic models, the stochastic ones are better because the dependent parameters of soil moisture and irrigation depth are random (Rodriguez-Iturbe et al. 1999a,b; Porporato et al. 2001; Laio et al. 2001; Ganji et al. 2006a,b).

Geerts and Raes (2009) discussed pros and cons of deficit irrigation, suggesting that it can increase water productivity without causing severe crop yield reductions. Tejero et al. (2011) studied three deficit irrigation (DI) strategies, sustained deficit irrigation (SDI), regulated deficit irrigation (RDI), and low-frequency deficit irrigation (LFDI) for commercial orchards of mature sweet orange. Considering water savings, water use was reduced by between 1,000 and 1,250 m3 ha−1applying RDI and LFDI.

Dattatray and Jyotiba (2011) formulated a multi Objective Fuzzy Linear Programming (MOFLP) irrigation planning model for deriving the optimal cropping pattern plan for the case study in Maharashtra State, India. Kloss et al. (2012) developed a simulation-based method to improve water productivity by applying controlled deficit irrigation subject to climate variability.

Various researchers have investigated optimal crop water allocation. Tsakiris (1982) optimized the intraseasonal distribution of irrigation water for grain sorghum under water shortage condition. The author extended an approach to derive crop sensitivity indices during certain stages (e.g. irrigation intervals). Further, the optimal water consumption was determined in each irrigation cycle to maximize crop yield throughout the irrigation season.

Shangguan et al. (2002) used an optimization method to allocate water under deficit irrigation. A non-linear programming optimization model with an integrated soil water balance is developed by Georgiou and Papamichail (2008) to determine the optimal reservoir release polices. Nikoo et al. (2012) proposed a methodology based on interval optimization and game theory to allocate benefits to water users. They used a linear water crop production function and applied it to incorporate deficit irrigation. Montazar (2013) coupled an integrated soil water balance algorithm to a non-linear optimization model. The author carried out water allocation planning in complex deficit agricultural water resources systems based on an economic efficiency criterion.

Optimization of crop patterns has been also the subject of many studies. Sethi et al. (2002) developed a linear programming model to maximize the economic returns by optimizing cropping patterns and groundwater management. Tsakiris and Spiliotis (2006) presents a methodology, based on the fuzzy set theory, for enhancing the goal programming approach to solve similar problems under various sets of criteria of a different nature to optimal crop pattern selection. Spiliotis and Tsakiris (2007)proposed an interactive fuzzy integer programming methodology for Minimum cost irrigation network design in order to incorporate obscure knowledge on these pressure requirements at the design stage. By using the proposed methodology significant economic gains may be achieved reducing the cost of the network, since the energy line is adapted more satisfactorily to the ranging pressure requirements. Mishra et al. (2009) developed a multi-objective optimization model to determine the optimal crop patterns and optimal size of auxiliary storage reservoir. In another study, Amini Fasakhodi et al. (2010) used a multi-objective fractional goal programming method to determine the optimal cropping pattern and sustain water availability in a rural farming system.

Fletcher and Ponnambalam (1995, 1988) proposed a stochastic continuous dynamic optimization model named Constraint-State (C-S), this is a stochastic optimization method to improve the efficiency of a reservoir. This method is similar to SDP model, but its state variables are not discrete and also use a continuous optimization method. Ganji et al. (2006a, b) proposed the use of Constraint-State model for optimization and simulation of soil moisture and irrigation depth. They extended this model by using means and variances of weekly rainfall, potential evapotranspiration, and a number of soil moisture characteristics as inputs. Ganji and Shekarriz-fard (2010) modified the proposed model in 2006 by incorporating irrigation depth and soil moisture uncertainties and developed a set of new formulations. They defined an equation representing the changes of soil moisture according to the root depth growth during the time.

It is obvious that the parameters of soil moisture and irrigation depth have uncertainties, but the important point is that, the stochastic variable is not always normal, so the results will be far from the reality. However, Mahootchi (2009) proposed a model to reservoirs management based on the assumption of nonnormal stochastic variable. His model was based on incorporation with Fletcher and Ponnambalam (1998) method and Kumaraswamy’s distribution function (1980). Mahootchi and Ponnambalam (2013) proposed a recently developed stochastic programming technique that includes reliability constraints which used to solve the operations optimization problem of the Parambikulam-Aliyar project (PAP), a multi reservoir system in India. The use of reliability constraints as chance constraints in reservoir operations optimization have been around for some time, but is still a challenging problem because either the results are not good enough or they cannot be applied to the cases with more than one or two reservoirs when such techniques depend on discretization. The new implementation of chance constraints based on a previous model extended to multi reservoir systems provides better results than so far known. Ganji and Kaviani (2013) proposed the new methodology to probability analysis of crop water stress index using Double Bounded Density Function and moment analysis of crop water stress index. The results show that in case of deficit irrigation, the probability of crop water stress occurrence is high and as a consequence, any unpredictable water shortage leads to yield reduction.

This paper proposes a new optimization model for crop water allocation based on Constraint-State model in arid and semi-arid regions by the assumption of nonnormal stochastic variable.

2 Materials and Methods

The soil moisture continuity equation for a specific plant on a weekly basis can be outlined as follows:

$$ n\left({z}_t{\theta}_t-{z}_{t-1}{\theta}_{t-1}\right)=I{r}_t+R{a}_t+n\left({z}_t-{z}_{t-1}\right){\theta}_r-E{T}_t-{L}_t+{\eta}_t $$
(1)

Where n is the soil porosity, z t is the root depth at the end of time t, θ t is the relative volumetric soil moisture at the end of a weekly period t, θ t − 1 is the relative soil moisture at the end of a weekly period t-1, θ r is the residual soil moisture at the end of a weekly period, Ir t is the weekly irrigation depth in period t, Ra t is the long-term average of the weekly effective rainfall depth, ET t is the long-term average of weekly actual evapotranspiration for a specific plant, L t is the long-term average of the weekly leaching fraction, and η t is the noise term of soil moisture balance equation that refers to an error in combining terms defined over short irrigation periods (soil moisture state variable) with terms defined over long term averages (rainfall and evapotranspiration).

The soil moisture balance equation (Eq. 1) can be represented using the indicator function developed by Fletcher and Ponnambalam (1996) originally for water reservoirs. The indicator function of the random variable θ t (for example, \( {1}_{\left({\theta}^{\min },{\theta}^{\max}\right)}\left({\theta}_t\right) \)) is itself a random variable such that:

$$ \left[{1}_{\left({\theta}^{\min },{\theta}^{\max}\right)}\left({\theta}_t\right)=\left\{\begin{array}{l}1\to {\theta}^{\min}\le {\theta}_t\le {\theta}^{\max}\\ {}0\to otherwise\end{array}\right.\right] $$
(2)

Where θ min is the lowest level of soil moisture state variable and θ max is the maximum allowable soil moisture at the end of time t. Applying the indicator function and considering three intervals for the soil moisture state variable, Eq. 1 is updated as:

$$ \begin{array}{l}n{z}_t{\theta}_t=n{z}_{t-1}{\theta}_{t-1}+\left[I{r}_t+R{a}_t+n\left({z}_t-{z}_{t-1}\right){\theta}_r-E{T}_t+{\eta}_t\right]{.1}_{\left({\theta}^{\min },{\theta}^{\max}\right)}\left({\theta}_t\right)\\ {}+\left[n{z}_t{\theta}^{\min }-n{z}_{t-1}{\theta}_{t-1}-n\left({z}_t-{z}_{t-1}\right){\theta}_r\right]{.1}_{\left(-\infty, {\theta}^{\min}\right)}\left({\theta}_t\right)\\ {}+\left[n{z}_t{\theta}^{\max }-n{z}_{t-1}{\theta}_{t-1}-n\left({z}_t-{z}_{t-1}\right){\theta}_r\right]{.1}_{\left({\theta}^{\max },+\infty \right)}\left({\theta}_t\right)\end{array} $$
(3)

Considering Eq. 3, the expected value of the soil moisture can be determined as follows:

$$ \begin{array}{l}E\left\{n{z}_t{\theta}_t\right\}=E\left(n{z}_{t-1}{\theta}_{t-1}\right)\\ {}+E\left\{\left[I{r}_t+R{a}_t+n\left({z}_t-{z}_{t-1}\right){\theta}_r-E{T}_t+{\eta}_t\right]{.1}_{{\left({\theta}^{\max },{\theta}^{\min}\right)}^{\left({\theta}_t\right)}}\right\}\\ {}+E\left\{\left[n{z}_t{\theta}^{\min }-n{z}_{t-1}{\theta}_{t-1}-n\left({z}_t-{z}_{t-1}\right){\theta}_r\right]{.1}_{{\left(-\infty, {\theta}^{\min}\right)}^{\left({\theta}_t\right)}}\right\}\\ {}+E\left\{\left[n{z}_t{\theta}^{\max }-n{z}_{t-1}{\theta}_{t-1}-n\left({z}_t-{z}_{t-1}\right){\theta}_r\right]{.1}_{{\left({\theta}^{\max },+\infty \right)}^{\left({\theta}_t\right)}}\right\}.\end{array} $$
(4)

Where the third part of the right hand side of Eq. 4 represents the probability of soil moisture deficit, considering θ min as the lower bound of soil moisture state variable. To derive the extended form of the Eq. 4, the expected value of the indicator function of soil moisture is determined. The final part in the right hand side of Eq. 4 is the probability of the upper limit of soil moisture content (θ max) violation. The failure probability is the sum of the probabilities of violations of lower and upper limits of soil moisture (see Ganji and Shekarriz-fard (2010) for more explanation about these formulations).

2.1 Theory of Nonnormal Probability for Stochastic Variable (\( \eta \))

The stochastic variable is considered as nonnormal terms, because in this way the results will be closer to reality. A generalized beta-equivalent distribution developed by Kumaraswamy (1980) is substituted for the Gaussian distribution. Before addressing details of this method, a brief introduction of this distribution is presented in the following section.

2.1.1 Double-Bounded Probability Density Function (DB-PDF)

Kumaraswamy (1980) suggested a beta-equivalent distribution function namely Double-Bounded Probability Density Function (DB-PDF). This is now more commonly called the Kumaraswamy distribution (Jones 2009). This function is used to examine different types of distributions models for random variables with lower and upper bounds as shown in Figs. 1 and 2. The general form of the density function for random process x using four different parameters including k 1, k 2 and Rf min, Rf max is shown in Eq. 5:

Fig. 1
figure 1

An example of DB-CDF (a = k1, b = k2)

Full size image
Fig. 2
figure 2

An example of DB-PDF (a = k1, b = k2)

Full size image
$$ \begin{array}{c}\hfill \mathrm{f}\left(\mathrm{x}\right)={\mathrm{k}}_1{\mathrm{k}}_2{\mathrm{x}}^{{\mathrm{k}}_1\hbox{-} 1}{\left({1\hbox{-} \mathrm{x}}^{{\mathrm{k}}_1}\right)}^{{\mathrm{k}}_1\hbox{-} 1}\hfill \\ {}\hfill \mathrm{x}=\frac{{\mathrm{Rf}\hbox{-} \mathrm{R}\mathrm{f}}_{\min }}{{\mathrm{Rf}}_{\max}\hbox{-} {\mathrm{Rf}}_{\min }},\mathrm{x}\in \left[0,1\right]\hfill \end{array} $$
(5)

where k 1, k 2 are two parameters playing the main role to create different functions such as exponential- or normal-shape distribution, and Rf min, Rf max are the lower and upper bounds of random variable x, respectively.

Deriving the Double-Bounded Cumulative Density Function (DB-CDF) from the density function (Eq. 5) is a very straightforward calculation, unlike in the Beta distribution that can be outlined as below:

$$ F(x)=1-{\left(1-{x}^{k_1}\right)}^{k_2} $$
(6)

The n th moment of x can be computed using the following equation:

$$ {x}^{-n}=\frac{\left[\left(\frac{n}{k_1}\right)!\right]\left({k}_2!\right)}{\left(\frac{n}{k_2}+{k}_2\right)}=\frac{\left[\varGamma \left(\frac{n}{k_1}+1\right)\right]\left(\varGamma \left({k}_2+1\right)\right)}{\varGamma \left(\frac{n}{k_2}+{k}_2+1\right)}={k}_2*\mathrm{B}\left(\frac{n}{k_1}+1,{k}_2\right) $$
(7)

Where B(·) is the beta function.

With historical or simulated data for random variables, all parameters in the probability functions can be computed using either moment equations or empirical cumulative distribution functions (CDF). It should be noted that the advantage of DB-PDF is the simple analytical forms for its DB-CDF, unlike the numerical integral required for beta CDF (see Mahootchi (2009) for more explanation about these formulations).

2.1.2 Presenting the Considered Formulas of this Theory

Applying the historical or simulated data of rainfall and implementing the foregoing equations, both parameters, k 1 and k 2 in the Eq. 5 can be computed throughoutthe growth periods. Proportional to the values of k 1 and k 2 in different growth stages, the density functions appear in different shapes, while in the previous methods the density functions were normal for all of the growth stages.

The soil moisture balance (Eq. 1), therefore can be represented as follows:

$$ \begin{array}{c}\hfill n{z}_t\theta =\left\{n{z}_{t-1}{\theta}_{t-1}+I{r}_t+Rf+n\left({z}_t-{z}_{t-1}\right){\theta}_r-E{T}_t+{\eta}_t\right\}{.1}_{\left({\theta}^{\min },{\theta}^{\max}\right)}\left({\theta}_t\right)\hfill \\ {}\hfill +\left\{n{z}_t{\theta}^{\min }-n{z}_{t-1}{\theta}_{t-1}-n\left({z}_t-{z}_{t-1}\right){\theta}_r\right\}{.1}_{\left(-\infty, {\theta}^{\min}\right)}\left({\theta}_t\right)\hfill \\ {}\hfill +\left\{n{z}_t{\theta}^{\max }-n{z}_{t-1}{\theta}_{t-1}-n\left({z}_t-{z}_{t-1}\right){\theta}_r\right\}{.1}_{\left({\theta}^{\max },+\infty \right)}\left({\theta}_t\right)\hfill \end{array} $$
(8)

The moments can be derived analogous to what have been performed in the other models. In this study, however, the numerical Integrations are used. Equations (9) and (11) considered as constraints of optimization model.

$$ \begin{array}{l}E\left(n{z}_t{\theta}_t\right)=\left[{k}_t+R{f}_{\min }+n\left({z}_t-{z}_{t-1}\right){\theta}_r-E{T}_t\right]*{\displaystyle \underset{L_1}{\overset{L_2}{\int }}f(x)dx}\\ {}+\left[R{f}_{\max }-R{f}_{\min}\right]*{\displaystyle \underset{L_1}{\overset{L_2}{\int }}x.f(x)dx}\\ {}+\left[n{z}_t{\theta}^{\min }-n{z}_{t-1}{\theta}_{t-1}-n\left({z}_t-{z}_{t-1}\right){\theta}_r\right]*{\displaystyle \underset{0}{\overset{L_1}{\int }}f(x)dx}\\ {}+\left[n{z}_t{\theta}^{\max }-n{z}_{t-1}{\theta}_{t-1}-n\left({z}_t-{z}_{t-1}\right){\theta}_r\right]*{\displaystyle \underset{L_2}{\overset{1}{\int }}f(x)dx}\end{array} $$
(9)
$$ {k}_t=I{r}_t+n{z}_{t-1}{\theta}_{t-1} $$
(10)
$$ \begin{array}{l}E{\left(n{z}_t{\theta}_t\right)}^2={\left[{k}_t+R{f}_{\min }+n\left({z}_t-{z}_{t-1}\right){\theta}_r-E{T}_t\right]}^2*{\displaystyle \underset{L_1}{\overset{L_2}{\int }}f(x)dx}\\ {}+2\left[R{f}_{\max }-R{f}_{\min}\right]*\left[{k}_t+R{f}_{\min }+n\left({z}_t-{z}_{t-1}\right){\theta}_r-E{T}_t\right]*{\displaystyle \underset{L_1}{\overset{L_2}{\int }}x.f(x)dx}\\ {}+2{\left[R{f}_{\max }-R{f}_{\min}\right]}^2*{\displaystyle \underset{L_1}{\overset{L_2}{\int }}{x}^2.f(x)dx}\\ {}+{\left[n{z}_t{\theta}^{\min }-n{z}_{t-1}{\theta}_{t-1}-n\left({z}_t-{z}_{t-1}\right){\theta}_r\right]}^2*{\displaystyle \underset{0}{\overset{L_1}{\int }}f(x)dx}\\ {}+{\left[n{z}_t{\theta}^{\max }-n{z}_{t-1}{\theta}_{t-1}-n\left({z}_t-{z}_{t-1}\right){\theta}_r\right]}^2*{\displaystyle \underset{L_2}{\overset{1}{\int }}f(x)dx}\end{array} $$
(11)
$$ \begin{array}{c}\hfill {L}_1=\frac{\left[n{z}_t{\theta}^{\min }-{k}_t-R{f}_{\min }-n\left({z}_t-{z}_{t-1}\right){\theta}_r+E{T}_t\right]}{\left[R{f}_{\max }-R{f}_{\min}\right]}\hfill \\ {}\hfill {L}_2=\frac{\left[n{z}_t{\theta}^{\max }-{k}_t-R{f}_{\min }-n\left({z}_t-{z}_{t-1}\right){\theta}_r+E{T}_t\right]}{\left[R{f}_{\max }-R{f}_{\min}\right]}\hfill \end{array} $$
(12)

It is worth mentioning because of using approximation techniques in finding Rf min, Rf max and during the optimization process two, the transformed lower and upper bounds (L 1 and L 2) in the above integrals might be determined logically meaningless (i.e., the lower or upper bound becomes less than zero or higher than one). The following rules need to be considered in setting the bounds:

$$ \left\{\begin{array}{l}{L}_1<0\Rightarrow {L}_1=0\\ {}{L}_2<0\Rightarrow {L}_1={L}_2=0\Rightarrow {\displaystyle \underset{L_1}{\overset{L_2}{\int }}\left[\dots \right]=0}\\ {}{L}_2>1\Rightarrow {L}_2=1\\ {}{L}_1\ge 1\Rightarrow {L}_1={L}_2=1\Rightarrow {\displaystyle \underset{L_1}{\overset{L_2}{\int }}\left[\dots \right]=0}\end{array}\right. $$
(13)

In the dynamic system of soil moisture changes, Eqs. 9 and 11 present mean and standard deviation of stochastic variables. These equations can be used to determine the optimum water allocation to plant during the growing season. For this purpose it is regular to define an optimization model for water allocation to plant. This model considers Eqs. 9 and 11 as constraints. These constraints state the random variables behavior (soil moisture and irrigation depth) affecting the allocated water as objective function.

2.2 Optimization Model

Generally, water resource models may be classified into two groups: optimization models and simulation models. Process of approaching to an optimum objective by changing decision variables is an optimization measure and any model performing this objective is an optimization model. In other word minimizing or maximizing the objective function subject to a set of constraints is optimization modeling process.

In fact, optimization models are a type of simulation models in which decision variables optimize the objective function. Each optimization model includes the following items: parameters, decision variables, objective function, and Constraints.

The Constraint-State optimization model has been used in this paper consisted of three main parts:

  1. 1-

    Main program: includes initial value of unknown parameters, the upper and the lower limit of unknown parameters, optimization program and outputs programs.

  2. 2-

    Objective function: the maximization of the expected net benefit is the objective function for a crop water allocation problem, which is based on the Jensen (1986) crop water production function. In this paper, the object is determining the maximum production (yields) of winter wheat based on the optimized irrigation.

    Among the proposed production functions in literature, thefunctions proposed by Jensen (1986) and Doorenbos and Kassam (1979) has been used widely in crop water allocation (Ghahraman and Sepaskhah 1997, 1999; Nagesh et al. 2006; Ganji et al. 2006a, b; 2010; Georgiou and Papamichail 2008; Grove and Lk 2010).

    Jensen (1986) divided the plant growing season into different phases and developed Eq. 14:

    $$ \frac{y_a}{y_{\max }}=\left\{\underset{i=1}{\overset{n}{\varPi }}{\left(\frac{E{T}_a}{E{T}_c}\right)}^{\lambda_i}\right\} $$
    (14)

    Where \( {y}_{{}_a} \) is the actual crop yield, y max is the potential or maximum crop yield, ET a is the actual crop evapotranspiration, ET c is the crop evapotranspiration, λ i is the crop water stress index for the growing phases, i is the growing phases and n is the number of the growing phases.

    The crop evapotranspiration can be calculated using the following equation:

    $$ E{T}_c=E{T}_0*{k}_c $$
    (15)

    Where, ET o is the reference evapotranspiration and k c is the crop coefficient. ET o , can be estimated using well known FAO Penman-Monteith equation.

    Doorenbos and Kassam (1979) proposed the relation between production and deficit irrigation as follows:

    $$ \frac{y_a}{y_{\max }}={\displaystyle \underset{i=1}{\overset{n}{\varPi }}}\left[\left(1-K{y}_i\right){\left(1-\frac{E{T}_a}{E{T}_c}\right)}_i\right] $$
    (16)

    Where, Ky i is the crop water stress index for the growing seasons.

    The objective function used is based on Jensen (1986) crop water production function:

    $$ f=E\left\{{\displaystyle \underset{t}{\overset{nperiod}{\varPi }}}\left\{1-{K}_t\left[1-\frac{E{T}_t}{E{T}_p}\right]\right\}.W-{\displaystyle \underset{t}{\overset{nperiod}{\varPi }}}\left(I{r}_t{W}_w\right)\right\} $$
    (17)

    Where, K t is the crop water stress index for period t (Jensen 1986), W is the price of yield per kg, ET t is actual evapotranspiration, ET p is the potential evapotranspiration and W w is the price of water per unit volume. It should be noted that, the crop water stress index can be translated to any appropriate growing period for a crop using the proposed methodology of Tsakiris (1982) and Kipkorir and Raes (2002). The first product term of Eq. 17 represents the gross benefit value and the second term is the water consumption cost in each period of time. Using the Taylor series approximation and neglecting the variance of the actual evapotranspiration and irrigation depth, the objective function is represented by Eq. 18. The Advance First Order Second Moment method analysis may be used to achieve a better approximation of Eq. 17.

    $$ f\approx \left\{{\displaystyle \underset{t}{\overset{nperiod}{\varPi }}}\left\{1-{K}_t\left[1-\frac{E\left(E{T}_t\right)}{E{T}_p}\right]\right\}.W-{\displaystyle \underset{t}{\overset{nperiod}{\varPi }}}\left[E\left(I{r}_t\right).{W}_w\right]\right\} $$
    (18)

    Where, E(ET t ) is the expected value of the actual evapotranspiration which is determined by the moment analysis as shown in Eq. 19.

    The evapotranspiration is a function of current soil moisture conditions and can be represented as follows:

    $$ E{T}_t=\left\{\begin{array}{l}0............................................{\theta}_t\le {\theta}_{pwp}\\ {}\frac{E{T}_{pt}\left({\theta}_t-{\theta}_{pwp}\right)}{\left(1-p\right)\left({\theta}_{FC}-{\theta}_{pwp}\right)}................{\theta}_{pwp}<{\theta}_t\le \left(1-p\right)\left({\theta}_{FC}-{\theta}_{pwp}\right)\\ {}E{T}_{pt}......................................{\theta}_t>\left(1-p\right)\left({\theta}_{FC}-{\theta}_{pwp}\right)\end{array}\right. $$
    (19)

    Where, (1 − p) is the fraction of total available soil water that can be depleted from the root zone before stress (reduction in ET) occurs, θ FC is relative soil moisture at field capacity and θ pwp is the relative soil moisture unavailable for plant growth or the water content at wilting point.

  3. 3-

    Constraints include linear and nonlinear equalities and inequalities. The constraints considered in this model are shown as Eqs. 9 and 11 and also the following inequalities:

    $$ \begin{array}{c}\hfill Ir\le \left[n{z}_t{\theta}^{\max }-R{a}_t-n\left({z}_t-{z}_{t-1}\right){\theta}_r\right.\hfill \\ {}\hfill \left.+\sqrt{2Var{\eta}_t}* erfinv\left(1-p\right)+E{T}_t-n{z}_{t-1}{\theta}_{t-1}\right]\hfill \end{array} $$
    (20)

Where p is the probability of not violating the available soil moisture capacity assigned by the decision maker and erfinv() is the inverse error function. A lower value of p leads to a higher probability of soil moisture capacity violation, resulting in a higher probability of water loss. The restriction of the actual evapotranspiration to the maximum potential evapotranspiration, and the restriction of irrigation depths to positive values are the other constraints that should be considered:

$$ E{T}_t\le E{T}_p $$
(21)
$$ I{r}_t={k}_t-n{z}_{t-1}{\theta}_{t-1}\ge 0 $$
(22)

The model was written in MATLAB and was run for winter wheat in Badjgah, south of Iran.

2.3 Simulation Model

Generally, to verify the accuracy and veracity of the output of optimization models and their uncertainty analysis mostly simulation models are employed. In fact, considering the simulation models outputs, the behavior and efficiency of system could be analyzed.

Simulation model’s inputs can be obtained from the local meteorological stations and collected data from the field. Input data should be for a long term to ensure that the system can experience all probable situations (flood, drought, lack of water, etc.). If adequate long term data were not available, dummy string data could be produced by historical data from the meteorological stations.

To verify the proposed optimization model, a simulation model was developed. To do this, the resulted irrigation strategy (from the optimization model) is used with fixed input values for the simulation model. The simulation model is mainly based on a simple soil water continuity equation, which uses the random generated rainfall and crop characteristics as input.

2.4 Reliability Index

There are different definitions presented by many researchers for reliability index in water resources science (e.g. Cai (1999), Ganji (2000) and Karamouz et al. (2003). In general, however, all have one main concept in common expressed through the following definition

The reliability of a time series is the number of data that are in a suitable state divided by all data of the series as following:

$$ \begin{array}{c}\hfill R=\frac{m}{n}\hfill \\ {}\hfill m\in \left[n{z}_t{\theta}^{\min }-n{z}_{t-1}{\theta}_{t-1}-n\left({z}_t-{z}_{t-1}\right){\theta}_r,n{z}_t{\theta}^{\max }-n{z}_{t-1}{\theta}_{t-1}-n\left({z}_t-{z}_{t-1}\right){\theta}_r\right]\hfill \end{array} $$
(20)

Where R is the reliability index, m is the number of data in a suitable state, n is the number of all data of the series, nz t θ min − nz t − 1 θ t − 1 − n(z t  − z t − 1)θ r is the probability of crop water stress and nz t θ max − nz t − 1 θ t − 1 − n(z t  − z t − 1)θ r is the probability of deep percolation (saturation).

2.5 Case Study

The application of the model was examined for winter wheat. Thus, the required information and data were collected from the agricultural meteorological station at Badjgah. The study area was located at the faculty of agriculture, Shiraz University located in Fars province, south of Iran (Fig. 3). Badjgah has a semiarid climate, with average annual rainfall of 404 mm, mostly occurs during winter and spring and annual potential evaporation of 1,800 mm. Evapotranspiration (using FAO Penman-Montith equation (Allen et al. 1998)) and rainfall data for the period 1983–2001 were used in this study. The daily rainfall records were extended using the Markov chain and Gamma distribution and the results were used to calculate the weekly mean and standard deviation of rainfall. The soil texture was silty-clay, the average soil field capacity (FC) was 0.35 (m 3/ m 3), the permanent wilting point (PWP) was 0.12 (m 3/ m 3) and the readily available water (RAW) was 0.23 (m 3/ m 3) (Ganji et al. 2006a).

Fig. 3
figure 3

The location of case study (Badjgah, Fars province, Iran)

Full size image

3 Results and Discussions

There is a high level of uncertainty with the determination of an irrigation policy as a result of soil moisture variability. In response to randomness in irrigation policy, a new formulation is developed. In this paper, the double bounded density function based on stochastic optimization model (developed by Ganji and Shekarriz-fard 2010), is applied to determine the optimum irrigation depth. For this purpose, Constraint-State optimization model which is a continuous stochastic dynamic model, representing the soil moisture behavior by mean and variance (first and second moments) (Eqs. 9 and 11) of the soil moisture and uses this nonlinear data as the constraint of the model is developed for 32 numbers each denoting to a week (32 weeks = period of winter wheat growth in the study area) as optimized weekly irrigation depth. Considering the result of the optimization model and the nature of soil moisture density function which has spikes at maximum and minimum soil moisture, DB-CDF method are applied to reliability analysis of the weekly irrigation depth.

To verify the proposed optimization model, a simulation model was developed. As the first step of model verification, the simulated mean soil moisture and variance are compared with corresponding optimized values. The result was very consistent with correlation coefficient of 99 %.

Figure 4 presents the comparison of the mean soil moisture resulting from the optimization and simulation models. According to this figure, the variance from the optimization model is very close to that from the simulation model for winter wheat. Figure 4 also illustrates the role of rainfall and its variability on the mean and standard deviation of the soil moisture.

Fig. 4
figure 4

Weekly mean and variance of the soil moisture during the growing season for winter wheat

Full size image

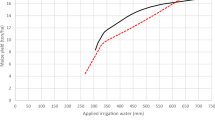
The weekly mean actual evapotranspiration values derived directly from the optimization model are compared with the corresponding results from the simulation as shown in Fig. 2. The mean actual evapotranspiration from the optimization is placed within a 95 % level of confidence interval for winter wheat. As Fig. 5 shows the maximum evapotranspiration in the study area occurs at week 25 with 36 mm/week and the results of optimization and simulation models are almost the same. The optimal irrigation strategy for winter wheat derived from the proposed optimization model is also presented in Fig. 5. As shown in this figure at the initial growth stage (germination period) more irrigation water is applied. During the winter time as rainfall is increased the irrigation water is reduced and in the spring time (mid growth stage) as rainfall is decreased and temperature is increased more irrigation water is applied and at the late season again irrigation water is reduced. T-test analysis was used to compare the simulation and optimization values that show a non-significant difference of results. The above verification results show that the model works well to determine the first and second moments of the soil moisture and actual evapotranspiration.

Fig. 5
figure 5

Weekly means actual evapotranspiration, rainfall and optimal irrigation strategy during the growing season for a winter wheat

Full size image

By definition, the reliability (R) is complementary to the failure (F), representing the probability of failure not occurring (R =1 − F). Figure 6 presents the mean weekly reliability of optimal irrigation strategy from the proposed optimization model. Based on Eq. 20, the upper and lower bounds of reliability indices are nz t θ max − nz t − 1 θ t − 1 − n(z t  − z t − 1)θ r and nz t θ min − nz t − 1 θ t − 1 − n(z t  − z t − 1)θ r .

Fig. 6
figure 6

Weekly reliability of optimal irrigation strategy during the growing season for winter wheat

Full size image

This factor only shows the possibility of failure occurrence in each week of growing season, but it can be applied to yield/benefit reliability analysis based on the Advance First Order Second Method (Ganji et al. 2006b).

Figure 3 shows that, model is always in the reliability range except for the first week, therefore the reliability of the Constraint-State model by assumption of nonnormal probability for the stochastic variable will be equal to 96.9 %. According to the efficiency criteria, the Constraint-State optimization model by assumption of nonnormal probability for the stochastic variable shows a good efficiency.

Using the proposed methodology, the expected value of the soil moisture, the variance of the soil moisture, the expected value of actual evapotranspiration, an optimal irrigation strategy and corresponding reliabilities and cumulative density function are determined, all achievable without the aid of the model simulation.

As a suggestion we recommend that, in addition to simulation results experimental verification in the field may be needed to uphold this claim. Also, due to the multiplicative yield function, we can’t realize that the yield obtained from the optimization model is at what level values of probability. It can’t be said conclusively that the resulting value for the objective function is mean value (or probability50%). So it is recommended to use AFOSMFootnote 1 method to improve this value.

4 Conclusions

A stochastic model was developed based on the Constraint-State formulation to determine the optimal weekly crop water allocation. The methodology presented incorporates minimum and maximum bounds on the soil moisture states explicitly in the dynamic systems. The current methodology considers a random irrigation policy in addition to the incorporation of crop demand uncertainty and nonnormal stochastic variable in the optimization of water allocation for a crop. The formulation also allows for the derivation of the reliability associated with the proposed optimal irrigation strategy during the growing season. The reliability is a useful index to realize the possibility of runoff and/or deep percolation events during the growing season. A weekly simulation model is used to validate the results of the proposed stochastic model. The outcomes are also justified by the results of Ganji and Shekarriz-fard (2010) that shows the possibility of achieving a higher relative net benefit by decreasing the allocated water. The derivation of near perfect estimates for soil moisture means and variances by using DB-CDF method which is comparable to simulation results, addressing physical bounds and both demand and allocation uncertainties has not been reported to date.