Abstract
Water utilities particularly in the developing countries continue to operate with considerable inefficiencies in terms of water and revenue losses. With increasing water demand and scarcity, utilities require effective strategies for optimum use of available water resources. Diverse water loss reduction options exist. Deciding on which option to choose amidst conflicting multiple criteria and different interests of stakeholders is a challenging task. In this paper, an integrated multi-criteria decision-aiding framework for strategic planning of water loss management is presented. The PROMETHEE II method was applied within the framework in prioritizing water loss reduction options for Kampala city. A strategic plan that combines selective mains and service lines replacement and pressure management as priorities is the best compromise based on preferences of the decision makers and seven evaluation criteria characterized by financial-economic, environmental, public health, technical and social impacts. The results show that the most preferred options are those that enhance water supply reliability, public health and water conservation measures. This study demonstrates how decision theory coupled with operational research techniques could be applied in practice to solve complex water management and planning problems.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
One of the main challenges facing water utilities worldwide is the high levels of water losses in the distribution networks. According to the World Bank study (Kingdom et al. 2006), about 32 billion m3 of treated water is lost annually as leakage from urban water distribution systems (WDSs) around the world, while 16 billion m3 is used but not paid for. They further estimate that these losses cost water utilities as much as US$ 14 billion per year, with a third of it occurring in the developing countries. In light of global pressures (climate change, urbanization, growing populations, increasing water demand and scarcity etc.), water utilities particularly in the developing countries need to operate more efficiently to provide sustainable water services.
Water loss management (WLM) has become an important decision issue in meeting utility’s strategic goals. Whereas strategic planning (SP) has proven to be a valuable tool for sustainable urban water management (Malmqvist et al. 2006), water utilities in developing countries often lack the necessary capabilities to carryout SP (Mugabi et al. 2007). SP is about setting a long-term direction based on sound predictions, analysis of options and key decisions about the future of an organisation. The Uganda National Water and Sewerage Corporation (NWSC) corporate plan (2009–2012) broadly categorises water loss reduction among other sub-goals under the main goal of revenue maximization (NWSC 2009a). This traditional way of evaluating water loss reduction strategies based on a single criterion of maximising revenue is unrealistic as water services management takes place in a multiple-criteria environment. Clearly, a more structured approach for SP is required to safeguard against asset stripping by a utility driven mainly to maximize profits.
Multi-criteria decision analysis (MCDA) is a tool developed in the field of decision theory for resolving operational research problems with a finite number of decision options amongst which decision-makers (DMs) have to evaluate and rank based on the weights of a finite set of evaluation criteria (EC) (Figueira et al. 2005; Lu et al. 2007; Simonovic 2009). The discrete MCDA techniques take into account a range of quantitative and qualitative criteria beyond the financial criterion and can deal with long-time horizons and uncertainties during the optimal decision-making process (NAMS 2004). They have the potential to provide well structured, rational, consistent, transparent and objective solutions to complex decision problems in water resources management and planning (Lai et al. 2008). A recent review of MCDA for water resource planning and management has shown that MCDA is mostly used for water policy evaluation, strategic planning and infrastructure selection (Hajkowicz and Collins 2007). The same review indicates that the most commonly applied methods were fuzzy set analysis, compromise programming (CP), analytic hierarchy process (AHP), elimination et choice translating reality (ELECTRE) and preference ranking and organization method for enrichment evaluation (PROMETHEE) respectively.
Many researchers have recently solved water resources management and planning problems by application of various MCDA techniques such as PROMETHEE (Morais and Almeida 2007; Silva et al. 2010), ELECTRE II (Bouchard et al. 2010), fuzzy TOPSIS (Afshar et al. 2011), and fuzzy AHP (Wang et al. 2011). The inexact two-stage fuzz-stochastic programming method developed for water resources management under uncertainty (Lu et al. 2008), could be a valuable tool for improving WDS efficiency (leakage reduction) and supply reliability by application of the flexible penalty policies incase water service providers fail to deliver the agreed upon amount of water to their customers. Of particular interest, is the leakage management study in Brazil (Morais and Almeida 2007). Although Morais and Almeida (2007) addressed the leakage strategy in WDSs, they did not tackle water loss in totality as the apparent water loss component that is often significant in developing countries (Mutikanga et al. 2009) was not considered. In addition, they did not carry out a water balance to identify whether the problem was leakage or apparent losses. They instead indicate a water loss of 60% for the case study. Use of percentage as a water loss indicator can be misleading as it is heavily influenced by consumption and has nothing to do with water loss control (Fanner et al. 2007).
The application of decision theory to real-world problems in practice is by far not trivial and could be one of the hardest parts of the decision-making process. According to Hajkowicz and Higgins (2008), the main challenge is not in developing more sophisticated MCDA methodologies but to develop more systematic frameworks to support the initial structuring of the decision problem in terms of selecting criteria and decision options. Clearly, there remains a gap between developed decision theories and applications. The knowledge gap is even bigger in developing countries where these methods and tools are hardly applied and therefore not very well understood and validated.
In this paper, an integrated MCDA framework for strategic water loss management planning (SWLMP) is proposed to aid urban water utility DMs in selecting and prioritizing water loss reduction strategies. The framework methodology is applied to a typical developing country city of Kampala, Uganda in East Africa. For the case study WDS, seven evaluation criteria under five main non-commensurate and conflicting objectives that include supply reliability, cost efficiency, water conservation, affordability and public health protection were identified and examined. The SWLMP framework includes the PROMETHEE outranking method of the MCDA family and its new computer software tool Decision Sights (D-Sight). The methodology explicitly includes the actors’ preferences in the evaluation of water loss reduction strategies and as such is able to support the DMs in the decision-making process. The D-Sight’s in-built sensitivity analysis tools were used to examine the influence of actor preference weighting on the final solution ranking. The SWLMP framework has shown to be a valuable tool for facilitating the decision process of prioritizing water loss reduction options.
This paper is organized as follows. Section 2 outlines the concepts and frameworks of decision making, group decision making, MCDA and the outranking PROMETHEE method of MCDA. Section 3 presents the integrated MCDA framework for SWLMP. In section 4, the application of the MCDA framework is presented together with the results and sensitivity analysis. The results discussion and some lessons learned are presented in section 5. Finally, conclusions are drawn in section 6.
2 Multi-criteria Decision Analysis
2.1 The Decision Making Process
Decision making has been defined differently by various researchers. Harris (1998) formally defines decision making as “the study of identifying and choosing alternatives based on the values and preferences of the decision makers”. According to Lu et al. (2007), decision making is “the cognitive process leading to the selection of a course of action among alternatives”. It can be deduced from these two definitions that decision making involves DMs, options and selecting a final solution in a clear and transparent manner.
In real-world, most decision environments are complex demanding multiple perspectives from different people, thus decisions are often made via group decision making (GDM). A group’s decision is usually understood to be the reduction of different individual preferences, among objectives in a given set, to a single collective preference (Ghanbarpour et al. 2005). The question that arises is how best to aggregate the DM’s preference structures. Most MCDA methods have been extended to GDM as group decision support methods (GDSM) such as PROMETHEE GDSM (Macharis et al. 1998) and fuzzy multi-criteria GDSM (Lu et al. 2007). The GDSM methods provide DMs with the freedom of having their own criteria, weights, and preference structure. The DMs generate their own individual solutions which are merged in the end and analyzed collectively in the evaluation matrix table to establish a group decision result. During aggregation, each member is considered as a separate criterion and could be given a weight corresponding to his influence and/or importance in the group. However, it is usually advised to assign equal weights to all DMs to indicate that their different points of view are of equal importance (Macharis et al. 2010). Lu et al. (2007) suggests other GDM methods based on rules such as authority rule, majority rule, negative minority rule, ranking rule and consensus rule. The processes of GDM have been reported to improve by using the aforementioned rules with techniques such as the Delphi method (Ghanbarpour et al. 2005; Lu et al. 2007). The Delphi method aims at building an interdisciplinary consensus about an opinion, without necessarily having people to meet face to face, such as through surveys, questionnaires and emails. It is more suitable in emotional decision environments, where strong factions exist and when dealing with a pre-selected group of experts.
Some studies have also evaluated the alternatives using the group median weight value for criteria as representative of the group preference (Hokkanen and Salminen 1994; Kodikara 2008). They argue that the median agrees with the majority of the group. In their recent application of the multi-actor multi-criteria analysis (MAMCA) methodology, Macharis et al. (2010) used the average value of individual respondents as representative of the points of view of each stakeholder group in evaluating the impact of policy measures on challenges affecting the Flanders in Action Process. The advantage of using the median value is that it is not as sensitive to extreme values as the mean value (Keller and Warrack 2003).
2.2 Multi-criteria Methods
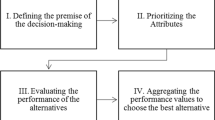
MCDA is a structured framework for analyzing decision problems characterized by complex multiple objectives and criteria. Guitouni and Martel (1998) described the MCDA methodology as a non-linear recursive process made up of four steps: (i) structuring the decision problem, (ii) articulating and modeling the preferences, (iii) aggregating the alternative evaluations (preferences) and (iv) making recommendations. It is generally used as an analytical tool but it can also be applied as an integrated framework by coupling with appropriate problem structuring methods. Mathematically, a typical MCDA problem can be modeled as follows (Brans and Mareschal 2005):
where A is a finite set of possible alternatives {a1,a2,…,ai,…, an} and {g1(.), g2(.),…, gj(.),…gk(.)} a set of evaluation criteria.
The basic data of a multi-criteria problem (Eq. 1) consists of an evaluation matrix (EM) shown in Table 1. The EM may contain a mix of ordinal and cardinal data. An MCDA model (Table 1) requires at least two non dominated decision options and discriminating criteria (Hajkowicz and Higgins 2008). Combining preference information (thresholds and weights) with performance data in the EM table provides the results.
There are various methods of MCDA. Lai et al. (2008) in their review paper on MCDA categorized these methods as follows:
-
1.
Elementary methods—are the simplest form of MCDA and are hardly applied in water resources management due to inadequacy of their simple preference models (e.g. weighted sum, conjunctive and disjunctive methods etc).
-
2.
Single synthesizing criterion approach—they reduce all criteria to a single criterion for comparison. They include multi-attribute utility theory (MAUT) methods, technique for order preference by similarity of ideal solution (TOPSIS), simple multi-attribute rating technique (SMART), Fuzzy (weighted sum and maxmin), AHP etc. These methods belong to the American school of thinking (Roy and Vanderpooten 1996).
-
3.
Outranking methods—use pairwise relations to compare actions, identifying preferences for one over the other and preference aggregation. They include novel approach to imprecise assessment and decision environments (NAIDE), ELECTRE, PROMETHEE, ORESTE, REGIME etc. These methods belong to the European school of thinking (Roy and Vanderpooten 1996).
-
4.
Goal or reference point method—identifies decision options that are closest to the ideal and furthest from the anti-deal. They include goal and compromise programming.
-
5.
Fuzzy set theory—the fuzzy set approach uses imprecise and uncertain information that provides a rigorous and flexible approach to complex resource management problems. Fuzzy set is used as a tool that can be applied to any MCDA methodologies rather than as a specific MCDA methodology itself.
MCDA methods are ideal for water resources management and planning and are usually preferred to other methods for various reasons including transparency and accountability to decision procedures, ability to resolve conflicts and use of formal axioms of decision theory to inform choice (Hajkowicz and Collins 2007). However, critics of MCDA say that the method is prone to manipulation, is very technocratic and provides a false sense of accuracy (Janssen 2001).
2.3 PROMETHEE II
The family of PROMETHEE methods were developed by Brans and Vincke (1985) to help a decision-maker rank partially (PROMETHEE I) or completely (PROMETHEE II) a finite number of options which are evaluated on a common set of non-commensurable multiple criteria. The method uses the outranking principle to rank options. The preference structure is based on pairwise comparisons. The method requires identification of different options and objectives of the decision problem. The objectives are expressed in form of evaluation criteria (EC) associated to the performance functions and weights. Once the actors have defined and weighted the EC and selected the preference thresholds, the next step is to complete the evaluation matrix (EM) table. Once these requisites are in place, then the PROMETHEE procedure can be applied (Brans and Mareschal 2005).
The preference structure of PROMETHEE is based on pairwise comparisons which is usually the deviation between evaluations of two options based on a particular criterion. The larger the deviation, the more the preference. The preference function (P j ) translates the difference between the evaluations (i.e. scores) obtained by the two option strategies (S n and S m ) in terms of a particular criterion, into a preference degree ranging from 0 to 1. This means that for each criterion the DM has in mind a function
and for which
And where g j is a non-decreasing function of the observed deviation (d) between f j (S n ) and f j (S m ). The pair { g j (.),P j (S n , S m )} is called the generalized criterion associated to criterion g j (.). Such generalised criterion has to be defined for each criterion. In PROMETHEE, there are six generalized criteria functions to choose from: the usual criterion (Type 1), U-shape criterion (Type 2), V-shape criterion (Type 3), level criterion (Type 4), V-shape with indifference criterion (Type 5), and Gaussian criterion (Type 6) (Brans and Mareschal 2005). Some functions require the definition of preference and indifference thresholds, p and q respectively. For working with ordinal scale criteria in PROMETHEE, De Keyser and Peeters (1996) recommend cardinalisation of evaluations in combination with the use of type I preference functions.
The principle is the construction and exploitation of the outranking preference index (π). The aggregated preference index over all criteria is defined as:
where, w j is a weight, measuring the relative importance allocated to criterion j. The weights are supposed to be normalized, so that
As each option faces (n–1) other options, the following positive (Ф+) and negative (Ф−) dominance flows express the dominating (strength) and the dominated (weakness) character of a strategy S n , respectively, over all the other strategies.
It is then possible to determine the overall score (net flow) for each option by calculating the balance of the dominance flow using Eq. 8.
The latter gives a quality measure of the strategy. The higher the net flow (Ф) value, the better the strategy (S n ). Accordingly, PROMETHEE II ranks the strategies in the order of their decreasing net flows. The associated D-Sight software allows sensitivity analysis to be carried out using additional tools such as “walking weights” and the decision stick. The graphical investigation of the conflicts between the criteria based on principal components analysis is enabled by means of the geometrical analysis for interactive assistance (GAIA) plane. This provides valuable visual insights into the trade-offs that need to be made by DMs.
The PROMETHEE method is easy to comprehend compared to other outranking methods and is widely applied in practice. A recent literature review identifies 217 scholarly papers based on the PROMETHEE method and about 90% were categorized as application papers solving real-life problems in water resources, environmental management, logistics and transport, forestry, chemistry, finance etc. (Behzadian et al. 2010). These methods are highly appreciated by end-users because they are easy to use, intuitive, auditable, and transparent with several graphical and interactive tools. Like all methods, PROMETHEE has some drawbacks that users must be aware of including lack of guidelines on how to determine criteria weights and it suffers from rank reversal on addition or removal of options particularly PROMETHEE II (De Keyser and Peeters 1996; Macharis et al. 2004; Mareschal et al. 2008). To avoid “black box” effects in PROMETHEE, Macharis et al. (2004) suggests use of a more manageable figure of seven EC and seven alternatives. However, this could be another weakness of the PROMETHEE by limiting complex MCDA problems to a few options and criteria. This weakness could be improved by hybrid methods that combine two or more methods for operational synergies such as PROMETHEE-AHP (Macharis et al. 2004), Fuzzy-AHP (Wang et al. 2011), and fuzzy multi-objective/criteria decision-making methods (Lu et al. 2007).
3 The Proposed Decision Framework
In this section we describe an integrated MCDA group decision-aiding framework for SWLMP in water utilities. The proposed decision-aiding framework is shown in Fig. 1.
Integrative framework is the problem structuring method which provides guidance for stakeholder engagement, criteria selection and alternative development (Lai et al. 2008).The method aids water utility DMs in selecting and prioritizing water loss reduction strategy options. The framework explicitly includes sustainability dimensions of WLM such as economic, technical, environmental and social. The prioritizing is enabled by PROMETHE II outranking method of the MCDA family. The framework method comprises of seven phases: (1) problem structuring phase; (2) design phase; (3) choice phase; (4) group decision phase; (5) testing phase; (6) implementation phase; and (7) monitoring phase. The application of the seven-step framework methodology in formulating water loss reduction priorities is briefly described.
3.1 Problem Structuring Phase
The aim at this stage is to come up with a clear and concise problem statement. To be able to do so requires identifying root causes, understanding the organizational context information, managerial assumptions and any related initial and desired conditions. Identification of actors and their participation in the decision process starts at this stage. Actors often referred to as stakeholders are people who have an interest, financial or otherwise, in the consequences of any decision taken (Macharis et al. 2010). In this study, actors refer to people other than the analyst involved in the decision process (DMs, experts and stakeholders). The analyst (in this case researcher) is responsible for the decision-aid process as a facilitator ensuring that the responsibility for the decision and its outcomes is of the DMs. The ultimate goal of this step is to come up with a clear problem statement agreed upon by all actors.
3.2 Design Phase
In this phase, the following decision tasks are accomplished:
Establishment of Objectives and Goals
Good decisions need clear objectives and goals. Goals are broad statements of intent and desirable long-term plans. The goals and objectives are derived from the utility’s vision and mission statements. The goals and objectives should include sustainability dimensions such as economic, environmental and social aspects. In practice, objectives are often conflicting and may be realized over a short, medium and long-term period.
Identification of Options or Alternatives
At this stage options that may contribute to the achievement of the objectives are identified. Water loss reduction options are selected after carrying out a water balance/audit. The water balance reveals the nature and magnitude of the decision problem and provides guidance on which strategy options to adopt. The strategy options can then be selected from a rich menu developed by the International Water Association (IWA) and the American Water Works Association (AWWA) based on many years of research (Alegre et al. 2006; AWWA 2009; Fanner et al. 2007). Each option should be clearly described as to how it will aid in solving the decision problem and how each differs from others.
Identification of Evaluation Criteria (EC)
In this step, criteria for evaluating performance of options are defined. The choice of the EC is based on the established objectives and the purpose of options considered. Criteria should be able to discriminate among options, complete, non-redundant, operational, measurable and minimal for sound decision making (Georgopoulou et al. 1998). Criteria should not be too many or too few. This means the selected criteria should be meaningful, relevant and completely cover all aspects of the objectives. Although large infrastructure projects may require over a hundred criteria, a more manageable typical range is six to twenty (UKDCLG 2009). Generally, actors should be engaged in developing criteria but in most cases analysts do develop the criteria to avoid influences from powerful DMs on other actors and when actors are not technically competent to generate criteria. The developed criteria should be able to measure the sustainability dimensions and are usually categorized in a similar manner as options into economic, environmental, technical and social aspects—usually in the AHP hierarchical structure.
Model Formulation
This step basically involves building the evaluation matrix (EM). Each entry in the EM represents the evaluation of an option according to its performance based on a criterion. Scoring of options is a technical activity, performed by a competent team especially when real outcomes of the decision options are often uncertain (Flug et al. 2000). The team may be composed of the analyst and experts on the subject matter. It requires experience and at times literature research especially in planning studies where outcomes are hard to predict with certainty. The EM could include quantitative (cardinal) data, qualitative (ordinal) data or both depending on the context information as most MCDA methods can work with both data. It has been urged that the presence of qualitative information in real-world problems involving environment, socio-economic and physical planning aspects, is a rule rather than an exception (Munda et al. 1994). Working with qualitative data usually requires scaling techniques of manipulating linguistic terms into interval scales. Linguistic terms reflect uncertainty, inaccuracy and fuzziness in the decision making process. Fuzzy sets coupled with MCDA could be explored to handle complex water resources planning problems—fuzzy multi-criteria methods (Lu et al. 2007).
Preference Elicitation
In this step, weights and preference functions for the EC and objectives reflecting their relative importance are defined by the actors. The actors must assign preference functions to each criterion using appropriate tools such as the generalized criteria functions in PROMETHEE (Brans and Mareschal 2005).
Weighting of criteria is subjective and has direct influence on the results of prioritizing strategy options. It is therefore critical that criteria weights are determined rationally and truthfully. Generally, there are two methods for weighting of criteria: the equal weights and the rank-order method. The equal weights method (wi = 1/n, i = 1, 2,…, n) is the most widely applied due to its simplicity. It requires minimal knowledge of the DM’s priorities and minimal input from the DM. The problem with this method is that it assumes equal importance for all criteria which is unrealistic and often not the case in practice. The rank-order method (w1 ≥ w2 ≥ … ≥ wn ≥ 0 and sum of all criteria weights must equal to one).
Wang et al. (2009), classifies the rank-order method into three categories: subjective weighting method, objective weighting method and combination weighting method. The subjective methods determine criteria weights based on the preferences of the DMs. They explain the elicitation process more clearly and are the most used for MCDA in water resources management. They include SMART, AHP, SIMOS and the Delphi method. The objective weights are obtained by mathematical methods based on the analysis of initial data. The objective weight procedure is not very clear and includes methods such as least mean square (LMS), minmax deviation, entropy, TOPSIS and multi-objective optimization. The combination or optimal weighting methods are a hybrid of methods that include multiplication and additive synthesis.
In this study, we apply the SIMOS procedure for weighting criteria (Figueira and Roy 2002). The main innovation of this procedure is relating a “playing card” to each criterion. The procedure can be summarized into four main steps as follows:
-
1.
Each DM is given n colored cards (or n criteria). Each card has the criterion name and its objective inscribed on it and objective of the criterion. A number of white cards (blank cards) are also provided.
-
2.
The DM is then asked to rank the cards from the least important to the most important. If certain criteria are perceived to be of equal importance (same weighting), the cards are grouped together (same rank position).
-
3.
The DMs are asked to insert the white cards between two successively ranked colored cards (or group of cards) in order to express their strong preference between criteria. The number of white cards is proportional to the difference between the importance of the considered criteria.
-
4.
The DM is finally asked to answer the question “how many times more important the first ranked criterion (or group of criteria) is, relative to the last ranked criterion (or group of criteria)?”
The ranking of criteria are then transformed using an appropriate algorithm that attributes a numerical value to the weights of each criterion (Figueira and Roy 2002). The main advantage of the SIMOS weighting method lies in its simplicity but yet intuitive procedure. The fact that the DM handles the cards in order to rank them, inserting white ones, allows indirect understanding of the aim of the procedure. In addition, DMs express the relative importance of criteria using ordinal preferences, allowing determining indirectly numerical values for weights. The respondents often find it easier to express their weightings on an ordinal scale rather than on a numerical scale. This procedure has been applied by other researchers in Greece (Georgopoulou et al. 1998), Austria (Madlener et al. 2007) and Australia (Kodikara 2008) and was found to be very well accepted by DMs.
3.2.1 Selecting the Decision-making Method
There are many MCDA methods for solving a decision problem. Munda et al. (1994) categorizes them as: (i) utility based models, (ii) outranking methods, (iii) the lexicographic model, and (iv) ideal point approaches and aspiration level models. Selecting an appropriate MCDA method based on criteria in literature and observing present institutional constraints, the selection of MCDA techniques is itself a multi-criteria problem (Abrishamchi et al. 2005). The guidelines on how to chose an appropriate MCDA method can be found in Guitouni and Martel (1998). Generally, selecting an appropriate MCDA method depends on the decision problem at hand, expertise, experience and the preference of the analyst or DM. Preferably, the simpler method should be chosen for the decision analysis.
There is no single MCDA method that can claim to be a superior method for all decision making problems. Different researchers have provided different views on this issue. Guitouni and Martel (1998) argue that different methods will yield different recommendations while Hajkowicz and Higgins (2008) argue that the ranking of decision options is unlikely to change markedly by using a different MCDA method provided ordinal and cardinal data are handled appropriately.
3.3 The Choice Phase
At this stage, the EM is complete with performance data of each option against each criterion. The options are then evaluated against objectives using the defined criteria, weightings of criteria, preference functions and thresholds by running the selected MCDA model. The results may be the ranking of options or a selected subset of the most promising options depending on the decision problem. The evaluation is usually of technical nature and must be executed by the analyst or any other experienced expert. Because the assignment of criteria weights is subjective and subject to errors during elicitation and in the aggregation process, it is important to verify the stability of the results by performing a sensitivity analysis to verify whether the result changes when the weights are modified. The results obtained in this phase must be recommended by the analyst to the actors for a final group decision.
3.4 Group Decision Phase
This stage is concerned with conflict resolution and reaching consensus. The analyst presents the results to the group with aid of visualization tools for clarity. Individual actor results as well as group decision results are presented including sensitivity analysis. In case of disagreements among the actors, the group could be asked to assign new weights to criteria and the evaluation repeated. If disagreements still arise, then new options and criteria could be selected and the evaluation repeated. Generally, the whole process is iterative and it is up to the analyst to determine the termination criteria in case of continued disagreements.
3.5 Testing Phase
Once the decision is made, pilot testing follows to validate whether the chosen option truly solves the identified decision problem based on real field measurements. This phase is very important in planning studies particularly when new strategy options have not been applied before in the organization and the MCDA results are based on uncertain performance predictions. In addition, implementation of water loss reduction strategies is very costly and must be based on accurate and reliable data. Depending on the findings, the earlier results of prioritized strategies could change before implementation. Once the solution is validated, it is recommended to DMs for consideration and onward implementation.
3.6 Implementation Phase
This final stage is to implement the final decision via well-scheduled action plans and available budgets. The implementation of prioritized strategy options could change along the way as more insight into the impact of different options on different components of water losses become available through the water balance. This provides flexibility during implementation. In practice, there is always some degree of overlap, where a mixture of strategies is applied concurrently to maximize the level of water loss reductions and cost optimization. For example pressure management could first be done at a macro level and later at a micro level after network zoning and District Meter Area (DMA) establishment.
3.7 Monitoring Phase
The final monitoring phase provides a continuous feedback loop on performance of each strategy based on actual field measurements and data collection to update the decision-making process. The whole MCDA framework methodology is actually iterative (Fig. 1) and should be considered as an exercise, which can always be revised and refined in the light of better data and information to support design of new options.
4 Application of the Integrated Framework Methodology
The methodology was applied to the NWSC’s Kampala Water Distribution System (KWDS) in Uganda’s capital city of Kampala. The KWDS service area encompasses an area of about 350 km2 with an estimated population of 1.5 million and 73% water coverage. Water supply has not kept pace with population growth with consequences of irregular supply in most parts of the city. The development of the KWDS commenced in the year 1928 and water production has since been gradually increasing up to the current average level of about 148,000 m3/day, serving about 150,000 service connections. The condition of the network has deteriorated over the years, due to poor operating practices and inadequate strategic asset management (Mutikanga et al. 2009). The major customer complaints are related to supply interruptions and low pressure as a result of frequent mains bursts and service line leakages. Apparent losses are also high with rampant illegal use of water, high metering inaccuracies and meter failure. The average number of failures reported during the year 2010 was 1175 breaks/100 km/year. This is rather very high compared to figures reported in the Netherlands of 8/100 km/year (Vloerbergh and Blokker 2009). Pipeline systems having an average annual pipe break ratio per 100 km of less than 40 are considered to be in an acceptable state (Pelletier et al. 2003). Non-revenue water averages about 43% of system input volume or 22 million m3 per year (NWSC 2009b).
4.1 Problem Formulation for the KWDS
Based on the case study information the agreed upon problem statement was documented as “identify and prioritize strategies to reduce water losses in KWDS”.
4.1.1 Requirements
The problem definition dictated the following key requirements for the decision problem:
-
1.
Strategy options should address both real and apparent losses.
-
2.
Cost of implementing a set of selected strategies should not exceed €3.6 million per year.
-
3.
Strategies should lead to a water loss reduction of at least 12 million m3 per year.
-
4.
Implementation period to achieve water loss reduction target should not exceed 10 years.
Actors
The actors were proposed by the analyst and approved by the General Manger of KWDS. They were all selected from within the utility apart from one actor. Three actor groups were identified to represent utility DMs, water users and environmentalists. In total eight DMs were selected for the preference elicitation process. In this study, actors are referred to as the eight DMs (DM1 to DM8). The senior manager in-charge of the Kampala Finance and Accounts Department together with three senior managers from the Kampala Water Supply Department represented utility interests (DM1, DM2, DM3, and DM4). One Branch Manager from the Commercial and Customer Care Department together with the GTZ Technical Adviser to NWSC represented customer’s interests (DM5, DM6). The NWSC’s Water Quality Manager and the Kampala Water Production Manager represented the environmental interests (DM7 and DM8). The environmental group was a hypothetical group due to time constraints to mobilize real environmental officials from relevant government departments.
Establishing Goals and Objectives
The goals and objectives of the study were derived from the utility’s mission of “providing safe and reliable water services to customers at a fair price and in an environmentally friendly manner”. The goal of this study was to reduce water losses in the KWDS. The goals were viewed in the broader national water sector policy of utility financial viability, environmental protection, public health protection, technically acceptable level of service and socio-economic aspects.
In light of the utility’s mission and problem statement, five main objectives were established:
-
1.
Maximize revenues and minimize costs.
-
2.
Maximize water savings.
-
3.
Maximize good quality water.
-
4.
Maximize water supply reliability.
-
5.
Maximize affordability of water.
Generating Options
In order to generate appropriate water loss reduction strategy options, a water balance was established by the utility water loss unit using the IWA/AWWA water balance methodology and the proposed methodology for assessing the apparent loss component (Mutikanga et al. 2010). The water balance for KWDS is shown in Table 2. Tabesh et al. (2009) applied the IWA/AWWA water balance methodology in their model for evaluating the WDS for an Iranian town. Although the methodology proposed by Tabesh et al. (2009) to evaluate water losses concurs with the IWA/AWWA water balance methodology, it had the following shortcomings:
-
In assessing legitimate night use during the hour of minimum night flow (MNF) they used default values (6% active population at night with 10 L/head/h) suggested by McKenzie (1999) for South African Cities, which are not likely to be valid for Iranian towns;
-
They introduced new terminologies of “operational error” and “management error” in assessment of apparent losses that are not part of the IWA/AWWA water balance methodology and are likely to cause confusion;
-
In assessing meter inaccuracies they did not consider user demand profiles yet meter accuracy is a function of water used at different flow rates (Arregui et al. 2011). In addition, they did not indicate which meter testing standards were used as different standards are likely to produce different meter accuracy results.
Based on the KWDS water balance (Table 2), the following seven strategy options were proposed by the analyst and accepted by the DMs.
-
1.
Meter replacement (S1).
-
2.
Illegal use control (S2).
-
3.
Improved speed and quality of repairs (S3).
-
4.
Selective mains and service line replacements (S4).
-
5.
Network zoning and establishing District Meter Areas (DMAs) (S5).
-
6.
Pressure management (S6).
-
7.
Active leakage control (S7).
Determining Evaluation Criteria
The seven EC shown in Table 3 were generated through a brainstorming session and agreed upon by all DMs as suitable for performance evaluation of the strategy options with aim of realizing the set objectives and goals.
Predicting Performance
The evaluation matrix (EM) for the case study is shown in Table 4. Each entry in the EM represents the evaluation of an option according to its performance based on a criterion. Scoring of options was based on experience and literature research as real outcomes of the decision options will be realized in future. In addition there was lack of reliable quantitative data for some options that are currently in use due to institutional challenges coupled with database limitations. To ensure accurate and objective evaluations, the evaluation matrix was completed by a team of the utility personnel in the water loss control unit who are experts on this subject matter. Since the criteria were qualitative in nature, the strategy options were evaluated using criteria measured on a Likert Scale ranging from 1 (poor performance) to 5 (very good performance) as shown in Table 5. This being an interval scale, the intervals between statements are meaningful but scale scores have no meaning.
Selecting the Multi-criteria Method
The MCDA method used was the PROMETHEE II and its D-Sight software tool.
Preference Modeling
The preference elicitation process in the case study comprised of an interviewer-assisted questionnaire survey to derive preference functions (PFs) and weights for the evaluation criteria (EC) and objectives. A survey was conducted on eight DMs and weights were assigned for each criterion and objective to reflect their relative importance to the decision. As the criteria were qualitative, the PF applied in this study was the type I (usual criterion) of the six generalized criteria as defined by the authors of the PROMETHEE method (Brans and Mareschal 2005). The preference thresholds can be chosen by means of the D-Sight software. In this way, a lot of flexibility is provided to represent the preferences of DMs.
Determining Criteria Weights
The weights were derived using the “Revised Simos” Procedure (Figueira and Roy 2002) and the criteria weight values are presented in Table 6. For the group decision, the median was considered as the representative value since it agrees with the majority view of the group.
4.1.2 Evaluating Options
The water loss reduction strategy options were evaluated and prioritized with the D-Sight Software tool, which uses the PROMETHEE algorithm. The PROMETHEE II individual decision and group decision rankings are shown in Tables 7 and 8. The prioritized strategies for the group decision are graphically depicted in Fig. 2. The evaluation of options was done by the analyst as it is a task of technical nature that needs expertise.
Sensitivity Analysis
The sensitivity of the results was analyzed using the capabilities of the D-Sight Software in-built tools. The results are presented in Table 9. The stability intervals indicate the range in which the weight of a criterion can be changed without affecting the ranking. For example, the technical criterion with an initial normalized weight of 30.4% may be weighted between 19.7% and 44.7% (stability interval of 25%) without affecting the ranking, provided all other factors remain constant. The sensitivity of the ranking can be considered as marginal with respect to the criteria weight values assigned.
Group Decision-making Phase
The PROMETHEE and GAIA plane provide both descriptive and prescriptive tools and were exploited during a group meeting organized to discuss the PROMETHEE II ranking of options, sensitivity of weighting criteria and agree on a compromise solution. During the discussions, most DMs were surprised that the current strategies (S1 and S2) being implemented by the utility were ranked among the last. Although the DMs were surprised by the outcome, consensus was reached that the global prioritized ranking was a group satisfactory solution that fully represented their preferences and met the set objectives and goals. Reaching consensus was rather easy as there was no dispute on the first two best options (S4 and S6) and minor disagreements on the third ranked option (S3) and last option (S2) as shown in Table 6. As a way forward, the DMs also unanimously agreed that since scoring of options was based on ordinal data and literature research, a testing phase (Fig. 1) was warranted to validate and quantify more precisely the impact of each strategy option before the implementation phase. This will provide information required to re-construct Fig. 2 on scale. This pilot testing approach has been used to justify implementation of pressure and leakage management strategies on the Gold Coast, Australia (Girard and Stewart 2007).
5 Results Discussion
The PROMETHEE net flows of strategy options S1 to S7 are as shown in Table 8. The strategy option S4 (mains and service lines replacement) is the best and strategy option S2 (illegal use control) is the least preferred. Whereas option S2 is the most preferred in terms of investment cost (Table 4), it is the least favorable in terms of performance. All DMs ranked option S4 as the best strategy (Table 7) and six DMs out of eight, ranked S2 last. This could be explained by the criteria weights in Table 6, where the most important criterion was water supply reliability. During the group discussion, the consensus was that reliable water supply must first be available before it is stolen and measured accurately. The current strategies (S1 and S2) being applied by NWSC-Kampala, are valid based on the traditional cost-benefit analysis (CBA) method rather than on the MCDA method that includes sustainability measures and incorporate other stakeholder views such as customers.
From Table 6, the most important criteria according to the DMs preferences are supply reliability, water savings and water quality respectively. According to Christodoulou et al. (2010a), “the driving forces behind pipe-replacement capital improvement projects have primarily been the mandate to safeguard the health of urban populations, the need to increase the reliability of the pipe networks and the service provided to people, as well as socioeconomic factors in relation to the cost of operations and maintenance of pipe networks”. This explanation coupled with the DMs’ preferences on EC clearly justifies why the most preferred options were S4 and S6 (pressure management) respectively. Since PROMETHEE II is a decision support tool, one could probably argue that since pressure management (PM) is less costly compared to option S4, it could be the best alternative, should there be budget constraints during implementation. Although PM is hardly applied in most utilities of the developing countries, it is now widely acknowledged that PM is the most cost effective and efficient tool for leakage reduction once pipes have been laid (Araujo et al. 2006; Nazif et al. 2010). Recent studies and research have shown that the general benefits of PM are three fold: reduction of background leakage, reduction in main break frequency and reduction of leakage flow rate (Charalambous 2008; Girard and Stewart 2007; Lambert and Thornton 2011).
The challenge likely to be faced by utility managers in implementing the best strategy option S4, is the question of which pipes to replace, when and where? The motivation to provide answers to this question has recently attracted a lot of research (Alvisi and Franchini 2009; Christodoulou et al. 2008; Christodoulou and Deligianni 2010). Although, the multi-objective procedure for optimal pipeline rehabilitation and leakage detection scheduling proposed by Alvisi and Franchini (2009) is a valuable tool, its application in developing countries with poor financial record keeping and no clear separation of proactive and reactive budget allocations for WDSs is doubtful. Christodoulou et al. (2008) and Christodoulou and Deligianni (2010) have developed a neurofuzzy decision-support system (DSS) that integrates risk analysis and asset management based on application of analytical and numerical methods, geographic information systems (GIS) and artificial neural networks (ANN). The DSS predicts risk of pipe failure and prioritizes which pipes to replace and where using GIS techniques to provide better visualization. Whereas the DSS has been successfully evaluated using 5-year period data sets for New York city (USA) and Limassol city (Cyprus), its application in developing countries is likely to be limited by the huge amount of reliable data required for training and re-training of the ANNs.
The third ranked strategy of improved speed and quality of repairs (S3) is more of a reactive strategy after failure has occurred. Although the first two ranked strategies are very good they don’t actually repair leaks and main breaks in practice. Strategy S3 is the only one that repairs actual failures and will always be used to supplement other strategies. The duration of real losses can be conceptually divided into awareness, location and repair times (AWWA 2009). The run time of a leak is a major factor contributing to the overall real loss volume and early detection and repair is essential. Online artificial intelligence systems have been reported to be effective tools for early detection of bursts according to a recent study carried out in the UK (Mounce et al. 2010). Improved supervision at the operational level coupled with online detection techniques offers hope for minimizing leakage in Kampala city among other options.
The fourth ranked strategy of active leakage control (S7) emerged low probably due to the fact that there is no sense in putting too much effort in detecting invisible underground leaks in a city like Kampala where the utility is overwhelmed by visible leaks everywhere. However, this is a very valuable strategy that enables utilities to address leakage proactively, in order to attain economic and sustainable levels of leakage. The sixth ranked strategy of network zoning and DMA establishment (S4) was considered of less importance probably because it is a complementary strategy to other strategies that allow leakage managers to divide the network into small discrete zones that are easy for monitoring flow and pressure measurements, to assess and quantify leakage and to enable leak detection. DMAs also require costly on-line hydraulic measurements (real-time) using wireless sensors, telemetry (e.g. SCADA) and other communication infrastructure for effective leakage management (Christodoulou et al. 2010b). Most DMs were not aware of these state-of-the-art techniques and underrated the usefulness of DMAs in WLM.
Although not determined scientifically but based on many years of experience, the general guidance provided to utilities in selecting the order of implementing real loss reduction strategies (Trow and Farley 2004), is in agreement with the developed prioritized water loss reduction strategy framework for Kampala city (Fig. 2). However, Fanner et al. (2007) suggest that mains replacement should always be carried out last as they require high investment costs. The decision on when to replace pipes should be based on local conditions, consideration of sustainability dimensions and preference of all stakeholders. According to Christodoulou et al. (2010a), proactive replacement of small-diameter pipes takes precedence over replacement of large diameter pipes. This seems to make much sense especially for Kampala city where most leaks occur on service lines and quick gains in terms of water savings are likely to be realized by prioritizing replacement of customer service lines and small distribution pipes.
5.1 Challenges and Lessons Learned
The main challenges and lessons learned during application of the SWLMP multi-criteria decision-aiding framework were as follows:
-
1.
The PROMETHEE MCDA outranking method is a powerful tool for solving decision problems under uncertain environment. It is very helpful in handling trade-offs between multiple criteria and conflicting decisions and is likely to break barriers hindering sustainable water loss reduction in utilities of the developing countries.
-
2.
The decision process exposed information gaps and has compelled the utility to establish a knowledge base to support future decision-making processes.
-
3.
Although the PROMETHEE method is a powerful tool, it does not provide specific guidelines for determining criteria weights and PROMETHEE II is likely to suffer from rank reversals (Macharis et al. 2004). In addition, defining the generalized criteria was not all that trivial for most participants.
-
4.
The foundation of the decision-making process is the problem structuring and design phases and their efficient execution is decisive for success.
-
5.
The D-Sight software is simple to use and its GAIA graphical descriptive interfaces were very valuable for the interactive group discussions.
-
6.
Public participation is not institutionalized in the utility which does not suit the MCDA consensus seeking-approach. This denies customers and other stakeholders chance to influence the decision process. For example road users are often inconvenienced whenever there is a pipe failure and their views could probably have added more social costs criteria that could have probably reversed the ranking.
-
7.
Although participation of more stakeholders makes the decision processes more credible, the process can be resource consuming if not well designed and carefully planned. In addition mobilizing DMs for brainstorming sessions away from their routine work was always a difficult task.
-
8.
The major drawback of the MCDA method was reducing each option to a single abstract value during data aggregation. Trade-offs between good performance on one criterion and poor performance on some other criterion often results into loss of important information. For example poor performance on water quality could be compensated with good performance on investment cost. The underlying value judgments of the aggregation procedure are therefore debatable and probably not acceptable from the public health and regulatory point of view. It is therefore critical that an appropriate non-compensatory aggregation method is selected for solving such decision problems.
6 Conclusions
This study presents an integrated strategic water loss management planning framework with emphasis on structuring the decision problem including careful selection of criteria and decision options. The proposed integrated MCDA framework explicitly considers sustainability dimensions of economic, environmental, technical and social objectives. The framework is capable of handling qualitative information and as such is useful for water loss reduction planning where numerical data is often lacking and imprecise. The framework includes the PROMETHEE outranking method with its D-Sight software tool in solving the decision problem.
The multi-criteria decision-aiding framework was illustrated on a real-developing world case study clearly highlighting the step-by-step group decision-making process in practice. For Kampala city, the prioritized options for water loss reduction were mains and service lines replacement followed by pressure management and improved speed and quality of repairs. The results show that the most preferred options are those that enhance water supply reliability, public health and water conservation measures. In addition, the results demonstrate that the cheapest option is not necessarily the best when multiple-criteria are considered in an explicit way. The D-Sight software proved to be a valuable tool for handling the complex water loss decision planning problem.
It can be concluded that the developed multi-criteria decision-aiding framework (SWLMP) is a valuable tool envisaged to help water utilities in evaluating and prioritizing water loss reduction strategies in urban water distribution systems particularly in the developing countries where the problem is more prominent.
References
Abrishamchi A, Ebrahimian A, Tajrishi M, Marino MA (2005) Case study: application of multicriteria decision making to urban water supply. J Water Resour Plann Manag 131(4):326–335
Afshar A, Marino MA, Saadatpour M, Afshar A (2011) Fuzzy TOPSIS multicriteria decision analysis applied to Karun reservoir system. Water Resour Manag 25:545–563
Alegre H, Baptista JM, Cabrera EJ, Cubillo F, Hirner W, Merkel W, Parena R (2006) Performance indicators for water supply services, IWA Manual of Best Practice, IWA Publishing, 2nd edn
Alvisi S, Franchini M (2009) Multiobjective optimization of rehabilitation and leakage detection scheduling in water distribution systems. J Water Resour Plann Manag 135(6):426–439
Araujo LS, Ramos H, Coelho ST (2006) Pressure control for leakage minimisation in water distribution systems management. Water Resources Management 20(1):133–149
Arregui FJ, Cobacho R, Cabrera E Jr, Espert V (2011) Graphical method to calculate the optimum replacement period for water meters. J Water Resour Plann Manag 137(1):143–146
AWWA (2009) Water audits and loss control programs: AWWA manual M36., American Water Works Association, Denver, USA
Behzadian M, Kazemzadeh RB, Albadvi A, Aghdasi M (2010) PROMETHEE: a comprehensive literature review on methodologies and applications. Eur J Oper Res 200:198–215
Bouchard C, Abi-zeid I, Beauchamp N, Lamontagne L, Desrosiers J (2010) Multicriteria decision analysis for the selection of a small drinking water system. J Water Supply: Res Technol-AQUA 59(4):230–242
Brans JP, Mareschal B (2005) PROMETHEE methods. In: Figueira J, Greco S, Ehrgott M (eds) Multiple criteria decision analysis: state of the art surveys. Springer, New York, pp 163–189
Brans JP, Vincke P (1985) A preference ranking organisation method: (The PROMETHEE method for multiple criteria decision-making). Manag Sci 31(6):647–656
Charalambous B (2008) Use of district metered areas coupled with pressure optimization to reduce leakage. Water Sci Technol: Water Supply 8(1):57–62
Christodoulou S, Deligianni A (2010) A neurofuzzy decision framework for the management of water distribution networks. Water Resour Manag 24:139–156
Christodoulou S, Charalambous C, Adamou A (2008) Rehabilitation and maintenance of water distribution network assets. Water Sci Technol: Water Supply 8(2):231–236
Christodoulou S, Agathokleous A, Charalambous B, Adamou A (2010a) Proactive risk-based integrity assessment of water distribution networks. Water Resour Manag 24:3715–3730
Christodoulou S, Agathokleous A, Kounoudes A, Mills M (2010b) Wireless sensor networks for water loss detection. European Water 30:41–48
De Keyser W, Peeters P (1996) A note on the use of PROMETHEE multicriteria methods. Eur J Oper Res 89:457–461
Fanner P, Thornton J, Liemberger R, Sturm R (2007) Evaluating water loss and planning loss reduction strategies, Awwa Research Foundation, AWWA;, Denver, USA; IWA, London, UK
Figueira J, Roy B (2002) Determining weights of criteria in the ELECTRE type methods with a revised Simos’ procedure. Eur J Oper Res 139:317–326
Figueira J, Greco S, Ehrgott M (2005) Multicriteria decision analysis: state of the art surveys. Springer, New York
Flug M, Seitz HL, Scott JF (2000) Multicriteria decision analysis applied to Glen Canyon Dam. J Water Resour Plann Manag 126(5):270–276
Georgopoulou E, Sarafidis Y, Diakoulaki D (1998) Design and implementation of a group DSS for sustaining renewable energies exploitation. Eur J Oper Res 109:483–500
Ghanbarpour MR, Hipel KW, Abbaspour KC (2005) Prioritizing long-term watershed management strategies using group decision analysis. Water Resour Dev 21(2):297–309
Girard M, Stewart RA (2007) Implementation of pressure and leakage management strategies on the Gold Coast, Australia: case study. J Water Resour Plann Manag 133:210
Guitouni A, Martel JM (1998) Tentative guidelines to help choosing an appropriate MCDA method. Eur J Oper Res 109:501–521
Hajkowicz S, Collins K (2007) A review of multiple criteria analysis for water resource planning and management. Water Resour Manag 21:1553–1566
Hajkowicz S, Higgins A (2008) A comparison of multiple criteria analysis techniques for water resources management. Eur J Oper Res 184:255–265
Harris R (1998) Introduction to decision making. Virtual Salt. http://www.virtualsalt.com/crebook.htm. (accessed15 February 2011)
Hokkanen J, Salminen P (1994) The choice of a solid waste management system using multicriteria decision analysis by using the ELECTRE III decision-aid method In: Paruccini M (ed) Applying MCDA for decision to environmental management. Kluwer, Dordretcht, Netherlands
Janssen R (2001) On the use of multi-criteria analysis in environmental impact assessment in The Netherlands. J Multicrit Decis Anal 10(2):101–109
Keller G, Warrack B (2003) Statistics for management and economics. Thomson, USA
Kingdom B, Liemberger R, Marin P (2006) The challenge of reducing non-revenue water (NRW) in developing countries. The World Bank, Washington, DC
Kodikara PN (2008) Multi-objective optimal operation of urban water supply systems, PhD thesis, Victoria University, Australia
Lai E, Lundie S, Ashbolt NJ (2008) Review of multi-criteria decision-aid for integrated sustainability assessment of urban water systems. Urban Water J 5(4):315–327
Lambert A, Thornton J (2011) The relationships between pressure and bursts—a “state-of-the-art” update. IWA Magazine Water 21:37–38
Lu J, Zhang G, Ruan D, Wu F (2007) Multi-objective group decision making: methods, software and applications with fuzzy set techniques. Imperial College, London
Lu HW, Huang GH, Zeng GM, Maqsood I, He L (2008) An inexact two-stage fuzzy-stochastic programming model for water resources management. Water Resour Manag 22:991–1016
Macharis C, Brans JP, Mareschal B (1998) The GDSS promethee procedure. J Decis Syst 7:283–307
Macharis C, Springael J, De Brucker K, Verbeke A (2004) PROMETHEE and AHP: The design of operational synergies in multicriteria analysis. Strengthening PROMETHEE with ideas of AHP. Eur J Oper Res 153:307–317
Macharis C, De Witte A, Turcksin L (2010) The Multi-Actor Multi-Criteria Analysis (MAMCA) application in the Flemish long-term decision making process on mobility and logistics. Transport Policy 17:303–311
Madlener R, Kowalski K, Stagl S (2007) New ways for the integrated appraisal of national energy scenarios: the case of renewable energy use in Austria. Energy Policy 35:6060–6074
Malmqvist P-A, Heinicke G, Karrman E, Stenstrom TA, Svensson G (2006) Urban water in context. In: Malmqvist, Heinicke, Karrman, Stenstrom, and Svensson (eds) Strategic planning of sustainable urban water management. IWA Publishing, London
Mareschal B, De Smet Y, Nemery P (2008) Rank reversal in the PROMETHEE II method: some new results. Proceedings of the 2008 IEEE IEEM, Singapore, pp 959–963
McKenzie RS (1999) SANFLOW user guide. South African Water Research Commission, WRC. Report TT 109/99
Morais DC, Almeida AT (2007) Group decision making for leakage management strategy of water network. Resour Conserv Recycl 52:441–458
Mounce SR, Boxall JB, Machell J (2010) Development and verification of an online artificial intelligence system for detection of bursts and other abnormal flows. J Water Resour Plann Manag 136(3):309–318
Mugabi J, Kayaga S, Njiru C (2007) Strategic planning for water utilities in developing countries. Utilities Policy 15:1–8
Munda G, Nijkamp P, Rietveld P (1994) Qualitative multicriteria evaluation for environmental management. Ecol Econ 10:97–112
Mutikanga HE, Sharma S, Vairavamoorthy K (2009) Water loss management in developing countries: challenges and prospects. Journal AWWA 101(12):57–68
Mutikanga HE, Sharma SK, Vairavamoorthy K (2010) Assessment of apparent losses in urban water systems. Water and Environment Journal. doi:10.1111/j.1747-6593.2010.00225.x
NAMS (2004) Optimised decision making guidelines. NZ National Asset Management Steering Group, Auckland, New Zealand
Nazif S, Karamouz M, Tabesh M, Moridi A (2010) Pressure management model for urban water distribution networks. Water Resour Manag 24:437–458
NWSC (2009a) Corporate Plan (2009–2012): “maximizing the cash operating margin”. National Water and Sewerage Corporation, Kampala
NWSC (2009b) NWSC annual performance report: financial year 2008–2009. Kampala
Pelletier G, Mailhot A, Villeneuve JP (2003) Modeling water pipe breaks-three case studies. J Water Resour Plann Manag 129(2):115–123
Roy B, Vanderpooten (1996) The european school of MCDA: emergency, basic features and current works. J Multicrit Decis Anal 5:22–38
Silva VBS, Morais DC, Almeida AT (2010) A multicriteria group decision model to support watershed committees in Brazil. Water Resour Manag 24:4075–4091
Simonovic SP (2009) Managing water resources: methods and tools for a systems approach. UNESCO Publishing, Paris
Tabesh M, Asadiyani Y, Burrows R (2009) An integrated model to evaluate losses in water distribution systems. Water Resour Manag 23(3):477–492
Trow S, Farley M (2004) Developing a strategy for leakage management in water distribution systems. Water Sci Technol: Water Supply 4(3):149–168
UKDCLG (2009) Multi-criteria analysis: a manual. UK Department of Communities and Local Government (UKDCLG), London. ISBN 978-1-4098-1023-0
Vloerbergh IN, Blokker EJM (2009) Failure data analysis—a Dutch case study. In: Alegre H, d. Almeida M (eds) Strategic asset management of water supply and wastewater infrastructures. IWA Publishing, London
Wang J-J, Jing Y-Y, Zhang C-F, Zhao J-H (2009) Review on multi-criteria decision analysis aid in sustainable energy decision-making. Renew Sust Energ Rev 13(9):2263–2278
Wang Y, Li Z, Tang Z, Zeng G (2011) A GIS-based spatial multi-criteria approach for flood risk management in the Dongting Lake Region, Hunan, Central China. Water Resources Management, DOI 10.1007/s11269-011-9866-2 (published online)
Acknowledgements
This work was funded under the Netherlands Fellowship Program and by National Water and Sewerage Corporation, Uganda. The authors are grateful to all the NWSC staff and the GTZ technical adviser to NWSC who participated in the questionnaire survey and brainstorming sessions. The authors are also grateful to Cathy Macharis (Free University of Brussels), Yves De Smet and Quinton Hayes (Université Libre de Bruxelles) for their support in acquiring the D-Sight software. Finally, the authors are very grateful to the anonymous reviewers for their insightful critique of the manuscript that greatly improved the article.
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Mutikanga, H.E., Sharma, S.K. & Vairavamoorthy, K. Multi-criteria Decision Analysis: A Strategic Planning Tool for Water Loss Management. Water Resour Manage 25, 3947–3969 (2011). https://doi.org/10.1007/s11269-011-9896-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11269-011-9896-9