Convergence Behavior of NLMS Algorithm for Gaussian Inputs: Solutions Using Generalized Abelian Integral Functions and Step Size Selection

Abstract

This paper studies the mean and mean square convergence behaviors of the normalized least mean square (NLMS) algorithm with Gaussian inputs and additive white Gaussian noise. Using the Price’s theorem and the framework proposed by Bershad in IEEE Transactions on Acoustics, Speech, and Signal Processing (1986, 1987), new expressions for the excess mean square error, stability bound and decoupled difference equations describing the mean and mean square convergence behaviors of the NLMS algorithm using the generalized Abelian integral functions are derived. These new expressions which closely resemble those of the LMS algorithm allow us to interpret the convergence performance of the NLMS algorithm in Gaussian environment. The theoretical analysis is in good agreement with the computer simulation results and it also gives new insight into step size selection.

1 Introduction

Adaptive filters are frequently employed to handle filtering problems in which the statistics of the underlying signals are either unknown a priori, or in some cases slowly-varying. Many adaptive filtering algorithms have been proposed and they are usually variants of the well known least mean square (LMS) [1] and the recursive least squares (RLS) [2] algorithms. An important variant of LMS algorithm is the normalized least mean square (NLMS) algorithm [3, 4], where the step size is normalized with respect to the energy of the input vector. Due to the numerical stability and computational simplicity of the LMS and the NLMS algorithms, they have been widely used in various applications [5]. Their convergence performance analyses are also long standing research problems. The convergence behavior of the LMS algorithm for Gaussian input was thoroughly studied in the classical work of Widrow et al. [1], in which the concept of independence assumption was introduced. Other related studies of the LMS algorithm with independent Gaussian inputs include [6–8]. On the other hand, the NLMS algorithm generally possesses an improved convergence speed over the LMS algorithm, but its analysis is more complicated due to the step size normalization. In [9] and [10], the mean and mean square behaviors of the NLMS algorithm for Gaussian inputs were studied. Analysis for independent Gaussian inputs in [11] also revealed the advantage of the NLMS algorithm over the LMS algorithm. Due to the difficulties in evaluating the expectations involved in the difference equations for the mean weight-error vector and its covariance matrix, general closed-form expressions for these equations and the excess mean square error (EMSE) are in general unavailable. Consequently, the works in [9, 10] only concentrated on certain special cases of eigenvalue distribution of the input autocorrelation matrix. In [12, 13], particular or simplified input data model was introduced to facilitate the performance analysis so that useful analytical expressions can still be derived. In [14], the averaging principle was invoked to simplify the expectations involved in the difference equations. Basically, the normalization term is assumed to vary slowly with respect to the input correlation term and the power of the input vector is assumed to have a chi-square distribution with L degrees of freedom. In [15], the difference equation was converted to a stochastic differential equation to simplify the analysis assuming a small step size. In [16], the normalization term mentioned above was recognized as an Abelian integral [17], which was explicitly integrated using a transformation approach into elementary functions.¹ Recently, Sayed et al. [18] proposed a unified framework for analyzing the convergence of adaptive filtering algorithms. It has been applied to different adaptive filtering algorithms with satisfactory results [19].

In this paper, the convergence behaviors of the NLMS algorithm with Gaussian input and additive noise are studied. Using the Price’s theorem [20] and the framework in [9, 10], new decoupled difference equations describing the mean and mean square convergence behaviors of the NLMS algorithm using the generalized Abelian integral functions are derived. The final results closely resemble the classical results for LMS in [1]. Moreover, it is found that the normalization process will always increase the maximum convergence rate of the NLMS algorithms over their LMS counterparts if the eigenvalues of the input autocorrelation matrix are unequal. Using the new solution for the EMSE, the step size parameters are optimized for white inputs which agrees with the approach previously proposed in [21] using calculus of variations. The theoretical analysis and some new bounds for step size selection are validated using Monte Carlo simulations.

The rest of this paper is organized as follows: In Section 2, the NLMS algorithm is briefly reviewed. In Section 3, the proposed convergence performance analysis is presented. Simulation results are given in Section 4 and conclusions are drawn in Section 5.

2 NLMS Algorithm

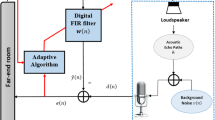
Consider the adaptive system identification problem in Fig. 1 where an adaptive filter with coefficient or weight vector of order L, ${\mathbf{W}}(n) = \left[ {w_1 (n),w_2 (n), \ldots, w_L (n)} \right]^T$, is used to model an unknown system with impulse response ${\mathbf{W}}^{ * } = \left[ {w_1, w_2, \cdots, w_L } \right]^T$. Here, (∙)^T denotes the transpose of a vector or a matrix. The unknown system and the adaptive filter are simultaneously excited by the same input x(n). The output of the unknown system d ₀(n) is assumed to be corrupted by a measurement noise η(n) to form the desired signal d(n) for the adaptive filter. The estimation error is given by e(n) = d(n) – y(n). The NLMS algorithm under consideration assumes the following form:

Figure 1

Adaptive system identification.

$$ {\mathbf{W}}\left( {n + 1} \right) = {\mathbf{W}}(n) + \frac{{\mu e(n){\mathbf{X}}(n)}}{{\varepsilon + \alpha X^T (n){\mathbf{X}}(n)}}, $$

(1)

where ${\mathbf{X}}(n) = \left[ {x(n),x\left( {n - 1} \right), \cdots, x\left( {n - L + 1} \right)} \right]^T$ is the input vector at time instant n, μ is a positive step size constant to ensure convergence of the algorithm, and ε and α are positive constants. In the ε -NLMS algorithm [10], ε is a small positive value used to avoid division by zero and α = 1. In the conventional LMS algorithm, ε = 1 and α = 0. The above model can also be used to model the effect of prior knowledge of noise power by choosing ε to be $\left( {1 - \alpha } \right)\hat{\sigma }_x^2$, where $\hat{\sigma }_x^2$ is some prior estimate of $E\left[ {{\mathbf{X}}^T (n){\bf X}(n)} \right]$ and α becomes a positive forgetting factor smaller than one.

3 Mean and Mean Square Convergence Analysis

To simplify the analysis, we assume that A1) the input signal x(n) is a stationary ergodic process which is Gaussian distributed with zero mean and autocorrelation matrix ${\bf R}_{XX} = E\left[ {{\bf X}(n){\mathbf{X}}^T (n)} \right]$, A2) η(n) is white Gaussian distributed with zero mean and variance $\sigma_g^2$, and A3) the well-known independent assumption [1] where W(n), x(n) and η(n) are considered statistically independent. Moreover, we denote ${\mathbf{W}}^{ * } = {\mathbf{R}}_{XX}^{- 1} {\mathbf{P}}_{dX}$ as the optimal Wiener solution, where ${\mathbf{P}}_{dX} = E\left[ {d(n){\mathbf{X}}(n)} \right]$ is the ensemble-averaged cross-correlation vector between X(n) and d(n).

3.1 Mean Behavior

From (1), the update equation for the weight-error vector v(n) = W ^* − W(n) is given by:

$${\mathbf{v}}{\left( {n + 1} \right)} = {\mathbf{v}}{\left( n \right)} - \frac{{\mu e{\left( n \right)}X{\left( n \right)}}}{{\varepsilon + a{\mathbf{X}}^{T} {\left( n \right)}{\mathbf{X}}{\left( n \right)}}}.$$

(2)

Taking expectation on both sides of (2), we get

$$ E\left[ {v\left( {n + 1} \right)} \right] = E\left[ {{\mathbf{v}}(n)} \right] - \mu {\mathbf{H}}_1, $$

(3)

where ${\mathbf{H}}_1 = E\left[ {{{e(n){\mathbf{X}}(n)} \mathord{\left/ {\vphantom {{e(n)X(n)} {\left( {\varepsilon + \alpha X^T (n)X(n)} \right)}}} \right. } {\left( {\varepsilon + \alpha {\mathbf{X}}^T (n){\mathbf{X}}(n)} \right)}}} \right]$ and E[∙] denotes the expectation over {v(n),X(n), η(n)} and is written more clearly as $E_{{\left\{ {v,X,\eta } \right\}}} \left[ \cdot \right]$. Since X(n) and η(n) are stationary, we can drop the time index n in the expectation to get ${\mathbf{H}}_1 = E\left[ {{{e{\mathbf{X}}} \mathord{\left/ {\vphantom {{eX} {\left( {\varepsilon + \alpha X^T X} \right)}}} \right. } {\left( {\varepsilon + \alpha {\mathbf{X}}^T {\mathbf{X}}} \right)}}} \right]$. Using the independence assumption A3, we further have ${\mathbf{H}}_1 = E_{{\left\{ v \right\}}} \left[ {\mathbf{H}} \right]$, where $H = E_{{{\left\{ {X,\eta } \right\}}}} {\left[ {{eX} \mathord{\left/ {\vphantom {{eX} {{\left\{ {\varepsilon + \alpha X^{T} X} \right\}}\left| v \right.}}} \right. \kern-\nulldelimiterspace} {{\left\{ {\varepsilon + \alpha X^{T} X} \right\}}\left| \mathbf{v} \right.}} \right]}$.

In the conventional NLMS algorithm studied in [9] and [10] with α = 1, similar difference equation for the mean weight-error vector (c.f. [10, Eq. 11])² was obtained:

$$ E\left[ {{\mathbf{v}}\left( {n + 1} \right)} \right] = \left( {{\mathbf{I}} - \mu {\mathbf{F}}_{\varepsilon } } \right)E\left[ {{\mathbf{v}}(n)} \right], $$

(4)

where ${\mathbf{F}}_{\varepsilon } = E\left[ {{{{\mathbf{X}}(n){\mathbf{X}}^T (n)} \mathord{\left/ {\vphantom {{X(n)X^T (n)} {\left( {\varepsilon + X^T (n)X(n)} \right)}}} \right. } {\left( {\varepsilon + {\mathbf{X}}^T (n){\mathbf{X}}(n)} \right)}}} \right]$ and I is the identity matrix. Moreover, F _ε was further diagonalized into H _ε whose i-th element is ${\left[ {{\mathbf{H}}_{\varepsilon } } \right]}_{{i,i}} = {\int_0^\infty {\frac{{\exp {\left( { - \beta \varepsilon } \right)}}}{{{\left| {{\mathbf{I}} + 2\beta {\mathbf{R}}_{{XX}} } \right|}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}} }}\,\frac{{\lambda _{i} }}{{1 + 2\beta \lambda _{i} }}} }$ (c. f. [10, Eq. 14]), where λλ _i is the i-th eigenvalue of R _XX . It was evaluated analytically in [9] for three important cases with different eigenvalue distributions (in [10], only the first case was elaborated): (1) white input signal with λλ ₁ = ... = λλ _L ; (2) two signal subspaces with equal powers λλ ₁ = ... = λλ _K  = αα and $\lambda_{K + 1} = \ldots = \lambda_L = b$; (3) distinct pairs, $\lambda_1 = \lambda_2$, $\lambda_3 = \lambda_4$, …, $\lambda_{L - 1} = \lambda_L$ (Assume L even). Besides these three special cases, no general solution to H _ε was provided. Therefore, general closed-form formulas for modeling the mean and mean square behaviors of the NLMS algorithm were unavailable in [9] and [10].

Here, we pursue another direction by treating some of these integrals as special functions and carry them throughout the analysis. The final formulas containing these special integral functions still allow us to clearly interpret the convergence behavior of the NLMS algorithm and determine appropriate step size parameters. More precisely, using Price’s theorem [20] and the approach in [9, 10], it is shown in Appendix A that:

$$ {\mathbf{H}}_1 = {\mathbf{U}}\Lambda {\mathbf{D}}_{\Lambda } {\mathbf{U}}^T E\left[ {{\mathbf{v}}(n)} \right] $$

(5)

where ${\mathbf{R}}_{XX} = {\mathbf{U}}\Lambda {\mathbf{U}}^T$ is the eigenvalue decomposition of R _XX and $\Lambda = {\text{diag}}\left( {\lambda_1, \lambda_2, \cdots, \lambda_L } \right)$ contains the corresponding eigenvalues. D _Λ is a diagonal matrix with the i-th diagonal entry given by (A-6):

$\left[ {{\mathbf{D}}_{\Lambda } } \right]_{i,i} = I_i \left( \Lambda \right) = \int_0^{\infty } {\exp \left( { - \beta \varepsilon } \right)\left[ {\prod\limits_{k = 1}^L {\left( {2\alpha \beta \lambda_k + 1} \right)^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}} } } \right]\left( {2\alpha \beta \lambda_i + 1} \right)^{- 1} d\beta }$,which is a generalized Abelian integral function where the conventional Abelian integral has the form $I_a (x) = \int_0^x {\left[ {q\left( \beta \right)} \right]}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}} d\beta$ with q(β ) being a polynomial in β. It is also similar to $\left[ {{\mathbf{H}}_{\varepsilon } } \right]_{i,i}$ in [10].

Substituting (5) into (3), the following difference equation for the mean weight-error vectors E[v(n + 1)] and E[v(n)] is obtained

$$ E\left[ {v\left( {n + 1} \right)} \right] = \left( {{\mathbf{I}} - \mu {\mathbf{U}}\Lambda {\mathbf{D}}_{\Lambda } {\mathbf{U}}^T } \right)E\left[ {{\mathbf{v}}(n)} \right] $$

(6)

(6) can also be written in the natural coordinate ${\mathbf{V}}(n) = {\mathbf{U}}^T {\mathbf{v}}(n)$ as

$$ E\left[ {{\mathbf{V}}\left( {n + 1} \right)} \right] = \left( {{\mathbf{I}} - \mu \Lambda {\mathbf{D}}_{\Lambda } } \right)E\left[ {{\mathbf{V}}(n)} \right], $$

(7)

which is equivalent to L scalar first order finite difference equations as follows:

$$ E\left[ {{\mathbf{V}}\left( {n + 1} \right)} \right]_i = \left( {1 - \mu \lambda_i I_i \left( \Lambda \right)} \right)E\left[ {{\mathbf{V}}(n)} \right]_i, $$

(8)

where E[V(n)] _i is the i-th element of the vector E[V(n)] for i = 1,2,∙∙∙,L.

For conventional LMS and NLMS algorithms, the above result agrees with the mean convergence result of the conventional NLMS algorithm in [10, Eq. 13], except that the effect of normalization is now more apparent. If all I _i(Λ)’s are equal to one, the analysis reduces to its un-normalized, conventional LMS counterpart. Therefore, the mean weight vector of the NLMS algorithm will converge if ${\left| {1 - \mu \lambda _{i} I_{i} {\left( \Lambda \right)}} \right|} < 1$, for all i, and the corresponding step size satisfies $\mu < 2 \mathord{\left/ {\vphantom {2 {{\left( {\lambda _{i} I_{i} {\left( \Lambda \right)}} \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {\lambda _{i} I_{i} {\left( \Lambda \right)}} \right)}}$, for all i. To determine the maximum possible step size μ _max, we need to examine the maximum of the product λλ _iI_i(Λ):

$$ \begin{array}{*{20}c} {\lambda_i I_i \left( \Lambda \right) = \lambda_i \int_0^{\infty } {exp\left( { - \beta \varepsilon } \right)\left[ {\mathop \Pi \limits_{k = 1}^L \left( {2\alpha \beta \lambda_k + 1} \right)^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. } 2}}} } \right]\left( {2\alpha \beta \lambda_i + 1} \right)^{- 1} d\beta } } \\ { = \int_0^{\infty } {exp\left( { - \beta \varepsilon } \right)\left[ {\mathop \Pi \limits_{k = 1}^L \left( {2\alpha \beta \lambda_k + 1} \right)^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. } 2}}} } \right]\left[ {2\alpha \beta + \left( {\lambda_i } \right)^{- 1} } \right]^{- 1} d\beta } } \\ \end{array} . $$

(9)

Since the factor $exp\left( { - \beta \varepsilon } \right)\left[ {\mathop \Pi \limits_{k = 1}^L \left( {2\alpha \beta \lambda_k + 1} \right)^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. } 2}}} } \right]$ is common for all the products and it is positive, the maximum value in (9) also occurs at the largest eigenvalue λλ _max with the corresponding value of I _i(Λ) given by $I_{{i\_\lambda_{{\max }} }} \left( \Lambda \right)$. Therefore,

$$ {{\mu < 2} \mathord{\left/ {\vphantom {{\mu < 2} {\left( {\lambda_{{\max }} I_{{i\_\lambda_{{\max }} }} \left( \Lambda \right)} \right)}}} \right. } {\left( {\lambda_{{\max }} I_{{i\_\lambda_{{\max }} }} \left( \Lambda \right)} \right)}} = \mu_{{\max }} $$

(10)

As a result, compared with the LMS algorithm, the maximum step size of the NLMS algorithm is scaled by a factor $1/I_{{i\_\lambda_{{\max }} }} (\Lambda )$. The fastest convergence rate of the algorithm occurs when μ = μ _max and it is limited by the mode corresponding to the smallest eigenvalue λλ _min with the corresponding value of I _i(Λ) given by $I_{{i\_\lambda_{{\min }} }} \left( \Lambda \right)$, that is ${{1 - \lambda_{{\min }} I_{{i\_\lambda_{{\min }} }} \left( \Lambda \right)} \mathord{\left/ {\vphantom {{1 - \lambda_{{\min }} I_{{i\_\lambda_{{\min }} }} \left( \Lambda \right)} {\left( {\lambda_{{\max }} I_{{i\_\lambda_{{\max }} }} \left( \Lambda \right)} \right)}}} \right. } {\left( {\lambda_{{\max }} I_{{i\_\lambda_{{\max }} }} \left( \Lambda \right)} \right)}}$. The smaller this value, the faster the convergence rate will be. From the definition of I _i(Λ) , it can be shown that ${{I_{{i\_\lambda_{{\min }} }} \left( \Lambda \right)} \mathord{\left/ {\vphantom {{I_{{i\_\lambda_{{\min }} }} \left( \Lambda \right)} {I_{{i\_\lambda_{{\max }} }} \left( \Lambda \right) \ge 1}}} \right. } {I_{{i\_\lambda_{{\max }} }} \left( \Lambda \right) \ge 1}}$. In other words, the eigenvalue spread ${{\lambda_{{\max }} } \mathord{\left/ {\vphantom {{\lambda_{{\max }} } {\lambda_{{\min }} }}} \right. } {\lambda_{{\min }} }}$ is reduced by a factor ${{I_{{i\_\lambda_{{\max }} }} \left( \Lambda \right)} \mathord{\left/ {\vphantom {{I_{{i\_\lambda_{{\max }} }} \left( \Lambda \right)} {I_{{i\_\lambda_{{\min }} }} \left( \Lambda \right)}}} \right. } {I_{{i\_\lambda_{{\min }} }} \left( \Lambda \right)}}$ after the normalization. Therefore, under the stated assumptions, the maximum convergence rate of the NLMS algorithm will always be faster than the LMS algorithm if the eigenvalues are unequal.

3.2 Mean Square Behavior

Post-multiplying (2) by its transpose and taking expectation gives

$$ {\mathbf{\Xi }}\left( {n + 1} \right) = {\mathbf{\Xi }}(n) - {\mathbf{M}}_1 - {\mathbf{M}}_2 + {\mathbf{M}}_3, $$

(11)

where ${\mathbf{\Xi }}(n) = E\left[ {{\mathbf{v}}(n){\mathbf{v}}^T (n)} \right]$,${\mathbf{M}}_1 = \mu {\mathbf{U}}\Lambda {\mathbf{D}}_{\Lambda } {\mathbf{U}}^T {\mathbf{\Xi }}(n)$, ${\mathbf{M}}_2 = \mu {\mathbf{\Xi }}(n){\mathbf{UD}}_{\Lambda } \Lambda {\mathbf{U}}^T$,${\mathbf{M}}_3 = \mu^2 E\left[ {{{e^2 {\mathbf{XX}}^T } \mathord{\left/ {\vphantom {{e^2 {\mathbf{XX}}^T } {\left( {\varepsilon + \alpha {\mathbf{X}}^T {\mathbf{X}}} \right)}}} \right. } {\left( {\varepsilon + \alpha {\mathbf{X}}^T {\mathbf{X}}} \right)}}^2 } \right] = E_{{\left\{ {\mathbf{v}} \right\}}} \left[ {{\mathbf{s}}_3 } \right]$, where ${\mathbf{s}}_3 = E_{{\left\{ {{\mathbf{X}},\eta } \right\}}} \left[ {{{e^2 {\mathbf{XX}}^T } \mathord{\left/ {\vphantom {{e^2 {\mathbf{XX}}^T } {\left( {\varepsilon + \alpha {\mathbf{X}}^T {\mathbf{X}}} \right)}}} \right. } {\left( {\varepsilon + \alpha {\mathbf{X}}^T {\mathbf{X}}} \right)}}^2 \left| {\mathbf{v}} \right.} \right]$. Here, we have used the previous result in (5) to evaluate M ₁ and M ₂.M ₃ is evaluated in Appendix B to be

$$ \begin{array}{*{20}c} {{\mathbf{M}}_3 = 2\mu^2 {\mathbf{U}}\left\{ {\Lambda \left[ {\left( {{\mathbf{U}}^T {\mathbf{\Xi }}(n){\mathbf{U}}} \right) \circ {\mathbf{I}}\left( \Lambda \right)} \right]\Lambda } \right\}{\mathbf{U}}^T + \mu^2 {\mathbf{U\bar{D}}}_2 {\mathbf{U}}^T } \\ {{\kern 1pt} + \mu^2 \sigma_g^2 {\mathbf{U}}\Lambda {\mathbf{I}}\prime \left( \Lambda \right){\mathbf{U}}^T } \\ \end{array} {\kern 1pt}, $$

(12)

where the diagonal matrix ${\mathbf{\bar{D}}}_2$ results from (B-7) and its i-th element $\left[ {{\mathbf{\bar{D}}}_2 } \right]_{i,i} = \mathop \Sigma \limits_k \lambda_k \lambda_i I_{ki} \left( \Lambda \right)\left[ {{\mathbf{U}}^T {\mathbf{\Xi }}(n){\mathbf{U}}} \right]_{k,k}$, $\circ$ denotes element-wise product of two matrices (Hadamard product), I(Λ) and I′(Λ) are defined in (B-5) and (B-8) and their elements are also generalized Abelian integral functions. Substituting (12) into (11) gives

$$ \begin{array}{*{20}c} {{\mathbf{\Xi }}\left( {n + 1} \right) = {\mathbf{\Xi }}(n) - \mu {\mathbf{U}}\Lambda {\mathbf{D}}_{\Lambda } {\mathbf{U}}^T {\mathbf{\Xi }}(n) - \mu {\mathbf{\Xi }}(n){\mathbf{UD}}_{\Lambda } \Lambda {\mathbf{U}}^T } \\ { + 2\mu^2 {\mathbf{U}}\left\{ {\Lambda \left[ {\left( {{\mathbf{U}}^T {\mathbf{\Xi }}(n){\mathbf{U}}} \right) \circ {\mathbf{I}}\left( \Lambda \right)} \right]\Lambda } \right\}{\mathbf{U}}^T + \mu^2 {\mathbf{U\bar{D}}}_2 {\mathbf{U}}^T } \\ { + \mu^2 \sigma_g^2 {\mathbf{U}}\Lambda {\mathbf{I}}\prime \left( \Lambda \right){\mathbf{U}}^T } \\ \end{array} . $$

(13)

(13) can be further simplified in the natural coordinate by pre- and post-multiplying Ξ(n) by U ^T and U to give:

$$ \begin{array}{*{20}c} {{\mathbf{\Phi }}\left( {n + 1} \right){\kern 1pt} = {\mathbf{\Phi }}(n) - \mu \Lambda {\mathbf{D}}_{\Lambda } {\mathbf{\Phi }}(n) - \mu {\mathbf{\Phi }}(n){\mathbf{D}}_{\Lambda } \Lambda } \\ { + 2\mu^2 \left[ {\Lambda \left( {{\mathbf{\Phi }}(n) \circ {\mathbf{I}}\left( \Lambda \right)} \right)\Lambda } \right] + \mu^2 {\mathbf{\tilde{D}}}_2 + \mu^2 \sigma_g^2 \Lambda {\mathbf{I}}\prime \left( \Lambda \right)} \\ \end{array}, $$

(14)

where ${\mathbf{\Phi }}(n) = {\mathbf{U}}^T {\mathbf{\Xi }}(n){\mathbf{U}}$ and $\left[ {{\mathbf{\tilde{D}}}_2 } \right]_{i,i} = \mathop \Sigma \limits_k \lambda_k \lambda_i I_{ki} \left( \Lambda \right)\left[ {{\mathbf{\Phi }}(n)} \right]_{k,k}$. From (14), we can get the i-th diagonal value of Φ(n) as follows

$$ \begin{array}{*{20}c} {\Phi_{i,i} \left( {n + 1} \right) = \Phi_{i,i} (n) - 2\mu I_i \left( \Lambda \right)\lambda_i \Phi_{i,i} (n)} \\ { + 2\mu^2 \lambda_i^2 I_{ii} \left( \Lambda \right)\Phi_{i,i} (n) + \mu^2 \mathop \Sigma \limits_k \lambda_k \lambda_i I_{ki} \left( \Lambda \right)\Phi_{k,k} (n)} \\ { + \mu^2 \sigma_g^2 \lambda_i I_i^{\prime } \left( \Lambda \right)} \\ \end{array} . $$

(15)

From numerical results, the term $\mu^2 \mathop \Sigma \limits_k \lambda_k \lambda_i I_{ki} \left( \Lambda \right)\Phi_{k,k} (n)$ is very small for small EMSE and (15) can be approximated as

$$ \Phi_{i,i} \left( {n + 1} \right) \approx \left( {1 - 2\mu I_i \left( \Lambda \right)\lambda_i + 2\mu^2 I_{ii} \left( \Lambda \right)\lambda_i^2 } \right)\Phi_{i,i} (n) + \mu^2 \sigma_g^2 \lambda_i I_i^{\prime } \left( \Lambda \right). $$

(16)

To study the step size for mean squares convergence of the algorithm, we first assume that the algorithm converges and then determine an upper bound of the EMSE at the steady state. From this expression, we are able to find the step size bound for a finite EMSE and hence mean square convergence. As we shall see below, this step size bound depends weakly on the signals. Alternatively, we can find an approximate signal independent upper bound for small EMSE by ignoring the term $\mu^2 \mathop \Sigma \limits_k \lambda_k \lambda_i I_{ki} \left( \Lambda \right)\Phi_{k,k} (n)$ since it is very small for small EMSE. Consequently, (16) suggests that the algorithm will converge in the mean squares sense when ${\left| {1 - 2\mu I_{i} {\left( \Lambda \right)}\lambda _{i} + 2\mu ^{2} I_{{ii}} {\left( \Lambda \right)}\lambda ^{2}_{i} } \right|} < 1$. This gives $\mu < {I_{i} {\left( \Lambda \right)}} \mathord{\left/ {\vphantom {{I_{i} {\left( \Lambda \right)}} {{\left( {\lambda _{i} I_{{ii}} {\left( \Lambda \right)}} \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {\lambda _{i} I_{{ii}} {\left( \Lambda \right)}} \right)}}$ for all i. From the definitions of I _i(Λ) and I _ii(Λ), we have $I_{{\text{i}}} {\left( \Lambda \right)}/{\left( {{\text{ $ \lambda $ }}_{i} I_{{ii}} {\left( \Lambda \right)}} \right)} = 2/{\left( {1 - I^{{′′}}_{{_{{ii}} }} {\left( \Lambda \right)}/I_{i} {\left( \Lambda \right)}} \right)} > 2$ for α = 1, where $I^{{\prime \prime }}_{i} {\left( \Lambda \right)} = {\int_0^\infty {\exp {\left( { - \beta \varepsilon } \right)}{\left[ {{\mathop \Pi \limits_{k = 1}^L }{\left( {2\beta \lambda _{k} + 1} \right)}^{{ - 1/2}} } \right]}} }{\left( {2\beta \lambda _{i} + 1} \right)}^{{ - 2}} d\beta$. Therefore, a conservative signal independent stability bound for small EMSE is μ < 2.

For a more precise upper bound, we first note that the EMSE at time instant n is given by ${\text{EMSE}}(n) = {\text{Tr}}\left( {{\mathbf{\Xi }}(n){\mathbf{R}}_{XX} } \right) = {\text{Tr}}\left( {{\mathbf{\Phi }}(n)\Lambda } \right)$. Assuming that algorithm converges, it is shown in Appendix B that the last two terms on the right hand side of (15) is upper bounded by $\mu^2 \sigma_e^2 \left( \infty \right)\lambda_i I_i^{\prime } \left( \Lambda \right)$ at the steady state. Hence, the steady state EMSE of the NLMS algorithm is approximately given by

$$ \xi_{\text{NLMS}} \left( \infty \right) = {\text{Tr}}\left( {{\mathbf{\Phi }}\left( \infty \right)\Lambda } \right) \approx \tfrac{1}{2}\mu \sigma_e^2 \left( \infty \right)\varphi_{\text{NLMS}}, $$

(17)

where $\varphi_{\text{NLMS}} = \sum\limits_{i = 1}^L {\frac{{\lambda_i I_i^{\prime } \left( \Lambda \right)}}{{I_i \left( \Lambda \right) - \mu \lambda_i I_{ii} \left( \Lambda \right)}}}$. Using the fact that $\sigma_e^2 \left( \infty \right) = \xi_{\text{NLMS}} \left( \infty \right) + \sigma_g^2$, one gets

$$ \xi_{\text{NLMS}} \left( \infty \right) \approx \frac{{\tfrac{1}{2}\mu \sigma_g^2 \varphi_{\text{NLMS}} }}{{1 - \tfrac{1}{2}\mu \varphi_{\text{NLMS}} }}. $$

(18)

It can be seen that $\xi_{\text{NLMS}} \left( \infty \right)$ is unbounded when either its denominator becomes zero or when ϕ _NLMS becomes unbound when any of the denominators of its partial sum becomes zero. This gives respectively the following two conditions:

$$ 0 < \mu < {{I_i \left( \Lambda \right)} \mathord{\left/ {\vphantom {{I_i \left( \Lambda \right)} {\lambda_i I_{ii} \left( \Lambda \right)}}} \right. } {\lambda_i I_{ii} \left( \Lambda \right)}}. $$

(19a)

$$ 0 < \mu < {{I_i \left( \Lambda \right)} \mathord{\left/ {\vphantom {{I_i \left( \Lambda \right)} {\lambda_i I_{ii} \left( \Lambda \right)}}} \right. } {\lambda_i I_{ii} \left( \Lambda \right)}}. $$

(19b)

For the LMS case, $I_{ii} \left( \Lambda \right) = I_i \left( \Lambda \right) = I_i^{\prime } \left( \Lambda \right) = 1$ and the corresponding conditions are:

$$ \mu < {2 \mathord{\left/ {\vphantom {2 {\varphi_{\text{LMS}} }}} \right. } {\varphi_{\text{LMS}} }}, $$

(20a)

$$ 0 < \mu < {1 \mathord{\left/ {\vphantom {1 {\lambda_i }}} \right. } {\lambda_i }}, $$

(20b)

where $\varphi_{\text{LMS}} = \sum\limits_{i = 1}^L {\frac{{\lambda_i }}{{1 - \mu \lambda_i }}}$. (20a) and (20b) are identical to the necessary and sufficient conditions for the mean square convergence of the LMS algorithm previously obtained in [6]. Similar results are obtained in [7] by solving the difference equation in Φ(n) and in [8] by a matrix analysis technique.

In [7], a lower bound of the maximum step size is also obtained. Using a similar approach, we now derive a step size bound for the NLMS algorithm. First we rewrite (19a) as:

$$ \sum\limits_{i = 1}^L {\frac{{\mu \lambda_i c_i }}{{1 - \mu \lambda_i d_i }}} < 2, $$

(21)

where $c_i = {{I_i^{\prime } \left( \Lambda \right)} \mathord{\left/ {\vphantom {{I_i^{\prime } \left( \Lambda \right)} {I_i \left( \Lambda \right)}}} \right. } {I_i \left( \Lambda \right)}}$ and $d_i = {{I_{ii} \left( \Lambda \right)} \mathord{\left/ {\vphantom {{I_{ii} \left( \Lambda \right)} {I_i \left( \Lambda \right)}}} \right. } {I_i \left( \Lambda \right)}}$. Let u = 2 μ ⁻¹ and rewrite (21) as

$$ \ell (u) - \sum\limits_{i = 1}^L {\lambda_i c_i l_i (u)} = \prod\limits_{i = 1}^L {\left( {u - \bar{u}_i } \right)} = \sum\limits_{i = 0}^L {\left( { - 1} \right)^{L - i} b_{L - i} } u^i = 0, $$

(22)

where, $\ell (u) = \prod\limits_{i = 1}^L {\left( {u - 2\lambda_i d_i } \right)}$, $l_i (u) = {{\ell (u)} \mathord{\left/ {\vphantom {{\ell (u)} {\left( {u - 2\lambda_i d_i } \right)}}} \right. } {\left( {u - 2\lambda_i d_i } \right)}}$, and $\overline{u} ^{{ - 1}}_{i}$ are the roots of (22). The largest root of (22) (smallest root of (21)) is upper bounded (lower bounded) by [26]

$$ u_{{N\_\max }} \le \frac{1}{L}\left( {s_1 + \sqrt {\left( {L - 1} \right)\left( {Ls_2 - s_1^2 } \right)} } \right) $$

(23)

where $s_1 = \sum\limits_{i = 1}^L {\bar{u}_i } = b_1$ and $s_2 = \sum\limits_{i = 1}^L {\bar{u}_i^2 } = b_1^2 - 2b_2$. By comparing the coefficients on different sides of (22), one also gets

$$ b_1 = \sum\limits_{i = 1}^L {\lambda_i \left( {2d_i + c_i } \right)} $$

and

$$ b_2 = 4\sum\limits_{{1 \le i \ne j \le L}} {\lambda_i } \lambda_j d_i d_j + \sum\limits_{i = 1}^L {\lambda_i c_i \left( {2\sum\limits_{{1 \le j \ne i \le L}} {\lambda_j d_j } } \right).} $$

(24)

From (23), a more convenient lower bound of μ _max can be obtained as follows

$$\begin{array}{*{20}c} {\mu _{{\max }} \geqslant \frac{{2L}}{{b_{1} + {\sqrt {{\left( {L - 1} \right)}^{2} b^{2}_{1} - 2L{\left( {L - 1} \right)}b_{2} } }}} \geqslant \frac{{2L}}{{b_{1} + {\sqrt {{\left( {L - 1} \right)}^{2} b^{2}_{1} } }}}} \\ { = \frac{2}{{b_{1} }} = \frac{2}{{Tr{\left( {\Lambda {\left( {{\mathbf{I}}\prime {\left( \Lambda \right)} + 2diag{\left( {{\mathbf{I}}{\left( \Lambda \right)}} \right)}} \right)}{\mathbf{D}}^{{ - 1}}_{\Lambda } } \right)}}}} \\ \end{array} $$

(25)

where diag(I(Λ)) is a diagonal matrix with the i-th diagonal value equal to I _ii (Λ).

From simulation results, we found that ϕ _NLMS is rather close to one. Hence, μ < 2 is a very useful rule of thumb estimate of the step size bound, since it does not depend on any prior knowledge of the Gaussian inputs.

Comparing (13) and the result in [10, Eq. 22], it can be found that they are identical except that all the integrals in [10] are coupled in their original forms. In contrast, the decoupled forms in terms of the generalized Abelian integral functions in (13)–(18) obtained with the proposed approach are very similar to those of the LMS algorithm. Moreover, we are also able to express the stability bound and EMSE in terms of these special functions, which are new to our best knowledge. When I _i(Λ), $I^{\prime}_i (\Lambda )$ and I _ii(Λ) are equal to one, our analysis will reduce to the classical results of the LMS algorithm. Next, we shall make use of these analytical expressions for step size selection.

3.3 Step Size Selection

For white input, I(Λ) and I′(Λ) will reduce respectively to $\tfrac{{\exp \left( {{\varepsilon \mathord{\left/ {\vphantom {\varepsilon {2\lambda }}} \right. } {2\lambda }}} \right)}}{{2\alpha \lambda }}E_{{{L \mathord{\left/ {\vphantom {L {2 + 1}}} \right. } {2 + 1}}}} \left( {\tfrac{\varepsilon }{{2\alpha \lambda }}} \right)$ and $\tfrac{{\exp \left( {{\varepsilon \mathord{\left/ {\vphantom {\varepsilon {2\lambda }}} \right. } {2\lambda }}} \right)}}{{\left( {2\alpha \lambda } \right)^2 }}\left[ {E_{L/2} \left( {\tfrac{\varepsilon }{{2\alpha \lambda }}} \right) - E_{L/2 + 1} \left( {\tfrac{\varepsilon }{{2\alpha \lambda }}} \right)} \right]$, where $E_n (x) = \int_1^{\infty } {\left( {{{\exp \left( { - xt} \right)} \mathord{\left/ {\vphantom {{\exp \left( { - xt} \right)} {t^n }}} \right. } {t^n }}} \right)} dt$ is the generalized exponential integral function (E _−n (x) is also known as the Misra function). For small ε, one gets $E_n \left( {{\varepsilon \mathord{\left/ {\vphantom {\varepsilon {2\lambda }}} \right. } {2\lambda }}} \right) \approx {1 \mathord{\left/ {\vphantom {1 {\left( {n - 1} \right)}}} \right. } {\left( {n - 1} \right)}}$ for n  > 1. In this case, the NLMS algorithm will have the same convergence rate of the LMS algorithm if $\mu_{\text{LMS}} = \mu \tfrac{{\exp \left( {{\varepsilon \mathord{\left/ {\vphantom {\varepsilon {2\lambda }}} \right. } {2\lambda }}} \right)}}{{2\alpha \lambda }}E_{{{L \mathord{\left/ {\vphantom {L {2 + 1}}} \right. } {2 + 1}}}} \left( {\tfrac{\varepsilon }{{2\alpha \lambda }}} \right) \approx \mu \tfrac{1}{{2\alpha \lambda \left( {{L \mathord{\left/ {\vphantom {L 2}} \right. } 2}} \right)}}$, or equivalently $\mu \approx \mu_{\text{LMS}} \alpha \lambda L$. For the maximum possible adaptation speed of the LMS algorithm, $\mu_{\text{LMS,opt}} = \tfrac{\lambda }{{\left( {L - 1} \right){}^2 + E\left[ {x^4 } \right]}} \approx {1 \mathord{\left/ {\vphantom {1 {\left( {\lambda L} \right)}}} \right. } {\left( {\lambda L} \right)}}$ for large L. As a result, μ ≈ α and one gets the following update

$$ {\mathbf{W}}\left( {n + 1} \right) = {\mathbf{W}}(n) + \frac{{e(n){\mathbf{X}}(n)}}{{\left( {{\varepsilon \mathord{\left/ {\vphantom {\varepsilon \alpha }} \right. } \alpha }} \right) + {\mathbf{X}}^T (n){\mathbf{X}}(n)}}, $$

(26)

which agrees with the optimum data nonlinearity for LMS adaptation in white Gaussian input obtained in [21] using calculus of variations. The MSE improvement of this NLMS algorithm over the conventional LMS algorithm was analyzed in detail in [21]. In general, one could set α = 1 and vary μ between 0 and 1 with a small ε to achieve a given MSE or match a given convergence rate as above. From simulation results, we found that the EMSE of the NLMS algorithm varies slightly with the eigenvalues for a given Tr(R _XX ). For small μ, (18) suggests that the LMS algorithm is almost independent of the eigenvalue spread for a given Tr(R _XX ) $\left( {\phi_{\text{LMS}} \approx \Sigma_{i = 1}^L \lambda_i } \right)$. Therefore, the relationship between μ and μ _LMS for the white input case, i.e. ${\mu \approx \mu _{{{\rm{LMS}}}} {\rm{TR}}{\left( {R_{{XX}} } \right)}}$, can be used as a reasonable approximation for the colored case and α = 1. The corresponding EMSE is approximately $\tfrac{1}{2}\mu_{\text{LMS}} \sigma_g^2 {\text{Tr}}\left( {{\mathbf{R}}_{XX} } \right) = \tfrac{1}{2}\mu \sigma_g^2$. From (17), $\phi_{\text{NLMS}} \approx \sum {{{_{i = 1}^L \lambda_i I_i^{\prime } \left( \Lambda \right)} \mathord{\left/ {\vphantom {{_{i = 1}^L \lambda_i I_i^{\prime } \left( \Lambda \right)} {I_i \left( \Lambda \right)}}} \right. } {I_i \left( \Lambda \right)}}}$, which can be shown to be independent of scaling of input for small ε. From simulation, we also found that the EMSE of the NLMS will increase slightly with the eigenvalue spread. Hence, $\tfrac{1}{2}\mu \sigma_g^2$ represents a useful lower bound for estimating the EMSE of NLMS algorithm. It is very attractive because it does not require the knowledge of the eigenvalues or eigenvalue spread of R _XX . The corresponding estimate of the misadjustment is then $\tfrac{1}{2}\mu$. A similar upper bound can be estimated empirically from simulation results to be presented.

4 Simulation Results

In this section we shall conduct computer experiments using both simulated and real world signals to verify the analytical results obtained in Section 3.

• (1) Simulated signals

These simulations are carried out using the system identification model shown in Fig. 1. All the learning curves are obtained by averaging the results of K = 200 independent runs. The unknown system to be estimated is a FIR filter with length L. Its weight vector W ^* is randomly generated and normalized to unit energy. The input signal x(n) = ax(n − 1) + v(n) is a first order AR process, where v(n) is a white Gaussian noise sequence with zero mean and variance $\sigma_v^2$. 0 < αα < 1 is the correlation coefficient. The additive Gaussian noise η(n) has zero mean and variance $\sigma_g^2$.

For the NLMS algorithm, we set α = 1, ε = 10⁻⁴ and vary μ. The values of the special integral functions, I _i(Λ) in (A-6), I _ij(Λ) in (B-5), and $I_i^{\prime } \left( \Lambda \right)$ in (B-8) are evaluated numerically using the method introduced in [22]. For the mean convergence, the norm of the mean square weight-error vector is used as the performance measure:

$$ ||{\mathbf{v}}_A (n)||_2 = \sqrt {\sum {_{i = 1}^L \left[ {\tfrac{1}{K}\Sigma_{j = 1}^K v_i^{{(j)}} (n)} \right]}^2 }, i = 1, \cdots, L,\,\;j = 1, \cdots, K, $$

where $v_i^{{(j)}} (n)$ is the i-th component of v(n) at time n in the j-th independent run. For the mean square convergence results, ${\text{EMSE}}(n) = {\text{Tr}}\left( {{\mathbf{\Phi }}(n)\Lambda } \right)$, or the misadjustment $M(n) = {{{\text{EMSE}}(n)} \mathord{\left/ {\vphantom {{{\text{EMSE}}(n)} {\sigma_g^2 }}} \right. } {\sigma_g^2 }}$, is used as the performance measure. The theoretical results are computed from (8) and (16).

Two experiments are conducted. In the first experiment, we compare our analytical results with those in [14] (Eq. 14) and [16] (Eq. 25) for mean square convergence. Two filter lengths with L = 8 and L = 24 are evaluated for two cases: (1) μ = 0.1, $\sigma_g^2 = 10^{- 5}$, and a less colored input with αα = 0.5; (2) μ = 0.1, $\sigma_g^2 = 10^{- 4}$, and a more colored input with αα = 0.9. From Fig. 2 (a) and (b), it can be seen that when the input is less colored, all the approaches show good agreement with simulation results. When the input is very colored, our approach gives more accurate results than [14] and [16]. When L is small, there are considerable discrepancies between the theoretical and simulation results in [14] and [16]. The main reason is that both [14] and [16] assume that the denominator in (2) is uncorrelated with the numerator and an “average” but constant normalization for all the eigen-modes results. When the input is very colored, the scaling constants according to (8), I _i(Λ), are considerably different for different modes. Hence, the averaging principle is less accurate in describing the convergence behavior.

Figure 2

Comparison of the proposed analytical results with those in [14] and [16]. a L = 8, b L = 24.

In experiment 2, we conduct extensive experiments to further verify our analytical results. The parameters are summarized in Table 1. The results concerning mean and mean square convergence are plotted in Fig. 3 (a), (b) and Fig. 3 (c)–(f) respectively. From these figures, it can be seen that the theoretical analysis agrees closely with the simulation results for all cases tested. The estimated lower bound $\tfrac{1}{2}\mu$ for misadjustment M obtained in Section 3.3 is also plotted. It is accurate for moderate filter lengths and serves as a useful bound for short filter lengths. As mentioned earlier, the steady state misadjustment M increases slightly with the eigenvalue spread of the input signal. Therefore, by introducing a correction factor CF, we can empirically estimate an upper bound of M as $CF \cdot \tfrac{1}{2}\mu$. This also serves as a reference for the selection of μ to achieve at least a given misadjustment for moderate eigenvalue spreads. This CF is found to decrease slightly as L increases. Other simulation results (omitted here due to page limitation) also give similar conclusion except when μ is near to one, where slightly increased discrepancies between theoretical and simulation results are observed due to the limitation of the independent assumption A3. In summary, the advantages of the NLMS algorithm over the LMS algorithm are its good performance in colored inputs and its ease in step size selection, which make it very attractive in speech processing and other applications with time-varying input signal level.

• (2) Real speech signals

Table 1 List of parameters in experiment 2 (χ: eigenvalue spread of R _XX , CF: correction factor).

Figure 3

Verification of the proposed analytical results with parameter settings given in Table 1, (a), (b) Mean convergence; (c)–(f) Mean square convergence.

To illustrate further the properties of the LMS and NLMS algorithms, real speech signals are employed to evaluate their performances in an acoustic echo cancellation application. The speech signals used for testing are obtained with courtesy from the open source in [24]. Figure 4 (a) represents the signal of a sentence articulated by a female speaker “a little black plate on the floor” plus a white Gaussian noise. The sampling rate is 8 kHz. The echo path used has a length of 128 and is a real one given as m ₁(k) in the ITU-T recommendation G.168 [25]. The background noise η(n) has a power of $\sigma_g^2 = 10^{- 4}$. For simplicity, no double talk is assumed in this experiment.

Figure 4

a A real speech signal of the sentence “a little black plate on the floor”. b, c The residual error in the acoustic echo cancellation application using the LMS and NLMS algorithms with different step sizes.

Two sets of step sizes for the LMS and NLMS algorithms are employed: 1) μ _LMS = 0.08, μ _NLMS = 0.5, and 2) μ _LMS = 0.02 and μ _NLMS = 0.1. These values are chosen so that when the two algorithms are excited by the additive noise (i.e. during nearly silent time period), both algorithms will give a similar MSE. The residual errors after echo cancellation are depicted in Fig. 4 (b) and (c), respectively. From Fig. 4 (b), we can see that due to the nonstationary nature of the speech signal and hence the unavailability a priori knowledge of the input statistics, the LMS algorithm with a fixed step size of 0.08 diverges and plots after time index 10000 are omitted. In contrast, the performance of the NLMS is rather satisfactory. At a smaller step size of 0.02, it can be seen from Fig. 4 (c) that LMS algorithm converges but its performance is severely degraded by the non-stationarity of the speech signal, whereas the NLMS algorithm again has a satisfactory performance. This is due to the rapidly changing input level and the colored nature of real speech signals.

5 Conclusions

A new convergence analysis of the NLMS algorithm using Price’s theorem and the framework proposed in [9, 10] in Gaussian input and noise environment is presented. New expressions are derived for stability bound, steady state EMSE and decoupled difference equations describing the mean and mean square convergence behaviors of the NLMS algorithm using the generalized Abelian integral functions. The theoretical models are in good agreement with the simulation results and guidelines for step size selection are discussed.

Appendix

1.1 Appendix A: Evaluation of H ₁

As η(n) and x(n) are assumed to be statistically independent, and X are jointly Gaussian with autocorrelation matrix R _XX , one gets

$$ {\mathbf{H}} = C_R \iint\limits_{{L + 1{\text{fold}}}} {\frac{{e{\mathbf{X}}}}{{\varepsilon + \alpha {\mathbf{X}}^T {\mathbf{X}}}}\exp \left( { - \frac{1}{2}{\mathbf{X}}^T {\mathbf{R}}_{XX}^{- 1} {\mathbf{X}}} \right)f\left( \eta \right)d\eta d{\mathbf{X}}}, $$

(A-1)

where $C_R = \left( {2\pi } \right)^{{{{ - L} \mathord{\left/ {\vphantom {{ - L} 2}} \right. } 2}}} \left| {{\mathbf{R}}_{XX} } \right|^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. } 2}}}$ and f (η) is the probability density function (PDF) of the Gaussian noise η. |·| denotes the determinant of a matrix. Similar to [9] and [10], let us consider the integral

$$ {\mathbf{F}}\left( \beta \right) = C_R \iint\limits_{{L + 1{\kern 1pt} {\text{fold}}}} {\frac{{e{\mathbf{X}}\exp \left( { - \beta \left( {\varepsilon + \alpha {\mathbf{X}}^T {\mathbf{X}}} \right)} \right)}}{{\varepsilon + \alpha {\mathbf{X}}^T {\mathbf{X}}}}}\exp \left( { - \tfrac{1}{2}{\mathbf{X}}^T {\mathbf{R}}_{XX}^{- 1} {\mathbf{X}}} \right)\, \times f\left( \eta \right)d\eta d{\mathbf{X}}. $$

(A-2)

It can be seen that H = F(0). Differentiating (A-2) w.r.t. β, one gets

$$ \frac{{d{\mathbf{F}}\left( \beta \right)}}{{d\beta }} = - \exp \left( { - \beta \varepsilon } \right)C_R \iint\limits_{{L + 1{\kern 1pt} {\text{fold}}}} {\left( {e{\mathbf{X}}} \right)\exp \left( { - \tfrac{1}{2}{\mathbf{X}}^T {\mathbf{B}}^{- 1} (n){\mathbf{X}}} \right)}\, \times f\left( \eta \right)d\eta d{\mathbf{X}}, $$

(A-3)

where ${\mathbf{B}}(n) = \left( {2\alpha \beta {\mathbf{I}} + {\mathbf{R}}_{XX}^{- 1} } \right)^{- 1}$. For notation convenience, we shall simply write B for B(n). To evaluate the integral, we use the eigenvalue decomposition of ${\mathbf{R}}_{XX} = {\mathbf{U}}\Lambda {\mathbf{U}}^T$, where Λ is a diagonal matrix whose elements are the eigenvalues of R _XX and U is a orthogonal matrix. The matrix B ⁻¹ can be written as ${\mathbf{B}}^{- 1} = {\mathbf{U}}\left( {2\alpha \beta {\mathbf{I}} + \Lambda^{- 1} } \right){\mathbf{U}}^T$, where D is a diagonal matrix with the i-th diagonal entry given by $d_{ii} (n) = \left( {2\alpha \beta + \lambda_i^{- 1} } \right)^{- 1}$. Noting that the determinants of U and D are respectively 1 and $\left| {\mathbf{D}} \right|^{- 1/2} = \mathop \Pi \limits_{i = 1}^L \left( {2\alpha \beta + \lambda_i^{- 1} } \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}}$, one can rewrite (A-3) as ${{d{\mathbf{F}}\left( \beta \right)} \mathord{\left/ {\vphantom {{d{\mathbf{F}}\left( \beta \right)} {d\beta }}} \right. } {d\beta }} = - \gamma \left( \beta \right){\mathbf{L}}_1$, where $C_B = \left( {2\pi } \right)^{{{{ - L} \mathord{\left/ {\vphantom {{ - L} 2}} \right. } 2}}} \left| {\mathbf{B}} \right|^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. } 2}}}$, ${\mathbf{L}}_1 = E_{{\left\{ {{\mathbf{X}},\eta } \right\}}} \left. {\left[ {e{\mathbf{X}}\left| {\mathbf{v}} \right.} \right]} \right|_{{E\left[ {{\mathbf{XX}}^T } \right] = {\mathbf{B}}}}$, and $\gamma \left( \beta \right) = \exp \left( { - \beta \varepsilon } \right)\mathop \Pi \limits_{i = 1}^L \left( {2\alpha \beta \lambda_i + 1} \right)^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. } 2}}}$. Using $e = {\mathbf{X}}^T {\mathbf{v}} + \eta$, we have $r_{{x_i e}} = \left. {E\left[ {x_i e\left| {\mathbf{v}} \right.} \right]} \right|_{{E\left[ {{\mathbf{XX}}^T } \right] = {\mathbf{B}}}} = E\left. {\left[ {x_i \left( {{\mathbf{X}}^T {\mathbf{v}} + \eta } \right)\left| {\mathbf{v}} \right.} \right]} \right|_{{E\left[ {{\mathbf{XX}}^T } \right] = {\mathbf{B}}}} = {\mathbf{B}}_i {\mathbf{v}}$, where B _i is the i-th row of B. Finally, we have L ₁ = B v(n).

Substituting it into (A-3) and integrating w.r.t. β yields

$$ {\mathbf{F}}\left( \beta \right) = {\mathbf{I}}\left( \beta \right){\mathbf{v}}(n), $$

(A-4)

where ${\mathbf{I}}\left( \beta \right) = - \int {^{\beta } } \gamma \left( \beta \right){\mathbf{B}}d\beta$ and the constant of integration is equal to zero because of the boundary condition F(∞) = 0. To evaluate I(0) and hence ${\mathbf{H}} = {\mathbf{F}}(0) = {\mathbf{I}}(0){\mathbf{v}}(n)$, we note that ${\mathbf{B}} = {\mathbf{UD}}(n){\mathbf{U}}^T$ and thus

$$ {\mathbf{I}}(0) = {\mathbf{U}}\left( { - \int {^0 } \gamma \left( \beta \right){\mathbf{D}}(n)d\beta } \right){\mathbf{U}}^T = {\mathbf{U}}\Lambda {\mathbf{D}}_{\Lambda } {\mathbf{U}}^T, $$

(A-5)

where ${\mathbf{D}}_{\Lambda } = {\text{diag}}\left( {I_1 \left( \Lambda \right),...,I_L \left( \Lambda \right)} \right)$ and

$$ \begin{array}{*{20}c} {I_i \left( \Lambda \right) = \int_0^{\infty } {exp\left( { - \beta \varepsilon } \right)\left[ {\mathop \Pi \limits_{k = 1}^L \left( {2\alpha \beta \lambda_k + 1} \right)^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. } 2}}} } \right]\left( {2\alpha \beta \lambda_i + 1} \right)^{- 1} d\beta }, } \\ {i = 1,2, \cdots, L,} \\ \end{array} $$

(A-6)

which can be numerically evaluated.

Finally, we have the desired result in (5)

$$ {\mathbf{H}}_1 = E_{{\left\{ {\mathbf{v}} \right\}}} \left[ {\mathbf{H}} \right] = E_{{\left\{ {\mathbf{v}} \right\}}} \left[ {{\mathbf{F}}(0)} \right] = {\mathbf{U}}\Lambda {\mathbf{D}}_{\Lambda } {\mathbf{U}}^T E\left[ {{\mathbf{v}}(n)} \right] $$

(A-7)

For the LMS algorithm, B will be equal to R _XX and accordingly D _Λ is equal to the identity matrix and $\sigma_e^2 \left( {\mathbf{v}} \right) = {\mathbf{v}}^T {\mathbf{R}}_{XX} {\mathbf{v}} + \sigma_g^2$.

1.2 Appendix B: Evaluation of s ₃ and M ₃

As in Appendix A, we write ${\mathbf{s}}_3 = E_{{\left\{ {{\mathbf{X}},\eta } \right\}}} \left[ {{{e^2 {\mathbf{XX}}^T } \mathord{\left/ {\vphantom {{e^2 {\mathbf{XX}}^T } {\left( {\varepsilon + \alpha {\mathbf{X}}^T {\mathbf{X}}} \right)^2 }}} \right. } {\left( {\varepsilon + \alpha {\mathbf{X}}^T {\mathbf{X}}} \right)^2 }}\left| {\mathbf{v}} \right.} \right]$ as:

$$ {\mathbf{s}}_3 = C_R \iint\limits_{{L + 1{\kern 1pt} {\text{fold}}}} {\frac{{e^2 {\mathbf{XX}}^T }}{{\left( {\varepsilon + \alpha {\mathbf{X}}^T {\mathbf{X}}} \right)^2 }}exp\left( { - \tfrac{1}{2}{\mathbf{X}}^{\mathbf{T}} {\mathbf{R}}_{XX}^{- 1} {\mathbf{X}}} \right)f\left( \eta \right)d\eta d{\mathbf{X}}}. $$

(B-1)

Let us define

$$ \begin{array}{*{20}c} {{\mathbf{\bar{F}}}\left( \beta \right) = C_R \iint\limits_{{L + 1{\text{ fold}}}} {\frac{{e^2 {\mathbf{XX}}^T exp\left( { - \beta \left( {\varepsilon + \alpha {\mathbf{X}}^T {\mathbf{X}}} \right)} \right)}}{{\left( {\varepsilon + \alpha {\mathbf{X}}^T {\mathbf{X}}} \right)^2 }}}} \\ { \cdot \exp \left( { - \tfrac{1}{2}{\mathbf{X}}^T {\mathbf{R}}_{XX}^{- 1} {\mathbf{X}}} \right)f\left( \eta \right)d\eta d{\mathbf{X}}.} \\ \end{array} $$

(B-2)

Comparing (B-2) with (B-1), it can be seen that ${\mathbf{s}}_3 = {\mathbf{\bar{F}}}(0)$. To evaluate ${\mathbf{\bar{F}}}\left( \beta \right)$, we differentiate (B-2) twice w.r.t. β to get ${{d^2 {\mathbf{\bar{F}}}\left( \beta \right)} \mathord{\left/ {\vphantom {{d^2 {\mathbf{\bar{F}}}\left( \beta \right)} {d\beta^2 }}} \right. } {d\beta^2 }} = \gamma \left( \beta \right){\mathbf{L}}_3$, where ${\mathbf{L}}_3 = E_{{\left\{ {{\mathbf{X}},\eta } \right\}}} \left. {\left[ {e^2 {\mathbf{XX}}^T \left| {\mathbf{v}} \right.} \right]} \right|_{{E\left[ {{\mathbf{XX}}^T } \right] = {\mathbf{B}}}}$, and γ(β), C _B , and B have been defined in Appendix A. Consider the (i, j)-th element of L ₃: ${\mathbf{L}}_{3,i,j} = E_{{\left\{ {{\mathbf{X}},\eta } \right\}}} \left[ {e^2 x_i x_j \left| {\mathbf{v}} \right.} \right]\left| {_{\mathbf{B}} } \right.$. Using Price’s theorem, we have ${{\partial {\mathbf{L}}_{3,i,j} } \mathord{\left/ {\vphantom {{\partial {\mathbf{L}}_{3,i,j} } {\partial r_{{x_i x_j }} }}} \right. } {\partial r_{{x_i x_j }} }} = E_{{\left\{ {{\mathbf{X}},\eta } \right\}}} \left[ {e^2 \left| {\mathbf{v}} \right.} \right]\left| {_{\mathbf{B}} } \right. = \sigma_e^2$, where $\sigma_e^2 = {\mathbf{v}}^T {\mathbf{Bv}} + \sigma_g^2$. Integrating ${{\partial {\mathbf{L}}_{3,i,j} } \mathord{\left/ {\vphantom {{\partial {\mathbf{L}}_{3,i,j} } {\partial r_{{x_i x_j }} }}} \right. } {\partial r_{{x_i x_j }} }}$ w.r.t. r _xixj gives ${\mathbf{L}}_{3,i,j} = \sigma_e^2 r_{{x_i x_j }} + c_{i,j}$, where $c_{i,j} = E\left. {\left[ {e^2 x_i x_j } \right]} \right|_{{r_{{x_i x_j = 0}} }}$ is the integration constant. Using Price’s theorem again, we have ${{\partial c_{i,j} } \mathord{\left/ {\vphantom {{\partial c_{i,j} } {\partial r_{{x_i e}} }}} \right. } {\partial r_{{x_i e}} }} = \left. {\left[ {E\tfrac{{de^2 }}{de}x_j } \right]} \right|_{{r_{{x_i x_j = 0}} }} = E\left[ {\tfrac{{d^2 e^2 }}{{de^2 }}} \right]r_{{x_j e}} = 2r_{{x_j e}}$. Integrating once again, we get $c_{i,j} = 2r_{{x_j e}} r_{{x_i e}}$. Combining, we have ${\mathbf{L}}_{3,i,j} = \sigma_e^2 r_{{x_i x_j }} + 2r_{{x_j e}} r_{{x_i e}}$, and hence ${\mathbf{L}}_3 = \sigma_e^2 {\mathbf{B}} + 2{\mathbf{Bvv}}^T {\mathbf{B}}$. Substituting it into ${{d^2 {\mathbf{\bar{F}}}\left( \beta \right)} \mathord{\left/ {\vphantom {{d^2 {\mathbf{\bar{F}}}\left( \beta \right)} {d\beta^2 }}} \right. } {d\beta^2 }} = \gamma \left( \beta \right){\mathbf{L}}_3$ gives

$$ {{d^2 {\mathbf{\bar{F}}}\left( \beta \right)} \mathord{\left/ {\vphantom {{d^2 {\mathbf{\bar{F}}}\left( \beta \right)} {d\beta^2 }}} \right. } {d\beta^2 }} = \gamma \left( \beta \right)\sigma_e^2 {\mathbf{B}} + 2\gamma \left( \beta \right){\mathbf{Bvv}}^T {\mathbf{B}}. $$

(B-3)

Integrating (B-3) w.r.t. β and using $\sigma_e^2 \left( {\mathbf{v}} \right) = {\mathbf{v}}^T {\mathbf{Bv}} + \sigma_g^2$ yields

$$ {\mathbf{s}}_3 = {\mathbf{I}}_1 + {\mathbf{I}}_2 + \sigma_g^2 {\mathbf{I}}_3, $$

where ${\mathbf{I}}_1 = 2\int_0^{\infty } {\int_{{\beta_1 }}^{\infty } {\gamma \left( {\beta_2 } \right){\mathbf{Bvv}}^T {\mathbf{B}}d\beta_2 d\beta_1 } } {\kern 1pt}, {\mathbf{I}}_2 = \int_0^{\infty } {\int_{{\beta_1 }}^{\infty } {\gamma \left( {\beta_2 } \right)\left( {{\mathbf{v}}^T {\mathbf{Bv}}} \right){\mathbf{B}}d\beta_2 d\beta_1 } },$ and ${\mathbf{I}}_3 = {\kern 1pt} \int_0^{\infty } {\int_{{\beta_1 }}^{\infty } {\gamma \left( {\beta_2 } \right){\mathbf{B}}d\beta_2 d\beta_1 } }$ with the boundary conditions: ${\mathbf{\bar{F}}}\left( \infty \right) = 0$ and ${{\partial {\mathbf{\bar{F}}}\left( \beta \right)} \mathord{\left/ {\vphantom {{\partial {\mathbf{\bar{F}}}\left( \beta \right)} {\partial \left. \beta \right|}}} \right. } {\partial \left. \beta \right|}}_{{\beta = \infty }} = 0$. The evaluation of the integrals I ₁, I ₂, and I ₃ is detailed below. Note, $E_{{\left\{ {\mathbf{v}} \right\}}} \left[ {\sigma_e^2 } \right] = E_{{\left\{ {\mathbf{v}} \right\}}} \left[ {{\mathbf{v}}^T {\mathbf{Bv}}} \right] + \sigma_g^2$ is upper bounded by $E_{{\left\{ {\mathbf{v}} \right\}}} \left[ {{\mathbf{v}}^T {\mathbf{R}}_{XX} {\mathbf{v}}} \right] + \sigma_g^2 = \sigma_e^2 (n)$, which is the MSE at time instant n. To simplify the derivation of the worse case EMSE, the term ${\mathbf{I}}_2 + \sigma_g^2 {\mathbf{I}}_3$ can be approximated by $\sigma_e^2 \left( \infty \right){\mathbf{I}}_3$.

Evaluation of I₁:

Using the eigenvalue decomposition of B, one gets

$$ {\mathbf{I}}_1 = 2\int_0^{\infty } {\int_{{\beta_1 }}^{\infty } {\gamma \left( {\beta_2 } \right){\mathbf{UD}}(n){\mathbf{U}}^T {\mathbf{vv}}^T {\mathbf{UD}}(n){\mathbf{U}}^T d\beta_2 d\beta_1 } } = {\mathbf{UD}}_1 {\mathbf{U}}^T, $$

(B-4)

where ${\mathbf{D}}_1 = 2\int_0^{\infty } {\int_{{\beta_1 }}^{\infty } {\gamma \left( {\beta_2 } \right){\mathbf{D}}(n){\mathbf{VV}}^T {\mathbf{D}}(n)d\beta_2 d\beta_1 } }$ and V = U ^T v. The (i, j)-th element of D ₁ is $[{\mathbf{D}}_1 ]_{i,j} = 2\left[ {{\mathbf{VV}}^T } \right]_{i,j} I_{i,j}$, where $I_{i,j} = \int_0^{\infty } {\int_{{\beta_1 }}^{\infty } {\gamma \left( {\beta_2 } \right)} d_{ii} (n)d_{jj} (n)d\beta_2 d\beta_1 } = \lambda_i \lambda_j I_{ij} \left( \Lambda \right)$ $= \lambda_i \lambda_j I_{ij} (\Lambda )$, and

$$ \begin{array}{*{20}c} {I_{ij} \left( \Lambda \right) = \int_0^{\infty } {\beta \exp \left( { - \beta \varepsilon } \right)\left[ {\mathop \Pi \limits_{k = 1}^L \left( {2\alpha \beta \lambda_k + 1} \right)^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. } 2}}} } \right]} \left( {2\alpha \beta \lambda_i + 1} \right)^{- 1} \times (2\alpha \beta \lambda_j + 1^{- 1} d\beta } \\ \end{array} . $$

(B-5)

Hence ${\mathbf{I}}_1 \, = {\mathbf{UD}}_1 {\mathbf{U}}^T$, where ${\mathbf{D}}_1 = 2\Lambda \left[ {\left( {{\mathbf{VV}}^T } \right) \circ {\mathbf{I}}\left( \Lambda \right)} \right]\Lambda$, $\left[ {{\mathbf{I}}\left( \Lambda \right)} \right]_{i,j} = I_{ij} \left( \Lambda \right)$, and $\circ$ denotes element-wise product of two matrices. I _ij(Λ) can be evaluated numerically.

Evaluation of I₂:

$$ \begin{array}{*{20}c} {{\mathbf{I}}_2 = \int_0^{\infty } {\int_{{\beta_1 }}^{\infty } {\gamma \left( {\beta_2 } \right){\text{Tr}}\left( {{\mathbf{vv}}^T {\mathbf{B}}} \right){\mathbf{B}}d\beta_2 d\beta_1 } } } \\ { = {\mathbf{U}}\left( {\int_0^{\infty } {\beta_2 \gamma \left( {\beta_2 } \right){\text{Tr}}\left( {{\mathbf{U}}^T {\mathbf{vv}}^T {\mathbf{UD}}} \right){\mathbf{D}}d\beta_2 } } \right){\mathbf{U}}^T } \\ {{\kern 1pt} = {\mathbf{U}}\left( {\int_0^{\infty } {\beta_2 \gamma \left( {\beta_2 } \right)\mathop \Sigma \limits_k d_{kk} \left[ {{\mathbf{U}}^T {\mathbf{vv}}^T {\mathbf{U}}} \right]_{k,k} {\mathbf{D}}d\beta_2 } } \right){\mathbf{U}}^T } \\ { = {\mathbf{UD}}_2 {\mathbf{U}}^T \,,} \\ \end{array} $$

(B-6)

where we have used ${\mathbf{B}}^{- 1} = {\mathbf{UD}}^{- 1} {\mathbf{U}}^T$and the property of trace operation Tr(·). D₂ is a diagonal matrix and its i-th diagonal element is given by:

$$ \begin{array}{*{20}c} {\left[ {{\mathbf{D}}_2 } \right]_{i,i} = \int_0^{\infty } {\beta_2 \gamma \left( {\beta_2 } \right)\mathop \Sigma \limits_k d_{kk} d_{ii} \left[ {{\mathbf{U}}^T {\mathbf{vv}}^T {\mathbf{U}}} \right]_{k,k} d\beta_2 } } \\ { = \mathop \Sigma \limits_k \left( {\int_0^{\infty } {\beta_2 \gamma \left( {\beta_2 } \right)} d_{kk} d_{ii} d\beta_2 } \right)\left[ {{\mathbf{VV}}^T } \right]_{k,k} } \\ { = \mathop \Sigma \limits_k \lambda_k \lambda_i I_{ki} \left( \Lambda \right)\left[ {{\mathbf{VV}}^T } \right]_{k,k} } \\ \end{array}, $$

(B-7)

where I _ki (Λ) has already been defined in (B-5).

Evaluation of I₃:

Since ${\mathbf{I}}_3 = \int_0^{\infty } {\int_{{\beta_1 }}^{\infty } {\gamma \left( {\beta_2 } \right){\mathbf{UD}}(n){\mathbf{U}}^T d\beta_2 d\beta_1 } } = {\mathbf{UD}}_3 (n){\mathbf{U}}^T$, it suffices to evaluate the integral of the diagonal elements of D ₃(n) as follows:

$$\begin{array}{*{20}c} {{\left[ {D_{3} {\left( n \right)}} \right]}_{{i,i}} = {\int_0^\infty {{\int_{\beta _{1} }^\infty {\gamma {\left( {\beta _{2} } \right)}d_{{ii}} {\left( n \right)}d\beta _{2} d\beta _{1} } }} }} \\ { = {\int_0^\infty {{\int_0^{\beta _{2} } {\gamma {\left( {\beta _{2} } \right)}d_{{ii}} {\left( n \right)}d\beta _{1} d\beta _{2} } }} }} \\ { = \lambda _{i} {\int_0^\infty {\beta \exp {\left( { - \beta \varepsilon } \right)}{\left[ {{\mathop {II}\limits_{k = 1}^L }{\left( {2\alpha \beta \lambda _{k} + 1} \right)}^{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-\nulldelimiterspace} 2}} } \right]}{\left( {2\alpha \beta \lambda _{i} + 1} \right)}^{{ - 1}} d\beta } }} \\ \end{array} .$$

Hence, ${\mathbf{D}}_3 (n) = \Lambda {\mathbf{I}}\prime \left( \Lambda \right)$, where I′(Λ) is a diagonal matrix with its i-th diagonal element (also can be numerically evaluated) given by

$$ I_i^{\prime } \left( \Lambda \right) = \int_0^{\infty } {\beta \exp \left( { - \beta \varepsilon } \right)\left[ {\mathop \Pi \limits_{k = 1}^L \left( {2\alpha \beta \lambda_k + 1} \right)^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. } 2}}} } \right]\left( {2\alpha \beta \lambda_i + 1} \right)^{- 1} } d\beta . $$

(B-8)

Finally, we have

$$\begin{array}{*{20}c} {{\mathbf{s}}_{3} = {\mathbf{UD}}_{1} {\mathbf{U}}^{T} + {\mathbf{UD}}_{2} {\mathbf{U}}^{T} + \sigma ^{2}_{g} {\mathbf{UD}}_{3} {\mathbf{U}}^{T} } \\ { = 2{\mathbf{U}}{\left\{ {\Lambda {\left[ {{\left( {{\mathbf{VV}}^{T} } \right)}\circ {\mathbf{I}}{\left( \Lambda \right)}} \right]}\Lambda } \right\}}{\mathbf{U}}^{T} + {\mathbf{UD}}_{2} {\mathbf{U}}^{T} + \sigma ^{2}_{g} {\mathbf{U}}\Lambda {\mathbf{I}}\prime {\left( \Lambda \right)}{\mathbf{U}}^{T} } \\ \end{array} $$

and

$$ \begin{array}{*{20}c} {{\mathbf{M}}_3 = E_{{\left\{ {\mathbf{v}} \right\}}} \left[ {{\mathbf{s}}_3 } \right] = 2\mu^2 {\mathbf{U}}\left\{ {\Lambda \left[ {\left( {{\mathbf{U}}^T {\mathbf{\Xi }}(n){\mathbf{U}}} \right) \circ {\mathbf{I}}\left( \Lambda \right)} \right]\Lambda } \right\}{\mathbf{U}}^T } \\ { + \mu^2 {\mathbf{U\bar{D}}}_2 {\mathbf{U}}^T + \mu^2 \sigma_g^2 {\mathbf{U}}\Lambda {\mathbf{I}}\prime \left( \Lambda \right){\mathbf{U}}^T } \\ \end{array} . $$

(B-9)

From numerical results, I ₂ is close to zero if the EMSE is small, and ${\mathbf{s}}_3 \approx {\mathbf{I}}_1 + \sigma_g^2 {\mathbf{I}}_3$. For the LMS algorithm, the normalization term in (B-2) is missing and L ₃ can be obtained by replacing B above by R _XX .