Finite Aperture Stereo

Abstract

Multi-view stereo remains a popular choice when recovering 3D geometry, despite performance varying dramatically according to the scene content. Moreover, typical pinhole camera assumptions fail in the presence of shallow depth of field inherent to macro-scale scenes; limiting application to larger scenes with diffuse reflectance. However, the presence of defocus blur can itself be considered a useful reconstruction cue, particularly in the presence of view-dependent materials. With this in mind, we explore the complimentary nature of stereo and defocus cues in the context of multi-view 3D reconstruction; and propose a complete pipeline for scene modelling from a finite aperature camera that encompasses image formation, camera calibration and reconstruction stages. As part of our evaluation, an ablation study reveals how each cue contributes to the higher performance observed over a range of complex materials and geometries. Though of lesser concern with large apertures, the effects of image noise are also considered. By introducing pre-trained deep feature extraction into our cost function, we show a step improvement over per-pixel comparisons; as well as verify the cross-domain applicability of networks using largely in-focus training data applied to defocused images. Finally, we compare to a number of modern multi-view stereo methods, and demonstrate how the use of both cues leads to a significant increase in performance across several synthetic and real datasets.

1 Introduction

The extraction of 3D geometry from digital images has a long and varied history, and continues to be an actively studied field. The understanding of a scene’s composition is central to many applications such as robotics, augmented reality and self-driving cars; and remains a challenging problem at the forefront of computer vision research.

Given a single 2D projection of a scene captured by a camera, the problem at hand is to estimate the underlying scene structure. Though the shape of this geometry is independent to its reflectance properities prior to capture, the projection of the scene to an image entangles these quantities as pixel intensities. Clearly, this process is not invertible, and any number of solutions exist that could describe the surface manifold.

Only recently has single-image 3D reconstruction achieved compelling results due to the adoption of learning-based methods. However, such methods are not perfect, and do not necessarily generalise well to unseen data. The reasoning behind unsatisfactory results in these scenarios are not always obvious, since the perception of the scene via contextual cues, image features and shape priors are learnt as implicit components of the framework. It is therefore difficult to evaluate why one scene may work better than another, or to fully understand the limitations of a particular method. This is true of any learning-based approach to varying extents.

It is apparent then that more information is required for generalised 3D reconstruction. For passive methods, this is usually some measurable change in the scene appearance arising from different viewpoints, camera settings, or environmental conditions such as lighting. By relating these observational cues to scene-centric or camera-centric models, 3D information can be inferred from multiple 2D images.

For example, multi-view stereo (MVS) aims to triangulate scene points from two or more images. Within the constraints of epipolar geometry, there exists a relationship between a given scene point and its projection across multiple views; providing candidate solutions of the original 3D coordinates. The search of this candidate space is sometimes referred to as the correspondence problem, and it is solved by comparing the similarity of pixels across neighbouring viewpoints.

Clearly, this principle strongly implies a number of properties about the scene content, and subsequently the performance of such methods is intrinsically linked to the data it is operating on. While capable of sub-millimeter accuracy in the presence of uniquely textured diffused materials, MVS reconstructions begin to degrade when applied beyond this ideal Lambertian surface model. Without the introduction of regularisation or scene priors, surfaces exhibiting complex light interactions such as specularities and sub-surface scattering cannot be recovered via multi-view consistency. Furthermore, regions of low or periodic texture make correspondence challenging, with concavities and thin structures often failing due to few observations.

While many previous works focus on developing approaches that work around these constraints, in this work we aim to overcome them by generalising image formation away from the traditional pinhole camera model. In doing so, we are able to exploit the characteristics of the camera to leverage additional information about the scene.

Specifically, the use of a lens introduces aberrations to the image that are not captured by the pinhole model. Traditionally, their appearance in the image serves only as sources of outlier that must be avoided or corrected. For example, while lens distortion can be detected during calibration, defocus blurring as a result of a finite aperture cannot. While this may not be a concern for large scale scenes such as buildings, the scene must nonetheless remain within the depth of field of the camera (DoF) where pixels can be considered sharp.

At first glance, it appears the formation of defocus is the prohibitive factor here; whose corruption of the scene radiance prevents the application of MVS. While this is true it is simply unavoidable - yet strangely presents an advantageous situation. Perhaps surprisingly, defocus itself can be considered a rich source of information about the scene structure. At its simplest, this could be the location of the focal plane according to a focus measure, which identifies focused pixels according to the axiom; defocus blur acts as a low-pass filter.

Instead, in this work we pursue the analysis of the defocus appearance, which in literature is best known as depth from defocus (DFD). While MVS introduces information through changes in viewpoint, DFD instead modifies the camera parameters; such as the focusing distance or aperture size. Defocus analysis is therefore monocular, and permits the recovery of view-dependent materials that would otherwise be challenging for MVS. However, for this reason traditional implementations only achieve partial reconstructions.

In this paper, we explore how MVS and DFD can be used together to recover geometry from macro-scale scenes with complex materials; and how the combination of these cues achieves higher quality reconstructions than if they were used individually. Though some previous works have demonstrated this, no work that we are aware of does so in the context of general 3D reconstruction. As part of our evaluation, we compare against and outperform a number of modern MVS approaches.

The majority of defocus-based literature hinges on the thin lens camera model. Here, we explain why this model is not robust enough for multi-view reconstruction, and instead develop our framework around the principles of a thick lens. To supplement this, we propose a novel and practical thick lens calibration procedure suitable for macro-lenses. The effectiveness of our calibration is demonstrated experimentally on a number of real-world datasets.

Defocus-based literature has only recently started shifting towards modern learning-based methodologies. Here, we evaluate the advantages of a feature-based cost function derived from a pre-trained convolutional neural network (CNN). Though networks trained end-to-end may have ambiguity as a whole regarding generalising to different inputs, it has been shown that image-based feature extraction transfers well across domains. Our results concur with these findings, and demonstrate a step improvement over traditional pixel-based comparison. Significantly, our results indicate the feature extractor pre-trained largely on pinhole images has the same capability with defocused images.

To summarise, this paper revisits the key aspects of image-based geometry recovery - image formation, calibration and multi-view reconstruction, and presents the following contributions:

• 1. An MRF-based reconstruction framework unifying stereo and defocus cues using deep features

• 2. A novel thick lens calibration procedure used to capture a number of real-world multi-view, multi-focus datasets

• 3. An extensive evaluation demonstrating the benefits of our approach, including an ablation study and comparisons against several modern MVS methods

• 4. Real and synthetic datasets released with this paper

This paper builds on our previous works Bailey and Guillemaut (2020); Bailey et al. (2021), and combines them to produce a complete pipeline for recovering geometry from finite aperture images using stereo and defocus cues. We introduce the feature-based cost function and have included an extended calibration derivation and evaluation to better illustrate the contributions of each cue under different conditions.

The remainder of this paper is structured as follows. Section 2 discusses previous work. Section 3 discusses image formation, and introduces the thick lens model. Section 4 explains our proposed calibration for this model, and Sect. 5 provides details on the reconstruction pipeline. Section 6 evaluates results on both synthetic and real data, and Sect. 7 concludes this work.

2 Previous Work

In this section, we survey related work. Here, stereo-based and focus-based reconstruction approaches are covered, and we include works considering these cues individually or in combination. To clarify the often interchanged terminology used in focus-based reconstruction and to keep the survey concise, we largely exclude approaches which evaluate the structure of a scene from a focal stack based on the response of a focus measure e.g. Moeller et al. (2015).

2.1 Multi-View Stereo

Perhaps one of the most widely understood reconstruction principles, MVS recovers 3D structure by identifying corresponding features from images of the scene taken at different viewpoints. Using geometric constraints arising from the pinhole camera model, 3D points can be triangulated from two or more of these features according to the pose of each view. Broadly speaking, the quality of reconstruction largely depends on three factors.

Scene Representation How surfaces are modelled not only affects the resolution of the final result, but also places restrictions on the reconstruction algorithm. For instance, voxel-based Vogiatzis et al. (2007); Logothetis et al. (2019); Hornung and Kobbelt (2006); Kar et al. (2017); Choy et al. (2016) and mesh-based Li et al. (2016); Delaunoy and Pollefeys (2014) representations allow for a globally optimal result, since all views can be evaluated jointly. Alternatively, view-dependent methods Schönberger et al. (2016); Tola et al. (2012) only use a subset of the input images to recover a depth map of each viewpoint. While they do not impose the strict initialisation of voxel-based and mesh-based methods, they require post processing and produce potentially less robust results.

Feature Matching At the heart of all MVS algorithms is a similarity metric used to identify corresponding points between images. Classical metrics implement per-pixel comparisons such as sum of squared differences (SSD) Li and Zucker (2010) and normalised cross correlation (NCC) Li et al. (2016); Bradley et al. (2008); Furukawa and Ponce (2010). Some works exploit perspective distortion to also estimate surface normals Bradley et al. (2008). More recent approaches generally use feature descriptors to extract richer information from the source images. Though initially hand-crafted Tola et al. (2010, 2012), the advent of deep learning introduced data-driven feature extraction with CNNs Zagoruyko and Komodakis (2015); Yao et al. (2018).

Regularisation To overcome the real-world limitations of standard MVS assumptions, most approaches use a regularisation framework to enforce scene priors. A popular traditional approach involves formulating these priors as part of an energy function, and solving with a Markov Random Field (MRF). Early deep learning works followed a similar idea, though recent approaches regularise with learnt priors.

Of particular interest to this survey is view-dependent methods. Many conventional approaches were able to produce compelling results despite the limitations of traditional feature matching, often resulting in creative methodologies Zhu et al. (2015); Liu et al. (2010); Tola et al. (2012). Notably, PMVS Furukawa and Ponce (2010) combine matched patches rather than point clouds, and refine the final mesh using an energy optimisation to impose smoothness constraints. COLMAP Schönberger et al. (2016), arguably one of the best performing conventional MVS methods, combines a structure from motion calibration with a view dependent reconstruction pipeline to produce high quality 3D models.

More recently, deep learning-based approaches have seen widespread success. SurfaceNet Ji et al. (2017) introduced the first method trained end-to-end based around a voxel grid. DeepMVS Huang et al. (2018) instead generates a plane sweep volume and aggregates matched features from an arbitary number of images. MVSNet Yao et al. (2018) introduces differentiable homography warping, and R-MVSNet Yao et al. (2019) improves the memory efficency with a recurrent architecture. PointMVSNet Chen et al. (2019) adopts a coarse-to-fine approach with multi-scale features. CasMVSNet Gu et al. (2019) develops a memory efficent cost volume and adapts it to existing methods. VisMVSNet Zhang et al. (2020) considers per-pixel visibility according to pair-wise observations and generates a cost volume via uncertainty maps. Though not advertised as MVS, neural radiance fields Mildenhall et al. (2020) achieve dense implicit reconstructions. Other notable works include Luo et al. (2019); Kuhn et al. (2020).

2.2 Depth from Defocus

By modelling the point spread function (PSF) of the camera, depth information of the scene can be leveraged from the formation of defocus on the image plane. DFD is a field of research that approaches this idea in many different and creative ways. Though techniques exist for evaluating depth from a single defocused image Chakrabarti and Zickler (2012); Anwar et al. (2021); Carvalho et al. (2019); Kashiwagi et al. (2019), we primarily focus on methods that require several defocused images captured with circular apertures.

Acquisition A convenient method for capturing multiple defocused images is with a lightfield camera Tao et al. (2013). However, lightfield cameras can only capture the scene at a limited resolution. With conventional camera lenses, there are two main approaches to generate differently focused images - with varying aperture size Pentland (1987); Martinello et al. (2015); Song and Lee (2018) or focusing distance Favaro et al. (2008); Namboodiri et al. (2008). Changing the aperture size is often simpler, but the scene reconstruction volume is limited due to the relative blur exhibiting a symmetrical transfer function Mannan and Langer (2015). Although focal stacks largely overcome this ambiguity, refocusing the camera in this way introduces scale and translational differences between images and subsequently requires correcting Watanabe and Nayar (1998); Tang et al. (2017); Ben-Ari (2014); Bailey and Guillemaut (2020). Some methods Hasinoff and Kutulakos (2009) vary both the aperture size and focus setting to capture dense information about the camera PSF.

PSF Modelling Most approaches assume a convolutional formation model, allowing the PSF to be approximated as a 2D kernel. Two popular choices include the Pillbox Watanabe and Nayar (1998); Favaro (2010) and Gaussian Favaro et al. (2008); Ben-Ari (2014); Persch et al. (2017) functions. These methods do not consider many of the aberrations present in optical systems, so some works Kashiwagi et al. (2019); Martinello et al. (2015) instead directly measure the blurring response of the camera. Other works do not model the PSF explicitly, instead depending on a data driven approach Hasinoff and Kutulakos (2009); Carvalho et al. (2019); Favaro and Soatto (2005). In many cases, a thin lens defocus model is assumed despite the fact this model does not hold in real-world optical systems. Lin et al. (2013) improves reconstruction accuracy through iterative refinement. Paramonov et al. (2016) considers a model beyond a thin lens, and formulates sub-aperture disparity relative to the entrance pupil in a colour coded-aperture camera. Bailey and Guillemaut (2020) proposes a formal calibration of a thick lens camera model, and applies it to capturing and reconstructing multi-view focal stacks.

Aside from Emerson and Christopher (2019) who utilise deep learning, most works adopt an MRF-based or numerical optimisation framework. Moreover, the overwhelming majority of DFD methods discussed only achieve single-view reconstructions. This is in part due to limitions modelling the PSF, as well as a lack of publically available datasets. To our knowledge, Bailey and Guillemaut (2020) is the only attempt at 3D reconstruction using only defocus cues; by fusing multiple single-view reconstructions together.

2.3 Hybrid Approaches

We will now discuss previous works that take advantage of multiple reconstruction cues. Most existing methods formulate their combination of stereo and defocus in an MRF framework. One approach is to combine cues with defocused stereo pairs Li et al. (2010); Rajagopalan et al. (2004); Chen et al. (2015); often expressing the relative blurring kernel in terms of pixel disparity. Takeda et al. (2013) applies coded apertures in this way. Acharyya et al. (2016) instead uses defocus to constrain stereo matching. Other methods apply single-image defocus constraints to better recover discontinuities Wang et al. (2016); Gheţa et al. (2007).

Alternative to pairwise-stereo, some methods use lightfield cameras to combine cues Lin et al. (2015); Tao et al. (2013); Tao et al. (2017), though reconstructions are limited to a very narrow baseline. Bhavsar and Rajagopalan (2012) considers multiple viewpoints, but does not apply this to 3D reconstruction. Chen et al. (2017) is the only approach we know of to use deep learning for combining cues. However, as with all works discussed, reconstructions remain limited to a single view.

Finally, shading cues have been proposed in combination with defocus Chen Li et al. (2016), stereo Wu et al. (2011) and both Tao et al. (2017) to alleviate the texture requirements of these cues.

2.4 Summary

Though many works have proposed methodologies considering stereo and defocus separately, far fewer have attempted combining them. Those who have limit reconstruction to a single view, and therefore do not recover a complete representation of the scene. In comparison to our previous works; though Bailey and Guillemaut (2020) remains the only method we know of that achieves 3D reconstruction using only defocus cues, it forgoes the explicit multi-view consistency of MVS. Bailey et al. (2021) demonstrates the advantages of using both stereo and defocus cues in 3D, but does not use a robust cost function or extensively illustrate the contribution of each cue. In this paper, we present the complete pipeline of our thick lens-based reconstruction approach, and address these shortcomings.

3 Image Formation

3.1 Projection Model

As discussed in the introduction, the pinhole camera model has become a key component to the theory behind MVS. Ignoring lens distortion, the projection of a world-space coordinate $\mathbf {X}$ to an image point on the camera sensor $\mathbf {x}$ is described by this model as Hartley (2000),

$$\begin{aligned} \mathbf {x} = K [ R \ \vert \ \mathbf {t} ] \ \mathbf {X}. \end{aligned}$$

(1)

Here, the intrinsic matrix K describes the projection itself, while rotation matrix R and translation vector $\mathbf {t}$ define the camera orientation in space. We define K as,

$$\begin{aligned} K = \begin{bmatrix} F &{} s &{} x_0 \\ 0 &{} F &{} y_0 \\ 0 &{} 0 &{} 1 \\ \end{bmatrix}, \end{aligned}$$

(2)

with F denoting the effective focal length, $x_0$ and $y_0$ describing the principal point (the centre of the image sensor relative to the centre of projection), and s the skew factor which is usually zero.

Let $r(\mathbf {x})$ define the radiance of the projected point. For a pinhole image, it is enough to simply assign the pixel colour according to r, as is the assumption in MVS. However, a more general expression can be used instead to describe the formation of a pixel $\mathbf {y}$ on image I Favaro et al. (2008),

$$\begin{aligned} I(\mathbf {y}) = \int _{}^{} k(\mathbf {y}, \mathbf {x}) \, r(\mathbf {x}) \, d\mathbf {x}. \end{aligned}$$

(3)

Here, $k(\mathbf {y}, \mathbf {x})$ represents the PSF, or the influence of the lens with respect to the formation of defocus. The pinhole model therefore becomes a special case of Eq. 3 where k assumes a Dirac delta centred around $\mathbf {y}$; thereby permitting the captured image to represent the incident radiance.

3.2 Defocus Model

In most DFD approaches, Eq. 3 is approximated as a convolution which imposes a fronto-parallel assumption about the scene. Although this technically becomes invalid at discontinuities, we found in our experiments the error introduced is negligble. Let us define $k_\sigma$ as a convolutional blurring kernel that estimates the PSF of the camera. Our image formation model then becomes a spatially variant convolution between the projected radiance and $k_\sigma$ Favaro et al. (2008); Favaro (2007)

$$\begin{aligned} I(\mathbf {y}) = (k_{\sigma } * r)(\mathbf {y}). \end{aligned}$$

(4)

The PSF kernel $k_{\sigma }$ resembles the shape of the aperture, and describes the distribution of light formed on the sensor in defocused regions. A popular choice in literature is to approximate the PSF as a 2D Gaussian function Favaro et al. (2008); Ben-Ari (2014). In this work, we also adopt this approach and define

$$\begin{aligned} k_{\sigma }(\mathbf {y}) = \frac{1}{2\pi \sigma ^2}e^{-\frac{1}{2}\left( \frac{\mathbf {y}}{\sigma }\right) ^2}. \end{aligned}$$

(5)

To complete our defocus camera model, we now need to derive the blur variance $\sigma$. This aspect of the defocus model is arguably the most important, since it relates the blurred appearance to scene depth d. Most existing literature consider a thin lens abstraction of the camera optics giving Favaro (2007)

$$\begin{aligned} \sigma (d) = \frac{\gamma a v}{2}\,\left( \,\frac{1}{d} + \frac{1}{v} - \frac{1}{f}\,\right) , \end{aligned}$$

(6)

where f is focal length, a is the aperture radius, v is the sensor distance from the lens, and $\gamma$ is a camera-specific constant.

Fig. 1

Comparison of pinhole (top) and thin lens (bottom) image formation models. Thin lens assumptions introduce defocus aberration by replacing the virtual pinhole with a principal plane $h_1$ at the same location. In both cases, the image distance v becomes the effective focal length derived in traditional stereo camera calibration

Fig. 2

Our camera model is a thick lens composed of two thin lenses each with focal length f separated by some distance. The effective pinhole location is at the entrance pupil $u_1$. Calculation of the defocus radius $\sigma$ for a given pixel is performed relative to the principal planes $h_1$ and $h_2$

This model has a number of drawbacks. First, the lens is assumed to be infinitesimally thin - simplifying the light transport to refract only once as it passes through the camera optics. In reality, light refracts at the boundary between two materials with differing refractive indices. For any physical glass lens suspended in air, light refracts once when it enters and again when it leaves.

Second, the thin lens model makes implicit and incorrect assumptions about the location of the principal plane of refraction. Comparing to the pinhole camera model, thin lens theory implies the centre of projection aligns with this refractive plane as seen in Fig. 1. This does not hold in practise, especially with macro-lenses. The implications of this become clear after realising defocus-based reconstructions are relative to the thin lens; while camera orientation and stereo-based reconstructions are relative to the pinhole. Therefore, any disparity between the locations of these quantities will introduce ambiguity between cues.

To overcome these problems, we model defocus formation according to thick lens principles. This model describes the camera lens as two principal planes $h_1$ and $h_2$ seperated by some distance as illustrated in Fig. 2; implying light refracts twice as it passes through the lens. Immediately, this addresses the first problem with the thin lens model.

This addition of another refractive plane in our model gives rise to a question - where is the aperture located? The answer to this is not immediately clear, but for our purposes this doesn’t matter. Instead, we need only consider the virtual images of the aperture as seen through the front or the back of the camera lens. These images are referred to as the entrance $u_1$ and exit $u_2$ pupils respectively, and control the amount of light entering or leaving each lens in the model.

If the pupil diameters are the same (a symmetric lens), then their positions converge on their respective principal planes. A more realistic model considers the scenario when their sizes differ, which has the effect of displacing the pupils. The size of this displacement is proportional to the ratio of pupil diameters, or pupillary magnification p Rowlands (2017)

$$\begin{aligned} p = \frac{u_{2}}{u_{1}}. \end{aligned}$$

(7)

Given that the effective pinhole location exists at the entrance pupil $u_1$, the second problem with the thin lens model can be addressed by finding p. Then, the displacement w of the front principal plane $h_1$ can be found Rowlands (2017)

$$\begin{aligned} w = f \left( \frac{1}{p} - 1\right) . \end{aligned}$$

(8)

To account for this offset, Eq. 6 now becomes

$$\begin{aligned} \sigma (d) = \frac{\gamma a v}{2}\,\left( \,\frac{1}{d-w} + \frac{1}{v} - \frac{1}{f}\,\right) , \end{aligned}$$

(9)

with scene depth d relative to the entrance pupil, and defocus observations relative to $h_1$. From the above it is clear that when $p \rightarrow 1$, $w \rightarrow 0$. Only under these conditions do thin lens assumptions become valid.

3.3 Camera Model Summary

Throughout this section, we have discussed three image formation models; pinhole, thin lens and thick lens. Hopefully, it is now apparent that the thick lens approach we take in this paper is a generalisation of the thin lens model; and by extension, thin lens assumptions are a generalisation of the traditional pinhole camera. In this way, it is interesting how the complexity of each model progresses by incrementally building on the principles of the previous one.

Fig. 3

The capture of a dataset is composed of two stages: aquisition and post-processing. During acquisition, an appropiate number of focal stack images are captured depending on the scene volume and aperture setting of the camera. Then, a series of images are taken concerning the thick lens calibration detailed in Sect. 4. Finally, with each camera setting calibrated, the capture of the actual scene can commence - with multi-view datasets achieved by orbiting the single camera around the scene. Using this data, the camera matrices describing image projection and pose are derived; with differences in image scale and translation as a result of refocusing the camera corrected. Finally, the parameters for the thick lens defocus model are estimated and refined

Could this dynamic be continued further, and would it be of any benefit? Consider, modern lenses are incredibly complicated pieces of equipment, with many optical elements involved in resolving the focused image. Surely, by incorporating more parameters into our model we could describe the camera behaviour with even higher precision? Certainly, additional factors could be included in the formation model - for example, we only consider light as a particle and disregard wavelength-dependent effects such as chromatic aberration. However, the majority of the complexity in modern lenses is to correct for such aberrations, so their appearance is far less significant than defocus blurring. It is not unreasonable to assume this will only continue to improve in future cameras, whereas defocus formation remains unavoidable. Moreover, the complexity of camera lenses is so great that we would argue only data-driven models, rather than our analytical model, can incorporate these less prominent features with any accuracy. That being said, we have already demonstrated in our previous work Bailey and Guillemaut (2020) the advantages our thick lens model has over traditional defocus analysis. For the scope of this paper, thick lens principles are sufficient for unifying stereo and defocus cues.

3.4 Cue Considerations

Let us now revisit Eq. 3, which describes the behaviour of all three camera models. Fundamentally, neither stereo nor defocus cues model the light reflected from a scene point beyond a simple projective transform. In other words, the light transport of the scene is not considered prior to the final surface interaction. Both cues are therefore dependent on the scene appearance alone as observed in the 2D projection. This is in contrast to shape from shading methods, that aim to recover geometry with consideration of the lighting conditions; and are well known for their independence of texture. Why then do we consider two cues that appear to depend on similar information?

First, it should be re-iterated that defocus information is monocular, and therefore remains coherent in the presence of view-dependent materials. On the other hand, MVS relies on multi-view consistency, and therefore degrades in performance when applied to materials exhibiting complex reflectance. Unlike shading information defocus is a camera-centric phenomena, and its reconstruction principles can be generalised across many complex environments and scenes with little regard to their content. Often, shading cues must make assumptions about the environment such as the number of light sources and may impose restrictions on the scene materials. Provided sufficent defocus-variant texture is present Favaro (2007), we argue defocus is one of the richest passive sources of information regarding the scene structure. At the macro-scale magnification explored in this paper, this texture limitation is not a concern.

4 Calibration

The calibration of the thick lens camera model is non-trivial for several reasons. First, unlike most approaches, we do not consider camera parameters provided by the manufacturer to be accurate for all focus settings. Rather, we only consider these values relevant when the camera is focused at infinity. Secondly, to our knowledge there is no standard approach for reliably calculating the pupil ratio p, whose value is of significant importance in our model. Finally, our calibration needs to correct for translation and scale differences between multi-focus images without dependance on DoF or texture content.

In this section, we will discuss how we solved these problems. We begin by defining a number of focus settings that sweep through the scene volume. In general, the more focus settings captured, the better our model can be applied to defocus-based reconstruction. Our calibration approach can then be broken down into several stages as summarised in Fig. 3. For each setting, the following key steps are made:

• 1. Calculate camera intrinsics and lens distortion

• 2. Derive affine transforms to register images

• 3. Estimate the defocus parameters in our model

• 4. Refine parameters in a per-viewpoint optimisation

From here onwards, we refer to parameters related to the i^th focus setting of this focal stack with a subscript. Without loss of generality, let us define a reference setting at $i=0$.

4.1 Camera Matrices

In this first step, we derive the intrinsic calibration of the camera using a standard approach proposed in Zhang (2000). A calibration plane is positioned in multiple orientations and captured for each focus setting. Images are taken with both a small and a large aperture. For each setting, feature points $\mathbf {c}$ are identified from the smaller aperture images. The intrinsic matrix $K_i$ and lens distortion coefficents for each setting are solved by minimising the reprojection error. In the following sections, images have lens distortion removed. R and $\mathbf {t}$ are calculated in a similar way for each viewpoint, using a set of scene features common to all views.

4.2 Registration

This step aims to register all images in a focal stack to a reference setting. A naive approach may be to directly use the parameters from the geometric calibration. Since $F_i$ is related to the projection magnification $m_i$ by Rowlands (2017)

$$\begin{aligned} F_i = f_i \left( 1 + \frac{m_i}{p_i} \right) , \end{aligned}$$

(10)

the scaling between two settings could be found quite easily if $p_i = 1$ and $f_i = f \ \forall \ i$. However, in our model neither of these conditions are guaranteed. In addition, while translation differences could be derived from the principal point in theory, in practise the estimation of this quantity is ill-posed and subject to unpredictable variations.

Instead, we exploit the detected features $\mathbf {c}$ from Sect. 4.1. By identifying corresponding features in the images, an optimal scale and translation can be calculated to best align them. The ratio of effective focal lengths between the reference ${F}_0$ and ${F}_i$ is used as an initial scaling factor $s_i$. This is refined in a least mean square optimisation:

$$\begin{aligned}&\min _{s_i}{ \sum _k \Vert \ \mathbf {t}_i^k - \bar{\mathbf {t}}_i \ \Vert ^2} \end{aligned}$$

(11)

$$\begin{aligned}&\mathbf {t}_i^k = \mathbf {c}_{0}^k - s_i\mathbf {c}_{i}^k \end{aligned}$$

(12)

where $\mathbf {c}_0$ and $\mathbf {c}_i$ are the feature coordinates, and $\bar{\mathbf {t}_i}$ is the mean of $\mathbf {t}_i^k \ \forall \ k$. Eq. 11 is solved as a function of $s_i$ using gradient descent. Once $s_i$ has been optimised, the corresponding ${\bar{t}}_i$ represents the required 2D translation. Images in the focal stack are then subject to the affine transform

$$\begin{aligned} T_i = \begin{bmatrix} s_i &{} 0 &{} \bar{t}_{ix} \\ 0 &{} s_i &{} \bar{t}_{iy} \\ \end{bmatrix}. \end{aligned}$$

(13)

After registration, all images in the focal stack share the camera matrices of the reference setting.

4.3 Parameter Estimation

In this section, we discuss how the parameters in Eq. 9$f_i$, $a_i$, $v_i$ and w are estimated. All parameters are implicitly assumed to be positive. We begin by calculating two intermediate variables $m_i$ and $p_i$.

Fig. 4

Calibration images of a uniform plane used for deriving average brightness focused at infinity (left) and at a focus setting (right). Besides the focus distance, all camera parameters and lighting conditions remain constant in both images. The observed change in brightness is therefore attributed to the pupil ratio. Images are white balanced and brightened for visualisation

Pupillary Magnification: Consider images of a uniform plane focused at infinity and at each of the defined focus settings (see Fig. 4). Our approach relates the change in observed brightness in these images to the pupil ratio $p_i$ at a particular focus setting under the following conditions:

Assumption 1

Exposure time and global illumination remain constant between the images.

Assumption 2

The pupil ratio has a value of 1 only when focused at infinity.

The amount of light incident to the image plane of the camera is related to the area of the smallest pupil. Therefore, assumption 2 implies that the maximum brightness observed will be when the camera is focused at infinity, since neither pupil is constricting the light entering the lens. Therefore, the value of $p_i$ will either be greater than or less than 1 depending on the camera lens. We will assume this is unknown, and show the derivation for $p_i < 1$ where $u_2 < u_1$. From assumption 1, the following must hold true:

$$\begin{aligned} \frac{b_{\infty }}{b_i} = \left( \frac{u_{2\infty }}{u_{2i}}\right) ^2. \end{aligned}$$

(14)

Here, $b_{\infty }$ and $u_{2\infty }$ are the average brightness and exit pupil diameter focused at infinity; and $b_i$ and $u_{2i}$ are the average brightness and exit pupil diameter at a given focus setting. Since $u_{1\infty } = u_{2\infty }$, Eq. 14 can be rewritten in terms of the entrance pupil according to Eq. 7

$$\begin{aligned} \frac{b_{\infty }}{b_i} = \left( \frac{u_{1\infty }}{u_{1i} \ p_i}\right) ^2. \end{aligned}$$

(15)

Knowing that Rowlands (2017)

$$\begin{aligned} u_1= & {} \frac{F_i}{N_i}, \end{aligned}$$

(16)

$$\begin{aligned} u_{1 \infty }= & {} \frac{f_{\infty }}{N_{\infty }}, \end{aligned}$$

(17)

where $f_{\infty }$ is the known focal length when focused at infinity, $N_{\infty }$ is the reported f-stop of the aperture and $N_i$ is the effective f-stop setting; Eq. 15 can be rewritten as:

$$\begin{aligned} \frac{b_{\infty }}{b_i} = \left( \frac{f_{\infty }N_i}{F_iN_{\infty }p_i}\right) ^2. \end{aligned}$$

(18)

Since Rowlands (2017)

$$\begin{aligned} N_i = N_{\infty } \left( 1 + \frac{m_i}{p_i} \right) , \end{aligned}$$

(19)

Equation 18 can be rearranged as a quadratic function of $p_i$ by substituting Eq. 19:

$$\begin{aligned} \frac{F_i}{f_{\infty }} \sqrt{\frac{b_{\infty }}{b_i}} p_i^2 - p_i - m_i = 0. \end{aligned}$$

(20)

The value of $p_i$ when $u_2 < u_1$ is given by the roots of Eq. 20.

$$\begin{aligned} p_i = \frac{f_{\infty }}{2F_i\sqrt{\frac{b_{\infty }}{b_i}}} \left( 1 \pm \sqrt{1 + \frac{4F_im_i}{f_{\infty }} \sqrt{\frac{b_{\infty }}{b_i}}} \right) . \end{aligned}$$

(21)

By definition, $b_\infty > b_i$ and $F_i > f_\infty$. As a result, the discriminant of Eq. 21 will always be greater than 1 which would render a negative solution. This is therefore discarded, leaving the single positive solution of $p_i$,

$$\begin{aligned} p_i = \frac{f_{\infty }}{2F_i\sqrt{\frac{b_{\infty }}{b_i}}} \left( 1 + \sqrt{1 + \frac{4F_im_i}{f_{\infty }} \sqrt{\frac{b_{\infty }}{b_i}}} \right) . \end{aligned}$$

(22)

Note here that Eq. 22 is only defined for $p_i < 1$. A similar derivation can be made for $u_2 > u_1$ by removing $p_i$ from Eq. 15. Conversely, in this case $p_i \ge 1$:

$$\begin{aligned} p_i = \frac{m_i}{\frac{F_i}{f_\infty }\sqrt{\frac{b_{\infty }}{b_i}} - 1}. \end{aligned}$$

(23)

Equations 22 and 23 represent a piecewise function describing the pupil ratio. The choice of either one when calculating $p_i$ is simply a case of whichever one gives a valid solution. See Appendix 1 for a proof that only one of these solutions is always valid. The only unknown here is $m_i$, which we derive next.

Projection Magnification The magnification $m_i$ in this context is the ratio of the object size in the scene to the projection of that object on the camera sensor. For a given focus setting, this is found by first finding the focusing distance $d_i$. This is the distance from the camera pinhole to the centre of the DoF. $m_i$ and $d_i$ are related as follows Kingslake (1992)

$$\begin{aligned} m_i = \frac{F_i}{d_i}. \end{aligned}$$

(24)

To calculate $d_i$, we apply the Sum Modified Laplacian (SML) Nayar and Nakagawa (1994) focus measure to the large aperture calibration pattern images captured in Sect. 4.1. Since the poses of the patterns are known, feature points on the calibration plane can be sampled and the distance to the camera found. Regions where a high response is measured indicates an area in-focus. Assuming the DoF is a parallel plane, samples from multiple calibration images can be collected to improve robustness. The weighted mean of the distribution above a threshold gives the value of $d_i$, from which $m_i$ is found.

Fig. 5

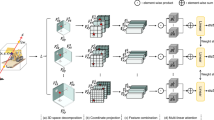
Diagram of the proposed iterative reconstruction framework. Defocus and stereo observations are generated from the calibrated focal stacks and synthetic pinhole images respectively. The cost function is generated from these observations via pixel values or extracted features, and weighted according to the value of $\alpha$. This weighted sum is input to an MRF framework, where spatial consistency is enforced according to second order smoothness priors. The output from the MRF is the estimated depth, which is used in the next iteration to re-generate pinhole images of the focal stacks. As iteration increases, $\alpha$ is updated and the effective resolution of the pipeline doubles. This process continues until the maximum number of iterations has been reached. To generate 3D models, the depth and normal maps from each viewpoint are converted to point clouds, and fused together

Focal Length Given $m_i$, $p_i$ and $F_i$, the value of $f_i$ is given by rearranging Eq. 10 as

$$\begin{aligned} f_i = \frac{F_i}{\left( 1 + \frac{m_i}{p_i} \right) }. \end{aligned}$$

(25)

Aperture The aperture radius $a_i$ is given by Kingslake (1992)

$$\begin{aligned} a_i = \frac{F_i}{2N_i}. \end{aligned}$$

(26)

Image Distance Usually, $v_i$ is defined by Kingslake (1992)

$$\begin{aligned} v_i = f_i(1 + m_i). \end{aligned}$$

(27)

While this is correct for a single image, this does not hold in the context of a focal stack. This is because, as the camera is refocused, there may be variance in the lens focal length f. Thus, for DFD observations to be relative to the same point (the reference focus setting at $i=0$), this drift needs to be accounted for when calculating $v_i$

$$\begin{aligned} v_i \ = \ f_i(1+m_i) - (f_0 - f_i) \ = \ f_i(2 + m_i) - f_0 . \end{aligned}$$

(28)

Equation 28 offsets Eq. 27 by the difference in focal length relative to $f_0$. Essentially, this adjustment aims to ensure the principal planes of each setting align with one another.

Pupil Displacement Finally, we can now define the value of w according to Eq. 8.

4.4 Parameter Refinement

An important practical consideration during acquisition is to capture multiple focal stacks with the same settings. So far, we have assumed the ideal case where the camera refocuses perfectly. However, throughout the calibration process the lens will not be returning to exactly the same focus setting. As a result, there may be a need to refine some parameters on a per-viewpoint basis, depending on the quality of the lens. In our experience, only the value of w needs adjusting in this way. All other parameters (including those used for image registration) appear sufficently accurate.

We optimise w using scene features with known position in the world reference frame. Our cost function is based on the relative blur between pairs of images in the focal stack. The cost function presented here is similar to the one used in Sect. 5 for reconstruction. First, we define the relative blur between settings i and j:

$$\begin{aligned} \sigma _{ij}(d) = \sqrt{\vert \sigma _i(d)^{2} - \sigma _j(d)^{2} \vert } \end{aligned}$$

(29)

where $\sigma (d)$ is defined in Eq. 9. Using this, we optimise w using images $I_a$ and $I_b$ from the focal stack.

$$\begin{aligned}&\min _{w}{ \sum _{\{ij\} \in {\Omega }} \sum _k \Vert \sigma _{ij}(d^k) \circ I_a \ - \ I_b \ \Vert ^2} \end{aligned}$$

(30)

$$\begin{aligned}&\{a,b\} \, = \, \left\{ \begin{aligned} \,&\{i,j\} \quad \sigma _i(d) < \sigma _j(d) \\ \,&\{j,i\} \quad \text {otherwise} \\ \end{aligned}\right. \end{aligned}$$

(31)

Here, ${\Omega }$ is a vector of paired image indices, $\circ$ is a defocus operator which we define later, and $d^k$ is the distance of the $k^{th}$ feature from the camera. Equation 30 blurs whichever image is sharpest to match the other for every feature, and compares the result with a pixel-wise square difference. This sparse optimisation can be thought of as a per-viewpoint global adjustment of all blurring functions describing the focal stack.

5 Reconstruction

Our approach combines defocus and stereo information to leverage the benefits of both cues to generate complete 3D models of macro-scale scenes. The proposed pipeline can be broken up into two sequential stages, as shown in Fig. 5.

Per-View Reconstruction Using stereo and defocus cues, we reconstruct per-viewpoint depth maps. As input, we take multi-view focal stacks captured and calibrated using the approach discussed in Sect. 4. These images have a narrow DoF, making them unsuitable for direct stereo matching. As part of our pipeline, we infer a focused image according to the current depth estimate, and perform stereo matching on these synthetically generated images. The two cues are then jointly optimised to find the surface estimate, which is refined in subsequent iterations. Our approach can be summarised as follows:

• 1. Calculate an initial thick-lens DFD reconstruction

• 2. Selectively composite the focal stack inputs using the camera model and estimated depth to approximate scene radiance

• 3. Find corresponding points from synthesised radiance

• 4. Combine defocus and correspondence information and recalculate surface at higher resolution

• 5. Repeat steps 2, 3 and 4 until maximum resolution or iteration reached

Point Cloud Fusion The point clouds from each view are combined to produce the final 3D model. We enforce consistency checks on each reconstructed point to reduce noise, before applying screened Poisson surface reconstruction Kazhdan and Hoppe (2013) to generate the final triangular surface mesh.

5.1 Energy Function

We formulate depth recovery of each view as a discrete labelling problem of N labels, which we generalise here to exploit both defocus and stereo cues. Each cue is represented as a data term in our energy function,

$$\begin{aligned} \begin{aligned}&E(\mathbf {x}, n) = (1 - \alpha (n)) \sum _{p \in \nu } \Phi _{D}(x_p) \ \ \\&\quad + \alpha (n) \sum _{p \in \nu } \Phi _{S}(x_p) \ + \frac{\lambda }{2^{n-1}} \sum _{(p,q) \in \epsilon } \Psi _{pq}(x_p, x_q). \end{aligned} \end{aligned}$$

(32)

Here, $\alpha$ is a scalar value between 0 and 1, and weights the contributions of the defocus term $\Phi _{D}$ and the stereo term $\Phi _{S}$. The proposed method linearly modulates its value with increasing iteration up to a maximum of 0.5. The value of $\lambda$ controls the amount of pairwise smoothness applied by $\Psi _{pq}$, which encourages second order smoothness as described in Olsson et al. (2013).

In our framework, we assume each pixel represents a surface and model it as a tangent plane. The orientation of each surface is estimated after every iteration by fitting a plane to neighbouring 3D points via singular value decomposition. During reconstruction, the candidate search space of each surface is independently reduced as a function of iteration n. Unlike traditional MRF formulations, this approach allows for high resolution reconstructions without requiring a corresponding number of labels; reducing memory usage and computational load. As n increases, the effect of the smoothness term is decreased to enable the recovery of higher fidelity surface details. Equation 32 is minimised using $\alpha$-expansion Boykov et al. (2001); Szeliski et al. (2008).

Each data term depends on a photometric cost function that compares the similarity of two image patches. In this paper we evaluate two such functions. For now, this is denoted $\Delta$ and will be explained in further detail later. We will now define each of the terms in Eq. 32.

5.2 Defocus Term

To calculate the defocus term for a pair of images $\{I_i$, $I_j\}$ in a given focal stack, a scale-space approach is taken. The relative blur between the images is found according to Eq. 29, and the sharper image is blurred to match the other. The cost function $\phi _{D}(x_{p})$ is defined by the similarity between the defocused and original image

$$\begin{aligned} \phi _{D}(x_{p}) = \sum _{\{ij\} \in {\Omega }} \Delta \left( \sigma _{ij}(x_p) \circ I_a, \ I_b \right) . \end{aligned}$$

(33)

As in Eq. 30, $\circ$ denotes the defocus operator, $\varvec{\Omega }$ contains indices of paired images, and $\{a,b\}$ are defined in Eq. 31. Since the accuracy of DFD is greatest when relative blur is small, only neighbouring images in the stack are paired together. When evaluating Eq. 33, we first remove harmonic texture components in the source images

$$\begin{aligned} I_i = I_i - (I_i \circ k_{\sigma }). \end{aligned}$$

(34)

This procedure, proposed in Favaro (2007), removes defocus-invariant texture components, and has been shown to improve the performance of focus analysis. We define our defocus operator $\circ$ as a linear diffusion operator as proposed in Favaro et al. (2008). Although this is equivalent to the Gaussian PSF discussed in Sect. 3.2, we found linear diffusion performs better with subpixel defocus radii. The forward diffusion constraint is enforced by starting Eq. 33 at the label closest to the depth $d_0$ where the relative blur $\sigma _{ij}(d_0) = 0$. We derive this from Eq. 29:

$$\begin{aligned} d_0 \ = \ \frac{a_i v_i \ \pm \ a_j v_j}{\frac{a_i}{f_i}(v_i - f_i) \ \pm \ \frac{a_j}{f_j}(v_j - f_j)} + w. \end{aligned}$$

(35)

The above simplifies to the result in Favaro et al. (2008) when $f_i = f_j$, $a_i = a_j$ and $w = 0$. Finally, the generated cost volume is normalised according to

$$\begin{aligned} \Phi _{D}(x_{p}) \, = \, 1 - \exp \left( -\frac{\phi _{D}(x_{p})}{\mu _D}\right) , \end{aligned}$$

(36)

where $\mu _D$ is the mean of the cost volume $\phi _{D}$.

5.3 Stereo Term

While the defocus term has a stable response in the presence of defocus-variant texture, it does not necessarily permit the recovery of high frequency surface detail. This is a consequence of the nature of defocus blur; surface details are attenuated by the aggregation of photons in out-of-focus regions. The stereo term is intended to improve the fidelity of the reconstruction by integrating correspondence information from synthetically generated images that approximate the scene radiance.

Compared to our previous work Bailey et al. (2021), we found that deblurring the focal stacks via non-blind deconvolution tends to be a source of instabililty; primarily in regions which do not have an accurate depth estimate. Overall, the benefits of a potentially sharper image vs the unstable conseqences when the reconstruction fails were not worthwhile. With our datasets, we found the radiance estimate produced through selective sampling of the focal stack produced a result that was perfectly adequate for stereo matching. As before, observations from either side of the reference view are used to improve robustness to occlusions.

Given an estimate of the depth map from the reference view, the surface is raymarched to determine the distance of all pixels from each view. Some pixels in the auxillary views will not intersect this surface, but this means they are probably not visible in the reference view anyway. With this estimate of the scene radiance, let us now look in detail at how a single pixel p is processed.

Assuming p is in the reference view, we define a square support patch $W_p$ centred around p, and cast rays into world-space. Unike Bailey et al. (2021), this is not done for every pixel in the support patch - only the four corners. As a result, computational efficiency is improved dramatically, and remains reasonably consistent regardless of the patch size.

These rays are intersected with sample tangent planes corresponding to p; at 3D locations determined by the candidate labels. By considering the surface orientation in this way, perspective distortion is applied to better resemble the patch appearance in the auxillary view. Pixels are then sampled between these corners, with subpixel sampling performed via bilinear interpolation. For label x, the vector of costs defining the similarity between a patch in the reference view $W_p$ and patches in the auxillary views $\hat{W_p}$ is defined by

$$\begin{aligned} \varphi _{S}(x_{p}) = \left\{ \Delta \left( W_p, \hat{W_p}^0 \right) , ..., \Delta \left( W_p, \hat{W_p}^j \right) \right\} , \end{aligned}$$

(37)

where $\varvec{\Omega _S}$ defines the vector of auxillary views with $j \in \varvec{\Omega _S}$. In our implementation, we consider 4 neighbouring views. To improve robustness, only the best 2 scores are considered per label from $\varphi _{S}(x_{\mathbf {p}})$, and are averaged together; denoted $\phi _{S}(x_{\mathbf {p}})$. Finally, the costs are normalised to produce the final stereo term, where $\mu _S$ is the mean of the cost volume $\phi _{S}$:

$$\begin{aligned} \Phi _{S}(x_{p}) \, = \, 1 - \exp \left( -\frac{\phi _{S}(x_{p})}{\mu _S}\right) . \end{aligned}$$

(38)

5.4 Smoothness Term

The purpose of the smoothness term is to ensure the reconstructions remain coherent in textureless or saturated regions while retaining surface edges. The general form of such a function can be written Szeliski et al. (2008)

$$\begin{aligned} \Psi _{pq}(x_{p}, x_{q}) = \text {min} \left( \Psi _{max}, V_{pq}(x_p, x_q) \right) . \end{aligned}$$

(39)

The above enforces pairwise smoothness between two pixels p and q taking labels $x_p$ and $x_q$ respectively, with the truncation preserving discontinuities. Following Bailey and Guillemaut (2020), we define $V_{pq}$ as a second-order prior and exploit the tangent plane surface model. For two world-points $\mathbf {P}$ and $\mathbf {Q}$ corresponding to labels $x_p$ and $x_q$ respectively, we define $V_{pq}$

$$\begin{aligned} V_{pq}(x_p, x_q) = \left( \frac{1}{\delta (n)(N-1)} \left| \frac{(\mathbf {Q} - \mathbf {P}) \cdot \mathbf {q^n}}{\mathbf {p^r} \cdot \mathbf {q^n}} \right| \right) ^2, \end{aligned}$$

(40)

similar to the definition proposed in Olsson et al. (2013). Here, $\mathbf {q^n}$ is the normal of the surface related to pixel q, $\mathbf {p^r}$ is a ray cast through pixel p and $\delta (n)$ is the metric distance between labels. This expression penalises label assignment based on the curvature of the surface, enabling a smooth piece-wise linear reconstruction. In our framework, we set $\Psi _{max} = 0.1$ and $\lambda = 10000$.

5.5 Photometric Cost Function

Throughout this section, our photometric cost has been abstracted away as some similarity score between two image inputs. Here, let’s consider the comparison of two image patches $\mathbf {a}$ and $\mathbf {b}$. In this paper, we explore two approaches in our implementation. The first takes the per-pixel sum of square differences (SSD) for all pixels contained within the patches,

$$\begin{aligned} \Delta _{SSD} (\mathbf {a}, \mathbf {b}) = \sum _{i} \left( a_i - b_i \right) ^2. \end{aligned}$$

(41)

This is a very simple and in some ways naive approach, but remains a popular choice in DFD. In fact, Eq. 41 was used exclusively in our previous work Bailey et al. (2021).

The second cost function we present in this paper is based on the extraction of learnt features. This is achieved using selected CNN layers of a pre-trained image classifier. In this work, we use ResNet-50 pre-trained on the ImageNet dataset. The model was obtained from the TorchVision package for PyTorch. It was trained using stochastic gradient descent with $10^{-4}$ weight decay and 0.9 momentum for 90 epochs; with a batch size of 32 and a learning rate of 0.1. Every 30 epochs, the learning rate was reduced by a factor of 0.1. All pooling layers and fully-connected layers are removed, and only the initial 7x7 convolutional layer and the first 2 bottleneck layers are used. These modifications were made because the training images are significantly larger than the image patches we wish to evaluate. Consequently, we can truncate the network and still maintain a receptive field that is appropiate for our use case.

Let the function R represent a forward pass of our ResNet-based feature extractor. Our similarity score then becomes a comparison between features instead of pixels,

$$\begin{aligned} \Delta _{CNN} (\mathbf {a}, \mathbf {b}) = \sum _{i} \left( R(\mathbf {a})_i - R(\mathbf {b})_i \right) ^2. \end{aligned}$$

(42)

Note that $\mathbf {a}$ and $\mathbf {b}$ remain subject to the usual image normalisation required by the network. In all experiments, we use a patch size of 11x11 pixels - an increase from the 5x5 patch size used in Bailey et al. (2021). When using $\Delta _{CNN}$, the output of R produces a 3x3 patch with 512 channels; which is flattened to a vector containing 4608 features.

Fig. 6

Materials simulated in our synthetic datasets: gold (top row), stone (middle row) and wood (bottom row)

Fig. 7

Example focal stack input images for our real datasets; Owl (top row), Bauble (middle row) and Temple (bottom row), with the focusing distance increasing from left to right. Only five of nine total images for the Bauble and Temple datasets are shown. Rightmost column shows the f/22 pinhole images used by the MVS methods we compare against

5.6 Point Cloud Fusion

To filter out significantly erroneous points in the point cloud outputs, a post-processing correspondence check is performed. This process retains corresponding points from neighbouring views that determined similar results during reconstruction, indicating a level of robustness in that region, and eliminates them otherwise. Our implementation requires each point to correspond in at least two adjacent views to within 0.5mm. We also exclude corresponding points where the difference in normal vectors exceeds 30 degrees. The position and normal vectors of all remaining points are averaged with their corresponding matches, and are subject to screened Poisson surface reconstruction to generate the final triangular mesh of the scene.

6 Evaluation

In this section we evaluate the performance of our approach on synthetic and real data. Here, we perform an ablation study to analyse the contribution of each cue, by comparing the proposed method against the performance of the stereo and defocus terms operating individually. This is achieved by fixing the weighting term $\alpha$ to 0 for defocus and 1 for stereo for all iterations except the first. In all experiments, the first iteration of the pipeline is defocus only to generate an initialisation of the surface and an estimate of the radiance required for stereo matching. Our evaluation considers two cost functions: sum of square differences (SSD) and a pre-trained feature-based cost (CNN). For all experiments, we process $N=100$ labels and run for 5 iterations with a visual hull initialisation. Real-world object silhouettes were generated using Rother et al. (2004), with any ambiguous regions manually corrected. Since the focal stack images are registered during calibration, only one silhouette is necessary per view. We found that the defocus term did not respond well without the object silhouettes shrunk to remove blurring due to background pixels. Our results are therefore missing some regions around the boundaries of objects, which is particularly apparent in the Dragon dataset. Note that, in principle, our approach does not necessarily require a visual hull initialisation.

This section begins by explaining how we generated our synthetic and real datasets. Next, a per-viewpoint evaluation is performed by comparing the accuracy of the depth maps our method produces across a range of metrics. We then explore the performance of our method in a 3D context. A quantitative analysis of the synthetic data is performed on the fused point clouds where we also compare to several modern MVS methods, before a qualitative comparison on the real datasets is conducted. Finally, an ablation study is performed to analyse the effect of the number of images in the focal stack.

Table 1 MAE of generated depth maps from datasets with 0% noise

6.1 Datasets

6.1.1 Synthetic

To generate the synthetic data, photo-realistic images of the Stanford Armadillo, Bunny and Dragon were rendered from 24 viewpoints using Blender. Each object was rendered with 3 different materials as seen in Fig. 6; gold, stone and wood. This initial output from the renderer represents the pinhole radiance of the scene. These images then had depth of field applied by blurring them with a Gaussian PSF according to our convolutional model, with f = 100mm, a = 4.55mm and w = 0mm. Each viewpoint is processed to create a 5-image focal stack, with the focusing distance uniformly incremented according to the ground truth depth maps. To simulate image noise, Eq. 4 is modified to become

$$\begin{aligned} I(\mathbf {y}) = (k_{\sigma } * r)(\mathbf {y}) + \eta , \end{aligned}$$

(43)

where $\eta$ is modelled as additive white Gaussian noise. For these experiments, the standard deviation of $\eta$ is set equal to 1% of the pixel value range. In combination with the noise-free data, this totals 18 synthetic datasets.

6.1.2 Real

Real-world datasets are acquired according to the procedure described in Sect. 4. In this paper we present three datasets; Owl (29 views, 5-image stacks), Bauble (18 views, 9-image stacks) and Temple (16 views, 9-image stacks). An example set of images from a single viewpoint are shown in Fig. 7. These are small objects that require relatively high magnification to photograph, and exhibit reflectance properties that resembles the synthetic data. Aperture values were chosen to be f/5.6 for Owl, and f/6.3 for Bauble and Temple. For camera pose estimation and comparison to MVS, small apertures images were taken with an f-stop of f/22.

The datasets were captured using a Canon EOS 5DS camera with a 100mm macro-lens. By physically measuring the pupil diameters as viewed from the front and back of the lens, we found the pupil ratio to be approximately 0.92 when focused at infinity - closely matching the assumptions made in Sect. 4.3. The images were downsampled to 2184 x 1464 pixels with 16-bit colour depth, before having lens distortion corrected and undergoing registration.

Table 2 MSE of generated depth maps from datasets with 0% noise

Table 3 % Bad pixels from depth maps with greater than 0.25 mm error generated from datasets with 0% noise

Table 4 MAE of generated depth maps from datasets with 1% noise

Table 5 MSE of generated depth maps from datasets with 1% noise

Table 6 % Bad pixels from depth maps with greater than 0.25mm error generated from datasets with 1% noise

6.2 Depth Map Evaluation

The per-viewpoint reconstruction approach we take permits us to evaluate performance by directly analysing the generated depth maps. This allows for a more direct evaluation of the cues, since the post-processing steps required to generate a 3D model often attenuate or remove significant regions of error.

6.2.1 Synthetic

We evaluate the performance of the single-view reconstructions using Mean Absolute Error (MAE), Mean Square Error (MSE) and % Bad Pixels above 0.25mm, and take the average across all views. Tables 1, 2 and 3 show the results of this evaluation under ideal 0% noise conditions, while Tables 4, 5 and 6 show results under 1% noise. In all cases, bold indicates the top performer determined by the lowest error reported for each column; with the proposed achieving the best performance in most instances.

Under noisy conditions, the performance of defocus degrades significantly, yet this does not appear to negatively influence the combination of cues; the contrary in fact. At first this seems strange - noise is not explicitly modelled in either cue, so why is only defocus sensitive to it? Our understanding is as follows. The basis of defocus modelling relies on texture analysis; specifically the appearance of high frequency textures under defocused conditions. By artifically injecting additive noise to the image, defocused regions now contain a large amount of unexpected high frequencies that confuse the cost function and degrade the resulting depth map. In contrast, the stereo term does not concern itself with the spectrum of texture components; simply the similarity of two image patches. Hence, the noise only increases the variance of the cost function, and does not impact the results a great deal. Even under adverse conditions, the defocus cue appears to positively influence the proposed method; and helps us achieve the best result in almost all cases.

Figures 8, 9 and 10 provide further insight by illustrating how each cue behaves recovering depth maps in the presense of different geometry and materials. These figures show both the SSD and CNN cost functions. In ideal 0% noise conditions, defocus appears to produce complete yet imprecise reconstructions, whereas stereo achieves higher accuracy at the expense of significant outliers. In combination, a balance of these benefits is achieved. The results under noisy conditions reflect the analysis above, with defocus alone highly sensitive to noise yet the proposed continuing to perform consistently.

6.2.2 Real

Figure 11 show a selection of depth map reconstructions on the real data. As with the synthetic data, the combination of cues appears to improve the depth map consistency and reduce significant error while also extracting detailed features. This figure shows the performance of both the SSD and CNN cost functions, and while this general trend is followed by both sets of results, the CNN cost produces the smoothest and most consistent output.

Fig. 8

Single view results on the gold Armadillo dataset with 0% and 1% noise. Rows 1 & 2 show the results from the SSD cost function; and rows 3 & 4 show results using the CNN cost function. Odd rows: depth maps produced by each variant of the method. Even rows: error maps when compared to the ground truth. Our method demonstrates robustness to noise despite the performance of both cues degrading when used seperately

Fig. 9

Single view results on the stone Bunny dataset with 0% and 1% noise. Rows 1 & 2 show the results from the SSD cost function; and rows 3 & 4 show results using the CNN cost function. Odd rows: depth maps produced by each variant of the method. Even rows: error maps when compared to the ground truth. The proposed achieves the highest overall precision and attenuates outliers resulting from specular regions

Fig. 10

Single view results on the wooden Dragon dataset with 0% and 1% noise. Rows 1 & 2 show the results from the SSD cost function; and rows 3 & 4 show results using the CNN cost function. Odd rows: depth maps produced by each variant of the method. Even rows: error maps when compared to the ground truth. Since this dataset has a largely diffused surface, failings in the stereo term are mostly due to occlusion. The proposed successfully captures the benefits of single-viewpoint reconstruction from the defocus term while retaining the higher accuracy afforded by the stereo term

Fig. 11

Single view results on the real datasets Owl (top row), Bauble (middle row) and Temple (bottom row). Depth maps normalised manually to the specified range

Table 7 Point cloud F-scores with $\tau$ = 0.5mm

Table 8 Point cloud F-scores with $\tau$ = 0.5mm

6.3 3D Reconstruction Evaluation

We compare performance on our datasets to three view-dependent MVS approaches; CasMVSNet Gu et al. (2019), VisMVSNet Zhang et al. (2020) and COLMAP Schönberger et al. (2016). Instead of operating on focal stacks, these methods take pinhole images as input. When operating on real data, these pinhole images are captured with an f/22 aperture. Though all of our datasets have a 16-bit colour depth, all MVS methods require 8-bit input images instead.

To share our pinhole camera calibration with COLMAP, we manually generated the configuration files that would otherwise be created by its structure from motion pipeline. Although CasMVSNet and VisMVSNet provide scripts to convert from the COLMAP format, we found overall these methods produced the best results when configured directly with our calibration and constrained to the same auxillary views our framework uses. These methods were run pre-trained with 256 labels on an Nvidia RTX 3070 graphics card; and the input images were downsampled to a maximum resolution of 1536 x 1024. For point cloud fusion, both methods use a threshold of 3 consistent views. Otherwise, parameters were left at their default values.

In all cases, our approach uses a visual hull initialisation for the first iteration, but is then disabled for all subsequent iterations. Since the MVS methods do not have access to our silhouette information, for fairness all points that are background are removed. For the synthetic data, this is based on the RGB value of the reconstructed point cloud. The real-world scene reconstructions are instead cleaned based on the position of the points; with the majority of points outside of the object volume removed. We do not perform similar post-processing on our own results. Finally, normals for the CasMVSNet point clouds were estimated prior to Poisson surface reconstruction since CasMVSNet does not provide this.

Fig. 12

Mesh reconstructions (top row) and error maps (bottom row) on the gold Armadillo dataset with 1% noise. On this dataset, defocus appears to perform best out of the comparisons shown, which we believe is due to the particularly high frequency appearance of the scratched gold material

Fig. 13

Mesh reconstructions (top row) and error maps (bottom row) on the stone Bunny dataset with 1% noise. Defocus appears to fail in improving performance over our stereo term alone

Fig. 14

Mesh reconstructions (top row) and error maps (bottom row) on the wooden Dragon dataset with 1% noise. The proposed compares well with the MVS methods

Fig. 15

Average recall (left) and precision (right) of point clouds across all synthetic experiments with 1% noise. Plots show the average percentage of points with respect to their distance from the ground truth mesh. Vertical line at 0.5mm represents the value of $\tau$ used when calculating the F-scores presented in Table 8. The proposed method with the CNN-based cost (shown in bold red) outperforms all methods by a clear margin when comparing against the recall, but trails the state-of-the-art MVS methods by around 5% in terms of precision at $\tau$ (Color figure online)

Fig. 16

Average recall (left) and precision (right) of reconstructed meshes across all synthetic experiments with 1% noise. Plots show the average percentage of vertices with respect to their distance from the ground truth mesh. For reference, the vertical line at 0.5mm represents the value of $\tau$ used when calculating the F-scores on the point clouds. The proposed method with the CNN-based cost (shown in bold red) achieves excellent recall and performs very competitively in terms of precision (Color figure online)

6.3.1 Synthetic

Figures 12, 13 and 14 show a comparison of 3D reconstructions on a selection of synthetic datasets with 1% noise. Recall under these conditions in the previous section defocus did not perform well. The results shown appear to indicate much the same, with the proposed depending heavily on the stereo term to produce a coherent output.

Tables 7 and 8 show an evaluation of our synthetic data on the fused point cloud outputs using the F-score metric provided by Knapitsch et al. (2017). In both tables, bold indicates the top performer of each column which maximises the score. In ideal 0% noise conditions where both cues are functioning at their best, we outperform all MVS methods, with the proposed outperforming the individual cues the majority of the time and achieving the best result on average. Under noisy conditions, the result is less clear-cut; though the proposed remains the best performer on average. Note the consistency in performance between Table 8 and Figs. 12, 13 and 14.

Figures 15 illustrates the average recall and precision of the point clouds across all experiments with 1% noise. Figure 16 shows the same, but on the Poisson meshes. Note the proposed approach achieves the best recall of all the methods, with the individual DFD and stereo terms consistently underperforming compared to the proposed. Interestingly, the stereo term achieves greater recall than defocus term, though this is probably due to the cross-correspondence check during point cloud fusion. Observe the difference between the CNN and SSD cost functions - the former achieves better performance in all cases. While they recover less overall completeness, all MVS methods appear to outperform in terms of precision; though the difference between the proposed and MVS closes when comparing meshes instead of clouds. This is to be expected to some extent, especially when compared to the performance of our stereo term by itself. If anything, this indicates more performance remains on the table that could be exploited by improving the robustness of each cue. However, the main objective of this paper is to explore their complementary nature rather than absolute performance, so this is left as future work.

In comparison to the depth evaluation in Sect. 6.2, the complete yet imprecise nature of the defocus term is less important due to the cross consistency checks performed when generating the point cloud. However, it remains useful for recovering the geometry of complex materials. This is reflected in the F-scores, with defocus performing best on the highly specular gold material while the stereo-based methods struggle to resolve a complete cloud. The decomposition of the F-scores showed the performance of the proposed exceeds that of both terms individually in recall and precision. A similar argument could be made from Sect. 6.2 regarding the performance of the ablation under noisy conditions.

Fig. 17

3D reconstructions of the real-world Owl dataset, and a comparison of several MVS methods (left) to an ablation of the proposed method (right). Top row: filtered point clouds produced by each method. Bottom row: triangular meshes generated from Poisson surface reconstruction

Fig. 18

3D reconstructions of the real-world Bauble dataset, and a comparison of several MVS methods (left) to an ablation of the proposed method (right). Top row: filtered point clouds produced by each method. Bottom row: triangular meshes generated from Poisson surface reconstruction

Fig. 19

3D reconstructions of the real-world Temple dataset, and a comparison of several MVS methods (left) to an ablation of the proposed method (right). Top row: filtered point clouds produced by each method. Bottom row: triangular meshes generated from Poisson surface reconstruction

Fig. 20

Alternative view of the Temple point clouds and mesh reconstructions using the CNN cost function. Defocus alone recovers a complete cloud but lacks surface details. Stereo alone recovers a point cloud with many holes present, making it unsuitable for recovering a stable mesh. The proposed achieves the best result; recovering a complete cloud and achieving a mesh reconstruction with many surface details

Table 9 Results from ablation study where the number of images in the focal stacks are varied from 2 to 5

6.3.2 Real

Figures 17, 18 and 19 show a comparison of the point cloud and triangular mesh reconstructions of our real-world datasets. The Owl object is the most diffused, and so performs the most consistently across all methods. In contrast, the MVS methods struggle to achieve a complete reconstruction of the Bauble, with the meshing algorithm smoothing over holes in the point cloud. The proposed approach performs much better; achieving a complete and detailed surface.

Finally, the MVS methods fail almost completely on the Temple object due to its highly specular and reflective appearance. Our ablative study illustrates the contribution of each cue very well on this object. Defocus alone achieves a complete cloud, yet lacks finer details such as the roof ornament. Stereo alone produces a noisy cloud with many holes due to a lack of robust matches, leading to a deformed mesh. The proposed recovers a complete point cloud suitable for recovering a stable mesh complete with many details. Figure 20 illustrates this point further.

6.4 Focal Stack Ablation

Finally, we present a set of experiments that explores how the number of images in the focal stack effects the performance of the approach. For this, each variant of the method was tested with 2, 3 and 5 images of the wood Bunny dataset. When using 2 images, only the nearest and furtherest images in the focal stack are seen by the method. Note the results with 5 images are the same as those seen previously - they are presented here again for ease of comparison. As with the other synthetic experiments, 24 viewpoints are made available to the method - only the number of images per view are modified. Since DFD has been shown to tolerate noise poorly, ideal 0% noise conditions were chosen for this test.

Table 9 combines the quantitive results from the 2D depth maps (MSE, MAE and % Bad Pixels) as well as evaluation on the fused point clouds (Recall, Precision and F-score). For the 2D results, there is a clear overall improvement in MSE and MAE when more images are used. Interestingly, DFD with the CNN cost function has fewer bad pixels when using only 2 images. The reasons for this are not immediately clear, but could be related to reduced ambiguity in the DFD cost when fewer images are used.

At first glance, the results from the fused point cloud analysis appear less clear. Although half of the results indicate better performance with 5 images, the rest appear to show the opposite. On closer inspection, the majority of these conflicting values are within one thousandth of the second best performer. This indicates that the influence of the focal stack size is either marginal or generally positive depending on the metric - at least with this dataset. It is also worth noting the proposed method almost always outperforms the individual stereo and defocus terms, even with less input data. However, these results only tell some of the story, as they do not consider the influence other parameters have on reconstruction such as the aperture diameter. Nevertheless, these results verify the proposed method continues to operate coherently with smaller focal stacks.

7 Conclusion

In this paper, we have presented a complete pipeline for reconstructing scenes from multi-view finite aperture images. We began by generalising the image formation process, and introduce a novel camera calibration procedure that characterises the unavoidable formation of defocus according to thick-lens principles. Next, an MRF-based reconstruction framework was proposed that unifies defocus and stereo cues and exploits the benefits of each; achieving performance greater than the sum of its parts. In our evaluation, we demonstrate how each cue contributes to the reconstruction with an ablation study; with the proposed method exhibiting robust and consistent performance across a range of complex materials. We also explored how a feature-based cost function could benefit our reconstruction. This became even more apparent in our comparison to several MVS methods, where in most cases we achieve similar or better performance.

There are several limitations with our current approach. While our stereo term is reasonably robust and achieves performance comparable to the other MVS methods tested, the defocus term can fail under the influence of noise. Though noise is less of a concern in macro photography where large apertures and exposure times are used, it remains an unavoidable feature of the image much like defocus itself. Though the proposed method continues to work well in most cases, under adverse conditions the defocus term does appear to contribute less useful information. In future work, the modelling of noise could be introduced to improve the robustness of the defocus term to noise.

Challenges also remain concerning how best to weight the contribution of each cue. Here, a scalar weighting was used that combined the stereo and defocus cues independent to the image context; leading to residual errors where the influence of an erroneous term is particularly strong. In our experiments, this usually originated from the stereo term in low noise data, and the defocus term in high noise data. In future work, it would be interesting to introduce a contextually aware weighting, where the contribution of a cue is conditional based on the appearance of the scene. Perhaps a classifier could be implemented that can perceive in a broad sense the reflectance function of the surface, and output a weighting of cues that extracts the most performance from our framework. Finally, there are additional variables that could be explored further relating to the focal stack, such as the aperture size and number of images.

A Mutually Exclusive Solution for Pupil Ratio

Recall that our calibration defines the pupil ratio $p_i$ as the piecewise function,

$$\begin{aligned} p_i = {\left\{ \begin{array}{ll} p_1, &{} \text {if } p_1 < 1 \\ p_2, &{} \text {if } p_2 \ge 1 \end{array}\right. } \end{aligned}$$

where,

$$\begin{aligned} p_1= & {} \frac{1}{2A} \left( 1 + \sqrt{1 + 4m_iA } \right) , \end{aligned}$$

(44)

$$\begin{aligned} p_2= & {} \frac{m_i}{A - 1}, \end{aligned}$$

(45)

$$\begin{aligned} A= & {} \frac{F_i}{f_\infty } \sqrt{\frac{b_\infty }{b_i}}. \end{aligned}$$

(46)

Let us show that one and only one solution of $p_i$ is valid. From Eq. 45,

$$\begin{aligned} A = \frac{m_i}{p_2} + 1. \end{aligned}$$

(47)

Substituting Eq. 47 in Eq. 44,

$$\begin{aligned} p_1 = \frac{1}{2 \left( \frac{m_i}{p_2} + 1 \right) } \left( 1 + \sqrt{1 + 4m_i \left( \frac{m_i}{p_2} + 1\right) } \right) , \end{aligned}$$

(48)

We need to show that $p_1$ is valid when $p_2$ is invalid. Since $p_1$ is valid when less than 1, we can show using Eq. 48,

$$\begin{aligned} \sqrt{1 + 4m_i \left( \frac{m_i}{p_2} + 1 \right) } < \frac{2m_i}{p_2} \end{aligned}$$

(49)

which simplifies to $p_2 < 1$. Similarly, when $p_1 \ge 1$ this implies $p_2 \ge 1$. Thus, only one function defining $p_i$ gives a valid solution for all cases. This completes the proof.