1 Introduction

Hydrogels are chemically crosslinked, hydrophilic polymer networks that swell in water or aqueous solvents. They are responsible for the low friction coefficients found in some biological systems, such as cartilage or the cornea [1]. Due to their tribological properties, hydrogels have been applied in soft contact lenses [2,3,4] and as synthetic articular cartilage materials [5,6,7].

Self-mated hydrogel-on-hydrogel frictional contacts, also known as Gemini hydrogels, have low friction coefficients at low sliding velocities [8]. It has been shown that the polymerization conditions define a hydrogel’s degree of crosslinking close to the surface [9, 10]. Hydrogels whose polymerization close to the surface is inhibited by the presence of oxygen exhibit pronounced crosslinking gradients and sparse surfaces. Conversely, the absence of oxygen during synthesis leads to a homogeneously crosslinked hydrogel [9, 10]. Due to the random nature of polymerization, not all chain ends are crosslinked, which leads to dangling chains and loops on the surface [11, 12]. The details of this interfacial structure might affect frictional behavior.

In weakly crosslinked hydrogel surfaces, hydrodynamics plays a significant role in the tribological response of the system [13]. For highly crosslinked surfaces, which are the focus of this work, the friction force is velocity independent or only weakly velocity dependent up to a threshold velocity [8, 14]. Past this threshold, experiments have shown that the friction coefficient increases approximately with the square root of the velocity for highly crosslinked surfaces [9, 13,14,15].

Competing models exist as explanations for this behavior: Pitenis et al. [15, 16] argue that for hydrogels with mesh size \(\xi\), solvent viscosity \(\eta\) and temperature T, friction is determined by a competition of fluctuation-induced polymer relaxation with time scale \(\tau _\text {r}=\xi ^3\eta /k_\text {B}T\) and the time scale introduced by the shear rate, \(\tau _\text {s}=\xi /v\). This gives rise to velocity-independent (Coulomb) friction at small velocities v, where \(\tau _\text {r}\ll \tau _\text {s}\). Friction measurements at high velocities collapse onto a single curve when plotted against the Weissenberg number [17], \(\textrm{Wi} = \tau _\text {r}/\tau _\text {s}\). This velocity-dependent friction regime can thus be attributed to the non-equilibrium behavior of strained polymer chains and possibly adhesive interactions between the surfaces [14]. Simple hydrodynamic-fluid-film friction models predict friction coefficients that scale with the square root of the velocity [18], but those models assume that surfaces are rigid and do not deform during sliding, which might not be representative of hydrogel-like biological surfaces. Furthermore, they require converging surfaces to generate hydrodynamic lift, a condition not met by parallel surfaces [19]. In contrast, soft elasto-hydrodynamic lubrication theory [18] allows the hydrogels to deform during sliding, but it also predicts friction coefficients that are lower than those measured experimentally and does not predict the scaling of friction with velocity observed in experiments [20]. These hydrodynamic lubrication theories also do not capture the transition between the velocity-independent and velocity-dependent friction regimes that appears to depend on the mesh size \(\xi\) [14, 15]. In particular, experiments by Urueña et al. [15] show the friction coefficient decreasing with increasing mesh size.

Fig. 1
figure 1

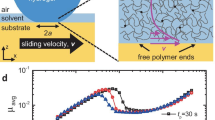
a Slice of the hydrogel network during shear. The network has been colored, to help distinguish the interface. The black line depicts the borders of the periodic simulation cell. The inset shows a detailed view of the interface before relaxation. b Coefficient of friction (CoF) as a function of sliding velocity v and chain lengths for our computational model. c Sketch of the interface for networks with and without surface variations. Monomers are colored in red and crosslinkers in green. d Schematic of the friction experiments using a flat, hydrogel pin on a flat, highly crosslinked gel. e Experimentally determined coefficients of friction for polyacrylamide hydrogels as a function of monomer concentration. The inset shows estimated mesh sizes \(\xi\) as a function of monomer weight percentage (Color figure online)

Full size image

We present evidence from molecular simulations in favor of the polymer-relaxation hypothesis in highly crosslinked hydrogels. By choosing a model with an implicit solvent, i.e. without long-range hydrodynamic momentum transport and no possibility of interfacial fluid-film formation, we disentangle the role played by the solvent from that of the polymer network. We find that hydrogel friction is a purely interfacial phenomenon at low contact pressures, i.e. pressures smaller than the network’s osmotic pressure. Furthermore, the shear response of interfacial polymers can be split into three speed-dependent regimes. For small velocities, the friction coefficient is speed independent due to the effect of thermal fluctuations overwhelming chain alignment. This is followed by a regime in which the friction coefficient increases linearly with velocity. We trace this observation back to the reorientation of interfacial polymer chains in the direction of shear. Once forces are strong enough, these interfacial chains start stretching, which leads to a friction coefficient that increases with the square root of velocity. A salient feature of our simulation model is its prediction that the friction coefficient increases with mesh size (chain length), which runs counter to the aforementioned reports by Urueña et al. [15]. In support of our simulation results, we here provide experimental data showing that the friction coefficient increases with increasing mesh size for highly crosslinked systems. We do so using a tribometer in a flat-on-flat configuration instead of a sphere-on-flat contact to minimize the potential influence of hydrodynamic lift.

2 Materials and Methods

2.1 Simulation Methods

Excluded volume interactions are modeled via a Weeks-Chandler-Anderson (WCA, cut-off radius \(2^{1/6}\sigma\)) potential [21] with an interaction energy of \(\varepsilon\) and a range \(\sigma\), defining the time scale \(\tau =\sigma (m/\varepsilon )^{1/2}\) of our simulations. Consecutive segments in a polymer chain are connected by finite extensible nonlinear elastic (FENE) bonds [22, 23] with spring constant \(30.0~\varepsilon \sigma ^{-2}\) and a maximum extension \(1.5~\sigma\) that prevents bond crossings. When adhesive interactions across the interface are included, we replace the WCA potential by an adhesive Lennard-Jones potential of energy \(\varepsilon _{\text {adh}}=0.5~\varepsilon\), range \(\sigma\) and cut-off radius \(2\cdot 2^{1/6} \sigma\) between dangling chains of each surface and all chains of the opposing surface. We report all simulation results in terms of the characteristic quantities \(\sigma\), \(\varepsilon\) and \(\tau\). For friction simulations, we need a profile-unbiased thermostat and employ dissipative particle dynamics (DPD) [24,25,26,27] with a linear weight function and a damping coefficient of \(\gamma =5.0~m\tau ^{-1}\). This thermostat is Galilean invariant and acts as an implicit solvent. Equations of motion are integrated using a timestep of \(\Delta t=0.001~\tau\).

Prior to running friction simulations, we equilibrate the networks using a Berendsen barostat [28], such that our networks are stress-free parallel to the interface. We push both interfaces together by applying a pressure of \(p_{zz}=-\sigma _{zz}=1\cdot 10^{-3}~m\sigma ^{-1}\tau ^{-2}\) at a temperature of \(T=1.0~\varepsilon /k_{\text {B}}\). The normal pressure is lower than the bulk modulus of the polymer network, so that the network does not collapse. The equilibration runs until the system size converges to a stable volume.

2.2 Experimental Methods

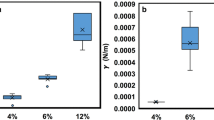
The polyacrylamide (PAAm) hydrogels were synthesized from acrylamide monomer (> 99%, Sigma-Aldrich, St. Louis, MO, USA), N,N’-methylene-bis-acrylamide cross-linker (> 99.5%, Sigma-Aldrich, St. Louis, MO, USA) and 2,2’-azobis-(2-methylpropionamidine)dihydrochloride (98%, Acros Organics, New Jersey) photo-initiator in MilliQ water. The molar ratio of the monomer to cross-linker was set to 50:1, where their total amount in the solution was set to 6, 7.5, 9, 11, 13, 15 and 17.5 wt%. The amount of the initiator was 0.5 wt%. Milli-Q water was bubbled with nitrogen for 30 minutes to remove the oxygen and then used to dissolve the set amounts of the monomer, the crosslinker and the initiator by gentle stirring. The solutions were poured into piranha-cleaned glass petri dishes to an approximate thickness of 3–4 mm and polymerized for 7 min by a UV light with an intensity of about 1 mW cm\(^{-2}\) at a wavelength of 365 nm (Stratalinker UV Crosslinker 2400, Stratagene Corp., La Jolla, CA, USA). After polymerization, the gels were removed from the molds and immersed in a large amount of Milli-Q water for at least 48 hours to remove unreacted species and allow swelling of the gels. Friction experiments were performed as described in Meier et al. [9]. In short, the coefficient of friction was measured using a tribometer (CSM, Needham, MA, USA) in reciprocating configuration. Flat discs of 10 mm diameter were punched out of 4–5 mm-thick hydrogel slabs and glued to flat-ended steel pins of the same diameter. The normal load was set to 0.5 N, which corresponds to a contact pressure of about 6 kPa. The stroke length was set to 10 mm and sliding speeds were varied from 0.1–15 mms\(^{-1}\). The tests consisted of 10–20 cycles at each condition, which was sufficient for the friction force to reach a steady state. The tests were performed at \(22~^{\circ }\text {C}\pm ~ 1~^{\circ }\text {C}\) with samples fully immersed in pure milli-Q water.

3 Results and Discussion

Our molecular-dynamics simulations [29] resolve polymer-chain dynamics on length scales of the order of a mesh size (5–20 nm). We use a purely repulsive, flexible bead-spring model [23], where a polymer chain is divided into uncorrelated segments (beads), each containing one or more monomers and of a size corresponding roughly to the Kuhn length [30]. The polymer chains are thermalized by a dissipative particle dynamics thermostat, which acts as an implicit solvent, but mediates no long-range hydrodynamic interactions [24,25,26,27].

Hydrogels are disordered networks with fourfold coordination, physical crosslinkers, entanglements and potentially dangling chains. Unfortunately, the detailed statistical properties of the connectivity of hydrogel networks are often unknown [11, 31] and influence frictional behavior [9, 13]. We therefore simplify our computational model and build the simplest regular structure with fourfold connectivity: a diamond lattice with dangling surface chains (see inset to Fig. 1a), as used in the past to, e.g., test mechanical properties of polymer networks [32]. Crosslinkers are connected to each other with polymer chains of length \(N_0\). The surface is a {111} crystallographic plane, with one dangling chain of length \(N_S\) per surface crosslinker. Our canonical model uses identical lengths for bulk and surface dangling chains (\(N_0=N_S\)), but we vary these lengths independently to test their individual influence on the frictional properties.

First, using our computational model, we look at the shear response of networks with the goal of unraveling the velocity dependence of the coefficient of friction. We do so by imposing shear on the polymer network by continuously deforming the periodic simulation cell at constant velocity v. The shear stress and normal stress are sampled every 10 time steps, for at least \(10^8\) time steps, so as to compute the friction coefficient (CoF), \(\mu =|\sigma _{xz}/\sigma _{zz}|\). We checked for selected configurations that friction follows Amontons law, i.e. the time-averaged shear stress \(\sigma _{xz}\) is proportional to the normal stress \(\sigma _{zz}\).

We observe two distinct regimes in the networks’ shear response, as seen in Fig.  1b. For all networks, above a certain threshold velocity, the friction coefficient increases approximately linearly with velocity. At low velocities, noise introduced by thermal fluctuations of the bulk chains prevent precise shear stress measurements. However, especially for networks with shorter chains, a change in friction behavior towards a speed-independent or only weakly speed-dependent friction regime can be observed. Our simulations indicate that the threshold velocity between friction regimes is chain-length dependent: The threshold velocity increases with decreasing chain length. We note that this dependency becomes clear when we nondimensionalize our simulation results in terms of the Weissenberg number below.

Next, we analyze the effect of surface chain density and length. Network 10S is a network with \(N_0=N_S=10\) beads/chain, in which dangling chains at the interface have been made sparse. (See our illustration of the near-surface network in Fig. 1c.) A lower surface chain-density slightly decreases the friction coefficient (Fig. 1b). The network 10S/30 has been constructed on the basis of network 10S, but extending the dangling chains to \(N_S=30\) beads/chain (Fig. 1c). In network 50/10, the surface chains have been shortened to \(N_S=10\) beads, while keeping the bulk network and chain density of \(N_0=50\) beads. Figure 1b shows that both the transition velocity and magnitude of the friction coefficient are closest to the results of the homogeneous network with \(N_S=N_0=\max (N_0,N_S)\). Hence, the longest chains present at the interface determine the frictional behavior.

We accompany our simulations by experiments on polyacrylamide gels with a highly crosslinked surface using a tribometer in reciprocating configuration (Fig. 1d), following the experimental design outlined in Meier et al. [9]. Mesh sizes were extrapolated from Urueña et al., but corrected with a factor of 0.15 [16, 33]. Urueña’s data shows how for a constant monomer/crosslinker ratio, the mesh size decreases with increasing monomer concentration due to an increase in physical crosslinks (entanglements) [15]. We observe that the friction coefficient increases with sliding velocity (Fig. 1e). Furthermore, for any given sliding velocity, the friction coefficient increases with mesh size. This behavior is also observed in our simulations (Fig. 1b). This last observation contradicts previous results by Urueña et al., who show an inverse relationship between mesh size and coefficient of friction [15]. This may be a consequence of Urueña et al. using a gel molded against polystyrene, whereas our gels were molded in glass petri dishes. The latter results in a more highly crosslinked surface [9, 10]. Furthermore, the flat-on-flat tribometer configuration used in our experiments differs from the spherical indenter used by Urueña et al. Their spherical indenter possibly introduces additional hydrodynamic lift.

Following the experimentally observed collapse of the friction curves [15, 16], we define the Weissenberg number as the product of the sliding velocity v and polymer relaxation time \(\tau _r\) divided by the radius of gyration \(R_\mathrm{{g}}\) of a single chain of length \(N_S\), \(\textrm{Wi}=v \tau _r R_\mathrm{{g}}^{-1}\). This takes advantage of the fact that in the semi-dilute regime, the mesh size is approximately equal to the radius of gyration of a single chain [34]. We compute the polymer relaxation time via the autocorrelation function of the gyration tensor [35]. For our experimental data we adopt the previously used definition of \(\textrm{Wi}=\xi ^2 v \eta /k_\mathrm{{B}}\mathrm T\) [15, 16], with a relaxation time of \(\tau _r\approx \eta \xi ^3/k_\textrm{B}T\) [35]. Figure 2a shows a collapse of our friction curves onto experimental and computational master curves. In our simulations, the transition between friction regimes takes place close to \(\textrm{Wi}\approx 0.01\). While both simulation and experiments show an increase in friction with velocity beyond this point, they differ qualitatively in the exponent. The simulations show \(\mu \propto \text {Wi}\) while the experiments scale as \(\mu \propto \text {Wi}^{0.5}\).

A crucial simplification of our mesoscale simulation model is that the interfacial chains only interact repulsively through excluded volume interactions. This type of model severely underestimates microscopic interchain friction and attractive interactions through hydrodynamic forces [36]— both phenomena that become relevant in nonequilibrium situations. We now mimic such interactions by introducing a simple adhesive pair-interaction between both surfaces (see methods for further details). Figure 2b shows that for the adhesive-interface model, the friction coefficient increases approximately as \(\mu \propto \text {Wi}\) at small sliding speeds, but then crosses over to \(\mu \propto \text {Wi}^{0.5}\), as in the experiment. In this regime, the simulation and experimental coefficients of friction have the same exponent at high speeds. Note that for weak adhesive interactions (\(\varepsilon _{\text {adh}}<0.5~\varepsilon\)), the frictional behavior is qualitatively similar to the non-adhesive model and we do not observe a change in exponent.

Fig. 2
figure 2

Coefficient of friction (CoF) as a function of the Weissenberg number \(\text {Wi}=v \tau _r R_\mathrm{{g}}^{-1}\) for the a non-adhesive and b adhesive models. Both are shown alongside experimental data for comparison

Full size image

The observed friction behavior is similar to what has been found in simulations for strongly compressed semi-dilute polymer brushes with explicit solvent [37, 38]. Given that sheared polymer brushes are subject to larger forces in explicit solvent compared to implicit solvent [38], our adhesive forces across the interface mimic the influence of an explicit solvent by increasing the shear forces acting on interfacial chains.

In order to understand the molecular origins of the interfacial shear stress and the differences in behavior between the adhesive and non-adhesive models, we analyze the conformational statistics of chain segments at the hydrogel interface. In equilibrium, flexible chains take on random-coil conformations. Polymer physics predicts that distorting equilibrium chain conformations reduces chain entropy and produces an entropic shear stress, defined as [35, 39]

$$\begin{aligned} \sigma _{xz}^\textrm{entr} = \frac{\rho k_\textrm{B}T}{C_\infty }\langle \mathcal {L}^{-1}(h)h \hat{r}_x \hat{r}_z \rangle \end{aligned}$$
(1)

Here, \(\rho\) is the number density of monomers and \(C_\infty\) is Flory’s characteristic ratio, which gives the average number of monomer bonds in one random-walk step of the equilibrium coil conformation. (For our model polymer chains \(C_\infty = 1.83\) [40].) The unit vector \(\hat{{\textbf {r}}}\) points along the end-to-end distance vector \(\textbf{R}_\mathrm{{ee}}\) connecting the ends of a chain segment, \(\mathcal {L}^{-1}\) is the inverse Langevin function [41] and the extension ratio is defined as \(h = |R_\mathrm{{ee}}|/nb\), with n the number of bonds in a chain segment and b the average monomer bond length.

Figure 3 plots this analytic entropic stress versus the total shear stress computed from the usual virial expression [29] in our simulations, where the ensemble average \(\langle \cdot \rangle\) is restricted to dangling chain segments at the interface. The two estimates agree, implying that the entropic stress of interfacial chains fully explains the shear stress for both the adhesive and non-adhesive models. This again shows that bulk chains do not contribute substantially to the shear stress.

Fig. 3
figure 3

Entropic stress as function of shear stress for the adhesive and non-adhesive models with \(N=50\) beads/chain. Each data point corresponds to a different sliding velocity

Full size image

Since the entropic stress of chains captures the interfacial friction for the full range of \(\textrm{Wi}\), we can analyze it to understand the molecular processes governing the rate-dependent friction. Equation 1 can be decomposed into an orientation tensor \(\hat{r}_\alpha \hat{r}_\beta\) that captures chain reorientation, and a Langevin hardening \(\mathcal {L}^{-1}(h)h\) that captures the nonlinear effects of chain elongation. Figure 4 plots these two terms separately for all systems and \(\textrm{Wi}\). At low \(\textrm{Wi}\), chains relax faster than deformation distorts their conformations, and show no change in orientation or elongation. This leads to a velocity-independent friction regime. As \(\textrm{Wi}\) increases, all systems show chain reorientation that grows with \(\textrm{Wi}\) as deformation tilts chain backbones towards the sliding plane. The adhesive system aligns more than the non-adhesive cases at the same \(\textrm{Wi}\), eventually saturating its alignment. While all systems reorient, only the adhesive system shows any increase in chain elongation.

Fig. 4
figure 4

a Hardening factor of the entropic stress tensor as a function of the Weissenberg number for the adhesive (\(N=50\)) and non-adhesive models (\(N=50\) and \(N=20\)). b Orientation tensor of the entropic stress tensor

Full size image

The shear stress is dominated by reorientation of interfacial chains for all systems at low sliding speeds (Fig. 4b). Since a chain’s relaxation time is proportional to its length, the velocity at which chains first noticeably reorient decreases with chain length. It follows that for any given velocity above the friction transition, longer chains should be further away from their equilibrium configurations than shorter chains (Fig. 4b). As a consequence, the friction coefficient increases with chain length or mesh size (Fig 1b).

We hypothesize that in the presence of explicit solvent, chain stretching would be more significant, even in the absence of additional adhesive interactions across the interface, since in the presence of explicit solvent, polymer chains are subject to larger shear forces than in equivalent implicit solvent simulations [38]. The loss of molecular detail when adopting the mesoscopic bead-spring model might also lead to lower intermolecular friction. Therefore, we view the adhesive and purely repulsive networks as providing the shear response across the range of intermolecular force strengths.

4 Summary and Conclusions

In summary, we have presented a coarse-grained computational model that reproduces the experimental phenomenology of self-mated hydrogel friction at low loads. A speed-independent, Coulomb-friction regime at low sliding velocities crosses over to speed-dependent friction. Simulation results quantitatively agree with experiments on hydrogels with a sharp gradient in surface density. Our simulations reveal that the frictional response is solely dominated by interfacial chains, not by the bulk hydrogels. The crossover to speed-dependent friction can then be attributed to the point where thermally driven relaxation of dangling polymer chains is slower than their excitation by sliding. Our simulations further show that the velocity-dependent regime can be split into two stages: interfacial polymer chains first reorient along the shear direction and then stretch only once significant shear forces act on the chains. These results show that tuning hydrogels for frictional properties should focus on engineering the surface, instead of the bulk structure.