1 Introduction

Many moving machine assemblies involve rolling-sliding parts, such as cam mechanisms, rolling bearings, gears, etc. and these typically operate under elastohydrodynamic lubrication (EHL) conditions. There are numerous examples of investigations of lubricant film formation and friction in the interfaces between the rolling-sliding parts. Most studies have been focused on high-load, low-speed conditions, but actual components also encounter low-load, high-speed conditions. Since severe wear and flaking may occur on the rolling-sliding surfaces due to insufficient oil film thickness, controlling the oil film thickness distribution is necessary for reliable performance over a wide range of operating conditions.

Johnson [1] divided the lubrication regimes in EHL into four parts. These regimes are the piezo viscous rigid (PR), the isoviscous rigid (IR), the piezo viscous elastic (PE), and the isoviscous elastic (IE). The analysis method to calculate oil film thickness for IR was described by Martin [2], PR by Grubin [3], PE by Dowson and Higginson [4], and IE by Herrebrugh [5]. Moes [6, 7] suggested a minimum film thickness formula that could be used over a wide range of operating conditions, which is an approximation formula including the transition regions PE, PR, IE, and IR. This approximation formula was curve-fitted with asymptotic lines for obtaining the minimum oil film thickness in PE, PR, IE, and IR regimes. For the transition regions between PE and PR, IE, and IR, the numerical calculation of the oil film thickness, does in many cases, experience convergence issues, which leads to inaccurate predictions.

Regarding numerical computation methods for EHL line contacts, Lubrecht [8], Venner [9], and Venner et al. [10] introduced a multigrid method based on a Gauss–Seidel solver for the Reynolds equation, applicable to the isothermal line contact problem. Venner [9] pointed out that “in some lowly loaded situations a larger inlet region was needed in order to avoid numerically starved lubrication”. Furthermore, the numerical computation method for the transition regions between IE and IR was not described in detail. Alakhramsing et al. [11], Habchi et al. [12, 13], and Hultqvist [14], investigated the effect of oil film thickness on friction based on a full-system finite element approach. They focused on high-load, low-speed conditions, under fully flooded lubrication. To this end, they applied the Hertzian radius as the normalization for the IE and PE regions, and the reduced radius of curvature for the IR and PR regions.

As Venner [8] concluded, “numerically starved lubrication” under lower load in the case of an inappropriate inlet distance, causes the divergence of the numerical results. This issue is a primary factor in the transition regions between the PE, IE regions, and the PR, IR regions, that causes instabilities in the numerical solution procedure.

Regarding the starved- and fully flooded conditions in EHL, Wedeven et al. [15] experimentally investigated the occurrence of starvation. Later, Hamrock et al. [16] suggested a simple expression of a computational inlet distance required to obtain a fully flooded simulation for EHL point contacts operating in the PE region. By means of this measure of the inlet distance, they also presented an approximative expression to estimate the oil film thickness for both starved and fully flooded EHL contacts operating within the PE region. For continued work devoted to EHL and starvation effects in the PE region, see [17,18,19,20,21]. Examples of work considering starved and fully flooded conditions in the IR region are the ones by Anandan [22, 23] and Biboulet [24], where the reduced radius of curvature was employed as a normalization of the computational domain that they used to numerically calculate the oil film thickness.

In this paper, an expression of the inlet distance that ensures fully-flooded conditions is employed to normalize the computational domain. The numerical EHL line contact calculation model, for isothermal conditions, is implemented in a fully-coupled finite element-based approach. By means of the present normalization method, the corresponding computational domain can be appropriately meshed, regardless of the variability of the inlet length, to accommodate changes in the operating conditions. This method can, therefore, be used to obtain accurate EHL film thickness and pressure data over a wide range of operating conditions, including the transition regions between PE, PR, IE, and IR.

2 The EHL Line Contact Model

This section presents the numerical EHL line contact model that incorporates an optimized inlet computational domain, which provides solutions that are not numerically starved.

2.1 Inlet Computation Domain Optimization

Let us first revisit the experimental research results by Wedeven et al. [15], who investigated starvation in ball bearings, by means of optical analysis.

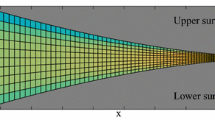
Figure 1 shows a cross-section of the contact geometry with particular emphasis on the inlet zone of the contact. The length of the inlet zone is crucial for the numerical computation of oil film thickness and pressure, since a too short inlet computational domain may lead to numerically starved conditions. This is, for instance, a big issue when simulating the conditions that are typical for the iso-viscous rigid (IR) regime. The numerically starved condition induces a reduction of oil pressure and converged solutions cannot be obtained.

Fig. 1
figure 1

Cross-section of contact geometry, where \({h}_{0}\) is the central film thickness, \({h}_{b}\) the film thickness at lubricant inlet boundary, \(a\) the Hertzian radius, \({S}_{f}\) the definition of a fully flooded inlet introduced in [15], \(b^{\prime}\) the optimal inlet distance defined herein, and \({U}_{i}\), are the velocities of the bearing surfaces (Color figure online)

Full size image

Wedeven et al. [15] presented an expression for the inlet zone length \({S}_{f}\) required to obtain fully flooded conditions, i.e.

$${S}_{f}=3.52{\left(\frac{{R^{\prime}}^{2}{h}_{0}^{2}}{a}\right)}^\frac{1}{3},$$
(1)

where

$$a=\sqrt{\frac{8R^{\prime}w}{\pi {E}^{^{\prime}}}},$$
(2)

is the Hertzian radius, \({R^{\prime}}^{-1}={R}_{1}^{-1}+{R}_{2}^{-1}\) the reduced radius of curvature, \({h}_{0}\) the central film thickness, and

$$\frac{2}{{E}^{^{\prime}}}=\frac{1-{\upsilon }_{1}^{2}}{{E}_{1}}+\frac{1-{\upsilon }_{2}^{2}}{{E}_{2}},$$
(3)

where \(E^{\prime}\) is the reduced elastic modulus, and \({E}_{i}\) and \({v}_{i}\) are Young’s modulus and the Poisson ratio of bodies \(i=1\) and \(2\), respectively.

They also discovered that the onset of starvation occurs if the ratio of \({h}_{b}/{h}_{0}\) of the oil film thickness at the inlet boundary \({h}_{b}=h\left({x}_{b}\right)\) to the central oil film thickness \({h}_{0}=h\left(0\right)\) falls below 9.

As previously mentioned, most EHL numerical calculation methods use a multiple of the Hertzian radius \(a\) to define the length of the computational domain. This may, however, lead to numerical starvation if the resulting inlet zone does not encompass the inlet distance \({S}_{f}\), as defined in [15]. This issue becomes a complication when performing calculations over a large range of operating conditions, which is often required when simulating an actual application, as it leads to less accurate oil film thickness and pressure estimates. If we can correctly adjust the inlet distance \({S}_{f}\) for fully flooded conditions independent of numerical calculation engineers’ technique, e.g. adjustment of required mesh size along with the inlet distance, the numerical calculation method can be used universally.

2.2 Governing Equations

In this section, the theoretical foundation of the fully-coupled finite element approach, in which the Reynolds equation and the equations governing linear elasticity are solved simultaneously, is presented. For line contacts, the Reynolds equation governing stationary flow is given by:

$$\frac{d}{\mathrm{d}x}\left(\frac{{\rho h}^{3}}{12\eta }\frac{\mathrm{d}p}{\mathrm{d}x}\right)={U}_{e}\frac{d\left(\rho h\right)}{\mathrm{d}x}+\theta\, \mathrm{in}\, {x}_{b}<x<{x}_{o} ,$$
(4)

where \(\rho\) is the oil density, \({\eta }_{0}\) the oil viscosity, \(h\) the oil film thickness, \(p\) the oil film pressure, \({U}_{e}=\left({{U}_{1}+U}_{2}\right)/2\) the mean entrainment speed and where \(\theta\) is a penalty term, see also [14]. The computational domain is defined by \([{x}_{b},{x}_{o}]\), where \({x}_{b}\) is the location where \(h={h}_{b}\) and \({x}_{o}\) is specified to ensure that it is larger than the point where the film ruptures and cavitation occur. The fluid–structure interaction in the EHL contact is manifested by the appearance of the total vertical displacement \({v}_{\partial\Omega }\) of the boundaries of the deforming solids’ \(\partial\Omega\), in the oil film thickness equation, i.e.

$$h={h}_{00}+\frac{{x}^{2}}{2R^{\prime}}-{v}_{\partial\Omega }$$
(5)

where \({h}_{00}\) is a measure of rigid body separation. This parameter is determined via force balance in the \(y\)-direction, i.e.

$${\int }_{{x}_{b}}^{{x}_{o}} p\left(x\right)\mathrm{d}x-w=0,$$
(6)

where \(w\) is the applied load per unit width. For a schematic illustration of the EHL line contact using present nomenclature, see Fig. 2.

Fig. 2
figure 2

Schematic illustration of the EHL line contact model, where \(R^{\prime}\), \(h(x)\), \({U}_{1}\), \({U}_{2}\) are the reduced radius of curvature, oil film thickness, and velocities of the surfaces, respectively

Full size image

The system of equations governing the mechanics of the linear elastic body is

$$\begin{gathered} - \frac{\partial }{{\partial x}}\left( {c_{1} \frac{{\partial u}}{{\partial x}} + c_{2} \frac{{\partial v}}{{\partial y}}} \right) - \frac{\partial }{{\partial y}}\left( {c_{3} \left( {\frac{{\partial u}}{{\partial y}} + \frac{{\partial v}}{{\partial x}}} \right)} \right) = 0, \hfill \\ - \frac{\partial }{{\partial x}}\left( {c_{3} \left( {\frac{{\partial u}}{{\partial y}} + \frac{{\partial v}}{{\partial x}}} \right)} \right) - \frac{\partial }{{\partial y}}\left( {c_{2} \frac{{\partial u}}{{\partial x}} + c_{1} \frac{{\partial v}}{{\partial y}}} \right) = 0 \hfill \\ \end{gathered}$$
(7)

where \(u\) and \(v\) are the displacements in the \(x\)- and \(y\)-direction, respectively, and \({c}_{i}, i=\mathrm{1,2},3\), are the equivalent components of the stiffness matrix given by

$${c}_{1}=\frac{\left(1-{\nu }_{\mathrm{eq}}\right){E}_{\mathrm{eq}}}{(1+{\nu }_{\mathrm{eq}})(1-2{\nu }_{\mathrm{eq}})}, \,{c}_{2}=\frac{{\nu }_{\mathrm{eq}}{E}_{\mathrm{eq}}}{(1+{\nu }_{\mathrm{eq}})(1-2{\nu }_{\mathrm{eq}})}, \,{c}_{3}=\frac{{E}_{\mathrm{eq}}}{2(1+{\nu }_{\mathrm{eq}})},$$
(8)

where \({E}_{\mathrm{eq}}\) and \({\nu }_{\mathrm{eq}}\) are the equivalent Young’s modulus and the equivalent Poisson's ratio of the contacting bodies, respectively. These are defined as in [25], i.e.,

$${E}_{eq}=\frac{{E}_{1}^{2}{E}_{2}{\left(1+{\nu }_{2}\right)}^{2}+{E}_{2}^{2}{E}_{1}{\left(1+{\nu }_{1}\right)}^{2}}{{\left({E}_{1}\left(1+{\nu }_{2}\right)+{E}_{2}\left(1+{\nu }_{1}\right)\right)}^{2}},$$
(9)
$${v}_{eq}=\frac{{E}_{1}{\nu }_{2}\left(1+{\nu }_{2}\right)+{E}_{2}{\nu }_{1}\left(1+{\nu }_{1}\right)}{{E}_{1}\left(1+{\nu }_{2}\right)+{E}_{2}\left(1+{\nu }_{1}\right)}.$$
(10)

As an approximate equation of the pressure-viscosity relationship, Roelands’ equation is used. This equation can be expressed as,

$$\eta \left(p\right)={\eta }_{0}\mathrm{exp}\left(\frac{\alpha {p}_{0}}{z} \left[-1+{\left(1+\frac{p}{{p}_{0}}\right)}^{Z}\right]\right),$$
(11)
$$\frac{\alpha {p}_{0}}{z}=\mathrm{ln}\left({\eta }_{0}\right)+9.67,$$
(12)

where \({p}_{0}=1.9608\times {10}^{8}\) Pa and \(\alpha\) is the Pressure-viscosity coefficient. To describe the density’s variation with pressure, Dowson and Higginson’s relationship is adopted here. That is,

$$\rho \left(p\right)={\rho }_{0}\frac{{p}_{r}+1.34p}{{p}_{r}+p}.$$
(13)

where \({p}_{r}=5.9\times {10}^{8}\) Pa and \({\rho }_{0}\) is lubricant’s density at zero pressure. This value for \({p}_{r}\) and the value 1.34 for the asymptote at infinite pressure are used to enable comparison with frequently available results, but it should be noticed that a much closer fit may be obtained by fitting to experimental data for a specific lubricant, see e.g. [26]. At high load conditions, the oil pressure distribution has fluctuations. This instability can be avoided with the Galerkin least-squares finite element method (GLS). For details, the reader is referred to [12].

2.3 Dimensionless Model

In this section, the dimensionless model of the elastohydrodynamic governing equations is introduced. In order to compare the results with the conventional model, the final calculation results in terms of minimum oil film thickness will be expressed in Moes's dimensionless parameters (\(M,L\)). However, a special non-dimensional model for numerical calculation is desired to avoid numerical starvation. A system of dimensionless equations based on \({b}^{^{\prime}}\) should be expressed by two dimensionless parameters including \({b}^{^{\prime}}\). The dimensionless parameters of Habchi's model were modified with \({b}^{^{\prime}}\), where the Hertzian radius \(a\) is used as the reference length. This way is reasonable that Habchi’s model governing equation can stay original formulas and only the dimensionless parameters are modified.

To ensure fully-flooded conditions, the computational domain for the EHL line contact model employed in the present analysis is normalized with the inlet distance \(a+{S}_{f}\), instead of the Hertzian radius \(a\). Moreover, since the minimum oil film thickness occurs at the center of the contact in the IR and PR regions, \({h}_{0}\) in Eq. (1) was replaced by Moes’ approximate expression of the dimensionless minimum oil film thickness, \({\tilde{h }}_{\mathrm{min}}^{\mathrm{Moes}}(M,L)\), presented in [7], and thus:

$$\frac{R^{\prime}{h}_{0}}{{a}^{2}}\approx \frac{\pi }{8}\frac{{\tilde{h }}_{\mathrm{min}}^{\mathrm{Moes}}\left(M,L\right)}{M}.$$
(14)

Based on this we define the formula for the inlet distance \({b}^{^{\prime}}\) as

$${b}^{^{\prime}}=a+{S}_{f}\approx a\left(1+3.52{\left(\frac{\pi }{8}\frac{{\tilde{h }}_{\mathrm{min}}^{\mathrm{Moes}}\left(M,L\right)}{M}\right)}^\frac{2}{3}\right)$$
(15)

As previously mentioned, the majority of the studies devoted to numerical calculations of EHL contacts are using a multiple of the Hertzian radius \(a\) to define the computational domain. The computational domain in the present approach is normalized by using an optimized definition of the inlet distance, i.e. \({b}^{^{\prime}}\), and the following normalization to transform the system of equations into the dimensionless form has been used:

$$\begin{array}{*{20}c} {X = \frac{x}{{b^{\prime}}},~~P = \frac{p}{{p^{\prime}_{h} }},~~H = \frac{{hR^{\prime}}}{{b^{\prime2}}},~~\bar{v} = \frac{{vR^{\prime}}}{{b^{\prime2}}},~~\bar{u} = \frac{{uR^{\prime}}}{{b^{\prime2}}},~~Y = \frac{y}{{b^{\prime}}},} \\ {H_{{00}} = \frac{{h_{{00}} R^{\prime}}}{{b^{\prime2}}},~~~\bar{\rho } = \frac{\rho }{{\rho _{0} }},~~\bar{\eta } = \frac{\eta }{{\eta _{0} }},~~\bar{\alpha } = \alpha p^{\prime}_{h} ,} \\ \end{array}$$
(16)
$${p}_{h}^{^{\prime}}=\frac{2w}{\pi {b}^{^{\prime}}}=\frac{a}{{b}^{^{\prime}}}\sqrt{\frac{w{E}^{^{\prime}}}{2\pi {R}^{^{\prime}}}} ,$$
(17)

ensuring that the number of dimensionless parameters (in the dimensionless system of equations) is minimized. In this case, the dimensionless representation of the Reynolds equation becomes

$$\frac{d}{\mathrm{d}X}\left(\frac{{\overline{\rho }H}^{3}}{\overline{\eta }\lambda }\frac{\mathrm{d}P}{\mathrm{d}X}\right)=\frac{\mathrm{d}\left(\overline{\rho }H\right)}{\mathrm{d}X}+\theta ,$$
(18)

where \(\lambda\) is given by

$$\lambda =\frac{12{\eta }_{0}{U}_{e}{R^{\prime}}^{2}}{{b}^{^{\prime}3}{p}_{h}^{^{\prime}}}.$$
(19)

At the same time, the dimensionless film thickness equation becomes

$$H={H}_{00}+\frac{{X}^{2}}{2}-{\overline{v} }_{\partial\Omega },$$
(20)

where \({H}_{00}\) is the dimensionless rigid-body displacement and \({\overline{v} }_{\partial\Omega }\) the dimensionless total displacement of the solid’s upper surface in the vertical direction.

The dimensionless form of the force balance equation can be described as,

$${\int }_{-4.5}^{2.5}P\left(X\right)dX=\frac{\pi }{2} ,$$
(21)

and, in dimensionless form, the system of equations for the elastic displacements is given by,

$$\begin{array}{*{20}c} { - \frac{\partial }{{\partial X}}\left( {c_{1} \frac{{\partial \bar{u}}}{{\partial X}} + c_{2} \frac{{\partial \bar{v}}}{{\partial Y}}} \right) - \frac{\partial }{{\partial Y}}\left( {c_{3} \left( {\frac{{\partial \bar{u}}}{{\partial Y}} + \frac{{\partial \bar{v}}}{{\partial X}}} \right)} \right) = 0,} \\ { - \frac{\partial }{{\partial X}}\left( {c_{3} \left( {\frac{{\partial \bar{u}}}{{\partial Y}} + \frac{{\partial \bar{v}}}{{\partial X}}} \right)} \right) - \frac{\partial }{{\partial Y}}\left( {c_{2} \frac{{\partial \bar{u}}}{{\partial X}} + c_{1} \frac{{\partial \bar{v}}}{{\partial Y}}} \right) = 0,} \\ \end{array}$$
(22)

where \({c}_{1}, {c}_{2}\), and \({c}_{3}\) are defined in Sect. 2.1. Notice that for the dimensionless representation Eq. (22), \({E}_{eq}\) in Eq. (9) has been redefined and is now given by

$${\overline{E} }_{\mathrm{eq}}=\frac{{E}_{\mathrm{eq}}}{{p}_{h}^{^{\prime}}}\frac{b^{\prime}}{R^{\prime}}.$$
(23)

In dimensionless form, Roelands’ equation can be defined as

$$\overline{\eta }\left(P\right)=\mathrm{exp}\left(\frac{\overline{\alpha }{P}_{0}}{z} \left[-1+{\left(1+\frac{P}{{P}_{0}}\right)}^{z}\right]\right),$$
(24)
$$z=\mathrm{ln}\left({\overline{\eta }}_{0}\right)+9.67,$$
(25)

where \({P}_{0}={p}_{0}/{p}_{h}^{^{\prime}}\). Notice that for the dimensionless representation Eq. (24), \(\overline{\eta }\left(P\right)\) in Eq. (11) has been defined \({p}_{h}^{^{\prime}}\). The dimensionless Dowson and Higginson relationship can be expressed as

$$\overline{\rho }\left(P\right)=\frac{{P}_{r}+1.34P}{{P}_{r}+P}.$$
(26)

where \({P}_{r}={p}_{r}/{p}_{h}^{^{\prime}}\). Notice that for the dimensionless representation Eq. (26), \(\overline{\rho }\left(P\right)\) in Eq. (13) has been defined \({p}_{h}^{^{\prime}}\).

In the case of a line contact, a 2D computational domain can be used for the linear elasticity equations, by assuming plane strain condition in the \(z\)-direction. The non-dimensional size of the computational domain \({\Omega }_{\mathrm{D}}\) is taken as 60 × 60, based on the study by Habchi et al. [12], which revealed that this is sufficiently large to capture the stresses and displacements with adequate accuracy. A graphical illustration of \({\Omega }_{\mathrm{D}}\) and its boundary \(\partial {\Omega }_{\mathrm{D}}=\partial {\Omega }_{\mathrm{E}}\cup \partial {\Omega }_{\mathrm{W}}\cup \partial {\Omega }_{\mathrm{S}}\cup \partial {\Omega }_{\mathrm{N}}\) is given in Fig. 3, where \({\Omega }_{\mathrm{C}}\subset \partial {\Omega }_{\mathrm{N}}\).

Fig. 3
figure 3

Graphical illustration of the computational domain \({\Omega }_{\mathrm{D}}\) for the elastic body, including the boundaries \(\partial {\Omega }_{\mathrm{D}}=\partial {\Omega }_{\mathrm{E}}\cup \partial {\Omega }_{\mathrm{W}}\cup \partial {\Omega }_{\mathrm{S}}\cup \partial {\Omega }_{\mathrm{N}}\), where \({\Omega }_{\mathrm{C}}\subset \partial {\Omega }_{\mathrm{N}}\). The latter represents the computational domain for the EHL line contact (Color figure online)

Full size image

The dimensionless computational domain \({\Omega }_{\mathrm{C}}\) for the EHL contact problem [where the Reynolds’ Eq. (18) and the film thickness Eq. (20) are defined], which is part of the upper boundary of \({\Omega }_{\mathrm{D}}\), is also depicted in Fig. 3. As illustrated in the insert to the right, the EHL contact spans the inlet region \(-4.5<X<-1.5\), the central region \(-1.5<X<1.5,\) and the outlet region \(1.5<X<2.5\). The same dimensionless domain was also used by Hultqvist [14], but in contrast to the present work where the inlet zone length \(b\mathrm{^{\prime}}\) is used to transform the equations into dimensionless form, Hultqvist used the Hertzian radius \(a\). As will be shown in the results section, this choice of the dimensionless computational domain renders a fully-flooded condition in the inlet region, thus numerical starvation is effectively avoided.

The boundary conditions are defined by

$$\left\{\begin{array}{c}{\sigma }_{n}=-P\, and\, { \sigma }_{t}=0, on\, {\Omega }_{\mathrm{C}}\\ {\sigma }_{n}=0, {\sigma }_{t}=0, on\, \partial {\Omega }_{\mathrm{D}}\setminus {\Omega }_{\mathrm{C}}\\ \overline{U }=\overline{V }=0, on\, \partial {\Omega }_{\mathrm{S}}\end{array}\right.$$
(27)

where \({\sigma }_{n}\) and \({\sigma }_{t}\) are the normal- and tangential stress, respectively.

3 Results and Discussion

This section describes the results produced using the numerical calculation model in Sect. 2. For verification of this numerical analysis, we confirmed the convergence of the numerical calculation model, oil pressure distribution, and oil film thickness distribution. We can describe Moes’ dimensionless load parameter \(M\) and dimensionless materials parameter \(L\) [7], by using the present dimensionless model parameters \(\lambda\), \(\overline{\alpha }\),

$$M={\left(\frac{8}{3{\pi }^{2}}\lambda \right)}^{-\frac{1}{2}}\left(\frac{{b}^{^{\prime}}}{a}\right),$$
(28)
$$L=\overline{\alpha }{\left(\frac{32}{3}\lambda \right)}^\frac{1}{4}{\left(\frac{b^{\prime}}{a}\right)}^\frac{1}{2},$$
(29)

and the relation between the present representation between the dimensionless film thickness \(H\) and the one presented by Moes in [7], i.e. \({\overline{h} }^{\mathrm{Moes}}\), reads

$${\overline{h} }^{Moes}=\frac{8M}{\pi }{\left(\frac{{b}^{^{\prime}}}{a}\right)}^{2}H$$
(30)

Values of \(M\) and \(L\) cover the IR-, IE-, PR-, and PE- lubrication regions, see Fig. 4 for a graphical illustration. Calculations are conducted with \(L=1, 2.5, 5,\) and \(10\), for 20 different values of \(M\) spanning the range \(\left[0.1, 200\right]\) going from 200 to 0.1, e.g. 20 corresponding to \(M=200\) and 1 corresponding to \(M=0.1\).

Fig. 4
figure 4

Overview of the numerical computation conditions in this study and the four different lubrication regions (Color figure online)

Full size image

3.1 Convergence

In this section, we describe how the mesh convergence of the current model was investigated in terms of accuracy. Regarding the accuracy of the elastic deformation along the boundary \({\Omega }_{\mathrm{C}}\), Habchi et al. [12] showed that could be computed with adequate accuracy even on a rather coarse mesh of the elastic body with a computational domain \({\Omega }_{\mathrm{D}}\). This result was confirmed herein by comparing the results obtained on a normal and an extremely coarse mesh for \({\Omega }_{\mathrm{D}}\), when the maximum mesh size of \({\Omega }_{\mathrm{C}}\) was specified as 0.00066, 0.001, and 0.00325. The normal and extremely coarse meshes when the maximum mesh size in \({\Omega }_{\mathrm{C}}\) was specified as 0.001 are depicted in Fig. 5.

Fig. 5
figure 5

The normal- (left) and extremely coarse (right) meshes employed to discretize \({\Omega }_{\mathrm{D}}\), when the maximum mesh size of \({\Omega }_{\mathrm{C}}\) is 0.001. The corresponding number of \(\partial {\Omega }_{\mathrm{D}}\) boundary elements are 3182 and 3116 for the normal and the extremely coarse mesh, respectively. The corresponding number of \({\Omega }_{\mathrm{D}}\) domain elements are 48,346 and 21,638, for the normal and the extremely coarse mesh, respectively (Color figure online)

Full size image

Table 1 shows the number of boundary elements \({N}_{\mathrm{C}}\) and the number of domain elements \({N}_{\mathrm{D}}\), of the extremely coarse mesh, corresponding to the three maximum boundary element sizes 0.00066, 0.001, and 0.00325.

Table 1 Number of boundary elements (\({N}_{\mathrm{C}}\)) and number of domain elements (\({N}_{\mathrm{D}}\)), corresponding to the non-dimensional maximum boundary element sizes on the first row
Full size table

The corresponding three extremely coarse domain meshes are shown in Fig. 6. As the maximum element size only affects the mesh of the upper boundary along the EHL contact, \({\Omega }_{\mathrm{C}}\), the change in the depth direction in the mesh of \({\Omega }_{\mathrm{D}}\) is marginal.

Fig. 6
figure 6

Domain meshes with 32,864, 21,638 and 7258 number of elements, corresponding to the maximum boundary element sizes 0.00066 (left), 0.001 (middle), but also depicted in Fig. 5 (right), and, 0.00325 (right) (Color figure online)

Full size image

The resulting oil film pressure distributions from an investigation of the accuracy of the representation of the pressure spike for \(\left(L,M\right)=\left(10, 200\right),\) obtained with three domain meshes corresponding to the maximum element size of \({\Omega }_{\mathrm{C}}\); 32,864, 21,638, and 7258, are depicted in Fig. 7. The right side presents a magnification of the pressure spike region, and a convergent trend in the location of the pressure spike can be observed. The location and magnitude of the pressure spike are both almost the same with 21,638 domain elements as with 32,864 domain elements. However, the mesh with 32,864 domain elements introduces an undesirable oscillation in the location of the pressure spike. Moreover, the mesh with 7258 domain elements seems not well enough to converge in the location of the pressure spike. Therefore, the mesh with 21,638 seems well enough to converge in the location of the pressure spike. This suggests that the mesh with 21,638 domain elements renders the best possible prediction, given the solver settings used. For this reason, this mesh is also employed when obtaining the reference solutions used in the comparison presented below.

Fig. 7
figure 7

Oil pressure distribution for three meshes, with the number of domain elements corresponding to the maximum element size of \({\Omega }_{\mathrm{C}}\); 32,864, 21,638, and 7258. On the right, is a magnification of the pressure spike region (Color figure online)

Full size image

The dimensionless minimum oil film thickness \({\overline{h} }_{\mathrm{min}}^{\mathrm{Moes}}\) obtained using the meshes with \({N}_{\mathrm{D}}=7258\) and \({N}_{\mathrm{D}}=21638\) elements, as well as the relative difference between them (using the solution at the finer mesh as reference) are shown in Table 2. The average computing time for \({N}_{\mathrm{D}}=7258\) and \({N}_{\mathrm{D}}=21638\) elements on an intel(R) core(TM) i7-8700 CPU was 23 s and 1 m 13 s, respectively. The calculation conditions were chosen using representative values of Moes’ dimensionless parameters \(M\) and \(L\) for each of the IR, PR, PE, and IE regions. The reason to focus on the minimum oil film thickness is that it is a key parameter in the expression of the inlet distance (15) which is investigated herein. As shown in Table 2, the dimensionless minimum oil film thickness decreases when the number of boundary elements \({N}_{\mathrm{C}}\) (used to discretize the domain for the EHL line contact) decreases. It is, however, reassuring that the maximum relative error of the dimensionless minimum oil film thickness \({\overline{h} }_{\mathrm{min}}^{\mathrm{Moes}}\) is less than 0.28% (in the case \(L=10\) and \(M=200\) representing the PE region) with the coarser mesh having 7258 domain elements.

Table 2 Results for the dimensionless minimum oil film thickness \({\overline{h} }_{\mathrm{min}}^{\mathrm{Moes}}\)
Full size table

Table 3, presents the dimensionless maximum oil pressure \({P}_{\mathrm{max}}\), and for the PE region the pressure spike \({P}_{s}\), obtained using the meshes with \({N}_{\mathrm{D}}=7258\) and \({N}_{\mathrm{D}}=21638\) elements, as well as the relative difference between them (using the solution at the finer mesh as reference). As the table shows, the dimensionless maximum oil pressure \({P}_{max}\) and the pressure spike \({P}_{s}\) decrease along with the decrease of boundary elements number on the EHL contact line \({\Omega }_{\mathrm{C}}\). It also shows that, the maximum relative difference of the dimensionless maximum oil pressure \({P}_{\mathrm{max}}\), for \(\left(L,M\right)=\left(10, 200\right)\) (PE), is less than 0.5%, for the mesh with 7258 domain elements. For \(\left(L,M\right)=\left(10, 0.73\right)\) (PR), and \(\left(L,M\right)=\left(10, 0.1\right)\) (IR), the relative difference of the dimensionless maximum oil pressure \(\Delta {P}_{\mathrm{max}}/{P}_{\mathrm{max}}\) is less than 0.03%. These relative differences are very small, but it is worth noticing that the results presented herein were obtained from the mesh with 21,638 domain elements, to ensure an adequate representation of the oil pressure distribution.

Table 3 Relative differences of dimensionless maximum pressure \(P\)
Full size table

3.2 Oil Pressure Distribution

In this section, the oil pressure distributions are shown for the computation domain to confirm the flooded conditions. As a verification, we confirmed both ends of the oil pressure distribution. If the oil pressure at the boundaries of the contact is zero, regardless of various inlet distances, the present numerical calculation method is shown to ensure the flooded condition.

The dimensionless oil pressure distribution on the computation domain is shown in Figs. 8, 9, 10, 11. Each of these figures shows the 20 numerical computations for \(M\) (enumerated from 1 to 20) starting from 200 and going down to 0.1, for \(L=1, 2.5, 5,\) and \(10\), respectively. It means that these results represent the oil pressure distributions spanning from the isoviscous elastic (IE) to the isoviscous rigid (IR) lubrication region.

Fig. 8
figure 8

Oil pressure distributions for \(L=1\), as \(M\) goes from \(200\) to \(0.1\) in 20 steps (Color figure online)

Full size image
Fig. 9
figure 9

Oil pressure distributions for \(L=2.5\), as \(M\) goes from \(200\) to \(0.1\) in 20 steps (Color figure online)

Full size image
Fig. 10
figure 10

Oil pressure distributions for \(L=5\), as \(M\) goes from \(200\) to \(0.1\) in 20 steps (Color figure online)

Full size image
Fig. 11
figure 11

Oil pressure distributions for \(L=10\), as \(M\) goes from \(200\) to \(0.1\) in 20 steps (Color figure online)

Full size image

As shown in Figs. 8,9,10,11, the derivative of the oil pressure distribution is 0 at both the inlet and exit, verifying that the inlet region in the present numerical calculation method effectively prevents starved conditions. It can also be seen that the oil pressure distribution expands towards the inlet boundary as the value of \(M\) reduces.

3.3 Oil Film Thickness

In this section, the Moes’ approximate expression \({\tilde{h }}_{\mathrm{min}}^{\mathrm{Moes}}(M,L)\) for the minimum oil film thickness is compared with the minimum oil film thickness obtained using the present model, and the comparison is conducted over a large portion of the Johnson chart [1].

The calculation results of the dimensionless oil film thickness \({\overline{h} }^{\mathrm{Moes}}\), for spanning the same range of the dimensionless load parameter \(M\) and material parameter \(L\) are depicted in Fig. 12. As shown here, the dimensionless minimum oil film thickness increases along with a decrease in \(M\). Moes’ approximate expression results [7] are in good agreement with the dimensionless minimum oil film thickness trend of the present model over a large portion of the Johnson chart [1]. A comparison of results of \({\tilde{h }}_{\mathrm{min}}^{\mathrm{Moes}}(M,L)\) calculated by Moes’ approximate expression vis a vis the present model is presented in Table 4, which shows that the relative difference between the two values is less than 2.7%

Fig. 12
figure 12

The minimum oil film thickness results obtained using the present model for \(L=1, 2.5, 5, 10\), and \(M\) going from 200 to 1 in 20 steps. Solid lines are Moes’ approximate solutions (Color figure online)

Full size image
Table 4 Comparison of \({\tilde{h }}_{\mathrm{min}}^{\mathrm{Moes}}\) calculated by Moes’ formula with present numerical analysis results
Full size table

4 Conclusions

In this paper, we have presented a numerical EHL calculation method for oil film thickness that ensures fully flooded conditions by employing the present inlet distance normalization. The results obtained with the present model were compared with results from Moes’ approximate minimum oil film thickness expression.

The main conclusions are:

  • With the definition of the inlet distance established herein, we confirmed that the oil pressure distributions obtained over the whole Johnson chart correspond to fully flooded conditions.

  • The maximum relative difference found in the mesh convergence study occurs in the PE region [represented here by \(\left(L,M\right)=\left(10, 200\right)\)] and a mesh with 21,638 domain elements was employed to get a sufficiently accurate representation of the pressure spike.

    • The maximum relative difference between dimensionless minimum oil film thickness obtained with the coarsest mesh (with 7258 domain elements) and the reference solution (obtained with the mesh with 21,638 domain elements) is less than 0.28%.

    • The maximum relative difference of the dimensionless maximum oil pressure obtained with the coarsest mesh (with 7258 domain elements) and the reference solution (obtained with the mesh with 21,638 domain elements) is less than 0.5%.

Regarding the oil film thickness, the relative difference between the prediction of the minimum oil film thickness using the present model and that by Moes’ approximate expression is less than 3% over the whole Johnson chart.