The Critical Pressure for Bulk Leakage of Non-planar Smooth Surfaces

Abstract

The sealing surfaces subjected to the hydrostatic load from the sealed fluid can deform to such an extent that leakage occurs when the sealed fluid pressure is sufficiently high, and this critical pressure that the seal can sustain without leakage is a fundamental aspect of the seal design. This paper presents a new numerical method based on the bisection algorithm and the boundary element method, which can be utilized to capture the critical pressure with high accuracy. The present method is employed to study the relationship between the critical pressure and the non-planar geometry of the sealing surfaces, under a wide range of loading conditions. The results show that the critical pressure can be acquired from the surface’s dry contact state with a dimensionless correction factor.

1 Introduction

Seals are widely used machine elements that are designed to prevent fluid flow through a gap between two assembled parts. One way of accomplishing this is by applying an external load to seal the gap between the parts. Once the gap is sealed, the first contacting point between the two surfaces at the high-pressure side of the seal marks the fluid front [1]. Leakage may, however, occur if the roughness of the contacting surfaces prevents the two surfaces from forming full contact. Persson and Yang [2] have proposed a theory to calculate the fluid leakage rate through the interface between rough surfaces, based on percolation theory [3] coupled with Persson’s contact mechanics theory for self-affine fractal rough surface [4]. The Persson and Yang theory has shown good agreement with the experiment for low leakage flow rate [5]. Some of the recent progress on the percolation-based model, such as those shown in [6,7,8,9], introduces the stochastic elements to reflect the random natural of surface roughness and leakage flow. It is considered better when compared with experiments [10], because the leakage rates near the percolation threshold are sensitive to the detailed distribution of the percolation paths [2, 11].

How the percolation paths are formed between the contacting surfaces is an important question for leakage inception. The experiments conducted in [1, 12, 13] show that bulk leakage at a high flow rate occurs when the sealed fluid pressure surpasses a critical value. The sealed fluid pressure at this critical point has been termed as blow-off pressure [14], breakthrough pressure [15], or threshold pressure [16] in different application scenarios. In this work, it is termed as critical pressure and is defined as the pressure at the high-pressure side of the seal, at which the pressurized fluid is displaced to an extent that continuous flow paths are formed between the high- and the low-pressure sides. Under this definition, there is no fluid leakage before the sealed fluid pressure reaches the critical pressure. The Persson and Yang theory, which is based on Bruggeman’s mean-field theory [17], is known to fail near critical points [18] when the leakage flow rate transits from zero to a finite value. Experiment data [1] have also shown that the Persson theory had difficulties predicting the critical pressure without incorporating the fluid load into contact mechanics. Dapp and Müser [19] coupled the contact mechanics of linear elastic bodies and Reynolds equation to study the fluid leakage near the percolation threshold, and they observed that the transition from zero to finite leakage has different critical exponents with small alteration on the fluid model. In their study, they assumed that the fluid pressure does not deform the contacting surfaces. This assumption is no longer valid when fluid pressure is comparable with the contact pressure, and, as shown in [14, 20,21,22,23], the fluid-structure interaction must be considered under this condition.

One cause of the bulk leakage is the failure of the sealing material. For instance, it has been observed that the elastomer O-ring can fail because of extrusion, explosive decompression, abrasion–friction, thermal and chemical degradation [24]. On the other hand, experiments [12, 13] have shown that bulk leakage can also happen without material failure, and the transition between zero and finite leakage is highly repeatable throughout the cycles of increasing and decreasing of the sealed fluid pressure. The critical pressure for the sealing system in [12] was computed with the force equilibrium relation between the fluid and the seal shear stress, with the assumption that both contacting surfaces are planar.

The contact between two non-planar surfaces (Fig. 1a) allows the pressurized fluid to percolate into the non-contact area that is connected to the high-pressure side. In this situation, the pressurized fluid at the contact interface provides the driving force to open up the contact and proceed the fluid front. The 2D elastic contact problem between a non-planar and a flat surface, incorporating the sealed fluid pressure, is studied in the present paper. The contact state is analyzed with increased sealed fluid pressure, until the solid–solid contact is lost. A criterion to determine the critical pressure is proposed, and a new numerical method is implemented based on this criterion for the computation thereof. The new implemented numerical method is then used to study how the critical pressure varies with the model input parameters, while keeping the total load constant.

2 The Contact Problem with Pressurized Fluid at the Contact Interface

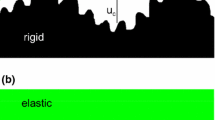
A sealing system consisting of one non-planar and one rigid flat surface is shown in Fig. 1, with the sealed fluid at the high-pressure side and air under standard temperature and pressure condition¹ (STP) at the low-pressure side. The displacement of the flat surface is fixed, and the non-planar surface is brought into contact with it under the total load $P_t$. It is assumed that the curvature of the non-planar surface is small enough so that the deformation satisfies the half-space assumptions.

Under the contact conditions studied in this work, we will use surface traction to refer to the surface stress orthogonal to the contact interface, following the naming convention in [25]. The surface traction p, under this definition, equals the fluid pressure in the fluid-filled regions and it is the contact pressure at the solid–solid contact regions. As the pressurized fluid at the contact interface carries a portion of the total load, the contact length decreases, and the contact stress is redistributed with respect to the corresponding dry contact condition [26,27,28]. Figure 1a–c displays the schematic views of the flow front position and the surface traction distribution at the contact interface, under elevated sealed fluid pressure conditions. The total load in the vertical direction, $P_t$, is assumed to be constant during the process depicted in Fig. 1a to c. The nominal traction is $p_0=P_t/A$, where A is the total load bearing area of the sealing interface. When the sealed fluid pressure, $p_f$, is small (Fig. 1a), the contact pressure prevents the fluid from penetrating through the contact interface, and there is no leakage. The fluid at the high-pressure side deforms and bends the non-planar surface toward the low-pressure side, resulting in a bigger gap between surfaces at the high-pressure side, as shown in Fig. 2. As the fluid pressure increases, more fluid enters from the high-pressure side, and the position of the fluid front moves forward. Meanwhile, the overshoot pressure $p_{over}$, which is defined as the difference between the maximum solid–solid contact pressure and the sealed fluid pressure, decreases.

The quantitative surface traction distribution under different $p_f$ conditions is obtained from the boundary element model [29], and it is also verified with the finite element model in [26]. When the total load,$P_t$, is constant and the sealed fluid pressure $p_f$ increases from zero, the solid–solid contact length decreases from both the high- and low-pressure side, and it is approaching zero while the overshoot pressure vanishes. Any further increase of the sealed fluid pressure will result in a discontinuity in surface traction [25], and the solid–solid contact is lost. At the moment when the contact opens, the high- and low-pressure side is connected, and the sealed fluid pressure is the critical pressure, $p_b$. The sealed fluid is, however, stationary, since it was in hydrostatic state before the critical pressure is reached. Meanwhile, the air at the low-pressure side is in its initial state. This suggests that the surface traction has the shape of step function with the pressure drop at the interface between the sealed fluid and the air, as shown in Fig. 1b.

A two-fluid system with an initial pressure condition as Fig. 1b should be considered as a multiphase shock tube problem [30]. The evolution rule governing this dynamical system is the Euler equation, which comprises equation for the conservation of mass, momentum, and energy of compressible fluids. Appendix A gives the exact solution of the 1D Euler equation for a non-reactive two-fluid system. The fluid pressure field from the solution of the Euler equation is composed of four regions, as shown in Fig. 1c. At the low-pressure side, the compression waves origins from the initial phase interface collide into a shock wave and it propagates inside the air. Before the shock wave, the air is at its initial state (STP), but the pressure rises abruptly when the shock wave sweeps over. Meanwhile, the so-called rarefaction fan propagates into the sealed fluid and decreases the pressure there. The sealed fluid pressure at the high-pressure side is preserved before the head of the rarefaction wave propagates through, and it decreases in a continuous manner, until the tail of the rarefaction wave enters. A pressure plateau is built up behind the rarefaction fan, which propagates to both the high- and low-pressure side with time. The sealed fluid front proceeds with the phase interface velocity, and it falls behind the shock wavefront because of the much faster shock wave speed.

The evolution of the surface traction profile from Fig. 1b, c is a very fast process because of the high wave speed, as explained in Eq. (26). So it is reasonable to assume that at the beginning of the leakage, the effect of fluid viscosity is minimal, and the leakage channel remains unchanged. However, these assumptions are no more valid as time evolves. In general, the conservation laws of the fluid system do not satisfy the total load constraint, so the non-planar surface can move up or down and alternate the height of the leakage channel. If the total fluid load becomes smaller than the applied load, the non-planar surface might be able to re-contact with the rigid surface, and the system returns to the state shown in Fig. 1a, with $p_f=p_b$, and the sealing system experiences an intermittent leakage process. On the other hand, if the total fluid load becomes higher than the applied load, the leakage channel will be further opened, and the leakage flow rate is uncontrollable beyond this point. The quantitative analysis of the long time behavior of the sealed fluid and the contact surface after the moment the sealed fluid pressure reaches the critical pressure is out of the scope of the current paper and will not be discussed further.

Based on the previous discussion, the critical pressure is the sealed fluid pressure at the moment the overshoot pressure vanishes. When quantifying the critical pressure using this definition, it matches well with the experiment carried out in [12], for a seal with displacement control. Our numerical experiment, resulting in the surface traction curves exhibited in Fig. 2, shows that the overshoot pressure also approaches zero under the total load control condition as the sealed fluid pressure increases.

Fig. 1

The schematic views of the flow front position and the surface traction distribution between two contacting surfaces with fluid at the contact interface. a $p_f<p_b$, b $p_f=p_b$ and $t_0=0$, c $p_f=p_b$ and $t_0>0$

Fig. 2

The surface traction distribution p and the deformed shape of the non-planar surface g under different sealed fluid pressure conditions, for a Parabolic profile $g_0(x)=4\Delta x^2/\lambda ^2$ in contact with a flat rigid surface, with the nominal traction $p_0=0.05p_s$. The pressure scaling factor $p_s$ is defined in Eq. (7)

3 The Numerical Method to Compute the Critical Pressure

The numerical method that can capture the critical pressure of bulk leakage requires incorporating the hydrostatic load at the contact interface. Multiple methods can achieve this, e.g., finite element method (FEM) with additional penalty term at the fluid-filled region [26]. The numerical practice has shown that computing the critical pressure with the total load control condition needs some artificial damping on the loading and constraints to improve its convergence properties, and it requires some trial and error, especially when the sealed fluid pressure ($p_f$) reaches the critical pressure ($p_b$). Furthermore, when $p_f \ge p_b$, the conventional finite element method (FEM) fails because the load balance is not preserved when the sealed fluid pressure ($p_f$) reaches the critical pressure ($p_b$). A new method, therefore, is required to simulate the critical pressure. Huang et al. [29] have developed a boundary element method (BEM) to study the elastic contact problem in combination with the hydrostatic fluid pressure load. The method solves the coupled solid-solid and fluid-solid contact problem by iterating the surface traction profile p, to minimize the total complementary energy. During each iteration, the surface traction profile needs to be adjusted to satisfy the total load condition, following the procedure described in [31]. The method is benchmarked with the FE Model in [29] for the cases of $p_f<p_b$. The BEM allows a fast computation of the contact problem with $p_{over}>0$, before it fails when $p_f=p_b$ and $p_{over}=0$ for the same reason for the FEM.

When $p_f \ge p_b$, the BEM method is jammed in an infinite loop at the surface traction adjustment step, because the load balance condition can never be satisfied. To break out of the infinite loop, three conditional statements are added in the surface traction adjustment step, viz.,

$$p_{f} > 0,$$

(1a)

$$\Omega _f=\emptyset ,$$

(1b)

$$\text {and} \quad p^{k}_{00}<p_f.$$

(1c)

The condition Eq. (1a) ensures that the sealed fluid pressure is applied, and the condition Eq. (1b) checks whether the hydrostatic fluid-filled region $\Omega _f$ is empty, with the algorithm implemented in [29]. When $\Omega _f \ne \emptyset$, the program is simulating the contact problem with hydrostatic load at the contact interface (Fig. 1a), following the workflow in [29]. Two possibilities can result in empty $\Omega _f$. One is that $p_f \ge p_b$, and the high- and low-pressure side is connected, so there is no fluid at hydrostatic state between the contacting surfaces. Another possibility is that the solid–solid contact happens at the high-pressure side, with a contact pressure higher than $p_f$ there. Therefore, the sealed fluid cannot enter the solution domain. The Eq. (1c) is applied to rule out the second possibility, with $p^{k}_{00}$ as the surface traction value at the high-pressure side, during the $k$th iteration step of the total complementary energy minimization. The simulation is terminated when the conditional statement Eqs. (1a) to (1c) is triggered, and a leakage identifier is returned as 1. Otherwise, the simulation will continue until convergence, and the leakage identifier is 0.

A bisection method is developed to identify the critical pressure. The method starts by simulating the contact problem with two sealed fluid pressure $p_f=p_l$ and $p_f=p_h$ and acquires their leakage identifiers. One convenient choice of $p_l$ is zero, and $p_h$ is chosen such that the leakage identifier is 1 when $p_f=p_h$. The interval $[p_l, p_h]$ is then repeatedly divided into two by their midpoint $p_{mid}=0.5(p_l+p_h)$, and the subinterval with different leakage identifiers at the endpoints is kept, by replacing one endpoint of $[p_l, p_h]$ with the value of $p_{mid}$. In this way, the width of the solution interval is reduced by half at each iteration, and the process is continued until the interval width $p_h-p_l$ is smaller than a specified tolerance $\epsilon$. The critical pressure $p_b$ is then returned as $0.5(p_l+p_h)$. With this method, the critical pressure for the case shown in Fig. 2 is computed as $p_b=1.789p_0$, or equivalent to $p_f=0.08945p_s$, when $\epsilon$ is set to $10^{-3}p_0$.

4 The Critical Pressure of Non-planar Surface in Contact with the Flat Rigid Surface

The 2D contact problem of the smooth non-planar surface in contact with a flat rigid surface is studied with the numerical method developed in Sect. 3. The solution domain covers the region from the high-pressure to the low-pressure side, and it is defined as $\Omega = [-0.5\lambda ,0.5\lambda ]$. The elastic modulus of the non-planar surface is $E$, and its Poisson’s ratio is $\nu$. Two factors thought to be influencing $p_b$ are explored in the current study. The first factor is the nominal traction in the vertical direction, and it is denoted as $p_0$. With higher $p_0$ to compress the two surfaces together, the required fluid pressure to open the contact increases correspondingly. The second factor that affects $p_b$ is the shape of the non-planar surface, because the change of the geometry can lead to different contact pressure distribution and maximum contact pressure. Three types of geometry are considered in the current study, i.e., shown in Fig. 3a–c. The three geometry profiles are the Parabolic profile:

$$\begin{aligned} y(x)=4\Delta \frac{(x-x_0)^2}{\lambda ^2}, \end{aligned}$$

(2)

the Cosine profile,

$$\begin{aligned} y(x)=\frac{\Delta }{2}\left( 1-\cos {\frac{2\pi (x-x_0)}{\lambda }}\right) , \end{aligned}$$

(3)

and the Catenary profile

$$\begin{aligned} y(x)= \frac{\Delta }{\left( \cosh {\frac{K}{2}}-1\right) }\left( \cosh {\left( K\frac{(x-x_0)}{\lambda }\right) }-1\right) . \end{aligned}$$

(4)

The geometry translation parameter $x_0$ is the x-coordinate of the first point brought into contact with the flat surface, and the parameter K in Eq. (4) controls the curvature of the Catenary profile. When $K \rightarrow \infty$, the Catenary profile approaches a flat surface. All surfaces generated from Eqs. (2) to (4) are confined to the range of $y \in [0, \Delta ]$, with points having $y>\Delta$ being cut off to $y=\Delta$.

Fig. 3

Top row (a–c): the initial gap depicted in Eqs. (2) to (4), with $x_0/\lambda =-0.25, 0, 0.25$, $\Delta /\lambda =0.01,$ and $K=10.0$. Bottom row (d-f): the fluid volume between the contacting surfaces before $p_b$ is reached, for the geometries depicted in the top row. The area under the dashed lines represents the possible $(p_f,Q)$ states after $p_f$ reaches $p_b$

The effect of $x_0$ on the critical pressure $p_b$ is readily understood by considering a rigid body case such as the one shown in Fig. 4. The force balance for the rigid body in contact with a flat surface is

$$\begin{aligned} p_fl_{f}+p_cl_0=p_0\lambda , \end{aligned}$$

(5)

with the initial fluid-filled length $l_f$ as the distance from the high-pressure side to the leading contact point position $x_{c0}$, $p_c$ as the solid–solid contact pressure and $l_0$ as the solid–solid contact length. Under constant loading condition, the solid–solid contact pressure $p_c$ decreases with increased $p_f$, and the critical pressure $p_b$ is reached when $p_f=p_c$. With $p_b=p_c=p_f$ in Eq. (5), we have

$$\begin{aligned} p_{b}=\frac{\lambda }{(l_{f}+l_0)}p_0. \end{aligned}$$

(6)

Since the critical pressure $p_b$ increases with the nominal traction in the vertical direction $p_0$, it is of interest to study their ratio $p_b/p_0$, and it is referred to as the critical pressure ratio in the following discussion. When $l_0$ is a constant, the critical pressure acquired from Eq. (6) decreases with larger $l_f$, because more fluid flows into the contact interface and shares the total load. The minimum critical pressure ratio is 1.0 when $l_f+l_0=\lambda$. The upper limit of the critical pressure ratio $p_b/p_0={\lambda }/{l_0}$ occurs when $l_f \rightarrow 0$. When $l_f=0$, there is no fluid at the sealing interface. The fluid is only present in the contact interface when $p_f>p_c$. It is equivalent to the condition Eq. (1c) in the elastic contact problem.

Fig. 4

A schematic view of the rigid body model problem with fluid at the sealing interface

The 2D elastic contact problem with pressurized fluid at the contact interface is studied for the geometries depicted in Eqs. (2) to (4) with $x_0/\lambda =-0.25, 0, 0.25$. The nominal traction $p_0$ is normalized with a pressure scaling factor $p_s$ in the simulation.

$$\begin{aligned} p_s=\frac{2\pi E}{(1-\nu ^2)}\frac{\Delta }{\lambda }. \end{aligned}$$

(7)

The simulations are conducted on an equidistantly spaced mesh with 2049 elements, with the maximum absolute error for the contact plane as $10^{-9} \lambda$. The sealed fluid pressure $p_f$ is increased from zero to $p_b$ in the simulation, and the tolerance for $p_b/p_0$ is set to $10^{-3}$. The ratio between $\Delta$ and $\lambda$ is 0.01 to fullfill the small slope requirement of the half-space approximation, while it is worth to point out that the surface traction solution is independent of $\Delta /\lambda$ when normalized with $p_s$ [26]. The fluid volume between the surfaces $Q=Q(p_f)$ is shown in Fig. 3d–f, for the case $p_0=0.035p_s$ and $K=10.0$. The fluid volume between the contacting surfaces Q is normalized with $Q_0=Q(p_f=0)$ and $Q_{ref}=\Delta \lambda$. By excluding the initial fluid volume between the contact interface, the fluid volume in Fig. 3d–f increases solely by the elevated sealed fluid pressure. The volume of fluid that flows into the contact interface grows with $p_f$, and its growth rate increases with higher sealed fluid pressure. The growth rate variation of Q when $p_f$ increasing from zero to $p_b$ is qualitatively consist with the measurement in [12]. Among the three types of geometries, the Cosine profile allows the largest volume of fluid to flow into the contact interface for a given applied fluid pressure $p_f$, and it also exhibits the highest critical pressure $p_b$. As anticipated, the Catenary profile has the smallest $p_b$ of the three. It is because of the large curvature of the Catenary geometry results in a more evenly distributed contact pressure, and its maximum dry contact pressure is the smallest of the three profiles. While the Catenary profile is easy to open, its volume of fluid Q is the smallest of the three under the same $p_f$. It suggests that the increase of Q mainly comes from the gap size increase at the high-pressure side, because of the deformation generated by the sealed fluid pressure $p_f$. The preceding of the fluid front also increases the fluid volume at the interface, but it only accounts for a small portion of Q because the insignificant gap size near the fluid front. The growth rate of Q for the Parabolic profile is in between the Cosine and Catenary profiles, and so is its critical pressure when the loading condition and $x_0$ are the same.

The critical pressure $p_b$ is higher with smaller $x_0$ in all the cases considered, because the initial fluid-filled length $l_f$ is smaller when the profile is closer to the high-pressure side. Since the pressurized fluid shares less load in the vertical direction, the pressure required to open the contact increases.

A parametric study is conducted for the three types of geometries depicted in Eqs. (2) to (4). Thirty uniformly spaced $p_0$ are chosen in the range $[0, p_{0m}]$ for each type of geometry, with

$$\begin{aligned} p_{0m}=K_p(1-2|x_0|)^2p_s. \end{aligned}$$

(8)

The empirical constant $K_p$ is 0.45 for the Parabolic profile, 0.25 for the Cosine profile, and 0.15 for the Catenary profile. The choices of $K_p$ guarantee a positive $l_f$ when $p_f \rightarrow 0$ and $p_0=p_{0m}$, so there is always initial fluid between the contact surfaces. Meanwhile, there is no solid–solid contact at the low-pressure side ($x=0.5\lambda$) when $p_0=p_{0m}$. The critical pressure ratio $p_b/p_0$ is set to a finite value $\lambda /x_{00}$ to avoid undefined critical pressure ratio when $p_0=0$ , with $x_{00}$ as the distance from the high-pressure side to $x_0$, and it is $0.5\lambda +x_0$ in the current coordinate system. Thirty uniformly spaced $x_0/\lambda$ are chosen from the interval [-0.25, 0.25], together with each value of $p_0$, this results in a total of 900 realizations for each type of geometry. The critical pressure $p_b$ acquired from the simulation is shown in Fig. 5, as a function of $p_0$ and coloring with $x_0$. The critical pressure ratio $p_b/p_0$ is always larger than 1.0, and it decreases with the nominal traction $p_0$. The drop rate of $p_b/p_0$ with $p_0$ depends on both $p_0$ and the geometry translation parameter $x_0$, and it is higher with smaller $p_0$ for a given $x_0$. Translating the geometry to the low-pressure side (bigger $x_0$) not only decreases $p_b/p_0$ but also leads to a slower decrease rate of the critical pressure ratio with $p_0$.

Fig. 5

The critical pressure ratio $p_b/p_0$ as a function of the nominal traction $p_0$ for the Parabolic (a), Cosine (b), and Catenary (c) profiles

The data shown in Fig. 5 are fitted into an empirical relationship:

$$\begin{aligned} \frac{p_b}{p_0}=f(x_0,p_0)=\frac{\lambda }{(0.5\lambda +x_{0})}-\alpha \left( \frac{p_0}{p_s}\right) ^{\beta }. \end{aligned}$$

(9)

The critical pressure ratio $p_b/p_0$ acquired from the simulation is plotted against the values from the fit equation Eq. (9) in Fig. 6. The relative error generated by Eq. (9) is 0.0026% on average and a maximum of 5.17%.

Fig. 6

The fitting error of $p_b/p_0$ generated by Eq. (9)

The first term on the right-hand side of Eq. (9) is the defined limit of $p_b/p_0$ when $p_0$ is equal to zero, and the fitting coefficients $\alpha , \beta$ are functions of $x_0/\lambda$, as shown in Fig. 7. The fitting coefficient $\alpha$ is negatively correlated with $x_0$ for the Parabolic and Cosine profile, while it increases with $x_0$ for the Catenary profile when $x_0/\lambda >0.1$. A simple linear relationship exists between $\beta$ and $x_0$ for the Cosine and Catenary profile, when $x_0/\lambda <0$. Furthermore, the $\beta$ value of Parabolic profile is a constant when $x_0/\lambda <0$. Overall, the $\beta (x_0/\lambda <0)$ can be written as follows:

$$\begin{aligned} \beta (x_0/\lambda <0)= {\left\{ \begin{array}{ll} 0.114x_0/\lambda +0.6188 &{} \text {for the Cosine profile},\\ 0.433 &{} \text {for the Parabolic profile},\\ -0.233x_0/\lambda +0.2666 &{} \text {for the Catenary profile}. \end{array}\right. } \end{aligned}$$

(10)

Fig. 7

The fitting coefficients $\alpha$ and $\beta$ depicted in Eq. (9), as the function of $x_0$

5 The Critical Pressure Factor

The simulations in Sect. 4 unveil the nonlinear relationship of the critical pressure with the surface geometry and the loading condition. To further the understanding of the critical pressure, a dimensionless parameter $\Lambda$ is introduced as the critical pressure factor:

$$\begin{aligned} \Lambda =\left( \frac{l_f+l_0}{\lambda }\right) \frac{p_b}{p_0}. \end{aligned}$$

(11)

The critical pressure factor for the rigid body contact is $\Lambda =1.0$, because of the force balance relation Eq. (6). In the rigid body contact case, the dry contact length $l_0$ is a constant for a given geometry, while it changes with the nominal traction $p_0$ when one or more surfaces in contact are elastic. The dry contact length $l_0$ from the elastic contact simulation is plotted against the critical pressure factor $\Lambda$ in Fig. 8. The critical pressure factor is larger than 1.0 in the elastic contact cases when $p_0>0$. It is anticipated since the elastic body deforms under the contact pressure, extra force is required to recover this deformation before the contact is open. One interesting finding from Fig. 8a is that the critical pressure factor of the Parabolic profile is a constant $\Lambda =1.108$ when $l_0/\lambda \geqslant 0.5$. When $l_0/\lambda <0.5$, the critical pressure factor $\Lambda$ increases with $l_0/\lambda$ with a declined growth rate. The minimum $\Lambda$ is achieved when $p_0 \rightarrow 0$, and its value increases with $x_0$. The minimum and maximum value of $\Lambda$, excluding the zero loading case ($p_0=0$), is shown in Table 1 for the values of $x_0/\lambda$ equal − 0.25, 0, and 0.25.

Table 1 The range of the critical pressure factor $\Lambda$ of the Parabolic profile at different values of $x_0/\lambda$

A constant critical pressure factor suggests that for a given nominal traction $p_0$, there is a reciprocal relationship exists between $l_f+l_0$ and the critical pressure ratio $p_b/p_0$. The reciprocal relationship does not hold for the Cosine and Catenary profiles, and the $\Lambda$ of the Cosine profile is larger for the smaller $x_0$ under the same $l_0/\lambda$ condition. A smaller $x_0$ leads to a shorter initial fluid fill length $l_f$ with the same $p_0$. It indicates that the increase of $p_b/p_0$ is faster than the decrease of $l_f+l_0$ when translating the geometry to the high-pressure side. The critical pressure factor of the Cosine profile, as shown in Fig. 8b, is positive correlative with the dry contact length, and it follows a linear trend for the positive $x_0$. When $x_0<0$, the critical pressure factor $\Lambda$ is nonlinear increasing with $l_0$. The maximum $\Lambda$ of Cosine profile is 1.161, for the case $x_{0} = - 0.0086$ and $l_{0} = 0.533$. This is also the maximum $\Lambda$ among the three types of geometries.

Figure 8c shows the critical pressure factor $\Lambda$ of the Catenary profile. It decreases with the dry contact length when $l_0/\lambda >0.3$. There is a bifurcation of $\Lambda$ when $l_0/\lambda \leqslant 0.3$, and the critical pressure factor becomes positive correlative with $l_0$ When $x_0>0.1$. The $\Lambda$ with different $x_0$ values collapses together when $l_0/\lambda \geqslant 0.4$. This suggests that $\Lambda$ is a function of the dry contact length $l_0$ for all $x_0$. The maximum $\Lambda$ for the Catenary profile is 1.095, and it is achieved when $x_0=-0.25$ and $l_0=0.166$.

Fig. 8

The critical pressure factor $\Lambda$ as the function of the dry contact length $l_0$ for the Parabolic (a), Cosine (b), and Catenary (c) profiles. The dashed line represents the linear fit given by Eq. (12) with coefficients in Table 2

The data shown in Fig. 8 are fitted into a linear relation:

$$\begin{aligned} \Lambda _{fit}(l_0/\lambda )= k_{\Lambda }l_0/\lambda +b_{\Lambda }, \end{aligned}$$

(12)

and the $\Lambda _{fit}$ acquired from Eq. (12) is shown in Fig. 8 as a dashed line. The parameters $k_{\Lambda }$ and $b_{\Lambda }$ in Eq. (12) are given for the three types of geometries in Table 2.

Table 2 Coefficients of Eq. (12)

By substituting Eq. (12) into Eq. (11), it is possible to compute the critical pressure ratio $p_b/p_0$ as follows:

$$\begin{aligned} \frac{p_b}{p_0}=\frac{\lambda \Lambda _{fit}}{l_f+l_0}. \end{aligned}$$

(13)

For a given geometry, the only unknown at the right-hand side of Eq. (13) is the dry contact length $l_0$, which can be acquired from the dry contact simulation. A parameter $\epsilon _b$ is defined to evaluate the relative error of $p_b/p_0$ generated from Eq. (13), viz.,

$$\begin{aligned} \epsilon _b=1- \frac{\Lambda _{fit}}{\Lambda }. \end{aligned}$$

(14)

Table 3 shows the mean and maximum values of $|\epsilon _b|$ for the three types of geometries. The average $|\epsilon _b|$ is $4.33\times 10^{-3}$ for the Parabolic profile, $1.10\times 10^{-2}$ for the Cosine profile, and $3.98\times 10^{-3}$ for the Catenary profiles, and the maximum $|\epsilon _b|$ are 6.5% , 3.8%, and 4.2%, respectively. The big errors occur when $x_0/\lambda =0.25$ and $p_0 \rightarrow 0$ for the Parabolic and Catenary profile, because the surface profile with large $x_0$ and light loading condition has a critical pressure factor closed to 1, while the $\Lambda _{fit}$ for the Parabolic and the Catenary profile is not converged to 1.0 when $l_0 \rightarrow 0$. The $\Lambda _{fit}$ for the Cosine profile, on the other hand, gives a good estimation of $p_b/p_0$ when $\Lambda \rightarrow 1.0$, but it fails to capture the nonlinearity of $\Lambda$ with small $x_0$, which results in a higher mean value of $|\epsilon _b|$.

Table 3 The relative error of the critical pressure factor computed with $\Lambda _{fit}$ in Eq. (12)

Equation (12), despite its simple form, allows one to quickly compute the critical pressure ratio without scarify much accuracy. It can be further illustrated by plotting the critical pressure factor $\Lambda$ and the critical pressure ratio $p_b/p_0$ of the Parabolic profile in Fig. 9. The blue point in Fig. 9 is the critical pressure ratio computed from simulation, and the red-dashed line is the value of $p_b/p_0$ computed from Eq. (11) with $\Lambda =\Lambda _{fit}$. The $p_b/p_0$ computed from Eq. (11) with $\Lambda =1.0$ is also plotted in Fig. 9 as a black-dashed line for the purpose of comparison, and the blue color bar in Fig. 9 is the critical pressure factor $\Lambda$ computed from the simulation results. Figure 9a shows the variation of $p_b/p_0, \Lambda$ under different loading conditions, with the geometry translation parameter $x_0=0$ and $\Delta /\lambda =0.01$. Figure 9b investigates the effect of curvature on the critical pressure ratio and $\Lambda$ under the constant loading conditions, by alternating the ratio $\Delta /\lambda$ with a normalized $\lambda$. Since the pressure scale factor $p_s$ is no more a constant with varying $\Delta /\lambda$ according to Eq. (7), the nominal traction is normalized with $E_s={2E}/{(1-\nu ^2)}$ instead, and $p_0/E_s$ is 0.0045 for the cases shown in Fig. 9b. Figure 9c shows the relationship of $p_b/p_0, \Lambda$ with $x_0$, for the Parabolic geometry with $\Delta /\lambda =0.01$ and $p_0/p_s=0.05$.

In general, the critical pressure ratio $p_b/p_0$ is nonlinear with the nominal traction $p_0$ (Fig. 9a), the curvature of the profile (Fig. 9b), and the geometry translation parameter (Fig. 9c). The critical pressure factor $\Lambda$, on the other hand, is much more stable. The $p_b/p_0$ computed with $\Lambda =\Lambda _{fit}$ gives a good estimation with the simulation results, whereas the $p_b/p_0$ computed with $\Lambda =1.0$ gives a relative error between 9 and 15%.

Fig. 9

The critical pressure factor $\Lambda$ and the critical pressure ratio $p_b/p_0$ of a Parabolic profile in contact with a rigid flat surface. The initial shape of the parabolic profile is $g_0(x) = 4\Delta (x-x_0)^2/\lambda ^2$. The blue points are $p_b/p_0,$ and the bars are $\Lambda$ obtained from the simulations. a $p_b/p_0, \Lambda$ as the functions of the nominal traction, with $x_0=0$ and $\Delta /\lambda =0.01$, b $p_b/p_0, \Lambda$ as the functions of $\Delta /\lambda$, with $x_0=0$ and $p_0=0.0045E_s$, c $p_b/p_0, \Lambda$ as the functions of the geometry translation parameter, with $\Delta /\lambda =0.01$ and $p_0/p_s=0.05$

One main difference among the three geometry types is their curvature. The curvature considered in the current study is the signed curvature defined as follows:

$$\begin{aligned} \kappa (x)=\frac{\frac{d^2y}{dx^2}}{\left( 1+\left( \frac{dy}{dx}\right) ^2\right) ^{\frac{3}{2}}}. \end{aligned}$$

(15)

According to Eq. (15), the curvature of the Parabolic profile Eq. (2) is $8\Delta /\lambda ^2$, and it is independent of the x-coordinate. While the curvatures of the Catenary and the Cosine profile are the functions of x, as shown in the upper right inset in Fig. 10 for the case $x_0=0$. In general, the curvature of the Catenary profile is positive and has its minimum at $x=x_0$. The curvature of the Cosine profile, on the other hand, is negative when $|x/\lambda |>0.25$ and $x_0=0$. The sign change of the curvature allows the osculating circle center to pass the surface, and the surface is not on the same side of its tangent plane. One consequence of this is that the Cosine profile will start to “kink” when the solid–solid contact front point $x=x_{c0}$ passes the zero-curvature point. Increasing the nominal traction $p_0$ beyond this condition will collapse the surface into the full contact state. This is the reason for the smaller range of the dry contact length $l_0$ for the Cosine profile in Fig. 8b. The critical pressure factor $\Lambda$ is plotted against the initial curvature at $x_{c0}$ in Fig. 10, and it decreases with $\kappa (x_{c0})$ for both the Cosine and Catenary profiles. This is because the smaller curvature requires a higher load to flatten out to the same contact length $l_0$ under dry contact condition, and it leads to higher maximum contact pressure. The sealed fluid pressure required to open it up, therefore, increases correspondingly. Since $\kappa (x_{c0})$ decreases with dry contact length $l_0$ for the Cosine profile, the critical pressure factor $\Lambda$ is positive correlative with $l_0$, as shown in fig. 8 (b). On the other hand, $\kappa (x_{c0})$ increases with $l_0$ for the Catenary profile, so its critical pressure factor $\Lambda$ decreases with the dry contact length $l_0$, as shown in fig. 8 (c). The critical pressure factor $\Lambda$ of the Catenary profile is independent of $x_0$ when $(\lambda ^2/{(8 \Delta )})\kappa (x_{c0})>0.3$, and the critical pressure factor of the Catenary profile can be fitted and represented as a power-law expression, viz.,

$$\begin{aligned} \Lambda _{catK}(\kappa )=1.045\left( \frac{\lambda ^2}{8\Delta }\kappa (x_{c0})\right) ^{-0.026}. \end{aligned}$$

(16)

The critical pressure factor acquired from Eq. (16) is depicted in Fig. 10 by a dashed line. The critical pressure factor $\Lambda$ of the Cosine profile depends on both $x_0$ and $\kappa (x_{c0})$, and the geometry translation parameter needs to be considered explicitly when computing the critical pressure ratio from $\Lambda$.

Fig. 10

The critical pressure factor as a function of the curvature $\kappa (x_{c0})$, for the Cosine and the Catenary profiles, with $x_{c0}$ as the leading contact point position under the dry contact condition (Fig. 4) . The upper right insert depicts the curvature $\kappa$ as the function of the x-coordinate for the two types of geometries

6 Concluding Remarks

A criterion is proposed to identify the critical pressure for two contacting surfaces under constant total load conditions. A numerical method based on the bisection algorithm and the boundary element method is implemented to capture this critical pressure. The critical pressure ratio is computed with the numerical method for Parabolic, Cosine, and Catenary profiles and represents as a nonlinear function of the nominal traction and the geometry translation parameter [Eq. (9)]. The introduction of the critical pressure factor [Eq. (11)] allows one to compute the critical pressure ratio with a simple algebraic equation [Eq. (13)]. Since both the dry contact length and the fluid initial filled length in Eq. (13) can be computed with high accuracy under dry contact conditions, the source of error for the critical pressure ratio is mainly delivered from the dimensionless critical pressure factor. The critical pressure factor is represented as a linear function of the dry contact length in Eq. (12). The relative error of the critical pressure ratio computed with the simple algebraic equation Eq. (13) is less than 1.2% on average, when compared with the values acquired from the simulation results.

The current study takes the first step to evaluate the sealability with the contact profile quantitatively. The simulation results suggest that translating geometry to the high-pressure side increases the critical pressure under the constant loading condition. It is because of the shorter fluid-filled length and the higher critical pressure factor. On the other hand, moving the geometry to the low-pressure side gives small critical pressure under the light loading condition, and the contacting objects behave close to the rigid bodies. The geometry translation parameter becomes less relevant for the critical pressure with the increased total load, because the critical pressure factor can be determined solely by the dry contact length and the geometry type.

The critical pressure ratio of rough surfaces could also be computed with the method described in the current paper. However, no simple formula has been found for the critical pressure factor, and it needs to be further investigated in detail. Despite the limitation of the current study on smooth surfaces, the study adds to our understanding of the contact profile design principle, which prefers a skewed contact profile toward the high-pressure side. Further research includes extending the present investigation to the elastoplastic and viscoelastic materials, by utilizing the influence coefficient conversion method [32].

Appendix A. The Exact Solution of Two-Phase Riemann Problem for 1D Euler Equation

The transition from zero to finite leakage of the sealed fluid when $p_f>p_b$ is modeled as a two-phase Riemann problem. The non-reactive two-phase Riemann problem has been solved numerically in [30, 33] and was compared with the analytical solution. However, the derivation of the corresponding analytical solution is missing in the literature, based on the authors’ knowledge. So it is presented in this appendix.

In one dimension, the conservation of mass, momentum, and energy for a system with two non-reactive inviscid fluids is

$$\begin{aligned} \mathbf {U}_t+\mathbf {F}(\mathbf {U})_x=0, \end{aligned}$$

(17)

where

$$\begin{aligned} \mathbf {U}=\left[ \begin{array}{c} \hat{\rho } \\ \hat{\rho } \hat{u} \\ \hat{E} \end{array}\right] , \quad \mathbf {F}=\left[ \begin{array}{c} \hat{\rho } \hat{u} \\ \hat{\rho } \hat{u}^{2}+\hat{p} \\ \hat{u}(\hat{E}+\hat{p}) \end{array}\right] , \end{aligned}$$

$\hat{u}$ is the fluid velocity, $\hat{\rho }$ is the fluid density, $\hat{p}$ is the fluid pressure, and $\hat{E}$ is the total energy per unit volume.

$$\begin{aligned} \hat{E}=\hat{\rho }(\frac{1}{2}\hat{u}^2+\hat{e}), \end{aligned}$$

where $\hat{e}$ is the specific internal energy given by the Equation of State (EOS):

$$\begin{aligned} \hat{e}=\hat{e}(\hat{\rho },\hat{p}). \end{aligned}$$

One widely used EOS for both solid, liquid, and gas is stiffened EOS [33].

$$\begin{aligned} \hat{e}=\frac{\hat{p}_i+\hat{\gamma }_i \hat{p}_i^{0}}{(\hat{\gamma }_i-1)\hat{\rho }_i}, \end{aligned}$$

with $i=L,R$ for the left and right phases, $\hat{\gamma }$ is the adiabatic constant, and $\hat{p}_i^{0}$ is the pressure correction coefficient. The stiffened EOS reduces to ideal gas law when $\hat{p}^0$ goes to zero. The detailed analysis on the thermal dynamics consistency of the stiffen EOS can be found in [34].

The Riemann problem describes the evolution of the dynamical system Eq. (17) with an initial condition:

$$\begin{aligned} \mathbf {U}=\mathbf {U}_L\quad \text {when} \quad x>0 \quad \text {and} \quad \mathbf {U}=\mathbf {U}_R \quad \text {when} \quad x<0. \end{aligned}$$

(18)

The Euler equation with the stiffen EOS satisfies the homogeneity property.

$$\begin{aligned} \mathbf {F}(\mathbf {U})=\mathbf {A}(\mathbf {U})\mathbf {U}, \end{aligned}$$

and the eigenvalues of the Jacobian matrix $\mathbf {A}$ are

$$\begin{aligned} \lambda _1=\hat{u}-\hat{a}, \lambda _2=\hat{u}, \lambda _3=\hat{u}+\hat{a}, \end{aligned}$$

where $\hat{a}$ is the fluid sound speed.

$$\begin{aligned} \hat{a}=\sqrt{\frac{\hat{\gamma } (\hat{p}+\hat{p}^{0})}{\hat{\rho }}}. \end{aligned}$$

(19)

It is proved in [35] that the wave corresponding to $\lambda _2$ is a degenerate wave with consistent pressure and velocity across it, and the density is discontinuous. In the two-phase non-reactive flow, this wave represents the phase interface.

The wave corresponds to $\lambda _{1,3}$ are nonlinear waves and have two possibilities. If the wave is a rarefaction wave, the isentropic relation [35] will be satisfied. The rarefaction wave has a fan shape and physics quantities change continuously within the fan region. If the wave is a shock wave, the physics quantities have an abrupt change when passing over it, and the Rankine-Hugoniot relation is satisfied. A case of a left rarefaction wave with a right shock wave is shown in Fig. 11.

Fig. 11

The characteristics lines of 1D Riemann problem. The space–time domain is separated by the shockwave $S_R$, the rarefaction waves with its head at $S_{HL}$ and its tail at $S_{TL}$, and the phase interface (dashed line). Physics quantities are uniform in each sub domain except the rarefaction area $x/t \in [S_{HL}, S_{TL}]$

The Rankine-Hugoniot relation for the right shock gives [36, 37]

$$\begin{aligned} \hat{u}^{*}-\hat{u}_R=f_R^{s}=\frac{\sqrt{2}(\hat{p}^{*}-\hat{p}_R)}{\sqrt{\hat{\rho }_{R}[2\hat{\gamma }_R(\hat{p}_R+\hat{p}^{0}_R)+(\hat{\gamma }_{R}+1)(\hat{p}^{*}-\hat{p}_R)]}}. \end{aligned}$$

(20)

Substituting the stiffen EOS into the first law of thermodynamics under the isentropic condition gives

$$\begin{aligned} \hat{u}_L-\hat{u}^{*}=f_L^{r}=\frac{2\hat{a}_L}{\hat{\gamma }_L-1}\left[ \left( \frac{\hat{p}^*+\hat{p}^{0}_L}{\hat{p}_L+\hat{p}^{0}_L}\right) ^{\frac{\hat{\gamma }_L-1}{2\hat{\gamma }_L}}-1\right] . \end{aligned}$$

(21)

Combining Eqs. (20) and (21) gives the middle state $u^{*}$ and $p^{*}$. The density $\hat{\rho }_L^{*}$ after the right rarefaction wave follows the isentropic relation:

$$\begin{aligned} \hat{\rho }_L^{*}=\hat{\rho }_L\left( \frac{\hat{p}^{*}+\hat{p}_L^{0}}{\hat{p}_L+\hat{p}_L^{0}}\right) ^{\frac{1}{\hat{\gamma }_L}}, \end{aligned}$$

(22)

and substitute Eqs. (22) into (19) gives the sound speed $\hat{a}_L^{*}$:

$$\begin{aligned} \hat{a}_L^{*}=\hat{a}_L\left( \frac{\hat{p}^{*}+\hat{p}_L^{0}}{\hat{p}_L+\hat{p}_L^{0}}\right) ^{\frac{\hat{\gamma }_L-1}{2\hat{\gamma }_L}}. \end{aligned}$$

(23)

The characteristics wave speed for the head and tail of the right rarefaction wave is

$$\begin{aligned} S_{HL}=\hat{u}_L-\hat{a}_L, \quad S_{TL}=\hat{u}^{*}-\hat{a}^{*}_L. \end{aligned}$$

The physics quantities in the fan area are given by the isentropic relation:

$$\begin{aligned} \mathbf {U}_{\text{ Lfan } }=\left\{ \begin{array}{l} \hat{\rho }=\hat{\rho }_{L}\left[ \frac{2}{(\hat{\gamma }_L+1)} +\frac{(\hat{\gamma }_L-1)}{\left( \hat{\gamma }_L+1\right) \hat{a}_{L}} \left( \hat{u}_{L}-\frac{x}{t}\right) \right] ^{\frac{2}{\hat{\gamma }_L-1}}, \\ \hat{u}=\frac{2}{(\hat{\gamma }_L+1)}\left[ \hat{a}_{L}+\frac{(\hat{\gamma }_L-1)}{2} \hat{u}_{L}+\frac{x}{t}\right] ,\\ \hat{p}=(\hat{p}_{L}+\hat{p}^0_L)\left[ \frac{2}{(\hat{\gamma }_L+1)} +\frac{(\hat{\gamma }_L-1)}{(\hat{\gamma }_L+1)\hat{a}_L}\left( \hat{u}_{L}-\frac{x}{t}\right) \right] ^{\frac{2 \hat{\gamma }_L}{\hat{\gamma }_L-1}}-\hat{p}^0_L. \end{array}\right. \end{aligned}$$

(24)

The density $\hat{\rho }_R^{*}$ is computed with the Rankine-Hugoniot relation:

$$\begin{aligned} \hat{\rho }_R^{*}=\hat{\rho }_R\left[ \frac{\frac{\hat{p}^*+\hat{p}_R^{0}}{\hat{p}_R+\hat{p}_R^{0}}+\frac{\hat{\gamma }_R-1}{\hat{\gamma }_R+1}}{\frac{\hat{\gamma }_R-1}{\hat{\gamma }_R+1}\frac{\hat{p}^*+\hat{p}_R^{0}}{\hat{p}_R+\hat{p}_R^{0}}+1} \right] , \end{aligned}$$

(25)

and the shock speed $S_R$ is acquired based on the mass conservation and Rankine-Hugoniot relation:

$$\begin{aligned} S_R=\hat{u}_R+\hat{a}_R\left[ \frac{\hat{\gamma }_R+1}{2\hat{\gamma }_R}\left( \frac{\hat{p}^*+\hat{p}_R^0}{\hat{p}_R+\hat{p}_R^0}\right) +\frac{\hat{\gamma }_R-1}{2\hat{\gamma }_R}\right] ^\frac{1}{2}. \end{aligned}$$

(26)

A water-air shock tube problem with 10MPa water at the left side ($x<0$) and STP air at the right side ($x>0$) is shown in Fig. 12. The initial water density is $997(kg/m^3)$, and its EOS parameters are $\hat{p}^{0}=375MPa$ and $\gamma =5.75$. These parameters are based on the curve-fitting results of IAPWS-97 [38]. The STP air follows the ideal gas law, with $\hat{p}^{0}=0$ and $\gamma =1.4$, and its initial density is $1.225(kg/m^3)$. Fig. 12 shows the physics quantities distribution at $t=2e-5s$, with the blue background represents the water, and the white background represents the air.

Fig. 12

The density, velocity, adiabatic constant, and the fluid pressure for a water-air shock tube problem at $t=2e-5$ seconds