Leakage Threshold of a Saddle Point

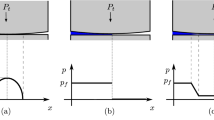
Abstract

The threshold condition for leakage inception is of great interest to many engineering applications, and it is essential for seal design. In the current study, the leakage threshold is studied by means of a numerical method for a mechanical contact problem between an elastic bi-sinusoidal surface and a rigid flat surface. The coalesce process of the contact patches is first investigated, and a generalized form of solution for the relation between the contact area ratio and the average applied pressure is acquired. The current study shows that the critical value of the average applied pressure and the corresponding contact area required to close the percolation path can be represented as a power law of a shape parameter, if the effect of the hydrostatic load from the pressurized fluid is ignored. With contact patches merged under a constant applied load, the contact breakup process is investigated with elevated sealed fluid pressure condition, and it is shown that the leakage threshold is a function of the excess pressure, which is defined as a ratio between the average applied pressure and the critical pressure under dry contact conditions.

Graphical abstract

1 Introduction

As a machine element that blocks the fluid flow, the seal achieves its function by compressing two surfaces together and closing the percolation paths between the high- and low-pressure sides. The contact patches are formed when two surfaces are pressed against each other. The initially isolated contact patches for rough surfaces can merge under increased contact load. The fluid leakage is stopped when the connected contact patches isolate the percolation paths between the high- and the low-pressure sides. Since the geometry connectivity of the contact patches decides the transition point of the leakage, it is of great interest to study the coalescence and breakup process of the contact patches.

The early contact mechanics models for the rough surfaces, such as the Greenwood–Williamson model [1] and the Greenwood–Tripp model [2, 3], assumed that the contact between the micro asperities could be decomposed into a group of Hertzian-like contacts and the deformation of each asperity is independent of each other. Since then, both experiments and simulations [4, 5] have shown that even for a simple contact problem between an elastic bi-sinusoidal and a rigid flat surface, the deformation of the contact patches is not independent of each other, suggesting that the contact patch interaction needs to be considered for the correct contact area, hence, also for the percolation threshold. Elastic contact mechanics accounting for the interaction between contact patches has been developed [6, 7]. It has also been utilized to study the percolation threshold for both the isotropic fractal rough surface and the anisotropic rough surface [8,9,10]. The contact area ratio at the leakage threshold predicted by both contact mechanics theory and numerical simulations [11,12,13,14,15,16] is smaller than the value predicted by the bond-percolation theory [17] and the bearing area model [2, 3], because the long-range elastic coupling between contact patches is ignored in the latter two.

Previous research on the leakage threshold of random rough surfaces usually builds on the assumption that the fluid pressure is much smaller than the contact pressure, and that the solid deformation generated by the fluid pressure is negligible. This assumption allows one to decouple the solid contact problem from the fluid leakage problem, and the leakage threshold is determined by the geometry connectivity of the deformed elastic surfaces without the fluid load. There are two situations where the fluid pressure is not negligible. First, the fluid can be trapped between the surface roughness due to the coalescing of the contact patches caused by a increase load. If the trapped fluid is further squeezed by the solid surfaces, its internal pressure will increase due to the volume decrease, thus providing additional load carrying capacity, and preventing further contact between the solid surfaces. Kuznetsov [18, 19] studied the contact problem with fluid entraps in the valleys of a sinusoidal profile. His solution shows that the increased total load can be balanced by the compressed fluid pressure with a constant solid–solid contact length. The experimental findings in [20] have also confirmed that the fluid entrapped between a bi-sinusoidal and a flat surface prevents the further close-up of the gap between them after the adjacent contact patches touch each other. The further increase of the average applied pressure mainly contributes to the deformation near the saddle point, with little variation on the solid–solid contact areas, and the trapped fluid does not leak with its increased hydrostatic pressure [21].

Another situation where the fluid pressure must be considered is when the sealed fluid pressure is comparable with the contact load. It is not a rare case, especially near the boundaries of the contact zones adjacent to the high-pressure side [22]. If there is no leakage, the pressurized fluid from the high-pressure side fills the gap between the contacting surfaces with uniform hydrostatic pressure. The hydrostatic fluid pressure will deform the contacting surfaces and change contact pressure distribution [23]. When the fluid is pressurized from the high-pressure side of an initially sealed system, leakage is observed when the sealed fluid pressure $p_{\text{f}}$ equals the maximum contact pressure [24]. The leakage threshold under this condition is governed by the initial geometries of the contact surfaces, the loading condition, and the sealed fluid pressure.

The contact mechanics problem between an elastic bi-sinusoidal and a rigid flat surface is probably the most simple one that may be used to show the coalescence of the contact patches and the disappearance of the percolation path. Hence, it serves as an important model problem involving the mechanics governing the leakage threshold, which has also been studied in the previous works [4, 5, 12], without considering the fluid load. In this work, we will revisit this problem and extend it to include the effect of the sealed fluid pressure at the high-pressure side. The main research objective here is to investigate the variability of leakage inception with the sealed fluid pressure in initially sealed contacts.

2 Problem Setup

The present study is devoted to the linear elastic contact problem between a non-planar smooth surface in contact with a rigid flat surface. The elastic surface has a initial bi-sinusoidal shape, i.e.,

$$g_{0} (x,y) = \Delta \left( {1 - \cos (2\pi x/\lambda ) + 0.5\alpha (1 + \cos (2\pi y/\lambda ))} \right),$$

(1)

with $(x,y) \in [-\lambda /2, \lambda /2]^2$, and $\lambda$ is the side length of the square solution domain. The geometry parameter $\Delta$ is chosen as $\Delta =0.01\lambda$ in the current study to satisfy the small slope requirement of the half-space approximation, while it is noteworthy that the solution in the current study is independent from $\Delta / \lambda$ when normalized with $\Delta / \lambda$ [25]. The shape parameter $\alpha$ controls the initial gap size at the saddle point $(x,y)=(0,0)$, and the gap equals $\alpha \Delta$ under zero loading condition. The initial geometry $g_0(x,y)$ reduces to a 1D cosine profile when $\alpha =0$. When $\alpha =2$, the geometry depicted in Eq. (1) is the bi-sinusoidal geometry studied in [4, 5, 12] under a rotation and a translation operation. In the current study, the shape parameter $\alpha$ is chosen as $\alpha =0.1, 0.2, 0.3, 0.4 \text { and } 0.5$, as shown in Fig. 1.

Fig. 1

The initial shape of the elastic bi-sinusoidal surface, mathematically described in Eq. (1), with the shape parameter $\alpha =0.1$ in (a), $\alpha =0.2$ in (b), $\alpha =0.3$ in (c), $\alpha =0.4$ in (d), and $\alpha =0.5$ in (e)

The non-planar smooth surface $g_0(x,y)$ is brought into contact with a rigid flat surface under the total load $P_{\text{t}}$, and the average applied pressure is $p_0=P_{\text{t}}/S_0$, with $S_0=\lambda ^2$ the area of the solution domain. The solid–solid contact problem is first studied with the DCD-FFT method [26] (which is a modification of the DC-FFT method with duplicated padding), in which the periodic boundary condition is applied at $y=\pm 0.5\lambda$. With the percolation path being sealed by the coalescence of the two contact patches under constant total load condition, the sealed fluid is filled in from the high-pressure side $x=-0.5 \lambda$ with its pressure equaling $p_{\text{f}}$. Under the elevated $p_{\text{f}}$ condition, the sealed fluid opens up the solid–solid contacts between the surfaces, allowing for the fluid front to move forward to the point that the percolation path is revealed once more, and the leakage is onset. The value of the sealed fluid pressure when the high- and low-pressure sides are first connected is defined as the critical pressure of leakage $p_{\text{b}}$, and the critical solid–solid contact area when $p_{\text{f}}=p_{\text{b}}$ is denoted as $S_{\text{b}}$. It is worth to mention that the $S_{\text{b}}$ defined in the current study is not the same as the critical area defined in the studies of [5, 12], in which the deformation of contacting surfaces by the sealed fluid pressure is ignored. The critical contact area under the dry condition is defined as $S^*$ in the current study and the corresponding average applied pressure when the solid–solid contact area S equals $S^*$ is defined as the critical pressure of dry contact, with the notation as $p_0^*$.

The values of $p_0^*$ are acquired by conducting the contact mechanics simulation under various $p_0$ conditions, and checking the geometry connectivity of the high- and low-pressure sides with a connected component labeling algorithm [23, 27]. A binary connectivity identifier is defined as 1 when the high- and low-pressure sides are connected, and 0 otherwise. A bisection method is utilized to narrow down the range of the average applied pressure $p_0$ based on the connectivity identifier, and the simulation is stopped when the range of $p_0$ is smaller than a specified tolerance $\epsilon =10^{-3}p_0$, and the critical pressure of dry contact is taken as the lower endpoint of the range of $p_0$.

The critical pressure of leakage $p_{\text{b}}$ is acquired with a boundary element method developed in [23]. The method is a further development of FFT-accelerated method [28] including the hydrostatic load at the contact interface. The mesh size is chosen as 1024 by 1024. The contact plane geometry tolerance is set to $10^{-5}\Delta$, and the total load tolerance is set to $10^{-9} p_0$ for both the dry contact and the cases with the hydrostatic load.

It is worth to emphasize that the periodic boundary condition is only applied at the y direction in the DCD-FFT method. It differentiates the current study from the previous studies on the bi-sinusoidal surface [4, 5, 12], in which the periodic boundary condition is applied to both the x and y directions. The $y$–only periodic boundary condition leads to contact pressure concentration when the contact patches touch the corner of the solution domain due to the flat punch effect, and the contact pressure at the corner is unbounded with large value of shape parameter $\alpha$. So $\alpha$ is set to be $\alpha \in (0.0,0.5]$ in the current study to avoid the contact pressure singularity under high loading conditions.

3 Results and Discussions

The merging of the two contact patches occurs continuously for non-adhesive solids, without considering the surface deformation by the sealed fluid pressure [12]. Both the critical pressure $p_0^*$ and the critical area $S^*$ under dry contact conditions depend on the shape of the merging contact patches. In this section, the critical quantities $p_0^*$ and $S^*$ are first studied for the initial geometries depicted in Eq. (1) and Fig. 1, followed by the analysis of the critical quantities $p_{\text{b}}$ and $S_{\text{b}}$ with hydrostatic load in consideration. The adhesion force between the contacting surfaces is ignored in the simulation, and the surface tension of the fluid is neglected. The surface stress orthogonal to the contact interface p is referred to as surface traction in the discussion below, following the naming convention in [29]. The surface traction p is the contact pressure under dry contact conditions. For the cases with hydrostatic load, the surface traction p equals the fluid pressure in the fluid-filled regions, and it is the contact pressure at the solid–solid contact regions. Both the force and pressure in the current study are normalized with a pressure scale factor $p_{\text{s}}$,

$$p_{\text{s}}= \frac{2\pi E}{1-\nu ^2} \frac{\Delta }{\lambda },$$

(2)

where E is the Young’s modulus of the elastic surface, and $\nu$ is its Poisson ratio.

3.1 Critical Quantities Under the Dry Contact Condition

Fig. 2

The surface traction distribution ${\text{p/p}}_{\text{s}}$ under dry contact conditions for the cases of $p_0/p_{\text{s}}=0.012$ in (a), $p_0/p_{\text{s}}=0.016$ in (b) and $p_0/p_{\text{s}}=0.020$ in (c). The shape parameter is $\alpha =0.3$ and the white regions represent the areas with surface traction equaling zero

Figure 2 shows the surface traction distribution ${{p/p}}_{{s}}$ under dry contact conditions for the initial geometry $g_0(x,y)$ depicted in Eq. (1), with the shape parameter $\alpha =0.3$. The average applied pressure is $p_0=0.012p_{\text{s}}$ in Fig. 2a, $p_0=0.016p_{\text{s}}$ in Fig. 2b, and $p_0=0.020p_{\text{s}}$ in Fig. 2c. At the beginning of the contact, the surfaces first touch at the crest positions $(x,y)=(0, \pm 0.5\lambda )$, and the shape of the contact patches can be approximated as two semiellipses. Johnson et al. [4] and Xu et al. [25] have shown that there exists a 2/3 power law between the contact area ratio $S/S_0$ and the average applied pressure $p_0$ if the contact patches are semiellipses. The contact area ratio deviates from the 2/3 power law with higher $p_0$, and it increases as a concave function of the average applied pressure. There is an inflection interval when $p_0 \rightarrow p_0^*$, in which the contact area ratio becomes a convex function of the average applied pressure, as shown in Fig. 3. This inflection interval is firstly discovered by Yastrebov et al. [5] for the isotropic bi-sinusoidal surface, and being confirmed by Xu et al. [25] for the anisotropic bi-sinusoidal surfaces. The contact area ratio transits back to the concave function of the average applied pressure after $p_0$ passes $p_0^*$, and the two contact patches merge together into a dumbbell shape. The size of the dumbbell contact patch, as shown in Fig. 2c, is further increased with elevated $p_0$.

Fig. 3

The relationship between the average applied pressure and the contact area ratio under dry contact conditions

The relationship between the contact area ratio $S/S_0$ and average applied pressure $p_0/p_{\text{s}}$, as shown in Fig. 3, can be fitted into an equation:

$$\begin{aligned} \frac{S}{S_0} = \frac{2}{\pi }\left( \arcsin {\sqrt{(1-\beta )\left( \frac{p_0}{p_S}\right) }} + \arcsin {\sqrt{\left( \frac{2\beta }{\alpha }\frac{p_0}{p_{\text{s}}}\right) }}\right) , \end{aligned}$$

(3)

see Appendix A, where $\beta =\beta (p_0;\alpha )$ is a partitioning function. The partitioning function $\beta$ (obtained by fitting Eq. (3) to the numerical simulation results shown in Fig. (3)) is illustrated in Fig. 4. Since the maximum value of $\beta$ is 0.041 under the current simulation conditions, and $p_0/p_{\text{s}} \in [0,0.05]$, Eq. (3) can be approximated as

$$\frac{S}{S_0} \approx \frac{2}{\pi }\left( 1 + {\sqrt{\frac{2\beta }{\alpha }}}\right) \sqrt{\frac{p_0}{p_{\text{s}}}}.$$

(4)

Fig. 4

The partition function $\beta$ obtained by fitting Eq. (3) to the numerical simulation results shown in Fig. 3

The critical pressure and the critical contact area under dry condition are represented as a function of the geometry parameter $\alpha$ in Fig. 5. They can be fitted in to the power laws of $\alpha$, which read

$$\begin{aligned} \begin{aligned} \frac{p_0^*}{p_{\text{s}}}&=0.076\alpha ^{1.292}, \\ \frac{S^*}{S_0}&=0.215\alpha ^{0.622}. \end{aligned} \end{aligned}$$

(5)

The power laws Eq. (5) give zero critical pressure and critical contact area ratio under dry contact condition when $\alpha =0$, this is coinciding with the 1D cosine contact problem, for which there is no percolation paths connecting the high- and low-pressure sides when the loading equals zero.

Fig. 5

The critical pressure (left) and critical contact area (right) under dry contact conditions, as function of the shape parameter $\alpha$. The dots are from simulation and the dashed lines are the power laws Eq. (5)

Substituting the power laws Eq. (5) into Eq. (4) gives

$$\begin{aligned} \begin{aligned} \frac{S}{S^*}&\approx \frac{2.564}{\pi }\alpha ^{0.024} \left( 1 + {\sqrt{\frac{2\beta }{\alpha }}}\right) \sqrt{\frac{p_0}{p_0^*}}\\&=\sqrt{C\frac{p_0}{p_0^*}}. \end{aligned} \end{aligned}$$

(6)

The coefficient C can be fitted as

$$\begin{aligned} C=c_0+c_1\arctan \left( c_2\frac{p_0}{p_0^*}+c_3\right) , \end{aligned}$$

(7)

with

$$\begin{aligned} c_0=0.943, \quad c_1=0.263, \quad c_2=3.107, \quad \text {and} \quad c_3=-2.838. \end{aligned}$$

(8)

The fitting coefficients $c_0$ to $c_3$ are independent from the shape parameter $\alpha$, as shown in Fig. 6 for $p_0/p_0^* \in (0,2.0]$. The fitting Eq. (6) agrees well with the simulation results when $p_0$ is closed to $p_0^*$, and the average and the maximum relative error of Eq. (6) are shown in Table 1 for different ranges of $p_0/p_0^*$. While Eq. (6) gives a poor estimation for the solid–solid contact area S when $p_0 \rightarrow 0$, the relative error decreases with increased applied load, and the maximum error is less than 2.5% when $p_0/p_0^*>0.5$.

Fig. 6

The relationship between the contact area ratio S and the average applied pressure $p_0$ under the dry contact conditions, with S normalized with $S^*$ and $p_0$ normalized with $p_0^*$

Table 1 The relative error of Eq. (6)

Equation (6), with the universal coefficients $c_0$ to $c_3$ in Eq. (8), suggests that the relationship between the contact area and the average applied pressure, when scaling with their critical values under the dry conditions, is weakly dependent on the initial gap shapes. Utilizing Eq. (6) can significantly simplify the computation of the solid–solid contact area at different loading conditions, and it is of a nature to scale the surface traction p with $p_0^*$. However, further analysis has shown that the surface traction $p/p_0^*$ at the saddle point $(x,y)=(0,0)$, after the percolation path is closed, depends on the shape parameter $\alpha$ (Fig. 7). Since the saddle point has the minimum non-zero surface traction after the percolation path closes, its value is closed relative to the hydrostatic pressure required to open up contact. Therefore, the critical pressure of leakage $p_{\text{b}}$ still depends on the initial gap shape.

Fig. 7

The surface traction at the saddle point

3.2 Critical Quantities with Hydrostatic Load

Fig. 8

The surface traction distribution $p/p_{\text{s}}$ for $p_{\text{f}}/p_0=2.5 \times 10^{-5}$ in (a), $p_{\text{f}}/p_0=0.285$ in (b), and $p_{\text{f}}/p_0=0.6125$ in (c). The average applied pressure is $p_0/p_{\text{s}}=0.04$, and the shape parameter for the initial gap is $\alpha =0.4$. The white regions represent the areas with surface traction equaling zero

Figure 8 shows the surface traction distribution $p/p_{\text{s}}$ for the initial geometry $g_0(x,y)$ depicted in Eq. (1), with the shape parameter $\alpha =0.4$. The average applied load is $p_0=0.04p_{\text{s}}$ in Fig. 8a–c, and the percolation path between the high- and low-pressure sides is disconnected under the dry contact condition. The sealed fluid enters from the low-pressure side $x=-0.5\lambda$ with its pressure equaling $p_{\text{f}}$, and the value of $p_{\text{f}}$ is $p_f/p_0=2.5 \times 10^{-5}$ in Fig. 8a, $p_f/p_0=0.285$ in Fig. 8b, and $p_f/p_0=0.6125$ in Fig. 8c. The fluid from the high-pressure side filled the gaps between the two contacting surfaces before being blocked by the contact patch. The surface traction distribution in the contact patch and the sealed fluid pressure together determined the fluid front before the contact is open, and the fluid front of the sealed fluid proceeds to the low-pressure side with increased $p_{\text{f}}$. Since the total load $P_{\text{t}}$ is constant in Fig. 8a–c, the maximum solid–solid contact pressure decreases with increased $p_{\text{f}}$, and the contact area S is decreased at the same time due to the proceeding of the sealed fluid. The loss of the solid–solid contact happens at both the high- and low-pressure sides, because of the global response of the elastic displacement with the surface traction distribution [23]. The contact patch has a dumbbell shape which is symmetric with $x=0$ when $p_{\text{f}}=0$, but loses the symmetry when the sealed fluid pressure increases, because the hydrostatic pressure is only applied at the high-pressure side. Since the neck position of the connected contact patches ($y=0$) has the smallest surface traction, the contact length at $y=0$ shrinks the fastest with increased $p_{\text{f}}$, and the contact is open along with it when the sealed fluid pressure reaches the critical pressure of leakage $p_{\text{b}}$.

In the current study, the critical pressure of leakage $p_{\text{b}}$ is defined as the value of the sealed fluid pressure when the high- and low-pressure sides are first connected, so it can only be uniquely determined when $p_0>p_0^*$. A normalized excess pressure ${\overline{\text{p}}} _{\text{es}}$ is defined as

$$\begin{aligned} {\overline{p}} _{es} =\frac{p_0}{p_0^*}-1, \end{aligned}$$

(9)

and the critical pressure of leakage $p_{\text{b}}$ is represented as the function of ${\overline{{p}}} _{{es}}$ for ${\overline{{p}}} _{{es}} \ge 0$, as shown in Fig. 9a. When ${\overline{{p}}} _{{es}} =0$, the two contact patches touch each other only at the saddle point $(x,y)=(0,0)$, any infinitesimal fluid pressure can open up the contact and $p_{\text{b}} \approx 0$. The ratio between $p_{\text{b}}$ and the average applied pressure $p_0$ firstly increases with ${\overline{{p}}} _{{es}}$, and slightly decreases with further growth of ${\overline{{p}}} _{{es}}$. The decrease of $p_{\text{b}}/p_0$ with the average applied pressure $p_0$ is consistent with the line contact problem studied in [30]. However, the critical pressure of leakage $p_{\text{b}}$ is always larger than the average applied pressure $p_0$ in the line contact problem, because the sealed fluid pressure must be increased to the level that all the contact area disappears to reveal the percolation path between the high- and low-pressure sides. On the other hand, the sealed fluid only needs to open up the contact at the saddle point to create leakage for the geometries Eq. (1), so the critical pressure of leakage $p_{\text{b}}$ can be smaller than $p_0$ in the current study. Another consequence of the existence of the saddle point is that the solid–solid contact area does not need to decrease to zero to initialize the leakage. The critical contact area $S_{\text{b}}$, which is the solid–solid contact area when the hydrostatic load opens the contact, is non-zero as depicted in Fig. 9b. The critical contact area $S_{\text{b}}$ equals $S^*$ when ${\overline{{p}}} _{{es}} =0$ for all geometries, since any infinitesimal fluid pressure increases will lead to contact open at the saddle point when $p_0=p_0^*$. When $p_0>p_0^*$, the solid–solid contact area S is larger than $S^*$, and it decreases with the increasing sealed fluid pressure $p_{\text{f}}$. The remaining solid–solid contact area when the contact is opened is generally higher than $S^*$ in the current study, and it increases with the shape parameter $\alpha$. The curvatures of $g_0(x,y)$ at the two crest positions ($(x=0,y=\pm 0.5\lambda )$) are

$$\begin{aligned} \kappa _x=\frac{4\pi ^2\Delta }{\lambda ^2}, \quad \kappa _y=0.5\alpha \frac{4\pi ^2\Delta }{\lambda ^2}, \end{aligned}$$

(10)

and $\kappa _y$ increases with $\alpha$. The higher curvature of the initial gap results in lager maximum contact pressure and steeper contact pressure distribution under the same total load condition, and the fluid front is harder to proceed with elevated hydrostatic pressure [30].

Fig. 9

The critical pressure (a) and the critical contact area of leakage (b), as the function of the excess pressure defined in Eq. (9)

The critical pressure of leakage $p_{\text{b}}$ illustrated in Fig. 9a is fitted into an empirical relationship:

$$\begin{aligned} \frac{p_{\text{b}}}{p_0}=2\left( 1-\frac{1}{1+ {\overline{\text{p}}} _{\text{es}}}\right) ^{1.266}-0.143\alpha ^{0.805}{ {\overline{p}} _{es} }^{0.935}. \end{aligned}$$

(11)

The relative error generated by Eq. (11) is 0.86% in average and maximize at 3.45%.

To further the understanding of the critical pressure ratio $p_{\text{b}}/p_0$, a dimensionless parameter $\Lambda$ is introduced as the critical pressure factor as follows [30]:

$$\begin{aligned} \Lambda =\left( \frac{S_{\text{f}}+S}{S_0}\right) \frac{p_{\text{b}}}{p_0}, \end{aligned}$$

(12)

with $S_{\text{f}}$ the flooded area at the high-pressure side when the sealed fluid pressure $p_{\text{f}}=0$ and the average applied pressure $p_0>p_0^*$. Due to the symmetry of the current problem under the dry contact condition, the $S_{\text{f}}$ can be written as

$$\begin{aligned} \frac{S_{\text{f}}}{S_0}=\frac{1}{2}\left( 1-\frac{S}{S_0}\right) . \end{aligned}$$

(13)

The critical pressure factor $\Lambda$ is plotted against the excess pressure $\overline{{p}} _{{es}}$ in Fig. 10, and it is fitted into an empirical relationship, viz.

$$\begin{aligned} \Lambda =\left( \tanh (1.283 {\overline{\text{p}}} _{\text{es}} ^{0.315})\right) ^{5.14}. \end{aligned}$$

(14)

The fitting coefficients in Eq. (14) are independent from the shape parameter $\alpha$. Substituting Eq. (14) into Eq. (12) allows one to calculate the critical pressure ratio $p_{\text{b}}/p_0$ with S and ${\overline{{p}}} _{{es}}$, which are quantities available from the dry contact simulation. The relative error of $p_{\text{b}}/p_0$ generated from Eq. (14) is 1.48% in average, when comparing with the simulation results, and the maximum relative error is 4.61%.

Fig. 10

The critical pressure factor, as the function of the excess pressure

4 Conclusions

A contact problem between a geometrically anisotropic bi-sinusoidal surface and a rigid flat surface is revisited in the current paper. The critical pressure and the critical solid–solid contact area are of main research interest since they are closely related to the leakage inception. The critical quantities are first studied without considering the hydrostatic load of the pressurized fluid. The relationship between the solid–solid contact area and the average applied load acquired from the current study qualitatively agrees with the previous studies from other researchers, and the detailed transition regime of the contact area is also observed. Instead of studying the asymptotic solution of this contact problem, a generalized form of solution Eq. (3) is constructed based on Westergaard’s solution of the 1D cosine contact. By introducing a partition function $\beta(p_0;\alpha)$, Eq. (3) can fit the contact area with high accuracy for a wide range of shapes and loading conditions. Moreover, it is found that the relationship between the contact area and the average applied pressure, when normalized with their critical quantities, is independent of the shape parameter.

The critical pressure and critical contact area for leakage are further studied by first applying a load to close the saddle point, and then filling the contact interface with fluid from the high-pressure side. The contact is lost due to increased sealed fluid pressure, and it was discovered that the sealed fluid pressure required to open up the contact and the remaining solid–solid contact area before the revealing of the percolation path can be represented as a function of excess pressure, which is defined as the difference between the applied pressure and the critical pressure under dry contact conditions. On top of that, a dimensionless parameter, called the critical pressure factor, is defined based on the previous studies from the same authors. It is shown that the critical pressure factor, when represented as a function of the excess pressure, is independent from the shape of the initial geometries. Utilizing the critical factor allows one to acquire the critical pressure for leakage using the quantities from the dry contact simulations, which are well studied and easily accessible from the previous research.

Appendix A. The relation between the contact area ratio and the average applied pressure under dry contact condition

The contact area S is a continuous function of the average applied pressure $p_0$ for non-adhesive elastic contact [12], and it depends on the geometries of the contact surfaces. Hence, the ratio of the contact area to the nominal area can be formulated as

$$\begin{aligned} \frac{S}{S_0}=f(p_0;\alpha ), \end{aligned}$$

(A.1)

where (the continuous function) $f(p_0;\alpha )$ should satisfy that:

$$\begin{aligned} f(0;\alpha )=0, \end{aligned}$$

(A.2)

for any value of $\alpha$ (the shape parameter that controls the initial gap size at the saddle point $(x,y)=(0,0)$) because the contact area is zero when there is no applied load.

In the current problem, the initial gap $g_0(x,y)$ in eq. (1) can be written as:

$$\begin{aligned} g_0(x,y)=g_x(x)+g_y(y), \end{aligned}$$

(A.3)

with

$$\begin{aligned} g_x(x)=\Delta \left( 1-\cos (2\pi x/\lambda )\right) , \end{aligned}$$

(A.4)

and

$$\begin{aligned} g_y(y)=0.5 \alpha \Delta \left( 1+\cos (2\pi y/\lambda )\right) . \end{aligned}$$

(A.5)

When $\alpha \rightarrow 0$, $g(x,y) \rightarrow g_x(x)$, the contact area S is a rectangular strip of shape $2l_{cx} \times \lambda$, as shown in Fig. 11 (e). The values of $l_{cx}$, according to the 1D Westergaard’s solution [31], is:

$$\begin{aligned} l_{cx}=\frac{\lambda }{\pi }\arcsin {\sqrt{\frac{p_0}{p_x^*}}}, \end{aligned}$$

(A.6)

with

$$\begin{aligned} p_x^*=\frac{\pi E}{1-\nu ^2} \frac{\Delta }{\lambda }=\frac{p_s}{2}. \end{aligned}$$

(A.7)

Therefore,

$$\begin{aligned} \left. \frac{S}{S_0}\right| _{\alpha =0}=f(p_0;0)=\frac{2}{\pi }\arcsin {\sqrt{\frac{2 p_0}{p_s}}}. \end{aligned}$$

(A.8)

When $\alpha \rightarrow \infty$, $g(x,y) \approx g_y(y)$, and the contact area S is a rectangular strip of shape $2\lambda \times l_{cy}$ as shown in Fig. 11 (f). The values of $l_{cy}$, according to the 1D Westergaard’s solution [31], is:

$$\begin{aligned} l_{cy}=\frac{\lambda }{\pi }\arcsin {\sqrt{\frac{p_0}{p_y^*}}}, \end{aligned}$$

(A.9)

with

$$\begin{aligned} p_y^*=\frac{\pi E}{1-\nu ^2} \frac{0.5 \alpha \Delta }{\lambda }=0.25 \alpha p_s. \end{aligned}$$

(A.10)

Therefore,

$$\begin{aligned} \left. \frac{S}{S_0}\right| _{\alpha \rightarrow \infty }=f(p_0;\infty )=\frac{2}{\pi }\arcsin {\sqrt{\frac{4 p_0}{\alpha p_s}}}. \end{aligned}$$

(A.11)

Fig. 11

Top row: the initial elastic surface $g_0(x,y)$ with the shape parameter $\alpha =0.5$ (a), the surface $g_x(x)$ depicted in eq. (A.4) (b), and the surface $g_y(y)$ depicted in eq. (A.5), with $\alpha =0.5$ (c). Bottom row: the schematic view of the contact region for the initial geometry depicted in (a)-(c) contacts with a flat rigid surface. The contact region is colored in red, and the initial elastic surface is $g_0(x,y)$ in (d), $g_x(x,y)$ in (e) and $g_y(x,y)$ in (f)

It is assumed that when $\alpha \in (0, \infty )$, the relation between contact area and average applied pressure eq. (A.1) can be reconstructed through function composition:

$$\begin{aligned} f(p_0;\alpha )=\frac{1}{2}(f(f_1(p_0;\alpha )p_0; 0)+f(f_2(p_0;\alpha )p_0; \infty )). \end{aligned}$$

(A.12)

The factor $\frac{1}{2}$ is applied in eq. (A.12) to normalize the contact area ratio, which is always less or equal to one. For the reconstruction to satisfy eq. (A.8) and eq. (A.11), one must have:

$$\begin{aligned} f(f_1(p_0;0)p_0;0)=2f(p_0;0), \quad f_2(p_0;0)=0, \end{aligned}$$

(A.13a)

$$\begin{aligned} f_1(p_0; \infty )=0, \quad f(f_2(p_0; \infty )p_0; \infty )=2f(p_0;\infty ). \end{aligned}$$

(A.13b)

Because the small values of $p_0$ in the current study, the function f can be approximated linearly, and eqs. (A.13a) and (A.13b) can be written as:

$$\begin{aligned} f_1(p_0;0)=2, \quad f_2(p_0;0)=0,\end{aligned}$$

(A.14a)

$$\begin{aligned} f_1(p_0; \infty )=0, \quad f_2(p_0; \infty )=2. \end{aligned}$$

(A.14b)

One way to satisfy both eqs. (A.14a) and (A.14b) is by choosing $f_1$ and $f_2$ so that

$$\begin{aligned} f_1(p_0;\alpha )+f_2(p_0;\alpha )=2, \end{aligned}$$

(A.15)

which can be achieved by introducing a partitioning function $\beta$ and letting

$$\begin{aligned} f_2(p_0;\alpha )=2 \beta (p_0;\alpha ), \quad f_1(p_0,\alpha )=2-2\beta (p_0;\alpha ). \end{aligned}$$

(A.16)

By substituting eq. (A.16) into eq. (A.12), and then using eq. (A.8) and eq. (A.11) gives:

$$\begin{aligned} \begin{aligned} \frac{S}{S_0}&= f(p_0; \alpha )= \frac{1}{\pi }\left( \arcsin {\sqrt{(2-2\beta )\left( \frac{2 p_0}{p_s}\right) }} + \arcsin {\sqrt{\left( \frac{8\beta }{\alpha }\frac{p_0}{p_s}\right) }}\right) \\&\approx \frac{2}{\pi }\left( \arcsin {\sqrt{(1-\beta )\left( \frac{p_0}{p_s}\right) }} + \arcsin {\sqrt{\left( \frac{2\beta }{\alpha }\frac{p_0}{p_s}\right) }}\right) . \end{aligned} \end{aligned}$$

(A.17)

It is worth mentioning that eq. (A.12) is not the only way to reconstruct $f(p_0;\alpha )$, e.g.,

$$\begin{aligned} f(p_0;\alpha )=h_1(p_0;\alpha )f(p_0;0)+h_2(p_0;\alpha )f(p_0;\infty ), \end{aligned}$$

(A.18)

with

$$\begin{aligned} h_1(p_0;\alpha =0)= & {} 1, \quad h_2(p_0;\alpha =0)=0, \end{aligned}$$

(A.19a)

$$\begin{aligned} h_1(p_0;\alpha \rightarrow \infty )= & {} 0, \quad h_2(p_0;\alpha \rightarrow \infty )=1, \end{aligned}$$

(A.19b)

also satisfies eq. (A.8) and eq. (A.11). However, the numerical experiment shows that the fitting equation based on eq. (A.18) gives a poor result with the current simulation data.