1 Introduction

Rolling contacts are widely found in mechanical systems, e.g. wheel and rail contact interfaces, cam and roller systems, gears, and rolling element bearings. The calculation of traction distribution and the stick/slip zones for rolling contact problems is significant for understanding traction control, lifespan prediction, wear and rolling contact fatigue. A lot of research has been conducted about this topic, and some sophisticated numerical models have been proposed by several researchers, such as CONTACT and FASTSIM algorithms proposed by Kalker [1] and the revised algorithms proposed by Vollebregt [2], the finite element method by Li [3, 4], the boundary element method by Abascal [5, 6], semi-analytical method by Wang [7] and the linear complementarity problem formulations by Xi [8, 9].

In order to improve and to adjust the contact interface behaviors without changing the bulk material, thin layers, usually in the form of surface coatings are often used. For example, the ceramic coatings, alloy/metal coatings and composite coatings [10], are often utilized. Moreover, sometimes the layers presented within the contact interfaces are unavoidable. For example, different third layers, such as leaves, dust and dirt, are often involved in wheel and rail contact problems [11].

To solve the rolling contact problems with elastic layers, many numerical studies have been proposed to obtain the traction distribution and the stick/slip zones. Among them, Meierhofer et al. proposed a model for calculating the traction characteristic for the wheel and rail contact with a third body layer [12]. The normal contact solution was simplified using the Hertz solution. A Winkler similar method was used for the tangential contact solution, and the layer deformation was assumed to be described by the independent brushes’ deformation. Guler et al. [13,14,15] focused on the solution of rolling contact problems with graded coatings. In their work, the relationship between the surface displacement gradients and the traction was derived by several integral equations, and the Goodman approximation was adopted to decouple the deriving singular integral equations. The solution of the integral equations was conducted using the Gauss–Chebyshev integration method. A similar method was also used in a recent work of Alinia et al. to analyze the stress for rolling contact problem with functionally graded material coating [16].

Most of the reports mentioned above are focused on two-dimensional rolling contact problems involving coating layers only. However, it is surprising that so little work has been done for three-dimensional ones with elastic coating layers. Here, it should be noted that, the three-dimensional rolling contact problems under viscoelastic layer conditions are considered by some researchers [17,18,19]. For viscoelastic materials, the imperfect elasticity plays a significant role for rolling traction force, that is different from the origin of elastic rolling traction forces. In our topic, for rolling contact problems of elastic materials, as important factors, creepages indicate the velocity differences within the rolling contact. For three-dimensional rolling contact problems, there are three kinds of creepages as per the different directions. Especially, the longitudinal creepage denotes the velocity difference in the rolling direction, the lateral creepage indicates the velocity difference in the lateral direction and the spin creepage denotes the angular velocity difference along the normal direction of the contact surfaces. Lateral and spin creepages are normally involved besides the longitudinal one, and they are also important for mechanical performance. For example, when wheels are negotiating with curved rails, squeal noise is often generated as the result of the lateral force [20, 21]. Moreover, asymmetrical wear profiles can also be found for the curved track because of the spin creepage [22, 23]. To understand and to explain these behaviors, it is required to take the effects of lateral and spin creepages into account. While for two-dimensional rolling contact conditions, only longitudinal creepage, or in other words slide-to-roll ratio (SRR), should be considered.

In this work, a three-dimensional rolling contact numerical model for point contact with one or two elastic layers are considered. The influence coefficients of the stress and the displacement for the contact with layers are obtained from the frequency response functions using the fast Fourier transform method. For calculating the normal contact and the tangential contact of the rolling contact problems, the conjugate gradient method is utilized during the iteration processes. Moreover, to speed up the calculation, the FFT technique is also employed. All possible creepages, i.e., the longitudinal, lateral and spin creepages are taken into account in the current rolling contact model. The results of traction distribution and the stick/slip zones are presented with various coating elastic modulus and thickness under different creepage combinations.

2 Problem Formulation

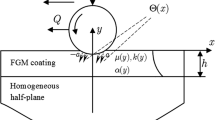
The schematic diagram of the current three-dimensional rolling contact problem is shown in Fig. 1, and \(\psi\), \(\varphi\) and \(\omega\) denote the angular velocities about x, y and z axes, respectively. In this work, each layer is homogeneous and linear elastic, and the interfaces are bounded perfectly. The elastic modulus for layer 1 and layer 2 are \({E}_{1}\) and \({E}_{2}\), respectively and \({v}_{1}\) and \({v}_{2}\) and \({h}_{1}\) and \({h}_{2}\) are the corresponding Poisson’s ratios and the layer thicknesses.

Fig. 1
figure 1

Schematic diagram of the 3D rolling contact problem

Full size image

2.1 The Normal Contact Solution

For the normal contact solution, the complementarity conditions for the normal gap \({g}_{z}\) and the corresponding normal pressure p are employed, and they can be given by

$$\left\{\begin{array}{c}p\bullet {g}_{z}=0,\\ p\ge 0,\\ {g}_{z}\ge 0.\end{array}\right.$$
(1)

The normal gap \({g}_{z}\) can be described by

$${g}_{z}-{h}_{z}={u}_{z}-{\delta }_{z}.$$
(2)

In which \({h}_{z}\) and \({\delta }_{z}\) are the initial separation and the rigid displacement between the contact surfaces, while \({u}_{z}\) is the displacement and can be calculated by

$${u}_{z}={C}_{p}^{{u}_{z}}*p.$$
(3)

where \({C}_{p}^{{u}_{z}}\) is the corresponding influence coefficient matrices (ICMs) and the derivation will be provided later. The normal force P can be calculated by

$$P=\mathrm{sum}\left({d}_{x}{d}_{y}p\right).$$
(4)

Here, \({d}_{x}\) and \({d}_{y}\) are the mesh sizes with respect to the x- and y-axis, respectively.

2.2 The Tangential Contact Solution

To solve the tangential contact problem, firstly the governing equations for three-dimensional rolling contact problems are given by [1]

$$\left\{\begin{array}{c}{S}_{x}={\xi }_{x}-{\xi }_{\varphi }y-\frac{\partial {u}_{x}}{\partial x},\\ {S}_{y}={\xi }_{y}+{\xi }_{\varphi }x-\frac{\partial {u}_{y}}{\partial x}.\end{array}\right.$$
(5)

In which \({S}_{x}\) and \({S}_{y}\) are the relative slip velocities in the x- and y-direction, and \({\xi }_{x}\), \({\xi }_{y}\) and \({\xi }_{\varphi }\) denote the longitudinal, lateral and spin creepages, respectively, while \({u}_{x}\) and \({u}_{y}\) are the corresponding deformations in the x- and y-direction.

An important characteristic, for rolling contact problems is that there are both stick and slip zones within the contact region. As per the report of Wang [7], mathematically, the basis to determine the stick and slip zones in this work can be expressed by

$$\left\{\begin{array}{c}\sqrt{{q}_{x}^{2}+{q}_{y}^{2}}\le \mu p,\mathrm{ and }\sqrt{{S}_{x}^{2}+{S}_{y}^{2}}=0. \mathrm{For the stick zone}.\\ \sqrt{{q}_{x}^{2}+{q}_{y}^{2}}=\mu p,\mathrm{ and }\sqrt{{S}_{x}^{2}+{S}_{y}^{2}}\ne 0. \mathrm{For the slip zone}.\end{array}\right.$$
(6)

where \({q}_{x}\) and \({q}_{y}\) are the traction results in x and y direction, \(\mu\) is the friction coefficient and \(p\) is the corresponding normal pressure.

In order to solve the current rolling contact model efficiently, the method proposed by Wang et al. [7] is adopted in this work, in which the conjugate gradient method is employed during the iteration processes. However, it should be noted that in Wang’s work the lateral and spin creepages are not considered, and in this work, the effects of these creepages on the traction distribution and the stick/slip zones are investigated. Therefore, based on Wang’s work, some necessary processes are adjusted to consider the lateral and spin creepages. To guarantee the completeness of the content in this work, the main methodology is also provided.

If there is no slip in the whole contact region, both \({S}_{x}\) and \({S}_{y}\) are zero. Therefore, the governing equation for 3D rolling contact problems can be expressed by

$$\left\{\begin{array}{c}\frac{\partial {u}_{x}}{\partial x}={\xi }_{x}-{\xi }_{\varphi }y,\\ \frac{\partial {u}_{y}}{\partial x}={\xi }_{y}+{\xi }_{\varphi }x.\end{array}\right.$$
(7)

By integrating both sides with respect to x, we have

$$\left\{\begin{array}{c}{u}_{x}={\xi }_{x}x-{\xi }_{\varphi }xy+f\left(y\right),\\ {u}_{y}={\xi }_{y}x+\frac{{\xi }_{\varphi }{x}^{2}}{2}+g\left(y\right).\end{array}\right.$$
(8)

In which \(f(y)\) and \(g(y)\) are functions of \(y\), after discretization they can be given by

$$\left\{\begin{array}{c}{f}_{j}={{u}_{{x}_{ij}}-\xi }_{x}{x}_{i}+{\xi }_{\varphi }{x}_{i}{y}_{j},\\ {g}_{j}={u}_{{y}_{ij}}-{\xi }_{y}{x}_{i}-\frac{{\xi }_{\varphi }{{x}_{i}}^{2}}{2}.\end{array}\right.$$
(9)

To obtain the results of \({u}_{{x}_{ij}}\) and \({u}_{{y}_{ij}}\), the ICMs to relate the deformation with the traction results are required. In contrast from the conditions without layers, it is hard to obtain the usable ICMs directly from the analytical solution, while for the layered condition, the ICMs can be derived from the corresponding frequency response functions [24]. In the work of Liu [25], the solution details for derivation of the ICMs with coating layers has been provided. Therefore, \({u}_{x}\) and \({u}_{y}\) can be calculated by

$$\left[\begin{array}{c}{u}_{x}\\ {u}_{y}\end{array}\right]=IFFT\left[\begin{array}{ccc}\widehat{\widehat{{C}_{{q}_{x}}^{{u}_{x}}}}& \widehat{\widehat{{C}_{{q}_{y}}^{{u}_{x}}}}& \widehat{\widehat{{C}_{p}^{{u}_{x}}}}\\ \widehat{\widehat{{C}_{{q}_{x}}^{{u}_{y}}}}& \widehat{\widehat{{C}_{{q}_{y}}^{{u}_{y}}}}& \widehat{\widehat{{C}_{p}^{{u}_{y}}}}\end{array}\right]*\left[\begin{array}{c}\widehat{\widehat{{q}_{x}}}\\ \widehat{\widehat{{q}_{y}}}\\ \widehat{\widehat{p}}\end{array}\right].$$
(10)

In which IFFT denotes inverse Fourier transform, \({C}_{{q}_{x}}^{{u}_{x}}\) indicates the influence coefficients to describe the relationship between traction \({q}_{x}\) and deformation \({u}_{x}\), and similar patterns for \({C}_{{q}_{y}}^{{u}_{x}}\), \({C}_{p}^{{u}_{x}}\), \({C}_{{q}_{x}}^{{u}_{y}}\), \({C}_{{q}_{y}}^{{u}_{y}}\) and \({C}_{p}^{{u}_{y}}\), while the symbol ^ is the discrete Fourier transform and the symbol * denotes the convolution calculation. For more details on the derivation of the ICMs, the reader is referred to the works of Liu, Cai and Sullivan [25,26,27].

In term of the Papkovich–Neuber potentials φ and \(\psi ({\psi }_{1},{\psi }_{2},{\psi }_{3})\), stress \(\sigma\) and displacement \(u\) can be given by

$${u}_{i}^{k}=\frac{1}{2{G}_{k}}\left[{\varphi }_{,i}^{k}+x{\psi }_{1,i}^{k}+{z}_{k}{\psi }_{3,i}^{k}-\left(3-4{v}_{k}\right){\psi }_{i}^{k}\right].$$
(11)
$${\sigma }_{ij}^{k}={\varphi }_{,ij}^{k}-2{v}_{k}\left({\psi }_{\mathrm{1,1}}^{k}+{\psi }_{\mathrm{3,3}}^{k}\right){\delta }_{ij}-\left(1-2{v}_{k}\right)\left({\psi }_{i,j}^{k}+{\psi }_{j,i}^{k}\right)+x{\psi }_{1,ij}^{k}+{z}_{k}{\psi }_{3,ij}^{k}.$$
(12)

In which k denotes the kth layer, and by double Fourier transform for x and y the stress and deformation can be expressed by

$${\mathop {u_{i}^{k} }\limits^{ \approx }} = \frac{1}{{2G_{k} }}FT_{{xy}} \left[ {\varphi _{{,i}}^{k} + x\psi _{{1,i}}^{k} + z_{k} \psi _{{3,i}}^{k} - \left( {3 - 4v_{k} } \right)\psi _{i}^{k} } \right],$$
(13)
$${\mathop {\sigma _{{ij}}^{k} }\limits^{ \approx }} = FT_{{xy}} \left( {\varphi _{{,ij}}^{k} - 2v_{k} \left( {\psi _{{{\text{1}},{\text{1}}}}^{k} + \psi _{{{\text{3}},{\text{3}}}}^{k} } \right)\delta _{{ij}} - \left( {1 - 2v_{k} } \right)\left( {\psi _{{i,j}}^{k} + \psi _{{j,i}}^{k} } \right) + x\psi _{{1,ij}}^{k} + z_{k} \psi _{{3,ij}}^{k} } \right).$$
(14)

In which both symbol \(\approx\) and \({FT}_{xy}\) denote double Fourier transform, and the solutions can be expressed by

$$\left\{\begin{array}{c}\stackrel{\sim }{\stackrel{\sim }{{\varphi }^{k}}}={A}^{k}{e}^{-\alpha z}+{\overline{A} }^{k}{e}^{\alpha z},\\ \stackrel{\sim }{\stackrel{\sim }{{\psi }_{1}^{k}}}={B}^{k}{e}^{-\alpha z}+{\overline{B} }^{k}{e}^{\alpha z},\\ \stackrel{\sim }{\stackrel{\sim }{{\psi }_{3}^{k}}}={C}^{k}{e}^{-\alpha z}+{\overline{C} }^{k}{e}^{\alpha z}.\end{array}\right.$$
(15)

In which \({A}^{k}\), \({\overline{A} }^{k}\), \({B}^{k}\), \({\overline{B} }^{k}\), \({C}^{k}\) and \({\overline{C} }^{k}\) are unknown coefficients needed to be solved.

There are several boundary conditions needed to acquire the solution, for the surface they can be given by

$$\left\{\begin{array}{c}{\sigma }_{zz}^{1}\left(x,y,0\right)=p\left(x,y\right),\\ {\sigma }_{zx}^{1}\left(x,y,0\right)=q\left(x,y\right),\\ {\sigma }_{zy}^{1}\left(x,y,0\right)=0.\end{array}\right.$$
(16)

For the layer interfaces the boundary conditions can be given by

$$\left\{\begin{array}{c}{\sigma }_{zx}^{k}\left(x,y,h\right)={\sigma }_{zx}^{k+1}\left(x,y,0\right),\\ {\sigma }_{zy}^{k}\left(x,y,h\right)={\sigma }_{zy}^{k+1}\left(x,y,0\right),\\ \begin{array}{c}{\sigma }_{zz}^{k}\left(x,y,h\right)={\sigma }_{zz}^{k+1}\left(x,y,0\right),\\ \begin{array}{c}{u}_{x}^{k}\left(x,y,h\right)={u}_{x}^{k+1}\left(x,y,0\right),\\ {u}_{y}^{k}\left(x,y,h\right)={u}_{y}^{k+1}\left(x,y,0\right),\\ {u}_{z}^{k}\left(x,y,h\right)={u}_{z}^{k+1}\left(x,y,0\right).\end{array}\end{array}\end{array}\right.$$
(17)

It can be seen that for the single layer condition there are 9 unknowns, while for the double layer conditions 15 unknowns are required to be solved. By using these equations \({A}^{k}\), \({\overline{A} }^{k}\), \({B}^{k}\), \({\overline{B} }^{k}\), \({C}^{k}\) and \({\overline{C} }^{k}\) can be solved, and the results can be found in [26, 27] for one and two layers.

When \({u}_{x}\) and \({u}_{y}\) are obtained, the residual vectors \({r}_{x}\) and \({r}_{y}\) can be expressed by

$$\left[\begin{array}{c}{r}_{{x}_{ij}}^{n}\\ {r}_{{y}_{ij}}^{n}\end{array}\right]=\left[\begin{array}{c}{u}_{{x}_{ij}}^{n}\\ {u}_{{y}_{ij}}^{n}\end{array}\right]-\left[\begin{array}{c}{\xi }_{x}{x}_{i}-{\xi }_{\varphi }{x}_{i}{y}_{j}+{f}_{j}\\ {\xi }_{y}{x}_{i}+\frac{{\xi }_{\varphi }{{x}_{i}}^{2}}{2}+{g}_{j}\end{array}\right].$$
(18)

To obtain the sum of squares of \({r}_{x}\) and \({r}_{y}\) in the stick zones, we have

$${r}^{n}=sum\left({{r}_{{x}_{ij}}^{n}}^{2}+{{r}_{{y}_{ij}}^{n}}^{2}\right).$$
(19)

If \(\frac{{r}^{n}}{{r}^{n-1}}<1\), the conjugate directions in both stick and slip zones can be calculated by

$$\left[\begin{array}{c}{t}_{x}^{n}\\ {t}_{y}^{n}\end{array}\right]=\left[\begin{array}{c}{r}_{x}^{n}\\ {r}_{y}^{n}\end{array}\right]+\frac{{r}^{n}}{{r}^{n-1}}\left[\begin{array}{c}{t}_{x}^{n-1}\\ {t}_{y}^{n-1}\end{array}\right].$$
(20)

In which \({t}_{x}^{n}\) and \({t}_{y}^{n}\) are the conjugate directions for the nth iteration, and if \(\frac{{r}^{n}}{{r}^{n-1}}\ge 1\) the old conjugate directions are employed.

The step length for the nth iteration \({\upalpha }^{n}\) can be calculated by

$${\alpha }^{n}=\frac{\left[\begin{array}{cc}{r}_{x}^{n}& {r}_{y}^{n}\end{array}\right]\bullet \left[\begin{array}{c}{r}_{x}^{n}\\ {r}_{y}^{n}\end{array}\right]}{\left[\begin{array}{cc}{t}_{x}^{n}& {t}_{y}^{n}\end{array}\right]\bullet IFFT\left[\begin{array}{cc}\widehat{\widehat{{C}_{{q}_{x}}^{{u}_{x}}}}& \widehat{\widehat{{C}_{{q}_{y}}^{{u}_{x}}}}\\ \widehat{\widehat{{C}_{{q}_{x}}^{{u}_{y}}}}& \widehat{\widehat{{C}_{{q}_{y}}^{{u}_{y}}}}\end{array}\right]*\left[\begin{array}{c}{t}_{x}^{n}\\ {t}_{y}^{n}\end{array}\right]}.$$
(21)

The traction distribution \({q}_{x}\) and \({q}_{y}\) can be given by

$$\left[\begin{array}{c}{q}_{x}^{n+1}\\ {q}_{y}^{n+1}\end{array}\right]=\left[\begin{array}{c}{q}_{x}^{n}\\ {q}_{y}^{n}\end{array}\right]-{\alpha }^{n}\bullet \left[\begin{array}{c}{t}_{x}^{n}\\ {t}_{y}^{n}\end{array}\right].$$
(22)

For the positions \(\sqrt{{q}_{{x}_{ij}}^{2}+{q}_{{y}_{ij}}^{2}}>\mu {p}_{ij}\), the traction values should be revised as

$$\left[\begin{array}{c}{q}_{{x}_{ij}}\\ {q}_{{y}_{ij}}\end{array}\right]=\frac{\mu {p}_{ij}}{\sqrt{{q}_{{x}_{ij}}^{2}+{q}_{{y}_{ij}}^{2}}}\left[\begin{array}{c}{q}_{{x}_{ij}}\\ {q}_{{y}_{ij}}\end{array}\right].$$
(23)

In which \(\mu\) is the friction coefficient. If the convergence condition is arrived, the results of \({q}_{x}\) and \({q}_{y}\) can be output. Otherwise, the iteration from Eq. 9 should be conducted again until the convergence condition is reached. A flowchart is provided in Fig. 2.

Fig. 2
figure 2

Flowchart of the numerical model

Full size image

3 Results and Discussion

3.1 Validation

To validate the normal pressure results from the current numerical model, dimensionless results of normal pressure against contact radius along the x-axis are provided in Fig. 3. In the following results, the sphere radius is set as 50 mm, the elastic modulus is 210 GPa and the Poisson ratio is 0.3. The normal load is set as 100 N. The potential contact area is selected as \(2\times 2 {\mathrm{mm}}^{2}\), and \(64\times 64\) mesh density is selected.

Fig. 3
figure 3

Dimensionless results of normal pressure along the x-axis for a a single layer and b two layers under different layer thickness and elastic modulus. The thickness values for the layer are 0.25a, 0.5a and a, in which a is the Hertz contact radius. The elastic modulus values for a single layer are \({{E}_{1}=0.5E}_{s}\) and \({{E}_{1}=2E}_{s}\), and for two layers they are \({{E}_{1}=0.5{E}_{2}=0.25E}_{s}\) and \({{E}_{1}=2{E}_{2}=4E}_{s}\)

Full size image

As shown in Fig. 3a, the results with one layer are given. The layer thickness parameters are varied from 0.25a to a, in which a is the Hertz contact radius. Two groups of elastic moduli are used, i.e. \({E}_{1}={0.5E}_{s}\) and \({E}_{1}={2E}_{s}\). Moreover, in order to provide a reference, the results with no layer are also provided. The normal pressure results are non-dimensionalized by the maximum Hertz pressure \({P}_{0}\), and the radial coordinate are non-dimensionalized by a. For the results with double layers, the thicknesses for each layer are varied from 0.25a to a. In this work, the thicknesses of the two layers are identical for each case, i.e. \({h}_{1}={h}_{2}\). Two groups of elastic modulus are employed, i.e., \({E}_{1}=0.5{E}_{2}={0.25E}_{s}\) and \({E}_{1}=2{E}_{2}={4E}_{s}\), and the results are given in Fig. 3b. The present results for a single layer with a thickness of a and the results of two layers, both with a thickness of 0.5a, are in good agreement with the results in Yu’s work [28].

Moreover, it can be seen that for layered conditions, the contact radius is increasing with the decreasing elastic modulus of layers. For compliant layers, i.e., the layer elastic modulus is smaller than the substrate material, the thicker the layer thickness, the larger the contact radius. Due to the larger contact area for compliant layer conditions, the maximum contact pressure results are much smaller by comparing with the hard one or no layer conditions. While for stiff layers, i.e. larger layer elastic modulus, the contact radius is decreasing with increasing layer thickness.

In order to validate the current results for traction distribution, the Linear Complementarity Problem (LCP) method for solving rolling contact problems is adopted [9]. Due to the high computation cost limitation of the LCP method, a coarse mesh, i.e., \(22\times 22\), is adopted. By the application of the FFT technique a much finer mesh may be used, and for the numerical solutions presented here, a \(64\times 64\) mesh was considered to yield representative results. Similar to the study of Nyqvist [29], for the depth direction the resolution of z can be coarser and set as 0.1a if the substrate stress results are required.

In this work, the relative tolerance for the normal contact is set as 1e-5, and for the tangential it is set as 1e-7. The relaxation factor for the normal contact is initiated from 64 and is decreasing with iterations but not smaller than 0.5. All the numerical simulations were performed on a computer with an i7-7820HQ CPU (2.9 GHz) and 16 G RAM, and the running time for each case is normally less than 6 s.

Different creepages combinations, including longitudinal, lateral and spin creepages, are employed. It should be noted that in this work the creepage parameters are seen as input parameters, and for each case the values are fixed in all iteration. As shown in Fig. 4a and b, pure longitudinal creepage condition, i.e., \({\xi }_{x}=0.002\), is compared. In Fig. 4c and d, both longitudinal and lateral creepages are applied, specifically, \({\xi }_{x}=0.002\) and \({\xi }_{y}=0.001\). While for Fig. 4e and f, spin creepage is involved, i.e., \({\xi }_{x}=0.002\) and \({\xi }_{\varphi }=0.01\). Lastly, as given in Fig. 4g and h, all possible creepages, i.e. longitudinal, lateral and spin creepages are employed in the numerical simulations, i.e., \({\xi }_{x}=0.002\), \({\xi }_{y}=0.001\) and \({\xi }_{\varphi }=0.01\). The slip zones are indicated by the filled circles on the corresponding grids. From the results presented in Fig. 4, it can be seen that the present results for all conditions agree well with the ones obtained with the LCP method.

Fig. 4
figure 4

Comparisons of the current results of the traction distribution with the LCP method. The friction coefficient \(\mu\) is set as 1. a Current results and b LCP results for \({\xi }_{x}=0.002\). c Current results and d LCP results for \({\xi }_{x}=0.002\) and \({\xi }_{y}=0.001\). e Current results and f LCP results for \({\xi }_{x}=0.002\) and \({\xi }_{\varphi }=0.01\). g Current results and h LCP results for \({\xi }_{x}=0.002\), \({\xi }_{y}=0.001\) and \({\xi }_{\varphi }=0.01\). The filled circles indicate the slip zones and the rest are stick zones

Full size image

3.2 Traction Distribution Results with Layers Under Pure Longitudinal Creepage

The traction distribution results under pure longitudinal creepage are provided in this section. Firstly, the traction distribution results along the x-axis with a single layer are given in Fig. 5, in which the layer thicknesses are varied from 0.25a to a and the elastic moduli are selected as 0.5 \({E}_{s}\) and 2 \({E}_{s}\). The longitudinal creepages from 0.02 to 0.1 are applied for each case. From Fig. 5a to 5c, it can be seen that for the compliant layer conditions the ratio of slip zones to the whole contact zones is increasing with increasing layer thickness, while the ratio of slip zones is decreasing with increasing layer thickness for the stiff layer conditions as shown from Fig. 5d to 5f. By comparing the compliant layer results with the stiff layer ones, it can be seen that the slip zones are more predominated for hard ones with the same longitudinal creepage conditions.

Fig. 5
figure 5

Traction distribution along the x-axis with single layer under pure longitudinal creepage. a 0.25a, 0.5 \({E}_{s}\), b 0.5a, 0.5 \({E}_{s}\), c a, 0.5 \({E}_{s}\), d 0.25a, 2 \({E}_{s}\), e 0.5a, 2 \({E}_{s}\) and f a, 2 \({E}_{s}\)

Full size image

In Fig. 6, the traction results with two layers under pure longitudinal creepage conditions are provided. Similar to the results for a single layer, larger slip zone ratios can also be found for the results of two hard layers, and smaller ones for the results of two compliant layers. Moreover, for the compliant layer conditions, slip zones also show more aggressive behavior for thick layers, while for the hard ones, more slip zones can be found for thinner layers.

Fig. 6
figure 6

Traction distribution along the x-axis with two layers under pure longitudinal creepage. a 0.25a, \({{E}_{1}=0.5{E}_{2}=0.25E}_{s}\), b 0.5a, \({{E}_{1}=0.5{E}_{2}=0.25E}_{s}\), c a, \({{E}_{1}=0.5{E}_{2}=0.25E}_{s}\), d 0.25a, \({{E}_{1}=2{E}_{2}=4E}_{s}\), e 0.5a, \({{E}_{1}=2{E}_{2}=4E}_{s}\), and f a, \({{E}_{1}=2{E}_{2}=4E}_{s}\)

Full size image

From the results of Fig. 5 and 6, it can be seen that the longitudinal creepage is a significant factor to determine the traction distribution and the stick/slip zones. Moreover, by employing suitable layer parameters the desired traction distribution and stick/slip results can be obtained.

These derived behaviors agree well with the conclusions proposed by Guler et al. [13, 15], in their works the traction distribution results for rolling contact problems are provided, but it should be noted that the graded elastic coatings are employed by them, which can be seen as a combination of multi-layered elastic coatings [30].

3.3 Traction distribution results with layers under longitudinal, lateral and/or spin creepages

The main purpose of this work is to provide the traction distribution and the stick/slip zones results with layers under different creepage conditions. In contrast to the results under pure longitudinal creepages, the results with lateral and spin creepages the traction distribution results are provided for the whole contact area. The mesh density parameters are the same as used in the previous section. The traction distribution results for a single layer are shown in Fig. 7 and Fig. 8, while in Fig. 9 and Fig. 10 the results of two layers are given.

Fig. 7
figure 7

Traction distribution under different creepage combinations with a single compliant layer of 0.5a and \({E}_{1}=0.5{E}_{s}\) for a \({\xi }_{x}=0.002\) and \({\xi }_{y}=0.001\), b \({\xi }_{x}=0.002\) and \({\xi }_{y}=0.002\), c \({\xi }_{x}=0.002\) and \({\xi }_{\varphi }=0.005\), d \({\xi }_{x}=0.002\) and \({\xi }_{\varphi }=0.01\), e \({\xi }_{x}=0.002\), \({\xi }_{y}=0.001\) and \({\xi }_{\varphi }=0.005\), and f \({\xi }_{x}=0.002\), \({\xi }_{y}=0.001\) and \({\xi }_{\varphi }=0.01\). With a single stiff layer of 0.5a and \({E}_{1}=2{E}_{s}\) for g \({\xi }_{x}=0.002\) and \({\xi }_{y}=0.001\), h \({\xi }_{x}=0.002\) and \({\xi }_{y}=0.002\), i \({\xi }_{x}=0.002\) and \({\xi }_{\varphi }=0.005\), j \({\xi }_{x}=0.002\) and \({\xi }_{\varphi }=0.01\), k \({\xi }_{x}=0.002\), \({\xi }_{y}=0.001\) and \({\xi }_{\varphi }=0.005\), and l \({\xi }_{x}=0.002\), \({\xi }_{y}=0.001\) and \({\xi }_{\varphi }=0.01\)

Full size image
Fig. 8
figure 8

Traction distribution under different creepage combinations with a single compliant layer of a and \({E}_{1}=0.5{E}_{s}\) for a \({\xi }_{x}=0.002\) and \({\xi }_{y}=0.001\), b \({\xi }_{x}=0.002\) and \({\xi }_{y}=0.002\), c \({\xi }_{x}=0.002\) and \({\xi }_{\varphi }=0.005\), d \({\xi }_{x}=0.002\) and \({\xi }_{\varphi }=0.01\), e \({\xi }_{x}=0.002\), \({\xi }_{y}=0.001\) and \({\xi }_{\varphi }=0.005\), and f \({\xi }_{x}=0.002\), \({\xi }_{y}=0.001\) and \({\xi }_{\varphi }=0.01\). With a single stiff layer of a and \({E}_{1}=2{E}_{s}\) for g \({\xi }_{x}=0.002\) and \({\xi }_{y}=0.001\), h \({\xi }_{x}=0.002\) and \({\xi }_{y}=0.002\), i \({\xi }_{x}=0.002\) and \({\xi }_{\varphi }=0.005\), j \({\xi }_{x}=0.002\) and \({\xi }_{\varphi }=0.01\), k \({\xi }_{x}=0.002\), \({\xi }_{y}=0.001\) and \({\xi }_{\varphi }=0.005\), and l \({\xi }_{x}=0.002\), \({\xi }_{y}=0.001\) and \({\xi }_{\varphi }=0.01\)

Full size image
Fig. 9
figure 9

Traction distribution under different creepage combinations with two compliant layers of 0.25a and \({{E}_{1}=0.5{E}_{2}=0.25E}_{s}\) for a \({\xi }_{x}=0.002\) and \({\xi }_{y}=0.001\), b \({\xi }_{x}=0.002\) and \({\xi }_{y}=0.002\), c \({\xi }_{x}=0.002\) and \({\xi }_{\varphi }=0.005\), d \({\xi }_{x}=0.002\) and \({\xi }_{\varphi }=0.01\), e \({\xi }_{x}=0.002\), \({\xi }_{y}=0.001\) and \({\xi }_{\varphi }=0.005\), and f \({\xi }_{x}=0.002\), \({\xi }_{y}=0.001\) and \({\xi }_{\varphi }=0.01\). With two stiff layers of 0.25a and \({{E}_{1}=2{E}_{2}=4E}_{s}\) for g \({\xi }_{x}=0.002\) and \({\xi }_{y}=0.001\), h \({\xi }_{x}=0.002\) and \({\xi }_{y}=0.002\), i \({\xi }_{x}=0.002\) and \({\xi }_{\varphi }=0.005\), j \({\xi }_{x}=0.002\) and \({\xi }_{\varphi }=0.01\), k \({\xi }_{x}=0.002\), \({\xi }_{y}=0.001\) and \({\xi }_{\varphi }=0.005\), and l \({\xi }_{x}=0.002\), \({\xi }_{y}=0.001\) and \({\xi }_{\varphi }=0.01\)

Full size image
Fig. 10
figure 10

Traction distribution under different creepage combinations with two compliant layers of 0.5a and \({{E}_{1}=0.5{E}_{2}=0.25E}_{s}\) for a \({\xi }_{x}=0.002\) and \({\xi }_{y}=0.001\), b \({\xi }_{x}=0.002\) and \({\xi }_{y}=0.002\), c \({\xi }_{x}=0.002\) and \({\xi }_{\varphi }=0.005\), d \({\xi }_{x}=0.002\) and \({\xi }_{\varphi }=0.01\), e \({\xi }_{x}=0.002\), \({\xi }_{y}=0.001\) and \({\xi }_{\varphi }=0.005\), and f \({\xi }_{x}=0.002\), \({\xi }_{y}=0.001\) and \({\xi }_{\varphi }=0.01\). With two stiff layers of 0.5a and \({{E}_{1}={2E}_{2}=4E}_{s}\) for g \({\xi }_{x}=0.002\) and \({\xi }_{y}=0.001\), h \({\xi }_{x}=0.002\) and \({\xi }_{y}=0.002\), i \({\xi }_{x}=0.002\) and \({\xi }_{\varphi }=0.005\), j \({\xi }_{x}=0.002\) and \({\xi }_{\varphi }=0.01\), k \({\xi }_{x}=0.002\), \({\xi }_{y}=0.001\) and \({\xi }_{\varphi }=0.005\), and l \({\xi }_{x}=0.002\), \({\xi }_{y}=0.001\) and \({\xi }_{\varphi }=0.01\)

Full size image

In order to show the input parameters more clearly for the following results from Fig. 7 to Fig. 10, the elastic modulus and the thickness of each layer for all the numerical simulations are summarized in Table 1, while the creepage parameters are provided in Table 2.

Table 1 Layer parameters for numeral simulations
Full size table
Table 2 Creepage parameters for numeral simulations
Full size table

Figure 7a to 7f show the traction distribution results with a single layer, and the layer thickness is 0.5a and the corresponding elastic modulus is \(0.5{E}_{s}\). The results for the creepage parameters are \({\xi }_{x}=0.002\), \({\xi }_{y}=0.001\) and \({\xi }_{x}=0.002\), \({\xi }_{y}=0.002\), can be found in Fig. 6a and 6b, respectively. The traction results are almost symmetric with respect to the x-axis, and the slip zones are located at the trailing edges. For larger lateral creepage, the slip zones become larger. The results with the combination of longitudinal and spin creepages are given in Fig. 7c and 7d, in which \({\xi }_{x}=0.002\), \({\xi }_{\varphi }=0.005\) and \({\xi }_{x}=0.002\), \({\xi }_{\varphi }=0.01\) are employed separately. Moreover, Fig. 7e and 7f show the results when the longitudinal, lateral and spin creepages, i.e. \({\xi }_{x}=0.002\), \({\xi }_{y}=0.001\), \({\xi }_{\varphi }=0.005\) and \({\xi }_{x}=0.002\), \({\xi }_{y}=0.001\), \({\xi }_{\varphi }=0.01\) are applied. Due to the involving spin creepage, the symmetrical behavior of the traction distribution is ruined. By comparing with the results of Fig. 7c with 7d, more stick zones can be found for smaller spin creepage condition, and the slip zones are located at the top part of the trailing end. Similar behavior can also be found in Fig. 7e and 7f. The spin creepage can be seen as the combined effects of longitudinal creepage and lateral creepage, and they are not fixed values but dependent on specific location. In the current conditions, at the area of \(x<0\) and \(y>0\), the spin creepage can enhance the traction and therefore to make more grids to reach the corresponding traction limits. While in the area of \(x<0\) and \(y<0\), the effects of the longitudinal and the lateral creepages on the traction are neutralized partly by the spin creepage, and some original slip zones are taken over by stick domain.

As shown in Fig. 7g to 7l, a stiff layer, i.e. \({E}_{1}=2{E}_{s}\), with 0.5a thickness is adopted. By comparing the results with the ones as provided in Fig. 7a to 7f, similar patterns for each case can be found, and it also can be seen that the contact areas are significantly smaller than the ones with a compliant layer, while for the same creepage conditions the slip zones account for larger ratio within the contact area.

Figure 8a to 8f illustrate the results with a single compliant layer of a and \({E}_{1}=0.5{E}_{s}\), by comparing the results with the ones from Fig. 7a to 7f, the effects of compliant layer thickness on the traction distribution and stick/slip results can be obtained. It can be noted that for the compliant layer larger traction results can be obtained with thinner layer under same creepage conditions, the slip portions are increasing for thicker compliant layer conditions. While the opposite behaviors can be found from the results as given by Fig. 8g to 8l and Fig. 7g to 7l for stiff layer conditions.

Traction distribution results with two compliant layers of 0.25a and \({{E}_{1}=0.5{E}_{2}=0.25E}_{s}\) are illustrated in Fig. 9a to Fig. 9f, while the results with two stiff layers of 0.25a and \({{E}_{1}=2{E}_{2}=4E}_{s}\) are presented in Fig. 9g to Fig. 9l. Here, 0.25a is the thickness for each layer and therefore the total thickness is 0.5a for each calculation. For compliant layer conditions, similar to the results of a single layer, for the conditions with both longitudinal and lateral creepages, the slip zones are located at the trailing edge and show symmetrical behaviors, and the slip zones are relatively small. For the cases with spin creepage, the slip zones prefer to locate at the top part of the trailing edge. For the stiff layer conditions, the contact areas are much smaller than the ones with compliant layers, and the ratios of slip zones are significantly higher.

From Fig. 10a to f, traction distribution results with two compliant layers of 0.5a and \({{E}_{1}=0.5{E}_{2}=0.25E}_{s}\) are shown, and the ones with two stiff layers of 0.5a and \({{E}_{1}=2{E}_{2}=4E}_{s}\) are given in Fig. 10g to l. It is interesting to note that for compliant layers, the ratios of slip zones are larger when the thicker layers are adopted by comparing the results of Fig. 10a to f with the results of Fig. 9a to f. While for the stiff layers, smaller ratios of slip zones can be found for thicker layers and this behavior can also be seen in the corresponding results of Figs. 8 and 9.

As can be seen from the above results, different layer thickness and elastic modulus parameters are employed in the numerical simulation under different creepage combinations. Opposite behaviors can be found for the conditions with compliant coating layers and hard coating layers. On one hand, for compliant coating layers, larger contact area can be achieved, and at the same time the mean contact pressure results are smaller. Under the same creepage combinations, for thicker compliant layers, the slip zone ratios are increasing. On the other hand, for hard coating layers, the contact area results are smaller and larger contact pressure results can be found. The slip zone ratios are decreasing with decreasing layer thickness. Therefore, it can be concluded that the traction distribution and stick/slip zone results can be modified using different coating layers.

4 Conclusions

In this work, the rolling contact problems with one or two elastic layers are considered. The influence coefficient relationship between the displacement and the stress is obtained from the corresponding frequency response functions, and we extend this method to solve the rolling contact problems with elastic layers. An efficient numerical model using the conjugate gradient iteration method and the FFT technique has been proposed. All possible creepages, such as the longitudinal creepage, lateral creepage and spin creepage, are considered in the current model to consider about the rolling contact problems with elastic coating layers.

Several numerical simulations have been carried out and as per the results, the following remarks can be derived:

  • Larger contact area and smaller normal pressure results can be obtained with compliant coating layers, while smaller contact area and larger normal pressure results can be achieved using hard coating layers.

  • The traction distributions can be significantly adjusted by different coating layers with the same creepage combinations, and it is found that the slip zones are more predominated for hard coating layers.

  • For compliant coating layers, the slip zone ratios are increasing with increasing layer thickness.

  • For hard coating layers, the slip zone ratios are increasing with decreasing layer thickness.

As for future work, we will improve the numerical model to include surface roughness, and to incorporate three or more coating layers.