1 Introduction

In order to increase vehicle efficiency and thereby limit CO2 emissions, there is a general trend to use lower and lower viscosity engine lubricants in order to reduce hydrodynamic friction losses. While engine oil viscosity is controlled primarily by the viscosity of the base oil present, it is considerably modified by dissolved polymeric additives known as viscosity index improvers or viscosity modifiers (VMs). The prime function of these additives is to increase the viscosity index of their blends, but it is now recognised that they may also contribute to reducing hydrodynamic friction by undergoing temporary shear thinning at the high shear rates present in some engine components. Unfortunately, while temporary shear thinning may be desirable, it is often accompanied by permanent shear thinning resulting from the scission of polymer molecular chains at high shear rates, and this is always undesirable. We thus require viscosity modifiers that show considerable temporary but very little permanent shear thinning.

This paper explores some aspects of permanent shear thinning of polymer solutions. First previous work on the permanent shear thinning of polymer solutions is outlined. This is followed by new experimental work in which an ultrashear viscometer (USV) is used to subject polymer solutions of viscosities comparable to those of engine oils to well-defined shear conditions. Using a range of different viscosity base fluids, it is confirmed that permanent shear thinning is controlled by applied shear stress rather than shear rate. A method is then developed that is able to extract and analyse the very small amount of sheared fluid in a USV to explore the molecular nature of the polymer breakdown that causes permanent shear thinning.

2 Background

It has long been known that solutions of high molecular weight polymers can show permanent shear thinning (permanent viscosity loss) when subject to high shear conditions. Thus a patent of 1937 describes both the milling of polymeric lubricating oil additives to reduce their average molecular weight and the development of a “shear viscosity breaking test” to assess the stability of viscosity-index-improved oils [1]. Throughout the 1950s to 1970s, there was considerable research work on permanent shear thinning with respect to both the mastication of solid polymers and viscosity loss of polymer solutions. Three useful reviews in the 1970s summarise the state of knowledge at this time [2,3,4]. Mackenzie and Jemmett noted the development of an early rule of thumb, that hydrocarbon-based polymer breakdown in solution is likely to occur when;

$$ {\text{solution}}\;{\text{viscosity}} \times {\text{shear}}\;{\text{rate}} \times {\text{MWt}}^{2} > \, 1 \times 10^{14} $$
(1)

where viscosity has units Poise, shear rate s−1, and MWt is the weight average molecular weight in g/mol. In the light of recent knowledge, this must be regarded as highly approximate—for example, it does not take any account of polymer architecture. It does, however, indicate the importance of molecular weight and viscosity in promoting permanent shear thinning.

Since the shear stress is the product of viscosity and shear rate, the above expression also suggests that it may be shear stress rather than shear rate that controls polymer breakdown. This question has been a matter of some debate. Early studies focused on the influence of shear rate on polymer breakdown and thus tended to give the impression that this was the driving factor [5,6,7]. However, the development of models to describe polymer breakdown [8] and also the observation that the rate of permanent shear thinning generally decreased with increasing temperature [9, 10] and increased with increasing viscosity [11] led to the gradual recognition that polymer breakdown might be dependent on the shear stress present in solution. This was confirmed by Yu et al. [12], who compared permanent shear thinning of polymer solutions in different viscosity base oils and found that it was more rapid in high-viscosity oils, in accord with it being controlled by shear stress rather than shear rate.

From Eq. 1, it can be very roughly estimated that, for a 10 cP solution of 105 MWt polymer, a shear rate of at least 106 s−1 is required for permanent shear thinning to occur. Such shear rates are difficult to obtain in conventional laminar flow viscometers and led to the early development of ultrasonic [13, 14], orifice [5], and engine bench test [15] methods of obtaining measurable permanent shear thinning. Studies were also carried out using capillary [16, 17] and concentric cylinder [10, 18, 19] viscometers, but these were generally employed to test very high molecular weight polymers whose solutions showed permanent viscosity loss at 104 or 105 s−1. They broadly confirmed the dependence of the onset of permanent viscosity loss on shear rate and molecular weight indicated by Eq. 1.

Up to the 1970s, there was considerable work to explore the mechanistic origins of permanent shear thinning. Early work by Frenkel [20], followed by an influential model of permanent shear thinning by Bueche [8], suggested that polymer molecule scission was most likely to occur at the central bond of a polymer chain due to the accumulation of stress at this location. In the 1960s the technique of gel permeation chromatography (GPC) was first applied to study the change in molecular weight distribution that accompanies permanent shear thinning. This gave variable results, with some studies and conditions producing a preponderance of fragments with half the molecular weight of the starting value [10, 12] but others showing randomly sized fragments or the formation of predominantly low molecular weight species [19].

Another experimental technique introduced in the 1960s was the use of radical trapping to monitor the rate of polymer bond breaking due to shear [21,22,23]. This is a potentially powerful technique but it was shown that the presence of such traps can increase the rate of polymer degradation by inhibiting the reformation of broken bonds, a role also accomplished by oxygen [24].

Various molecular-based models have been developed to describe the way that applied shear causes polymer scission, of which the most influential are those of Beuche [8] and de Gennes [25]. Both of these are based on the concept of stress-augmented thermal activation in which the activation energy in the normal Arrhenius rate equation is reduced by a mechanical work term originating from the action of applied force on molecular bonds, so that the rate of bond scission, R, depends on

$$ R = K{\text{e}}^{{ - \left( {E - F\delta } \right)/k_{\text{B}} T}} $$
(2)

where E is the energy needed to break the bond, F is the tensile force applied to the bond and δ is a distance approximately equal to the distance the bond will stretch before breaking. K is a prefactor, k B the Boltzmann constant, and T the absolute temperature. For polymers, the force F depends on a friction factor that describes the viscous force applied to a polymer segment and on the number of segments over which this force accumulates [8].

Since the 1970s, research on permanent shear thinning has been more fragmentary, especially concerning the breakdown of viscosity modifier additives. The main focus has been practical, i.e., on refining and correlating polymer breakdown tests with performance in engine [26,27,28,29,30], automatic transmission [31], hydraulic [32], and gear [33] systems. This is most problematic with respect to engine oils since many other factors influence change of viscosity during use including fuel dilution and oxidation [34]. In addition to engine tests, three main bench tests have emerged, based, respectively, on a diesel injector [35], sonic degradation [36] and a taper roller bearing [37]. Mortier has compared the main bench test methods for measuring shear stability of VM-containing lubricants [38]. In most bench tests, viscosity loss is quantified by comparing the low shear rate viscosity of the test lubricant before and after severe shearing, but Alexander has noted that in terms of engine performance it might be more relevant to compare the high shear rate viscosities of the sheared and unsheared oils [39].

Most comparisons of different test methods for assessing permanent shear stability find that those where the lubricant is subject to elastohydrodyamic (EHD) conditions, such as in rolling bearings and gears, give higher levels of permanent viscosity loss than injector tests [31, 40]. This is to be expected on the basis that shear stress drives polymer breakdown, since the high pressures in EHD contacts result in large increases in lubricant viscosity and thus high shear stresses, even at quite low shear rates. In an ingenious study, Walker et al. extracted small volumes of polymer-containing and polymeric lubricants from a sliding EHD contact and, based on viscosity loss and GPC, found very severe breakdown of the polymers [41].

Many studies have compared the shear stability of different VM types, though Mortier has noted that the ranking varies depending on the test employed [38]. Covitch has studied the influence of polymer molecular architecture on shear stability and found strong dependence on polymer structure, with star polymers giving greater stability than linear ones, with branched structures intermediate [42].

Recently there has been growing interest in the influence of polymer shear stability on fuel economy of engine oils, and van Dam has shown that fuel economy of heavy-duty engine oils correlates with the high temperature viscosity of the oils as measured after extraction from engine tests or after an injector test [43, 44]. This is not unexpected but does suggest that fuel economy prediction models should be based, at least in part, on the properties of degraded rather than fresh oils.

Compared with early work, the main focus of VM work in recent years has been on permanent changes in viscosity resulting from shear, with less consideration of the causative molecular weight reductions produced by high shear, although a few researchers have continued to apply GPC to analyse shear thinned oils [27, 41]. Herbeaux et al. noted that for dilute polymer solutions the specific viscosity, η sp, and thus the polymer solution viscosity η are proportional to the concentration c and weight average molecular weight \( \bar{M}_{\text{w}} \);

$$ \eta_{\text{sp}} = \frac{\eta }{{\eta_{\text{base}} }} - 1 = Kc\bar{M}_{\text{w}} $$
(3)

where η base is the base oil viscosity [45]. They used this, together with a model of how MWt changes with shearing time, to develop and apply a model for how viscosity should vary during shearing tests. Covitch et al. also used a similar, though somewhat more complex approach applicable to more concentrated, semidilute, polymer solutions, to develop a model of viscosity loss of heavy-duty diesel lubricants;

$$ \eta_{\text{sp}} = k^{\prime } c\bar{M}_{\text{w}}^{a} + k^{\prime \prime } c^{2} \bar{M}_{\text{w}}^{a} $$
(4)

where k′, k″ and a are constants, with a having the value 1.1 [46].

Fundamental research on polymer breakdown under shear outside of the VM literature has continued since the 1970s, with particular emphasis on polymer response to different types of flow field. In laminar shear, the fluid is exposed to a combination of rotation and deformation and this combination is relatively benign in terms of the forces experienced by polymer chains in solution. Odell et al. studied polymer breakdown in pure elongation flow and found very rapid polymer breakdown to occur above a critical shear rate that could be related to the relaxation time of the polymer molecules [47,48,49]. GPC showed rupture of molecules at or close to the central bond and a critical shear rate for rupture that was inversely proportional to the square of the MWt, reminiscent of Eq. 1. These researchers interpreted their findings in terms of the stress-augmented thermal activation described by Eq. 2 [48]. Recently Vanapalli et al. [50] have examined polymer breakdown in turbulent flow and developed general scaling rules for polymer breakdown. In non-turbulent conditions, they suggest that the onset of polymer scission depends linearly on the viscosity while in turbulent flow this dependence is much weaker at η 0.25, due to tension-inducing velocity fluctuation in the flow. By analysing previous literature on polymer shear degradation, they concluded that many studies that were presumed to be in laminar flow must actually have involved some turbulence, for example at the inlet and outlet of capillaries, and that it should be very difficult to obtain polymer scission in pure laminar flow.

From the above, it can be seen that the extensive literature on polymer permanent shear thinning of polymer solutions can be divided broadly into two groups, work looking specifically at VM polymer solutions and more fundamental studies of polymer scission under shear. Considering all of the research conducted, it is perhaps surprising that we still have no ability to predict VM polymer degradation and consequent viscosity loss and are thus reliant on bench tests. There are several key problems. One is that almost all studies of VM polymer degradation are carried out in spray nozzles, rolling bearings or ultrasonic systems where permanent shear thinning can be quite easily achieved. However, the shear rate and indeed the shear conditions in most such devices are impossible to quantify accurately so that results from such studies cannot be interpreted at a fundamental level. Also in many tests carried out on these devices, only a fraction of the fluid actually passes through the high shear system from where it is returned to a reservoir. This makes analysis of the rate of polymer breakdown and the effect of this on overall viscosity change very difficult to analyse, although valiant attempts have been made to do so [51,52,53].

To be relevant to polymer degradation in the highly laminar flow conditions likely to be present in thin film plain bearing conditions, polymer degradation should be studied at such conditions, though it is interesting to note that physics-based studies of polymer degradation suggest that little polymer breakdown ought to take place in laminar flow [49]. One possibility is to use capillary flow, but this gives a variation of shear rate across the diameter, and it has also been shown that polymer degradation is dominated by the conditions at the capillary inlet [54]. Another important issue in studies of polymer breakdown using capillaries and orifices is that, unless a series of carefully chosen capillaries of different diameters are used, solutions flowing at high shear rate will spend less time in a capillary than those flowing at low shear rate. This has to be taken into account when comparing polymer degradation rates, which should describe how much degradation occurs per unit time of shear rather per pass through the capillary.

The most promising alternative to a capillary is a narrow gap concentric cylinder or truncated cone geometry. Viscometers based on this geometry have been employed since the 1980s to measure the viscosity of lubricants up to 106 s−1 [55, 56] and, more recently, up to 107 s−1 [57]. In a recent study, it was shown that the application of shear rates above 106 s−1 in a concentric cylinder viscometer results in significant permanent viscosity loss of polymer solutions and that this can be used to compare the shear stability of VMs [58]. From the point of view of fundamental research, a key limitation of this type of viscometer is that the volume of fluid being sheared is very small and quite inaccessible. This makes it problematic to use chemical methods such as GPC to study the sheared sample posttest. An ingenious way around this problem was employed by Porter et al. [19], who used a continuous flow of test fluid through a concentric cylinder gap.

The current paper describes work in which a high shear rate concentric viscometer is employed to study polymer breakdown in solution at high shear rates. Care is taken when comparing polymer breakdown rates to compensate for the different times that fluids are sheared at different shear rates. A series of different base fluids having very similar chemical structure but with different viscosities is used to confirm previous studies and show that polymer degradation rate depends on shear stress and not shear rate. Finally, a method is developed to extract the sheared volume of fluid from the concentric viscometer and analyse it using GPC.

3 Materials

In order to explore the mechanism of permanent shear thinning, well-characterised polymers with low polydispersity are desirable. Polystyrenes were chosen since these are commercially available as chromatography standards at a series of molecular weights and with polydispersity indices below 1.04. Since these polymers do not dissolve in predominantly aliphatic base oils such as mineral oils, phthalate esters were used as solvents. The aromatic structure of these fluids mean that they are good solvents for polystyrene while, because they are widely used as plasticisers, they are commercially available in pure form with a series of alkyl groups and thus viscosities.

Table 1 lists the phthalate ester solvents used as base oils and their viscometric properties, Table 2 lists the polystyrene polymers, and Table 3 shows the solutions studied and their low shear rate viscometric properties.

Table 1 Ester base oils used
Full size table
Table 2 Polystyrene polymers
Full size table
Table 3 Solutions tested
Full size table

4 Test Methods

4.1 Ultrashear Viscometer Method

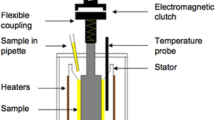
Permanent shear thinning was measured using a method devised by Holtzinger et al. [58] and further developed in the current study. This employs a PCS Instruments Ultra Shear Viscometer (USV) to subject a small lubricant sample to a very high shear rate at controlled temperature.

The USV is based on a concentric cylinder geometry with a very small gap of typically between 1 and 1.5 μm. Normally, viscometers with such geometry are limited to a maximum shear rate of ca 106 s−1 since above this level the temperature rise due to shear heating becomes excessive. In the USV this problem is overcome by using a very short shearing time to ensure any such temperature rise is very small. A motor accelerates a flywheel to high speed and then a clutch system engages to transmit the rotational energy to the inner cylinder (rotor) for just a few revolutions at a set shear rate. Depending on the lubricant viscosity and thus the shear stress applied, a small amount of shear heating can still occur within this time frame, but the USV is able to measure the increase in temperature on the stator and, using heat transfer theory, estimate the temperature rise within the contact. The temperature of the chamber is then reduced slightly using this temperature offset to ensure that in the next engagement the lubricant sample reaches the sought test temperature just when the viscosity is measured.

In the USV, a series of engagements is generally made, namely one to obtain the temperature offset and then three consecutive engagements for measurement. A torque sensor is fitted to the outer concentric cylinder (stator), and the average measurements of the last three engagements are used to determine a viscosity value. Holtzinger et al. [58] defined this process as one cycle but in the current study, in order to more accurately describe the shear history of the test sample, each engagement will be termed one shear cycle, so there will be four shear cycles for every data point measured.

As found previously by Holtzinger, most high MWt polymer-containing test samples show a progressive fall in viscosity in the USV at high shear rates due to permanent shear thinning.

Figure 1 compares the reduction in viscosity against number of shear cycles at two applied shear rates, 3 × 106 and 6 × 106 s−1 for a 2 wt% solution of 100 k g/mol MWt PS in DEHP at 80 °C.

Fig. 1
figure 1

Variation of viscosity with number of shear cycles. 2 wt% 100 k PS in DEHP at 80 °C

Full size image

The reduction in viscosity is linear at first, although it levels out eventually after a high number of shear rate cycles. It is important to note that as well as being a means to study permanent shear thinning, this permanent loss of viscosity must also be considered when using the USV to study temporary shear thinning. Thus the viscosity at 3 and 6 × 106 s−1 prior to any permanent shear thinning can be estimated by extrapolating the straight lines shown in Fig. 1 back to zero cycles. It also means that a series of viscosity measurements of the same test sample should not be made in the USV at different shear rates to derive viscosity versus shear rate dependence since this will accumulate permanent shear thinning. Instead, a separate test on a new sample should be made at each shear rate of interest.

In this study, after each test, the cylinders were dismantled from the USV and cleaned in an ultrasonic bath in toluene and then acetone. A fresh lubricant test sample of a few mm3 was then applied to the clean rotor and stator, which were then reassembled in the USV and a test carried out. This method differs considerably from the conventional flushing cycle recommended by PCS Instruments but was found to improve viscosity measurement accuracy considerably. Furthermore, use of a known and small quantity of sample made it possible to distinguish between the permanently shear thinned sample within the USV gap and the excess oil required outside the contact and thus enabled a chromatographic study of permanent shear thinning as outlined below.

4.2 Chromatography Method

The above USV procedure subjects a polymer solution sample to a well-defined shear rate and shear stress and monitors the resulting permanent viscosity loss. In order to relate this to actual polymer molecule breakdown it is necessary to be able to measure the change in polymer MWt distribution that causes the viscosity loss. Most previous molecular-based studies of polymer degradation have used gel permeation chromatography (GPC), and this is particularly well suited to the polystyrene solutions studied in this work since polystyrene is used as a chromatographic standard to calibrate GPC systems. However, the method is quite difficult to apply in the current study because the volume of oil sample subject to high shear rate is very small. Based on the concentric cylinder length and diameter of 16 and 12 mm, respectively, and the gap of 1.28 μm, the contained volume is only 0.77 mm3. Also there is a considerable additional reservoir of solution that is contained above and below the concentric cylinder geometry itself, which serves to ensure the gap is filled. This fluid is not sheared. In the normal use of the USV the test solution is injected into the apparatus and this reservoir is very large. However, by applying the assembly method outlined above, this volume is much reduced to typically 7 mm3. The ratio of the volume within the concentric cylinders to that outside is also known and was typically 1:10.

In the current study the USV was carefully disassembled after a test and the stator and rotor rinsed in 1 ml of tetrahydrofuran (THF) to dissolve the polymer solution. An Agilent 1260 Infinity GPC was employed to analyse the degraded solution. The instrument was calibrated against narrow polystyrene standards (Mn 1300—446,500 g/mol). 2 × Agilent PLgel Mixed-D columns were used with a guard column. Refractive index was employed for detection and the injection volume of the sample was 100 µL. The THF flow rate was set at 1 mL/min. Temperature was thermostatically controlled to 30 °C by a column oven and Agilent GPC/SEC software (2013 edition) was employed for analysis.

The efficiency of extraction of polymer solution into THF was determined by using different polymer solution volumes in the USV without shear, as shown in Fig. 2 for 2 wt% 200 k PS in DEHP. These chromatograms were obtained by applying a known volume of solution to the rotor and stator, assembling and disassembling the test rig without shearing the test sample, and then carrying out the extraction and GPC analysis outlined above. Extraction efficiency was measured to be 66%. Since it was known (1) that the polymer solution sample consisted of 0.77 mm3 of sheared sample from the concentric cylinders and a variable amount of unsheared sample from the surrounding reservoir and (2) that 66% of this total was eventually analysed, it was possible to explore the impact of shear thinning on the polymer solution MWt distribution.

Fig. 2
figure 2

GPCs of different volumes of unsheared 2 wt% solution of 200 k PS in DEHP extracted from the USV using THF

Full size image

5 Quantification and Interpretation of Permanent Shear Thinning

In most studies of permanent shear thinning the level of permanent viscosity loss of VM solutions is quantified by a non-dimensional value, of which the two most common are the permanent viscosity loss (PVL) and the permanent shear stability index (PSSI). These are defined in terms of the kinematic viscosities at 100 °C of the sheared (KVsheared), unsheared (KVfresh), and base oil (KVbase).

$$ {\text{PVL}} = \frac{{{\text{KV}}_{\text{fresh}} - {\text{KV}}_{\text{sheared}} }}{{{\text{KV}}_{\text{fresh}} }} $$
(5)
$$ {\text{PSSI}} = \frac{{{\text{KV}}_{\text{fresh}} - {\text{KV}}_{\text{sheared}} }}{{{\text{KV}}_{\text{fresh}} - {\text{KV}}_{\text{base}} }} $$
(6)

PVL thus describes the fractional loss of polymer solution viscosity due to shear while PSSI is the fraction of the original thickening by the polymer that is lost due to shear.

It is not possible to evaluate the above two measurements of permanent shear thinning in the USV since it is not possible to extract enough sample to measure its KVsheared. It is, however, possible to measure the viscosity at 106 s−1 within the USV after degradation. Therefore, as was suggested by Holtzinger et al. [58], the two expressions equivalent to PVL and PSSI were calculated in this study:

$$ {\text{PVL}}\left( {10^{6} } \right) = \frac{{\eta_{\text{fresh}} - \eta_{\text{sheared}} }}{{\eta_{\text{fresh}} }} $$
(5)
$$ {\text{PSSI}}\left( {10^{6} } \right) = \frac{{\eta_{\text{fresh}} - \eta_{\text{sheared}} }}{{\eta_{\text{fresh}} - \eta_{\text{base}} }} $$
(6)

where η sheared is the dynamic viscosity measured in the USV at 106 s−1 and the test temperature after shearing, η fresh is the dynamic viscosity value measured in the USV at 106 s−1 and the test temperature before shearing and η base is the base oil dynamic viscosity at the test temperature.

It is important to note that neither PVL nor PSSI is a system property since both will depend on the conditions under which they are measured and on the viscosity of the base oil and the concentration of polymer [59]. PSSI is, however, much less dependent on concentration than PVL since it measures the fraction of polymer thickening lost rather than fraction of blend viscosity lost. PSSI(106) can also be expressed in terms of specific viscosities as defined in Eq. 3 as;

$$ {\text{PSSI}}\left( {10^{6} } \right) = \frac{{\eta_{\text{sp,fresh}} - \eta_{\text{sp,sheared}} }}{{\eta_{\text{sp,fresh}} }} $$
(7)

where the polymer solution viscosities are measured at 106 s−1.

Equation 7 relates the PSSI(106) to the specific viscosity at 106 s−1. Based on this, and assuming that the high-shear-rate-specific viscosity varies linearly with concentration and molecular weight, as indicated by Eq. 3 for low shear rate, and that we can sum the contributions to specific viscosity of the undegraded and degraded polymer, we obtain from Eq. 7;

$$ {\text{PSSI}}\left( {10^{6} } \right) = \frac{{kc_{0} \bar{M}_{\text{w}} - \left( {kc\bar{M}_{\text{w}} + k\left( {c_{0} - c} \right)\bar{M}_{\text{w,sheared}} } \right)}}{{kc_{o} \bar{M}_{\text{w}} }} $$
(8)

or

$$ {\text{PSSI}}\left( {10^{6} } \right) = \frac{{\left( {c_{0} - c} \right)\left( {\bar{M}_{\text{w}} - \bar{M}_{\text{w,sheared}} } \right)}}{{c_{0} \bar{M}_{\text{w}} }} $$
(9)

where c 0 and \( \bar{M}_{\text{w}} \) are the initial concentration and average molecular weight of the sample prior to shear, c is the concentration of the undegraded polymer after shear and \( \bar{M}_{\text{w,sheared}} \) is the average molecular weight of the sheared sample. It should be noted that polymer concentrations are based on weight, not number of molecules, so the increase in concentration of lower molecular weight polymer due to degradation will be identical to the reduction in concentration of the higher molecular weight polymer.

This suggests that the PSSI(106) should vary linearly with the reduction in concentration of the undegraded polymer and thus be proportional, at least in the early stages of degradation, to the rate of polymer scission.

6 Permanent Shear Thinning Rate: Time Effect

As discussed in the background in this paper, when comparing shear thinning at different conditions, it is important to take account of any differences in the times that shear is applied to the fluid during a test when comparing rates of shear thinning. In the USV single cycle, the fluid shear force is monitored over 8 revolutions of the rotor. Prior to this, there is a short period of about 1.5 revolutions after the fluid has reached its set shear rate and torque has stabilized. Upon clutch disengagement, deceleration is very rapid. Since the rotor speed increases with increasing shear rate, so the time that the fluid is subjected to its set shear rate decreases with shear rate. Table 4 lists the estimated times for which the fluid is within 10% of its stabilized torque in a single cycle at different shear rates. To compare shear thinning rates at different shear rates, the measured loss of viscosity must be divided by this corresponding shear time. It should be noted that these times per cycle are calculated for the 1.28 μm gap used and will vary inversely with the gap size.

Table 4 Variation of fluid shear time with applied shear rate
Full size table

7 Results

7.1 Effect of Polymer Concentration and Molecular Weight on Viscosity at 106 s−1

Since PVL(106) and PSSI(106) are based on measurements at 106 s−1, it is of interest to look at the way that polymer viscosity measured at this shear rate varies with polymer concentration and molecular weight prior to any permanent shear thinning. Three different MWt PS polymers were studied in solution in DEHP at 80 °C.

Figure 3 shows the dependence of both viscosity and specific viscosity on concentration at 106 s−1. The specific viscosity is as defined in Eq. 3 except that the polymer solution viscosity is measured at 106 s−1. All solutions except for 4 and 6 wt% of 100 k PS in DEHP are in the dilute regime; for this polymer the transition from dilute to semidilute is around 3.5 wt% for 100 k PS in DEHP at low shear rate. As expected, both the viscosity and specific viscosity at 106 s−1 increase with polymer concentration and MWt. The dependence on concentration is practically linear up to 3 wt%, but greater than linear above this concentration. This type of dependence is similar to that of low shear rate viscosity.

Fig. 3
figure 3

Dependence of viscosity and specific viscosity at 106 s−1 on polymer concentration and MWt for solutions in DEHP at 80 °C

Full size image

The dependence on MWt is complex since both thickening and temporary shear thinning depend strongly on molecular weight and compete against one another. In Fig. 3 it can be seen that at 2 wt% concentration, high shear rate viscosity is only weakly dependent on MWt over the range studied.

7.2 Effect of Number of Shear Cycles on Permanent Shear Thinning Rate

Permanent shear thinning tests were carried out on blends of 2 wt% 100 k MWt polystyrene in DEHP at 80 °C using different numbers of shear cycles. For each data point, a fresh oil sample was used and the test consisted of 4 cycles at 1 × 106 s−1 to determine η fresh, followed by a variable number of cycles at the test shear rate, and finally four final cycles at 1 × 106 s−1 to determine η sheared. Figure 4 shows the variation of PSSI(106) with number of shear cycles. Separate tests were run at shear rates of 1(not shown), 3, 6 and 10 × 106 s−1. The number of cycles shown is only the number at the high shear rate of interest, excluding the first and last four-cycle sets at 106 s−1. Permanent shear thinning increases with the number of cycles in an approximately linear fashion, although it starts to level out after 20 cycles at the highest shear rate.

Fig. 4
figure 4

PSSI(106) plotted against number of shear cycles at three applied shear rates for 2 wt% 100 k PS in DEHP at 80 °C

Full size image

Figure 5 shows the same data but now plotted as rate of PSSI(106) change versus number of cycles. This emphasizes the constancy of the rate of shear thinning with number of cycles except at the highest shear rate. It also shows how strongly the rate of shear thinning depends on shear rate when the fact that the test fluid is sheared for shorter times at higher shear rates is taken into account.

Fig. 5
figure 5

PSSI(106) rate plotted against number of shear cycles at three applied shear rates for 2 wt% 100 k PS in DEHP at 80 °C

Full size image

7.3 Influence of Shear Stress and Shear Rate on Permanent Shear Thinning

As described earlier in this paper, one issue of interest is whether permanent shear thinning is controlled by the shear rate or the shear stress experienced by the polymer solution. The most compelling evidence in support of shear stress control is given by Yu et al. [12]. To explore whether permanent shear thinning is, indeed, controlled by shear stress or shear rate we need to measure the rate of permanent shear thinning while varying shear rate independently of shear stress. In the USV the shear rate is directly controlled as u s/h where u s is the surface speed of the rotor and h the gap. The shear stress, τ, is obtained from the torque transmitted from rotor to stator but is expressed as the dynamic viscosity, η of the test sample calculated from the ratio of shear stress and the shear rate. The shear stress can thus be back-calculated from \( \tau = \eta \dot{\gamma } \).

This equation indicates that the shear stress can be varied independently from the shear rate by varying the viscosity of the solution used. In principle this can be achieved by simply varying the temperature or the polymer concentration, but both of these might themselves lead to a change in the rate of polymer breakdown. Therefore, in this work, the viscosities of a series of polymer test solutions all having the same polymer at the same concentration were varied by using a series of different phthalate ester solvents as listed in Table 1. These esters are considered sufficiently alike that the solvency and thus shear thinning properties of the PS should be similar in all of them.

Polystyrene of MWt 200 k was dissolved at the same concentration by weight in the four phthalate ester base fluids listed in Table 1. The samples were then subjected to 40 cycles at a test shear rate, followed by 4 cycles at 106 s−1. Four different shear rates were used, 1, 3, 6 and 10 × 106 s−1, to give 16 different combinations of solution viscosity and shear rate. Figure 6 compares the reduction in viscosity over 40 cycles for the polymer solutions in the four base fluids at 3 × 106 s−1. As expected, the rate of permanent shear thinning increases with the viscosity of the blend.

Fig. 6
figure 6

Variation of viscosity with number of shear cycles for 2 wt% PS 200 k MWt at 3 × 106 s−1 and 80 °C

Full size image

PSSI(106) values were then calculated using η sheared from viscosity measurements made at 106 s−1 at the end of each shear thinning test and η fresh measured at 106 s−1 on fresh samples in separate tests. Finally PSSI(106) rates of change were estimated by dividing PSSI(106) values by the appropriate shear time for 40 cycles using the times per cycle listed in Table 4.

Figures 7 and 8 show the resulting PSSI(106) rates plotted against shear rate and shear stress, respectively. Error bars are shown corresponding to an estimated accuracy of the shear thinning rate of ±15%.

Fig. 7
figure 7

Dependence of PSSI(106) rate of change on shear rate for 2 wt% 200 k PS in DEHP at 80 °C. Error bars are ±15%

Full size image
Fig. 8
figure 8

Dependence of PSSI(106) rate of change on shear stress for 2 wt% 200 k PS in DEHP at 80 °C. Error bars are ±15%

Full size image

It can be seen that the permanent shear thinning rates in different viscosity base fluids lie on separate lines when plotted against shear rate but approximately coincide when plotted against shear stress. This suggests that permanent shear thinning is more likely to be controlled by shear stress than shear rate. The following results in this paper are thus shown as a function of shear stress rather than shear rate.

Figure 9 plots the permanent shear thinning data for 2% PS in DEHP already shown in Fig. 5 but now as PSSI(106)/time of shear versus shear stress, where time of shear is the number of cycles multiplied by the shear time per cycle from Table 4. It can be seen that essentially all results lie on the same master curve indicating that shear thinning expressed as PSSI(106) varies linearly with shear time. This is further confirmation that polymer degradation is driven by shear stress. Figure 9 also indicates that the dependence of shear thinning rate on shear stress is close to exponential, in agreement with the stress-augmented thermal activation model for polymer breakdown shown in Eq. 2.

Fig. 9
figure 9

Dependence of PSSI(106) rate of change on shear stress after different shear times for 2 wt% 100 k PS in DEHP at 80 °C

Full size image

7.4 Effect of Polymer Molecular Weight on Permanent Shear Thinning

The permanent shear thinning behaviour of 2 wt% solutions of three different MWt PS solutions in DEHP was measured at four applied shear rates, 1, 3, 6 and 10 × 106 s−1. For each data point, a fresh oil sample was used and PSSI(106) rates were calculated after the same 40 cycle protocol outlined in the previous section. Figure 10 shows PSSI(106) rate as a function of shear stress. As expected, higher molecular weight polymers degrade faster than lower molecular weight ones at a given shear stress. It is interesting to consider what might happen if, hypothetically, all 200 k MWt molecules in a 2 wt% solution were to rupture in the centre, as might be the case in an extreme degradation process. This would result in a 2 wt% 100 k MWt solution. According to the temporary shear thinning measurements shown in Fig. 3, this would result in very little change in high shear rate viscosity. The fact that PSSI(106) rate does vary with molecular weight, suggests that fragmentation to smaller molecules occurs.

Fig. 10
figure 10

Dependence of PSSI(106) rate of change on shear stress for three different MWt 2 wt% PS solutions in DEHP at 80 °C

Full size image

At the test conditions applied, it is interesting to notice that the 100 k MWt PS solution does not degrade at the lowest applied shear rate. This makes it an ideal test specimen for the modified PSSI equation since there will be no possible permanent shear thinning during the 1 × 106 s−1 shear rate cycles applied at the start and end of a shear thinning test in order to calculate PSSI(106). Thus we will focus on this polymer in the concentration study below.

7.5 Effect of Polymer Concentration on Permanent Shear Thinning

The permanent shear thinning behaviour of four different concentration solution of 100 k MWt PS in DEHP were studied after 20 shear cycles. Tests were carried out at four applied shear rates, 1, 3, 6 and 10 × 106 s−1. For each data point, a fresh oil sample was used.

The results are shown in Fig. 11 and indicate that degradation rate as described by PSSI(106) rate increases with shear stress and is greatest at low concentration. This reflects the way that PSSI is defined as the fractional loss of thickening power and is most easily understood by reference to Eq. 7, where the denominator is η sp,fresh. From Eq. 3 this is proportional to the polymer concentration, so the lower the concentration, the lower the denominator in PSSI(106).

Fig. 11
figure 11

Dependence of PSSI(106) rate of change on shear stress for four different concentrations of 100 k PS solution in DEHP at 80 °C after 20 cycles

Full size image

7.6 Chromatography Results

Figure 12 shows chromatograms taken after three tests in which 2 wt% 200 k MWt PS in DEHP was sheared at 3 × 106 s−1 for 40 cycles at 80 °C. The resulting PSSI(106) was 0.38 ± 0.03. In one test a minimum sample volume of 2 mm3 was used in the USV (at this condition there was some risk of starvation) while in the other two tests total volumes of 5 and 10 mm3, respectively, were used. The peak at 200 k g/mol represents the undegraded PS. Most of this comes from fluid outside the sheared contact since the sheared fluid volume is only 0.77 mm3. The extraction system is designed to extract only about 4 mm3 of fluid in and around the sheared region on the rotor and stator surfaces so the signal strengths of this peak are similar when 5 and 10 mm3 of fluid are used in the USV.

Fig. 12
figure 12

Post-shear GPCs from USV tests using three different starting volumes of PS solution. 2 wt% 200 k PS in DEHP, 40 shear cycles at 3 × 106 s−1

Full size image

Figure 13 shows the same data with an expanded y-axis scale to show more clearly the low molecular weight component formed during shear. This is centred in the 10–20 k range, indicating that PS has fragmented rather than undergoing only mid-chain scission. Figure 14 compares sheared and fresh PS solution and shows that the low MWt peak is not present in the fresh solution and is thus a product of shearing.

Fig. 13
figure 13

Magnified scale from GPCs in Fig. 11 showing degraded PS peak

Full size image
Fig. 14
figure 14

Comparison of GPCs of fresh and sheared 2 wt% 200 k PS solutions. The sheared sample GPC is from Fig. 11

Full size image

By careful calibration, it was possible to obtain an estimate of the proportion of degraded to undegraded PS. This required estimation of the proportion of the peak centred at 200 k g/mol that originated from the sheared volume compared to the total. To do this, fixed volumes of PS solution were supplied to the USV which was then dismantled and the solutions extracted and analysed without any shear. This enabled the efficiency of THF extraction and analysis to be determined so that the volume of oil extracted could be estimated from the peak height, and the volume of sheared oil was then a known proportion of this. The ratio of the integrated area of the low molecular weight peak to the integrated area of the scaled 200 k peak gave an estimate of the proportion of degradation.

Figure 15 shows the resulting estimates of the percentage of 200 k PS degraded in six repeat tests of 40 cycles at 3 × 106 s−1. The results show an average loss of 30% of the 200 k peak of lubricant inside the contact after 40 cycles. This suggests that a PSSI(106) of 0.38 corresponds to about 30% polymer molecule degradation. This is in quite good accord with Eq. 9.

Fig. 15
figure 15

Estimated percentage of 2 wt% 200 k PS degraded after 40 cycles at 3 × 106 s−1 and 80 °C

Full size image

Figure 16 shows unsheared and sheared GPCs using the much higher concentration of 10 wt% 200 k PS in DEHP. In this case there is an evident new peak formed due to shear, centred around 100 k g/mol, suggesting that in these conditions mid-chain scission occurs. The differences in the size of the peak at 200 k simply reflect differences in total extract volume but the differences in the 100 k peak arise solely from the sheared region of the viscometer. As expected, the magnitude of this latter peak increases with both shear rate and number of shear cycles.

Fig. 16
figure 16

Comparison of unsheared and sheared 10 wt% 200 k PS in DEHP at different shear rates and for different amounts of shear cycles at 80 °C. Black curve is the unsheared case

Full size image

At first sight, it is counterintuitive that a concentrated solution gives primarily mid-chain scission while a low concentration gives fragmentation since one might expect a more concentrated solution with more direct polymer–polymer entanglement points to produce multiple rupture sites. The higher concentration solution will have higher viscosity and thus higher shear stress at a given strain rate. It is possible that at high shear stress a stress-augmented thermal activation process dominates to produce rapid mid-chain scission while at lower shear stress polymer degradation is much slower, and has a larger thermal activation component. To test this, an extended study with different shear stresses and at various temperatures would be necessary.

8 General Discussion

This study has shown the utility of the USV to measure the permanent shear thinning of polymer solutions at high shear rates and thus high shear stresses. In practice, since it can measure the viscosity of liquids up to 20 cP at 107 s−1, the USV is able to apply shear stresses up to 0.2 MPa at this strain rate. This combination of shear rate and shear stress is much higher than in most viscometers and is only possible because the short duration of shear precludes significant shear heating. At such high shear stresses, considerable permanent shear thinning of the polystyrene polymer solutions studied occurs, and this can be monitored by subjecting the solution sample to repeated cycles of shear.

One limitation of this approach is that it is only possible to monitor the change in viscosity measured at high shear rate since insufficient shear-degraded fluid is available for low shear rate viscosity measurement. This can be viewed as a disadvantage or an advantage. It means that it is not straightforward to relate the results directly to polymer solution viscosity theory, especially in terms of the impact of molecular weight, since the measured viscosity will incorporate a temporary shear thinning effect of any polymer present. However, it has been suggested that the impact of polymer shear degradation measured at high shear rate is more relevant to engine friction than that measured at low shear rate [44].

When interpreting permanent shear thinning in the USV, it is very important to take account of the fact that the polymer solution is subjected to different shearing times at different shear rates, so the shear thinning rate must be determined by dividing the amount of shear thinning by this time of shear. This issue is also present and may have been neglected, in some previous shear thinning studies using capillary and orifice viscometers where the time of passage of the lubricant through a capillary depends on the shear rate.

It has been found that the amount of shear thinning is usefully expressed in terms of the permanent shear stability index, PSSI, since, as shown in Eq. 7, this can be related directly to the specific viscosity change and thus, from Eq. 9, to the rate of change of concentration of polymer. Equation 9 applies formally only if the polymer solution viscosities are measured at low shear rate, in which case the PSSI should be proportional to the initial polymer concentration change and to the change in average MWt. When PSSI(106) is measured at 106 s−1 in the USV its dependence on the change in MWt should be much lower since, as shown in non-shear thinning measurements, specific viscosity increases only slowly with MWt.

The study has confirmed that the rate of shear thinning depends on shear stress rather than strain rate and increases approximately exponentially with shear stress in accord with the stress-augmented thermal activation model. This dependence on shear stress has practical importance when we consider the fact that there is a trend towards lower and lower lubricant viscosities. In pure sliding hydrodynamic conditions the lubricant film thickness depends on viscosity and sliding speed according to

$$ h \propto \left( {\eta u_{\text{s}} } \right)^{a} $$
(10)

where a is typically ca. 0.5. Assuming this value for a, the shear rate thus depends on η and u s according to;

$$ \dot{\gamma } = \frac{{u_{\text{s}} }}{h} \propto \left( {\frac{{u_{\text{s}} }}{\eta }} \right)^{0.5} $$
(11)

By contrast, shear stress dependence on η and u s is;

$$ \tau = \eta \dot{\gamma } = \eta \frac{{u_{\text{s}} }}{h} \propto \left( {u_{\text{s}} \eta } \right)^{0.5} $$
(12)

These relationships imply that reductions in lubricant viscosity will tend to increase shear rates but reduce shear stresses in hydrodynamic contacts. Therefore, if permanent shear thinning is shear stress controlled, it will become less of a problem as oil viscosities are reduced, but if it is shear rate controlled it will become worse. However, this does not take account of another trend in lubricated components, which is towards higher power densities and thus larger contact pressures. This will tend to increase viscosity within contacts due to a piezoviscous response, which will increase shear stress.

It is of interest to compare the observation of permanent shear thinning in this study with the long-standing rule of thumb described in Eq. 1. If we assume a representative high shear rate viscosity of 10 cP, then the product of shear rate with viscosity and MWt2 varies with shear rate and MWt as shown in Table 5. Based on the threshold of 1014 in Eq. 1, we would thus expect to see significant permanent shear thinning of the 50 k polymer at 106 s−1. In practice, this is not the case and a more appropriate threshold for the onset of permanent shear thinning for the PS studied would appear to be 1015.

Table 5 Range of product (viscosity (Poise) × shear rate × MWt2) in this study
Full size table

9 Conclusions

This study has shown that the ultrashear viscometer (USV) is a powerful tool for studying the permanent shear thinning of polymer solutions having viscosities representative of engine oils at very high shear rates and thus high shear stresses. However, for quantitative studies it is essential to take into account the time of shear, which varies with both the number of cycles and the shear rate. By using polymers dissolved in different viscosity solvents, it has been shown that permanent shear thinning depends on shear stress and not directly on shear rate. This implies that the use of low viscosity lubricants should help ameliorate the problem of permanent shear thinning. It has also been found that the dependence of shear thinning on shear stress is in accord with the stress-augmented thermal activation model of polymer degradation.

The permanent shear stability index is found to be a good way to describe permanent shear thinning because it can be related theoretically to the change in polymer concentration and, at least at low shear rate, to the change of polymer MWt.

One potential limitation of the USV is that the very small volume of sheared fluid and its location within a concentric cylinder geometry might preclude the possibility of carrying out GPC to study the impact of shear on molecular weight distribution. However, it has been shown that careful calibration enables analysis of the sheared polymer solution by GPC. This indicates striking differences in the ways that the polystyrene polymer degrades at different polymer concentrations.

A key feature of the USV is that, unlike other methods currently used to measure permanent shear thinning behaviour of engine oils, it subjects the test fluid to well-defined, controllable high shear conditions. Coupled with the use of GPC this makes it possible for the first time to relate quantitatively the permanent shear thinning of engine oils to shear conditions and to polymer degradation response.