Comparisons of Slip-Corrected Reynolds Lubrication Equations for the Air Bearing Film in the Head-Disk Interface of Hard Disk Drives

Abstract

Slip-corrected Reynolds equations have not been widely used in the air bearing simulations for the head-disk interface in hard disk drives since Fukui and Kaneko [Trans ASME J Tribol 110:253–262, 1988] published a more accurate generalized lubrication equation (FK model) based on the linearized Boltzmann equation for molecular gas lubrication. However, new slip models and slip-corrected Reynolds equations continue to be proposed with certain improvements or with the more physical basis of kinetic theory. Here, we reanalyze those slip models and lubrication equations developed after the FK model was published. It is found that all of the slip-corrected Reynolds equations are of limited use in the air bearing simulations, and that these new slip-corrected Reynolds equations cannot replace the FK model for calculating an accurate pressure distribution of molecular gas lubrication.

1 Introduction

Slip-corrected Reynolds lubrication equations are important in the modeling of the low subsonic air bearing film in the head-disk interface of hard disk drives. The classical compressible Reynolds lubrication equation was derived from the Navier–Stokes equation with the continuum no-slip boundary condition. It is not accurate when the gas rarefaction comes into effect, as happens when the slider to disk spacing is on the order of the mean free path of the ambient gas molecules. In the past as the slider-disk gap was reduced from microns to nanometers, the velocity slip was taken into consideration. However, slip-corrected Reynolds equations have not been widely used in the air bearing simulations for hard disk drives since Fukui and Kaneko [1] derived a more accurate generalized lubrication equation (FK model) based on the linearized Boltzmann equation with the Bhatnager–Gross–Krook (BGK) model [2]. The slip-corrected Reynolds equations may not be valid for ultra-thin air bearing films with local transition flows or free molecular flows, due to limitations of the velocity slip models. On the other hand, the FK lubrication equation, which has a similar form as that of slip-corrected Reynolds lubrication equations, is valid for arbitrary Knudsen numbers.

A slip-corrected Reynolds lubrication equation is based on a slip model of the velocity boundary condition. The first-order slip model, which was originally developed by Maxwell [3], was incorporated into the Reynolds equation by Burgdorfer [4]. Hsia and Domoto [5] derived a second-order slip model using a Taylor expansion of the bulk mean velocity and obtained a new Reynolds equation. Mitsuya [6] developed a kinetic-theory based so-called “1.5-order” slip model and modified the Reynolds equation accordingly. Recently, Wu and Bogy derived a pressure gradient model [7] and new first- and second-order slip models [8] from a more physical point of view. Shen and Chen [9] analyzed the linearized Boltzmann equation with the BGK model for Poiseuille flow and derived a “first-order” slip model. Peng et al. [10] modified the gas molecule’s mean free path due to the existence of boundaries of the air bearing film and applied this modification to different slip models and the corresponding Reynolds equations. Bahukudumbi and Beskok [11] obtained a Reynolds equation valid in a wide range of Knudsen numbers, using a modified slip boundary condition for steady plane Couette flows [12] and a generalized higher-order slip model for pressure-driven flows [13].

All of these efforts on slip-corrected Reynolds equations uncover certain physical aspects of rarefaction effects on an air bearing; however, they do not show any important advantages over the generalized Reynolds equation derived by Fukui and Kaneko [1], except for Wu’s work [7], Shen and Chen’s “first-order” model [9], and Peng’s modification of the mean free path [10]. Wu showed that, unlike the FK model, the 1.5- and second-order slip-corrected Reynolds equations do not have the unbounded air pressure singularities when the air bearing is at or near contact. The physics mechanism emphasized in Shen and Chen’s “first-order” slip model makes the model in close agreement with the FK model, but no complicated solving process of the linearized Boltzmann equation is needed in their model. Peng et al. [10] applied the gas molecule’s modified mean free path to the slip model and Reynolds lubrication equations and changed the Poiseuille flow rate coefficient in different gas lubrication equations.

The question arises as to whether or not these improvements should be incorporated into the numerical simulation of the air bearing film in a head-disk interface. Here we reanalyze these slip models and the corresponding slip-corrected Reynolds equations. It is found that the improvements of these slip models and the corresponding slip-corrected Reynolds equations are of limited use in the air bearing simulation of molecular gas lubrication. The problem of a contact pressure singularity inherent in the FK model needs to be further analyzed.

2 Slip Models and Slip-Corrected Reynolds Equations

Slip models are the bases of slip-corrected compressible Reynolds equations. A compressible Reynolds equation is derived from the Navier–Stokes equations with the conservation of the mass flow rates, the equation of state of the compressible flow and the velocity boundary conditions. In hard disk drives, the disk’s rotation velocity is low subsonic. Usually, it is assumed that the flow is isothermal, the pressure field is uniform in the film thickness direction, the inertial effects are negligible, and the viscosity change with position and velocity is also negligible. The equation of state of the compressible flow in hard drives is the ideal gas law. The slip model prescribes the velocity boundary condition due to rarefaction, which usually depends on the velocity profile near the wall, the Knudsen number, the surface accommodation coefficient, the flow velocity gradient or pressure gradient, or shear stress at the wall.

In general, the obtained slip-corrected Reynolds equations have the form,

$$ \nabla \cdot [(\bar{Q}_{{\text{P}}} ph^{3} \nabla p) - (6U\mu ph)] = 12\mu\; {\frac{{\partial (ph)}}{{\partial t}}}, $$

(1)

where $\bar{Q}_{\text{P}}$ is the relative Poiseuille flow rate coefficient. The deviation of its value from 1 represents the effect of the velocity slip on the gas flow. Its’ expression in terms of the (inverse) Knudsen number depends on the slip model used in the derivation.

Usually, a compressible slip-corrected Reynolds equation does not contain the relative Couette flow rate coefficient, provided that the surface accommodation coefficients on the two boundaries are close to each other. The surface accommodation coefficient is defined for the tangential momentum exchange of gas molecules with surfaces, and it determines the velocity slip property of the boundary for slip flows. Due to the skew symmetry of Couette flow with respect to its center plane, the Couette flow rate does not depend on the velocity slip at the boundaries, provided that the slip conditions at the upper and lower boundaries are the same. On the contrary, the symmetry of Poiseuille flow with respect to the center plane results in a strong dependence of the Poiseuille flow rate on the slip conditions at the boundaries.

2.1 First-Order [4] and Classical Second-Order [5] Models

Usually, the temperatures of the slider and the disk surfaces are close to the ambient temperature. So the air bearing film can be assumed to be isothermal, which has been validated using the linearized Boltzmann equation with the BGK model [1], and the thermal creep effect can be neglected in the velocity slip at the boundaries. Hence, the first-order slip model, which was originally proposed by Maxwell in 1879 and contains the velocity jump and thermal creep, can be reduced to [3],

$$ u_{\text{slip}} = {\frac{2 - \alpha }{\alpha }}\;\lambda\;{\frac{{{\text{d}}u}}{{{\text{d}}n}}}. $$

(2)

Burgdorfer [4] used this velocity slip model based on Schaaf and Sherman’s work on slip flow [14] and derived a first-order slip-corrected Reynolds equation. A second-order slip model,

$$ u_{\text{slip}} = {\frac{2 - \alpha }{\alpha }}\left( {\lambda {\frac{{{\text{d}}u}}{{{\text{d}}n}}} - {\frac{{\lambda^{2} }}{2}}{\frac{{{\text{d}}^{2} u}}{{{\text{d}}n^{2} }}}} \right), $$

(3)

was derived by Hsia and Domoto [5] and a new slip-corrected Reynolds equation was obtained. Hsia and Domoto also compared this Reynolds equation to their experimental results. This slip model has more of a mathematical basis than a physical basis. These first- and second-order models were developed earlier than the FK model. Different types of slip models continue being proposed to search for a better slip-corrected Reynolds equation.

2.2 1.5-Order Model [6]

Equating the kinetic-theory based momentum transfer rate on a stationary wall and the macroscopic shear stress $\tau = \mu {\frac{\partial u}{\partial z}},$ Mitsuya [6] derived a “1.5-order” slip model,

$$ u_{\text{slip}} = {\frac{2 - \alpha }{\alpha }}\;\lambda\;{\frac{{{\text{d}}u}}{{{\text{d}}n}}} - {\frac{1}{2}}\left( {{\frac{2\lambda }{3}}} \right)^{2} {\frac{{{\text{d}}^{2} u}}{{{\text{d}}n^{2} }}}. $$

(4)

Although it is referred to as a 1.5-order slip model, it is actually a second-order type model, since the slip velocity contains the second-order effect of the mean free path (or Kn in a nondimensional sense). The methodology of equating two shear stresses on a wall is also used in the derivation of Wu’s pressure gradient slip model [7] and new first- and second-order slip models [8] as well as Shen and Chen’s slip model [9].

2.3 Wu’s Pressure Gradient Model [7] and New First- and Second-Order Models [8]

Equating the macroscopic shear stress at the wall and the shear stress obtained from kinetic theory, Wu and Bogy proposed a pressure gradient model [7] and new first- and second-order slip models [8]. In the first model, the macroscopic shear stress is obtained from the balance of forces on a control volume with its height equal to the mean free path, which is shown in Fig. 1(a), and it is expressed in the form,

$$ \tau |_{z = 0} = \mu\;{\frac{\partial u}{\partial z}}|_{z = 0} - \lambda\;{\frac{\partial P}{\partial x}}|_{z = 0} , $$

(5)

which is different from the conventional formula $\tau = \mu {\frac{\partial u}{\partial z}}$ of fluid mechanics for slip and continuum flows.

Fig. 1

Control volume with different heights used to derive the force balance equation. a Control volume used by Wu and Bogy [7]. b Control volume used by Shen and Chen [9]

The kinetic-theory based shear stress is the momentum transfer rate from the gas molecules to the solid wall [3], which is expressed as

$$ \tau = {\frac{{\rho \bar{v}\alpha u_{\text{slip}} }}{2(2 - \alpha )}}. $$

(6)

The slip velocity, obtained by equating these two expressions, is then,

$$ u_{\text{slip}} = {\frac{2 - \alpha }{\alpha }}\left( {\lambda {\frac{\partial u}{\partial z}} - {\frac{2\lambda }{{\rho \bar{c}}}} {\frac{\partial P}{\partial x}}} \right). $$

(7)

The existence of the pressure gradient in the model is consistent with the fact that it is essentially a second-order slip-type model. Using one of the reduced Navier–Stokes equations of Wu [7],

$$ 0 = -{\frac{\partial p}{\partial x}} + \mu\;{\frac{{\partial^{2} u}}{{\partial y^{2} }}}, $$

(8)

and the viscosity of the hard sphere model $\mu = mN\bar{\nu }\lambda /2$ [3], the slip model in Eq. 7 changes to a second-order form,

$$ u_{\text{slip}} = {\frac{2 - \alpha }{\alpha }}\left( {\lambda {\frac{\partial u}{\partial z}} - \lambda^{2} {\frac{{\partial^{2} u}}{{\partial z^{2} }}}} \right). $$

(9)

In the derivation of the new first- and second-order slip models [8], the conventional formula $\tau = \mu {\frac{\partial u}{\partial z}}$ is used for the macroscopic shear stress at the boundary instead of Eq. 5. The kinetic analysis of the momentum transfer rate, which still uses integration based on the continuum media assumption, obtains an expression of viscosity,

$$ \mu = {\frac{1}{3}} mN\bar{\nu }\lambda . $$

(10)

This equation is slightly different from the conventionally used expression of viscosity for the hard elastic sphere gas molecule model [15],

$$ \mu \approx \sqrt {{\frac{2RT}{\pi }}} \rho \lambda = {\frac{1}{2}}mN\bar{\nu }\lambda , $$

(11)

which is also used in the derivation of the pressure gradient model [7]. With Eq. 11 for the viscosity, new first- and second-order slip models are produced.

2.4 Shen and Chen’s Model [13]

Shen and Chen [9] did not solve the Boltzmann equation for the air bearing film, although the derivation of their slip model started from the linearized Boltzmann equation. With the linearized Boltzmann equation and a restriction of the flow to Poiseuille type with u = u(y) and P = P(x), shown in Fig. 1(b), Shen and Chen [9] obtained the shear stress in the flow in the form of,

$$ \tau = n\tau kT{\frac{{{\text{d}}u}}{{{\text{d}}y}}} = \mu {\frac{{{\text{d}}u}}{{{\text{d}}y}}}, $$

(12)

and the shear stress at the wall in the form of,

$$ \tau |_{y = 0} = \alpha \left[ {\sqrt {{\frac{kT}{2\pi m}}} u|_{y = 0} mn + {\frac{1}{2}} n\iota kT{\frac{{{\text{d}}u}}{{{\text{d}}y}}}|_{y = 0} } \right], $$

(13)

For the hard sphere ideal gas molecule model, we have $P = \rho RT$ and $\mu = n\tau kT$. Hence the above Eq. 13 can be rewritten as,

$$ \tau |_{y = 0} = \alpha \left[ {{\frac{\mu }{2\lambda }}u|_{y = 0} mn + {\frac{\mu }{2}} {\frac{{{\text{d}}u}}{{{\text{d}}y}}}|_{y = 0} } \right]. $$

(14)

Instead of equating the internal shear stress at the flow boundary, shown by Eq. 12 evaluated at the wall (y = 0), and the shear stress at the wall, i.e., Eq. 13, and then producing the classical first-order slip model, Shen and Chen [9] adopted the balance equation of forces on a control volume at the wall. The control volume has a height equal to the so-called effective mean free path. The force balance equation produces an expression for the slip velocity,

$$ u_{\text{slip}} = u|_{y = 0} = {\frac{2 - \alpha }{\alpha }}\iota \left( {{\frac{\pi kT}{2m}}} \right)^{2} {\frac{{{\text{d}}u}}{{{\text{d}}y}}}|_{y = 0} - {\frac{{\lambda_{m} }}{\alpha }}\sqrt {{\frac{2\pi m}{kT}}} {\frac{1}{mn}}\,{\frac{{{\text{d}}p}}{{{\text{d}}x}}}. $$

(15)

Using the hard sphere gas molecule model, this can be changed to

$$ u_{\text{slip}} = u|_{y = 0} = {\frac{2 - \alpha }{\alpha }}\left( {\lambda_{m} {\frac{{{\text{d}}u}}{{{\text{d}}y}}}|_{y = 0} - {\frac{2}{2 - \alpha }} {\frac{{\lambda_{m}^{2} }}{\mu}}\,{\frac{{{\text{d}}p}}{{{\text{d}}x}}}} \right). $$

(16)

As in the derivation of the pressure gradient model [7], the force balance equation does not produce the final slip velocity expression in Eq. 16 until the approximation ${\frac{{{\text{d}}u}}{{{\text{d}}y}}}|_{{y = \lambda_{m} {\text{ (or }}\lambda )}} \approx {\frac{{{\text{d}}u}}{{{\text{d}}y}}}|_{y = 0}$ is used, which is not based on any kinetic theories. It is seen that this approximation is not valid for a transition flow, which has 0.1 < Kn < 10. For a transition flow, the mean free path is comparable to the thickness of the gas film, so it cannot be approximated as zero.

It is interesting to note that this slip model is very similar to Wu’s pressure gradient model [7], except for the mean free path and the factor 2/(2 − α) in the second term. With Eq. 15 and the conservation of linear momentum for the Poiseuille flow, the slip velocity can be finally expressed as,

$$ u_{\text{slip}} = u|_{y = 0} = {\frac{2 - \alpha }{\alpha }}\left( {\lambda_{m} {\frac{{{\text{d}}u}}{{{\text{d}}y}}}|_{y = 0} - {\frac{2}{2 - \alpha }}\lambda_{m}^{2} {\frac{{{\text{d}}^{2} u}}{{{\text{d}}y^{2} }}}} \right). $$

(17)

Essentially, this is still a second-order slip-type model, since its nondimensional expression contains the square of the Knudsen number.

2.5 Bahukudumbi and Beskok’s Model [15]

Using a modified slip boundary condition for steady plane Couette flow [12],

$$ u_{\text{slip}} = {\frac{2 - \alpha }{\alpha }}(1.2977 + 0.71851\tan^{ - 1} ( - 1.17488{\text{Kn}}^{0.58642} ))\lambda {\frac{{{\text{d}}u}}{{{\text{d}}y}}}, $$

(18)

and a generalized high-order slip boundary condition for the pressure-driven flow [13],

$$ u_{\text{slip}} = {\frac{2 - \alpha }{\alpha }}\left( {{\frac{{K_{n} }}{{1 + {\text{Kn}}}}}} \right)\lambda {\frac{{{\text{d}}u}}{{{\text{d}}y}}}. $$

(19)

Bahukudumbi and Beskok [11] derived a phenomenological Reynolds equation valid for a wide range of Knudsen numbers. An interesting point is that Eq. 19 is only valid for the nondimensional velocity profile of Poiseuille flow. The Poiseuille flow rate coefficient based on Eq. 19 differs greatly from the DSMC results [13]. With a modification of dynamic viscosity, a modified Poiseuille flow rate coefficient is proposed [11, 13],

$$ Q_{\text{p}} = (1 + \delta {\text{Kn}})\left( {1 + {\frac{{6{\text{Kn}}}}{{1 + {\text{Kn}}}}}} \right), $$

(20)

where the rarefaction correction parameter δ (also denoted by α in [11, 13]) is obtained by matching the modified flow rate coefficient with the Poiseuille flow rate database via the solution of a two-dimensional linearized Boltzmann equation [16]. So it is not surprising that their analytical lubrication equation gives similar results to those of the FK lubrication equation with its numerically obtained look-up table [16]. A good point is that their model also gives the analytical expressions for the flow velocity profile and shear stress at the boundaries with good accuracy for flows with Kn < 12. This is an advantage over the FK lubrication equation; however, there is no accuracy improvement to the air bearing simulation.

2.6 Other Kinetic-Theory Based Slip Models

Although not integrated into the Reynolds lubrication equation, several second-order slip models have been proposed for shear or pressure-driven flows, such as the models by Schamberg [17], Beskok and Karniadakis [13], Cercignani and Daneri [18], Deissler [19], and Hadjiconstantinou [20]. Beskok and Karniadakis [13] also derived higher-order slip models.

The slip velocity of all of the second-order slip models can be expressed in a general form, when the surface accommodation coefficient is 1,

$$ U_{\text{slip}} = C_{1} {\text{Kn}}\left( {{\frac{\partial U}{\partial n}}} \right)|_{\text{boundary}} - C_{2} {\text{Kn}}^{2} \left( {{\frac{{\partial^{2} U}}{{\partial n^{2} }}}} \right)|_{\text{boundary}} $$

(21)

These models are only valid in the slip flow regime and not for the entire Knudsen number regime. Table 1 lists the coefficients C ₁ and C ₂ for all of the second-order slip models referred to in this paper. In this table, the first- and 1.5-order slip models are viewed as second-order slip models with special coefficients C ₁ and C ₂.

Table 1 Coefficients for second-order slip models expressed in a general form

Corresponding to the general slip model in Eq. 21, the Poiseuille flow rate coefficient can be calculated and expressed in the form,

$$ Q_{\text{p}} = {\frac{D}{6}} + C_{1} {\frac{\sqrt \pi }{2}} + C_{2} {\frac{\pi }{2D}}. $$

(22)

Figure 2 shows plots of the Poiseuille flow rate of the FK model [1], the first-, second- and 1.5-order slip models [4–6], the pressure gradient model [7], and Shen and Chen’s model [9] without using the effective mean free path. All of the second-order type models have a similar trend different from that of the first-order model. It is seen that in the transition flow and free molecular flow regions (D < 8.86) all of the slip models, which can be expressed by Eq. 21, differ greatly from the FK model in predicting the Poiseuille flow rate. This is expected, since the slip model is only valid in the slip flow region.

Fig. 2

Relation between the Poiseuille flow rate coefficient (nondimensional Poiseuille flow rate) and the inverse Knudsen number in the FK model [1], the first-, second-, and 1.5-order models [4–6], the pressure gradient model [7], Shen and Chen’s model [9]

3 Modification of the Mean Free Path

The mean free path of gas molecules is the mean value of the free distances that gas molecules can travel between two collisions in the equilibrium state. It depends on the molecule’s internal structure, gas pressure, and temperature. Based on kinetic theory, different air molecule models give different expressions for the mean free path.

3.1 Probabilistic Mean

It is obvious that the free distance that a gas molecule in an air bearing film can travel before a collision with another molecule or the boundary is reduced due to the existence of the boundaries. The second-order slip models [5–7, 9] either take the Taylor expansion of the bulk velocity with respect to the mean free path or employ a control volume with a height related to the mean free path. So it may be more accurate if the mean free path in the second-order slip models is replaced by a modified mean free path in considering the existence of boundaries. Peng et al. [10] obtained the probabilistic mean of the mean free path considering the boundary effects,

$$ \lambda_{m} = \left\{ {\begin{array}{*{20}c} {\lambda \left( {1 - {\frac{\lambda }{4h}}} \right),} \hfill & {h \ge \lambda } \hfill \\ {\lambda \left( {{\frac{3h}{4\lambda }} - {\frac{h}{2\lambda }}\ln \left( {{\frac{h}{\lambda }}} \right)} \right),} \hfill & {h < \lambda. } \hfill \\ \end{array} } \right. $$

(23)

Three assumptions are adopted in the derivation process. For the air flow, it is assumed that the air molecules are uniformly distributed in the air film and the velocity directions of air molecules are uniformly distributed in the three-dimensional space. In their derivation, it is also assumed that collision with another molecule is almost sure to happen when one molecule travels a distance of its mean free path. This inherent assumption can be seen from their result that the mean free path of molecules with a distance d > λ from the boundary is not affected by the boundary effect. Specifically, Fig. 3 shows it is not possible for the molecule to travel more than λ in the direction to the boundary before collision, while the possibility is finite if there is no boundary. This boundary effect is neglected under that inherent assumption.

Fig. 3

One molecule and one boundary

With the mean free path modification, an agreement between high-order slip-corrected Reynolds equations and the FK model is obtained. The mean free path in the slip models can be replaced by the modified mean free path in Eq. 23, resulting in a more reasonable choice of the Taylor expansion variable and the control volume’s height. With this replacement, the 1.5- or second-order slip-corrected Reynolds equations predict a pressure distribution and a load capacity close to that of the FK model, although the first-order slip-corrected Reynolds equation does not change much; and the Poiseuille flow rates of the 1.5- and second-order slip models have a similar trend to that of the FK model in the entire Knudsen number regime. As an example, in Fig. 2 the classical second-order slip model with the modified mean free path gives a Poiseuille flow rate coefficient much closer to that predicted by the FK model than the classical second-order slip model.

However, it appears that the approach of modifying the mean free path cannot replace the FK model. It is obvious that these three assumptions used in Peng’s derivation are not valid for a real air bearing flow. The distribution of molecular velocities is described by the Boltzmann equation. For an ideal gas, the number density of the air molecules, related to the density, is proportional to the gas pressure which is not necessarily uniform. The third assumption neglects the randomness of molecular collisions. Thus, it is supposed to be better if the true mean free path considering the boundary effects can be calculated directly from the velocity distribution function of gas molecules in the Boltzmann equation for the air bearing film. On the other hand, after the solution of the Boltzmann equation for the air bearing film is obtained, the air bearing problem is solved and the air pressure, the macroscopic flow velocity, the shear stress and so on can be obtained in terms of integrals with the molecular velocity distribution, as shown by Fukui and Kaneko [1]. The slip-corrected Reynolds equation then becomes unnecessary. In this sense, one should not expect to replace the FK model with a slip-corrected Reynolds equation by modifying the gas molecular mean free path.

The mean free path modification is not necessary for the FK model. In that model, the mean free path is a characteristic value of the BGK gas molecules in the equilibrium state. The boundary effect is considered by the boundary conditions for the linearized Boltzmann equation. So Peng’s further implementation of the modified mean free path into the FK model is not necessary.

3.2 The Matthiessen Rule

The effective mean free path in Shen and Chen’s slip model [9] is calculated using the Matthiessen rule [21],

$$ {\frac{1}{{\lambda_{m} }}} = {\frac{1}{\lambda /\sqrt 3 }} + {\frac{1}{h/2}}. $$

(24)

The Matthiessen rule is widely used in considering the boundary scattering effects on electron and phonon transport. However, it is seldom used for rarefied gas dynamics. This effective mean free path cannot be taken as a modified mean path of air molecules. A discrepancy occurs when the air film thickness h becomes much larger than the mean free path. As h increases, the boundaries move away from most of the air molecules, the boundary effect diminishes and the mean free path should approach the original mean free path λ instead of $\lambda /\sqrt 3$. Without this effective mean free path, Shen and Chen’s slip model is a second-order type, and the corresponding Poiseuille flow rate is no longer close to that predicted by the FK model. This can be seen from Fig. 2. However, the application of the Matthiessen rule to rarefied gases is not supported by the Boltzmann equation. And, it does not work better than the usage of the modified mean free path in Peng et al. [10], since both Shen and Chen’s model and the classical second-order model with the modified mean free path are close to the FK model in Fig. 2.

3.3 Air Molecule Models

Instead of the hard sphere model, which is usually used to calculate the mean free path used in the slip models, Sun et al. [22] took the results of a variable hard sphere (VHS) model [23] and variable soft sphere (VSS) model [24] and applied the modified mean free path to the classical second-order slip model. However, they compared their results to those of the slip-corrected Reynolds equations and the linearized Boltzmann equation with the BGK model. Using only this comparison may not validate the application of VHS and VSS models to an air bearing lubrication.

4 Contact Pressure Singularity

It was stated by Wu and Bogy [7] that the second-order slip-corrected Reynolds equation does not predict an unphysical unbounded pressure singularity in the limit of contact between the bearing surface and the moving surface. Following Wu’s analysis [7], the form of the Reynolds equation, i.e., Eq. 1, can be changed by using the second-order slip flow’s Poiseuille flow rate coefficient in Eq. 22 to the following form for the steady state one-dimensional air bearing equation,

$$ {\frac{\partial }{\partial X}}\left[ {\left( {{\frac{{p_{\text{a}} h_{0}^{2} }}{6\mu UL}}PH^{3} + {\frac{{\beta p_{\text{a}} \lambda_{\text{a}} h_{0} }}{6\mu UL}}H^{2} + {\frac{{\gamma p_{\text{a}} \lambda_{\text{a}}^{2} }}{6\mu UL}}{\frac{H}{P}}} \right){\frac{\partial P}{\partial X}}} \right] = {\frac{\partial }{\partial X}}(PH), $$

(25)

where β = 6a and γ = 6a (12a) for Hsia and Domoto’s second-order slip model [5], and β = 6a and γ = 12a for Wu’s pressure gradient model [7]. In the near-contact regime, H approaches zero. With the high-order terms of H in Eq. 25 neglected in Wu’s analysis, the Reynolds equation can be reduced to,

$$ {\frac{\partial }{\partial X}}\left[ {\Upgamma {\frac{H}{P}}{\frac{\partial P}{\partial X}}} \right] = {\frac{\partial }{\partial X}}(PH), $$

(26)

where the dimensionless parameter $\Upgamma = {\frac{{\gamma p_{\text{a}} \lambda_{\text{a}}^{2} }}{6\mu UL}}.$ Wu’s asymptotic solution of Eq. 26 for an asperity with actual contact at X = 0, the profile of which is $H = (AL^{2} /h_{0} )X^{2} + 1$ and shown in Fig. 4, is

$$ P = \left\{ {\begin{array}{*{20}c} {{\frac{{P_{\text{L}} \Upgamma }}{{\Upgamma - P_{\text{L}} (1 + X)}}},} \hfill & { - 1 \le X < 0}, \hfill \\ {{\frac{{P_{\text{R}} \Upgamma }}{{\Upgamma + P_{\text{R}} (1 - X)}}},} \hfill & { \, 0 < X \le 1}. \hfill \\ \end{array} } \right. $$

(27)

where P _L and P _R are the nondimensional air bearing pressures at the left and right side of the contact regime. As shown by Wu, this solution has a shock wave-like discontinuity at the contact point. However, one special situation is not discussed by Wu. Provided that the same boundary condition is taken with P _L = P _R = 1, Eq. 27 may produce an unbounded air pressure before the contact point X = 0 if Γ = 1. The parameter values used by Wu [7] for an asperity in near contact with the disk are p _a = 0.101 MPa, λ_a = 65 nm, U = 10 m/s, μ = 1.85 × 10⁻⁵ N s/m² and L = 0.5 μm. It is obvious that if the accommodation coefficient is 1 and L = 2.284 μm for γ = 6 (L = 4.568 μm for γ = 12), which are still reasonable parameter values for the characteristic length of an asperity, unbounded pressure values can be obtained near the contact point. So it is possible that a second-order slip-corrected Reynolds equation also predicts an unphysical unbounded pressure singularity in the limit of contact with a certain asperity profile, which partially contradicts Wu’s conclusion.

Fig. 4

Parabolic profile of an asperity in near-contact with the disk [7]

Numerical simulations are carried out here to compare with this asymptotic analysis. A slider with a length of 0.04 mm and a width of 0.04 mm has an asperity at the center of the flat air bearing surface. The asperity has a parabolic shape of $H = {\frac{{AL^{2} }}{{h_{0} }}}r^{2} + 1,$ where r is the distance from the center. The slider has fixed zero pitch and roll angles on a disk with 10000 RPM. The CML air bearing program with a finite volume method is used to solve the Reynolds equation for the air bearing pressure profile. The FK model, the pressure gradient model [7] and the classical second-order slip model [5] are used in the air bearing simulation, respectively. The pressure singularity is numerically analyzed with the slider’s minimum flying height at 0.1, 0.01, and 0.001 nm, as done by Wu and Bogy [7]. Three cases with different parameter values are analyzed—Case 1 with A = 10⁴/m and L = 0.5 μm; Case 2 with A = 10²/m and L = 5 μm and Case 3 with A = 25/m and L = 10 μm. These micron level values are reasonable for L, the radius of the base of a parabolic asperity. A is the shape parameter of the parabolic profile and here a value of A is chosen so that the asperity tip has a height of 2.5 nm above its base in each case, which is a reasonable height value.

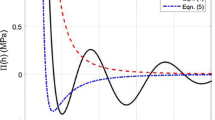
Simulation results of Case 1 are shown in Fig. 5, including the ABS profile and air bearing pressure profile along the center line for a minimum flying height (min FH, i.e., the gap between the asperity tip and the disk) of 0.1, 0.01, and 0.001 nm. They are similar to Wu’s simulation results. The air bearing pressure along the center line obtained using the pressure gradient model has a shock wave-like shape across the near-contact regime, while the air bearing pressure obtained using the FK model has a very large value in the near-contact regime. As the min FH decreases from 0.1 nm to 0.001 nm, the pressure profile obtained using the pressure gradient model converges to a bounded value, while the pressure profile obtained using the FK model has an increasing air pressure in the near-contact regime. These conclusions with Case 1 agree well with Wu’s conclusions.

Fig. 5

ABS profile and air bearing pressure profile along the center line from the leading edge to the trailing edge in Case 1 (A = 10⁴/m and L = 0.5 μm). a Air bearing surface profile. b Air bearing pressure profile along the ABS’s center line using the FK model. c Air bearing pressure profile along the ABS’s center line using the pressure gradient model

The ABS profiles and air bearing pressures along the slider’s center line of Cases 2 and 3 are plotted in Figs. 6 and 7, respectively. It is obvious in both of these cases that the air bearing pressures obtained using either the FK model or the pressure gradient model do not converge to a bounded value. The air bearing pressure at the near-contact regime increases beyond 100p _a or even 1000p _a, as the min FH decreases. Further, the results of the classical second-order slip-corrected Reynolds equation for Cases 1, 2, and 3 are shown in Fig. 8. The rapid increase of the air bearing pressure at the near-contact region as the gap decreasing does not change for Cases 2 and 3. A shock wave-like profile of the air bearing pressure at the near-contact region is not a universal result of a second-order type slip-corrected Reynolds equation.

Fig. 6

ABS profile and air bearing pressure profile along the center line from the leading edge to the trailing edge in Case 2 (A = 10²/m and L = 5 μm). a Air bearing surface profile. b Air bearing pressure profile along the ABS’s center line using the FK model. c Air bearing pressure profile along the ABS’s center line using the pressure gradient model

Fig. 7

ABS profile and air bearing pressure profile along the center line from the leading edge to the trailing edge in Case 3 (A = 25/m and L = 10 μm). a Air bearing surface profile. b Air bearing pressure profile along the ABS’s center line using the FK model. c Air bearing pressure profile along the ABS’s center line using the pressure gradient model

Fig. 8

Air bearing pressure profile along the center line from the leading edge to the trailing edge obtained using the classical second-order model. a Case 1 (A = 10⁴/m and L = 0.5 μm). b Case 2 (A = 10²/m and L = 5 μm). c Case 3 (A = 25/m and L = 10 μm)

Wu’s asymptotic approach may not be valid for a general slider-disk contact situation. For an isothermal gas flow, the mean free path of the gas molecules is inversely proportional to the gas pressure, i.e., λp = λ_a p _a. Thus, the Knudsen number of the air flow at a local position with a slider-disk gap of h can be written as Kn = λ/h = λ_a/(h _o PH). With this expression of Kn, Eq. 25 can be written in the form of,

$$ {\frac{\partial }{\partial X}}\left[ {{\frac{{\gamma p_{\text{a}} \lambda_{\text{a}}^{2} }}{6\mu UL}}{\frac{1}{P}}\left( {{\frac{1}{{\gamma {\text{Kn}}^{2} }}}H + {\frac{\beta }{{\gamma {\text{Kn}}}}}H + H} \right){\frac{\partial P}{\partial X}}} \right] = {\frac{\partial }{\partial X}}(PH). $$

(28)

The slider-disk gap is negligible near a contact region; hence H can be taken as a first-order term near the contact region. However, the first and second terms on the left hand side of Eq. 28 are not necessarily higher-order terms in H, unless 1/Kn is a first- or higher-order term in H. The numerically obtained Knudsen numbers in Cases 1, 2, and 3 with Wu’s pressure gradient model, FK model and the classical second-order slip model are listed in Table 2. It is seen that the product of Kn and H in Case 1 almost remains constant, which indicates that 1/Kn may be a first-order term in H. So Wu’s asymptotic approach is supported by the numerical results in Case 1. However, in Cases 2 and 3, Kn almost remains constant as H reduces dramatically. The first and second terms in Eq. 25 and 28 are no longer higher-order terms in H, and they cannot be directly neglected in the asymptotic analysis. So the numerical data here do not support Wu’s asymptotic approach. From this point of view, it can be concluded that Wu’s asymptotic result of a bounded air pressure at the contact region may not always be valid at a general slider-disk contact region.

Table 2 Knudsen number at the center of the near-contact region in the slider-disk contact Cases 1, 2, and 3

As a conclusion, neither the pressure gradient model nor the classical second-order slip model always predicts a bounded air bearing pressure at the contact or near-contact region. In fact this contact pressure singularity may be associated with the usage of the ideal gas law p = ρRT. As the film thickness approaches zero at the near-contact region, the gas density there approaches infinity, due to the continuity equation, which is the basis of different types of Reynolds equations. As a result, the pressure also approaches infinity at the near-contact region. On the other hand, the ideal gas law may not be a good approximation when the gas film thickness is close to zero. Therefore, the contact singularity of the Reynolds lubrication theory needs further analysis.

5 Conclusions

A valid slip model for Poiseuille flow is critical to deriving a slip-corrected Reynolds equation, when the surface accommodation coefficients at the slider surface and bearing surface are the same or close to each other. Different slip models predict different slip conditions at the slider and the disk surfaces, and then lead to different Poiseuille flow rate coefficients, i.e., the nondimensional Poiseuille flow rates, which are the only varying part in different slip-corrected Reynolds equations.

Through modifying the mean free path or mathematically matching the Poiseuille flow rate to the kinetic simulation results, some slip-corrected Reynolds equations can obtain results close to that of the FK model based on the linearized Boltzmann equation. However, it is not expected that these can replace the FK model and give more accurate results. The contact pressure singularity is a common problem of the second-order type slip-corrected Reynolds equation as well as the FK lubrication equation and the first-order slip-corrected equation. It may be related to the application of the ideal gas law, and it needs further consideration.