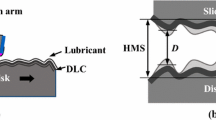
The head–disk interface (HDI), as shown in Fig. 1, is the region between a slider and a disk in hard disk drives. The slider, carrying a read–write transducer at the trailing edge, flies over the disk which rotates and has a local speed U around 10–30 m/s. A specifically designed pattern called the air-bearing surface (ABS) exists on the slider’s surface facing the disk. In the HDI, the flow of air, setup by the moving disk and compressed by the ABS, creates pressure that balances the suspension load on the slider, and it serves as a cushion layer to stabilize the motion of the slider and reduce contact between the slider and the disk. To further reduce the possibility of the slider’s impact on the disk, and mitigate its effect when contact occurs, a layer of lubricant, with thickness of about 1 nm, is coated on the disk. In modern hard disk drives, the minimum flying height of the slider has been reduced to less than 5 nm. This leads to strong interactions between the slider, the air flow, and the lubricant. Experiments have shown that the lubricant, due to its mobility, deforms and creates specific patterns due to these interactions [1, 2]. It has also been experimentally observed that the lubricant in some cases transfers from the disk to the slider [3], which decreases the effect of the lubricant as a protecting layer for the disk and may alter the performance of the slider. Thus, despite its very small thickness, the lubricant layer plays an important role in the reliability of hard disk drives [4].

Fig. 1
figure 1

The geometry of the HDI, composed of a slider and a moving disk. A lubricant layer covering the disk serves to reduce impact damage of the slider on the disk. This figure is not to scale

Full size image

Although the thickness of the lubricant layer is often less than 1 nm, experiments have shown that it can still be modeled using continuum theory with a modification to its viscosity [5]. Inspired by this finding, many papers, mostly numerical analyses, have been published on the deformation and instability of the lubricant layer in the framework of continuum theory [3, 4, 6–10]. It is generally agreed [4, 8, 10] that the shear force induced by the air flow is a dominant factor determining the lubricant dynamics. However, in all of these studies, the shear force was represented by either an oversimplified model [4, 6] that contains only the Couette flow component or a model based on the first-order slip theory [8]. Wu [8] compared results based on these two models and showed that the approach to modeling the shear force is essential to the analysis of lubricant dynamics. Since the gap spacing between the slider and the disk, h, changes from several nanometers at the trailing edge to near 1 μm, the Knudsen number, defined as the ratio of h to the mean free path λ, covers a wide range of values from larger than 10 to less than 0.1 based on the value λ = 65 nm for air. In view of the fact that the first-order slip theory is only applicable for Kn < 0.1 [11], it can not be expected that a shear model based on the first-order slip theory would be applicable in the HDI.

Although Kang et al. [12] numerically studied the shear stress in a HDI flow, their database for the shear force was not widely available, and Wu [8] instead resorted to a model based on the first-order slip theory. It has been demonstrated that the shear force based on this model compares well with numerical results from a Direct Simulation Monte Carlo (DSMC) analysis for several ABS designs [13]. This, however, does not guarantee that the model Wu used uniformly holds for all ABS designs. The underlying reason why the numerical results and the results based on the first-order slip theory are close to each other is therefore not yet clear. Thus, given the importance of the shear force in lubricant dynamics, a further study of it is needed. In this communication, we present an analytical formula for the shear force induced by the air flow in the HDI. This formula reduces to that based on the first-order slip theory when the hard sphere model for air molecules is used, and it thus validates previous studies that rely on the latter formula.

In the HDI, the shear forces on the slider and the disk are each a linear combination of contributions from two parts [14]: a Couette flow with one boundary fixed and the other one moving at a speed U, and a Poiseuille flow driven by a pressure gradient dp/dx. Since Couette flow has been thoroughly investigated, we restrict our attention to the Poiseuille flow part and consider a Poiseuille flow of a rarefied gas between two planes lying at y = −h/2 and y = h/2.

The motion of a rarefied gas is described by the Boltzmann equation, whose form is complex and difficult to analyze. Since we are mainly interested in a macroscopic quantity, i.e., the shear force, detailed information on the velocity distribution function of the molecules moving between the slider and the disk is not of concern. So we can bypass the Boltzmann equation and instead work with the conservation equations. The conservation equations can be derived directly from the basic principle of the conservation of mass, momentum, and energy, and they apply to any kind of air flow rarefied or not [11]. These equations are not closed since they involve several unknown quantities such as the stress tensor, which needs to be determined through other means. From another point of view, these conservation equations are the first three moments of the Boltzmann equation with respect to the molecular velocity. According to the theory of partial differential equation, a partial differential equation is equivalent to a full set of all its moment equations, and, for the Boltzmann equation, these moment equations form the so-called BBGKY hierarchy. Since the conservation equations are the first three components of the BBGKY hierarchy, they are not fully equivalent to the Boltzmann equation and they are not closed. The Euler equation and the Navier–Stokes equation are two special cases of the conservation equations where the stress tensor is related to the air flow velocity gradient through a constitutive relation.

Since Fukui and Kaneko [14] have shown that the air flow in the HDI is isothermal, we only need to deal here with the conservation equations of mass and momentum to get the shear force [11]. Under the same assumptions as used by Fukui and Kaneko [14], i.e., the thickness of the air gap in the HDI is much less than the length and the width of the slider, and the air flow in the direction perpendicular to the disk is negligible, the conservation equations for a steady flow reduce to

$$ \frac{\partial}{\partial x}\left(\rho v_x\right)=0 $$
(1)
$$ \frac{\partial}{\partial x}\left(\rho v_x^2+\sigma_{xx}\right)+ \frac{\partial}{\partial y}\left(\sigma_{xy}\right)=0 $$
(2)

where σ xx and σ xy are components of the stress tensor. Again, we note that Eqs. 1 and 2 are not closed due to the appearance of σ xy and σ xx which can only be determined by some kind of constitutive relations. We next investigate the order of each term in Eq. 2 and show that all the terms in Eq. 2 are not of the same order. Through this approach, Eq. 2 can be further reduced.

Since the Boltzmann equation is very complex, a widely used model for the Boltzmann equation was proposed by Bhatnagar et al. [15]. This model equation, the so-called BGK–Boltzmann equation, gives results that compare well with experiments for most problems [11]. Since the flow velocity in the present case is on the order of the disk speed, and it is much less than the average thermal speed of air molecules, which is comparable to the speed of sound in air, the BGK–Boltzmann equation can be linearized with respect to a reference ambient state with temperature T 0 and density ρ0. Its form, with only linear terms retained, is:

$$ \xi_i\frac{\partial \phi}{\partial x_i}=\nu\left(-\phi-1+{\frac{\rho}{\rho_0}}+{\frac{\xi_iv_i} {RT_0}}\right) $$
(3)

where ξ i is the molecular velocity, ϕ = (f/f 0)−1, f is the velocity distribution function of the air molecules, f 0 is a Maxwellian in a quiescent flow at the reference state, ν is a collision frequency related to the mean free path, ρ is the density of air, v i is the flow velocity, and R is the specific gas constant. In plane Poiseuille flow, the air flow is setup by the pressure gradient. The requirement that the air speed is much less than the thermal speed of air molecules further requires that the pressure gradient dp/dx is small as well. More specifically, this requires that (h/p 0)dp/dx≪ 1 where p 0 = ρ0 RT 0 is the ambient pressure. Since the flow is induced by the pressure gradient, it can be shown that the air speed is of the same order as the pressure gradient.

For a plane Poiseuille flow of a rarefied gas, a solution satisfying Eq. 3 and compatible with the associated boundary conditions in the HDI is [14]

$$ \phi={\frac{1}{\rho_0RT_0}}\,{\frac{\hbox{d}p}{\hbox{d}x}}x+{\frac{\xi_x}{\sqrt{2RT_0}}}\,\phi_1(y,\xi_y,\xi_i\xi_i) $$
(4)

with ϕ1 determined by

$$ \xi_y \frac{\partial \phi_1}{\partial y} +{\frac{1}{\nu}}\phi_1=-{\frac{\sqrt{2RT_0}} {\rho_0RT_0}}{\frac{\hbox{d}p}{\hbox{d}x}} $$
(5)

where L is the length of the slider, x points to the flow direction, and y points to the direction perpendicular to the disk. In Eq. 4, the dependence of p on y is neglected given that h≪L.

From the definition of the shear stress in kinetic theory [11] and Eq. 4

$$ \begin{aligned} \sigma_{xx} = & -p_0 - {\frac{2}{\pi^{3/2}}}\,{\frac{p_0} {(2RT_0)^{5/2}}}\int\xi_x^2\phi\exp\left(-{\frac{\xi_i\xi_i} {2RT_0}}\right)\hbox{d} {\varvec{\xi}}\notag \\ = & -p_0 - {\frac{2}{\pi^{3/2}}}\,{\frac{p_0}{(2RT_0)^{5/2}}}\,{\frac{1} {\rho_0RT_0}}\,{\frac{\hbox{d}p}{\hbox{d}x}}x \int\limits_{-\infty}^\infty\int\limits_{-\infty}^\infty\int\limits_{-\infty}^\infty\xi_x^2\exp \left(-{\frac{\xi_x^2+\xi_y^2+\xi_z^2} {2RT_0}}\right)\hbox{d}\xi_x\hbox{d}\xi_y\hbox{d}\xi_z\notag \\ & -{\frac{2}{\pi^{3/2}}}\,{\frac{p_0}{(2RT_0)^{5/2}}}\,{\frac{1}{\sqrt{2RT_0}}} \int\limits_{-\infty}^\infty\int\limits_{-\infty}^\infty\int\limits_{-\infty}^\infty\xi_x^3\phi_1\exp \left(-{\frac{\xi_x^2+\xi_y^2+\xi_z^2}{2RT_0}}\right) \hbox{d}\xi_x\hbox{d}\xi_y\hbox{d}\xi_z\notag \\ = & -p_0-{\frac{\hbox{d}p}{\hbox{d}x}}x \end{aligned} $$

where the integral involving ϕ1 vanishes since the limits of the integral for ξ x are symmetric and the associated integrand is odd in ξ x , the latter of which is further due to the oddness of ξ 3 x and the fact that ϕ1 is functions of y, ξ y , ξ 2 x , ξ 2 y , ξ 2 z but not ξ x itself. For σ xy , we have

$$ \sigma_{xy}={\frac{2}{\pi^{3/2}}}\,{\frac{p_0} {(2RT_0)^{5/2}}}\int\xi_x\xi_y\phi\exp\left(-{\frac{\xi_i\xi_i} {2RT_0}}\right)\hbox{d}{\varvec{\xi}}\neq 0 $$

As discussed above, the linearized Boltzmann equation is a reduced Boltzmann equation where we only retain terms of an order lower than or equal to the order of the flow speed which is the same as the order of the pressure gradient (L/p 0)dp/dx. In the framework of the linearized Boltzmann equation, σ xx and σ xy are different from zero, so they each have an order the same as or lower than (L/p 0)dp/dx. Then, in view of (L/p 0)dp/dx ≪ 1, we can neglect terms of an order higher than (L/p 0)dp/dx in Eq. 2 for the analysis of σ xy . The first term in Eq. 2, ∂(ρv 2 x )/∂x, after using Eq. 1 to eliminate ∂v x /∂x, turns out to be −v 2 x ∂ρ/∂x, which is of second order of \(U/\sqrt{2RT_0}.\) This term is therefore negligible since the other terms in Eq. 2 are of first order or lower. So Eq. 2 finally reduces to

$$ -{\frac{\hbox{d}p}{\hbox{d}x}}+ \frac{\partial \sigma_{xy}}{\partial y}=0 $$
(6)

Since the accommodation coefficients of engineering surfaces are close to each other, we here assume the accommodation coefficients of the slider and the disk are the same. Then, the Poiseuille flow is symmetric with respect to the centerline y = 0 in our coordinate system. Under these conditions, the shear forces on the two boundaries are equal to each other, i.e., σ xy n y |y=-h/2 = σ xy n y |y=h/2, and the normal directions of the two boundaries are opposite to each other, i.e., n y |y=-h/2 = −n y |y=h/2. Thus, σ xy |y=-h/2 = −σ xy |y=h/2. Then, integrating Eq. 6 from y = −h/2 to y = h/2, we get

$$ \sigma_{xy}\vert_{y=h/2}={\frac{h}{2}}\,{\frac{\hbox{d}p}{\hbox{d}x}} $$
(7)

This result is the same as would be obtained through Valougeorgis’ force balance approach [17] where the shear force is regarded as being balanced by the pressure gradient alone. Our approach is, however, more rigorous since we work with the Boltzmann equation and demonstrate that the contribution from the momentum flux is of higher order when the velocity of the flow is much less than the average thermal velocity of the air molecules, and thus it is negligible. We note that Eq. 7 can also be obtained from an integral form of the momentum equation, i.e., by extending Valougeorgis’ approach to include the momentum flux. But the linearized Boltzmann equation and intrinsic symmetry of Poiseuille flow are still needed for finally arriving at Eq. 7. Equation 7 also agrees with the numerical results from the DSMC method [13].

For the shear force contributed by the Couette flow part, we adopt the formula obtained by Liu and Lees [18] through the method of moments. The shear force calculated through Liu and Lees’ formula compares well with numerical results based on the linearized Boltzmann equation [19]. Then the total shear forces on the disk and the slider are

$$ \tau_w\vert_{\rm disk}= -\rho\lambda\sqrt{{\frac{RT_0} {2\pi}}}\,{\frac{U}{2\lambda+h}}-{\frac{h}{2}}\,{\frac{\hbox{d}p}{\hbox{d}x}} $$
(8)
$$ \tau_w\vert_{\rm slider}= \rho\lambda\sqrt{\frac{RT_0} {2\pi}}\,{\frac{U}{2\lambda+h}}-{\frac{h}{2}}\,{\frac{\hbox{d}p}{\hbox{d}x}} $$
(9)

Generally speaking, the pressure gradient dp/dx changes with x, and the generalized Reynolds equation [14] needs to be solved for dp/dx before Eqs. 8 and 9 can be used.

Let us now compare the present formula Eq. 8 with that based on the first-order slip theory which, on the disk, has the form [8]:

$$ \tau_w= -\mu{\frac{U}{2\lambda+h}}- {\frac{h}{2}}{\frac{\hbox{d}p}{\hbox{d}x}} $$
(10)

Equations 8 and 10 are the same when a hard sphere model is used for air molecules because in this case the viscosity for a rarefied gas is \(\mu=\rho\lambda\sqrt{RT_0/(2\pi)}\) [20]. Since μ does not change very much as the Knudsen number increases, the shear force calculated through Eq. 10 with μ taking its value in a continuum flow does not deviate much from the exact results calculated from Eq. 8. This underlies Wu’s reasoning [8] that the shear force based on a first-order slip model is a good approximation. We note that the correct way to implement Eq. 10 is to use Eq. 8 where the viscosity in a rarefied gas has been taken into account explicitly. In Dai et al.’s model [4], only the shear force contributed by the Couette flow part was considered. Whereas, as argued by Wu [8] and shown by the numerical results in Fig. 2, the second terms in Eqs. 8 and 9 produced by the Poiseuille flow are not always negligible. Thus, the use of the full form of Eqs. 8 and 9 is not only preferred but it is required.

Fig. 2
figure 2

The shear force on the layer of lubricant under the CML Femto slider calculated through Eq. 8 with a disk speed of 32.5 m/s. a The ABS of the slider. b The ratio of the shear force contributed by the Poiseuille flow part to that contributed by the Couette flow part. Although not shown here, the magnitude of the shear force contributed by the Couette flow part is not always negligible in the region where the ratio is on the order of 1. The flow field in the HDI is obtained via the CML ABS design program [16], which uses the finite volume method to solve the generalized Reynolds equation [14]. The dependence of the mean free path on air pressure has been included here

Full size image

In summary, the shear force in the HDI in hard disk drives is investigated in this communication. Based on some results obtained from the linearized BGK–Boltzmann equation, we make use of an order analysis to simplify the conservation equations, and obtain an analytical formula for the shear stress in plane Poiseuille flow. It is shown that the shear forces on the two boundaries in plane Poiseuille flow are the same and are equal to (−h/2)dp/dx. Making use of Liu and Lees’ formula for the shear force in plane Couette flow, we then present formulae for the total shear force on the slider and on the disk in the HDI based on the information obtained from the linearized Boltzmann equation that the total shear force is a linear combination of the contributions from Couette and Poiseuille flows. When a hard sphere model is used for air molecules, our formula reduces to that based on the first-order slip model, and it thus validates the use of the latter formula for analyzing lubricant dynamics on the slider and the disk, lubricant transfer from the disk to the slider, or vice versa as well as the dynamics and stability of the slider itself.