1 Introduction

The Fischer–Tropsch synthesis (FTS) reaction is a well-established, industrially significant, catalytic reaction involving the conversion of synthesis gas (CO and H2) into a wide range of hydrocarbon products, which can be further processed to produce high value chemical intermediates utilised in the chemical manufacturing industry [1,2,3]. Co and Fe based catalysts dominate the industrial FTS scene; this work concentrates solely on iron-based FTS systems. Despite wide industrial application of iron FTS, there remains uncertainty in the mechanistic operation of these catalysts. This may be due in part to the ‘evolutionary’ phase in the initial stages of reaction that can result in a variety of molecular entities including iron oxides, iron carbides, metallic Fe, carbon, and a hydrocarbonaceous overlayer; with the final composition dependent on the reaction conditions [2, 4,5,6,7,8].

Previous work has utilised neutron spectroscopic techniques, in particular inelastic neutron scattering (INS) for the investigation of iron FTS systems, allowing for identification of hydrogenous moieties in post-reaction iron FTS catalysts [9, 10]. Alongside complimentary analytical techniques such as XRD, Raman, temperature-programmed oxidation (TPO) and TEM, INS has been used to investigate both the evolutionary profile of the active phase of the catalyst as well as the development of a hydrocarbonaceous overlayer [8, 11,12,13,14]. These investigations have utilised a promoter-free iron-based catalyst (α-Fe2O3) and have examined its evolutionary profile over a 24 h period using ambient pressure CO hydrogenation conditions as a representative FTS reaction [8]. Consequently, a qualitative model has been proposed indicating a role for the hydrocarbonaceous overlayer in the process chemistry, where the overlayer ‘templates’ access to two active sites: one primarily supporting dissociative hydrogen adsorption and the other supporting dissociative CO adsorption and, sequentially, product formation. A component of this model requires adsorbed hydrogen to diffuse through the overlayer, with the expectation that the rate of diffusion will change as the overlayer evolves [8]. More recently, the period of reaction under examination by INS has been extended from 24 h to 10 days (240 h) time-on-stream [15], with that work revealing further complexity within the catalyst conditioning period. Specifically, catalytic performance was observed to be decoupled from certain aspects of the evolving catalyst matrix: whereas CO hydrogenation activity had stabilised by 9 h time-on-stream, carbide formation and maturing of the hydrocarbonaecous overlayer, comprising sp3- and sp2-hybridized C-H components, exhibited different temporal profiles [15].

In order to test the hypothesis of moderated hydrogen diffusion throughout the iron based FTS catalyst conditioning period, here we report a preliminary investigation employing the technique of quasi-elastic neutron scattering (QENS) to examine the diffusion characteristics of an iron based FTS catalyst that has experienced different times-on-stream. Hydrogen was selected as a probe molecule because it is directly linked with the process chemistry under consideration. In this role, the hydrogen molecule is viewed as existing as a physisorbed entity that can access porosity within the various phases of the catalyst matrix, viz. iron oxides, iron carbides, amorphous carbon and hydrocarbonaceous overlayer [16].

Within the context of this application of QENS, it is informative to consider how neutrons interact with matter. Due to their lack of charge, neutrons generally interact only weakly with matter. When they do interact, they may either be scattered or absorbed. If we assume absorption to be negligible in our system, we can limit our interpretation to four types of scattering. Neutrons may be scattered elastically or inelastically, and coherently or incoherently. Whilst the theoretical basis for the separation of these components is well understood, we can only measure the neutrons that are scattered and infer from our knowledge of the system the most likely source [17]. Coherent elastic scattering is the most common and familiar event, where there is no change in the energy of the neutron, which interacts as a wave interfering with the extended lattice and leads to diffraction. Coherent inelastic scattering occurs where a neutron scatters from a correlated lattice motion (phonon). Incoherent inelastic scattering provides information about uncorrelated atomic motion. At higher energies this may represent molecular vibrations, but around the elastic peak this represents the stochastic diffusion processes occurring within a sample. Incoherent elastic scattering also occurs, but does not carry useful information.

The probability of a neutron scattering from an atom is given by its scattering cross section. This can be split into coherent and incoherent cross sections, which determine the relative strengths of these two modes of scattering and is isotope dependent. 1H has such a uniquely high incoherent cross that in hydrogenous samples all incoherent scattering is generally treated as scattering from hydrogen. In a system with a solid phase and a hydrogen-containing liquid the incoherent inelastic scattering will represent the stochastic motions of the liquid, whilst the coherent elastic scattering represents the structural order of the solid. This simplification allows us to neglect the effects of correlated motions in the solid, and structure in the liquid, although we should remember that this is an approximation that becomes decreasingly accurate with as the percentage of hydrogen in our sample reduces.

In this study, QENS has been used for the first time to investigate the diffusion of the hydrogen reactant in FTS catalysts that have been exposed to CO hydrogenation conditions at 623 K for 0, 12 and 24 h. The three samples have previously been analysed by INS by Warringham et al. [8]. Specifically, this preliminary QENS study seeks to investigate whether this technique may provide any insight towards how the evolving hydrocarbonaceous overlayer affects reactant diffusion.

2 Experimental

2.1 Catalyst Preparation

The iron oxide catalyst sample used for this investigation was prepared using the co-precipitation of iron nitrate (Sigma Aldrich, 99.99%) and sodium carbonate (Sigma-Aldrich, 99.99%). The preparative procedure utilises a batch reactor apparatus for reproducible sample synthesis and is described elsewhere [14]. The resulting slurry is filtered and washed with warm deionised water followed by a calcination step involving a step wise heating programme, with a maximum temperature of 623 K [14]. The procedure produces hematite (α-Fe2O3) and an absence of promoters/modifiers. The surface area of the samples examined in this work was 70.8 m2 g−1. All samples were ground and sieved to a particle size range of 250–500 µm. Catalyst characterisation has been carried out in previous investigations [8, 14].

2.2 Quasielastic Neutron Measurements

In previous studies, approximately 10 g of iron oxide catalyst was exposed to CO hydrogenation conditions (heated to 623 K at 5 K min−1 under a flow of H2, 150 sccm, CK Gas, 99.9%, and CO, 75 sccm, CK Gas, 99.9%, in a carrier gas He, 600 sccm, CK Gas, 99.9%, total WHSV of 1.47 h−1) in a custom built sample preparation rig [8, 9]. Each sample was exposed to reaction conditions for varying lengths of time on stream: 0, 12 and 24 h; labelled as FT0, FT12 and FT24 respectively. Following exposure to reaction conditions, each of the reacted samples were subjected to a passivation procedure involving the introduction of small amounts of O2 to the reactor, gradually increasing to atmospheric levels (i.e. 20% O2 in the gas feed) [18]. Each sample was sealed into cylindrical aluminium sample cans that had an annular sample space of 2 mm and allowed connection to gas handling facilities. The three samples were first dried in a vacuum furnace at 363 K overnight. They were then mounted onto a gas handling sample stick to allow control of the gas atmosphere in the sample space whilst the sample was cooled in a closed cycle refrigerator (CCR) in the neutron beam. For the hydrogen-containing samples the gas was admitted to the cell and an attached gas buffer of 500 cm3 to approximately 1 bar at 300 K and sealed. The pressure drop upon cooling was significant due to adsorption/condensation of the hydrogen gas. Data was collected using the IRIS spectrometer at ISIS using the 002 reflection of the pyrolitic graphite analyser bank [19, 20]. This gives an energy transfer range of − 0.5 to 0.5 meV with an energy resolution of 17.5 µeV. IRIS has 51 spectroscopy detectors viewing the graphite analyser that cover a 2θ range of 27.07–158.4 degrees. In the PG002 configuration, this corresponds to 0.442–1.854 Å−1. It is common to group these detectors to improve the signal to noise ratio at the expense of Q resolution. The choice of groups was optimised for quasielastic signal, with detectors coincident with strong Bragg scattering peaks from the reacted catalysts omitted from the analysis.

3 Results and Discussion

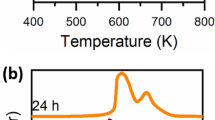
An initial assessment of the interaction between hydrogen and the sample utilised elastic window scans under varying temperature [17]. The total integrated elastic peak intensity was obtained by integration between − 0.0175 and + 0.0175 meV energy transfer (the instrumental resolution) for the FT24 sample with and without hydrogen. Results are shown in Fig. 1. At temperatures of 100 K and above the samples with and without hydrogen show little difference, indicating that hydrogen is only present in the sample space as a rarefied gas, which scatters too weakly to be detected. Below 100 K, however a condensed phase forms on the catalyst, presumably within pores present in the sample indicated by additional scattering from the hydrogen atoms. As the liquid range of hydrogen is 14–20 K at one atmosphere the difference in the elastic peak intensities in the range 20–100 K suggests that there is a favourable interaction between the catalyst and the hydrogen leading to an absorptive process. Any information that may be obtained about the nature of this sorbed phase and its interaction with the catalyst could lead to increased understanding of the catalytic reaction mechanism.

Fig. 1
figure 1

Elastic peak intensity as a function of temperature for FT24 without (a, grey) and with (b, red) an overpressure of hydrogen. Decreasing elastic intensity indicates increasing molecular motion

Full size image

Figure 1 therefore allows the temperature region of interest to be defined (20–100 K); longer data accumulation times were then used for all subsequent measurements to allow line-shape analysis. The data summed across Q for all three samples (FT0, FT12 and FT24) and conditions (30, 50, 70 K with and without H2) is presented in Fig. 2.

Fig. 2
figure 2

Variation in quasielastic peak maxima summed across Q for catalyst samples before and during hydrogen exposure: a FT0, b FT12, c FT24, d FT0 + H2, e FT12 + H2, f FT24 + H2

Full size image

Figure 2 presents the peak maxima for the six samples considered. For the samples without hydrogen dosing (Fig. 2a–c), the differing intensity between catalyst samples is attributed to differing sample masses. Figure 2a shows the unreacted sample (FT0) to exhibit little increase in motion over the temperature range studied, as would be expected for a rigid, coherently-scattering structure. However, for the FT12 and FT24 samples (Figs. 2b and c), there is a more pronounced change in motion with temperature, indicating that there is increasing incoherent scattering with temperature from hydrogen contained within these samples. Moreover, as previous characterisation of the FT12 and FT24 samples has shown the only hydrogeneous entities present are encompassed with the hydrocarbonaceous overlayer [8], the motion observed in Fig. 2b and c is uniquely assigned to the presence of the hydrocarbonaceous overlayer [8].

The addition of hydrogen was performed in situ and the increased intensity of the quasielastic peak reflects the increased number of scatters in the neutron beam. This is visible in the increased intensity for the lower temperatures (Fig. 2d–f). The increase in quasielastic peak intensity on hydrogen adsorption across all samples is remarkably similar in magnitude, suggesting that the sorption capacity of the α-Fe2O3 pre-catalyst does not significantly change during the transformation to the active carbided form. It should be remembered however that the quality of the data recorded was limited by the weak interaction with the sample. At lower temperatures the dynamics were too slow to be observed. At higher temperatures, equilibrium shifted towards the gas phase, resulting in decreased signal, preventing determination of the activation energy of diffusion.

3.1 Quasielastic Fitting

Fitting of the data was carried out using the DAVE software package [21] with a two component fit. The experimentally measured resolution function was convoluted with a delta function to represent the elastic scattering, and a single Lorentzian was used to represent the quasielastic broadening. Many fitting models were attempted, with the most consistent results obtained using un-subtracted data. The elastic component in this model represents both the coherent and incoherent elastic scattering, which is the sum of the static and dynamic structure factors, and reduces the number of variables in our interpretation. Attempts to fit the subtracted data, where the static structure from the immobile phase has been removed, resulted in negative peaks at higher Q values.

Even with this restricted model, it was not possible to achieve reliable fitting for the H-dosed sample at 30 K or for the evacuated samples. An example fit for a subset of the hydrogen loaded 50 K data is shown in Fig. 3. Various diffusion models were considered, with little to recommend one over another. For illustration purposes, the simple Fickian model is selected for discussion. In this case the width at half-maximum of the Lorentzian component, FWHM = DsQ2, where Ds is the self-diffusion coefficient. Figure 4 shows plots of the FWHM as a function of Q2 along with linear fits to the data for the hydrogen dosed samples analysed at 50 and 70 K. The error bars shown correspond to the standard error obtained through least squares data fitting. The calculated diffusion coefficients are presented in Table 1 and are comparable to previous reports of hydrogen diffusing on carbon [22]. Little difference is apparent between 50 and 70 K for FT0 in Fig. 4a, and the rate is similar at 50 K for all three catalysts. The 70 K data for the FT12 and FT24 catalysts (Fig. 4b and c) show an increase in diffusion rate that is more pronounced with increasing reaction time. The significant result is that the difference in gradient increases with time on stream, with the FT24 sample showing a pronounced difference. Importantly, Fig. 4 and Table 1 show that hydrogen diffusion within the overlayer is physically feasible and that the more lengthy the catalyst conditioning period, the greater the diffusion rate, whether or not this diffusion follows the Fickian model. These results provide additional evidence for a role of hydrogen diffusion within the evolving catalyst matrix. However, whereas the experimental constraints associated with Fig. 2a–c (absence of probe molecule) permitted deductions to be made concerning an exclusive contribution from the hydrocarbonaceous overlayer, such distinction in not possible when examining the mobility of the liquid hydrogen data. The hydrogen is present in various components of the catalyst matrix, e.g. iron carbide, amorphous carbon or hydrocarbonaceous overlayer, with the hydrogen in each environment having different dynamics. Diffusion for adsorbed hydrogen was observed over the molecular length scales accessed by the QENS measurement (< 2.7 nm), suggesting a bulk-like liquid in contact with the solid below 70 K. Though not directly comparable with the FTS reaction conditions, the differences observed suggest that the changing nature of the evolving catalyst is apparent using cryogenic hydrogen as a surface probe.

Fig. 3
figure 3

Example fits for FT24 loaded with hydrogen at 50 K and Q = 0.48 (a), 0.96 (b), 1.27 (c) and 1.77 Å− 1 (d); limited Q values shown for clarity to illustrate broadening of Lorentzian with increasing Q

Full size image
Fig. 4
figure 4

FWHM variation with Q2; linear fit corresponding to Fickian long-range diffusion of hydrogen dosed onto a FT0, b FT12 and c FT24 catalysts at 50 (grey) and 70 K (red)

Full size image
Table 1 Diffusion constants for Fickian diffusion of hydrogen in catalyst samples
Full size table

The FTS model catalyst is able to sorb hydrogen throughout its life cycle at cryogenic temperatures, either through chemisorption or encapsulation. As the condensed phase only forms within a limited temperature range, complete characterisation of the hydrogen interaction with QENS remains challenging. Use of a sorption probe with a wider liquid range is recommended for future studies. The use of methane as a probe molecule is proposed as an alternative to hydrogen [16].

3.2 Diffraction

The IRIS spectrometer has the additional capability to collect time of flight neutron diffraction data, across a limited Q range in parallel with normal spectroscopic measurement. Diffraction data collected from the three evacuated samples at base temperature is shown in Fig. 5. All patterns show weak peaks from the Al sample holder corresponding to d-spacings of 3.37 and 3.65 Å. The FT0 sample displays a single reflection at 3.68 from the hematite (012) plane. The FT12 and FT24 catalysts show (111) reflections at d-spacings of 3.16 and 3.32 Å. This is consistent with the transformation of the hematite FT0 pre-catalyst into Hägg carbide in samples FT12 and FT24 [8]. Phases were assigned using neutron diffraction patterns computed by the PowderCell software [23] from literature CIF files [24, 25]. No significant differences in diffraction were seen due to temperature or hydrogen loading.

Fig. 5
figure 5

Neutron diffraction data for FT0 (a, yellow), FT12 (b, green) and FT24 (c, orange). Peaks labelled ‘hem’ are assigned to hematite; ‘car’ refers to the Hägg carbide. Vertical lines indicate the position of background from the aluminium sample holder

Full size image

4 Conclusions

With reference to an iron based un-promoted FTS catalyst, samples that have previously experienced 12 and 24 h time on stream in ambient pressure CO hydrogenation at 623 K were investigated for hydrogen diffusion by QENS. The following conclusions can be drawn.

  • An elastic peak intensity scan as a function of temperature for the 24 h sample shows hydrogen incorporation into the catalyst surface structure over the range 20–100 K (Fig. 1).

  • The structure of the unreacted catalyst is rigid over the temperature range 30–70 K but catalysts possessing a hydrocarbonaceous overlayer show increased incoherent scattering (Fig. 2b, c).

  • The analysis of samples loaded with hydrogen at 50 and 70 K suggests diffusion within a condensed hydrogen phase. That the diffusion rate qualitatively varies with catalyst time-on-stream is consistent with the hydrogen associating with the evolving catalyst matrix.

  • QENS has the potential to probe diffusion issues connected with iron-based FTS catalysts however, better correspondence between molecular interactions, superior signal:noise ratio spectra, and spectrometer temporal range is desirable.