Abstract
Pulsed field gradient NMR diffusion measurements provide a non-invasive measure of the mass transport (self-diffusion) characteristics of liquids confined to porous catalyst materials. Here we explore the ability of this technique to probe the diffusive behaviour of a series of short-chain primary alcohols within a mesoporous catalyst support material; through the comparison of our results with highly surface-sensitive NMR relaxation data, we show that the evaluation of bulk-pore diffusion dynamics may provide a simple and indirect method to access and explore surface interaction phenomena occurring at the catalyst-liquid interface.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
It is well-established that the implementation of heterogeneous catalytic process is fundamental to the future of sustainable chemistry [1, 2]. The development of liquid-phase reaction processes is of particular importance regarding the enhanced utilisation of biomass—waste organic matter derived from food refuse, animal waste and used vegetable oils—which may be processed to produce renewable platform chemicals and fuels [3,4,5]. While it is clear that relevant catalytic processes are necessary to facilitate such transformations [6,7,8,9], such reaction systems can differ significantly from the gas-phase processes encountered in more traditional catalyst applications [10]. Most notably, biomass-derived compounds typically possess multiple polar functional groups; the resulting intermolecular interactions lead these materials to exhibit notably low volatilities and vapour pressures, such that effective transportation relies heavily on the addition of solvents [11]. It follows that the relevant chemistry and mass transport phenomena are dominated by the liquid-phase; while this is favourable for efficient macrokinetic transport processes, the high molecular density within such systems can lead to complex and competitive dynamics at the catalyst surface [11]. As a result, the development of robust approaches for the investigation of liquid-phase dynamics within catalytically relevant porous media has become a significant goal within modern catalytic research.
Nuclear magnetic resonance (NMR) relaxation and diffusion measurements have shown significant promise in this area [12]. Obtaining useful insight from traditional NMR chemical shift phenomena is challenging when considering liquid-saturated porous material as a result of significant line-broadening effects due to adsorption interactions and magnetic susceptibility differences at the solid–liquid interface. While such effects may be mitigated through the observation of nuclei known to exhibit a wide range of chemical shift values (e.g. 13C), the resolution of such measurements is often limited by their inherently low natural abundance. The measurement of nuclear spin relaxation rates and molecular self-diffusion coefficients are, however, broadly independent of observable chemical shift phenomena. Rather, such measurements depend on the rate of decay of relevant NMR signals as a result of molecular dynamics. NMR relaxation studies have been particularly successful in determining adsorption phenomena within liquid-saturated catalyst materials; such measurements probe the longitudinal (\(T_{1}\)) and/or transverse (\(T_{2}\)) relaxation time constants of the confined liquid. Notably, the ratio of these time constants \(T_{1} /T_{2}\) is now well-established as a measure of relative surface affinity exhibited by liquids and liquid mixtures at the catalyst pore surface [13,14,15], and we have recently extended such analysis to demonstrate that this ratio may be interpreted as a quantitative indicator of adsorption energetics [16, 17].
Alternatively, pulsed field gradient (PFG) NMR diffusion measurements rely on the application of a series of short magnetic field gradient pulses to encode and then decode the position of nuclear spins either side of an observation period (see Sect. 2). Such measurements have been widely applied to the elucidation of mass transport phenomena in materials of relevance to heterogeneous catalysis [18], including mass-transfer limitations [19] and the influence of pore structure design [20,21,22]. Intriguingly, we note that liquids confined to porous materials will be subject to significant and repeated interactions with the pore walls, such that the measurement of their diffusive characteristics may present a potential method for the elucidation of surface interaction phenomena. While PFG NMR diffusion measurements have previously been applied to obtain direct insight into surface diffusion phenomena within liquid-saturated catalyst materials [23], the direct observation of dynamics associated with the adsorbed surface layer is challenging due to its small population and self-diffusion coefficient, as well as the inherently rapid rates of nuclear spin relaxation of species near the pore surface; such characteristics significantly reduce the observable signal from this layer, relative to that obtained from the bulk-pore population. It follows that this approach is only possible with access to NMR hardware capable of producing both large static magnetic fields and field gradient pulses ranging in the several \({\text{T m}}^{ - 1}\). Herein, with the aid of preliminary diffusion data obtained from a series primary alcohols within a silica catalyst support, we discuss how the observation of self-diffusion phenomena associated with the bulk-pore population of confined liquids may be utilised as an indirect method for the elucidation of surface phenomena within liquid-saturated mesoporous materials. This approach is predicted to be applicable to experiments using a range of NMR hardware, including low magnetic field benchtop systems [24].
2 Theory
2.1 Pulsed Field Gradient NMR
Given the general relationship between static magnetic field strength \(B_{0}\), gyromagnetic ratio \(\gamma\) and Larmor frequency \(\omega_{0}\),
the application of a spatially varying magnetic field (a gradient) \({\mathbf{g}} = \left( {g_{x} ,g_{y} ,g_{z} } \right)\) causes the precessional frequency of the spin system to vary with position \({\mathbf{r}}\) [25],
For a gradient applied in only the z-direction the frequency is
and so when viewed from the rotating frame of reference—that being a frame of reference which precesses at \(\omega_{0}\)—results in a spatially-dependent offset [26]
The time-evolution of the Larmor precession therefore exhibits a clear dependence on the spatial coordinate \(z\). Indeed, provided that the sample magnetisation has been excited into the transverse plane through the application of an appropriate radio frequency (RF) pulse sequence, the spatial dependence of \({{\Omega }}\left( z \right)\) results in rotation of the transverse magnetisation by a phase factor \(\exp \left( {i\phi } \right)\). The phase \(\phi\) is given by
where \(t_{g}\) defines the length of the applied gradient pulse. Neglecting any details of relaxation effects or chemical shift phenomena, and assuming the absence of any phase offset, the complex transverse magnetisation following this gradient pulse may then be expressed as
where \(M_{0}\) is the magnitude of the transverse magnetisation immediately prior to the pulse. Importantly, this expression describes a spatially varying magnetisation helix of pitch \(2\pi \left( {\gamma g_{z} t_{g} } \right)^{ - 1}\) which encodes the position of the nuclear spins under study [27].
PFG NMR diffusion experiments extend the ability to encode the spatial positioning of nuclear spins to the measurement of molecular displacement rates. Such measurements are performed by employing multiple field gradient pulses separated by a diffusion observation time \(t_{{{\Delta }}}\). Consider, for example, the displacement of a single spin by a factor \({{\Delta }}z = z^{\prime} - z\) in which the z-coordinate changes from \(z\) at time \(t = 0\) to \(z'\) at \(t = t_{{{\Delta }}}\). Displacement of the spin during the observation time results in a phase shift of the form
The application of a second gradient pulse of equal magnitude but opposite polarity aims to remove the spatial encoding defined by Eq. (6). In the absence of any diffusive displacement \(\Delta z = 0\) and the transverse magnetisation returns to its original state. If molecular motion has occurred, however, \(\Delta z \ne 0\) and the original magnetisation is not recovered. For a spin system of arbitrary size the corresponding NMR signal is given by
where \(S\left( 0 \right)\) is the signal obtained in the absence of any applied field gradient. The propagator \(P\left( {\Delta ,t_{\Delta } } \right)\) describes the probability that a randomly selected spin will experience a displacement \(\Delta z\) during \(t_{{{\Delta }}}\), and for normal diffusion is described by the Gaussian function
where \(D\) is the self-diffusion coefficient which quantifies the rate of displacement. It follows that for \({{\Delta }}z \ne 0\) diffusive attenuation of the signal \(S(g_{z} )\) will be observed. Combining Eqs. (8) and (9) we obtain the general expression [28]
where \(t_{eff}\) is an effective observation time which accounts for diffusion during the gradient pulses, and depends on the NMR pulse sequence employed. It follows that \(D\) may be obtained by incrementing \(g_{z}\) through a range of values and fitting the acquired attenuation data to Eq. (10).
2.2 Diffusion in Restricted Systems
The diffusive behaviour of liquids confined to porous media is complicated by restrictions arising from the geometrical features of the accessible pore structure [29]. The application of PFG NMR measurements to such systems provides an effective self-diffusion coefficient \(D_{eff}\), which is dependent on the characteristics of the confining pore system and on the diffusion observation time employed [27, 30]. Differing degrees of diffusive restriction may be characterised by the dimensionless parameter [25]
where \(D_{0}\) is the self-diffusion coefficient of the unrestricted liquid and \(\ell\) is a characteristic length scale defining the pore structure. This expression provides a simple comparison between pore size and the mean squared displacement (MSD) of the diffusing species \(\left( {\Delta z} \right)^{2}\), which, for the evolution of a system over a time period \(t\) may be related to the self-diffusion coefficient of the system according to the Einstein expression,
For restricted diffusion observed with short \(t_{{{\Delta }}}\) a short-time diffusion limit emerges for which Eq. (11) gives \({{\Xi }} \ll 1\). Within this diffusive regime the majority of molecular displacements are not large enough for significant restrictions to occur from interactions with the pore walls, such that the observed effective self-diffusion coefficient tends towards \(D_{0}\). An intermediate regime emerges for longer \(t_{\Delta }\) values, and is characterised by \(\Xi \approx 1\). This regime corresponds to a substantial portion of the diffusing molecules experiencing restrictions due to encounters with the pore walls, such that the MSD is reduced relative to that associated with unrestricted diffusion occurring over the same \(t_{{{\Delta }}}\). An effective self-diffusion coefficient is observed which depends on both \(t_{\Delta }\) and the surface-to-volume (\(S/V\)) of the confining pore structure according to [27]
In the present work we concentrate on diffusive characteristics observed at long \(t_{{{\Delta }}}\) values, wherein all of the diffusing molecules are subject to significant interactions with the pore walls. This long-time diffusion limit is characterised by \(\Xi \gg 1\). For isolated pores the MSD is limited to the square of the pore diameter and \(D_{eff} = 0\); for a well-connected pore network, however, the effective self-diffusion coefficient \(D_{eff} \left( {t_{\Delta } \to \infty } \right) \equiv D_{\infty }\) is reduced from that of the unrestricted liquid according to [28]
where \(\tau\) is the tortuosity of the accessible pore network.
We note here that while Eq. (14) suggests that knowledge of the pore structure tortuosity may simply be obtained through the ratio \(D_{0} /D_{\infty }\), this is typically far from the case. Indeed, deviations in this ratio across a range of molecular liquids within the same pore structure are common, implying sensitivity to interactions between the probe liquid and porous matrix. The results of such measurements are instead described in terms of the so-called PFG interaction parameter [31],
For weakly interacting non-viscous liquids (such as short-chain alkanes) restricted within mesoporous media this ratio is often considered equal to the tortuosity of the accessible pore network, \(\xi = \tau\) [32]. The observation that \(\xi > \tau\) may be facilitated by non-negligible adsorption interactions at the solid liquid interface, or by the occurrence of hindered diffusion, whereby region of the porous materials exhibit pore diameters of a similar size to the diffusion probe molecule employed. Prevalent examples of such are configurational diffusion through the pore network of zeolites, and the effects of coke deposition [33, 34]. Conversely, the observation that \(\xi < \tau\) has been proposed to originate from the disruption of dynamic hydrogen bonding networks by the presence of the pore walls [20, 32]. Herein, we present a brief investigation into the PFG interaction parameter presented by a homologous series of short-chain primary alcohols within an industrial silica catalyst support; the diffusion of cyclohexane is also investigated as a weakly interacting reference, and the assumption that such liquids may be used to provide an estimate of the pore structure tortuosity addressed.
3 Materials and Methods
3.1 Sample Preparation
A commercial G57 silica catalyst support was obtained from Johnson Matthey; material textural properties are summarised in Table 1. Methanol, ethanol, 1-propanol, 1-butanol and cyclohexane (\(\ge 99 \%\) purity, Sigma Aldrich) were used as received. The silica support material was first dried at 105 °C for 12 h. Imbibed samples were then prepared by soaking in excess liquid for at least 24 h under ambient conditions. The silica was then separated from each liquid and rolled over a pre-soaked filter paper to remove any liquid on the outer surface of the material. Finally, the imbibed material was transferred to sealed 5 mm NMR tubes to a height of approximately 15 mm, which were sealed with a plug of soaked filter paper so as to saturate the atmosphere within each NMR tube.
3.2 Pulsed Field Gradient NMR Measurements
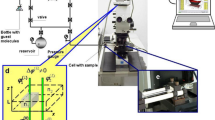
A summary of the PFG NMR acquisition parameters employed in this work is provided in Table 2; all measurements were performed at 20.0 ± 0.1 °C and at ambient pressure. 1H PFG NMR diffusion experiments were performed using a Bruker DMX spectrometer equipped with a 7.1 T superconducting magnet (corresponding to a 1H frequency of 300.13 MHz) and a Bruker Biospin Diff-30 diffusion probe capable of producing magnetic field gradient pulses of up to 11.76 \({\text{T m}}^{ - 1}\). The diffusion of unrestricted liquids was analysed using the pulsed gradient stimulated echo (PGSTE) sequence illustrated in Fig. 1a [35]. Unrestricted self-diffusion coefficients \(D_{0}\) were obtained from this analysis by fitting the acquired signal attenuation data to the Stejskal–Tanner equation [35],
where
PFG NMR diffusion pulse sequence diagrams for a PGSTE and b APGSTE analysis. Each pulse sequence consists of a radio frequency (RF) and gradient pulse (\(\mathrm{g}\)) axis. All remaining symbols are defined within the main text and Table 2
Our PGSTE measurements were performed by holding \(t_{g} = 1\) ms constant and varying the magnetic field gradient strength; 16 linearly spaced \(g_{z}\) values were employed while the observation time was set to \(t_{\Delta } =\) 50 ms. Trapezoidal gradient pulses of area \(t_{g} g_{z}\) were employed to ensure consistent pulse shaped across all values of \(g_{z}\). A homospoil gradient of magnitude \(g_{max} /3\) (where \(g_{max}\) is the magnitude of the maximum applied gradient) and length \(t_{H} =\) 5 ms was also applied during the storage interval \({\text{T}}\) to remove any remaining coherent transverse magnetisation. The echo time was \(\tau_{e} =\) 3.2 ms.
The diffusion of liquids restricted to mesoporous silica was analysed using the alternating pulsed gradient stimulated echo (APGSTE) sequence illustrated in Fig. 1b [36]; this sequence was employed to minimise the influence of any background magnetic field gradients resulting from susceptibility differences at the solid–liquid interface [37]. The effective self-diffusion coefficients of restricted liquids \(D_{eff}\) were therefore obtained by fitting the acquired signal attenuation data to
where [36]
In analogy to our PGSTE experiments, APGSTE analysis was carried out by holding \(t_{g} =\) 1 ms constant and varying \(g_{z}\) across 16 linearly spaced values; in this case, however, the observation time was set to \(t_{\Delta } =\) 100 ms to allow for sufficient self-diffusion throughout the silica pore network. Trapezoidal gradient pulse lobes (in this case of area \(t_{g} g_{z} /2\)) and a homospoil gradient of magnitude \(g_{max} /3\) and length \(t_{H} =\) 10 ms were employed, while the echo time was \(\tau_{e} =\) 2.7 ms.
4 Results and Discussion
Our acquired PGSTE and APGSTE diffusion attenuation data are show in Fig. 2a and b, respectively. The resulting self-diffusion coefficients are detailed in Table 3. In all cases the diffusion observation time for our APGSTE analysis was set to \(t_{\Delta } =\) 100 ms; given the resultant effective self-diffusion coefficients \(D_{eff}\) obtained from these experiments we may readily calculate that the corresponding root mean squared displacements (\(RMSD = \sqrt {2t_{\Delta } D_{eff} }\)) of the confined liquids fall within the range 0.64–1.59 µm. Clearly these displacements are far larger than the average pore size of the silica material employed here (\(d_{pore} =\) 15 nm), resulting in molecular self-diffusion across a significant number of pore diameters during this observation time. In turn, this suggests that we may define \(D_{eff} \left( {t_{\Delta } = 100\, {\text{ms}}} \right) \approx D_{\infty }\). Calculation of the restricted diffusion parameter \({{\Xi }}\) according to Eq. (11) supports this assumption, with each of the five liquids investigated here exhibiting \(\Xi \gg 1\), indicative of the long-time diffusion limit. It follows that our acquired \(D_{eff}\) values may be used to calculate the PFG interaction parameter according to Eq. (15); these value are also provided in Table 3.
PFG NMR signal attenuation data for short-chain primary alcohols and cyclohexane in a the unrestricted bulk and b restricted within mesoporous silica. Solid lines in a represent a fit to Eqs. (16) and (17) while solid lines in b represent a fit to Eqs. (18) and (19). The resultant self-diffusion coefficients are detailed in Table 3
It is clear from our calculated \(\xi\) values that the primary alcohols investigated here exhibit larger \(D_{0} /D_{eff}\) values than expected from the tortuosity of our silica material, which may be approximated from our cyclohexane diffusion data, such that \(\tau \approx \xi \approx 1.5\). This value is in good agreement with previous investigations into the tortuosity of similar mesoporous catalyst support materials [32]. The observed increase in \(\xi\) away from this value suggest that adsorption interactions at the solid–liquid interface have a non-negligible effect on the self-diffusion of our primary alcohols within this material. Furthermore, there is a clear increase in \(\xi\) with increasing alcohol carbon chain length; notably, this trend is similar to that previously observed when considering the nuclear spin relaxation characteristics (\(T_{1} /T_{2}\) ratio) of these same adsorbate/adsorbent systems at intermediate magnetic field [17]. This observation is of particular interest as we have shown that the \(T_{1} /T_{2}\) ratio obtained under such conditions may be directly related to adsorption energetics [16]. As such, we provide in Fig. 3 a direct comparison of our calculated \(\xi\) data with these \(T_{1} /T_{2}\) values. We find that there exists a remarkably strong, positive correlation between these two measurements. Given the well-established sensitivity of the ratio \(T_{1} /T_{2}\) to surface phenomena, this observation implies that the restricted diffusion observed through our APGSTE analysis exhibits significant sensitivity to adsorption interactions at the pore surface. The solid diagonal line within Fig. 3 illustrates a linear fit to the data and suggests that \(D_{0} /D_{\infty } \approx \left( {T_{1} /T_{2} } \right)/10 + 1.3\). Of particular interest is the solution to this equation for \(T_{1} /T_{2} = 1\), indicative of unrestricted—and therefore totally non-interacting—liquids [38]. In this case our data fit predicts that in the absence of any adsorption interactions \(D_{0} /D_{\infty } \approx 1.4\). This value is clearly in excellent agreement with the tortuosity implied through our cyclohexane diffusion data, providing validation for the use of short chain alkanes as a measure of tortuosity in such systems.
Comparison of the PFG interaction parameter \(\xi\) with ratio of NMR relaxation time constants \(T_{1} /T_{2}\) (a measure of surface affinity) obtained for these same adsorbate/adsorbent systems. NMR relaxation data is taken from Ref [17]
It is appropriate here to briefly interrogate how our self-diffusion measurements might exhibit such sensitivity to adsorption phenomena. To a simple approximation our liquid-saturated silica may be treated as a biphasic system, consisting of an adsorbed surface layer and a bulk-like liquid population towards the centre of the pores. The observed diffusion characteristics of such systems is highly dependent upon the rate of exchange between the two populations, relative to the diffusion observation time employed. If the observation time is short with respect to this exchange process (biphasic slow-exchange) then the resulting PFG data will attenuate as
Here \(S\left( {g_{z} } \right)/S\left( 0 \right)\) is the normalised signal attenuation, \(D_{1}\) and \(D_{2}\) are the self-diffusion coefficients associated with populations \(P_{1}\) and \(P_{2}\) respectively (with \(P_{1} = 1 - P_{2}\)), and \(b\) depends on the NMR pulse sequence employed. Data of this form will be highly apparent in the resulting log-attenuation plot as a curve with limiting gradients \(- D_{1}\) and \(- D_{2}\). [23] Conversely, if the diffusion observation time is long with respect to the exchange process (biphasic fast-exchange) then the resulting PFG attenuation data will follow
with
In this case a single self-diffusion coefficient \(D\) is observed, defined by the weighted average of the rates of diffusion within the two populations. Given the long diffusion observation time employed in our APGSTE measurements it is reasonable to assume that this biphasic fast-exchange approach is applicable to the self-diffusion processes explored here; this interpretation is supported by the log-attenuation plots in Fig. 2, which present a single diffusion coefficient as characterised by a straight line on the log-scale.
In the present case we must also take account of the influence of the pore structure tortuosity on our observed self-diffusion characteristics. In particular, the effective self-diffusion coefficient of our restricted liquids may be defined according to
Here \(D_{0}\) is again the self-diffusion coefficient of the unrestricted bulk, while \(D_{surf}\) is the self-diffusion coefficient for species within an adsorbed surface layer of population \(P\); \(\tau\) is again the tortuosity of the overall pore structure while \(\tau_{surf}\) is an apparent surface tortuosity which influences diffusion through the adsorbed surface layer [39]. This tortuosity parameter relates to the topology of the pore surface on the length scale \(\ell_{s} \sim \sqrt {D_{surf} \tau_{s} }\) [30], where \(\tau_{s}\) is the mean surface residence time of the adsorbate at the pore surface. It follows from this expression that for \(\left( {1 - P} \right)D_{0} /\tau \gg PD_{surf} /\tau_{surf}\) we obtain \(D_{0} /D_{\infty } \approx \tau\). However, if the surface term \(PD_{surf} /\tau_{surf}\) is non-negligible then \(D_{0} /D_{\infty } > \tau\). It follows that our observed trend in PFG interaction parameter might be explained through the increased prominence of this surface term with increasing alcohol carbon chain length. Furthermore, we note that for a series of similar adsorbates (e.g. short-chain primary alcohols) within the same mesoporous material, the prominence of this surface term will be dominated by the surface diffusion coefficient \(D_{surf}\). This diffusion coefficient provides a potential link to adsorption energetics through the usual Arrhenius form
where \(E_{a}\) is the activation energy for the surface diffusion process, typically considered some fraction of the adsorption energy [40], \(R\) is the gas constant, \(T\) the absolute temperature, and \(D_{surf,0}\) the Arrhenius pre-exponential factor for activated surface diffusion. While this expression does not provide a direct explanation for the strong linear relationship observed between the two data sets in Fig. 3, perturbation of the observed self-diffusivity behaviour by activated surface dynamics clearly presents a promising link between these different measurements. Indeed, recalling that the surface diffusion coefficient may also be expressed in terms of the average adsorption site residence time \(\tau_{m}\) and the mean distance between adsorption sites \(\lambda\) as \(D_{surf} = \lambda^{2} /4\tau_{m}\) [41], and that the expression \(T_{1} /T_{2} \propto - 1/\ln \left( {\tau_{m} } \right)\) has been derived elsewhere [16], some simple algebraic manipulation suggests that the relationship between surface relaxation and self-diffusion should be exponential in nature, rather than the linear expression obtained from the data in Fig. 3. We note, however, that a far more detailed evaluation of this relationship over a wider range of data points is necessary to determine whether such an expression is robust; such experiments are the subject of future investigation.
5 Conclusion
This work has detailed a brief evaluation of the diffusive characteristics of a series of short-chain primary alcohols and cyclohexane within a commercial mesoporous silica catalyst support material. Through the application of PFG NMR diffusion measurements we have revealed a distinct inequality in the ratio of unrestricted-to-restricted self-diffusion coefficients across the series of liquids investigated. Indeed, while this ratio is often defined as a measure of the tortuosity of the accessible pore space, our results illustrate a notable increase in this parameter with increasing carbon chain length. A direct comparison of this data with the results of nuclear spin relaxation measurements reported previously reveal a strong, positive correlation, and suggests that our NMR diffusion data is sensitive to adsorption interactions occurring at the solid–liquid interface. A biphasic fast-exchange theory has been presented which suggests that the sensitivity of bulk-pore diffusivity to surface phenomena occurs as a result of the influence of a surface diffusion term. Overall, the results described here demonstrate that such measurements may be a potential source of additional insight for providing rational connections between adsorption phenomena and mass transfer characteristics within systems of relevance to heterogeneous catalysis.
References
Friend CM, Xu B (2017) Heterogeneous catalysis: a central science for a sustainable future. Acc Chem Res 50:517–521
Christensen CH, Rass-Hansen J, Marsden CC et al (2008) The renewable chemicals industry. Chemsuschem 1:283–289
Wilson K, Lee AF (2016) Catalyst design for biorefining. Philos Trans R Soc A Math Phys Eng Sci 374:20150081
Huber GW, Iborra S, Corma A (2006) Synthesis of transportation fuels from biomass: chemistry, catalysts, and engineering. Chem Rev 106:4044–4098
Corma Canos A, Iborra S, Velty A (2007) Chemical routes for the transformation of biomass into chemicals. Chem Rev 107:2411–2502
Resasco DE, Wang B, Sabatini D (2018) Distributed processes for biomass conversion could aid UN Sustainable Development Goals. Nat Catal 1:731–735
Gallezot P (2012) Conversion of biomass to selected chemical products. Chem Soc Rev 41:1538–1558
Kunkes EL, Simonetti DA, West RM et al (2008) Catalytic conversion of biomass to monofunctional hydrocarbons and targeted liquid-fuel classes. Science 322:417–421
Chheda JN, Huber GW, Dumesic JA (2007) Liquid-phase catalytic processing of biomass-derived oxygenated hydrocarbons to fuels and chemicals. Angew Chem Int Ed 46:7164–7183
Murphy BM, Xu B (2018) Foundational techniques for catalyst design in the upgrading of biomass-derived multifunctional molecules. Prog Energy Combust Sci 67:1–30
Sievers C, Noda Y, Qi L et al (2016) Phenomena affecting catalytic reactions at solid-liquid interfaces. ACS Catal 6:8286–8307
Gladden LF (2013) Magnetic resonance in reaction engineering: beyond spectroscopy. Curr Opin Chem Eng 2:331–337
Weber D, Mitchell J, McGregor J, Gladden LF (2009) Comparing strengths of surface interactions for reactants and solvents in porous catalysts using two-dimensional NMR relaxation correlations. J Phys Chem C 113:6610–6615
Pini R, Joss L (2019) See the unseen: applications of imaging techniques to study adsorption in microporous materials. Curr Opin Chem Eng 24:37–44
Kinn BE, Myers TR, Allgeier AM (2019) Surface enhanced nuclear magnetic resonance relaxation mechanisms and their significance in chemical engineering applications. Curr Opin Chem Eng 24:115–121
D’Agostino C, Mitchell J, Mantle MD, Gladden LF (2014) Interpretation of NMR relaxation as a tool for characterising the adsorption strength of liquids inside porous materials. Chem A Eur J 20:13009–13015
Robinson N, Robertson C, Gladden LF et al (2018) Direct correlation between adsorption energetics and nuclear spin relaxation in a liquid-saturated catalyst material. ChemPhysChem 19:2472–2479
Chmelik C, Kärger J (2010) In situ study on molecular diffusion phenomena in nanoporous catalytic solids. Chem Soc Rev 39:4864–4884
D’Agostino C, Ryabenkova Y, Miedziak PJ et al (2014) Deactivation studies of a carbon supported AuPt nanoparticulate catalyst in the liquid-phase aerobic oxidation of 1,2-propanediol. Catal Sci Technol 4:1313–1322
Rottreau TJ, Parlett CMA, Lee AF, Evans R (2017) Diffusion NMR characterization of catalytic silica supports: a tortuous path. J Phys Chem C 121:16250–16256
Isaacs MA, Robinson N, Barbero B et al (2019) Unravelling mass transport in hierarchically porous catalysts. J Mater Chem A 7:11814–11825
Schneider D, Mehlhorn D, Zeigermann P et al (2016) Transport properties of hierarchical micro-mesoporous materials. Chem Soc Rev 45:3439–3467
Weber D, Sederman AJ, Mantle MD et al (2010) Surface diffusion in porous catalysts. Phys Chem Chem Phys 12:2619–2624
Mitchell J, Gladden LF, Chandrasekera TC, Fordham EJ (2014) Low-field permanent magnets for industrial process and quality control. Prog Nucl Magn Reson Spectrosc 76:1–60
Price WS (1997) Pulsed-field gradient nuclear magnetic resonance as a tool for studying translational diffusion: Part 1. Basic theory. Concepts Magn Reson 9:299–336
Stallmach F, Galvosas P (2007) Spin echo NMR diffusion studies. Annu Rep NMR Spectrosc 61:51–131
Callaghan PT (2011) Translational dynamics and magnetic resonance: principles of pulsed gradient spin echo NMR. Oxford University Press, Oxford
Price WS (2009) NMR studies of translational motion. Cambridge University Press, Cambridge
Stallmach F, Kärger J (1999) Potentials of pulsed field gradient NMR for investigation of porous media. Adsorption 5:117–133
Valiullin R (2016) Diffusion NMR of confined systems. Royal Society of Chemistry, London
Mantle MD, Enache DI, Nowicka E et al (2011) Pulsed-field gradient NMR spectroscopic studies of alcohols in supported gold catalysts. J Phys Chem C 115:1073–1079
D’Agostino C, Mitchell J, Gladden LF, Mantle MD (2012) Hydrogen bonding network disruption in mesoporous catalyst supports probed by PFG-NMR diffusometry and NMR relaxometry. J Phys Chem C 116:8975–8982
Wood J, Gladden LF (2003) Effect of coke deposition upon pore structure and self-diffusion in deactivated industrial hydroprocessing catalysts. Appl Catal A Gen 249:241–253
Zhou B, Liao Z, Mattea C et al (2018) Solvents molecular mobility in coked catalyst ZSM-5 studied by NMR relaxation and pulsed field gradient techniques. Ind Eng Chem Res 57:6647–6653
Stejskal EO, Tanner JE (1965) Spin diffusion measurements: spin echoes in the presence of a time-dependent field gradient. J Chem Phys 42:288–292
Cotts R, Hoch MJ, Sun T, Markert J (1989) Pulsed field gradient stimulated echo methods for improved NMR diffusion measurements in heterogeneous systems. J Magn Reson 83:252–266
Mitchell J, Chandrasekera TC, Johns ML et al (2010) Nuclear magnetic resonance relaxation and diffusion in the presence of internal gradients: the effect of magnetic field strength. Phys Rev E 81:026101
Kowalewski J, Mäler L (2017) Nuclear spin relaxation in liquids: theory, experiments, and applications, 2nd edn. CRC Press, Boca Raton
Komiyama H, Smith JM (1974) Surface diffusion in liquid-filled pores. AIChE J 20:1110–1117
Medveď I, Černý R (2011) Surface diffusion in porous media: a critical review. Microporous Mesoporous Mater 142:405–422
Lombardo SJ, Bell AT (1991) A review of theoretical models of adsorption, diffusion, desorption, and reaction of gases on metal surfaces. Surf Sci Rep 13:3–72
Acknowledgements
N.R. acknowledges the Catalysis@Cambridge initiative, University of Cambridge, for the award of a studentship. The authors also thank Prof Lynn F. Gladden, University of Cambridge, for access to the NMR equipment.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors have no conflicts of interest to declare.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Robinson, N., D’Agostino, C. NMR Investigation into the Influence of Surface Interactions on Liquid Diffusion in a Mesoporous Catalyst Support. Top Catal 63, 319–327 (2020). https://doi.org/10.1007/s11244-019-01209-7
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11244-019-01209-7