1 Introduction

Diffusion, i.e. the random movement of objects, is among the omnipresent and most fundamental phenomena in our world. It may be encountered with objects of any size, ranging from atoms and molecules up to the plants and animals spreading in their habitat, and may even refer to non-physical “objects” such as words and technological knowhow. The fundamental relations of diffusion are, correspondingly, applicable to a wide range of different problems (Bunde et al. 2018). Definite predictions, however, necessitate an exact knowledge about the elementary phenomena, giving rise to the type of movement under consideration. It is therefore no surprise that our knowledge about the diffusion of atoms in a solid (Philibert 1991; Mehrer 2007) or of molecules in a liquid (Cussler 2009), with trillions of identical objects under study is far more advanced than our options to predict, for example, the spreading or extinction of a given species in a certain habitat (Vogl 2019).

Within this spectrum of possibilities, molecular diffusion within nanoporous host systems (Kärger et al. 2012) occupies a medium position. Molecules of a certain species, on the one hand, may indeed be considered to be identical and, except in the very smallest systems, the numbers are sufficiently large to ensure reliable statistics. Problems with diffusion studies in nanoporous materials tend to arise, however, due to the fact that the host systems under study are often of only microscopic extension. Diffusion measurement over displacements small in comparison with these extensions (i.e., the application of “microscopic” measuring techniques) presents a particular challenge for the experimentalist, which increases the risk of inaccuracies in the experimental data. Alternatively, application of “macroscopic” techniques with the aim of extracting the “microscopic” diffusivities by using a suitable model is subject to the risk of misinterpretation arising from the use of an incorrect or inadequate model. The “real” structure of a given nanoporous material is, moreover, known to depend on numerous influences, including the procedures of synthesis, storage and activation (Ruthven 2012). For example, with seemingly identical crystals of commercially produced zeolites of type SAPO-34 from the same batch, surface permeabilities were found to vary over almost two orders of magnitude (Remi et al. 2015), suggesting that very minor differences in synthesis conditions may have a major effect.

Molecular diffusion determines the performance of nanoporous materials in numerous processing applications involving selective adsorption (Ruthven et al. 1994; Schüth et al. 2002) and catalytic conversion (Ertl et al. 2008; van de Voorde and Sels 2017) since the production rate of the value-added products can never exceed the rate of mass transfer between the pore space and the surrounding fluid. In addition to its relevance to fundamental science, knowledge about mass transfer and diffusion-controlled reactions is therefore of immediate practical relevance for performance enhancement by the application of transport-optimized materials (Mitchell et al. 2015; Hartmann and Schwieger 2016; Schneider et al. 2016; Trogadas et al. 2016). Correlated with the numerous mechanisms which, for a given host–guest system, may become rate controlling for overall mass transfer, there are many options for transport enhancement. Which of these options is the most promising depends on the given circumstances. There is scarcely any better way towards their elucidation than direct measurement of the relevant transport characteristics, particularly the diffusivities. However, in practice, it is not always easy to determine which features of mass transfer are really under observation in a given experiment (Valiullin 2015).

The present special issue of the Adsorption journal deals with such measurements. Diversity in the host structure and, related to it, in the processes and phenomena under study, together with a spread over many orders of magnitude in the relevant diffusivities have led to the development of numerous techniques, which all have their strengths and weaknesses; these are discussed in detail in the papers in this issue. The contents are rounded off with a discussion of diffusion in the individual nanoporous particles, superimposed on mass transfer in a macroscopic column, with examples illustrating the application of diffusion theory and modelling. In addition to their relevance for fundamental research such an approach can also enhance the accuracy and reliability of diffusion measurement.

The present contribution serves as a general introduction to diffusion phenomena in nanoporous materials. In Sect. 2 we start by introducing the main relations of diffusion within an infinitely extended, isotropic and homogeneous medium. Section 3 goes a step further by considering possible deviations, including diffusion anisotropy, internal barriers and pore hierarchies. Section 4 deals with the problems that emerge from the microscopic size of the particles/crystallites under study. The concluding Sect. 5 summarizes some of the issues, which commonly arise during experimental measurements. It refers, in particular, to the benefits that can be derived from parallel simulations and theoretical analysis.

2 Diffusion fundamentals

2.1 The “different” diffusivities

We start by considering a porous host large enough so that the overwhelming majority of guest molecules do not come into contact with the boundary. The host material is assumed to be isotropic and homogeneous with reference to the considered diffusion path lengths (Titze et al. 2015b) and inert to the presence of the guest molecules. It therefore serves as an ideal coordinate system for indicating the positions of the individual guest molecules and their fluxes. Figure 1 illustrates typical situations under which information about the relevant transport parameters may be obtained (Kärger 2015). The presence of a gradient of molecular concentration as a prerequisite of transport diffusion, considered in Fig. 1a, is immediately understood to give rise to a flux in the direction of decreasing concentration. This flux increases in direct proportion with the concentration gradient (Kärger and Ruthven 2016) leading to Fick’s 1st law of diffusion

$$ j = - D_{T} \frac{\partial c}{{\partial x}} $$
(1)
Fig. 1
figure 1

Definition of the various coefficients of molecular transport in microporous materials and schemes of measurement: a transport diffusivity, b self-diffusivity by tracer exchange and Fick’s first law, c self-diffusivity by the Einstein relation, d barrier permeability. Reprinted with permission from Kärger (2015)

Full size image

The factor of proportionality correlating the flux j with the concentration gradient is referred to as the transport or Fickian diffusivity; alternatively also the terms collective or chemical diffusivity are in use. The term “diffusivity” is synonymous with “diffusion coefficient” and “coefficient of diffusion”.

Combination of (1) with the law of matter conservation (the “continuity equation”)

$$ \frac{\partial c}{{\partial t}} = - \frac{\partial j}{{\partial x}} $$
(2)

yields Fick’s 2nd law (for a unidimensional system):

$$ \frac{\partial c}{{\partial t}} = \frac{\partial }{\partial x}\left( {D_{T} \frac{\partial c}{{\partial x}}} \right) = D_{T} \left( c \right)\frac{{\partial^{2} c}}{{\partial x^{2} }} + \frac{{dD_{T} \left( c \right)}}{dc}\left( {\frac{\partial c}{{\partial x}}} \right)^{2} $$
(3)

Equation (3) simplifies to

$$ \frac{\partial c}{{\partial t}} = D_{T} \frac{{\partial^{2} c}}{{\partial x^{2} }} $$
(4)

if the diffusivity is either independent of concentration or if, over the concentration interval considered in the measurement, the influence of concentration dependence (as represented by the second term on the right hand side of (3)) is negligibly small. Note that, for attaining reasonably defined concentrations and fluxes, the unit volumes and areas considered for their definition have to notably exceed the pore extensions.

Self-diffusion measurements are performed under equilibrium conditions as considered in Fig. 1b. There are no changes in the overall guest distribution so that information about molecular diffusion can only be attained by making guest molecules distinguishable from each other. This is conventionally achieved by the use of isotopes (Dyer 1970; Goddard and Ruthven 1986). In Fig. 1b two different types of isotopes (of one and the same chemical species and, thus, implied to be of identical microdynamic properties) are indicated by different shades of color. With the same reasoning as applied already with reference to transport diffusion in Fig. 1a, the flux of either of the two isotopes may be correlated with their concentration gradients by Fick’s 1st law

$$ j^{*} = - D\frac{{\partial c^{*} }}{\partial x} $$
(5)

The asterisk indicates that fluxes and concentrations of only “labelled” molecules (i.e. of one or the other isotope) are considered. The factor of proportionality is referred to as the self- or tracer diffusivity. Given the different physical situations (namely non-equilibrium vs. equilibrium conditions), self- and transport diffusivities generally differ from each other. Only in the limit of sufficiently small concentrations (“loadings”), when guest-guest interactions are of only minor relevance, both parameters converge. This finding follows the more general rule that a distinction between equilibrium and non-equilibrium phenomena in a system becomes meaningless in the absence of mutual interactions (Prigogine 1997).

Like the transport diffusivity, the self-diffusivity also depends on the concentration. It is important to emphasize that this dependence refers to the overall concentration, i.e. (with the view on Fig. 1b) to the sum of the concentrations of the differently labelled but microdynamically identical components since the diffusivity of a labelled component does not depend on its share of the total concentration. For following the spreading of labelled molecules within an unlabeled surrounding (with a constant overall concentration) it is therefore sufficient to operate with Fick’s 2nd law in the form of (4), i.e. for a diffusivity, independent of concentration, with the transport diffusivity replaced by the self- (or tracer) diffusivity:

$$ \frac{{\partial c^{*} }}{\partial t} = D\frac{{\partial^{2} c^{*} }}{{\partial x^{2} }} $$
(6)

One may determine the probability (density) that, over a given time interval t, a molecule will have diffused over a distance x, by solving (6) for an infinitely extended medium and with Dirac’s delta function for the initial concentration \(c^{*} \left( {x,t = 0} \right) = \delta \left( x \right)\). i. e. by assuming that all molecules are initially positioned in the origin (at \(x = 0)\). By inserting into (6) one easily recognizes the Gaussian

$$ P\left( {x,t} \right) = \left( {4\pi Dt} \right)^{ - 1/2} {\exp}\left( { - \frac{{x^{2} }}{4Dt}} \right) $$
(7)

as its solution. By considering the limit of \(t \to 0\) it is, moreover, easily seen to obey the required initial condition. With (7) the mean squared displacement of the molecules

$$ x^{2} \left( t \right) = \mathop \smallint \limits_{ - \infty }^{\infty } x^{2} P\left( {x,t} \right)dx = 2Dt $$
(8)

is found to increase in proportion with the observation time. Equation (8) is generally referred to as the Einstein equation. It is an alternative to (6) for defining self- or tracer diffusivities and serves, correspondingly, also as a basis for experimental measurement.

This is relevant, in particular, to the pulsed field gradient (PFG) technique of NMR (also known as pulsed gradient spin-echo (PGSE) NMR or NMR diffusometry) (Stejskal and Tanner 1965; Price 2009; Kärger et al. 2012; Valiullin 2016), which allows recording of the (sample average of the) probability distribution \(P\left( {x,t} \right)\) of molecular displacements (the “mean propagator” (Kärger and Heink 1983; Cotts 1991) over space and time scales of typically micrometers and milliseconds. Displacements over notably shorter space and time scales, namely from Ångstroms to nanometers and from pico- to nanoseconds, respectively, can be recorded by quasi-elastic neutron scattering (QENS) (Jobic and Theodorou 2007; Jobic 2008; O’Malley et al. 2016).

Both PFG NMR and QENS determine the mean displacements by considering the “ensemble average”, i.e. the mean value resulting as the average over all molecules. The advent of single-particle tracking (SPT) (Kirstein et al. 2007; Bräuchle et al. 2010, Weckhuysen 2010) has enabled determining the mean value of displacements over a time interval t by following the trajectory of a single molecule over a time interval \(T \gg t\). In combined PFG NMR and SPT diffusion studies within a nanoporous glass (Enke et al. 2003; Chmelik et al. 2011) using Atto532 (ATTO532-COOH, ATTOTEC, Siegen, Germany) dissolved in deuterated methanol as a probe molecule observable by both techniques (Feil et al. 2012) agreement between time and ensemble averages of molecular displacements under equilibrium conditions has been confirmed by experimental evidence, as predicted by the Ergodic Theorem of theoretical physics (Birkhoff 1931).

In most practical cases, nanoporous materials accommodate mixtures of different molecular species rather than only a single component. Following the reasoning leading to (1), fluxes of the individual components have then to be denoted as

$$ j_{i} = - \mathop \sum \limits_{j} D_{ij} \frac{{\partial c_{j} }}{\partial x} $$
(9)

The diffusion coefficient has thus become a diffusion matrix, with the element \(D_{ij}\) indicating the influence of a concentration gradient of component j on the flux of component i. \(D_{ij}\) is, in general, a function of all concentrations. For sufficiently small concentrations, all off-diagonal elements of the diffusion matrix are easily understood to disappear, yielding

$$ \mathop {\lim }\limits_{c \to 0} D_{ij} = \delta_{ij} D_{i} $$
(10)

with \(\delta_{ij} = 1\) for i = j and = 0 otherwise. With the reasoning following (5), the quantity \(D_{i}\) is immediately recognized as the (mutually coinciding) coefficient of self- and transport diffusion of component i. We note that, with increasing loading, the matrix elements \(D_{ij}\) are, in general, a function of all concentrations \(c_{i}\).

2.2 The driving force of diffusion

All relations so far introduced could be directly, i.e. without any ambiguity, derived from the perspective on random molecular [the “Brownian” (Vogl 2019)] motion as illustrated by Fig. 1c. Further advancement in understanding and, notably, the establishment of correlations between the different diffusivities leads to the question of what is the underlying driving force for diffusion. Starting with the pioneering work by Maxwell (Maxwell 1860) and Stefan (Stefan 1872) it was, in particular, Krishna and co-workers who—by adopting the Stefan–Maxwell model to diffusion in nanoporous materials (Wesslingh and Krishna 2000; Krishna 2014, 2019) [see also chapter 3 in (Kärger et al. 2012)]—explored and exploited in greater detail the role of the gradient of the chemical potential as the driving force of diffusion.

Recognizing the gradient of the chemical potential (\(- (\partial \mu /\partial x)\)) as the driving force for diffusion, the equilibrium condition with the resistance experienced by the diffusing molecules may be expressed as

$$ fu = - \frac{d\mu }{{dx}} $$
(11)

where u and f stand for the molecular mean velocity and a friction coefficient reflecting the resistance experienced by the molecules on their diffusion path. The diffusive flux, resulting as the product of concentration and mean velocity, is given by

$$ j = uc = - \frac{{R_{g} T}}{f}\frac{{d\left( {\ln p} \right)}}{{d\left( {\ln c} \right)}}\frac{dc}{{dx}} $$
(12)

With the second equality, we used the relation

$$ \mu \left( c \right) = \mu_{0} + R_{g} T\ln \left[ {\frac{p\left( c \right)}{{p\left( {c_{0} } \right)}}} \right] $$
(13)

correlating the chemical potential with the (inverse of the) adsorption isotherm c(p). \(R_{g} \) is the gas constant and \(\mu_{0}\) stands for the chemical potential for the reference concentration \(c_{0}\). Combining (12) with Fick’s 1st law (1), the transport diffusivity is seen to be given by the relation

$$ D_{T} = \frac{{R_{g} T}}{f}\frac{{d\left( {\ln p} \right)}}{{d\left( {\ln c} \right)}} = D_{0} \frac{{d\left( {\ln p} \right)}}{{d\left( {\ln c} \right)}} $$
(14)

It is thus recognized as the product of two factors, which represent different influences. The first factor (\(D_{0} \equiv (R_{g} T/f)\)), known as the “corrected” or Maxwell–Stefan diffusivity, is a measure of the molecular mobility. \(d\left( {\ln p} \right)/d\left( {\ln c} \right) \) is referred to as the thermodynamic (correction) factor and is seen to affect the concentration dependence of the transport diffusivity (in addition to any such effect arising from the molecular mobility).

With the reasoning leading to (11) we may correlate self- and transport diffusion by considering the resistance opposing the flux of one component under counter-diffusion of two differently labelled components as shown in Fig. 1b. The resistance experienced by one component is, obviously, brought about by the pore walls and by the counter flux of the other component. Having in mind that the reciprocal value of the diffusivity is a measure of the resistance encountered by the diffusing molecules we may note

(15)

The first term on the right hand side refers to the friction with the pore walls, which guest molecules experience during also transport diffusion. However, since the rate of mass transfer during transport diffusion is additionally affected by the “thermodynamic factor”, it is only the “corrected” diffusivity, which has to appear. Ɖii is referred to as the self-exchange diffusivity, with its reciprocal value being a measure of the mutual resistance of the counter-diffusing molecules (Paschek and Krishna 2001; Krishna 2012).

With (15) we easily recognize the situation with vanishing loading, where self- and transport diffusion coincide. We note that, with the adsorption isotherms becoming linear as to be expected for sufficiently small loadings, the thermodynamic factor becomes 1 so that, with (14), transport and corrected diffusivity coincide. Since the second term is a measure of the mutual resistance of counter-diffusing molecules, it vanishes with decreasing loading. This situation is sometimes explicitly taken account of with a slightly modified definition of Ɖii so that, in the second term on the right hand side of (15), the relative pore filling appears as an additional factor.

Ɖii may assume, under certain conditions, two limiting values, independent of the given concentration. One limiting case is encountered with, e.g., zeolites and MOFs when the critical diameter of the guest molecules approaches the size of the “windows” between adjacent cavities. In such a situation the rate of molecular propagation is determined by the probability of the passage through these windows, so that the intermolecular “friction” becomes negligibly small, corresponding with an infinitely large self-exchange diffusivity, i.e. with 1/Ɖii = 0. With (15), the self-diffusivity is seen to coincide, in such cases, with the corrected diffusivity. Diffusion of light hydrocarbons in MOF ZIF-8 (Chmelik 2015) has been observed to follow this pattern. Host–guest systems of this type offered, in addition, the possibility to predict the concentration dependence of the diffusivities by application of conventional transition theory (Ruthven and Derrah 1972b) on, exclusively, the basis of the adsorption isotherm (Chmelik and Kärger 2016).

The opposite situation is encountered under the conditions of single-file diffusion (Kukla et al. 1996; Rödenbeck et al. 1999; Dutta et al. 2016) where molecules contained in channel pores are unable to pass each other. In such a situation, Ɖii drops to zero so that, with (15), also the self-diffusivity vanishes, irrespective of the fact that the transport and corrected diffusivity may assume finite values. Vanishing of the self-diffusivity in an (infinitely extended) single-file system correlates with the fact that the mean square displacement of the molecules within this file scales with the square root of time rather than with the time itself as required—via (8)—for normal diffusion [see chapter 5 in (Kärger et al. 2012)]. Normal diffusion postulates (for sufficiently large time intervals) independence of subsequent displacements. This requirement is indeed easily seen to be violated in single-file systems where successive displacements are more likely to occur in opposite directions than in the same direction.

3 Diffusion in more complex pore spaces

3.1 Pore space anisotropy

We have so far assumed system isotropy. It was therefore sufficient to confine our discussion to diffusion in one direction. However, numerous, notably crystalline, nanoporous materials are known to be of anisotropic structure. In such cases, (1) has to be replaced by the more general relation

$$ \vec{j} = - \overrightarrow {{\overrightarrow {D} }}_{T} {\text{grad}}c $$
(16)

which correlates the flux vector with the concentration gradient. The diffusion coefficient appearing in (1) is replaced by a diffusion tensor. Differing from the situation under isotropic conditions, now the flux direction does not necessarily coincide with the direction of the concentration gradient. It is always possible, however, to choose a coordinate system in which the diffusion tensor takes on diagonal shape. With reference to the coordinates of such a system (the “principal directions” of the diffusion tensor, as pre-determined by the pore space geometry), (16) assumes the shape of (1) with

$$ j_{i} = - D_{Ti} \frac{\partial c}{{\partial x_{i} }} $$
(17)

where the \(D_{Ti}\) are the principal diffusivities, i.e. the elements of the diagonalized diffusion tensor. Fick’s 2nd law, noted in three dimensions, becomes

$$ \frac{\partial c}{{\partial t}} = - \mathop \sum \limits_{i = 1}^{3} D_{Ti} \frac{{\partial^{2} c}}{{\partial x_{i}^{2} }} $$
(18)

3.2 Diffusion and reaction

For their application as porous catalysts, the pore space of nanoporous materials is designed to give rise to specific catalytic reactions. For reactions with n molecules involved the conversion rate of component i may, quite generally, be noted as

$$ \left( {\frac{{\partial c_{i} }}{\partial t}} \right)_{{{\text{conv}}.}} = f_{i} \left( {c_{1} \ldots c_{i} \ldots c_{n} } \right) $$
(19)

where \(f_{i} \left( {c_{1} \ldots c_{i} \ldots c_{n} } \right)\) indicates the increase in the concentration of component i per time, with \(c_{1} \ldots c_{i} \ldots c_{n}\) denoting the set of given concentrations. For a first-order reaction, e.g., (19) simplifies to \(f_{i} \left( {c_{1} \ldots c_{i} \ldots c_{n} } \right) = - k_{i} c_{i} + \mathop \sum \limits_{j \ne i} k_{ij} c_{j}\) with the parameters \(k_{ij}\) and \(k_{i} = \mathop \sum \limits_{j \ne i} k_{ji}\) denoting the respective conversion rates from component j to i and from i to any of the components j (\(\ne i\)). Again, as mentioned already in the context of (4), the unit volumes serving as a basis for the definition of concentrations ci are implied to be large enough to allow such a notation (Titze et al.2015a, b).

Application of the continuity equation (2) to Eq. (9) and taking account of (19) for considering the change in local concentration due to catalytic conversion yields the diffusion reaction equation

$$ \frac{{\partial c_{i} }}{\partial t} = \mathop \sum \limits_{j} D_{ij} \frac{{\partial^{2} c_{j} }}{{\partial x^{2} }} + f_{i} \left( {c_{1} \ldots c_{i} \ldots c_{n} } \right) $$
(20)

3.3 Internal barriers

With the advent of the microscopic techniques for diffusion measurement, the bulk phase of microporous materials is known to be often traversed by transport resistances (Vasenkov et al. 2001; Vasenkov and Kärger 2002; Karwacki et al. 2007, 2009; Stavitski et al. 2008; Feldhoff et al. 2009). The effect of such resistances may be quantified by considering the situation depicted in Fig. 1d. Here, the flux j through the barrier is equated with the difference in the concentrations on the right and left sides (\(c_{r} , c_{l}\)) of the barrier yielding

$$ j = - \alpha \left( {c_{r} - c_{l} } \right) $$
(21)

with the factor of proportionality \(\alpha\) referred to as the barrier permeance (or permeability). In Sect. 4.3 the influence of transport resistances on the outer surface of the porous particles (“surface barriers”) shall be considered in a related manner.

For a first-order estimate of the influence of internal barriers on the overall mass transfer we consider, as a simplified, special case, parallel resistances of (equal) mutual separation l and identical permeance \(\alpha\). Considering the flux perpendicular to these barriers over distances large in comparison with the barrier separation l, combination of (1) and (21) leads to an overall diffusivity

$$ \frac{1}{D} = \frac{1}{{D_{{{\text{micro}}}} }} + \frac{1}{\alpha l} $$
(22)

where \(D_{{{\text{micro}}}}\) stands for the diffusivity in the genuine (micro)pore space. (22) holds as an estimate for both transport and self-diffusion. Similarly as with (15) it is seen to result by adding the relevant resistances, which appear as the reciprocal values of the associated diffusivities.

3.4 Pore hierarchies

Technical application of nanoporous materials for both mass separation and catalytic conversion is largely based on the intimate contact of the guest molecules with the internal surface of these materials. Best conditions for this contact are given with pore sizes matching the critical dimensions of the molecules. This intimate contact, on the other hand, notably reduces the propagation rate and leads, correspondingly, to a reduced output of the value-added products. This conflict, which is inherent to the application of microporous materials in general, may be circumvented by the use of hierarchically organized pore spaces. In such materials, a microporous bulk phase is permeated by larger “transport” (i.e. meso- or macro-) pores, which ensure sufficiently fast exchange between the microporous bulk phase and the surroundings (Groen et al. 2007; García-Martínez and Li 2015; Mitchell et al. 2015; Hartmann and Schwieger 2016; Schneider et al. 2016).

The top of Fig. 2 shows the scheme for such a material. We note that instead of a single diffusivity overall mass transfer is now described by at least four parameters, namely the diffusivities in the two mutually penetrating pore spaces, the relative populations of the two pore spaces and the rate of mutual exchange. Equation (4) is now to be replaced by (Hwang et al. 2020)

$$ \frac{{\partial c_{{{\text{micro}}}} }}{\partial t} = D_{{{\text{micro}}}} \frac{{\partial^{2} c_{{{\text{micro}}}} }}{{\partial x^{2} }} - \frac{{c_{{{\text{micro}}}} }}{{\tau_{{{\text{micro}}}} }} + \frac{{c_{{{\text{transport}}}} }}{{\tau_{{{\text{transport}}}} }} $$
(23)
$$ \frac{{\partial c_{{{\text{transport}}}} }}{\partial t} = D_{{{\text{transport}}}} \frac{{\partial^{2} c_{{{\text{transport}}}} }}{{\partial x^{2} }} - \frac{{c_{{{\text{transport}}}} }}{{\tau_{{{\text{transport}}}} }} + \frac{{c_{{{\text{micro}}}} }}{{\tau_{{{\text{micro}}}} }} $$
(24)

where we are adopting the formalism introduced for the measurement of two-region diffusion via PFG NMR (Kärger 1985; Kärger et al. 1988).

Fig. 2
figure 2

Modelling mass transfer in a hierarchically ordered pore space (top) with density evolution of selected simulation runs of molecular uptake showing the limiting cases of fast exchange (upper presentations) and slow exchange (lower presentations). The density profiles, i.e. density ρ as a function of position x, during uptake are displayed on the left-hand side for two relative densities \((\rho /\rho^{{{\text{eq}}}})_{{{\text{cryst}}}} \), with the respective cross sections showing the distribution of the guest molecules on the right. Reprinted with permission from Schneider et al. (2015)

Full size image

These relations take into account that changes in local concentration arise from the combined effect of diffusion within, departure from and access to the respective pore system. The relative populations of the two pore spaces are correlated with the mean life times by the detailed-balance relation

$$ \frac{{p_{{{\text{micro}}}} }}{{p_{{{\text{transport}}}} }} = \frac{{\tau_{{{\text{micro}}}} }}{{\tau_{{{\text{transport}}}} }} $$
(25)

Among very different transport patterns resulting as the functions of microdynamics and pore structure classes (Schneider et al. 2016), one may easily identify two limiting cases. If the relevant time scales of observation notably exceed the mean life time in the two pore spaces, overall mass transfer can be adequately represented by a single diffusivity, resulting in the weighted mean of the diffusivities in both pore spaces

$$ D = p_{{{\text{micro}}}} D_{{{\text{micro}}}} + p_{{{\text{transport}}}} D_{{{\text{transport}}}} $$
(26)

Such a situation is depicted in the second row of Fig. 2. The density profiles shown on the left hand side have been evaluated by considering a cylinder-shaped cut of radius R = 15 lattice nodes through the center of the model system during uptake where each single \(\rho \left( x \right)\) corresponds to the average over the cross-sectional area of the cylinder for a given x. The right-hand side shows longitudinal cuts through the model systems at mean relative guest densities \(\rho_{{{\text{cryst}}}} /\rho_{{{\text{cryst}}}}^{{{\text{eq}}}} = 0.4\) (center) and 0.7 (right).

Since, in general, \(p_{{{\text{micro}}}} \gg p_{{{\text{transport}}}}\) and \(D_{{{\text{micro}}}} \ll D_{{{\text{transport}}}}\), there is no common rule for predicting the significance of the two terms appearing on the right of (26) for overall mass transfer. However, since the ratio \(p_{{{\text{transport}}}} /p_{{{\text{micro}}}}\) is known to follow an Arrhenius dependence \({\exp}\left( { - E/kT} \right)\) with E being of the order of the heat of adsorption, the contribution of the transport pores is easily seen to become increasingly dominant at higher temperatures.

In the limiting case of “slow exchange”, filling of the two pore systems occurs in two steps, starting with an essentially immediate filling of the transport pores. Such a situation is shown in the lower row of Fig. 2.

Whether one may indeed refer to one of these limiting cases depends on the time of molecular exchange between the nanoporous particle under study and its surroundings which, in turn, is a function of the particle size (Hwang et al. 2020). In the following section, we consider the effects brought about by the finite extension of the particles under study, quite in general.

4 Finite size effects

4.1 Diffusion-controlled molecular uptake and release

The fractional approach to equilibrium (\(m_{t} /m_{\infty }\)) for a spherical adsorbent particle exposed to a step change in the gas pressure of guest molecules in the surrounding atmosphere results as a solution of Fick’s 2nd law yielding (Crank 1975; Kärger et al. 2012)

$$ \frac{{m_{t} }}{{m_{\infty } }} = \frac{{\overline{c}\left( t \right) - c_{0} }}{{c_{\infty } - c_{0} }} = 1 - \frac{6}{{\pi^{2} }}\mathop \sum \limits_{n = 1}^{\infty } \frac{1}{{n^{2} }}{\exp}\left( { - \frac{{n^{2} \pi^{2} Dt}}{{R^{2} }}} \right) $$
(27)

with \(c_{0}\), \(c_{\infty }\) and \(\overline{c}\left( t \right)\) denoting, respectively, the initial and (new) equilibrium guest concentrations as well as the mean guest concentration at time t. The diffusivity D (which, likewise, may be the self- or transport diffusivity) has been assumed to be constant for simplicity [for more complex situations see, e.g., (Kärger et al. 2012)] and the shape of the host particle is approximated by a sphere of radius R. Limiting expressions of (27) are

$$ \frac{{m_{t} }}{{m_{\infty } }} \approx \frac{6}{\sqrt \pi }\sqrt {\frac{Dt}{{R^{2} }}} $$
(28)

for short times and

$$ \frac{{m_{t} }}{{m_{\infty } }} \approx 1 - \frac{6}{{\pi^{2} }}{\exp}\left( { - \frac{{\pi^{2} Dt}}{{R^{2} }}} \right) $$
(29)

for long times. Eqs. (27) to (29) are reasonable approximations for any particle geometry if R is understood as the radius of a sphere whose surface-to-volume ratio (A/V) coincides with that of the particle under study, that is, with

$$ R = \frac{3V}{A} $$
(30)

Quantification of the time constant of uptake and release may conveniently be based on the concept of the first statistical moment (Kocirik and Zikanova 1974; Dubinin et al. 1975; Barrer 1978; Kärger et al. 2012) defined by the relation

$$ m_{1} = \mathop \smallint \limits_{0}^{\infty } \left( {1 - \frac{m\left( t \right)}{{m_{\infty } }}} \right)dt $$
(31)

For diffusion-limited uptake and release one obtains (Kocirik and Zikanova 1974; Dubinin et al. 1975; Barrer 1978; Kärger et al. 2012)

$$ m_{{1{\text{Diff}}}} = \frac{{R^{2} }}{15D} $$
(32)

4.2 External transport resistances

During practical application one is, as a rule, concerned with nanoporous particles in loose beds or in compacted form rather than with infinitely extended bodies. Mass transfer has to overcome, therefore, a series of resistances acting in parallel with intraparticle (-crystalline) diffusion which, in the previous section, was assumed to be the only transport resistance. Additional resistances have, in particular, to be taken into account with reference to mass transfer between the particles and an external “reservoir” of guest molecules and the macro-pore diffusion through the bed/pellet of particles (crystallites). It is important to emphasize that each of these influences may become rate-determining in overall uptake and release as exemplified in numerous experimental studies (Garg and Ruthven 1972; Ruthven and Derrah 1972a; Kocirik et al. 1973).

Equally importantly, molecular uptake and release may also be affected by the rate of thermal exchange between the host material and the surroundings. It is true that any process of adsorption is accompanied by the release of the heat of adsorption and, correspondingly, by temperature increase just as, vice versa, desorption gives rise to a decrease in temperature. This change in temperature is accompanied by a change in the equilibrium concentration for the given guest pressure and, hence, by a variation in the boundary conditions of uptake and release (Chihara et al. 1976; Ruthven et al. 1980; Ruthven and Lee 1981; Haynes 1988). Final equilibration therefore includes heat exchange with the surrounding which, especially for high intraparticle diffusivities, may become rate-determining for the overall kinetics.

The development of strategies for keeping the influence of extra-particle effects on mass transfer as small as possible has served as a major driving force for the development and further accomplishment of experimental techniques for transient diffusion measurement, including the chromatographic methods (Haynes 1988), notably the zero-length column (ZLC) technique (Eic and Ruthven 1988; Brandani and Ruthven 1995; Ruthven and Brandani 2000), and the frequency response (FR) technique (Yasuda 1994; Rees and Song 2000; Wang and Levan 2005; Giesy et al. 2012).

Tests for evaluating the influence of extra-particle resistances on overall mass transfer include variation of the size and configuration of the bed of particles under study since the time constants of both “macropore” diffusion through and heat exchange with the particle bed/pellet increase with an increase in the critical dimension of the bed. Problems with these types of limitation are, correspondingly, largely excluded with measuring techniques such as microimaging via IR microscopy (IRM) and interference microscopy (IFM) which allow uptake and release measurements with single crystals/particles (Heinke et al. 2007; Kärger et al. 2014).

It has to be emphasized, however, that similar reasoning does not apply to variation of the pressure step: Invariance of an experimental uptake or release curve to the size of the concentration step provides no evidence that the system is effectively isothermal (Chihara et al. 1976). It should be kept in mind, however, that heat release during transient sorption is accessible to direct measurement and may thus, in turn, contribute to elucidating the properties of the samples under study, including their transport properties. Measurements of this type even offer the option of high throughput screening (Wollmann et al. 2012).

4.3 Surface barriers

In many cases, mass transfer through the external surface must be assumed to occur at a finite rate, following the relation

$$ j = - \alpha \left[ {c\left( {r = R} \right) - c_{0} } \right] $$
(33)

similarly to (21), now with \(\alpha\) denoting the surface permeance (or permeability) and j the flux entering the particle. \(c\left( {r = R} \right)\) and \(c_{0}\) stand for the current intraparticle/-crystalline concentration close to the surface and for the concentration in equilibrium with the given external atmosphere. The time constant (first statistical moment) of barrier-limited uptake/release results as (Barrer 1978; Kärger et al. 2012)

$$ m_{{1{\text{Bar}}}} = \frac{R}{3\alpha } $$
(34)

Deviating from the external resistances considered in Sect. 4.2, there is no way to circumvent the influence of surface resistances on overall uptake and release by appropriate arrangement of the nanoporous crystals/particles under study (such as, e.g., by spreading as an ultra-thin layer). In general, both resistances must rather be considered to act simultaneously.

Within the formalism of the statistical moments [see (31)], the first statistical moments of the individual resistances simply sum up to the overall effect, yielding

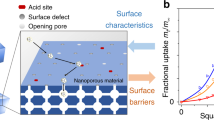
$$ m_{1} = m_{{1{\text{Diff}}}} + m_{{1{\text{Bar}}}} = \frac{{R^{2} }}{15D} + \frac{R}{3\alpha } $$
(35)

With (35), material miniaturization is immediately recognized as the main avenue towards transport enhancement by reducing the time constants of molecular uptake, release and exchange. Simultaneously, the relative significance of surface barriers for the overall process is seen to increase with decreasing particle sizes since the time constant (and, correspondingly, the associated resistance) scales only linearly rather than with the square of the particle size. Permeances of, e.g., zeolite membranes must therefore be expected to be increasingly controlled by surface effects rather than by their intracrystalline diffusivities with decreasing thickness (Caro and Kärger 2020; Kumar et al. 2020). Teixeira et al. (2013) nicely demonstrates this behavior by evidencing, in ZLC diffusion measurements with cyclohexane in silicalite, transition from internal diffusion control with large crystals to surface resistance control for small crystals.

However, it is important to emphasize that this marked difference in the dependence of the transport resistances by diffusion and by surface permeation on particle size does not always provide a secure means for elucidating their relevance by, e.g., a variation of the particle sizes. Such a procedure requires constancy of both the diffusivity D and the surface permeance \(\alpha\). The assumption of a constant internal diffusivity is normally (but not invariably) a valid approximation, but the surface permeance has been found to vary substantially even between different crystals from the same batch (Hibbe et al. 2011, 2012; Remi et al. 2015). Enhanced susceptibility of crystal structure close to the surface is not unexpected so that already small differences in environmental conditions may indeed be expected to give rise to a breakdown of the genuine pore architecture and, as a consequence, to additional transport resistances. In accordance with such reasoning, surface barriers of different faces of one and the same microporous crystal are usually found to coincide while those on different crystals may differ significantly from each other.

4.4 Single-file diffusion

In concluding Sect. 2.2, self-diffusion in single-file systems has been shown to drop to zero. This was attributed to the fact that subsequent molecular displacements are anti-correlated so that, as a result, the mean square displacement may be shown to increase with only the square root of time rather than with the time itself. This drop to zero does, in particular, refer to also the diffusivities \(D_{ij}\) appearing in (20) as a measure of the diffusivity of a particular molecular species under the influence of all of the species participating in chemical reactions.

The situation changes in single-file systems of finite size with which, as a matter of course, we are exclusively confronted in reality. Now, in addition to the displacements occurring in an infinitely extended single file (namely in consequence of fluctuations in guest density), displacements may also be caused by the access and departure of guest molecules at the file margins. Access and departure on either side of the file and also in subsequent instants of time is uncorrelated. Subsequent displacements of this type are, as a consequence, uncorrelated, giving rise to a genuine diffusion process as described by the Einstein relation (8). The resulting self-diffusivity is found to scale with file length (Hahn and Kärger 1998; Nelson and Auerbach 1999a, 1999b; Rödenbeck and Kärger 1999; Wollmann et al. 2012).

With (32), the time constants of uptake and release under single-file conditions are thus seen to scale with even the third power of the file length and, thus, of the crystal size for crystalline material. Such a situation would be given during tracer exchange but, more importantly, also for chemical reactions if the diffusion properties of the species under consideration do not appreciably differ so that, under stationary conditions, their diffusion properties are reasonably well approximated by the self-diffusivities (Carvill et al. 1993; Liu et al. 1996; Rödenbeck et al. 1999; Gauw et al. 2001) [see also chapter 5 of (Kärger et al. 2012)].

5 Summary and conclusions

There are two main stimuli that promote a steadily growing interest in the elucidation of guest diffusion in nanoporous host materials. Firstly, there are few, if any, other classes of materials which are so important for application in environmentally benign processes for the production of value-added products. In all these processes, notably including mass separation and heterogeneous catalysis, diffusion is among the rate- and, hence, profit-limiting processes since the gain in value-added products can never exceed the limit imposed by the mass transport rate.

The relevance of diffusion studies emerges, secondly, from the intrinsic interest of the information that such studies provide concerning the fundamental physics of molecular interactions. Diffusion in nanoporous materials is dominated by interactions between the fluid phase (the individual guest molecules) and the host material, leading to a wide range of remarkable effects. Depending on the particular host–guest system, enhancement of the guest concentration may give rise to both increasing and decreasing molecular mobilities, resulting in a spectrum of quite different patterns for the concentration dependence of the self-diffusivity as observed, some years ago, in PFG NMR diffusion studies (Kärger and Pfeifer 1987) and progressively rationalized, over the subsequent years, by molecular modelling (Keil et al. 2000; Beerdsen et al. 2004, 2005, 2006; Krishna and van Baten 2008).

The presence of guest molecules is, moreover, known to affect the structure of the nanoporous host lattice (Fyfe et al. 1984, 1988; Tezel and Ruthven 1990; Snurr et al. 1993, 1994; Song et al. 2005; Kärger et al. 2014). These generally modest effects may become important with representatives of the metal organic frameworks (MOFs), when the presence of guest molecules gives rise to a significant swelling (“breathing”) of the host lattice, accompanied by dramatic diffusivity enhancement (Devic and Serre 2009; Salles et al. 2010; Rives et al. 2013).

Remarkably, an increase in confinement by the host lattice does not automatically result in a reduction of the guest diffusivities. There are a number of model considerations where, under certain conditions, guest mobilities have been shown to increase rather than decrease with increasing confinement, brought about by either an enhancement of guest size or a reduction of pore space. Such effects have been assigned different names by different authors; for example “resonant diffusion” (Runnebaum and Maginn 1997; Tsekov and Evstatieva 2005), “levitation effect” (Ghorai et al. 2003; Kumar and Bhatia 2006; Borah et al. 2010), “commensurate adsorption” (Krishna and van Baten 2009; Wu et al. 2012; Wang et al. 2014) and “incommensurate diffusion” (Dubbeldam and Smit 2003; Krishna and van Baten 2017).

It is interesting to note that the search for such anomalies dates back to 1973 when Gorring measured the variation of uptake rate with carbon number for linear alkanes in beds of zeolite T (Gorring 1973). He observed a surprising trend with a pronounced minimum at n-C8. Assuming that the rate was controlled by intra-crystalline diffusion he postulated that this minimum arose because the n-octane molecule can just fit within a single cage in the channel structure and would encounter a high activation energy on passing through the distorted 8-ring (the window) to an adjacent cage. He coined the term “window effect” to describe this phenomenon and this paper has been widely cited in the literature as an example of anomalous behavior. However, subsequent experimental studies failed to replicate this trend (Cavalcante et al. 1995; Magalhães et al. 1996) and a detailed analysis of Gorring’s data (Ruthven 2006) showed clearly that, under his experimental conditions, the uptake rate was probably controlled by the combined effects of heat transfer and extra-crystalline diffusion and certainly not by intra-crystalline diffusion. Of course one cannot completely exclude the possibility of such an anomaly (Jobic et al. 2004, 2005; Hwang et al. 2018) but the Gorring saga does suggest that claims of bizarre behavior should be viewed skeptically.

It is worth noting that nanoporous materials were successfully developed and applied in industrial processes long before it was possible to understand the underlying behavior in detail. However, it is reasonable to assume that an increased understanding of the fundamentals will lead to new discoveries as well as allowing optimization of existing materials and processes.

In this paper it was our aim to provide an introduction to the challenges involved in measuring diffusion in nanoporous solids. The experimental techniques are quite varied and the conditions under which they can yield accurate data are different. Recognition of the limitations and experimental checks to ensure that the operating conditions fall within the required boundaries are obviously critical but have not always been carried out, leading to the publication of many erroneous results. The advantages and limitations of the various techniques are discussed in detail in subsequent papers and it is our hope that this will help to eliminate such errors in the future.