Skip to main content

Advertisement

SpringerLink
Log in

On the Structure Sensitivity of Formic Acid Decomposition on Cu Catalysts

  • OriginalPaper
  • Published:
Topics in Catalysis Aims and scope Submit manuscript

Abstract

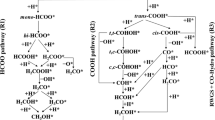
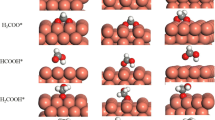
Catalytic decomposition of formic acid (HCOOH) has attracted substantial attention since HCOOH is a major by-product in biomass reforming, a promising hydrogen carrier, and also a potential low temperature fuel cell feed. Despite the abundance of experimental studies for vapor-phase HCOOH decomposition on Cu catalysts, the reaction mechanism and its structure sensitivity is still under debate. In this work, self-consistent, periodic density functional theory calculations were performed on three model surfaces of copper—Cu(111), Cu(100) and Cu(211), and both the HCOO (formate)-mediated and COOH (carboxyl)-mediated pathways were investigated for HCOOH decomposition. The energetics of both pathways suggest that the HCOO-mediated route is more favorable than the COOH-mediated route on all three surfaces, and that HCOOH decomposition proceeds through two consecutive dehydrogenation steps via the HCOO intermediate followed by the recombinative desorption of H2. On all three surfaces, HCOO dehydrogenation is the likely rate determining step since it has the highest transition state energy and also the highest activation energy among the three catalytic steps in the HCOO pathway. The reaction is structure sensitive on Cu catalysts since the examined three Cu facets have dramatically different binding strengths for the key intermediate HCOO and varied barriers for the likely rate determining step—HCOO dehydrogenation. Cu(100) and Cu(211) bind HCOO much more strongly than Cu(111), and they are also characterized by potential energy surfaces that are lower in energy than that for the Cu(111) facet. Coadsorbed HCOO and H represents the most stable state along the reaction coordinate, indicating that, under reaction conditions, there might be a substantial surface coverage of the HCOO intermediate, especially at under-coordinated step, corner or defect sites. Therefore, under reaction conditions, HCOOH decomposition is predicted to occur most readily on the terrace sites of Cu nanoparticles. As a result, we hereby present an example of a fundamentally structure-sensitive reaction, which may present itself as structure-insensitive in typical varied particle-size experiments.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Scheme 1
Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

References

  1. Alonso DM, Bond JQ, Dumesic JA (2010) Catalytic conversion of biomass to biofuels. Green Chem 12(9):1493–1513

    Article  CAS  Google Scholar 

  2. Bozell JJ, Petersen GR (2010) Technology development for the production of biobased products from biorefinery carbohydrates-the US Department of Energy’s “Top 10” revisited. Green Chem 12(4):539–554

    Article  CAS  Google Scholar 

  3. Xingwen Y, Pickup PG (2011) Codeposited PtSb/C catalysts for direct formic acid fuel cells. J Power Sources 196(19):7951–7956

    Article  Google Scholar 

  4. Liu C, Chen M, Du C, Zhang J, Yin G, Shi P, Sun Y (2012) Durability of ordered mesoporous carbon supported Pt particles as catalysts for direct formic acid fuel cells. Int J Electrochem Sci 7(11):10592–10606

    CAS  Google Scholar 

  5. Yinghui P, Ruiming Z, Blair SL (2009) Anode poisoning study in direct formic acid fuel cells. Electrochem Solid State Lett 12(3):B23–B26

    Article  Google Scholar 

  6. Xingwen Y, Pickup PG (2008) Recent advances in direct formic acid fuel cells (DFAFC). J Power Sources 182(1):124–132

    Article  Google Scholar 

  7. Boddien A, Loges B, Junge H, Gaertner F, Noyes JR, Beller M (2009) Continuous hydrogen generation from formic acid: highly active and stable ruthenium catalysts. Adv Synth Catal 351(14–15):2517–2520

    Article  CAS  Google Scholar 

  8. Fellay C, Yan N, Dyson PJ, Laurenczy G (2009) Selective formic acid decomposition for high-pressure hydrogen generation: a mechanistic study. Chem Eur J 15(15):3752–3760

    Article  CAS  Google Scholar 

  9. Gan W, Dyson PJ, Laurenczy G (2009) Hydrogen storage and delivery: immobilization of a highly active homogeneous catalyst for the decomposition of formic acid to hydrogen and carbon dioxide. React Kinet Catal Lett 98(2):205–213

    Article  CAS  Google Scholar 

  10. Columbia MR, Thiel PA (1994) The interaction of formic-acid with transition metal surfaces, studied in ultrahigh vacuum. J Electroanal Chem 369(1–2):1–14

    Article  CAS  Google Scholar 

  11. Madix RJ (1980) Surface reaction modifiers—general overview. Abstracts of Papers of the American Chemical Society 180 (Aug): 26

  12. Larson LA, Dickinson JT (1979) Decomposition of formic acid on Ru(1010). Surf Sci 84(1):17–30

    Article  CAS  Google Scholar 

  13. Solymosi F, Kiss J, Kovacs I (1987) Adsorption of HCOOH on Rh(111) and its reaction with preadsorbed oxygen. Surf Sci 192(1):47–65

    Article  CAS  Google Scholar 

  14. Senanayake SD, Mullins DR (2008) Redox pathways for HCOOH decomposition over CeO2 surfaces. J Phys Chem C 112(26):9744–9752

    Article  CAS  Google Scholar 

  15. Kubota J, Bandara A, Wada A, Domen K, Hirose C (1996) IRAS study of formic acid decomposition on NiO(111)/Ni(111) surface: comparison of vacuum and catalytic conditions. Surf Sci 368:361–365

    Article  CAS  Google Scholar 

  16. Dilara PA, Vohs JM (1993) TPD and HREELS investigation of the reaction of formic acid on ZrO2(100). J Phys Chem 97(49):12919–12923

    Article  CAS  Google Scholar 

  17. Iglesia E, Boudart M (1983) Decomposition of formic acid on copper, nickel, and copper–nickel alloys. 2. Catalytic and temperature-programmed decomposition of formic acid on Cu/SiO2, Cu/Al2O3, and Cu powder. J Catal 81(1):214–223

    Article  CAS  Google Scholar 

  18. Bowker M, Madix RJ (1981) XPS, UPS and thermal desorption studies of the reactions of formaldehyde and formic acid with the Cu(110) surface. Surf Sci 102(2–3):542–565

    Article  CAS  Google Scholar 

  19. Marcinkowski MD, Murphy CJ, Liriano ML, Wasio NA, Lucci FR, Sykes ECH (2015) Microscopic view of the active sites for selective dehydrogenation of formic acid on Cu(111). ACS Catal 5(12):7371–7378

    Article  CAS  Google Scholar 

  20. Youngs TGA, Haq S, Bowker M (2008) Formic acid adsorption and oxidation on Cu(110). Surf Sci 602(10):1775–1782

    Article  CAS  Google Scholar 

  21. Bowker M, Haq S, Holroyd R, Parlett PM, Poulston S, Richardson N (1996) Spectroscopic and kinetic studies of formic acid adsorption on Cu(110). J Chem Soc Faraday Trans 92(23):4683–4686

    Article  CAS  Google Scholar 

  22. Gokhale AA, Dumesic JA, Mavrikakis M (2008) On the mechanism of low-temperature water gas shift reaction on copper. J Am Chem Soc 130(4):1402–1414

    Article  CAS  Google Scholar 

  23. Grabow LC, Gokhale AA, Evans ST, Dumesic JA, Mavrikakis M (2008) Mechanism of the water gas shift reaction on Pt: first principles, experiments, and microkinetic modeling. J Phys Chem C 112(12):4608–4617

    Article  CAS  Google Scholar 

  24. Yang Y, Evans J, Rodriguez JA, White MG, Liu P (2010) Fundamental studies of methanol synthesis from CO2 hydrogenation on Cu(111), Cu clusters, and Cu/ZnO(000(1)over-bar). Phys Chem Chem Phys 12(33):9909–9917

    Article  CAS  Google Scholar 

  25. Quinn DF, Taylor D (1965) Decomposition of formic acid and methanol on copper–nickel alloys. J Chem Soc 5248–5251

  26. Rundell DN, Saltsburg HM, Smith WD (1980) the role of multiple gas-solid collisions in the catalytic decomposition of formic acid. Chem Eng Sci 35(5):1113–1119

    Article  CAS  Google Scholar 

  27. Inglis HS, Taylor D (1969) Decomposition of formic acid on titanium, vanadium, chromium, manganese, iron, cobalt, nickel and copper. J Chem Soc Inorg Phys Theor 19:2985–2987

    Article  Google Scholar 

  28. Nakano H, Nakamura I, Fujitani T, Nakamura J (2001) Structure-dependent kinetics for synthesis and decomposition of formate species over Cu(111) and Cu(110) model catalysts. J Phys Chem B 105(7):1355–1365

    Article  CAS  Google Scholar 

  29. Hu ZM, Boyd RJ (2000) Structure sensitivity and cluster size convergence for formate adsorption on copper surfaces: a DFT cluster model study. J Chem Phys 112(21):9562–9568

    Article  CAS  Google Scholar 

  30. Bowker M, Rowbotham E, Leibsle FM, Haq S (1996) The adsorption and decomposition of formic acid on Cu{110}. Surf Sci 349(2):97–110

    Article  CAS  Google Scholar 

  31. Grabow LC, Mavrikakis M (2011) Mechanism of methanol synthesis on Cu through CO2 and CO hydrogenation. ACS Catal 1(4):365–384

    Article  CAS  Google Scholar 

  32. Perdew JP, Chevary JA, Vosko SH, Jackson KA, Pederson MR, Singh DJ, Fiolhais C (1992) Atoms, molecules, solids, and surfaces—application of the generalized gradient approximation for exchange and correlation. Phys Rev B 46(11):6671–6687

    Article  CAS  Google Scholar 

  33. Perdew JP, Wang Y (1992) Accurate and simple analytic representation of the electron-gas correlation-energy. Phys Rev B 45(23):13244–13249

    Article  Google Scholar 

  34. Greeley J, Norskov JK, Mavrikakis M (2002) Electronic structure and catalysis on metal surfaces. Annu Rev Phys Chem 53:319–348

    Article  CAS  Google Scholar 

  35. Hammer B, Hansen LB, Norskov JK (1999) Improved adsorption energetics within density-functional theory using revised Perdew–Burke–Ernzerhof functionals. Phys Rev B 59(11):7413–7421

    Article  Google Scholar 

  36. Greeley J, Mavrikakis M (2002) Methanol decomposition on Cu(111): a DFT study. J Catal 208(2):291–300

    Article  CAS  Google Scholar 

  37. Herron JA, Scaranto J, Ferrin P, Li S, Mavrikakis M (2014) Trends in formic acid decomposition on model transition metal surfaces: a density functional theory study. ACS Catal 4(12):4434–4445

    Article  CAS  Google Scholar 

  38. Chadi DJ, Cohen ML (1973) Special points in Brillouin zone. Physical Review B 8(12):5747–5753

    Article  Google Scholar 

  39. Monkhorst HJ, Pack JD (1976) Special points for Brillouin-zone integrations. Phys Rev B 13(12):5188–5192

    Article  Google Scholar 

  40. Vanderbilt D (1990) Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys Rev B 41(11):7892–7895

    Article  Google Scholar 

  41. Kresse G, Furthmuller J (1996) Efficiency of ab initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput Mater Sci 6(1):15–50

    Article  CAS  Google Scholar 

  42. Bengtsson L (1999) Dipole correction for surface supercell calculations. Phys Rev B 59(19):12301–12304

    Article  CAS  Google Scholar 

  43. Straumanis ME, Yu LS (1969) Lattice parameters, densities, expansion coefficients and perfection of structure of Cu and of Cu-In alpha phase. Acta Crystallogr Sect A (Cryst Phys Diffract Theor Gen Crystallogr) A25:676–682

    Article  Google Scholar 

  44. Greeley J, Mavrikakis M (2003) A first-principles study of surface and subsurface H on and in Ni(111): diffusional properties and coverage-dependent behavior. Surf Sci 540(2–3):215–229

    Article  CAS  Google Scholar 

  45. Henkelman G, Uberuaga BP, Jonsson H (2000) A climbing image nudged elastic band method for finding saddle points and minimum energy paths. J Chem Phys 113(22):9901–9904

    Article  CAS  Google Scholar 

  46. Singh S, Li S, Carrasquillo-Flores R, Alba-Rubio AC, Dumesic JA, Mavrikakis M (2014) Formic acid decomposition on Au catalysts: DFT, microkinetic modeling, and reaction kinetics experiments. AIChE J 60(4):1303–1319

    Article  CAS  Google Scholar 

Download references

Acknowledgments

This work was supported by the U.S. Department of Energy (DOE)–Basic Energy Sciences (BES), Office of Chemical Sciences, grant DE-FG02-05ER15731. We thank Lars C. Grabow for performing the calculations on Cu(111), as reported originally in Ref. [31] and utilized here. Calculations were performed at supercomputing centers located at the Environmental Molecular Sciences Laboratory, which is sponsored by the DOE Office of Biological and Environmental Research at the Pacific Northwest National Laboratory; Center for Nanoscale Materials at Argonne National Laboratory, supported by DOE contract DE-AC02-06CH11357; and National Energy Research Scientific Computing Center, supported by DOE contract DE-AC02-05CH11231. We thank Anthony Plauck, Luke Roling and Dr. Srinivas Rangarajan for carefully proofreading this manuscript.

Author information

Authors and Affiliations

  1. Department of Chemical and Biological Engineering, University of Wisconsin-Madison, Madison, WI, 53706, USA

    Sha Li, Jessica Scaranto & Manos Mavrikakis

Authors
  1. Sha Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jessica Scaranto
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Manos Mavrikakis
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Manos Mavrikakis.

Electronic supplementary material

Below is the link to the electronic supplementary material.

Supplementary material 1 (DOCX 39 kb)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Li, S., Scaranto, J. & Mavrikakis, M. On the Structure Sensitivity of Formic Acid Decomposition on Cu Catalysts. Top Catal 59, 1580–1588 (2016). https://doi.org/10.1007/s11244-016-0672-1

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11244-016-0672-1

Keywords

Search

Navigation