How Theoretical Simulations Can Address the Structure and Activity of Nanoparticles

Abstract

Theoretical simulations in the field of heterogeneous catalysis started about two decades ago when the main goal was to understand the activation of small molecules on infinite surfaces. The improvements in the accuracy and the large availability of computers with increasing power have raised the quality of the calculations, the reliability of the results and prompted the interest in their predictions. Such changes have also allowed the study of nanoparticles by the combined investigation of different facets or by taking into account the complete structures. As for the reactivity, theoretical simulations allow the comparison of different synthetic conditions within the same approximation. Consequently, large systematic studies with the same theoretical models can provide databases for properties, structures, prove and disprove hypothetical reaction paths, identify intermediates, and complete the understanding of reaction mechanisms. In some cases, simulations support and give explanations to experiments but new emerging aspects such as the prediction of new properties or the analysis of complex systems are possible. Several challenges are ahead the simulations of reactions on nanoparticles: (i) how to drive the synthesis to achieve the desired architectures and (ii) how to stabilize the active phase under reaction conditions.

Introduction

Nanoparticles have a wide range of application from plasmonics to heterogeneous catalyst. Reactions that can be catalysed by nanoparticles have been known and employed industrially since more than a hundred years [1]. As the reactions take place between a gas or liquid phase reactant and a solid surface it is usually described as heterogeneous process. Due to the interaction of molecules with the solid surface, reactants get activated and reduce the energetic requirement for the reaction. Therefore, the number of active sites available is crucial and this number of sites depends on the surface to volume ratio. As a consequence, the use of nanoparticles is crucial to enhance the catalytic activity. This fact was very early established as one of the fathers of Catalysis, Humphry Davy, reported that Pt was more active when finely divided [2]. As catalyst are made of expensive or rare metals there is a need to reduce the amount of material used and thus oxide supports or other carriers with high surface areas are routinely employed. In the case of active industrial catalysts, there are a few more components including binders, secondary metals and molecular modifiers which finely tune the electronic structure, and improve the activity, selectivity and stability under reaction conditions.

Nanoparticles have been employed with different catalytic purposes [3] but still it is a main challenge how to achieve a given dispersion, shape and size distribution that is optimum to catalytic performance. The last synthetic and characterization techniques have proven to enhance the degree of architecture control. For instance, different synthetic methods have been devised to achieve narrow distributions for sizes and shapes, but their effectiveness depends on the application. In heterogeneous catalysis maintain finely distributed nanoparticles might be difficult under typical harsh conditions. The main reason for the stability issue is based on the large interaction between the reactants (intermediates or products) and the nanoparticles or the oxides serving as supports. From a theoretical point of view nanoparticles supported on oxides can be studied through the direct comparison to physical methods. Those are well-suited to detailed analysis, as atomistic modelling and benchmarking can be directly performed [4–6]. Care shall be taken though because the stable or metastable structures prepared in such manner are extremely sensitive to changes in temperature and partial pressures. Many of the so-prepared structures are dynamic and thus the representativity of these systems is compromised.

There are different ways to create nanoparticles for the chemical wet preparations. In particular the use of soft-templates and surfactants have been found as flexible, very versatile platforms that can adjust the size distribution and shape control [7]. However, attempting to remove the surfactants by increasing the temperature may induce metal coalescence and reduction of the surface area, and therefore reduces the benefits of wet synthesis. Such complex multicomponent and multiphase systems are difficult to represent from a computational perspective, so we are going summarize the major points that need to be taken into account to model the structure and reactivity of such nanoparticles.

In Fig. 1 we schematically show different representations of nanoparticles that can be studied through theoretical means and that will be described in the following.

Fig. 1

Sketch of the different models for nanoparticles: a gas-phase, b solvated, c surfactant covered, d in solution, surfactant-covered, e supported, f supported, in solution, g supported, surfactant-covered, and h supported surfactant-covered nanoparticle in solution

Theoretical Simulations

Theoretical simulations are usually based on the solution of the time-independent version of the Schrödinger equation. The analytical solution for the wavefunction can only be obtained for monoelectronic atoms, therefore approximations need to be used with polyelectronic systems. In the traditional view of chemists this was achieved through a hierarchy of Quantum Chemistry methods. This list of methods starts with the Hartree–Fock (HF) approach, i.e. a mean field approximation, and then higher accuracy is achieved by including more terms in the expression of the wavefunction. Thus, in traditional molecular studies, expansions to the Møller–Plesset perturbation methods or more sophisticated formulations based on Configuration Interaction expansion were used to analyse particular properties, but they were excessively expensive in terms of computational resources. Besides, a localized basis set depicting the atomic and molecular orbitals that provided a relatively easy interpretation of the chemical bond has been employed for molecules and extended to small clusters. This approach is however not viable for systems containing more than 10 metal atoms as they strongly depend on the number of basis set functions which can rise from N⁴ (HF) to N⁶⁻⁷ in Configuration Interaction approaches.

The alternative comes from the use of Density Functional Theory, DFT, which employs the electronic density as a function that only depends on the Cartesian coordinates and spin. The ultimate quality of the density is that it is a fundamental observable that can be directly compared to results from X-ray or neutron diffraction. The drawback of this simplification is the addition of an unknown exchange–correlation term to the energy. DFT energies are usually taken as the reference for more sophisticated approaches, such as medium field theories, or schemes that describe larger time and length scales suitable to be compared to experiments in both Materials Science and Catalysis [8].

The accuracy and efficiency of DFT-based methods depend on several technical choices [9], including the particular exchange–correlation functional, the basis set for the expansion of the Kohn–Sham (KS) orbitals and the algorithms employed to solve the KS equations. The choice of exchange–correlation functionals and the completeness of the basis set account for the accuracy, whereas the numerical algorithms are responsible for the efficiency. The hierarchy of exchange–correlation functionals was described by John Perdew in “the Jacob’s ladder of DFT” with the computational demands and the accuracy as shown in Fig. 2 [10].

Fig. 2

Jacob’s ladder of Density Functional Theory with the different approximations linking the Hartree World of Independent Electrons and the Heaven of Chemical Accuracy [11]. E _XX stands for the exact exchange, n for the density, τ for the kinetic terms and Ψ for the orbitals. Notice that no comparison to computational Chemical methods is presented and only from rung 4 upwards exact exchange (i.e. Hartree–Fock form) is taken into account

The lowest part of the ladder is the local density approximation (LDA) [12], where the exchange–correlation energy (E _xc) is expressed as that of a homogeneous electron gas of the same density, n(r). The E _xc is parameterized from quantum Monte-Carlo simulations [13]. LDA solves many bulk [14] and surface systems but it usually leads to over-binding [15]. The second rung in the ladder is formed by a family of methods termed as generalised gradient approximation (GGA) [16, 17]. There E _xc depends not only on the electron density but on its local gradient, ∇n(r). The GGAs solves the over-binding of the LDA, with a tendency to over-correct it [18] but the attained accuracy is enough for many chemical reactions [19]. PW91 [20], PBE [21], revised PBE [18], PBEsol [22], MA05 [23], and WC [24] belong to this family of methods. PW91 and PBE have been the standard in reactivity during the last decade. However, GGAs have two serious drawbacks. First, they do not account for van der Waals (vdW) interactions resulting from dynamical correlations between fluctuating charge distributions [9]. The second weak point is related to the non-zero interaction of a single electron with its own density, known as self-interaction error (SIE). SIE is the cause of many of the failures of approximate functionals, such as excessively narrow band gaps [25, 26], wrong dissociation energies for molecules [27], and incorrect description of systems with localised f electrons [28]. Therefore a proper SIE correction is required for the nanostructures of oxides. Fixes to strong-correlated systems based on the Hubbard model have been applied to address issues such as the incorrect description of band gaps, and are known as DFT + U [29]. Normally the DFT employed is of the GGA level. The main concern is that the U, a parameter to describe interelectronic repulsion in d or f strongly correlated levels, depends on the particular observable to be calculated; this enters in contradiction with the universality claimed for the functional.

Meta-GGA includes higher-order terms of the gradient of the local kinetic energy density, ∇^² n(r), and constitutes the third rung on the DFT ladder [30]. Unfortunately such methods do not systematically improve the properties from those obtained with GGA. Examples of this lack of consistency have been reported, such as the adsorption of small molecules on transition- and noble-metal surfaces [9] and the hydrogenation of benzene to cyclohexene on Ni(111) [31].

The next step in the ladder corresponds to hybrid functional, that mix exact E _XX, i.e. HF and DFT exchange, and describe correlation at the standard DFT level. The most popular hybrid in chemistry has been for more than one decade the B3LYP functional [32, 33], providing high accuracy for almost all properties of molecules, but failing when applied to metals and semiconductor solids, because the correlation part of the functional is incorrect in the homogeneous electron gas limit [34, 35]. Other hybrid approaches typically employed for solids are PBE0 [36] and HSE03 [37], which show better estimates for lattice parameters and bulk moduli of solids, and for the band gaps in semiconductors and insulators [34, 35]. In general, these hybrid functionals properly describe both insulating antiferromagnetic rare-earth and transition metal oxides which are not correct with GGAs [38, 39]. Atomisation energies and magnetic properties of metals are more accurate through standard PBE. A difficulty in the use of hybrid functional is their great computational cost than standard DFT.

Dispersion interactions (vdW) are lacking in standard DFT calculations. Methods based on the random-phase approximation, combined with the adiabatic connection and fluctuation dissipation theorem [40] can account for these terms but they are extremely computationally demanding. As a consequence they can mostly be employed as benchmark for simplified models. To account for vdW effects, cheaper alternatives with modified functionals have been put forward. However there is a lack of robustness in some of the approaches that makes difficult to assess their long-term viability [41, 42]. The simplest way to introduce dispersive terms was given by semi-empirical force fields of Grimme [43] (DFT-D2). They are calculated through the London formula [44] leading to the ΣC₆/R⁶ term and thus the choice of the C₆ parameter becomes crucial. Still, it has been applied to water layers on metals (one of the most complex systems to model) and holds promise for the modelling of complex solid/liquid interfaces, layered compounds, and weakly interacting systems [45].

Clusters, Nanoclusters and Their Simulations

Two types of approximations can be employed to the study of clusters in the nanometric regime. On one side nanoparticles are finite-size structures. Therefore, they can be modelled as large molecules, where the total amount of atoms is truly represented (i.e. through the use force fields, or first-principles approaches). However, if we are interested in complex electronic structures, the use of large molecules may not possible. Clusters with large sizes imply the treatment of 1,000 or more atoms which cannot be handled with traditional molecular codes, like Gaussian [46]. Newer algorithms implemented are more suited to address such large structures. For instance, the real space implementation of DFT in GPAW [47] can take into account large metal nanoparticles and oxide clusters and large metal oxide polyanions like -polyoxometallates.

In the description of nanoparticles two different regions can be identified. At small diameters non-scalable regimes appear: this means that the properties of a system with N constituents cannot be directly extrapolated to those of N + 1. From a technological point of view this is a dangerous path as the degree of control in the synthesis and long-term stability cannot ensure that the “active” species can be maintained for sufficiently large time scales. Scalability appears at larger diameters, and thus there is a systematic way to understand the properties of an N + 1 system provided that the N is known. The normal behaviour or activity as a function of the diameter of the particles is shown in Fig. 3.

Fig. 3

Turn-over frequency (activity) as a function of the particle diameter. Scalable versus non-scalable (shadowed) regimes are shown. In the non-scalable regime, below 1.5 nm in diameter, the properties depend on the explicit number of atoms, but at higher diameters the properties are continuous. The dashed red line corresponds to the density of corners atoms in nanoparticles that scales as 1/r ³

Non-scalable Regime

Structure

The chemical properties of systems in the non-scalable regimes have been described for several examples. In the limit, the formation of benzene from ethylene on isolated Pd atoms on defects in MgO were described to show that one atom is enough for some interesting chemistry [48]. Larger cluster agglomerates, containing from a few to tenths of atoms, show some of the properties of molecules like (i) the fluxionality, the flexibility of the structure and (ii) a relatively large the number of low-lying configurations where different spin-states, separated by a finite energy, easily surmounted. In many cases, the study of such nanostructures is limited to the electronic and geometric ground state. This simplification can only be employed for applications where the temperatures considered are low and the systems are chemically insulated (such as memory storage) then the individual properties of ground state structures might be enough to represent these systems [49].

In chemical environments or where several relevant configurations might play a role, complex algorithms, usually based on basin hopping and minimization techniques, could serve as a first indication of the number of low-lying states within a small energy difference [50]. The role of these alternative structures implies that the proper description of the chemical phenomena taking place on these scales would require considering at least low-lying structures and weighting the properties by a distribution (i.e. Boltzmann for the equilibrium). Obviously this limits the availability of the atomistic theoretical simulations as they imply a large number of structures and wide sampling. The representativity of low-lying states and their corresponding properties, in particular those related to the chemistry, might be completely irrelevant.

For discrete clusters the energy levels are well separated. This has been exemplified in the comparison of the Density of States for the bulk of gold and two nanoparticles presented in Fig. 4. The HOMO–LUMO gaps are shown so that the convergence with the metal character represented by the bulk is clearly seen and this would account for the scalability at medium to large sizes. For small clusters, there is a group of structures that might behave as noble (or inert) as the parent compounds. These correspond to the appearance of magic numbers, which show the following properties: (i) a large energy difference of the ground state from the lowest to the next configuration, (ii) a close-shell structure with a large gap in the electronic structure and thus a HOMO–LUMO gap. In the case of monoelectronic metals it is very easy to identify which structures will behave as magic clusters. This can be extended to pseudo-monoelectronic metals such as Cu, Ag, and Au. The concept is more complex for metals in which the electronic configuration is less straightforward. Magic numbers can be understood in chemical terms as a kind of aromaticity that has been reported for clusters of carbon (the well-known fullerenes) [51], boron and other compounds.

Fig. 4

Projected Density of States for two clusters of gold Au₁₃, Au₅₅ compared to the Au_bulk. For the nanoparticles, the HOMO–LUMO gap opens indicated by the blue arrows

Magic clusters might also appear for other chemical structures as they are potential energy wells and their appearance depends on (i) the nature of the system (i.e. type of material: metals, oxides, salts); (ii) the redox state of the metals and (iii) the environment (i.e. oxidative, reductive, solvent, surfactants…). Environmental factors might modify not only the surface structure with partial oxides but also generate new stoichiometries for which no models are known, therefore altering the composition and structure of magic clusters. As a consequence, synthetic processes carried out under mild conditions are more prone to show complexity compared to other preparations for which usual “cleaning” procedures, i.e. reduction at high temperatures, simplify the stoichiometry and composition.

Activity

Examples of potential activity in the non-scalable regime have been presented for a number of reactions including the trimerization of ethylene [48], oxidation of CO by Au₈ [52] and the selective epoxidation of propyne [53]. For the first case it is clear that the well-anchored structure with a charge-promoted Pd atom sitting on a vacancy site could be enough for the reaction, as it is still active and sufficiently electronic rich to perform the transformation. Moreover, Pd would tend to sit on steps and oxygen vacancies on MgO, if those are present in significant amounts [48]. The concept above is a proof of site isolation presented by several groups in different context. If the isolation of the active centre (and even its promotion) is possible, then the catalyst would have the optimum activity, selectivity and stability. Obviously, the ensemble control would be easier for reactions taking place on isolated atoms than for other requiring more complex configurations. For the second case [52], the CO oxidation on Au₈ particles, it was clearly shown that the activity in the reaction has a lateral path, i.e. an O atom remains on the nanocatalyst. This can be detrimental to the overall stability as the O can fill the vacancy healing the anchoring site. So, after one or a few reaction cycles, the active centre is no longer present. The final example, even more interesting from a technological point of view, is the catalyst for epoxidation of ethylene, Ag, cannot be used for propylene due to the high basicity of the oxygen atoms carrying out the reaction [54]. Experiments and computational models have shown that for small clusters, i.e. containing less than ten atoms, the amount of oxygen on the surface might be reduced, leading to a sharp selectivity for the desired compound [53]. Again, the issue for the long-term stability of these silver-based epoxidation nanocatalysts is compromised if enough oxygen is around as agglomeration of the silver catalyst and thus its death is likely.

Scalable Regime

Structure

Scalable regimes corresponds to sizes larger than 1.5 nm diameter, where the properties of a system tend to converge and do not explicitly depend on the number of atoms. The main problem of representing such structures is that at least 10³ atoms need to be considered. These are not suited to traditional physic models that exploit plane waves and periodic boundary conditions as they do not benefit for further contractions of the reciprocal space once the direct lattice has a side of about 3 nm. To check for the convergence of cluster properties to the scalable regime, calculations with real space codes have been presented in the literature. For instance, they have shown how the extension and shape of the Au molecular orbitals converge with a diameter of nanoparticles of around 2.7 nm, or 561 atoms [55]. Also the algorithms at the core of the SIESTA package, which employs localized basis sets [56] with a cutoff for the interaction, allows the linear scalability for large enough systems.

Instead of this brute force approach that contains 10³ atoms in the calculations of nanoparticles, the traditional view was to separate and study the contribution from different facets of the crystal and then add them up. This approach has been widely employed to understand the activity of nanoparticles and can be summarized as follows. First, the calculations are performed on different facets of the crystal. Thus, the surface energy (i.e. the energy needed to cut a particular facet) for each of the j cuts, γ _j , is obtained. Finally, the Wulff construction [57] is applied. The Wulff theorem, developed in 1901, states that the lower the surface energy of a facet, the largest contribution it has in the equilibrium structure of a given material. The Gibbs function of the equilibrium nanoparticle, ΔG _i , thus minimizes the summation for all the surface energies, times the area O _j of this particular facet:

$$\Updelta G_{i} = \mathop \sum \limits_{j} \gamma_{j} O_{j} .$$

The Wulff construction allows a smart evaluation of the exposed facets of a material with just few cheap calculations, and has been proven exceedingly successful predicting nanoparticle structures. Examples of these structures can be found in Fig. 5 for a prototypical fcc metal and two rutile compounds relevant in industrial processes. Still the Wulff model is oversimplified because it does not consider the energy required to form steps and edges [58]. Obviously, this approximation is less valid when considering small nanoparticles as the number of low-coordinated sites on them is larger. Also, relatively large structures, i.e. >1.5 nm, need to be included for the model to be relevant. Other approximations can be added on top of the simplified Wulff model. One of them relates to the effect of the environment. Clearly when growing under different conditions, e.g. the oxygen pressure, the surface energies change and this might control the facets exposed. This can be transferred to the Wulff’s model and then the surface energy, under oxygen-rich or -lean conditions or with other compounds like CO [58], can be investigated instead of the raw value. The estimation of the surface free energy at a given temperature and pressure can be addressed through first-principles thermodynamics [59], thus adding extra degree of freedoms (and another source of error linked to the ideal gas models employed to account for temperature and pressure effects). This methodology includes the effect of the surroundings through the computation of the corresponding surface Gibbs free energies, by introducing the reaction temperature and the pressures or concentrations of the environment. These constructions are more approximated than the static calculations described before, but provide an insight on the real state of the catalyst that otherwise would be very difficult to determine under experimental conditions; when a sufficiently large pool of configurations is taken into account, a good description of the surface state is obtained. Recent examples on the nature of the self-poisoned Deacon catalyst have pointed out the full coverage of RuO₂ surfaces, which might in turn be important for the further development of the reaction. In the Deacon process, coverage effects make surface reoxidation the rate-determining step [60]. This implies that, when growing under different conditions, the nature of the exposed metals is changed. Therefore, instead of the surface energy for the clean surface, γ, that of the environment acting on it N _k , γ _j (N _k ), shall be used. The modified equations look then as follows:

Fig. 5

Wulff construction for typical nanoparticles of fcc metals and two oxides with rutile structure

$$\Updelta G_{i} = \mathop \sum \limits_{j} \gamma_{j} \left( {N_{k} } \right)O_{j} .$$

Finally, when considering real systems, the role of the interface between different parts (e.g. metal–oxide junctions or oxide–oxide interactions) should also be included within the Wulff construction. As one of the surfaces will be affected by the interaction with the support, symmetric structures will no longer exist, leading to differently wetting types of particles. The wetting equation derived by Young can be written in terms of the new surface energy at the interface between the cluster and the carrier, γ and the clean reference, γ ₀. Taking into account the interaction energy per surface, $\frac{\Updelta E}{O},$ the equation reads as follows [61]:

$$\frac{\gamma }{{\gamma_{0} }} = \frac{{(\gamma_{\text{int}} - \gamma_{0} )}}{{\gamma_{0} }} = 1 + \frac{\Updelta E}{{O\gamma_{0} }}.$$

In turn, the state of the carrier can be affected by the presence of reducing or oxidising environments that modify the quality of the surface (i.e. number of oxygen vacancies) such as for Cu/ZnO [62], or by the presence of water [63]. Furthermore, on some of the carrier surfaces, special active places for nucleation might exist due to the preparation methods [64].

Once the electronic structure is obtained, the different contributions to the activity and selectivity of a given reaction can be calculated in an isolated manner, employing the tools from first principles applied to slabs, and weighting the contributions corresponding to different facets [60]. In principle, the surface amount can be identified in the Wulff construction and then the reaction evaluated and added up. It might result that one of these high energy facets is more active or more selective and thus would be more interesting to show to a larger extent. While this result is important by itself, sometimes this design parameter cannot be employed as the Wulff construction is a thermodynamic sink and the nanoparticle structure will end up being of this kind.

Although the Wulff construction constitutes the simplest model to describe the structure of a nanoparticle, it has several drawbacks related to the lack of information of defects or low-coordinated sites, together with the fact that only nanoparticles that share the same crystal lattice than the bulk can be retrieved. More detailed thermodynamic investigations in the literature have accounted for unusual metal coordinations. Those models can provide a wide description of the morphologies and even phase diagrams, which can then be compared to tomographic experiments [65–68]. Still, they are being developed and do not consider environment effects, which in heterogeneous catalysis turn out to be more important.

In some cases, as a consequence of adopting different preparation methods controlled by kinetics, new crystal structures that would be metastable under other conditions might be the ground state. A beautiful example is Co nanocrystals, for which a different packing configuration, known as the ε crystal, has been shown. Formation of ε-Co is only possible by solution-phase chemistry, namely organometallic route, and generally using a combination of tight binding ligands or surfactants [69]. As this liquid route is not thermodynamically controlled, the surfactants might change the energetics by binding tightly around the growing crystal and the dissolved Co atoms. This is paradigmatic but in the small range confinement might allow magnetization, availability of different spin orderings, or other particular properties. On this issue, calculations are difficult as they need to assess varied structures in order to understand the nucleation and this task is cumbersome [70].

A good example of the complexity that can affect the theoretical study of nanoparticles, is given by Co and Fe containing clusters. Experiments have shown that such Fe- or Co-based nanoparticles form mixed oxides with rather undefined stoichiometries [71, 72]. Even if they keep an important magnetic moment useful during the separation process, the variable oxygen content adds an extra difficulty to the simulations. Actually, DFT-based calculations for Fe oxides have shown the large complexity in assessing properly even only the electronic structure of such strong-correlated systems. Special care shall be taken in correcting the SIE through DFT + U methods. The coupling between spin and orbital moments leads to intricate electronic structures that depend on the U value. Thus, the present theoretical models cannot yet be employed as black-boxes for this type of calculations [73, 74]. In summary, for some nanoparticles in the form of mixed oxides, to address the issue of the nature, stoichiometry, surface termination, dispersion and stability is still a challenge.

Activity

In many cases, when employing nanoparticles, a strong dependence of the activity on the number of atoms is found. The paradigmatic clear example for this corresponds to the activity of gold nanoparticles. While gold is known to be completely inert, when prepared as small particles usually between 2 and 3 nm in diameter, it presents an enhanced activity for oxidation and hydrogenation reactions [75, 76]. In the scalable regime, catalytic properties are closely linked to the large number of low-coordinated sites on these compounds compared to the total number of atoms. Obviously adsorption energies and vacancy formation energies (i.e. either molecule or site activation) do depend on the coordination number and accordingly, the larger the relative number of sites, the better the reactivity.

The case of sponges and membranes is particularly interesting because, under certain conditions, some metals can change their structure by incorporating a large amount of a second compound and obviously these properties might change when nanoparticles are considered. This is the case of Pd for which hydrides are easy to obtain [77]. The contribution of the hydride phase depends on the environment [78]. The hydrogenation capacity acts as a buffer if solvents are present, like in the hydrogenation of alkynes in the presence of alkenes through the Lindlar catalyst; in fact it reduces the amount of hydrogen that is in contact with the metal surface, thus allowing the use of selectivity modifiers as quinoline, that would not be stable otherwise [79]. This kind of cooperative chemistry which relies on multiple elements to achieve a single property is very common in liquid-phase chemistry, but the implications at high pressure conditions or even electrochemical conditions have been less explored. Interestingly enough, some experiments have indicated that there is a difference in the storage ability when reaching the nanosize that enhance the activity in the hydrogenation of large olefins [80].

The Role of Surfactants

Wet synthesis methods usually employ soft-templates to control the shape of nanoparticles. These procedures are highly flexible and can generate a large number of morphologies. Due to their nature, only few examples have been reported in the heterogeneous catalysis literature. In most cases this can be attributed to structural properties. An example was presented by Häkkinen and co-workers [81], showing the structure of a capped nanoparticle as a function of a sulphide-based surfactant. However, the model did not include solvent effects. The final geometry of the nanocluster is thus given by a delicate balance between the metal–metal, surfactant–metal and surfactant–surfactant interactions. In a way, the effect of the surfactant might be seen as the modification of the surface energies, as described in the Wulff model in the previous section [58].

Yet another example on the electronic structure modifications induced by surfactants was presented for the materials that can be employed in quantum dots. Calculations on CdSe nanoparticles show that it is possible to fine tune the HOMO–LUMO gap by adsorbing different types of surfactants without changing the structure (i.e. the local coordination number of the surface atoms). The dipolar moment of the head adsorbed on the surface can slightly modify the position of the states, already different from the bulk values due to the final nature of the structure, resulting in more suitable light adsorption [82].

In the case of wet synthesis, the reactions take place in a liquid phase, where a number of solutes are presented. The system contains at least the metal salt out of which the nanoparticles are generated, the reductive agent, and the surfactant. In many cases morphology modifiers are also added. Such kind of synthesis exhibits a large degree of control for particles with interesting properties in sensing. The enhanced plasmons are then based on the asymmetry that can be induced by controlling the growth. Calculations with charged fragments present some difficulties but in principle a Born cycle can be prepared with different contributions. An example is shown in the cleaning of gold ores which is the inverse of the process [83].

In understanding the activity when surfactants have not been removed, the issue of diffusion to the active site (for reactants) and out to the liquid phase (for products) might be fundamental and compromise the activity of the catalyst. Transport problems of this kind are usually overlooked but they need to be addressed properly if the chemical properties are to be studied [84].

Understanding Activity

Heterogeneous catalysis as performed by nanoparticles usually follows the well-known Langmuir–Hinshelwood reaction scheme. This mechanism states that reactants are bonded to the surface, either to competitive sites or to different positions. Adsorption weakens the internal bonds reducing their strength and thus favouring either dissociative or associative paths. Then the activated reactants can interchange some of their fragments and generate the products that can leave the surface. There are several implications to the mechanism described above. First, coordination to the surface will depend on the properties of the nanoparticles, which in principle are different for the extended metals. As nanoparticles exhibit a larger number of low-coordinated sites, they are more prone to adsorb reactants, therefore they are believed to be more active than the rest of the surface. However it also implies the ability to break unwanted bonds, form impurities on the surface, get preferentially decorated, generate cokes or carbides and ultimately ruin the activity by poisoning.

The ability of different heterogeneous catalyst for a given reaction has been proven to follow the Sabatier principle, which states that the maximum activity for a given reaction is obtained by a balance at which relevant species are not coordinated too weakly (as then none would be adsorbed) or too strongly (as the surface would be poisoned). Therefore for large interaction energies, the catalyst surface is permanently blocked by one of the species of the catalytic cycle (either reactants, products or intermediates), while in the opposite case, when the binding energy is too small, the activation does not occur as the catalyst is empty for long time, rendering it inactive. For instance, this can be transferred to the activity of gold. When prepared as a surface, the binding energies of many atoms or molecules (particularly O₂) is far too low, therefore no oxidations can occur on those surfaces. On the contrary, if nanoparticles are prepared, the binding energy of oxygen lays on the highest activity point of the volcano curve representing the Sabatier principle, and thus maximum activity is retrieved in oxidation processes even at low temperatures. Alternatively, if a molecule or a fragment is easily adsorbed to the surface, it will adsorb even stronger to the defects. This can be explained by the d-band model [85]. Therefore, small nanoparticles would be likely completely poisoned by these strongly interacting fragments rendering them inactive. As a general rule the binding energies of fragments to the isolated atoms (or even when present as complexes) are higher than for the metal nanoparticles followed by regular surfaces, resulting in a way to improve activity (for inactive metals) or poison them (for already active metal surfaces).

Figure 6 presents the link between the different systems summarized in Fig. 1, ranging from individual nanoparticles, supported or surfactant-covered ones. Theoretical simulations hold the key to answer the role of different phases, as simplified hierarchical models can be constructed adding complexity in steps. For instance, modifications in the structure of clusters with respect to bulk can be summarized mainly in two terms: electronic and geometric. The final state of the cluster either as a free nanoparticle, or supported or surfactant covered, might affect the number of low-coordinated sites (likely blocked in the surfactant preparations). Other electronic effects can be charge modifications likely induced by the presence of a support (although these are smoothed out for medium size nanoparticles) or by the presence of the surfactant. With respect to geometric effects, the fluxionality, exposed facets and ensembles, depend on the formation on nanoparticles, carriers and/or surfactants. Such electronic and geometric modifications affect the storage and transport properties to a large extent especially when interfaces are present.

Fig. 6

List of potential modifications induced by the individual nanoparticles, adsorbed and surfactant-covered ones

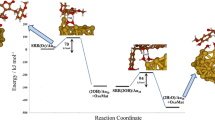
An example of the transferability of the theoretical procedures to both organometallic homogeneous and heterogeneous catalysts has been recently presented. Selective activation of alkynes in the presence of alkenes on gold systems constitutes a paradigm. Experiments for nanoparticles have shown the exquisite selectivity for the hydrogenation of alkyne groups in the presence of alkenes. Alkynophilicity has also been termed in the field of homogeneous catalysis, indicating the preference in the activation of these C≡C bonds in multifunctionalized molecules. Theoretical modelling has found that on the nanoparticles there is a preferential adsorption of triple C–C bonds. This is due to the presence of two π-states that are able to interact with the high energy states of low-coordinated sites on the metal nanoparticles. For the homogeneous catalysts, states of the correct symmetry are not available for both π states resulting in lower energy interactions. This explains why the adsorption energy is more favourable for the alkene and how the activity cannot be expressed directly in the same manner for the homogeneous and heterogeneous cases [86]. Our results are not conclusive at this stage, while a wide set of experiments performed in the groups of Toste and co-workers [87], found some type of correlation between tridimensional surfaces and surfactant-covered clusters.

As for oxides the reaction can even be more complex. Our investigations have found that the tridimensional nature of the catalysts and its curvature can have a role in the activity of oxygen species on polyoxometallates. Activation of species that require two sites depends on spatial 3D configuration. Clearly, the structure for the atoms in the nanoparticles can have curvatures different from those on planar surfaces, leading to different activities and selectivities [88].

Conclusions

Theoretical simulations based on the extensive application of DFT coupled to models like first-principles thermodynamics and the Wulff construction, can give a good description of several aspects of the nature, structure, shape and surface stoichiometry of these nanoparticles under different environments. Although these methods are very powerful in the sense that a hierarchical knowledge can be retrieved for the role of the different contributions, many challenges remain ahead of us. On one side non-equilibrium structures, or with many configurations and those with strong coupling between composition and electronic structure, are difficult to address in part due to the deficiencies associated to DFT and in part due to the large number of structures that need to be to be surveyed. On the other hand, the study of the reactivity of these particles can be strongly modified by adding diverse degrees of freedom, such as including supports, solvent, surfactants or a combination of all these issues. Even for those extremely complex cases, theoretical models represent a consistent way to identify leading contributions and fundamental property descriptors, which can be employed to address the synthesis of new, more industrially appealing compounds.